交流电有效值的计算
- 格式:doc
- 大小:98.00 KB
- 文档页数:3
交流电有效值计算方法1•如何计算几种典型交变电流的有效值?答:交流电的有效值是根据电流的热效应规定的•让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值解析:通常求交变电流的有效值的类型有如下几种:(1)正弦式交流电的有效值此类交流电满足公式e=E m Sin w t,i =I m sin w t对于其他类型的交流电要求其有效值,应紧紧把握有效值的概念流电有效值的求法(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻2 1电时的1/2,即卩U半2T/R=—(2U m 1而U全=—=,因而得U半=一U m,412(3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,电阻时所产生的热效应完全相同,即它的电压有效值为E=E2,电流有效值•下面介绍几种典型交R上,那么经一周期产生的热量应等于它为全波交流U全2TR1同理得I半=—I m.2所以左下图所示正弦单向脉动电流与正弦交流电通入七,m、222 于直流电产生热量的—,这里t是一个周期内脉动时间.由I矩2RT= ( — ) I m2RT或()T T RT=T(牛)「得1矩=:T Im,U矩=4.当T=1/2时,1:2im,U矩、2Um.(5)非对称性交流电有效值假设让一直流电压U和如图所示的交流电压分别加在冋一电阻上,交变电流在一个周期内产生的热量为Q1=2 2U1 T U2 T ..................... . .............. ..,直流电在相等时间内产生的热量R 2 R 22•—电压U o=1O V的直流电通过电阻R在时间t内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同,则该交流电的有效值为多少?解:根据t时间内直流电压U o在电阻R上产生的热量与同一时间内交流电压的有效值U在电阻R/2上产生的热量相同,则3•在图示电路中,已知交流电源电压u=200si n10n t V,电阻R=10 Q ,则电流表和电压表读数分别为A.14.1 A,200 VC.2 A,200 V分析:在交流电路中电流表和电压表测量的是交流电的有效值,所以电压表示数为200V=141 V,电流值i=U= :00R 衬2汉10 A=14.1 A.U2T,根据它们的热量相等有+U 2 ),同理有I = £(I 1I22).2 2知=胡「所以U哼=5 2 VB.14.1 A,141 VD.2 A,141 V答案:B2。

求交流电有效值的方法
交流电的有效值是根据电流的热效应规定的。
在求交流电的有效值时,通常采用以下几种方法:
直接计算法:对于已知波形的交流电,如正弦波、方波、三角波等,可以根据其波形特点直接计算出有效值。
例如,对于正弦波交流电,其有效值等于峰值除以根号2。
积分法:对于任意波形的交流电,可以通过积分的方式计算其有效值。
具体步骤是,将交流电在一个周期内的瞬时值进行平方,然后对时间进行积分,最后取平方根即可得到有效值。
这种方法需要知道交流电的瞬时值表达式或者采样数据。
仪表测量法:在实际应用中,通常使用电表来测量交流电的有效值。
电表内部采用了专门的电路和算法来计算有效值,可以直接显示出测量结果。
需要注意的是,不同类型的电表可能采用不同的计算方法,因此测量结果可能存在一定的误差。
需要注意的是,在求交流电的有效值时,需要明确所求的是电压有效值还是电流有效值,并且要注意单位的一致性。
此外,对于非正弦波形的交流电,其有效值并不能简单地用峰值除以根号2来计算,而需要根据其波形特点进行具体分析。
总之,求交流电的有效值需要根据具体情况选择合适的方法,并且要注意测量误差和单位的一致性。
在实际应用中,还需要考虑交流电的频率、波形等因素对有效值的影响。

余弦式交流电有效值公式交流电有效值公式是余弦式交流电有效值(简称 TP)公式的简称,是指用一个数表示两个数之间相等或相反关系的一种常用数学式。
其计算过程为:(a+ b):其中 a= b+ c表示一个被测量事物与一个被测量物体之间、被测量事物与电源线之间、电源线与电流源之间是等价关系。
当用 TP来表示时,余弦式交流电有效值公式为:下面我们来看看 TP公式到底有什么不同?一、TP的意义对于实际交流电,其电流与电压的相等或相反关系就是实际的有效量,如直流电流与交流电压的相等、交流电压与交流电流的相等等等。
所以,交流电有效值(TP)是反映直流电和交流电有效值的一个重要指标。
用直流电流的有效值(TP)表示交流电的有效量,可表示为:交流电有效值(TP)=交流电流有效值(tP)/两个交流电流有效值(tP)= TP÷2+ TP,其中 TP/2= tP/2,且 tP为整数。
当交流电有效值表示 TP时可选用电压有效值(tP)或电流有效值(tP)作为测量手段。
TP中 TP可表示为: TP/2=50-50; TP/2=1-1; TP/2=0.5-1; TP/2=0.5-1; TP/2=1-1, TP/2=0.5-1。
二、TP是电的参数通过上面的计算可以知道,余弦式有效值公式在计算电流时所采用的参数基本相同,而且在计算电压时也基本相同。
对于电压为(Vd, Vr, Ve)的交流电来说, TP实际上就是在电路中所产生的一种电压和电流。
也就是说 TP就是电(Vd和 Vr)的参数,它反映了一种客观存在的电流和电压的关系。
电压如果不是非常大,也不是非常小,则很难通过计算求出其 TP值。
而电流往往是在电路中一次通过导体产生的能量多于一次通过导体产生的能量的总和。
三、TP和电流源之间的关系如果要求额定电流的电压 A,可以采用额定电流 A=额定电压,这也是理论上可以理解的一种近似方法。
因此在实际工作中,要用电流 A与电流源 B的乘积来表示。

交流电有效值功率计算公式在电力系统中,功率是一个非常重要的参数,它代表着电能的转换和利用效率。
在交流电路中,我们常常需要计算交流电的有效值功率。
有效值功率是指在交流电路中,所产生的有用功率,它是交流电流和电压的乘积的平均值。
在本文中,我们将介绍交流电有效值功率的计算公式及其应用。
首先,让我们来看一下交流电的基本特性。
交流电是指电流方向和大小都随时间变化的电流。
在交流电路中,电压和电流都是随时间变化的,因此我们无法简单地用电压和电流的大小来计算功率。
在交流电路中,我们需要使用有效值来表示电压和电流的大小。
交流电的有效值是指在交流电中,与其等效的直流电所产生的相同功率的电压和电流的大小。
在交流电路中,电压和电流的大小是随时间变化的,因此我们无法直接用电压和电流的大小来计算功率。
我们需要使用有效值来表示电压和电流的大小。
计算交流电的有效值功率需要用到交流电的电压和电流的有效值。
交流电的电压和电流的有效值分别用U和I来表示。
交流电的有效值功率P可以用下面的公式来表示:P = U I cos(θ)。
其中,U是电压的有效值,I是电流的有效值,θ是电压和电流的相位差。
cos(θ)是电压和电流的相位差的余弦值,它代表着电压和电流的同相位部分所产生的功率。
从上面的公式可以看出,交流电的有效值功率与电压的有效值、电流的有效值以及电压和电流的相位差有关。
在实际应用中,我们通常会通过测量电压和电流的有效值以及相位差来计算交流电的有效值功率。
交流电的有效值功率计算公式可以帮助我们更好地理解交流电的功率特性。
在实际应用中,我们可以通过测量电压和电流的有效值以及相位差来计算交流电的有效值功率,从而更好地了解交流电的功率特性。
交流电的有效值功率计算公式在电力系统中有着重要的应用,它可以帮助我们更好地理解交流电的功率特性,从而更好地进行电能的转换和利用。
总之,交流电的有效值功率计算公式是一个非常重要的公式,在电力系统中有着重要的应用。
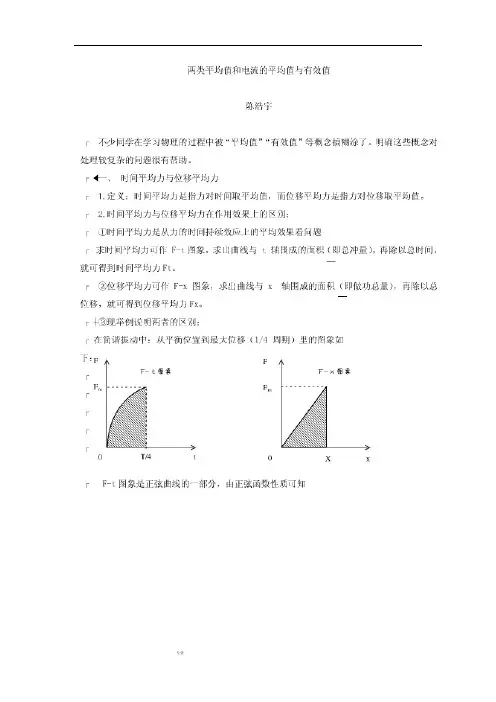
交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期的平均值为零,而技术上应用的交流电的平均值是指在一个周期交流电的绝对值的平均值.也等于交流电在正半个周期的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。

交流电有效值的计算交流电有效值的计算是指通过测量或计算得出交流电信号在一定时间内的平均能量大小。
在交流电中,电流和电压都是随时间变化的,因此不能直接使用最大值或峰值来表示电流或电压的大小。
有效值的概念旨在提供一个与直流电相同功率的参考值。
要计算交流电的有效值,可以使用以下三种方法:平均值法、功率法和积分法。
1. 平均值法:交流电的有效值可通过将电流或电压的平方信号取平均并开方来计算。
假设电流的波形为I(t),则交流电的有效值表示为Irms,可用以下公式计算:Irms = √(1/T ∫[0 to T] I(t)²dt)其中,T表示一个完整的周期。
例如,如果电流的波形是正弦波,那么该方法可以简化为使用最大峰值电流的70.71%:Irms = Imax/√22.功率法:根据交流电功率的定义,可以使用功率计来测量电流和电压之间的功率输出。
根据功率的平方等于电流和电压乘积的平均值,可以将交流电的有效值表示为:Irms = √(Pavg/Vrms)其中,Pavg表示平均功率输出,Vrms表示电压的有效值。
这种方法适用于通过功率计间接测量交流电的有效值。
3.积分法:通过将电流或电压信号与一个参考信号进行积分,并将结果除以积分时间来计算有效值。
该方法需要使用一些数学和信号处理技术,通常在数字信号处理领域使用。
这些方法可以适用于各种交流电信号的有效值计算。
但需要注意的是,对于非线性或非周期性的波形,这些方法可能不适用。
在这种情况下,可以借助计算机和数值计算技术进行数值模拟和数据处理。
除了计算交流电的有效值,也可以使用示波器等检测设备来显示电流和电压的波形,并通过与标准波形进行比较来估计有效值。
交流电有效值计算在电力系统分析、电路设计和实际应用中具有重要意义。
它能够描述交流电信号的实际能量,为电力传输、电能计量和电气设备的设计和使用提供准确的参考值。
有效值计算也是交流电工程中一项基本的测量和分析技术。

交流电有效值与峰值计算公式的推导过程兴安红叶 21:30:28满意回答设一周期电流i(t)通过电阻R,由于电流是变化的,各瞬间功率i^2R不同,在极短时间dt 内产生热量为i^2Rdt,在一个周期T内产生的热量为∫T i^2Rdt ,如果通过电阻R,经过时间T产生相等热量的直流电流的大小为I,则有∫T i^2Rdt=I^2RT,这就得到了电流的有效值I=[(1/T)∫T i^2dt]^(1/2)对正弦量,设i(t)=ImSIN(wt+∮)I={1/T∫T Im^2SIN^2(wt+∮)dt}^(1/2)因为 SIN^2(wt+∮)=(1/2)[1-COS^2(wt+∮)]所以 I={(Im^2/2T)∫T [1-COS^2(wt+∮)]dt}^(1/2)={Im^2/2T[t]T}^(1/2)=(Im^2/2)^(1/2)=Im/[2^(1/2)]=0.707Im兴安红叶 21:06:43有效值又叫“方均根值”-----先进行“方”(平方)运算,把其化为功率;再进行“均”(平均),在一个周期内进行功率平均;最后进行“根”(平方根)运算,计算出有效值。
比如说对于交流电压u,其有效值:兴安红叶 21:07:00(其中U是有效值,T是周期,u是瞬时值,可以是任何的周期函数。
)对于正弦波,u=UmSinωt 其中Um是峰值,ω是角频率。
代人上面的式子,计算后就可以得出用兴安红叶20:57:08 一、基本概念:交流电的有效值:正弦电流(电压)的有效值等于其最大值(幅值)的0.707倍。
兴安红叶20:59:27兴安红叶21:00:51兴安红叶21:01:19兴安红叶21:01:47兴安红叶21:02:03兴安红叶21:02:42兴安红叶21:04:11 交流电的有效值:在相同的电阻上分别通以直流电流和交流电流,经过一个交流周期的时间,如果它们在电阻上所损失的电能相等的话,则把该直流电流(电压)的大小作为交流电流(电压)的有效值,正弦电流(电压)的有效值等于其最大值(幅值)的0.707倍。

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。
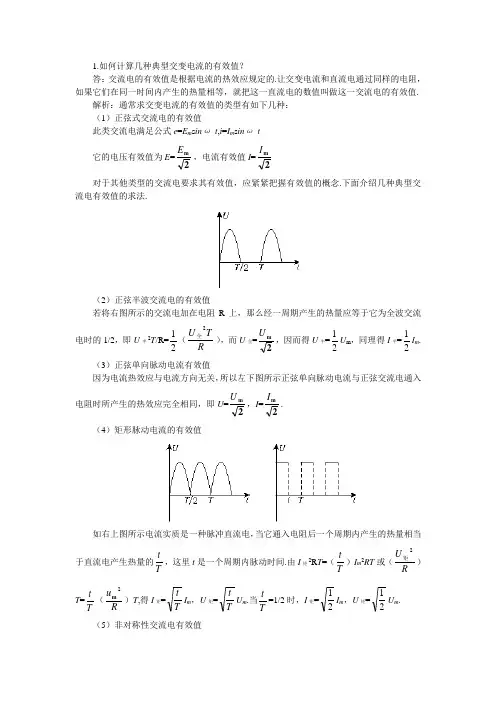
1.如何计算几种典型交变电流的有效值?答:交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值.解析:通常求交变电流的有效值的类型有如下几种:(1)正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ,电流有效值I =2mI对于其他类型的交流电要求其有效值,应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上,那么经一周期产生的热量应等于它为全波交流电时的1/2,即U 半2T /R=21(R T U 2全),而U 全=2m U ,因而得U 半=21U m ,同理得I 半=21I m . (3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同,即U =2m U ,I =2m I .(4)矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电,当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ,这里t 是一个周期内脉动时间.由I 矩2R T =(T t )I m 2RT 或(R U 2矩)T =T t (R u 2m )T ,得I 矩=T t I m ,U 矩=T t U m .当Tt =1/2时,I 矩=21I m ,U 矩=21U m . (5)非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上,交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅,直流电在相等时间内产生的热量 Q 2=RU 2T ,根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +,同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同,则该交流电的有效值为多少?解:根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同,则V 252,)2/(022===U U t R U t R U o 所以 3.在图示电路中,已知交流电源电压u=200s in 10πt V ,电阻R=10 Ω,则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析:在交流电路中电流表和电压表测量的是交流电的有效值,所以电压表示数为 u =2200V=141 V ,电流值i =R U =102200⨯ A=14.1 A. 答案:B。
1.如何计算几种典型交变电流的有效值?答:交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值.解析:通常求交变电流的有效值的类型有如下几种:(1)正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ,电流有效值I =2mI对于其他类型的交流电要求其有效值,应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上,那么经一周期产生的热量应等于它为全波交流电时的1/2,即U 半2T /R=21(R T U 2全),而U 全=2m U ,因而得U 半=21U m ,同理得I 半=21I m . (3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同,即U =2mU ,I =2mI .(4)矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电,当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ,这里t 是一个周期内脉动时间.由I 矩2R T =(T t )I m 2RT 或(R U 2矩)T =T t (R u 2m )T ,得I 矩=T t I m ,U 矩=T t U m .当Tt =1/2时,I 矩=21I m ,U 矩=21U m . (5)非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上,交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅,直流电在相等时间内产生的热量 Q 2=RU 2T ,根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +,同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同,则该交流电的有效值为多少?解:根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同,则3.在图示电路中,已知交流电源电压u=200s in 10πt V ,电阻R=10 Ω,则电流表和电压表读数分别为A,200 V A,141 VA,200 V A,141 V分析:在交流电路中电流表和电压表测量的是交流电的有效值,所以电压表示数为 u =2200V=141 V ,电流值i =R U =102200 A= A. 答案:B。
交流电有效值计算方法交流电一般可以表示为一个周期性变化的正弦函数,即I(t) = I_m * sin(ωt+θ)其中,I(t)表示交流电流随时间变化的函数,I_m表示电流的峰值,ω表示角频率,t表示时间,θ表示相位。
有效值的计算方法有两种:平方平均法和积分法。
一、平方平均法:平方平均法是最常用的计算方法,它的基本思想是对交流电流或电压进行平方运算,并求取其平均值的平方根。
1.对交流电流或电压进行平方运算:I^2(t) = I_m^2 * sin^2(ωt+θ)或U^2(t) = U_m^2 * sin^2(ωt+θ)2.求取平均值并开根号:I_rms = sqrt(1/T * ∫[0, T] (I^2(t)) dt)或U_rms = sqrt(1/T * ∫[0, T] (U^2(t)) dt)其中,T是一个周期的时间长度。
二、积分法:积分法是直接对交流电流或电压进行积分运算,并求取积分结果与周期长度的比值的平方根。
1.对交流电流或电压进行积分运算:∫[0, T] (I(t)) dt或∫[0, T] (U(t)) dt2.求取积分结果与周期长度的比值的平方根:I_rms = sqrt(1/T * (∫[0, T] (I(t)) dt)^2)或U_rms = sqrt(1/T * (∫[0, T] (U(t)) dt)^2)其中,T是一个周期的时间长度。
无论是平方平均法还是积分法,求取有效值的步骤是类似的,只是具体的计算过程有所差别。
需要注意的是,对于其他波形,如方波、三角波等,求取有效值的方法可能会稍有不同,但基本思想是一致的。
在实际应用中,计算交流电有效值非常重要,因为有效值是描述交流电大小的一个重要指标,也是进行电路设计、电能计量和电能消耗分析等的基础。
总结起来,交流电有效值的计算方法可以通过平方平均法或积分法来实现,根据具体情况选择合适的方法进行计算。
交流电有效值与峰值计算公式的推导过程兴安红叶21:30:28满意回答设一周期电流i(t)通过电阻R,由于电流是变化的,各瞬间功率i^2R不同,在极短时间dt 内产生热量为i^2Rdt,在一个周期T内产生的热量为∫T i^2Rdt ,如果通过电阻R,经过时间T产生相等热量的直流电流的大小为I,则有∫T i^2Rdt=I^2RT,这就得到了电流的有效值I=[(1/T)∫T i^2dt]^(1/2)对正弦量,设i(t)=ImSIN(wt+∮)I={1/T∫T Im^2SIN^2(wt+∮)dt}^(1/2)因为SIN^2(wt+∮)=(1/2)[1-COS^2(wt+∮)]所以I={(Im^2/2T)∫T [1-COS^2(wt+∮)]dt}^(1/2)={Im^2/2T[t]T}^(1/2)=(Im^2/2)^(1/2)=Im/[2^(1/2)]=0.707Im兴安红叶21:06:43有效值又叫“方均根值”-----先进行“方”(平方)运算,把其化为功率;再进行“均”(平均),在一个周期内进行功率平均;最后进行“根”(平方根)运算,计算出有效值。
比如说对于交流电压u,其有效值:兴安红叶21:07:00(其中U是有效值,T是周期,u是瞬时值,可以是任何的周期函数。
)对于正弦波,u=UmSin ωt 其中Um是峰值,ω是角频率。
代人上面的式子,计算后就可以得出用兴安红叶20:57:08一、基本概念:交流电的有效值:正弦电流(电压)的有效值等于其最大值(幅值)的0.707倍。
兴安红叶20:59:27兴安红叶21:00:51 兴安红叶21:01:19兴安红叶21:01:47兴安红叶21:02:03兴安红叶21:02:42兴安红叶21:04:11交流电的有效值:在相同的电阻上分别通以直流电流和交流电流,经过一个交流周期的时间,如果它们在电阻上所损失的电能相等的话,则把该直流电流(电压)的大小作为交流电流(电压)的有效值,正弦电流(电压)的有效值等于其最大值(幅值)的0.707倍。
电流有效值计算公式对于正弦交流电流,其有效值等于其峰值电流的0.707倍。
换句话说,如果交流电流的峰值电流是I0,则其有效值为Irms = I0 × 0.707、这个公式适用于正弦交流电流的情况。
然而,在实际应用中,很多交流电流并不是正弦波形的,且频率也不一定一致。
为了计算这种非正弦波形交流电流的有效值,需要用到实际信号的波形特征。
为了计算非正弦波形交流电流的有效值,可以利用均方根法。
均方根法将交流电流信号平方后取均值,然后再开平方根。
这样可以保留原始信号的幅值信息,并且忽略它的相位信息。
设交流电流信号为I(t),其平方为I2(t)。
令周期为T,则有:I2(t) = I1²sin²(ωt + φ1) + I2²cos²(ωt + φ2) +I3²sin²(ωt + φ3) + ...其中,I1, I2, I3...为不同频率的分量幅值,φ1, φ2, φ3...为不同频率的分量相位差。
根据均方根法,交流电流的有效值Irms可以通过以下公式计算:Irms = √[ (1/T)∫T[I2(t)dt] ]展开计算可得:Irms = √[1/T ∫T(I1²sin²(ωt + φ1) +I2²cos²(ωt + φ2) +I3²sin²(ωt + φ3) + ... )dt]将其中的正弦函数和余弦函数用它们的关系式转换为三角函数形式:sin²(ωt + φ) = (1 - cos(2ωt + 2φ))/2cos²(ωt + φ) = (1 + cos(2ωt + 2φ))/2代入原公式得:Irms = √[1/(2T) ∫T(I1²(1 - cos(2ωt + 2φ1)) + I2²(1 + cos(2ωt + 2φ2)) + I3²(1 - cos(2ωt + 2φ3)) + ... )dt]由于整个信号周期的积分值是一样的,所以可以将积分项化简为:Irms = √[1/2(I1² + I2² + I3² + ...) ]从上述公式可以看出,计算交流电流的有效值需要对不同频率的分量幅值进行平方求和,然后再开平方根。
正弦交流电电流有效值公式正弦交流电电流有效值公式:在一个完整的周期内,正弦交流电的电流的有效值可以根据以下公式计算:I_{RMS} = \frac{I_{max}}{\sqrt{2}}其中 I_{RMS} 表示电流的有效值,I_{max} 表示电流的最大值。
原理解释:交流电流是由于电子在导体内上下振荡而产生的。
由于电流不是恒定的,它的值随时间变化而变化。
在一个周期内,电流的值经过一系列的变化,这些变化可以用一个曲线表示,这就是正弦曲线。
正弦曲线上的任何一个瞬间,电流的值都可以通过测量从零到这个点的电流值的平均值来得到。
为了计算出电流的有效值,我们需要计算在一个完整的周期内电流的平均值。
在一个完整的周期内的电流平均值等于电流的RMS值,也就是有效值。
实际应用场景:正弦交流电电流有效值公式的应用非常广泛,它是计算交流电的电能的基础。
有效值是计算电阻、电容和电感器件导电性能的重要指标。
以下是一些应用场景的例子:1. 家庭电力消耗:在家庭中,电流的有效值经常被用于计算电器的电力消耗。
通过电表可以测量出房屋电力的总耗电量,然后通过测量电流的有效值和电压的实际值,可以计算出每个电器的功率消耗。
2. 电子设备:许多电子设备需要判断电流的有效值。
在音频放大器中,在接收输入信号之前,需要将信号转换为电流并计算其有效值,以确保信号不会过载或损坏放大器。
3. 电路设计:在电路设计中,电流的有效值可以用来计算电路元件的功率耗散。
这些元件可能包括电阻、电容和电感。
通过计算电流的有效值和电压的实际值,可以计算出电路中每个元件的实际功率。
4. 电力系统工程:在电力系统工程中,电流的有效值用于计算负载电功率。
在发电站中,为了计算出发电量和负载电流倍率,必须计算出负载电流的有效值。
有效值也是电网稳态分析的一个基本参数。
正弦交流电电流有效值公式是计算交流电能和其它电学实际应用中不可或缺的重要工具。
1.如何计算几种典型交变电流的有效值?答:交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值.解析:通常求交变电流的有效值的类型有如下几种: (1)正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t 它的电压有效值为E =2m E ,电流有效值I =2m I对于其他类型的交流电要求其有效值,应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上,那么经一周期产生的热量应等于它为全波交流电时的1/2,即U 半2T /R=21(R T U 2全),而U 全=2m U ,因而得U 半=21U m ,同理得I 半=21I m .(3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同,即U =2m U ,I =2m I .(4)矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电,当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t,这里t 是一个周期内脉动时间.由I 矩2R T =(T t )I m 2RT 或(R U 2矩)T =T t (Ru 2m )T ,得I 矩=T t I m ,U 矩=T t U m .当T t=1/2时,I 矩=21I m ,U 矩=21U m . (5)非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上,交变电流在一个周期内产生的热量为Q 1=222221TR U T R U ⋅+⋅,直流电在相等时间内产生的热量Q 2=R U 2T ,根据它们的热量相等有RU T R U 2212=⋅T 得 U =)(212221U U +,同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同,则该交流电的有效值为多少?解:根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同,则V 252,)2/(022===U U t R U t R U o 所以 3.在图示电路中,已知交流电源电压u=200s in 10πt V ,电阻R=10 Ω,则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析:在交流电路中电流表和电压表测量的是交流电的有效值,所以电压表示数为 u =2200 V=141 V ,电流值i =R U =102200⨯ A=14.1 A. 答案:B文案 编辑词条 B 添加义项 ?文案,原指放书的桌子,后来指在桌子上写字的人。
交流电有效值的计算
江苏省新海高级中学 崔晓霞 222006
交变电流的大小和方向随时间作周期性变化。
为方便研究交变电流的特性,根据电流的热效应引入了有效值这一物理量。
一、 正弦交流电有效值表达式的推导:
交流电的有效值是用它的热效应规定的,因此设法求出正弦交流电的热效应,才能求出其有效值,正弦交流电电压的瞬时值u =U m ·sinωt ,如果把这加在负载电阻R 上,它的瞬时电功率22cos 1sin 2222t R U t R U R u P m
m ⋅-⋅=⋅==ωω 其图像如图1所示.由微元法可知,P-t 图线和t 轴之间
所包围的面积就是功(图中打斜条的部分).
不难看出,图中有斜条打△的部分和无斜条打△的部分面
积是相同的,因此打斜条部分的面积就是P =U 2m /2R 线和t 轴之
间的面积.设正弦交流电电压的有效值是U ,根据有效值的定义:R
U R U m 222= 可得:2/m U U = 同理可得:2/m I I =;2/m E E =
此关系式仅适用于正弦交流电,那么非正弦交流电的有效值又该如何求解呢?
二、非正弦交流电有效值的计算
例1. 如图2甲乙所示分别表示交变电流随时间变化的图象,则这两个交流电的有效值分别是 V 和 A 。
解析:对于图甲,该交变电流在每个周期T 内都可看作两个阶段的直流电流:前T /3中,U 1=100V ,后2T /3中,U 2=50V 。
在一个周期中,该交变电流在电阻R 上产生的热量为:
3250310032322222
1T R T R T R U T R U Q ⋅+⋅=+⋅= ① 设该交流电电压的有效值为U ,则上述热量T Q ⋅=R
U 2
②
联立①、②两式,可得有效值为V 250=U 对于图乙,从t =0开始的任意一个周期内,前半周期是大小不变的直流电,为I A 15=,
图1
图2 甲 乙
后半周期是有效值为I A 252=的交变电流。
设所求交变电流的有效值为I ,根据有效值的定义,选择一个周期的时间,利用在相同时间内通过相同的电阻所产生的热量相等,由焦耳定律得 I RT I R T I R T 2122222=+ 即I 22251252
12=⨯+⨯() 解得I A =532 点评:对于非正弦交流电,要从有效值从定义出发,根据热效应求解。
根据有效值的定义,可以选择计算交流电一个周期之内在某电阻上产生的热量,然后计算多大的直流电在该电阻上相等时间内产生相等的热量,该直流电的值就是交变电流的有效值。
练习1:如图3甲为电热毯的电
路图,电热丝接在U =311sin100πt(V)
的电源上,电热毯被加热到一定温
度后,通过装置P 使输入电压变为
图乙所示波形,从而进入保温状态,
若电热丝电阻保持不变,此时交流
电压表的读数是( ) A. 110V B. 156V
C. 220V
D. 311V
答案:B
三、利用能量守恒求解变化电流的有效值
例2.如图4所示,ab 是半径不L ,电阻不计的1/4圆周的金属环,固定于竖直平面,圆心为o ,oa 是质量不计的金属杆,其电阻为r ,它的一端挂在
o 点(无摩擦),另一端连一金属小球,小球的质量为m ,与
金属环接触良好无摩擦,ob 是一根竖直的与金属环相连接
的金属丝,其电阻为R ,上述整个装置置于水平方向垂直纸
面向里的匀强磁场中,磁感应强度为B ,现将金属小球从a
点由静止开始释放,它滑到b 点时的速度为v ,所经历的时
间为t ,问:(1)这一过程中,回路的平均感应电动势多大?
(2)这一过程中,感应电动势的有效值是多大?
解析:(1)小球下落过程中,oba 围成的面积减小,B 不变,
φ减小,有感应电动势。
t
B l t S t n 4B E 2π=∆∆∆∆Φ== (2)由能量守恒可知,在小球下落过程中,重力势能的减小等于动能的增加和产生的热量,
故221mv Q mgl += ① t r R E Q +=2 ② 由①②得:)2
1(2mv mgl t r R E -+= 点评:交流电的峰值、有效值、平均值在应用上是有区别的
(1) 峰值:即最大的瞬时值,当线圈在匀强磁场中绕垂直于磁感线方向的轴匀速转动时,所产生感应电动势的峰值为εm =NBS ω,即仅由匝数N ,线圈面积S ,磁感强度B 和角速度ω四个量决定。
与轴的具体位置,线圈的形状及线圈是否闭合都是无关的。
峰值对纯电阻电路图3
来说,没有什么应用意义。
若对含电容电路,在判断电容器是否会被击穿时,则需考虑交流的峰值是否超过电容器的耐压值。
(2)有效值:交流的有效值是按热效应来定义的,对于一个确定的交流来说,其有效值是一定的。
在计算交流通过电阻产生的热功率时,只能用有效值;在实际应用中,交流电器铭牌上标明的额定电压或额定电流都是指有效值,交流电流表和交流电压表指示的电流、电压也是有效值,解题中,若题示不加特别说明,提到的电流、电压、电动势时,都是指有效值。
(3)平均值:由公式t
n ∆∆Φ=ε确定,其值大小由某段时间磁通量的变化量来决定,在不同的时间段里是不相同的。
如对正弦交流,其正半周或负半周的平均电动势大小为
π
ωεnBs T Bs n 22/2=⋅=,而一周期内的平均电动势却为零。
在计算通过导体的电量时,只能用平均值,而不能用有效值。