计算交变电流有效值的三种方法

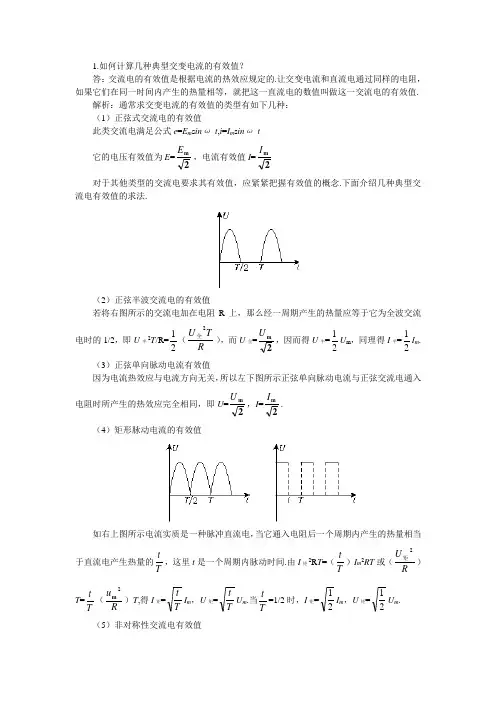
1.如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值.解析：通常求交变电流的有效值的类型有如下几种： （1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t 它的电压有效值为E =2m E ，电流有效值I =2m I对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（RT U 2全），而U 全=2mU ，因而得U 半=21U m ，同理得I 半=21I m .（3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2mU ，I =2m I .（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的Tt ，这里t 是一个周期内脉动时间.由I矩2R T =（Tt ）I m 2RT 或（RU 2矩）T =Tt （Ru 2m ）T ,得I 矩=Tt I m ，U 矩=Tt U m .当Tt =1/2时，I 矩=21I m ，U 矩=21U m .（5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T RU T RU ⋅+⋅，直流电在相等时间内产生的热量Q 2=RU 2T ，根据它们的热量相等有RUT RU 2212=⋅T 得U =)(212221U U +，同理有I =)(212221I I +.2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同，则V 252,)2/(022===U U t R Ut RU o 所以3.在图示电路中，已知交流电源电压u=200s in 10πt V ，电阻R=10 Ω，则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为 u =2200 V=141 V ，电流值i =RU =102200⨯ A=14.1 A.答案：B。

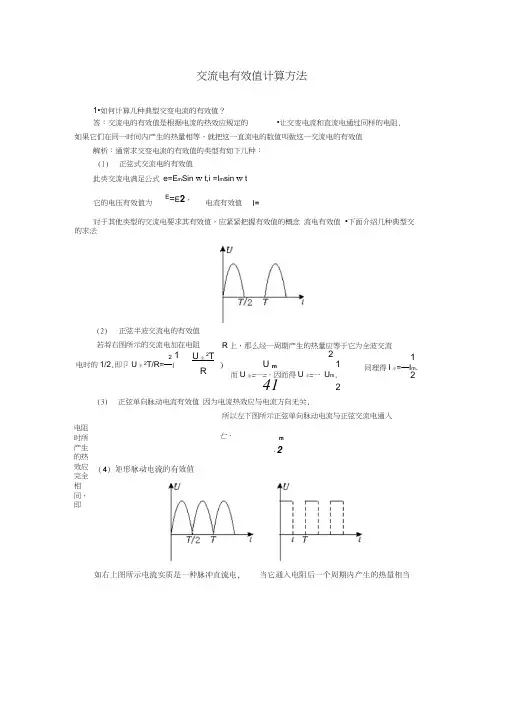
交流电有效值计算方法1•如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的•让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值解析：通常求交变电流的有效值的类型有如下几种：(1)正弦式交流电的有效值此类交流电满足公式e=E m Sin w t,i =I m sin w t对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念流电有效值的求法(2)正弦半波交流电的有效值若将右图所示的交流电加在电阻2 1电时的1/2,即卩U半2T/R=—(2U m 1而U全=—=，因而得U半=一U m,412(3)正弦单向脉动电流有效值因为电流热效应与电流方向无关,电阻时所产生的热效应完全相同，即它的电压有效值为E=E2，电流有效值•下面介绍几种典型交R上，那么经一周期产生的热量应等于它为全波交流U全2TR1同理得I半=—I m.2所以左下图所示正弦单向脉动电流与正弦交流电通入七，m、222 于直流电产生热量的—，这里t是一个周期内脉动时间.由I矩2RT= ( — ) I m2RT或()T T RT=T(牛)「得1矩=：T Im，U矩=4.当T=1/2时，1：2im，U矩、2Um.(5)非对称性交流电有效值假设让一直流电压U和如图所示的交流电压分别加在冋一电阻上，交变电流在一个周期内产生的热量为Q1=2 2U1 T U2 T ..................... . .............. ..，直流电在相等时间内产生的热量R 2 R 22•—电压U o=1O V的直流电通过电阻R在时间t内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t时间内直流电压U o在电阻R上产生的热量与同一时间内交流电压的有效值U在电阻R/2上产生的热量相同，则3•在图示电路中，已知交流电源电压u=200si n10n t V,电阻R=10 Q ,则电流表和电压表读数分别为A.14.1 A,200 VC.2 A,200 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为200V=141 V,电流值i=U= ：00R 衬2汉10 A=14.1 A.U2T,根据它们的热量相等有+U 2 )，同理有I = £(I 1I22).2 2知=胡「所以U哼=5 2 VB.14.1 A,141 VD.2 A,141 V答案：B2。

交流电有效值计算方法1。

如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值.解析：通常求交变电流的有效值的类型有如下几种：（1)正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ，i =I m s in ω t它的电压有效值为E =2m E ，电流有效值I =2m I对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念。

下面介绍几种典型交流电有效值的求法。

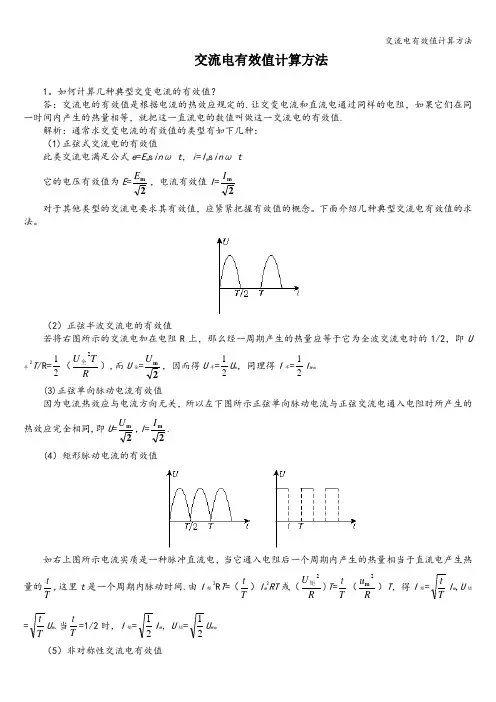
（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全）,而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m 。

(3)正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同,即U =2m U ,I =2mI .(4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ,这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或（RU 2矩)T =T t （R u 2m ）T ，得I 矩=T t I m ,U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m 。

（5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 R U T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +。

求交流电有效值的方法
交流电的有效值是根据电流的热效应规定的。

在求交流电的有效值时，通常采用以下几种方法：
直接计算法：对于已知波形的交流电，如正弦波、方波、三角波等，可以根据其波形特点直接计算出有效值。

例如，对于正弦波交流电，其有效值等于峰值除以根号2。

积分法：对于任意波形的交流电，可以通过积分的方式计算其有效值。

具体步骤是，将交流电在一个周期内的瞬时值进行平方，然后对时间进行积分，最后取平方根即可得到有效值。

这种方法需要知道交流电的瞬时值表达式或者采样数据。

仪表测量法：在实际应用中，通常使用电表来测量交流电的有效值。

电表内部采用了专门的电路和算法来计算有效值，可以直接显示出测量结果。

需要注意的是，不同类型的电表可能采用不同的计算方法，因此测量结果可能存在一定的误差。

需要注意的是，在求交流电的有效值时，需要明确所求的是电压有效值还是电流有效值，并且要注意单位的一致性。

此外，对于非正弦波形的交流电，其有效值并不能简单地用峰值除以根号2来计算，而需要根据其波形特点进行具体分析。

总之，求交流电的有效值需要根据具体情况选择合适的方法，并且要注意测量误差和单位的一致性。

在实际应用中，还需要考虑交流电的频率、波形等因素对有效值的影响。

计算交变电流有效值的三种方法交变电流的有效值是指通过交变电流产生的等效直流电流的大小。

它是交流电流的一个重要参数，用于描述交流电流的强度。

计算交变电流的有效值一般有以下三种方法：插入均方根，通过峰值和周期进行计算，以及通过功率计进行测量。

1.插入均方根法插入均方根法是计算交变电流有效值的一种常用方法，也是最常见的方法之一、它利用电流的瞬时值进行测量和计算。

具体步骤如下：a. 在交流电路中插入一个测量电流的均方根（rms）电流表。

b.记录电流表显示的数值。

这个数值就是交变电流的有效值。

这种方法适用于所有频率的交流电流。

2.峰值与周期计算法峰值与周期计算法是计算交变电流有效值的另一种方法，它利用电流的峰值和周期进行计算。

具体步骤如下：a.通过示波器或其他测量仪器测量交流电流的峰值。

b.通过频率计或其他测量仪器测量交流电流的周期。

c.将测得的峰值除以根号2，再除以测得的周期的一半，即可得到交变电流的有效值。

这种方法适用于周期性波形的交流电流。

3.通过功率计进行测量通过功率计进行测量是最直接和准确的方法之一，它既可以测量已经连入电路中的交变电流，也可以测量未连入电路的交变电流。

具体步骤如下：a.将功率计与电路连接，使之成为电路中的一部分。

b.读取功率计显示的数值。

这个数值即为交变电流的有效值。

这种方法适用于电路中的交变电流。

除了以上三种方法，还有一些其他的计算交变电流有效值的方法，如采用傅里叶变换、数值模拟等。

但这些方法通常需要较高的计算能力和专业知识，并不适用于常规的电流测量。

根据具体的使用情景和测量要求，可以选择适合的方法计算交变电流的有效值。

需要注意的是，在实际测量中，要注意测量仪器的精度、测量环境的影响以及电流波形的非理想性等因素，以确保测量结果的准确性和可靠性。

交流电有效值计算方法1。

如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的。

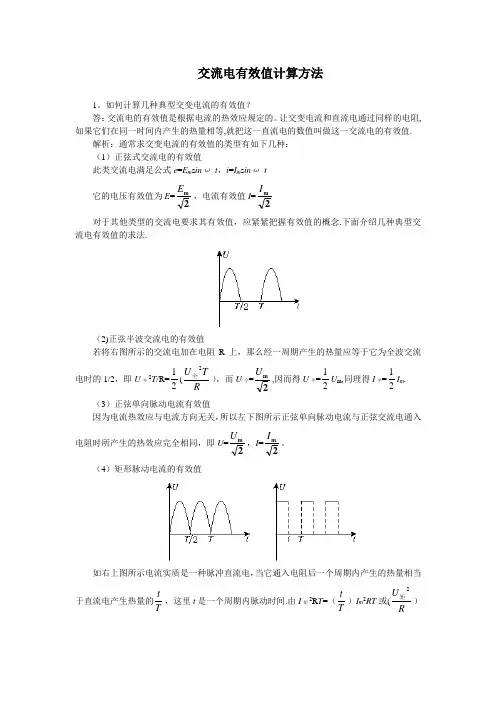
让交变电流和直流电通过同样的电阻,如果它们在同一时间内产生的热量相等,就把这一直流电的数值叫做这一交流电的有效值. 解析：通常求交变电流的有效值的类型有如下几种：（1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ，i =I m s in ω t它的电压有效值为E =2m E ，电流有效值I =2m I对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2)正弦半波交流电的有效值 若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21(R T U 2全），而U 全=2m U ,因而得U 半=21U m ,同理得I 半=21I m . （3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2m U ，I =2m I 。

（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或(R U 2矩）T =T t (R u 2m )T ,得I 矩=T t I m ，U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m . （5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +。

专题64交变电流有效值的计算与“四值”的理解应用一、计算交变电流有效值的方法1．利用有效值的定义计算(非正弦式电流)交变电流的有效值是根据电流的热效应(电流通过电阻生热)进行定义的，所以进行有效值计算时，要紧扣电流通过电阻生热(或热功率)．注意“三同”：即“相同电阻”，“相同时间”内产生“相同热量”．计算时“相同时间”要取周期的整数倍，一般取一个周期．2.公式法 利用E ＝E m2、U ＝U m2、I ＝I m2计算，只适用于正(余)弦式交变电流．3. 多种形式组合的有效值的计算（1）分段计算电热求和得出一个周期内产生的总热量．（2）利用两个公式Q ＝I 2Rt 和Q ＝U 2Rt 可分别求得电流有效值和电压有效值．（3）若图象部分是正弦(或余弦)式交变电流，其中的14(但必须是从零至最大值或从最大值至零)和12周期部分可直接应用正弦式交变电流有效值与最大值间的关系I ＝I m 2、U ＝U m2求解．【典例1】如图所示为一交变电流随时间变化的图象，此交流电的有效值是( )． A ．5 2 AB ．5 AC ．3.5 2 AD ．3.5 A 【答案】 B【典例2】如图所示的区域内有垂直于纸面的匀强磁场，磁感应强度为B .电阻为R 、半径为L 、圆心角为45°的扇形闭合导线框绕垂直于纸面的O 轴以角速度ω匀速转动(O 轴位于磁场边界)．则线框内产生的感应电流的有效值为( )．A.BL 2ω2RB.2BL 2ω2RC.2BL 2ω4RD.BL 2ω4R【答案】 D【解析】 线框转动的角速度为ω，进磁场的过程用时18周期，出磁场的过程用时18周期，进、出磁场时产生的感应电流大小均为I ′＝12BL 2ωR，则转动一周产生的感应电流的有效值I 满足：I 2RT ＝⎝ ⎛⎭⎪⎪⎫12BL 2ωR 2R ×14T ，解得I ＝BL 2ω4R ，D 项正确．【典例3】如图所示，图甲和图乙分别表示正弦脉冲波和方波式的交变电流与时间的变化关系．若使这两种电流分别通过两个完全相同的电阻，经过1 min 的时间，则( )A ．图甲所示交变电流的有效值为33 A B ．图乙所示交变电流的有效值为22A C ．两电阻消耗的电功之比为1∶3D ．两电阻消耗的电功之比为3∶1 【答案】AC【跟踪短训】1．某交流电的电流随时间变化图像如图所示，则此交变电流的有效值为A． l A B． 3 A C． D． 2 A【答案】C【解析】据有效值的定义可得：，代入数据解得：此交变电流的有效值。

几种常见的交变电流的有效值和平均值的计算湖北省襄樊市第一中学（441000）赵兴华 高中物理第二册（实验修订本） 《交变电流》一章中列举了几种常见交变电流，即：正 弦交变电流、锯齿波电流、矩形脉冲电流和尖脉冲电流。

交变电流的有效值和平均值是两个 不同的概念，不少学生在解题中不能很好地区分， 造成解题失误。

交变电流的有效值是根据 电流的热效应来规定的，让交流电和直流电通过相同阻值的电阻， 如果它们在相同的时间里 产生的热量相等，就把这一直流电的数值叫这一交流电的有效值； 交变电流的平均值是指交 变电流在一个周期内交流电的绝对值的平均值。

教材中只给出了正弦交变电流的有效值， 没 有给出其他几种交变电流的有效值， 也没有给出平均值的大小。

笔者在这里给出它们供大家 参考。

一、交变电流的有效值 1、正弦交变电流的有效值 方法一：设有一直流电和一正弦交流电，分别通过同样的电阻 R ，经过时间T （ T 为该 交流电的周期）内产生的热量分别为： Q 直=I 2RT , Q 交=P T , 则有: 正弦交流电的瞬时功率: P = i 2R = l ；Rsin 2 t = 1；只？丄(1 cos2 t) 21 .2 1 . 2 _ =—l m R l m Rcos2 t 2 2 上式中第一项是不随时间变化的常量， 第二项是按余弦变化的量, 1 2项的平均值是零，故有： P 丄l ；R 2 在一个周期内，第二r% I 方法二：用积分的方法对于 1= I m sin dQ ，则有：dQ = i 2Rdt =( I m sin t ) 2Rdt 在1个周期内，t=T , R 产生的热量：T22 T1Q = 0 (I m sin t) Rdt = I m R 0 (-可得:0.7071mt ，通过阻值为R 的电阻在dt 时间里产生的热量1 1 2sin2 t ）dt = I m RT 2 2而等效电流I 在相等的时间产生的热量也为Q ,则有：Q = I 2RT所以正弦交变电流的有效值与最大值之间的关系为:2、锯齿波电流的有效值: 设有一锯齿波电流的最大值为0.7071I =|m,周期是3、矩形脉冲电流的有效值:为T ，(如图所示)。

几种常见的交变电流的有效值和平均值的计算湖北省襄樊市第一中学（441000）赵兴华 高中物理第二册（实验修订本） 《交变电流》一章中列举了几种常见交变电流，即：正 弦交变电流、锯齿波电流、矩形脉冲电流和尖脉冲电流。

交变电流的有效值和平均值是两个 不同的概念，不少学生在解题中不能很好地区分， 造成解题失误。

交变电流的有效值是根据 电流的热效应来规定的，让交流电和直流电通过相同阻值的电阻， 如果它们在相同的时间里 产生的热量相等，就把这一直流电的数值叫这一交流电的有效值； 交变电流的平均值是指交 变电流在一个周期内交流电的绝对值的平均值。

教材中只给出了正弦交变电流的有效值， 没 有给出其他几种交变电流的有效值， 也没有给出平均值的大小。

笔者在这里给出它们供大家 参考。

一、交变电流的有效值 1、正弦交变电流的有效值 方法一：设有一直流电和一正弦交流电，分别通过同样的电阻 R ，经过时间T （ T 为该 交流电的周期）内产生的热量分别为： Q 直= I 2RT, Q 交=P T, 则有:I = 正弦交流电的瞬时功率: 1 P= i 2R = i m Rsin 2t = i m R?-(1 cos2 t) 2 1|2_ 1 . 2 _ =—I m R — I m Rcos2 t 2 2 上式中第一项是不随时间变化的常量， 第二项是按余弦变化的量, — 1 2项的平均值是零，故有：P 丄i m R 2在一个周期内，第二I J % 必og 方法二：用积分的方法对于 1= I m sin dQ ，则有：dQ = i 2Rdt =( I m sin t ) 2Rdt 在1个周期内，t=T , R 产生的热量：T2 2 T 1 Q= n (Imsin t) Rdt = ImR (0 0 2 可得:t ，通过阻值为R 的电阻在 dt 时间里产生的热量1 12 — Sin2 t ）dt = TmRT 2 - 而等效电流I 在相等的时间产生的热量也为 Q,所以正弦交变电流的有效值与最大值之间的关系为: 1.2“ 2则有：Q= I 2RT J 沧0.7071m2、锯齿波电流的有效值:设有一锯齿波电流的最大值为I m ,周期是T ，且 I m = k —,2在半个周期内瞬时电流: 在dt 时间里通过电阻 dQ=( kt) 2Rdt3、矩形脉冲电流的有效值:在t= T 时间通过电阻 R 上产生热量为:^k 2t 2Rdt — k 2RT 01. 2_3 12 .....故有：|2=丄k 2T 212丄（玉）2T 212 T即锯齿波电流的有效值与最大值之间的关系为: Im /Z/3i = kt R 上产生热量为:(1) 若有一矩形脉冲电流，正反向的电流值相等为 为T,(如图所示)。