2017-2018七年级数学上册 截面与三视图习题 (新版)新人教版

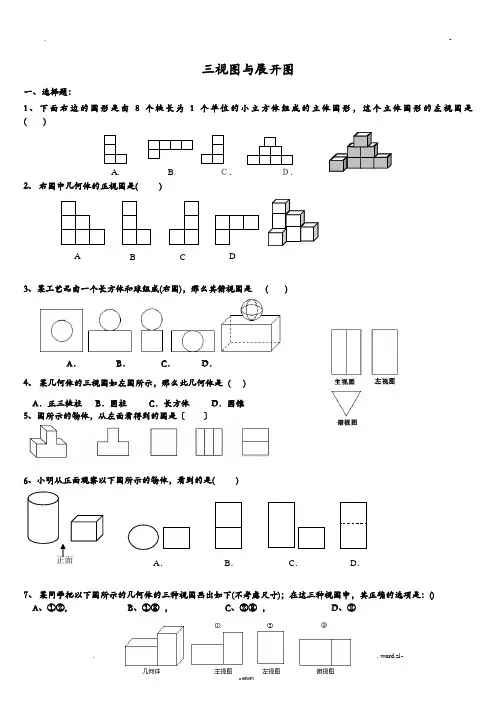
. -三视图与展开图一、选择题：1、下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )A. B.Ｃ．Ｄ．2、右图中几何体的正视图是( )A B C D3、某工艺品由一个长方体和球组成(右图)，那么其俯视图是( )A．B．C．D．4、某几何体的三视图如左图所示，那么此几何体是( )A．正三棱柱B．圆柱C．长方体D．圆锥5、图所示的物体，从左面看得到的图是〔〕6、小明从正面观察以下图所示的物体，看到的是( )正面A．B．C．D．7、某同学把以下图所示的几何体的三种视图画出如下(不考虑尺寸)；在这三种视图中，其正确的选项是：()A、①②,B、①③，C、②③，D、②. -8、 由假设干个同样大小的正方体堆积成一个实物，不同侧面观察到如图8所示的投影图，那么构成该实物的小正方体个数为 ( )A. 6B. ７C. 8D. 9 9、 某超市货架上摆放着“康师傅〞红烧肉面，如图1是它们的三视图，那么货架上的“康师傅〞红烧肉面至少有 ( ) Ａ．8桶 Ｂ．9桶 Ｃ．10桶 Ｄ．11桶10、 图2中几何体的正视图是( )11、由一些完全一样的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数 ( ) A 、6个 B 、7个 C 、8个 D 、9个主视图 左视图 俯视图 (第12题)12、 如图是一些一样的小正方体构成的几何体的正视图和左视图，在这个几何体中，小正方体的个数不可能是( )A 、7B 、8C 、9D 、1013、如图是正方体的展开图，那么原正方体相对两个面上的数字和最小的是( ). A. 4 B. 6 C. 7 D.8 14、 右图所示是一个三棱柱纸盒，在下面四个图中，只有一个是这个纸盒的展开图，那么这个展开图是( )15、 如下图，右面水杯的俯视图是()AB C D 1 42 5 36第13题图主视图 左视图 俯视图 图1A B C D16、以下几何体，正(主)视图是三角形的是( )A．B．C．D．17、有一实物如下图，它的主视图是( )18、骰子是一种特别的数字立方体，它符合规那么：相对两面的点数之和总是7.下面四幅图中可以折成符合规那么的骰子的是19、一个画家有14个边长为1m的正方体，他在地面上把它们摆成如下图的形式，然后他把露出的外表都涂上颜色，那么被涂上颜色的总面积为〔〕A. 19m2B. 21m2C. 33m2D. 34m220、如图，以Rt△ABC为直角边AC所在直线为轴，将△ABC旋转一周所形成的几何体的俯视图是( )21、下面的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )DCBA22、有6个大小一样的正方体搭成的几何体如下图，那么关于它的视图说确的是( )A 主视图的面积最大B 左视图的面积最大C 俯视图的面积最大D 三个视图的面积一样大23、想一想：将左边的图形折成一个立方体，右边的四个立方体哪一个是由左边的图形折成的〔〕 24、如下图的立方体，如果把它展开，可以是以下图形中的〔 〕25、以下四个图形中，每个小正方形都标上了颜色. 假设要求一个正方体两个相对面上的颜色都一样，那么不可能是这一个正方体的展开图的是〔 〕26、 以下展开图中，不是正方体是A 、B 、C 、D 、-27、 一个由假设干个一样的正方体搭成的物体的主视图与左视图都是右边的图形，这个物体有( )种不同的搭建方法.A 、2B 、3C 、4D 、5二、填空题：1. 如图是一个几何体的三视图，根据图中提供的数据 (单位：cm)可求得这个几何体的体积为．2、如下图，用字母M 表示与A 相对的面，请主视图 左视图 12俯视图1323黄红 黄 红 绿 绿黄 红绿 红 绿 黄 绿 红红 绿 黄 黄 绿 红黄 红 黄绿A ．B ．C ．D ．. -主视图左视图在下面的正方体展开图中填写相应的字母．3、如图是一个由假设干个正方体搭建而成的几何体的主视图与左视图，那么以下图形中可以作为该几何体的俯视图的序号是:4、 如图，是由假设干个一样正方体组成的几何体的主视图和左视图，那么组成这个几何体最少的正方体的个数是-个.5、 桌上摆着一个由假设干个一样正方体组成的几何体，其主视图和左视图如下图，这个几何体最多可以由个这样的正方体组成。

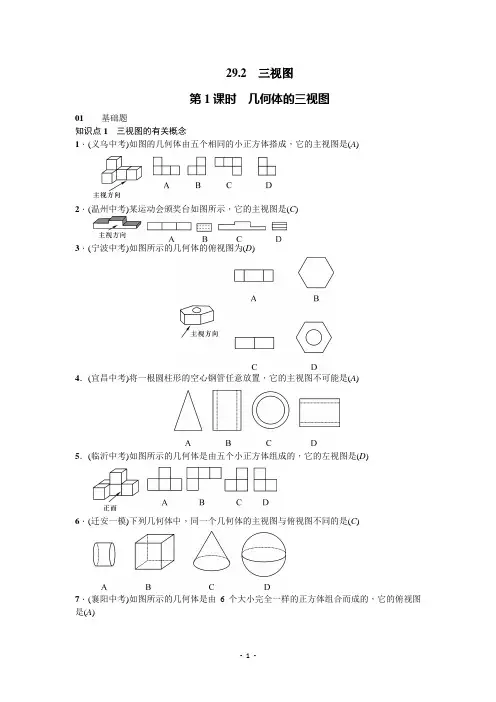
29.2三视图第1课时几何体的三视图01基础题知识点1三视图的有关概念1．(义乌中考)如图的几何体由五个相同的小正方体搭成，它的主视图是(A)2．(温州中考)某运动会颁奖台如图所示，它的主视图是(C)3．(宁波中考)如图所示的几何体的俯视图为(D)4．(宜昌中考)将一根圆柱形的空心钢管任意放置，它的主视图不可能是(A)5．(临沂中考)如图所示的几何体是由五个小正方体组成的，它的左视图是(D)6．(迁安一模)下列几何体中，同一个几何体的主视图与俯视图不同的是(C)7．(襄阳中考)如图所示的几何体是由6个大小完全一样的正方体组合而成的，它的俯视图是(A)8．(丽水中考)如图是底面为正方形的长方体，下面有关它的三个视图的说法正确的是(B)A．俯视图与主视图相同B．左视图与主视图相同C．左视图与俯视图相同D．三个视图都相同9．(济宁中考)下列几何体中，主视图、俯视图、左视图都相同的是(B)10．用12个大小相同的小正方体搭成的几何体如图所示，标有正确小正方体个数的俯视图是(A)知识点2三视图的画法11．(杭州中考)下列选项中，如图所示的圆柱的三视图画法正确的是(A)12．画出如图所示几何体的三视图．解：如图．02中档题13．(河北中考)如图是由相同的小正方体木块粘在一起的几何体，它的主视图是(A)14．(邢台临城县一模)如图所示的几何体的俯视图是(D)15．(菏泽中考)下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是(C)16．一位美术老师在课堂上进行立体模型素描教学时，把由圆锥与圆柱组成的几何体(如图所示，圆锥在圆柱上底面正中间放置)摆在讲桌上，请分别画出这个几何体的三视图(从正面、左面、上面看得到的视图)．解：如图.17．一种机器上有一个进行转动的零件叫燕尾槽(如图)，为了准确做出这个零件，请画出它的三视图．解：如图.03综合题18．中央电视台有一个非常受欢迎的娱乐节目叫《墙来了！》．选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞，则该几何体为下列几何体中的哪一个？选择并说明理由．解：比较各几何体的三视图，考虑是否有短形，圆及三角形即可．对于A，三视图分别为短形、三角形、圆(含直径)，符合题意；对于B，三视图分别为三角形、三角形、圆(含圆心)，不符合题意；对于C，三视图分别为正方形、正方形、正方形，不符合题意；对于D，三视图分别为三角形、三角形、矩形(含对角线)，不符合题意．故选A.第2课时由三视图确定几何体01基础题知识点由三视图确定几何体1．(金华中考)一个几何体的三视图如图所示，则这个几何体是(D)A．球体B．圆锥C．立方体D．圆柱2．(新疆中考)某几何体的三视图如图所示，则该几何体是(D)A．球B．圆柱C．三棱锥D．圆锥3．(承德六校一模)如图是某几何体的三视图，则该几何体是(C)A．圆锥B．圆柱C．正三棱柱D．正三棱锥4．(云南中考)若一个几何体的主视图、左视图、俯视图是半径相等的圆，则这个几何体是(C)A．圆柱B．圆锥C．球D．正方体5．(武汉中考)某物体的主视图如图所示，则该物体可能为(A)6．(唐山古冶区一模)如图是由三个相同小正方体组成的几何体的主视图，那么这个几何体可以是(A)7．(聊城中考)如图是由若干个小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是(C)8．(河北中考)图中的三视图所对应的几何体是(B)9．(深圳模拟)如图是一个几何体的俯视图，则该几何体可能是(B)02中档题10．(金华中考)一个几何体的三视图如图所示，那么这个几何体是(D)11．(唐山路南区一模)如图为某几何体的三视图，则组成该几何体的小正方体的个数是(A)12．(怀化中考)如图，甲、乙、丙图形都是由大小相同的正方体搭成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，其中主视图相同的是(B)A．仅有甲和乙相同B．仅有甲和丙相同C．仅有乙和丙相同D．甲、乙、丙都相同13．(保定莲池区模拟)一张桌子上摆放有若干个大小、形状完全相同的碟子，现从三个方向看，其三种视图如图所示，则这张桌子上碟子的总数为(B)A．11 B．12 C．13 D．14解析：因为右上角的盘子有5个，左下角的盘子有3个，左上角的盘子有4个，3＋4＋5＝12(个)，故选B.14．用4个棱长为1的正方体搭成一个几何体模型，其主视图与左视图如图所示，则该立方体的俯视图不可能是(D)15．如图是由一些完全相同的小正方体搭成的几何体的俯视图和左视图，则组成这个几何体的小正方体的个数是(C)A．5或6或7 B．6或7C．6或7 或8 D．7或8或916．根据如图所示的几何体的三视图描述物体的形状．解：几何体的形状为：03综合题17．某个长方体的主视图是边长为1 cm的正方形．沿这个正方形的对角线向垂直于正方形的方向将长方体切开，截面是一个正方形．那么这个长方体的俯视图是(D)第3课时由三视图确定几何体的表面积或体积01基础题知识点1几何体的展开图1．(保定章末测试)一个几何体的表面展开图如图所示，则这个几何体是(A)A．四棱锥B．四棱柱C．三棱锥D．三棱柱2．(宜昌中考)如图是一个小正方体的展开图，把展开图折叠成小正方体后，与“爱”字一面的相对面上的字是(C)A．美B．丽C．宜D．昌3．(唐山路南区模拟)下列图形中可以作为一个三棱柱的展开图的是(A)4．(梧州中考)如图是一个圆锥，下列平面图形中既不是它的三视图，也不是它的侧面展开图的是(D)5．(舟山中考)一个正方体的表面展开图如图所示，将其折叠成立方体后，“你”字对面的字是(C)A．中B．考C．顺D．利6．(唐山丰南区一模)如图是一个几何体的三视图，则这个几何体的展开图可以是(A)知识点2由三视图确定几何体的表面积或体积7．(连云港中考)由6个大小相同的正方体搭成的几何体如图所示，比较它的主视图、左视图和俯视图的面积，则(C)A．三个视图的面积一样大C．主视图的面积最小C．左视图的面积最小D．俯视图的面积最小8．(湖州中考)如图是按1∶10的比例画出的一个几何体的三视图，则该几何体的侧面积是(D)A．200 cm2B．600 cm2C．100πcm2D．200πcm29．(河北模拟)如图是一个长方体的三视图(单位：cm)，根据图中数据计算这个长方体的体积是24cm3.10．如图是某几何体的展开图．(1)这个几何体的名称是圆柱；(2)画出这个几何体的三视图；(3)求这个几何体的体积．(π取3.14)解：(2)三视图为：(3)体积为πr2h≈3.14×52×20＝1 570.02中档题11．(呼和浩特中考)一个几何体的三视图如图所示，则该几何体的表面积为(D)A．4πB．3πC．2π＋4 D．3π＋412．(呼和浩特中考)如图是某几何体的三视图，根据图中数据，求得该几何体的体积为(B)A．60πB．70πC．90πD．160π13．(滨州中考)如图，一个几何体的三视图分别是两个矩形、一个扇形，则这个几何体表面积的大小为15π＋12．解析：由三视图可以看出这是一个残缺的圆柱，侧面是由一个曲面和两个长方形构成，上下底面是两个扇形，S 侧＝34×2π×2×3＋2×3＋2×3＝9π＋12，S 底面＝2×34×π×22＝6π.所以这个几何体的表面积为15π＋12.14．(石家庄四十二中一模)由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示．方格中的数字表示该位置的小立方块的个数．(1)请在下面方格纸中分别画出这个几何体的主视图和左视图．(2)根据三视图，请你求出这个组合几何体的表面积(包括底面积)．解：(1)如图．(2)几何体的表面积为：(3＋4＋5)×2＝24.15．如图是某工件的三视图，求此工件的全面积．解：由三视图可知，该工件是底面半径为10 cm ，高为30 cm 的圆锥． 圆锥的母线长为302＋102＝1010(cm )，圆锥的侧面积为12×20π×1010＝10010π(cm 2)， 圆锥的底面积为102×π＝100π(cm 2)，圆锥的全面积为100π＋10010π＝100(1＋10)π(cm 2)．03 综合题16．如图是一个几何体的三视图(单位：厘米)．(1)写出这个几何体的名称；(2)根据图中数据计算这个几何体的表面积；(3)如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC的中点D，请你求出这个线路的最短路程．解：(1)圆锥．(2)S表＝S扇形＋S圆＝πrl＋πr2＝12π＋4π＝16π(平方厘米)．(3)如图，将圆锥侧面展开，线段BD为所求的最短路程．由条件得，∠BAB′＝120°，∵C为弧BB′的中点，AB＝6厘米，∴BD＝33厘米．。

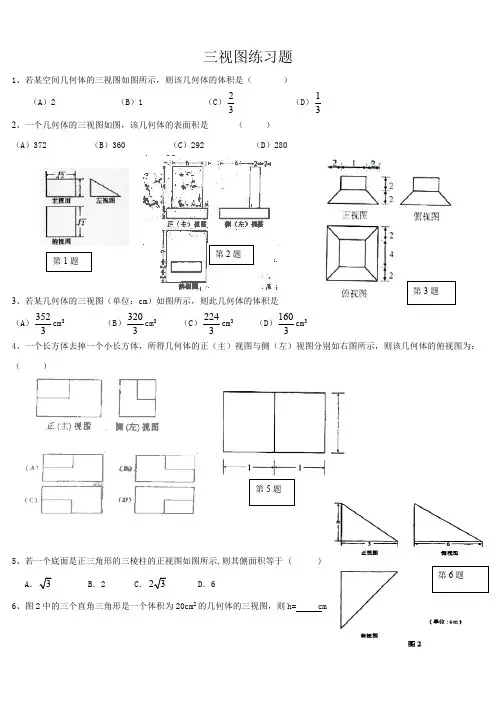
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

三视图习题50道(含答案)三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（ ）（A ）2 （B ）1 （C ）23 （D ）132、一个几何体的三视图如图，该几何体的表面积是 （ ） （A ）372 （B ）360 （C ）292 （D ）2803、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 （A ）3523cm 3（B ）3203cm3（C ）2243cm 3（D ）1603cm 34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（ ）第1第2第35、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面．．积．等于 ( )A．3 B．2 C．23 D．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.第69、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B.423π+ C. 2323π+ D. 2343π+22侧22 2 正俯第俯视图 正(主)视图 侧(左)视图 2 3 22 第1111、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A．9πB．10πC．11πD．12π12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c2m）为（）（B）48+24（C）36+12（A）48+1213、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是3cm．14、设某几何体的三视图如上图所示。

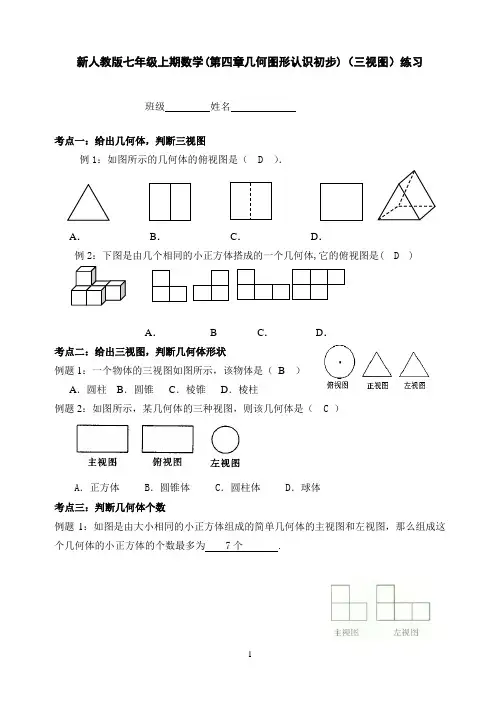
新人教版七年级上期数学(第四章几何图形认识初步)（三视图）练习班级姓名考点一：给出几何体，判断三视图例1：如图所示的几何体的俯视图是（ D ）．A．B．C．D．例2：下图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( D )A． B C．D．考点二：给出三视图，判断几何体形状例题1：一个物体的三视图如图所示，该物体是（B ）A．圆柱B．圆锥C．棱锥D．棱柱例题2：如图所示，某几何体的三种视图，则该几何体是（ C ）A．正方体 B．圆锥体 C．圆柱体 D．球体考点三：判断几何体个数例题1：如图是由大小相同的小正方体组成的简单几何体的主视图和左视图，那么组成这个几何体的小正方体的个数最多为 7个 .例题2：下图是由几个相同的小正方体搭成的几何体的三视图， 则搭成这个几何体的小正方体的个数是 （ A ）A ．5B ．6C ．7D ．8考点四：只给出俯视图，并根据俯视图上的数字画出它的主视图、左视图。

例题：如图，是由正方形搭成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数。

请你画出它的主视图和左视图。

解：俯视图主视图 左视图试一试，练一练1. 下面简单几何体的左视图是( )．2. 如图所示，右面水杯的俯视图是( )3、如图(1)放置的一个机器零件，若从正面看是如图(2)，则其左面看是（ ）4. 图所示的物体，从左面看得到的图是（ ）5、如图所示是由四个相同的小正方体组成的立体图形，它的俯视图为（ ）A ．BC ．D ．6、如图2，这是一个正三棱柱，则从上面看到的图为（ ）7、如图是由七个相同的小正方体堆成的物体，从上面看这个物体的图是（ ）8、由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数 ( ) A 、6个 B 、7个 C 、8个 D 、9个主视图 左视图 俯视图9、如图1，是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的主视图是 （ ）图11112A B C D10．下面是一些立体图形的三视图（如图），•请在括号内填上立体图形的名称．11．如图，从不同方向看下面左图中的物体，右图中三个平面图形分别是从哪个方向看到的？12．一个由几个相同的小立方体搭成的几何体的俯视图如图所示，方格里的数字表示该位置的小立方体的个数，请你画出这个几何体的主视图和左视图．13．由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图的方格中的字母和数字表示该位置上小立方体的个数，求x，y的值．。

截面与三视图（讲义）课前预习1.制作一个长方体的土豆块，试着切一刀，观察切出的面是什么形状．再换一种切法，看能否切出不同形状的面．下面是几种不同的切法，请你观察切出的面形状分别是什么，并填在对应的横线上．2.我们知道从不同的角度观察同一个物体时，可能会看到不同形状的图形，如图，桌面上放着一个圆柱体和一个三棱锥，请说出下面的三幅图分别是从“上面”、“正面”、“左面”中哪个方向看到的？知识点睛1.正方体截面有．2.观察一个几何体的形状通常从三个方向看，从正面看（主视图），从左面看（左视图），从上面看（俯视图）．从正面看可以看到物体的和；从左面看可以看到物体的和；从上面看可以看到物体的和．精讲精练1.圆柱体截面的形状可能是（至少写出两个）．2.用一个平面去截：①圆锥；②圆柱；③球；④五棱柱，能得到截面是圆的几何体是（）A．①②④ B．①②③ C．②③④D．①③④3.如图所示，用一个平面去截一个圆柱，则截得的形状应为（）A．B．C．D．4.圆锥的截面不可能为（）A．三角形 B．四边形 C．圆 D．椭圆5.如图所示，用一个平面沿与棱平行的方向去截一个棱柱，则截面的形状是．6.正方体的截面不可能是（）A．四边形B．五边形C．六边形D．七边形7.写出两个三视图形状都一样的几何体：．8.一个直立在水平面上的圆柱的主视图、俯视图、左视图分别是（）A．长方形、圆、长方形B．长方形、长方形、圆C．圆、长方形、长方形D．正方形、长方形、圆9. 如图，该物体的俯视图是（ ）A ．B ．C ．D ．10. 下图是由 7 个完全相同的小立方块搭成的几何体，那么这个几何体的左视图是（ ）A ．B ．C ．D ．1. 下图是由五块积木搭成的几何体，这几块积木都是相同的立方块，请画出这个几何体的主视图、左视图和俯视图．12. 下图是由五块积木搭成的几何体，这几块积木都是相同的立方块，请画出它的三视图．13. 如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，请你画出它的主视图与左视图．2 3 1 2 414. 如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，请你画出它的主视图与左视图．15. 如图是由一些相同的小立方块构成的几何体的三视图，那么构成这个立体图形的小立方块有（ ） A ．4 个 B ．5 个 C ．6 个D ．7 个主视图左视图俯视图16. 如图是由一些相同的小立方块构成的几何体的三视图，那么构成这个立体图形的小立方块有（ ） A ．4个 B ．5 个 C ．6 个D．7 个主视图左视图俯视图17.用小立方块搭一几何体，使得它的主视图和俯视图如图所示， 这样的几何体最多要 个立方块，最少要 个立方块．主视图俯视图18. 如图是一个由若干个相同的小立方块组成的几何体的主视图和俯视图，则能组成这个几何体的小立方块的个数最多是个，最少是个．主视图 俯视图19. 用小立方块搭成的几何体，主视图和俯视图如下．它最多需要多少个小立方块？最少需要多少个小立方块？请画出最多和最少时的左视图．主视图俯视图20. 用小立方块搭成的几何体，主视图和俯视图如下．它最多需要多少个小立方块？最少需要多少个小立方块？请画出最多和最少时的左视图．主视图 俯视图21. 如图是由大小相同的小立方块组成的简单几何体的主视图和左视图，那么组成这个几何体的小立方块最多为 个．主视图 左视图2. 一个几何体是由一些大小相同的小立方块摆成的，其主视图和左视图如图所示，则组成这个几何体的小立方块最多是块．主视图左视图23. 一个几何体是由若干个相同的小立方块组成的，其主视图和左视图如图所示，则组成这个几何体需要的小立方块的个数最多是 块．24. 已知下图为一几何体的三视图：（1）写出这个几何体的名称；左视图（2）任意画出它的一种表面展开图；（3）若主视图的长为8 cm ，俯视图中圆的半径为 3 cm ，求这个几何体的表面积和体积．（结果保留 π）主视图：长方形左视图： 长方形俯视图：圆【参考答案】课前预习1.长方形平行四边形梯形三角形2.左面上面正面知识点睛1.三角形、四边形、五边形、六边形2.列数、层数行数、层数行数、列数精讲精练1.圆、长方形（答案不唯一，圆、长方形、椭圆任选两个即可）2. B3. B4. B5.长方形6.D7.球体、正方体8.A9. C10.A11.略12.略13.略14.略15. B16. B17. 13 918. 13 919.最多需要 8 个立方块，最少需要 7 个立方块，图略．20.最多需要 14 个立方块，最少需要 10 个立方块，图略．21. 722. 1023. 1324. （1）圆柱；（2）略；（3）表面积为(66π) cm2，体积为(72π) cm3．。

七年级数学截面与三视图（丰富的图形世界）基础练习试卷简介:全卷共8个选择题，5个填空题，1个大题，分值100分，测试时间30分钟。

本套试卷立足基础，主要考察了学生对特殊几何体的截面与三视图基础知识及基本运用的掌握。

各个题目难度有阶梯性，学生在做题过程中可以回顾本章知识点，认清自己对知识的掌握及灵活运用程度。

学习建议:本章主要内容是特殊几何体的截面与三视图的概念及运用，不仅是中考常考的内容之一，更是整个数学学科的重要内容之一。

本讲题目灵活多变，同学们可以在做题的同时体会截面与三视图在诸多方面的运用，并且关注问题的解决过程。

一、单选题(共8道，每道5分)1.用一个平面去截①圆锥；②圆柱；③球；④五棱柱，能得到截面是圆的图形是（）A.①②④B.①②③C.②③④D.①③④答案：B解题思路：空间几何体①②③的水平截面均为圆，④沿各种方向的截面都不是圆；答案为B易错点：对空间体的截面问题判断失误试题难度：三颗星知识点：截一个几何体2.如下图1所示，用一个平面去截一个圆柱，则截得的形状应为（）A.B.C.D.答案：B解题思路：圆柱沿水平方向的截面是圆，即A，而沿倾斜方向的截面图形是椭圆；答案为B 易错点：误将圆柱沿倾斜方向的截面图形判断为沿水平方向的截面图形试题难度：三颗星知识点：截一个几何体3.正方体的截面不可能是（）A.四边形B.五边形C.六边形D.七边形答案：D解题思路：平面与正方体的几个面相交就得到几边形，与四面相交是四边形，与五面相交是五边形，与六面相交是六边形，而正方体只有六个面，所以不可能是七边形；答案为D易错点：对正方体的各种截面掌握不全试题难度：三颗星知识点：截一个几何体4.一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是（）A.长方形、圆、长方形B.长方形、长方形、圆C.圆、长方形、长方形D.正方形、长方形、圆答案：A解题思路：对于圆柱体，主视图与左视图是一样的，都是长方形或正方形，而俯视图是一个圆；答案为A易错点：对三种视图概念的混淆试题难度：三颗星知识点：简单几何体的三视图5.下图是由7个完全相同的小立方块搭成的几何体，那么这个几何体的左视图是（）A.B.C.D.答案：A解题思路：从左边来看实际的物体，物体有两列，所以排除C、D两项，又因为从左边来看第一列能看到三个小正方体，所以答案为A易错点：对左视图概念的不理解试题难度：三颗星知识点：简单组合体的三视图6.如图是由一些相同的小正方体构成的立体图形的三种视图．那么构成这个立体图形的小正方体有（）A.4B.5C.6D.7答案：B解题思路：结合主视图和左视图在俯视图中标注数字来解决问题，如图：因此答案为B易错点：对三种视图之间关系的不理解试题难度：三颗星知识点：由三视图判断几何体7.下面几何体的截面图不可能是圆的是（）A.圆柱B.圆锥C.球D.棱柱答案：D解题思路：A、B、C的水平截面图形都是圆，而D的各种截面图形都不是圆；答案为D易错点：截面图概念的理解试题难度：三颗星知识点：截一个几何体8.正方体的各个侧面分别标上字母a，b，c，d，e，f；其中a在后面，b在下面，c在左面，则下列结论错误的是（）A.d在上面B.e在前面C.f在右面D.d在前面答案：D解题思路：由图可知，因为a在后面，b在下面，c在左面，所以容易判断，e在前面，d 在上面，f在右面；答案为：D易错点：正方体展开后各对面位置的判断试题难度：三颗星知识点：几何体的展开图二、填空题(共5道，每道8分)1.如图，是一个由若干个相同的小正方体组成的几何体的主视图和俯视图，则能组成这个几何体的小正方体的个数最少是______个.答案：9个解题思路：结合主视图，在俯视图中标注数字来解决问题，通过主视图可以知道俯视图中的第一列至少有一格中是3个小正方体，第二列中只能是一个，第三列中至少有一格中是2个小正方体，因此数量最少如图：易错点：对实际物体中小正方体数量的判断试题难度：三颗星知识点：由三视图判断几何体2.写出两个三视图形状都一样的几何体：______答案：球、正方体.解题思路：在常见的几何体中，球的三视图都是圆，正方体的三视图都是正方形；答案为：球、正方体.易错点：要求三视图的形状都一样试题难度：三颗星知识点：简单几何体的三视图3.用小立方块搭一几何体，使得它的主视图和俯视图如图所示，这样的几何体最少要______个立方块，最多要______个立方块.答案：9个，13个解题思路：结合主视图，在俯视图中标注数字来解决问题，通过主视图可以知道俯视图中的第一列至少有一格中是2个小正方体，第二列至少有一格中是3个小正方体，第三列中只能是一个，因此数量最少（如图1），数量最多（如图2）易错点：对实际物体中小正方体数量的判断试题难度：三颗星知识点：由三视图判断几何体4.如图是由大小相同的小正方体组成的简单几何体的主视图和左视图那么组成这个几何体的小正方体的个数最多为______.答案：7个解题思路：通过主视图和左视图将俯视图先画出来，通过主视图和左视图可知实际物体有两列，三行，又因为题目中求的是最多数量，因此图为：易错点：对实际物体中小正方体数量的判断试题难度：三颗星知识点：由三视图判断几何体5.如图所示，用一个平面沿与棱平行的方向去截一个棱柱，则截面的形状可能为______.答案：长方形解题思路：如题中的图，沿竖直方向的截面是长方形，但可以通过调整截面的角度，得到正方形，而正方形也是长方形的一种，所以答案为：长方形.易错点：通过对截面角度的调整，会得到不同的截面图形试题难度：三颗星知识点：截一个几何体三、作图题(共1道，每道20分)1.如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.答案：解题思路：假设俯视图是立在屏幕上的，则从下往上来看图的形状，即为主视图，因此第一列、第二列、第三列分别只能看到三个、两个、四个.易错点：错误判断主视图与左视图的形状试题难度：三颗星知识点：由三视图判断几何体。

学生做题前请先回答以下问题问题1：举出一个几何体，使得从正面、左面、上面看到的这个几何体的形状都一样，你能举出几种？问题2：观察一个几何体的形状通常从三个方向看，从正面看（主视图），从左面看（左视图），从上面看（俯视图），从正面看可以看到几何体的________和________；从左面看可以看到几何体的________和________；从上面看可以看到几何体的________和________．问题3：在利用三视图确定小木块个数时，数字一般标在________图上．截面与三视图（人教版）一、单选题(共16道，每道6分)1.用一个平面去截五棱柱，则截面不可能是( )A.三角形B.四边形C.五边形D.圆答案：D解题思路：五棱柱的面均为平面，面面相交得直线，而不可能成为曲线，圆是由曲线构成的，所以五棱柱的截面不可能是圆．故选D．试题难度：三颗星知识点：几何体的截面2.用一个平面去截如图所示的圆锥，得到的图形不可能是( )A. B.C. D.答案：C解题思路：如果用平面去截圆锥，平面过圆锥顶点时得到的截面图形是一个等腰三角形；如果不过顶点，且平面与底面平行，那么得到的截面就是一个圆；如果不与底面平行且与底面相交，得到就是选项A中的图形；不可能是C中的直角三角形．故选C．试题难度：三颗星知识点：几何体的截面3.用一个平面去截下面的几何体，所得截面是三角形，则这个几何体不可能为( )A. B.C. D.答案：B解题思路：选项A中：正方体的截面可能是三角形、四边形、五边形或六边形；选项B中：圆柱的截面可能是长方形、圆或椭圆，不可能出现三角形；选项C中：用平行于上下底面的平面就可截出三角形；选项D中：用经过顶点且垂直于底面的平面可截出三角形．因此以上几种几何体只有圆柱的截面不可能是三角形．故选B．试题难度：三颗星知识点：几何体的截面4.如图是一个用5个完全相同的小立方块搭成的几何体，那么这个几何体的主视图是( )A. B.C. D.答案：C解题思路：主视图是从正面看，可以看到列数和层数，此几何体有3列，第1列最高2层，第2列最高1层，第3列最高1层，所以主视图是C．试题难度：三颗星知识点：几何体的三视图5.如图是一个用6个完全相同的小立方块搭成的几何体，那么这个几何体的俯视图是( )A. B.C. D.答案：D解题思路：俯视图是从上面看，可以看到列数和行数，此几何体有3行3列，第1列3行，第2列1行，第3列1行，所以俯视图是D．试题难度：三颗星知识点：几何体的三视图6.如图是由几个相同的小立方块组成的一个几何体，它的左视图是( )A. B.C. D.答案：B解题思路：左视图是从左面看，可以看到行数和层数，此几何体有2行，第1行最多2层，第2行最多1层，所以左视图是B．试题难度：三颗星知识点：几何体的三视图7.主视图、左视图、俯视图分别是下列三个图形的物体是( )A. B.C. D.答案：D解题思路：主视图是从正面看，可以看到列数和层数；左视图是从左面看，可以看到行数和层数；俯视图是从上面看，可以看到列数和行数．因此在俯视图上标数字，表示此位置上小立方块的个数．从主视图可以看出该几何体的第1列最多有2层，第2列最多有1层，第3列最多有1层；从左视图可以看出该几何体的第1行最多有2层，第2行最多有1层，如图所示，故选D．试题难度：三颗星知识点：几何体的三视图8.某几何体的三种视图如图所示，则该几何体是( )A.三棱柱B.长方体C.圆锥D.圆柱答案：D解题思路：根据几何体的主视图和左视图都是长方形，俯视图是圆，可知这个几何体是圆柱．故选D．试题难度：三颗星知识点：几何体的三视图9.如图是一个由多个相同小立方块堆积而成的几何体的俯视图，图中所示数字为该位置小立方块的个数，则这个几何体的主视图是( )A. B.C. D.答案：C解题思路：俯视图是从上面看，可以看到列数和行数；主视图是从正面看，可以看到列数和层数．又由俯视图中的每个数字是该位置小立方块的个数，可得此几何体有3列，第1列最多有3层，第2列最多有3层，第3列最多有2层，如图所示，所以其主视图为：故选C．试题难度：三颗星知识点：几何体的三视图10.如图是由几个完全相同的小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置上小立方块的个数，则这个几何体的左视图是( )A. B.C. D.答案：A解题思路：俯视图是从上面看，可以看到列数和行数；左视图是从左面看，可以看到行数和层数．又由俯视图中的每个数字是该位置小立方块的个数，可得此几何体有2行，第1行最多有1层，第2行最多有2层，如图所示，故选A．试题难度：三颗星知识点：几何体的三视图11.如图所示是由一些相同的小正方体构成的几何体的三视图，则这些相同的小正方体的个数是( )A.3个B.4个C.5个D.6个答案：B解题思路：主视图是从正面看，可以看到列数和层数；左视图是从左面看，可以看到行数和层数；俯视图是从上面看，可以看到列数和行数．因此在俯视图上标数字，表示此位置上小正方体的个数．由主视图可得该几何体有3列，第1列最多有1层，第2列最多有1层，第3列最多有2层；由左视图可得该几何体只有1行，且该行最多有2层，如图所示，因此小正方体一共有1+1+2=4（个）．故选B．试题难度：三颗星知识点：几何体的三视图12.如图所示是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体的个数是( )A.6个B.5个C.4个D.3个答案：C解题思路：主视图是从正面看，可以看到列数和层数；左视图是从左面看，可以看到行数和层数；俯视图是从上面看，可以看到列数和行数．因此在俯视图上标数字，表示此位置上小正方体的个数．由主视图可得该几何体有2列，第1列最多有2层，第2列最多有1层；由左视图可得该几何体有2行，第1行最多有1层，第2行最多有2层，如图所示，因此小正方体一共有1+2+1=4（个）．故选C．试题难度：三颗星知识点：几何体的三视图13.用小正方体搭建成的几何体，下面三个图分别是它的主视图、左视图和俯视图，那么构成这个几何体的小正方体有( )A.10个B.6个C.9个D.11个答案：A解题思路：主视图是从正面看，可以看到列数和层数；左视图是从左面看，可以看到行数和层数；俯视图是从上面看，可以看到列数和行数．因此在俯视图上标数字，表示此位置上小正方体的个数．如图，所以小正方体一共有2+1+3+2+1+1=10（个）．故选A．试题难度：三颗星知识点：几何体的三视图14.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数最少有( )A.4个B.5个C.6个D.7个答案：B解题思路：从俯视图可得该几何体是2行2列，从主视图可得第1列最多2层，第2列最多1层．当小正方体最少时（第1列只有一个为2），如图所示，所以小正方体的个数最少为1+1+1+2=5（个）．故选B．试题难度：三颗星知识点：由三视图求最多、最少问题15.如图是由一些大小相同的小正方体搭成的一个几何体的左视图和俯视图，则组成这个几何体的小正方体的个数最多有( )A.5个B.6个C.8个D.9个答案：D解题思路：从俯视图中可得该几何体是3行3列，从左视图可得第1行最多有1层，第2行最多有2层，第3行最多有1层，当小正方体最多时，如图所示，因此小正方体的个数最多有1+1+2+2+2+1=9（个）．故选D．试题难度：三颗星知识点：由三视图求最多、最少问题16.用小正方体积木搭出一个主视图和俯视图如图所示的几何体，它最多需要( )个小正方体积木．A.8B.9C.10D.11答案：B解题思路：从俯视图可得该几何体是3行3列，从主视图可得第1列最多3层，第2列最多1层，第3列最多1层．当小正方体最多时，如图所示，因此小正方体积木的个数最多有3+3+1+1+1=9（个）．故选B．试题难度：三颗星知识点：由三视图求最多、最少问题第11页共11页。

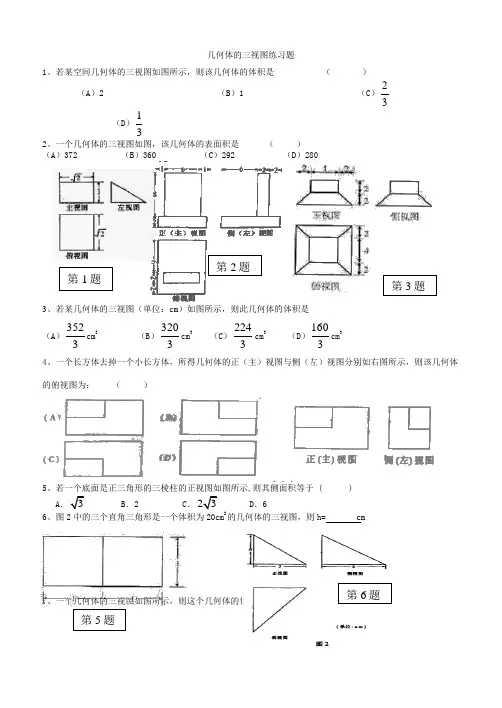
几何体的三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是 （ ） （A ）2（B ）1（C ）23（D ）132、一个几何体的三视图如图，该几何体的表面积是 （ ） （A ）372 （B ）360 （C ）292 （D ）2803、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 （A ）3523cm 3（B ）3203cm 3（C ）2243cm 3（D ）1603cm 34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为： （ ）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( ) A ．3 B ．2 C ．23 D ．66、图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h= cm7、一个几何体的三视图如图所示，则这个几何体的体积为 。

第1题第2题第3题第5题第6题8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,则该几何体 的体积为( ). A.223π+ B. 423π+C. 2323π+D. 2343π+11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ） A ．9πB ．10πC ．11πD ．12π12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （ ）（A ）48+122 （B ）48+242 （C ）36+122 （D ）36+24213、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．第7题第8题2 2侧(左)视2 22 正(主)视俯视第10俯视图 正(主)视图 侧(左)视图2 32 2第1114、设某几何体的三视图如上图所示。

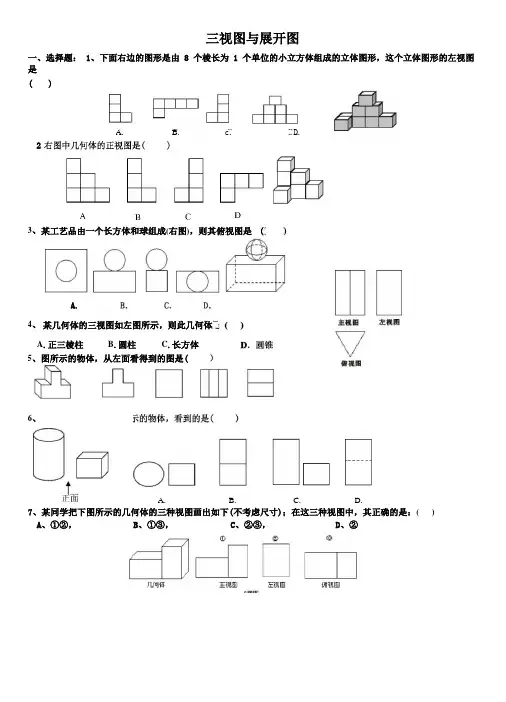
一、选择题： 1、下面右边的图形是由 8 个棱长为 1 个单位的小立方体组成的立体图形，这个立体图形的左视图是( )7、某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸)；在这三种视图中，其正确的是：( )A 、①②，B 、①③，C 、②③，D 、② 三视图与展开图3、 4、 A. B. c. 某工艺品由一个长方体和球组成(右图)，则其俯视图是 (6、C . D.某几何体的三视图如左图所示，则此几何体A .正三棱柱B .圆柱C .长方体5、图所示的物体，从左面看得到的图是(2A.A .B . D .8、由若干个同样大小的正方体堆积成一个实物，不同侧面观察到如图8所示的投影图，则构成该实物的小正方体个13、如图是正方体的展开图，则原正方体相对两个面上的数字和最小的是（ ）.数为A. 6 ()B. 7C. 8D. 9 田田俯视图 左聊图 主视图9、某超市货架上摆放着“康师傅”红烧肉面，如图1是它们的三视图，则货架上的“康师傅”红烧肉面至少有A. 8 桶B. 9 桶C. 10 桶D.11 桶 10、 图2中几何体的正视图是（ ） 11、由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数A 、6个B 、7个C 、8个D 、9个俯视图 （第12题） 12、 A 、7如图是一些相同的小正方体构成的几何体的正视图和左视图，在这个几何体中，小正方体的个数不可能是（B 、8C 、9D 、10 A. 414、B. 6C. 7D.8 16、 下列几何体，正（主）视图是三角形的是俯视图主视图 左视图图1 主视图 左视图15、 右图所示是一个三棱柱纸盒，在下面四个图中，只有一个是这个纸盒的展开图，那么这个展开图是（如图所示，右面水杯的俯视图是（）A ．B ．C ．D ． 17、 有一实物如图所示，它的主视图是（ ） 1 O HE A B C D18、骰子是一种特别的数字立方体，它符合规则：相对两面的点数之和总是7.下面四幅图中可以折成符合规则的骰子 的是19、一个画家有14个边长为1m 的正方体，他在地面上把它们摆成如图所示的形式，然后他把露 出的表面都涂上颜色，那么被涂上颜色的总面积为（）A. 19m 2B. 21m 2C. 33m 2D. 34m 220、如图，以Rt△ABC 为直角边AC 所在直线为轴，将AABC 旋转一周所形成的几何体的俯视图是）21、下面的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是（ ）有6个大小相同的正方体搭成的几何体如图所示，则关于它的视图说法正确的是（ ）23、想一想：将左边的图形折成一个立方体，右边的四个立方体哪一个是由左边的图形折成的（）C 22、A 主视图的面积最大 C 俯视图的面积最大B 左视图的面积最大D 三个视图的面积一样大Be（A ） 回 （匚） 。

立体图形的截面与三视图【知识要点】1．截面：一个平面与一个几何体相交所截得的图形叫做截面．2．三视图：（1）主视图（2）左视图（3）俯视图三视图之间有什么关系？3．多边形：在平面内，由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形．三角形、四边形、五边形、六边形等都是多边形．【典型例题】# 例1 用一个平面去截一个正方体，可能出现哪些图形？请分别画出．# 例2 如果用一个平面截一个正方体的一个角，剩下的几何体有几个顶点、几条棱、几个面？# 例3桌子上放着一个长方体和圆柱(如下图)，说出下列三幅图分别是_____.# 例4 如图是11个小立方体搭成的几何体,从不同方向看几何体,分别画出它们的三种视图，并在小正方形内填上表示该位置的小正方体的个数.（1）（2）例5 如图，是由几个小正方体所搭成的两个几何体的俯视图.小正方形中的数字表示该位置小正方体的个数，请画出相应几何体的主视图和左视图．例6 用小方块搭成的一个几何体，从不同的方向观察得到三视图如下图，试确定该几何体用了多少块小方块．主视图左视图（1）（2）* 例7 如图所示的积木是由16块棱长为1cm的正方体堆积而成的，请求出它们的表面积.* 例8 用小立方块搭一几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中的字母表示在该位置小立方块的个数，请问：（1）a，b，c各表示几？（2）这个几何体最少由几个小正方块搭成？最多呢？（3）当d=e=1，f=2时，画出这个几何体的左视图.* 例9 如图：是由几个小立方体所搭的几何体的俯视图，小正方体中的数字表示该位置小正方体的个数，如果每个小正方体的棱长是1，求该几何体的表面积．** 思考：棱长为a的正方体，摆放成如下图所示的形状. （1）如果这一物体摆放三层，试求该物体的表面积：（2）依图中摆放方法类推，如果该物体摆放了上下20层，求该物体的表面积；（3）第n层，该物体的表面积是多少？初试锋芒姓名： 成绩：一：选择题：# 1、在下列立体图形中，不属于多面体的是（ ）A ．正方体B ．三棱柱C ．长方体D ．圆锥体# 2、下列图形中左视图和主视图不一样的图形是( )A ．C ．长方体B ．圆柱C ．圆锥D ．球# 3、如下图，是由几个小立方体块搭成的几何体，小正方形内的数字表示在该位置小立方块的个数，其主视图、左视图正确的是（ ）二：解答题：1、如右图是由小立方体搭成的几何体的俯视图，小立 方体的数字表示在该位置的小立方体的个数，请画出 它的主视图和左视图．2、如右图，是由小正方体块搭成的几何体的俯视图，小正方体中的数字是表示在该位置的小立方体块的个数，再根据左视图所提供的信息，求x,y的值，并画出主视图．* 3、如右图是由若干块小立方体积木堆成的实体,在这个基础上要把它堆成一个大立方体, 至少需要多少块立方体积木?大显身手姓名：成绩：# 1．截去四边形的一个角，剩余图形不可能是（）A．三角形; B．四边形;C．五边形; D．圆# 2．用一个平面去截一个几何体，如果截面的形状是圆，则这个几何体不可能是（）A．圆柱; B．圆锥;C．正方体; D．球3、正方体被一个平面所截，所得边数最多的多边形是（）A、四边形B、五边形C、六边形D、七边形4．用平面去截一个三棱柱，很容易截出一个三角形，你还能截出一个平行四边形吗？能截出一个梯形吗？能截出一个五边形吗？（借助下图进行分析，不必画出截面）5、一个平面去截一个几何体两次，一次所成截面是圆，另一次是等腰三角形，那么这个几何体是．6、如图是由一些相同的小正方体构成的主体图形的三种视图构成这个立体图形的小正方体的个数是（）A．3; B．4; C．5; D．67、观察图形，问：圆锥的三视图是（）A. 主视图和俯视图是三角形，侧视图是圆．B. 主视图和侧视图是三角形，俯视图是圆．C. 主视图和侧视图是三角形，俯视图是圆和圆心．D. 主视图和俯视图是三角形，侧视图是圆和圆心．8、观察长方体，判断它的三视图是（）A. 三个大小不一样的长方形，但其中有两个可能大小一样．B. 三个正方形．C. 三个一样大的长方形．D.两个长方形，一个正方形# 9、物体的形状如图所示，则此物体的俯视图是（）# 10、甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边，桌上一张纸上写着数字“9”，甲说他看到的是“6”，乙说他看到的是“”，丙说他看到的是“”，丁说他看到的是“9”，则下列说法正确的是( )A.甲在丁的对面，乙在甲的左边，丙在丁的右边B.丙在乙的对面，丙的左边是甲，右边是乙C.甲在乙的对面，甲的右边是丙，左边是丁D.甲在丁的对面，乙在甲的右边，丙在丁的右边11、如图，是由一些相同的小正方体构成的立体图形的三视图这些小正方体的个数是（）A 4B 5C 6D 7主视图左视图俯视图# 12、下面是用几个小正方体搭成的四种几何体，分别画出它们的三视图．13.由几个小立方体组成的几何体的俯视图如右图所示，小正方形中的数字和字母表示叠在该位置上的小立方块的个数.根据主视图求出y x ,的值并说明你的理由.14. 如图是一个立体图形的三视图,这个立体图形是由一些相同的小正方形搭成的,这些小正方的个数为( ) A 6 B 7 C 8 D 9# 15.如图1-4-16是小明用八块小正方体搭的积木，该几何体的俯视图是（ ）x 3 2 y 俯视图主视图 左视图 主视图 俯视图16.作出如下图所示立体图形的三视图.* 17. 把一个正方体截去一个角剩下的几何体最多有（ ）A ．4个面B ．5个面C ．6个面D ．7个面* 18.一个球的内部挖去一个最大的正方体（正方体的八 个顶点都在球的表面上），用一个平面去截这个几何体， 是截面形状的有（ ）* 19.一个画家有14个边长为1的正方体，他在地 上把它们摆成如下图所示的形式，然后他把露出的 表面涂上颜色，求：涂上颜色的表面积．A ．1个B ．2个C ．3个D ．4个。

2019年七年级数学上册图形认识三视图 A卷一、选择题1、“2019年平昌冬季奥运会”的颁奖台如图所示，它的俯视图是（）A． B． C． D．2、下图中的图形绕虚线旋转一周，可得到的几何体是（）A． B． C． D．3、如图是由相同小正方体组成的立体图形，它的左视图为（）A． B． C． D．4、如图，将甲乙丙丁四个小正方形中的一个剪掉，使余下的部分不能围成一个正方体，剪掉的这个小正方形是（）A．甲 B．乙 C．丙 D．丁5、如图，是由若干个相同的小立方体搭成的几何体的俯视图和左视图．则小立方体的个数可能是（）A．5或6 B．5或7 C．4或5或6 D．5或6或76、如图是用八块完全相同的小正方体搭成的几何体，从左面看几何体得到的图形是（）A． B． C． D．7、如图所示的几何体的俯视图是（）A． B．C．D．8、下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是（）A． B． C．D．9、如图是由若干小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是（）A． B．C．D．10、如图，小桥用黑白棋子组成的一组图案，第1个图案由1个黑子组成，第2个图案由1个黑子和6个白子组成，第3个图案由13个黑子和6个白子组成，按照这样的规律排列下去，则第8个图案中共有个黑子．A. 37B. 42C. 73D. 121二、填空题11、如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，应剪去（填序号）.12、如图是由棱长相等的小立方体摆成的几何体的主视图与俯视图，根据视图可以判断组成这个几何体至少要个小立方体.13、一个几何体的主视图和俯视图如图所示，若这个几何体最多有m个小正方体组成，最少有n个小正方体组成，m+n= ．14、如图所示的某种玩具是由两个正方体用胶水粘合而成的，它们的棱长分别为1分米和3分米，为了美观，现要在其表面喷涂油漆，已知喷涂1平方分米需用油漆3克，那么喷涂这个玩具共需油漆克．15、一个零件的主视图、左视图、俯视图如图所示（尺寸单位：厘米），这个零件的体积为立方厘米。

截面与三视图（讲义）一、知识点睛1.正方体截面有____________________________________．2.从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成____________个三角形．3.n边形的内角和为________________．4.几何体的三视图有_________，__________，___________．主视图可以看到___________和______________；左视图可以看到___________和______________；俯视图可以看到___________和______________．二、精讲精练1.圆柱体的截面的形状可能是____________（至少写出两个）．2.用一个平面去截：①圆锥；②圆柱；③球；④五棱柱，能得到截面是圆的几何体是（）A．①②④B．①②③C．②③④D．①③④3.如图所示，用一个平面去截一个圆柱，则截得的形状应为（）A．B．C．D．4.如图所示，用一个平面沿与棱平行的方向去截一个棱柱，则截面的形状是．5.正方体的截面不可能是（）A．四边形B．五边形C．六边形D．七边形6.从多边形的一个顶点出发，分别连接这个顶点与其余各个顶点，可以把五边形分割成3个三角形，把六边形分割成4个三角形，…，如果是十二边形，可以分割成个三角形．7.一个多边形的内角和为1 800°，则它是_____________边形．8.从一个多边形的某个顶点出发，分别连接这个顶点和其余各顶点，可以把这个多边形分割成5个三角形，则这个多边形的边数为，这个多边形的内角和为___________．9.从多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2 012个三角形，则这个多边形的边数为（）A．2 011 B．2 012 C．2 013 D．2 01410.写出两个三视图形状都一样的几何体：________________．11.一个直立在水平面上的圆柱的主视图、俯视图、左视图分别是（）A．长方形、圆、长方形B．长方形、长方形、圆C．圆、长方形、长方形D．正方形、长方形、圆12.如图，该物体的俯视图是（）A．B．C．D．13.下图是由7个完全相同的小立方块搭成的几何体，那么这个几何体的左视图是（）A．B．C．D．14.下图是由五块积木搭成的几何体，这几块积木都是相同的正方体，请画出这个几何体的主视图、左视图和俯视图．15.下图是由五块积木搭成的几何体，请画出它的三视图．16. 如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，请你画出它的主视图与左视图．4213217. 如图，这是一个由小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数，请你画出它的主视图与左视图．31121118. 如图是由一些相同的小正方体构成的几何体的三视图，那么构成这个立体图形的小正方体有（ ） A ．4个 B ．5个 C ．6个 D ．7个19. 如图是由一些相同的小正方体构成的几何体的三视图，那么构成这个立体图形的小正方体有（ ） A ．4个 B ．5个 C ．6 个 D ．7个20. 用小立方块搭一几何体，使得它的主视图和俯视图如图所示，这样的几何体最多要_______个立方块，最少要______个立方块．左视图主视图俯视图主视图左视图俯视图主视图俯视图21.如图是一个由若干个相同的小正方体组成的几何体的主视图和俯视图，则能组成这个几何体的小正方体的个数最多是________个，最少是________个．主视图俯视图22.用小立方块搭成的几何体，主视图和俯视图如下，问这样的几何体有多少可能？它最多需要多少个小立方块，最少需要多少个小立方块，请画出最多和最少时的左视图．主视图俯视图23.如图是由大小相同的小正方体组成的简单几何体的主视图和左视图，那么组成这个几何体的小正方体的个数最多为_____________个．左视图主视图24.一个几何体是由一些大小相同的正方体摆成的，其主视图和左视图如图所示，则组成这个几何体的小正方体最多是________块．25.一个几何体是由若干个相同的小正方体组成的，其主视图和左视图如图所示，则组成这个几何体需要的小正方体的个数最多是________块．主视图左视图26.已知下图为一几何体的三视图：（1）写出这个几何体的名称；（2）任意画出它的一种表面展开图；（3）若主视图的长为10cm，俯视图中正方形的边长为4cm，求这个几何体的侧面积和体积．主视图：长方形左视图：长方形俯视图：正方形27.已知下图为一几何体的三视图：（1）写出这个几何体的名称；（2）任意画出它的一种表面展开图；（3）若主视图的长为8cm，俯视图中圆的半径为3cm，求这个几何体的表面积和体积（结果保留π）．主视图：长方形左视图：长方形俯视图：圆三、回顾与思考__________________________________________________________ __________________________________________________________ ______________________【参考答案】一、知识点睛1.三角形、四边形、五边形、六边形．2.(n-2)3.(n-2)×180°4.主视图，左视图，俯视图；层数，列数；层数，行数；行数，列数二、精讲精练1.圆，长方形（或矩形）2. B3. B4.长方形5. D6.107.十二8.7，900°9. C10.球、正方体11.A12.C13.A14.略15.略16.略17.略18.B19.B20.13，921.13，922.这样的几何体有三种可能，最多需要8个立方块，最少需要7个立方块，图略．23.724.1025.1326.（1）四棱柱；（2）略；（3）侧面积为160cm2，体积为160cm3．27.（1）圆柱；（2）略；（3）表面积为66π(cm2)，体积为72π(cm3)．。

⎨54 ⎨⎪ 几何体与展开图（习题）例题示范例：已知一不透明的正方体的六个面上分别写着 1 至 6 六个数字， 如图是我们能看到的三种情况，那么 2，3，4 的对面数字分别是 ， ， .思路分析正方体六个面中，每一个面和四个面相邻，和一个面相对．从图中出现次数最多的面找起，先找出和它相邻的面，进而确定和它相对的面．具体操作如下： 3 1 相 对 面 261 2 3 4 5相对面6所以，剩余的“4”和“5”是相对面． 巩固练习1.将如图所示的直角梯形绕直线 l 旋转一周，得到的几何体是（ ）lA ．B ．C ．D ．2. 下列立体图形中，有五个面的是（ ）A ．四棱锥B ．五棱锥C ．四棱柱D ．五棱柱3.下列说法中，正确的是（ ）A ．棱柱的侧面可以是三角形B ．棱柱的各条棱都相等C ．正方体的各条棱都相等D ．六个大小一样的正方形所拼成的图形是正方体的表面展开图1 345316 154.如图是正方体的表面展开图，每一个面标有一个汉字，则与“和”相对的面上的字是（ ） A ．构B ．建C ．社D ．会第 4 题图第 5 题图第 6 题图5.一个正方体的每个面上都写着一个汉字，其表面展开图如图所示，那么在该正方体中，与“享”相对的面上的字是（ ） A ．众 B ．视 C ．在 D ．频 6.一个正方体的表面展开图如图所示，每一个面上都写有一个数，并且相对两个面上所写的两个数之和都相等，那么（ ） A ．a =3，b =5 B ．a =5，b =7 C ．a =3，b =7 D ．a =5，b =6 7.如图，下列四个图形折叠后，能得到如图所示正方体的是 （ ）A ．B ．C ．D ．8.骰子是一种特殊的数字立方体，它符合规则：相对两面的点数之和总是 7，下面四幅图中可以折成符合规则的骰子的是 （ ）A ．B ．C ．D ．在众享 线视 频68 4 b 5 a③ ① ②① ② ③①②③③② ①③ ② ①9.快速旋转一枚竖立的硬币（假定旋转轴在原地不动），旋转形成的几何体是 .10. 正方体有 个顶点，经过每个顶点有条棱．11. 长方体有个顶点，有条棱，有个面，这些面的形状都是.12. （1）三棱锥有条棱，十棱柱有条棱；（2） 棱锥有 30 条棱， 棱柱有 60 条棱；（3）一个棱锥的棱数是 10，则这个棱锥的面数是 ．13. 表面展开图如图所示的几何体是．第 13 题图第 14 题图14. 若要使得图中表面展开图折叠成正方体后，相对面上的两个数之和为 10，则 xyz =_．15. 一个正方体六个面上分别写着 1，2，3，4，5，6，从三个不同角度看正方体如图所示，请判断：1 对面的数字是，2 对面的数字是 ，3 对面的数字是．16. 一个正方体的六个面分别标上 1，2，3，4，5，6 这六个数字， 从三个不同角度看正方体如图所示，那么标有数字 2 的面的对面数字是．2 3x y z 96 142315 345 461625 31l10 711思考小结1. 图形都是由、 、组成，而我们在研究 一个几何体的过程中，往往是按照 、 、的顺序来进行的． 2. 如图是一个直角三角形，现将它绕直线 l 旋转，则旋转后可以得到一个圆锥的是图．ll①②③3. 将一个正方体的表面沿某些棱剪开，展成一个平面图形，你剪开了条棱，你是怎样思考的？4. 一个正方体的六个面上写着六个连续的整数，且相对面上的两个数之和相等，如图所示，你能看到的数为 7，10，11，则六个整数的和为（ ） A ．51 B ．52 C ．57D ．58【参考答案】例题示范1，6，5巩固练习1.D2.A3. C4.D5.D6. C7.A8. C9.球体10. 8，311. 8，12，6，长方形12. （1）6，30；（2）十五，二十；（3）613. 三棱柱14. 5615. 5，4，616. 5思考小结1. 点，线，面；面，棱，顶点2. ①②3.7，正方体表面展开图中有六个面，被 5 条棱连着，正方体共12 条棱，5 条连接各面，因此剪开的棱有 7 条．4. C。

人教版2018年七年级数学上册图形认识三视图 B卷含答案2019年七年级数学上册图形认识三视图 B卷一、选择题:1、将下列平面图形绕轴旋转一周，可得到图中所示的立体图形是A． B． C． D．2、将两个长方体如图放置，则所构成的几何体的左视图可能是（）A． B． C．D．3、如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面，与“友”相对的面上的汉字是（）A.爱 B．国 C．诚D．善A． B． C．D．9、在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能是下列数中的（）A．5 B．4 C．3 D．1 10、将图①中的正方形剪开得到图②，图②中共有个正方形；将图②中一个正方形剪开得到图③，图③中共有个正方形；将图③中一个正方形剪开得到图④，图④中共有个正方形…如此下去，则第个图中共有正方形的个数为（）.A．20 B．22 C．24 D．26二、填空题:11、一个几何体是由一些大小相同的小立方块摆成的，如下图是从正面、左面、上面看这个几何体得到的平面图形，那么组成这个几何体所用的小立方块的个数是__________．12、如图是由一些大小相同的小正方体搭成的几何体的主视图和俯视图，则搭成该几何体的小正方体最多是___个．13、一个几何体的三视图如图，根据图示的数据计算该几何体的全面积为__________(结果保留π)．14、如图，要使图中平面展开图按虚线折叠成正方体后，相对面上两个数之和为0，则x－2y= ．15、如图，下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么黄色的对面是．16、．如图，观察下列图案，它们都是由边长为1cm 的小正方形按一定规律拼接而成的，依此规律，则第16个图案中的小正方形有个．三、解答题：17、如图是由一些棱长都为1cm的小正方体组合成的简单几何体．（1）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；（2）如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加块小正方体．18、如图①是一个组合几何体，右边是它的两种视图. （1）在右边横线上填写出两种视图名称；（2）根据两种视图中尺寸（单位：cm），计算这个组合几何体的表面积．（π取3.14）19、如图是一个正方体盒子的侧面展开图，该正方体六个面上分别标有不同的数字，且相对两个面上的数字是一对相反数.（1）请把－10，8，10，－3，－8，3分别填入六个小正方形中.（2）若某相对两个面上的数字分别满足关系式，求20、用小立方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体只有一种吗？它最多需要多少个小立方体？它最少需要多少个小立方体？请你画出这两种情况下的左视图．21、（1）由大小相同的小立方块搭成的几何体如图1，请在图2的方格中画出该几何体的俯视图和左视图．（2）用小立方体搭一几何体，使得它的俯视图和左视图与你在图2方格中所画的一致，则这样的几何体最少要个小立方块，最多要个小立方块．22、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式请你观察下列几种简单多面体模型，解答下列问题：（1）根据上面多面体的模型，完成表格中的空格：多面体顶点数（V）面数（F）棱数（E）四面体 4 4长方体8 6 12正八面体8 12你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是；（2）一个多面体的棱数比顶点数大10，且有12个面，则这个多面体的棱数是；（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，每个顶点处都有3条棱，共有棱36条．若该多面体外表面三角形的个数比八边形的个数的2倍多2，求该多面体外表面三角形的个数．参考答案1、B2、C3、D4、D5、B．6、A7、C8、D9、D10、B11、8．12、713、24π14、615、答案为：绿色．16、136个．17、答案为：6．18、解：（1）主，俯；（2）表面积19、解：（1）前后两个面的数字符合要求即可（2）依题意得：解得：20、解：由主视图可知，它自下而上共有3列，第一列2个，第二列2个，第三列3个．由俯视图可知，它自左而右共有3列，第一列3个，第二列1个，第三列2个，从空中俯视的个数只要最底层有一个即可．因此，综合两图可知：这个几何体的形状不能确定；并且最多时为第一列有三个二层，第二列有一个二层，第三列有两个三层，共14个，其左视图如图1；最少时为第一列与第二列各有一个二层，第三列有一个三层，共10个，其左视图不唯一，共五种情况，如图2．21、(1)如图；(2)9；14．22、解：（1）根据题意得：四面体的棱数为6，正八面体顶点数为6，∵4+4﹣6=2，8+6﹣12=2，6+8﹣12=2，∴顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F﹣E=2；故答案为：6，6，V+F﹣E=2；（2）∵一个多面体的棱数比顶点数大10，且有12个面，∴这个多面体是十二面体，∴顶点数为20，∵V+F﹣E=2，∴棱数E=20+10=30；故答案为：30；（3）∵=36=E，V=24，V+F﹣E=2，∴F=14，设八边形的个数为y个，则三角形的个数为2y+2个，由题意得y+2y+2=14，解得：y=4，∴2y+2=10，答：该多面体外表面三角形的个数为10个．。

2截⾯与三视图（讲义及答案）截⾯与三视图（讲义）课前预习1.点动成____，线动成_____，⾯动成_____．⾯和⾯相交得到_____，线和线相交得到_____．2.正⽅体有_____个⾯，每个⾯都是_______；圆锥有____个⾯，底⾯形状是____，侧⾯是_______（填“平⾯”或“曲⾯”）；球有____个⾯，是_______．3.制作⼀个长⽅体的⼟⾖块，试着切⼀⼑，观察切出的⾯是什么形状．再换⼀种切法，看能否切出不同形状的⾯．下⾯是⼏种不同的切法，请你观察切出的⾯形状分别是什么，并填在下⾯对应的横线上．_________ _______ ________ ________4.我们知道从不同的⾓度观察同⼀个物体时，可能会看到不同形状的图形，如图：桌⾯上放着⼀个三棱锥和⼀个圆柱体，请说出下⾯的三幅图分别是从“上⾯”、“正⾯”、“左⾯”中哪个⽅向看到的？________ ________ ________知识点睛1.正⽅体截⾯有_______________________________________．2.从⼀个n边形的同⼀个顶点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成____________个三⾓形．3.n边形的内⾓和为________________．4.观察⼀个⼏何体的形状通常从三个⽅向看，从正⾯看（主视图），从左⾯看（左视图），从上⾯看（俯视图）．精讲精练1.圆柱体截⾯的形状可能是____________（⾄少写出两个）．2.⽤⼀个平⾯去截：①圆锥；②圆柱；③球；④五棱柱，能得到截⾯是圆的⼏何体是（）A．①②④B．①②③C．②③④D．①③④3.如图所⽰，⽤⼀个平⾯去截⼀个圆柱，则截得的形状应为（）A．B．C．D．4.圆锥的截⾯不可能为（）A．三⾓形B．四边形C．圆D．椭圆5.如图所⽰，⽤⼀个平⾯沿与棱平⾏的⽅向去截⼀个棱柱，则截⾯的形状是_______________．6.正⽅体的截⾯不可能是（）A．四边形B．五边形C．六边形D．七边形7.形分割成3个三⾓形，把六边形分割成4个三⾓形，…，如果是⼗⼆边形，可以分割成_____个三⾓形．8.⼀个多边形的内⾓和为1 800°，则它是_____________边形．9.从⼀个多边形的某个顶点出发，分别连接这个顶点和其余各顶点，可以把这个多边形分割成5个三⾓形，则这个多边形的边数为_________，这个多边形的内⾓和为___________．10.写出两个三视图形状都⼀样的⼏何体：________________．11.⼀个直⽴在⽔平⾯上的圆柱的主视图、俯视图、左视图分别是（）A．长⽅形、圆、长⽅形B．长⽅形、长⽅形、圆C．圆、长⽅形、长⽅形D．正⽅形、长⽅形、圆12.如图，该物体的俯视图是（）A．B．C．D．13.下图是由7个完全相同的⼩⽴⽅块搭成的⼏何体，那么这个⼏何体的左视图是（）A．B．C．D．14.下图是由五块积⽊搭成的⼏何体，这⼏块积⽊都是相同的⽴⽅块，请画出这个⼏何体的主视图、左视图和俯视图．15.下图是由五块积⽊搭成的⼏何体，这⼏块积⽊都是相同的⽴⽅块，请画出它的三视图．16.如图，这是⼀个由⼩⽴⽅块搭成的⼏何体的俯视图，⼩正⽅形中的数字表⽰该位置的⼩⽴⽅块的个数，请你画出它的主视图与左视图．4213217.如图，这是⼀个由⼩⽴⽅块搭成的⼏何体的俯视图，⼩正⽅形中的数字表⽰该位置的⼩⽴⽅块的个数，请你画出它的主视图与左视图．31121118.如图是由⼀些相同的⼩⽴⽅块构成的⼏何体的三视图，那么构成这个⽴体图形的⼩⽴⽅块有（）A．4个B．5个C．6个D．7个俯视图左视图主视图19. 如图是由⼀些相同的⼩⽴⽅块构成的⼏何体的三视图，那么构成这个⽴体图形的⼩⽴⽅块有（） A ．4个B ．5个C ．6个D ．7个20. ⽤⼩⽴⽅块搭⼀⼏何体，使得它的主视图和俯视图如图所⽰，这样的⼏何体最多要_____个⽴⽅块，最少要_____个⽴⽅块．俯视图主视图21. 如图是⼀个由若⼲个相同的⼩⽴⽅块组成的⼏何体的主视图和俯视图，则能组成这个⼏何体的⼩⽴⽅块的个数最多是________个，最少是________个．俯视图主视图22. ⽤⼩⽴⽅块搭成的⼏何体，主视图和俯视图如下．它最多需要多少个⼩⽴⽅块？最少需要多少个⼩⽴⽅块？请画出最多和最少时的左视图．俯视图主视图23. ⽤⼩⽴⽅块搭成的⼏何体，主视图和俯视图如下．它最多需要多少个⼩⽴⽅块？最少需要多少个⼩⽴⽅块？请画出最多和最少时的左视图．主视图俯视图24. 如图是由⼤⼩相同的⼩⽴⽅块组成的简单⼏何体的主视图和左视图，那么组成这个⼏何体的⼩⽴⽅块最多为________个．俯视图主视图左视图左视图主视图25. ⼀个⼏何体是由⼀些⼤⼩相同的⼩⽴⽅块摆成的，其主视图和左视图如图所⽰，则组成这个⼏何体的⼩⽴⽅块最多是________块．26. ⼀个⼏何体是由若⼲个相同的⼩⽴⽅块组成的，其主视图和左视图如图所⽰，则组成这个⼏何体需要的⼩⽴⽅块的个数最多是27. 已知下图为⼀⼏何体的三视图：（1）写出这个⼏何体的名称；（2）任意画出它的⼀种表⾯展开图；（3）若主视图的长为8 cm ，俯视图中圆的半径为3 cm ，求这个⼏何体的表⾯积和体积．（结果保留π）俯视图：圆左视图：长⽅形主视图：长⽅形截⾯与三视图（随堂测试）要点回顾1.正⽅体截⾯有_______________________________________．2.从⼀个n边形的同⼀个顶点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成____________个三⾓形．3.n边形的内⾓和为________________．4.观察⼀个⼏何体的形状通常从三个⽅向看，从正⾯看（_____图），从左⾯看（______图），从上⾯看（________图）．典型题测试1.⽤平⾯去截⼀个⼏何体，如果截⾯的形状是长⽅形，那么原来的⼏何体不可能是（）A．正⽅体B．棱柱C．圆柱D．圆锥2.如果从⼀个多边形的⼀个顶点出发，分别连接这个顶点与其余各顶点，可将这个多边形分割成2 015个三⾓形，那么此多边形的边数为__________．3.如图是由⼀些相同的⼩⽴⽅块构成的⼏何体的三视图，则构成这个⼏何体的⼩⽴⽅块有（）A．3个B．4个C．5个D．6个俯视图左视图主视图4.⽤⼩⽴⽅块搭成的⼏何体的主视图和俯视图如下．它最多需要多少个⼩⽴⽅块？最少需要多少个⼩⽴⽅块？请画出最多和最少时的左视图．主视图俯视图截⾯与三视图（习题）要点回顾1.⾯与⾯相交得到______，正⽅体只有______个⾯，因此它的截⾯边数不会超过________．2.在观察由⼩⽊块组成的⼏何体时，从正⾯看可以看到它的列数和层数，从左⾯看可以看到它的______和______；从上⾯看可以看到它的______和________．巩固练习1.⽤⼀个平⾯去截某⼀⼏何体，⽆论如何截，它的截⾯都是⼀个圆，则这个⼏何体是________.2.从n边形的⼀个顶点出发，分别连接这个点与其余各个顶点，得到7个三⾓形，则这个多边形为_________边形，这个多边形的内⾓和是__________．3.如图是由6个形状相同的⼩⽴⽅块搭成的⼀个⼏何体，则它的俯视图是（）A．B．C．D．4.如图是⼀个⽤5个⼩⽴⽅块搭成的⼏何体，请画出它的三视图．5.如图是⼀个⽤7个⼩⽴⽅块搭成的⼏何体，请画出它的三视图．6. 由⼩⽴⽅块搭成的⼏何体的俯视图如图所⽰，⼩正⽅形中的数字表⽰在该位置的⼩⽴⽅块的个数，请画出这个⼏何体的主视图和左视图．112117. 由⼩⽴⽅块搭成的⼏何体的俯视图如图所⽰，⼩正⽅形中的数字表⽰在该位置的⼩⽴⽅块的个数，请画出这个⼏何体的主视图和左视图．1121328. ⽤⼩⽴⽅块搭建成⼀个⼏何体，下⾯三个图分别是它的主视图、左视图和俯视图，那么构成这个⼏何体的⼩⽴⽅块有________个．俯视图左视图主视图9. ⽤⼩⽴⽅块搭⼀个⼏何体，使得它的主视图和俯视图如图所⽰，这样的⼏何体最多要______个⼩⽴⽅块，最少要_______个⼩⽴⽅块．主视图俯视图10. ⽤⼩⽴⽅块搭成的⼏何体的主视图和俯视图如图所⽰，它最多需要多少个⼩⽴⽅块？最少需要多少个⼩⽴⽅块？请画出最多和最少时的左视图．俯视图主视图11. ⼀个⼏何体是由若⼲个相同的⼩⽴⽅块组成的，其主视图和左视图如图所⽰，则这个⼏何体最多可由_________个⼩⽴⽅块组成．主视图左视图12. 如图是⼀个⼏何体的三视图，请写出这个⼏何体的名称，并计算这个⼏何体的表⾯积和体积．（结果保留π）俯视图主视图左视图思考⼩结1. ⽤⼀个平⾯截五棱柱，所得截⾯的边数最多是______．2. ⼀个⽴⽅体截去⼀个⾓以后，剩下的⼏何体有多少条棱？多少个⾯？多少个顶点？请根据图形，进⾏说明．图1图2图3图4如图1，有_______个⾯，______条棱，_______个顶点．如图2，有_______个⾯，______条棱，_______个顶点．如图3，有_______个⾯，______条棱，_______个顶点．如图4，有_______个⾯，______条棱，_______个顶点． 3. 在利⽤三视图确定⼩⽊块个数时，数字⼀般标在______图上．。