信号与系统_高等教育何子述版课件及答案

《信号与系统》ppt-2-5线性时不变系统的时域分析卷积的性质卷积成⽴的条件⼀个连续（离散）时间LTI 系统的特性完全由它的单位冲激（脉冲）响应来决定。

但是，单位脉冲响应不能完全表征⾮LTI 系统的特性。

卷积和（积分）成⽴的前提是系统是LTI 的。

下⾯讨论卷积积分的性质，卷积和也有同样的结论。

()2[][][1]y n x n x n =+-()[]max [],[1]y n x n x n =- 1 0,1[]0 n h n otherwise =?=??[][][1]y n x n x n =+-交换律交换律：⼀个单位冲激响应是的LTI 系统对输⼊信号所产⽣的响应，与⼀个单位冲激响应是的LTI 系统对输⼊信号所产⽣的响应相同。

()()()()()()()()()y t x t h t x h t d x t h d h t x t ττττττ∞-∞∞-∞=*=-=-=*?()h t ()h t ()x t ()x t分配律：两个LTI 系统并联，其总的单位脉冲(冲激)响应等于各⼦系统单位脉冲(冲激)响应之和。

*+=*+*x t h t h t x t h t x t h t ()[()()]()()()()1212有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）结合律：两个LTI 系统级联时，系统总的单位冲激(脉冲)响应等于各⼦系统单位冲激(脉冲)响应的卷积。

1212[()()]()()[()()]x t h t h t x t h t h t **=**这表明：两个LTI 系统级联的先后次序可以调换。

产⽣以上结论的前提条件：系统必须是LTI 系统；所有涉及到的卷积运算必须收敛。

1221()[()()]()[()()]x t h t h t x t h t h t **=**卷积的微分与积分微分：两个函数卷积后的微分等于其中⼀个函数的微分与另⼀个函数的卷积，即：如果，那么。

何子述信号与系统习题解答第5章拉普拉斯变换(2012新)何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!第5章拉普拉斯变换习题解答一、基本概念与基本运算习题题5.1 解：当f t u t 时，0能使信号g t 的傅里叶变换存在。

当f t u t 时，0能使信号g t 的傅里叶变换存在。

当f t 1时，找不到一个实数使信号g t f t e t绝对可积。

题5.2 解：（a）由拉普拉斯变换的定义式F(s) e 2tu t 1 e1j tdte 2te te j tdt1 s 2e, 2s 2（b）由拉普拉斯变换的定义式j ttδt12δt1eut1edt利用积分的分配律及单位冲激信号的筛选性，可得F s es 2e s ete te j tdt- 1e1 se 2e , 11 sss（c）由拉普拉斯变换的定义式F s e 2tsin 3t u t e-j tdte2tej3t e j3t t j teedt2j239, 2157何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!（d）由拉普拉斯变换的定义式F sf t ej tdtete te j tdt 20e 2te te j t 2dts 12s 2e2 11 es 1 s 2,（e）由拉普拉斯变换的定义式e 2t j tedt不存在使上式积分收敛，故信号f(t) e 2t的拉普拉斯变换不存在。

（f）由拉普拉斯变换的定义式F s2δ j tt δ t 2 e dt2 s2 se 2s,题5.3 解：（a）有拉普拉斯变换对e 2tu t L 1s 2, 2 e 4tu t L1s 4, 4由拉普拉斯变换的线性，信号f t 的拉普拉斯变换为f t L11s 2s 4, 4 2 零极点图如图J5.3.1所示。

（b）有拉普拉斯变换对e2tsin 5t u t Ls 2 225, 2δ t L1,由拉普拉斯变换的线性，信号f t 的拉普拉斯变换为f t L15s s2 4s 34s 2 s 2 2225s2 4s 29 s 2 j5s 2 j5,1582何子述老师2012年最新高等教育出版社出版《信号与系统习题解答》发布,对考研同学帮助极大!零极点图如图J5.3.2所示。

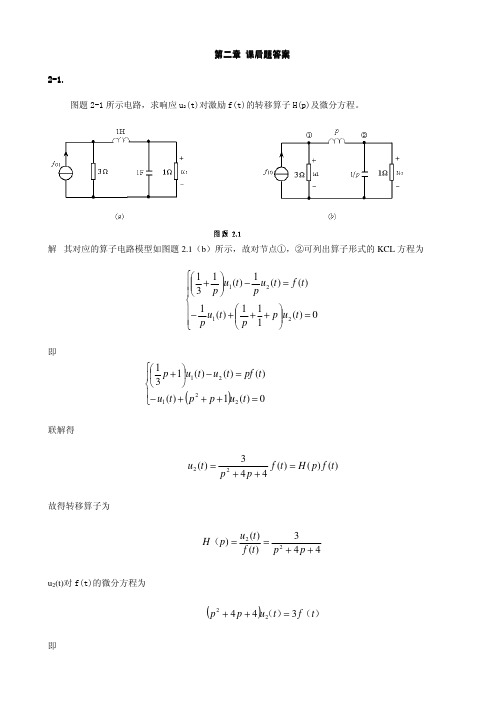
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路，求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图题2.1（b ）所示，故对节点①，②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H （u 2(t)对f(t)的微分方程为()）（）（t f t u p p 34422=++即）（t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。

解 其对应的算子电路模型如图2.2（b）所示。

故得）（）（t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路，已知u C (0-)=1 V, i(0-)=2 A。

求t>0时的零输入响应i(t)和u C (t)。

解 其对应的算子电路模型如图题2.3（b）所示。

故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根（即电路的自然频率）为p 1=-1，p 2=-2。