伍德里奇计量经济学第六版答案Chapter-10

伍德里奇计量经济学导论第6版笔记和课后答案
第1章计量经济学的性质与经济数据
1.1 复习笔记
考点一：计量经济学及其应用★
1计量经济学
计量经济学是在一定的经济理论基础之上，采用数学与统计学的工具，通过建立计量经济模型对经济变量之间的关系进行定量分析的学科。

进行计量分析的步骤主要有：①利用经济数据对模型中的未知参数进行估计；②对模型进行检验；③通过检验后，可以利用计量模型来进行相关预测。

2经济分析的步骤
经济分析是指利用所搜集的相关数据检验某个理论是否成立或估计某种关系的方法。

经济分析主要包括以下几步，分别是阐述问题、构建经济模型、经济模型转化为计量模型、搜集相关数据、参数估计和假设检验。

考点二：经济数据★★★
1经济数据的结构（见表1-1）
表1-1 经济数据的结构
2面板数据与混合横截面数据的比较（见表1-2）
表1-2 面板数据与混合横截面数据的比较
考点三：因果关系和其他条件不变★★
1因果关系
因果关系是指一个变量的变动将引起另一个变量的变动，这是经济分析中的重要目标之一。

计量分析虽然能发现变量之间的相关关系，但是如果想要解释因果关系，还要排除模型本身存在因果互逆的可能，
否则很难让人信服。

2其他条件不变
其他条件不变是指在经济分析中，保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

第12章时间序列回归中的序列相关和异方差性12.1复习笔记考点一：含序列相关误差时OLS 的性质★★★1．无偏性和一致性当时间序列回归的前3个高斯-马尔可夫假定成立时，OLS 的估计值是无偏的。

把严格外生性假定放松到E（u t ｜X t ）＝0，可以证明当数据是弱相关时，∧βj 仍然是一致的，但不一定是无偏的。

2．有效性和推断假定误差存在序列相关，即满足u t ＝ρu t－1＋e t ，t＝1，2，…，n，｜ρ｜＜1。

其中，e t 是均值为0方差为σe 2满足经典假定的误差。

对于简单回归模型：y t ＝β0＋β1x t ＋u t 。

假定x t 的样本均值为零，因此有：1111ˆn x t tt SST x u -==+∑ββ其中：21nx t t SST x ==∑∧β1的方差为：()()122221111ˆ/2/n n n t j xt t x x t t j t t j Var SST Var x u SST SST x x ---+===⎛⎫==+ ⎪⎝⎭∑∑∑βσσρ其中：σ2＝Var（u t ）。

根据∧β1的方差表达式可知，第一项为经典假定条件下的简单回归模型中参数的方差。

因此，当模型中的误差项存在序列相关时，OLS 估计的方差是有偏的，假设检验的统计量也会出现偏差。

3．拟合优度当时间序列回归模型中的误差存在序列相关时，通常的拟合优度指标R 2和调整R 2便会失效；但只要数据是平稳和弱相关的，拟合优度指标就仍然有效。

4．出现滞后因变量时的序列相关（1）在出现滞后因变量和序列相关的误差时，OLS 不一定是不一致的假设E（y t ｜y t－1）＝β0＋β1y t－1。

其中，｜β1｜＜1。

加上误差项把上式写为：y t ＝β0＋β1y t－1＋u t ，E（u t ｜y t－1）＝0。

模型满足零条件均值假定，因此OLS 估计量∧β0和∧β1是一致的。

误差{u t }可能序列相关。

虽然E（u t ｜y t－1）＝0保证了u t 与y t－1不相关，但u t－1＝y t －1－β0－β1y t－2，u t 和y t－2却可能相关。

第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★1计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。

2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。

根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。

(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。

②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。

③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。

考点二:经济数据★★★1经济数据的结构(见表1-3)2面板数据与混合横截面数据的比较(见表1-4)考点三:因果关系和其他条件不变★★1因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之计量分析虽然能发现变量之间的相关关系,但是如果想要解释因果关系,还要排除模型本身存在因果互逆的可能,否则很难让人信服。

2其他条件不变其他条件不变是指在经济分析中,保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

1.2课后习题详解一、习题1.假设让你指挥一项研究，以确定较小的班级规模是否会提高四年级学生的成绩。

(i)如果你能指挥你想做的任何实验，你想做些什么?请具体说明。

(ii)更现实地，假设你能搜集到某个州几千名四年级学生的观测数据。

你能得到它们四年级班级规模和四年级末的标准化考试分数。

你为什么预计班级规模与考试成绩成负相关关系?(iii)负相关关系一定意味着较小的班级规模会导致更好的成绩吗?请解释。

答:(i)假定能够随机的分配学生们去不同规模的班级，也就是说，在不考虑学生诸如能力和家庭背景等特征的前提下，每个学生被随机的分配到不同的班级。

第二篇时间序列数据的回归分析第10章时间序列数据的基本回归分析10.1 复习笔记考点一：时间序列数据★★1．时间序列数据与横截面数据的区别（1）时间序列数据集是按照时间顺序排列。

（2）时间序列数据与横截面数据被视为随机结果的原因不同。

（3）一个时间序列过程的所有可能的实现集，便相当于横截面分析中的总体。

时间序列数据集的样本容量就是所观察变量的时期数。

2．时间序列模型的主要类型（见表10-1）表10-1 时间序列模型的主要类型考点二：经典假设下OLS的有限样本性质★★★★1．高斯-马尔可夫定理假设（见表10-2）表10-2 高斯-马尔可夫定理假设2．OLS估计量的性质与高斯-马尔可夫定理（见表10-3）表10-3 OLS估计量的性质与高斯-马尔可夫定理3．经典线性模型假定下的推断（1）假定TS.6（正态性）假定误差u t独立于X，且具有独立同分布Normal（0，σ2）。

该假定蕴涵了假定TS.3、TS.4和TS.5，但它更强，因为它还假定了独立性和正态性。

（2）定理10.5（正态抽样分布）在时间序列的CLM假定TS.1～TS.6下，以X为条件，OLS估计量遵循正态分布。

而且，在虚拟假设下，每个t统计量服从t分布，F统计量服从F分布，通常构造的置信区间也是确当的。

定理10.5意味着，当假定TS.1～TS.6成立时，横截面回归估计与推断的全部结论都可以直接应用到时间序列回归中。

这样t统计量可以用来检验个别解释变量的统计显著性，F统计量可以用来检验联合显著性。

考点三：时间序列的应用★★★★★1．函数形式、虚拟变量除了常见的线性函数形式，其他函数形式也可以应用于时间序列中。

最重要的是自然对数，在应用研究中经常出现具有恒定百分比效应的时间序列回归。

虚拟变量也可以应用在时间序列的回归中，如某一期的数据出现系统差别时，可以采用虚拟变量的形式。

2．趋势和季节性（1）描述有趋势的时间序列的方法（见表10-4）表10-4 描述有趋势的时间序列的方法（2）回归中的趋势变量由于某些无法观测的趋势因素可能同时影响被解释变量与解释变量，被解释变量与解释变量均随时间变化而变化，容易得到被解释变量与解释变量之间趋势变量的关系，而非真正的相关关系，导致了伪回归。

CHAPTER 11TEACHING NOTESMuch of the material in this chapter is usually postponed, or not covered at all, in an introductory course. However, as Chapter 10 indicates, the set of time series applications that satisfy all of the classical linear model assumptions might be very small. In my experience, spurious time series regressions are the hallmark of many student projects that use time series data. Therefore, students need to be alerted to the dangers of using highly persistent processes in time series regression equations. (Spurious regression problem and the notion of cointegration are covered in detail in Chapter 18.)It is fairly easy to heuristically describe the difference between a weakly dependent process and an integrated process. Using the MA(1) and the stable AR(1) examples is usually sufficient.When the data are weakly dependent and the explanatory variables are contemporaneously exogenous, OLS is consistent. This result has many applications, including the stable AR(1) regression model. When we add the appropriate homoskedasticity and no serial correlation assumptions, the usual test statistics are asymptotically valid.The random walk process is a good example of a unit root (highly persistent) process. In a one-semester course, the issue comes down to whether or not to first difference the data before specifying the linear model. While unit root tests are covered in Chapter 18, just computing the first-order autocorrelation is often sufficient, perhaps after detrending. The examples in Section 11.3 illustrate how different first-difference results can be from estimating equations in levels. Section 11.4 is novel in an introductory text, and simply points out that, if a model is dynamically complete in a well-defined sense, it should not have serial correlation. Therefore, we need not worry about serial correlation when, say, we test the efficient market hypothesis. Section 11.5 further investigates the homoskedasticity assumption, and, in a time series context, emphasizes that what is contained in the explanatory variables determines what kind of hetero-skedasticity is ruled out by the usual OLS inference. These two sections could be skipped without loss of continuity.129130SOLUTIONS TO PROBLEMS11.1 Because of covariance stationarity, 0γ = Var(x t ) does not depend on t , so sd(x t+hany h ≥ 0. By definition, Corr(x t ,x t +h ) = Cov(x t ,x t+h )/[sd(x t )⋅sd(x t+h)] = 0/.h h γγγ=11.2 (i) E(x t ) = E(e t ) – (1/2)E(e t -1) + (1/2)E(e t -2) = 0 for t = 1,2, Also, because the e t are independent, they are uncorrelated and so Var(x t ) = Var(e t ) + (1/4)Var(e t -1) + (1/4)Var(e t -2) = 1 + (1/4) + (1/4) = 3/2 because Var (e t ) = 1 for all t .(ii) Because x t has zero mean, Cov(x t ,x t +1) = E(x t x t +1) = E[(e t – (1/2)e t -1 + (1/2)e t -2)(e t +1 – (1/2)e t + (1/2)e t -1)] = E(e t e t+1) – (1/2)E(2t e ) + (1/2)E(e t e t -1) – (1/2)E(e t -1e t +1) + (1/4(E(e t-1e t ) – (1/4)E(21t e -) + (1/2)E(e t-2e t+1) – (1/4)E(e t-2e t ) +(1/4)E(e t-2e t-1) = – (1/2)E(2t e ) – (1/4)E(21t e -) = –(1/2) – (1/4) = –3/4; the third to last equality follows because the e t are pairwise uncorrelated and E(2t e ) = 1 for all t . Using Problem 11.1 and the variance calculation from part (i),Corr(x t x t+1) = – (3/4)/(3/2) = –1/2.Computing Cov(x t ,x t+2) is even easier because only one of the nine terms has expectation different from zero: (1/2)E(2t e ) = ½. Therefore, Corr(x t ,x t+2) = (1/2)/(3/2) = 1/3.(iii) Corr(x t ,x t+h ) = 0 for h >2 because, for h > 2, x t+h depends at most on e t+j for j > 0, while x t depends on e t+j , j ≤ 0.(iv) Yes, because terms more than two periods apart are actually uncorrelated, and so it is obvious that Corr(x t ,x t+h ) → 0 as h → ∞.11.3 (i) E(y t ) = E(z + e t ) = E(z ) + E(e t ) = 0. Var(y t ) = Var(z + e t ) = Var(z ) + Var(e t ) + 2Cov(z ,e t ) = 2z σ + 2e σ + 2⋅0 = 2z σ + 2e σ. Neither of these depends on t .(ii) We assume h > 0; when h = 0 we obtain Var(y t ). Then Cov(y t ,y t+h ) = E(y t y t+h ) = E[(z + e t )(z + e t+h )] = E(z 2) + E(ze t+h ) + E(e t z ) + E(e t e t+h ) = E(z 2) = 2z σ because {e t } is an uncorrelated sequence (it is an independent sequence and z is uncorrelated with e t for all t . From part (i) we know that E(y t ) and Var(y t ) do not depend on t and we have shown that Cov(y t ,y t+h ) depends on neither t nor h . Therefore, {y t } is covariance stationary.(iii) From Problem 11.1 and parts (i) and (ii), Corr(y t ,y t+h ) = Cov(y t ,y t+h )/Var(y t ) = 2z σ/(2z σ + 2e σ) > 0.(iv) No. The correlation between y t and y t+h is the same positive value obtained in part (iii) now matter how large is h . In other words, no matter how far apart y t and y t+h are, theircorrelation is always the same. Of course, the persistent correlation across time is due to the presence of the time-constant variable, z .13111.4 Assuming y 0 = 0 is a special case of assuming y 0 nonrandom, and so we can obtain the variances from (11.21): Var(y t ) = 2e σt and Var(y t+h ) = 2e σ(t + h ), h > 0. Because E(y t ) = 0 for all t (since E(y 0) = 0), Cov(y t ,y t+h ) = E(y t y t+h ) and, for h > 0,E(y t y t+h ) = E[(e t + e t-1 + e 1)(e t+h + e t+h -1 + + e 1)]= E(2t e ) + E(21t e -) + + E(21e ) = 2e σt ,where we have used the fact that {e t } is a pairwise uncorrelated sequence. Therefore, Corr(y t ,y t+h ) = Cov(y t ,y t+ht11.5 (i) The following graph gives the estimated lag distribution:wage inflation has its largest effect on price inflation nine months later. The smallest effect is at the twelfth lag, which hopefully indicates (but does not guarantee) that we have accounted for enough lags of gwage in the FLD model.(ii) Lags two, three, and twelve have t statistics less than two. The other lags are statistically significant at the 5% level against a two-sided alternative. (Assuming either that the CLMassumptions hold for exact tests or Assumptions TS.1' through TS.5' hold for asymptotic tests.)132(iii) The estimated LRP is just the sum of the lag coefficients from zero through twelve:1.172. While this is greater than one, it is not much greater, and the difference from unity could be due to sampling error.(iv) The model underlying and the estimated equation can be written with intercept α0 and lag coefficients δ0, δ1, , δ12. Denote the LRP by θ0 = δ0 + δ1 + + δ12. Now, we can write δ0 = θ0 - δ1 - δ2 - - δ12. If we plug this into the FDL model we obtain (with y t = gprice t and z t = gwage t )y t = α0 + (θ0 - δ1 - δ2 - - δ12)z t + δ1z t -1 + δ2z t -2 + + δ12z t -12 + u t= α0 + θ0z t + δ1(z t -1 – z t ) + δ2(z t -2 – z t ) + + δ12(z t -12 – z t ) + u t .Therefore, we regress y t on z t , (z t -1 – z t ), (z t -2 – z t ), , (z t -12 – z t ) and obtain the coefficient and standard error on z t as the estimated LRP and its standard error.(v) We would add lags 13 through 18 of gwage t to the equation, which leaves 273 – 6 = 267 observations. Now, we are estimating 20 parameters, so the df in the unrestricted model is df ur =267. Let 2ur R be the R -squared from this regression. To obtain the restricted R -squared, 2r R , weneed to reestimate the model reported in the problem but with the same 267 observations used toestimate the unrestricted model. Then F = [(2ur R -2r R )/(1 - 2ur R )](247/6). We would find thecritical value from the F 6,247 distribution.[Instructor’s Note: As a computer exercise, you might have the students test whether all 13 lag coefficients in the population model are equal. The restricted regression is gprice on (gwage + gwage -1 + gwage -2 + gwage -12), and the R -squared form of the F test, with 12 and 259 df , can be used.]11.6 (i) The t statistic for H 0: β1 = 1 is t = (1.104 – 1)/.039 ≈ 2.67. Although we must rely on asymptotic results, we might as well use df = 120 in Table G.2. So the 1% critical value against a two-sided alternative is about 2.62, and so we reject H 0: β1 = 1 against H 1: β1 ≠ 1 at the 1% level. It is hard to know whether the estimate is practically different from one withoutcomparing investment strategies based on the theory (β1 = 1) and the estimate (1ˆβ= 1.104). But the estimate is 10% higher than the theoretical value.(ii) The t statistic for the null in part (i) is now (1.053 – 1)/.039 ≈ 1.36, so H 0: β1 = 1 is no longer rejected against a two-sided alternative unless we are using more than a 10% significance level. But the lagged spread is very significant (contrary to what the expectations hypothesis predicts): t = .480/.109≈ 4.40. Based on the estimated equation, when the lagged spread is positive, the predicted holding yield on six-month T-bills is above the yield on three-month T-bills (even if we impose β1 = 1), and so we should invest in six-month T-bills.(iii) This suggests unit root behavior for {hy3t }, which generally invalidates the usual t -testing procedure.133(iv) We would include three quarterly dummy variables, say Q2t , Q3t , and Q4t , and do an F test for joint significance of these variables. (The F distribution would have 3 and 117 df .)11.7 (i) We plug the first equation into the second to gety t – y t-1 = λ(0γ + 1γx t + e t – y t-1) + a t ,and, rearranging,y t = λ0γ + (1 - λ)y t-1 + λ1γx t + a t + λe t ,≡ β0 + β1y t -1 + β2 x t + u t ,where β0 ≡ λ0γ, β1 ≡ (1 - λ), β2 ≡ λ1γ, and u t ≡ a t + λe t .(ii) An OLS regression of y t on y t-1 and x t produces consistent, asymptotically normal estimators of the βj . Under E(e t |x t ,y t-1,x t-1, ) = E(a t |x t ,y t-1,x t-1, ) = 0 it follows that E(u t |x t ,y t-1,x t-1, ) = 0, which means that the model is dynamically complete [see equation (11.37)]. Therefore, the errors are serially uncorrelated. If the homoskedasticity assumption Var(u t |x t ,y t-1) = σ2 holds, then the usual standard errors, t statistics and F statistics are asymptotically valid.(iii) Because β1 = (1 - λ), if 1ˆβ= .7 then ˆλ= .3. Further, 2ˆβ= 1ˆˆλγ, or 1ˆγ= 2ˆβ/ˆλ= .2/.3 ≈ .67.11.8 (i) Sequential exogeneity does not rule out correlation between, say, 1t u - and tj x for anyregressors j = 1, 2, …, k . The differencing generally induces correlation between the differenced errors and the differenced regressors. To see why, consider a single explanatory variable, x t . Then 1t t t u u u -∆=- and 1t t t x x x -∆=-. Under sequential exogeneity, t u is uncorrelated with t x and 1t x -, and 1t u - is uncorrelated with 1t x -. But 1t u - can be correlated with t x , which means that t u ∆ and t x ∆ are generally correlated. In fact, under sequential exogeneity, it is always true that 1Cov(,)Cov(,)t t t t x u x u -∆∆=-.(ii) Strict exogeneity of the regressors in the original equation is sufficient for OLS on the first-differenced equation to be consistent. Remember, strict exogeneity implies that theregressors in any time period are uncorrelated with the errors in any time period. Of course, we could make the weaker assumption: for any t , u t is uncorrelated with 1,t j x -, t j x , and 1,t j x + for all j = 1, 2, …, k . The strengthening beyond sequential exogeneity is the assumption that u t is uncorrelated w ith all of next period’s outcomes on all regressors. In practice, this is probably similar to just assuming strict exogeneity.(iii) If we assume sequential exogeneity in a static model, the condition can be written as。

第7章含有定性信息的多元回归分析：二值（或虚拟）变量7.1 复习笔记考点一：带有虚拟自变量的回归★★★★★1．对定性信息的描述定性信息是指通常以二值信息（0-1）的形式出现的信息，如性别、是否结婚等。

在计量经济学中，二值变量又称为虚拟变量。

2．只有一个虚拟自变量（1）只有一个虚拟自变量的简单模型考虑决定小时工资的简单模型：wage＝β0＋δ0female＋β1educ＋u。

根据多元回归的解释方式，δ0表示控制educ不变时，female变化1单位给wage带来的变化。

假定零条件均值假定E（u｜female，educ）＝0成立，那么：δ0＝E（wage｜female＝1，educ）－E（wage｜female＝0，educ），其中female＝1表示女性，female＝0表示男性。

可以发现，在任意教育水平下，男性与女性的工资差异是固定的，女性工资比男性工资多δ0。

除了β0之外，模型中只需要引入一个虚拟变量。

因为female＋male＝1，所以引入两个虚拟变量会导致完全多重共线性，即虚拟变量陷阱。

（2）当因变量为log（y）时，对虚拟解释变量系数的解释当变量中有一个或多个虚拟变量，且因变量以对数的形式存在时，虚拟变量的系数可以理解为百分比的变化。

将虚拟变量的系数乘以100，表示的是在保持所有其他因素不变时y的百分数差异，精确的百分数差异为：100·[exp （β∧1）－1]。

其中β∧1是一个虚拟变量的系数。

3．使用多类别虚拟变量 （1）在方程中包括虚拟变量的一般原则如果回归模型具有g 组或g 类不同截距，一种方法是在模型中包含g －1个虚拟变量和一个截距。

基组的截距是模型的总截距，某一组的虚拟变量系数表示该组与基组在截距上的估计差异。

如果在模型中引入g 个虚拟变量和一个截距，将会导致虚拟变量陷阱。

另一种方法是只包括g 个虚拟变量，而没有总截距。

这种方法存在两个实际的缺陷：①对于相对基组差别的检验变得更繁琐；②在模型不包含总截距时，回归软件通常都会改变R 2的计算方法。

伍德⾥奇《计量经济学导论》（第6版）复习笔记和课后习题详解-多元回归分析：推断【圣才出品】第4章多元回归分析：推断4.1复习笔记考点⼀：OLS估计量的抽样分布★★★1．假定MLR.6（正态性）假定总体误差项u独⽴于所有解释变量，且服从均值为零和⽅差为σ2的正态分布，即：u～Normal（0，σ2）。

对于横截⾯回归中的应⽤来说，假定MLR.1～MLR.6被称为经典线性模型假定。

假定下对应的模型称为经典线性模型（CLM）。

2．⽤中⼼极限定理（CLT）在样本量较⼤时，u近似服从于正态分布。

正态分布的近似效果取决于u中包含多少因素以及因素分布的差异。

但是CLT的前提假定是所有不可观测的因素都以独⽴可加的⽅式影响Y。

当u是关于不可观测因素的⼀个复杂函数时，CLT论证可能并不适⽤。

3．OLS估计量的正态抽样分布定理4.1（正态抽样分布）：在CLM假定MLR.1～MLR.6下，以⾃变量的样本值为条件，有：∧βj～Normal（βj，Var（∧βj））。

将正态分布函数标准化可得：（∧βj－βj）/sd（∧βj）～Normal（0，1）。

注：∧β1，∧β2，…，∧βk的任何线性组合也都符合正态分布，且∧βj的任何⼀个⼦集也都具有⼀个联合正态分布。

考点⼆：单个总体参数检验：t检验★★★★1．总体回归函数总体模型的形式为：y＝β0＋β1x1＋…＋βk x k＋u。

假定该模型满⾜CLM假定，βj的OLS 量是⽆偏的。

2．定理4.2：标准化估计量的t分布在CLM假定MLR.1～MLR.6下，（∧βj－βj）/se（∧βj）～t n－k－1，其中，k＋1是总体模型中未知参数的个数（即k个斜率参数和截距β0）。

t统计量服从t分布⽽不是标准正态分布的原因是se（∧βj）中的常数σ已经被随机变量∧σ所取代。

t统计量的计算公式可写成标准正态随机变量（∧βj－βj）/sd（∧βj）与∧σ2/σ2的平⽅根之⽐，可以证明⼆者是独⽴的；⽽且（n－k－1）∧σ2/σ2～χ2n－k－1。

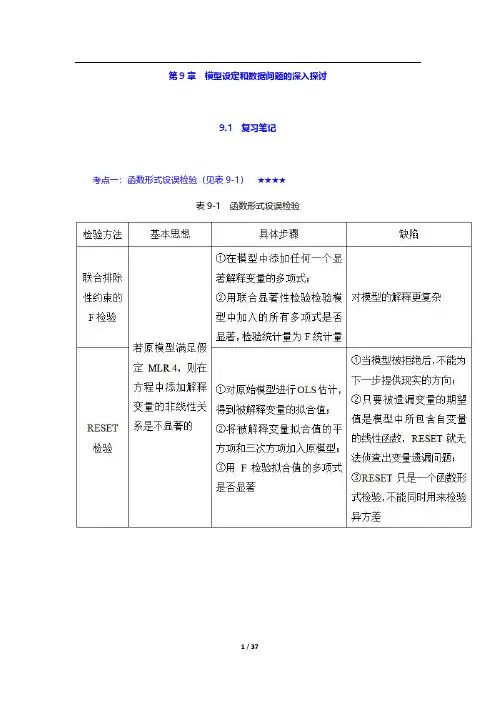
第9章模型设定和数据问题的深入探讨9.1复习笔记考点一：函数形式设误检验（见表9-1）★★★★表9-1函数形式设误检验考点二：对无法观测解释变量使用代理变量★★★1．代理变量代理变量就是某种与分析中试图控制而又无法观测的变量相关的变量。

（1）遗漏变量问题的植入解假设在有3个自变量的模型中，其中有两个自变量是可以观测的，解释变量x3*观测不到：y＝β0＋β1x1＋β2x2＋β3x3*＋u。

但有x3*的一个代理变量，即x3，有x3*＝δ0＋δ3x3＋v3。

其中，x3*和x3正相关，所以δ3＞0；截距δ0容许x3*和x3以不同的尺度来度量。

假设x3就是x3*，做y对x1，x2，x3的回归，从而利用x3得到β1和β2的无偏（或至少是一致）估计量。

在做OLS之前，只是用x3取代了x3*，所以称之为遗漏变量问题的植入解。

代理变量也可以以二值信息的形式出现。

（2）植入解能得到一致估计量所需的假定（见表9-2）表9-2植入解能得到一致估计量所需的假定2．用滞后因变量作为代理变量对于想要控制无法观测的因素，可以选择滞后因变量作为代理变量，这种方法适用于政策分析。

但是现期的差异很难用其他方法解释。

使用滞后被解释变量不是控制遗漏变量的唯一方法，但是这种方法适用于估计政策变量。

考点三：随机斜率模型★★★1．随机斜率模型的定义如果一个变量的偏效应取决于那些随着总体单位的不同而不同的无法观测因素，且只有一个解释变量x，就可以把这个一般模型写成：y i＝a i＋b i x i。

上式中的模型有时被称为随机系数模型或随机斜率模型。

对于上式模型，记a i＝a＋c i和b i＝β＋d i，则有E（c i）＝0和E（d i）＝0，代入模型得y i＝a＋βx i＋u i，其中，u i＝c i＋d i x i。

2．保证OLS无偏（一致性）的条件（1）简单回归当u i＝c i＋d i x i时，无偏的充分条件就是E（c i｜x i）＝E（c i）＝0和E（d i｜x i）＝E（d i）＝0。

伍德里奇计量经济学第六版答案AppendixBAPPENDIX BSOLUTIONS TO PROBLEMSB.1 Before the student takes the SAT exam, we do not know – nor can we predict with certainty – what the score will be. The actual score depends on numerous factors, many of which we cannot even list, let alone know ahead of time. (The student’s innate abil ity, how the student feels on exam day, and which particular questions were asked, are just a few.) The eventual SAT score clearly satisfies the requirements of a random variable.B.2 (i) P(X≤ 6) = P[(X–5)/2 ≤ (6 –5)/2] = P(Z≤ .5) ≈.692, where Z denotes a Normal (0,1) random variable. [We obtain P(Z≤ .5) from Table G.1.](ii) P(X > 4) = P[(X– 5)/2 > (4 – 5)/2] = P(Z > -.5) = P(Z≤ .5) ≈ .692.(iii) P(|X– 5| > 1) = P(X– 5 > 1) + P(X– 5 < –1) = P(X > 6) + P(X < 4) ≈ (1 – .692) + (1 – .692) = .616, where we have used answers from parts (i) and (ii).B.3 (i) Let Y it be the binary variable equal to one if fund i outperforms the market in year t. By assumption, P(Y it = 1) = .5 (a 50-50 chance of outperforming the market for each fund in each year). Now, for any fund, we are also assuming that performance relative to the market is independent across years. But then the probability that fund i outperforms the market in all 10 years, P(Y i1 = 1,Y i2 = 1, , Y i,10 = 1), is just the product of the probabilities: P(Y i1 = 1)?P(Y i2 = 1) P(Y i,10 = 1) = (.5)10 = 1/1024 (which is slightly less than .001). In fact, if we define a binary random variable Y i such that Y i = 1 if and only if fund i outperformed the market in all 10 years, then P(Y i = 1) = 1/1024.(ii) Let X denote the number of funds out of 4,170 that outperform the market in all 10 years. Then X = Y1 + Y2 + + Y4,170. If we assume that performance relative to the market is independent across funds, then X has the Binomial (n,θ) distribution with n = 4,170 and θ =1/1024. We want to compute P(X≥ 1) = 1 – P(X = 0) = 1 –P(Y1 = 0, Y2= 0, …, Y4,170 = 0) = 1 –P(Y1 = 0)? P(Y2 = 0)P(Y4,170 = 0) = 1 –(1023/1024)4170≈.983. This means, if performance relative to the market is random and independent across funds, it is almost certain that at least one fund will outperform the market in all 10 years.(iii) Using the Stata command Binomial(4170,5,1/1024), the answer is about .385. So there is a nontrivial chance that at least five funds will outperform the market in all 10 years.B.4 We want P(X ≥.6). Because X is continuous, this is the same as P(X > .6) = 1 –P(X≤ .6) =F(.6) = 3(.6)2– 2(.6)3 = .648. One way to interpret this is that almost 65% of all counties havean elderly employment rate of .6 or higher.B.5 (i) As stated in the hint, if X is the number of jurors convinced of Simpson’s innocence, then X ~ Binomial(12,.20). We want P(X≥ 1) = 1 – P(X = 0) = 1 –(.8)12≈ .931.263264 (ii) Above, we computed P(X = 0) as about .069. We need P(X = 1), which we obtain from(B.14) with n = 12, θ = .2, and x = 1: P(X = 1) = 12? (.2)(.8)11 ≈ .206. Therefore, P(X ≥ 2) ≈ 1 – (.069 + .206) = .725, so there is almost a three in four chance that the jury had at least two members convinced of Simpson’s innocence prior to the trial.B.6 E(X ) = 30()xf x dx ? = 320[(1/9)] x x dx ? = (1/9) 330x dx ?.But 330x dx ? = (1/4)x 430| = 81/4. Therefore, E(X ) = (1/9)(81/4) = 9/4, or 2.25 years.B.7 In eight attempts the expected number of free throws is 8(.74) = 5.92, or about six free throws.B.8 The weights for the two-, three-, and four-credit courses are 2/9, 3/9, and 4/9, respectively. Let Y j be the grade in the j th course, j = 1, 2, and 3, and let X be the overall grade point average. Then X = (2/9)Y 1 + (3/9)Y 2 + (4/9)Y 3 and the expected value is E(X ) = (2/9)E(Y 1) + (3/9)E(Y 2) + (4/9)E(Y 3) = (2/9)(3.5) + (3/9)(3.0) + (4/9)(3.0) = (7 + 9 + 12)/9 ≈ 3.11.B.9 If Y is salary in dollars then Y = 1000?X , and so the expected value of Y is 1,000 times the expected value of X , and the standard deviation of Y is 1,000 times the standard deviation of X . Therefore, the expected value and standard deviation of salary, measured in dollars, are $52,300 and $14,600, respectively.B.10 (i) E(GPA |SAT = 800) = .70 + .002(800) = 2.3. Similarly, E(GPA |SAT =1,400) = .70 + .002(1400) = 3.5. The difference in expected GPAs is substantial, but the difference in SAT scores is also rather large.(ii) Following the hint, we use the law of iterated expectations. SinceE(GPA |SAT ) = .70 + .002 SAT , the (unconditional) expected value of GPA is .70 + .002 E(SAT ) = .70 + .002(1100) = 2.9.。