伍德里奇---计量经济学第6章部分计算机习题详解(STATA)

R2 = 1−
SSR /(n − k − 1) SSR n − 1 n −1 = 1− ⋅ = 1 − (1 − R 2 ) ⋅ SST /(n − 1) SST n − k − 1 n − k −1
n −1 n − k −1
2
自由度惩罚因子：
在方程中增加一个（组）x，R2 一定增加，但只有该 x 的 t＞1（F＞1） R 才增加。 ，
2 3
三、含交叉项的模型 粮食产量＝β 0 + β1 （施肥量）+β（降水量）+β 3 （施肥量 × 降水量）+随机误差项 2
yi = β 0 + β1 xi + β 2 zi + β3 xi zi + ui
或
E ( y | xi , zi )＝β 0 + β1 xi +β 2 zi +β3 xi zi
（B）
将（B）式中的 X 用
yt − yt −1 替换，则（A）式可近似地表示为 yt −1
Δ ln yt ≈
yt − yt −1 yt −1
即表明对数变化相当于变量的变化率（相对变化） 。 该近似计算在系数数值小时比较准确， 但数值大的时候， 不太准确。 准确的变化率： 由于 ln y = β 0 + β1 x1 + β 2 x2 + .... + u ，如果 x1 变化一个绝对单位，其他 x 保持不 变，则有
ji j i
2
2
ˆ βj
ˆ 普通最小二乘回归系数 β j ( j = 1, 2, L , k ) 表示在其它变量不变的情况下，自变量 ˆ x j 每变化一个绝对单位引起的因变量的平均变化量；标准化回归系数 b j 表示在其它变

第六章自相关二、问答题1、那些原因可以造成自相关；2、存在自相关时，参数的OLS估计具有哪些性质；3、如何检验是否存在自相关；4、当存在自相关时，如何利用广义差分法进行参数估计；5、当存在自相关时，如何利用广义最小平方估计法进行参数估计；6、异方差与自相关有什么异同；三、计算题1、证明：当样本个数较大时，)d。

≈-1(2ρα2、通过D-W检验，判断下列模型中是否存在自相关，显著性水平%5=（1）样本大小：20；解释变量个数（包括常数项）：2；d=0.73；（2）样本大小：35；解释变量个数（包括常数项）：3；d=3.56；（3）样本大小：50；解释变量个数（包括常数项）：3；d=1.87；（4）样本大小：80；解释变量个数（包括常数项）：6；d=1.62；（5）样本大小：100；解释变量个数（包括常数项）：5；d=2.41；3、假定存在下表所示的时间序列数据：请回答下列问题：（1）利用表中数据估计模型：t t t x y εββ++=10；（2）利用D-W 检验是否存在自相关？如果存在请用d 值计算估计自相关系数ρ；（3）利用广义差分法重新估计模型：'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。

第三部分 参考答案二、问答题1、那些原因可以造成自相关？答：造成自相关的原因大致包括以下六个方面：（1）经济变量的变化具有一定的倾向性。

在实际的经济现象中，许多经济变量的现值依赖于他的前期值。

也就是说，许多经济时间序列都有一个明显的相依性特点，这种现象称作经济变量所具有的惯性。

（2）缺乏应有变量的设定偏差。

（3）不正确的函数形式的设定错误。

（4）蛛网现象和滞后效应。

（5）随机误差项的特征。

（6）数据拟合方法造成的影响。

2、存在自相关时，参数的OLS 估计具有哪些性质？答：当存在自相关，即I D ≠ΩΩ=,)(2σε时，OLS 估计的性质有：（1）βˆ是观察值Y 和X 的线性函数；（2）βˆ是β的无偏估计；（3）βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ；（4）βˆ不是β的最小方差线性无偏估计；（5）如果nX X n Ω'∞→lim存在，那么βˆ是β的一致估计；（6）2σ 不是2σ的无偏估计；（7）2σ不是2σ的一致估计。

伍德里奇计量经济学第6章计算机习题详解 STATA引言本文档旨在对伍德里奇计量经济学第6章的计算机习题进行详解和解答，使用计量经济学软件STATA进行操作和分析。

本文档将逐步解答各个习题，并给出相应的STATA代码和结果展示。

习题1假设我们有一个数据集data.dta，其中包含了变量y和x。

现在我们想要估计下列回归模型的系数：$$y = \\beta_0 + \\beta_1 x + \\beta_2 x^2 + u$$使用STATA进行分析，首先加载数据集：use data.dta然后我们可以采用如下代码进行回归分析：reg y x c.x#c.x这里的c.x#c.x表示将变量x进行平方。

执行上述代码后，STATA将输出回归结果。

习题2在第6章的习题2中，我们需要进行假设检验。

假设我们想要检验系数$\\beta_1=0$和$\\beta_2=0$的原假设。

我们可以使用STATA进行对应的假设检验。

首先，我们需要执行回归分析，并保存回归结果：reg y x c.x#c.xestimates store reg1然后，我们可以使用如下代码进行假设检验：test x#c.x=0执行上述代码后，STATA将输出相应的假设检验结果。

习题3在第6章的习题3中，我们需要计算残差的平方和（Sum of Squared Residuals）。

我们可以使用STATA来计算残差的平方和。

首先，我们需要执行回归分析，并保存回归结果：reg y x c.x#c.xestimates store reg1然后，我们可以使用以下代码计算残差的平方和：predict u, residegen ssr = sum(u^2)scalar ssr_sum = r(ssr)执行上述代码后，STATA将输出残差的平方和。

习题4在第6章的习题4中，我们需要计算拟合度（Goodness of Fit）度量指标，如R2，调整后R2等。

我们可以使用STATA计算拟合度指标。

文章主题：探寻计量经济学伍德里奇第六版stata代码的应用与意义1. 引言计量经济学作为经济学的一个重要分支，旨在运用数学、统计学和计算机科学的方法来分析经济问题和经济现象，从而为实证经济研究提供理论和方法。

而伍德里奇的《计量经济学》第六版，作为该领域的经典教材，常常被用来进行实证研究和教学。

在本文中，我们将深入探讨这本教材中的stata代码部分，分析其应用与意义。

2. 计量经济学伍德里奇第六版stata代码的意义在《计量经济学》第六版中，作者伍德里奇通过stata代码来展示实证分析的方法和过程。

这些代码不仅仅是为了教学目的，更重要的是为了让读者能够学会如何用计量经济学的方法来研究实际经济问题。

通过学习这些stata代码，读者可以掌握实证分析的基本技能，了解如何处理实际数据、构建模型、进行估计和推断，从而在实际研究中能够灵活运用计量经济学的方法。

3. 深入理解计量经济学伍德里奇第六版stata代码在伍德里奇的《计量经济学》第六版中，stata代码涵盖了从简单的OLS回归分析到复杂的面板数据模型的估计方法，涉及了各种实证问题和分析工具。

通过深入学习这些代码，读者可以逐步理解和掌握计量经济学的核心内容，包括数据的处理与清洗、模型的构建与估计、假设检验与推断等方面的知识和技能。

这样的深入理解将使读者能够更好地应用计量经济学的方法来解决实际经济问题，并且能够进行批判性思考和创新性研究。

4. 个人观点和理解作为一名计量经济学的研究者和教学者，我深切理解学习和掌握计量经济学伍德里奇第六版stata代码的重要性。

这些代码不仅仅是一种工具，更是一种思维方式和方法论，是我们用来研究经济现象和问题的利器。

通过不断地学习和实践，我相信我们能够更好地理解和应用计量经济学的方法，为经济学研究和实践带来更多的启发和进步。

5. 总结通过本文的探讨，我们深入了解了《计量经济学》第六版中stata代码的应用与意义。

这些代码的存在不仅仅是为了让我们学会如何进行实证分析，更重要的是让我们深刻理解和掌握计量经济学的思想和方法。

考点五：对多个线性约束的检验：F 检验 ★★★★★
1．对排除性约束的检验 对排除性约束的检验是指检验一组自变量是否对因变量都没有影响，该检验不适用于不 同因变量的检验。F 统计量通常对检验一组变量的排除有用处，特别是当变量高度相关的时 候。 含有 k 个自变量的不受约束模型为：y＝β0＋β1x1＋…＋βkxk＋u，其中参数有 k＋1 个。 假设有 q 个排除性约束要检验，且这 q 个变量是自变量中的最后 q 个：xk－q＋1，…，xk， 则受约束模型为：y＝β0＋β1x1＋…＋βk－qxk－q＋u。 虚拟假设为 H0：βk－q＋1＝0，…，βk＝0，对立假设是列出的参数至少有一个不为零。 定义 F 统计量为 F＝[（SSRr－SSRur）/q]/[SSRur/（n－k－1）]。其中，SSRr 是受约束模型 的残差平方和，SSRur 是不受约束模型的残差平方和。由于 SSRr 不可能比 SSRur 小，所以 F 统计量总是非负的。q＝dfr－dfur，即 q 是受约束模型与不受约束模型的自由度之差，也是 约束条件的个数。n－k－1＝分母自由度＝dfur，且 F 的分母恰好就是不受约束模型中σ2＝ Var（u）的一个无偏估计量。 假设 CLM 假定成立，在 H0 下 F 统计量服从自由度为（q，n－k－1）的 F 分布，即 F～ Fq，n－k－1。如果 F 值大于显著性水平下的临界值，则拒绝 H0 而支持 H1。当拒绝 H0 时，就 说，xk－q＋1，…，xk 在适当的显著性水平上是联合统计显著的（或联合显著）。

∧
∧
∧
∧
注：β1，β2，…，βk 的任何线性组合也都符合正态分布，且βj 的任何一数检验：t 检验 ★★★★
1．总体回归函数 总体模型的形式为：y＝β0＋β1x1＋…＋βkxk＋u。假定该模型满足 CLM 假定，βj 的 OLS 量是无偏的。

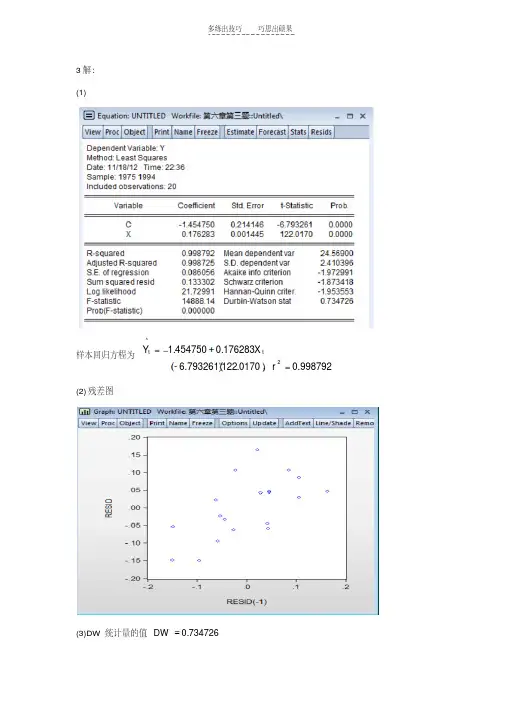
3解:(1)样本回归方程为998792.00170.1226.793261-176283.0454750.12^t r X Y t，(2)残差图(3)DW 统计量的值734726.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tX e e 000420.0060923.0638831.01因为84.3998223.7,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。

首先估计自相关系数^，得632637.02734726.0121^DW 对原变量做广义差分变换。

令1t 632637.0t t Y Y GDY ，1t 632637.0t t X X GDX 以年1994~1975,,t t GDX GDY 为样本再次回归，得tGDX GDY 173740.0391490.0t 回归方程拟合的效果仍然比较好,651914.1DW 对于给定05.0，查表得，。

43.1,24.1U L d d 因为75.243.11651914.1DW ,依据判别规则，误差项已消除自相关。

由391490.0^*0，得06568.1632637.01/391490.01/^^*0^0则原模型的广义最小二乘估计结果是t X Y 173470.006568.1^t 。

4解：（1）样本回归方程为tGDP Y 694454.0674.2816^t（2）残差图(3)3397.0DW(4)BG LM 自相关检验辅助回归式估计结果是t t t tGDP e e 029062.07871.334985257.01因为84.309615.30,84.31205.0LM ,所以LM 检验量也说明样本回归方程的误差项存在一阶正自相关。

首先估计自相关系数^，得83015.023397.0121^DW对原变量做广义差分变换。

令1t 83015.0t t Y Y GDY ，183015.0t t tGDGDP GDP GDGDP ，以年1994~1975,,t t GDGDP GDY 为样本再次回归，得。

第1章计量经济学的性质与经济数据1.1复习笔记考点一:计量经济学★1计量经济学的含义计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。

2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。

根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。

(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。

②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。

③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。

考点二:经济数据★★★1经济数据的结构(见表1-3)2面板数据与混合横截面数据的比较(见表1-4)考点三:因果关系和其他条件不变★★1因果关系因果关系是指一个变量的变动将引起另一个变量的变动,这是经济分析中的重要目标之计量分析虽然能发现变量之间的相关关系,但是如果想要解释因果关系,还要排除模型本身存在因果互逆的可能,否则很难让人信服。

2其他条件不变其他条件不变是指在经济分析中,保持所有的其他变量不变。

“其他条件不变”这一假设在因果分析中具有重要作用。

1.2课后习题详解一、习题1.假设让你指挥一项研究，以确定较小的班级规模是否会提高四年级学生的成绩。

(i)如果你能指挥你想做的任何实验，你想做些什么?请具体说明。

(ii)更现实地，假设你能搜集到某个州几千名四年级学生的观测数据。

你能得到它们四年级班级规模和四年级末的标准化考试分数。

你为什么预计班级规模与考试成绩成负相关关系?(iii)负相关关系一定意味着较小的班级规模会导致更好的成绩吗?请解释。

答:(i)假定能够随机的分配学生们去不同规模的班级，也就是说，在不考虑学生诸如能力和家庭背景等特征的前提下，每个学生被随机的分配到不同的班级。

第六章 经典联立方程计量经济学模型：理论与方法一、内容提要联立方程计量经济学模型是相对于单一方程模型提出来的，旨在在讨论多个经济变量相互影响的错综复杂的运行规律，或者说讨论多个内生变量被联立决定的问题。

本章学习内容的一个重点是关于联立方程计量经济学模型区别于单方程模型的若干基本概念，包括内生变量、外生变量、前定变量的概念；结构式模型、简化式模型的概念；随机方程、恒等方程的概念；行为方程、技术方程、制度方程、统计方程、定义方程、平衡方程等相关概念。

本章学习的另一个重点是联立模型的识别问题。

需掌握模型识别的基本概念、模型识别的类型（不可识别、恰好识别、过渡识别）、模型的结构式识别条件、模型的简化式识别条件以及实际应用中的经验识别方法。

本章学习的第三个重点是联立模型的估计问题。

首先明确联立模型估计时会遇到的三个方面的问题。

一是随机解释变量问题，即模型中的某些解释变量也能是与随机扰动项相关的随机解释变量；二是损失变量信息的问题，即以单方程方法估计模型时会损失其他方程变量所提供的信息；三是损失方程之间的相关性信息问题，即以单方程方法估计模型时会损失不同方程随机扰动项间的相关性方面的一些信息。

其次，需要掌握联立模型两大类估计方法中的主要估计方法，如单方程估计方法中的狭义工具变量法（IV ）、间接最小二乘法（ILS ）、二阶段最小二乘法（2SLS ），系统估计方法中的三阶段最小二乘法（3SLS ）等。

本章学习中不容忽视的还有联立方程计量经济学模型估计方法的比较，以及联立方程模型的检验问题。

前者需要考察大样本估计量特性与小样本估计量的特性；后者包括拟合效果检验、预测性检验、方程间误差传递检验等方面的内容。

二、典型例题分析1、如果我们将“供给”1Y 与“需求”2Y 写成如下的联立方程的形式：222221111211u Z Y Y u Z Y Y ++=++=βαβα其中，1Z 、2Z 为外生变量。

（1）若01=α或02=α，解释为什么存在1Y 的简化式？若01≠α、02=α，写出2Y 的简化式。

伍德里奇计量经济学导论第6版考研笔记和课后习题详解伍德里奇《计量经济学导论》（第6版）笔记和课后习题详解内容简介伍德里奇所著的《计量经济学导论》（第6版）是我国许多高校采用的计量经济学优秀教材，也被部分高校指定为“经济类”专业考研考博参考书目。

本书遵循伍德里奇《计量经济学导论》（第6版）教材的章目编排，共分3篇19章，每章由两部分组成：第一部分为复习笔记，总结本章的重难点内容；第二部分为课（章）后习题详解，对第6版的所有课（章）后习题都进行了详细的分析和解答。

作为该教材的学习辅导书，本书具有以下几个方面的特点：（1）整理名校笔记，浓缩内容精华。

每章的复习笔记以伍德里奇所著的《计量经济学导论》（第6版）为主，并结合国内外其他计量经济学经典教材对各章的重难点进行了整理，因此，本书的内容几乎浓缩了经典教材的知识精华。

（2）解析课后习题，提供详尽答案。

本书参考大量经济学相关资料对伍德里奇所著的《计量经济学导论》（第6版）的课（章）后习题进行了详细的分析和解答，并对相关重要知识点进行了延伸和归纳。

（3）补充相关要点，强化专业知识。

一般来说，国外英文教材的中译本不太符合中国学生的思维习惯，有些语言的表述不清或条理性不强而给学习带来了不便，因此，对每章复习笔记的一些重要知识点和一些习题的解答，我们在不违背原书原意的基础上结合其他相关经典教材进行了必要的整理和分析。

•试看部分内容第1章计量经济学的性质与经济数据1.1复习笔记考点一：计量经济学及其应用★1计量经济学计量经济学是在一定的经济理论基础之上，采用数学与统计学的工具，通过建立计量经济模型对经济变量之间的关系进行定量分析的学科。

进行计量分析的步骤主要有：①利用经济数据对模型中的未知参数进行估计；②对模型进行检验；③通过检验后，可以利用计量模型来进行相关预测。

2经济分析的步骤经济分析是指利用所搜集的相关数据检验某个理论是否成立或估计某种关系的方法。

经济分析主要包括以下几步，分别是阐述问题、构建经济模型、经济模型转化为计量模型、搜集相关数据、参数估计和假设检验。

伍德⾥奇---计量经济学第8章部分计算机习题详解（STATA）班级：⾦融学×××班姓名：××学号：×××××××C8.1SLEEP75.RAWsleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u 解：（ⅰ）写出⼀个模型，容许u的⽅差在男⼥之间有所不同。

这个⽅差不应该取决于其他因素。

在sleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u模型下，u⽅差要取决于性别，则可以写成：Var u︳totwork,educ,age,yngkid,male =Var u︳male =δ0+δ1male。

所以，当⽅差在male=1时，即为男性时，结果为δ0+δ1；当为⼥性时，结果为δ0。

将sleep对totwork，educ，age，age2，yngkid和male进⾏回归，回归结果如下：（ⅱ）利⽤SLEEP75.RAW的数据估计异⽅差模型中的参数。

u的估计⽅差对于男⼈和⼥⼈⽽⾔哪个更⾼？由截图可知：u2=189359.2?28849.63male+r20546.36 (27296.36)由于male 的系数为负，所以u 的估计⽅差对⼥性⽽⾔更⼤。

（ⅲ）u 的⽅差是否对男⼥⽽⾔有显著不同？因为male 的 t 统计量为?1.06，所以统计不显著，故u 的⽅差是否对男⼥⽽⾔并没有显著不同。

C8.2 HPRICE1.RAW price =β0+β1lotsize +β2sqrft +β3bdrms +u 解：（ⅰ）利⽤HPRICE 1.RAW 中的数据得到⽅程（8.17）的异⽅差—稳健的标准误。

讨论其与通常的标准误之间是否存在任何重要差异。

●先进⾏⼀般回归，结果如下：●再进⾏稳健回归，结果如下：由两个截图可得：price =?21.77+0.00207lotsize +0.123sqrft +13.85bdrms29.48 0.00064 0.013 (9.01)37.13 0.00122 0.018 [8.48]n =88，R 2=0.672⽐较稳健标准误和通常标准误，发现lotsize 的稳健标准误是通常下的2倍，使得 t 统计量相差较⼤。

（完整版）计量经济学（伍德里奇第五版中文版）答案第1章解决问题的办法1.1（一）理想的情况下，我们可以随机分配学生到不同尺寸的类。

也就是说，每个学生被分配一个不同的类的大小，而不考虑任何学生的特点，能力和家庭背景。

对于原因，我们将看到在第2章中，我们想的巨大变化，班级规模（主题，当然，伦理方面的考虑和资源约束）。

（二）呈负相关关系意味着，较大的一类大小是与较低的性能。

因为班级规模较大的性能实际上伤害，我们可能会发现呈负相关。

然而，随着观测数据，还有其他的原因，我们可能会发现负相关关系。

例如，来自较富裕家庭的儿童可能更有可能参加班级规模较小的学校，和富裕的孩子一般在标准化考试中成绩更好。

另一种可能性是，在学校，校长可能分配更好的学生，以小班授课。

或者，有些家长可能会坚持他们的孩子都在较小的类，这些家长往往是更多地参与子女的教育。

（三）鉴于潜在的混杂因素- 其中一些是第（ii）上市- 寻找负相关关系不会是有力的证据，缩小班级规模，实际上带来更好的性能。

在某种方式的混杂因素的控制是必要的，这是多元回归分析的主题。

1.2（一）这里是构成问题的一种方法：如果两家公司，说A和B，相同的在各方面比B公司à用品工作培训之一小时每名工人，坚定除外，多少会坚定的输出从B公司的不同？（二）公司很可能取决于工人的特点选择在职培训。

一些观察到的特点是多年的教育，多年的劳动力，在一个特定的工作经验。

企业甚至可能歧视根据年龄，性别或种族。

也许企业选择提供培训，工人或多或少能力，其中，“能力”可能是难以量化，但其中一个经理的相对能力不同的员工有一些想法。

此外，不同种类的工人可能被吸引到企业，提供更多的就业培训，平均，这可能不是很明显，向雇主。

（iii）该金额的资金和技术工人也将影响输出。

所以，两家公司具有完全相同的各类员工一般都会有不同的输出，如果他们使用不同数额的资金或技术。

管理者的素质也有效果。

（iv）无，除非训练量是随机分配。

型中未知参数的个数（即 k 个斜率参数和截距β0）。
∧
∧
t 统计量服从 t 分布而不是标准正态分布的原因是 se（βj）中的常数σ已经被随机变量σ
所取代。t
∧
∧
统计量的计算公式可写成标准正态随机变量（βj－βj）/sd（βj）与
σ∧ 2/σ2
的平方
根之比，可以证明二者是独立的；而且（n－k－1）σ∧ 2/σ2～χ2n－k－1。于是根据 t 随机变量
有一个联合正态分布。
考点二：单个总体参数检验：t 检验 ★★★★
1．总体回归函数 总体模型的形式为：y＝β0＋β1x1＋…＋βkxk＋u。假定该模型满足 CLM 假定，βj 的 OLS 量是无偏的。
2．定理 4.2：标准化估计量的 t 分布
∧
∧
在 CLM 假定 MLR.1～MLR.6 下，（βj－βj）/se（βj）～tn－k－1，其中，k＋1 是总体模
定理 4.1（正态抽样分布）：在 CLM 假定 MLR.1～MLR.6 下，以自变量的样本值为条
∧
∧
∧
∧
件，有：βj～Normal（βj，Var（βj））。将正态分布函数标准化可得：（βj－βj）/sd（βj）～
Normal（0，1）。
1 / 89
∧
∧
∧
∧
注：β1，β2，…，βk 的任何线性组合也都符合正态分布，且 βj 的任何一个子集也都具
1．对排除性约束的检验 对排除性约束的检验是指检验一组自变量是否对因变量都没有影响，该检验不适用于不 同因变量的检验。F 统计量通常对检验一组变量的排除有用处，特别是当变量高度相关的时 候。 含有 k 个自变量的不受约束模型为：y＝β0＋β1x1＋…＋βkxk＋u，其中参数有 k＋1 个。 假设有 q 个排除性约束要检验，且这 q 个变量是自变量中的最后 q 个：xk－q＋1，…，xk，则 受约束模型为：y＝β0＋β1x1＋…＋βk－qxk－q＋u。 虚拟假设为 H0：βk－q＋1＝0，…，βk＝0，对立假设是列出的参数至少有一个不为零。 定义 F 统计量为 F＝[（SSRr－SSRur）/q]/[SSRur/（n－k－1）]。其中，SSRr 是受约束模型 的残差平方和，SSRur 是不受约束模型的残差平方和。由于 SSRr 不可能比 SSRur 小，所以 F 统计量总是非负的。q＝dfr－dfur，即 q 是受约束模型与不受约束模型的自由度之差，也是 约束条件的个数。n－k－1＝分母自由度＝dfur，且 F 的分母恰好就是不受约束模型中σ2＝ Var（u）的一个无偏估计量。 假设 CLM 假定成立，在 H0 下 F 统计量服从自由度为（q，n－k－1）的 F 分布，即 F～ Fq，n－k－1。如果 F 值大于显著性水平下的临界值，则拒绝 H0 而支持 H1。当拒绝 H0 时，就 说，xk－q＋1，…，xk 在适当的显著性水平上是联合统计显著的（或联合显著）。

第六章1、答：给定显著水平α，依据样本容量n 和解释变量个数k’，查D.W.表得d 统计量的上界du 和下界dL ，当0<d<dL 时，表明存在一阶正自相关，而且正自相关的程度随d 向0的靠近而增强。

当dL<d<du 时，表明为不能确定存在自相关。

当du<d<4-du 时，表明不存在一阶自相关。

当4-du<d<4-dL 时，表明不能确定存在自相关。

当4-dL<d<4时，表明存在一阶负自相关，而且负自相关的程度随d 向4的靠近而增强。

前提条件：DW 检验的前提条件：（1）回归模型中含有截距项；（2）解释变量是非随机的（因此与随机扰动项不相关）（3）随机扰动项是一阶线性自相关。

；（4）回归模型中不把滞后内生变量（前定内生变量）做为解释变量。

（5）没有缺失数据，样本比较大。

DW 检验的局限性：（1）DW 检验有两个不能确定的区域，一旦DW 值落在这两个区域，就无法判断。

这时，只有增大样本容量或选取其他方法（2）DW 统计量的上、下界表要求n ≥15, 这是因为样本如果再小，利用残差就很难对自相关的存在性做出比较正确的诊断(3) DW 检验不适应随机误差项具有高阶序列相关的检验.(4) 只适用于有常数项的回归模型并且解释变量中不能含滞后的被解释变量2、答：（1）当回归模型随机误差项有自相关时，普通最小二乘估计量是有偏误的和非有效的。

判断：错误。

当回归模型随机误差项有自相关时，普通最小二乘估计量是无偏误的和非有效的。

（2）DW 检验假定随机误差项u i 的方差是同方差。

判断：错误。

DW 统计量的构造中并没有要求误差项的方差是同方差 。

（3）用一阶差分法消除自相关是假定自相关系数为-1。

判断：错误。

用一阶差分法消除自相关是假定自相关系数为1，即原原模型存在完全一阶正自相关。

（4）当回归模型随机误差项有自相关时，普通最小二乘估计的预测值的方差和标准误差不再是有效的。

第三篇高级专题第13章跨时横截面的混合：简单面板数据方法13.1复习笔记考点一：跨时独立横截面的混合★★★★★1．独立混合横截面数据的定义独立混合横截面数据是指在不同时点从一个大总体中随机抽样得到的随机样本。

这种数据的重要特征在于：都是由独立抽取的观测所构成的。

在保持其他条件不变时，该数据排除了不同观测误差项的相关性。

区别于单独的随机样本，当在不同时点上进行抽样时，样本的性质可能与时间相关，从而导致观测点不再是同分布的。

2．使用独立混合横截面的理由（见表13-1）表13-1使用独立混合横截面的理由3．对跨时结构性变化的邹至庄检验（1）用邹至庄检验来检验多元回归函数在两组数据之间是否存在差别（见表13-2）表13-2用邹至庄检验来检验多元回归函数在两组数据之间是否存在差别（2）对多个时期计算邹至庄检验统计量的办法①使用所有时期虚拟变量与一个（或几个、所有）解释变量的交互项，并检验这些交互项的联合显著性，一般总能检验斜率系数的恒定性。

②做一个容许不同时期有不同截距的混合回归来估计约束模型，得到SSR r。

然后，对T个时期都分别做一个回归，并得到相应的残差平方和，有：SSR ur＝SSR1＋SSR2＋…＋SSR T。

若有k个解释变量（不包括截距和时期虚拟变量）和T个时期，则需检验（T－1）k个约束。

而无约束模型中有T＋Tk个待估计参数。

所以，F检验的df为（T－1）k和n－T－Tk，其中n为总观测次数。

F统计量计算公式为：[（SSR r－SSR ur）/SSR ur][（n－T－Tk）/（Tk－k）]。

但该检验不能对异方差性保持稳健，为了得到异方差-稳健的检验，必须构造交互项并做一个混合回归。

4．利用混合横截面作政策分析（1）自然实验与真实实验当某些外生事件改变了个人、家庭、企业或城市运行的环境时，便产生了自然实验（准实验）。

一个自然实验总有一个不受政策变化影响的对照组和一个受政策变化影响的处理组。

自然实验中，政策发生后才能确定处理组和对照组。

Only change will happen to the intercept. log(cyi)=log(c)+log(yi), the new intercept will be β0-log(c) log(dxi)=log(d)+log(xi), the new intercept will be β0+βjlog(d)
bwght =child birth weight, in ounces cigs =number of cigarette smoked by the mother while pregnant, per day faminc =annual family income, in thousands of dollars.
3

4
[Example]: Infant birth weight on cigarette smoking and family income (cont.)

[Example]: Infant birth weight on cigarette smoking and family income (cont.)
taking the natural log ― the most popular device in econometrics ― of x, y or both;
― ― ―

using quadratic forms of x; use interactions of x variables.
Occasional you’ll see reference to a “standardized coefficient” or “beta coefficient” which has a specific meaning. Idea is to replace y and each x variable with a standardized version – i.e. subtract mean and divide by standard deviation. Coefficient reflects how many y standard deviation of y change with respect to an one standard deviation change in x, holding other factors fixed. So we are measuring effects not in terms of the original units of y and x, but in standard deviation units.

clear,clc;% c6.13 by% 打开文字文件和数据文件importdata('meap00_01.des');data=xlsread('meap00_01');% 检验所用数据是否为非空Isnan=isnan(data(:,[3,5,8,9]));a=sum(Isnan')';b=find(a==0);data1=data(b,:);% 变量命名math4=data1(:,3);lunch=data1(:,5);lenroll=data1(:,8);lexppp=data1(:,9);% OLS估计result1=ols(math4,[ones(length(math4),1),lunch,lenroll,lexppp]);vnames=char('math4','constant','lunch','lenroll','lexppp');prt(result1,vnames)% 回归结果% Ordinary Least-squares Estimates% Dependent Variable = math4% R-squared = 0.3729% Rbar-squared = 0.3718% sigma^2 = 234.1638% Durbin-Watson = 1.7006% Nobs, Nvars = 1692, 4% ***************************************************************% Variable Coefficient t-statistic t-probability% constant 91.932484 4.605444 0.000004% lunch -0.448743 -30.647631 0.000000% lenroll -5.399153 -5.741265 0.000000% lexppp 3.524742 1.680172 0.093109% 由回归结果中的p值发现lunch,lenroll是在5%的水平上显著的,而lexppp在5%水平上不显著,% 但在10%的显著水平上是显著的.% 求出回归的拟合值及其取值范围yhat=result1.yhat;std_yhat=std(yhat);mean_yhat=mean(yhat);yhat_qujian=[mean_yhat-2*std_yhat,mean_yhat+2*std_yhat]% yhat的取值范围是(49.1090 ,96.2665)% 求出math4的实际取值范围math4_qujian=[min(math4),max(math4)]% math4的实际取值范围是(0 ,100),可见拟合值的取值范围要比实际范围窄% 求出回归残差resid=result1.resid;max_resid=max(resid);row=find(resid==max_resid)school_code=data1(row,2)% 学校类型是school_code=1141,说明该学校的实际数学考试通过率要比估计的数学考试通% 过率高很多,也就这所学校的数学教学质量较高% 求取解释变量数据的平方项lenroll2=lenroll.^2;lexppp2=lexppp.^2;lunch2=lunch.^2;%在方程中加入所有解释变量的平方项进行回归result2=ols(math4,[ones(length(math4),1),lunch,lenroll,lexppp,lunch2,lenroll2,lexppp2]); vnames=char('math4','constant','lunch','lenroll','lexppp','lunch2','lenroll2','lexppp2');prt(result2,vnames)% 检验联合显著性rsqr1=result1.rsqr;rsqr2=result2.rsqr;F=((rsqr2-rsqr1)/3)/((1-rsqr2)/(1692-6-1))p=1-fcdf(F,3,1685)% F =0.5180% p =0.6699% 所以这几个解释变量的平方项是联合不显著的,所以不应该把他们放到模型中% 求所用数据值除以其标准差lenroll_new=lenroll/std(lenroll);lunch_new=lunch/std(lunch);lexppp_new=lexppp/std(lexppp);math4_new=math4/std(math4);% 重新进行回归result3=ols(math4_new,[ones(length(math4_new),1),lunch_new,lenroll_new,lexppp_new]); vnames=char('math4_new','constant','lunch_new','lenroll_new','lexppp_new');prt(result3,vnames)% 回归结果% Ordinary Least-squares Estimates% Dependent Variable = math4_new% R-squared = 0.3729% Rbar-squared = 0.3718% sigma^2 = 0.6282% Durbin-Watson = 1.7006% Nobs, Nvars = 1692, 4% ***************************************************************% Variable Coefficient t-statistic t-probability% constant 4.761759 4.605444 0.000004% lunch_new -0.612853 -30.647631 0.000000% lenroll_new -0.114620 -5.741265 0.000000% lexppp_new 0.034743 1.680172 0.093109% 由结果lunch,lenroll和lexppp分别提高一倍,会使数学通过率分别变化0.613,0.115和% 0.035个标准差,所以lunch对数学考试通过率影响最大。