电路微分方程解法
- 格式:doc
- 大小:565.00 KB
- 文档页数:12




rlc电路微分方程例题全文共四篇示例,供读者参考第一篇示例:RLC电路是一种常见的电路类型,由电阻(R)、电感(L)、电容(C)三种元件组成。
在电路中,产生电压和电流的关系可以用微分方程表示。
本文将为大家介绍关于RLC电路的微分方程例题,希望能帮助大家加深对此知识的理解。
假设我们有一个串联RLC电路,电阻的阻值为R欧姆,电感的电感值为L亨利,电容的电容值为C法拉。
当电路中的电压源为E(t)伏特时,可以通过基尔霍夫定律建立电路的微分方程。
根据基尔霍夫定律,在电路中,电压源E(t)等于电阻、电感和电容元件上的电压之和。
电阻上的电压可以表示为IR,电感上的电压可以表示为L(di/dt),电容上的电压可以表示为Q/C,其中Q为电容器上的电荷。
根据电压和电流的关系可以得到以下方程:E(t) = IR + L(di/dt) + Q/CI为电流强度,di/dt为电流的变化率,Q为电容器上的电荷。
我们知道电流等于电荷的导数,即I = dQ/dt,根据此关系可以对方程进行求导整理得到:对上式做微分运算,可以得到RLC电路的微分方程:这个微分方程描述了RLC电路中电荷Q随时间的变化情况。
通过解这个微分方程,我们可以得到电荷Q随时间的具体变化规律,从而了解电路中电流的行为。
下面我们通过一个具体的例题来演示如何解决RLC电路的微分方程。
假设一个串联RLC电路中,电阻R = 2欧姆,电感L = 1亨利,电容C = 0.5法拉,电压源为E(t) = 6sin(2t)伏特。
我们需要求解电路中电荷Q随时间的变化情况。
根据上述微分方程,我们有:带入已知的数值,得到:这是一个二阶常系数非齐次线性微分方程。
我们可以通过常数变易法或者拉普拉斯变换等方法进行求解。
在这里,我们选择通过试解法来求解该微分方程。
假设Q(t) = A cos(2t) + B sin(2t)是微分方程的一个特解,代入原方程,整理后可得到:Q(t) = -2.4sin(2t) + 0.224cos(2t) + (6/5)sin(2t)电路中电荷Q随时间的变化规律可表示为:通过上述例题的求解过程,我们可以看到如何使用微分方程求解RLC电路中电荷的变化情况。

微分方程与电路问题的建模与解法电路问题是现代科学与工程领域中常见的实际问题之一,而微分方程则是解决这些问题的重要工具之一。
本文将探讨微分方程与电路问题的建模与解法,并通过实例来说明其应用。
一、电路问题的建模电路问题通常涉及电流、电压、电阻等物理量之间的关系。
为了解决这些问题,我们需要将电路中的各个元件进行建模,并建立它们之间的数学关系。
微分方程提供了一种有效的建模方法。
以简单的电路为例,假设一个由电阻R、电感L和电容C组成的串联电路,电源为直流电源V(t)。
我们可以根据基尔霍夫定律建立以下微分方程:L(di/dt) + Ri + q/C = V(t)其中,i是电流,q是电容器的电荷量。
这个微分方程描述了电感、电阻和电容之间的关系。
二、微分方程的解法解决微分方程可以采用不同的方法,如分离变量法、变量代换法、特解法等。
在电路问题中,我们通常使用拉普拉斯变换和复变函数等方法来求解微分方程。
以上述电路问题为例,我们可以通过拉普拉斯变换将微分方程转化为代数方程,进而求解电流i(t)和电荷量q(t)的表达式。
通过求解微分方程,我们可以获得电路中各个物理量随时间的变化规律。
三、实例分析为了更好地理解微分方程与电路问题的应用,我们来看一个实际的例子。
假设有一个由电阻R和电感L组成的串联电路,电源为交流电源V(t) = V0 sin(ωt)。
我们希望求解电路中的电流i(t)。
根据基尔霍夫定律和欧姆定律,我们可以建立以下微分方程:L(di/dt) + Ri = V0 sin(ωt)通过拉普拉斯变换,我们可以将上述微分方程转化为代数方程:(sL + R)I(s) = V0/[(s^2 + ω^2)]其中,I(s)是电流的拉普拉斯变换,s是复变函数。
通过求解代数方程,我们可以得到电流的拉普拉斯变换表达式:I(s) = V0/[(s^2 + ω^2)(sL + R)]然后,我们可以通过拉普拉斯逆变换将I(s)转化为时间域的电流i(t)。


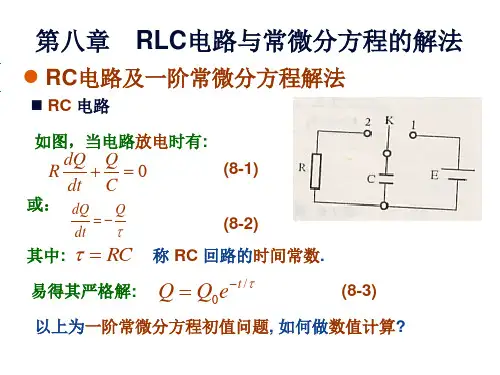
关于RLC 二阶电路的分析方法——电路的微分方程与初始条件
由两个独立储能元件组成的电路,其过渡过程的特征性用二阶微分方程描述,故称为二阶电路。
RLC 串联电路,是典型的二阶电路。
通过对它的分析来明确二阶电路过渡过程的基本概念和分析方法,着重讨论RLC 串联电路的放电过程,即电路的固有响应也就是零输入响应。
也介绍RLC 串联电路的充电过程,即零状态响应和完全响应。
1.电路的微分方程与初始条件
如图4-5所示RLC 串联二阶电
路,0≥t 时以电容电压C u 为变
量描述动态过程特性的微分方程
是图 4-5 RLC 串联二阶电路 022=++C C C u dt du RC dt u d LC
过渡过程中电容电压C u 随时间变化的规律,就是微分方程的解。
方程的求解,需有如下两个初始条件:
)0(C u
C i dt du u L t C C )
0()0(0=='=
只要知道电路的两个初始状态)0(C u 和)0(L i ,按上式便可得出初始条件)0(C u 和)0(C u '。
于是,RLC 串联电路的放电过程的C u ,就是满足上述初始条件齐次微分方程的解;充电过程的C u ,就是满足初始条件非齐次微分方程的解。
+-
C u。


rlc电路微分方程RLC电路微分方程是一种常用的电路理论,用于描述RLC电路的时变行为。
它将电路的物理参数如电阻、电感和电容以方程的形式表达出来,并通过求解该方程,可以求出电路中的电流和电压的时变特性。
RLC电路微分方程的公式为:L\frac{di}{dt} + Ri +\frac{1}{C}\int_{0}^{t}{i(t)dt} = E(t)式中,L、R、C分别代表电路中的电感、电阻和电容,而E(t)是外加电源的电压,单位是伏特(V);i(t)为电路中的电流,单位是安培(A);t为时间,单位是秒(s)。
首先,左边的第一项,即L* d/dt (i),表示电感对电流的时变的影响,电感的电流随时间的变化而变化,即电流的增加会使电感的电流减少;而右边的第二项,即Ri,表示电阻对电路中电流的影响,电阻会限制电流的通过,因此电流与电阻之间存在着成正比的关系;最后,第三项,即1/C * ∫0t i(t) dt,表示电容对电路中电流的影响,电容能够储存电量,因此电容会阻碍电路中电流的通过,当电路中的电流减少时,电容就会向电路中释放电量,从而抵消电路中电流的减少。
最后,右边的E(t)表示外加电源的电压,它受外部环境的影响而发生变化,从而影响电路中电流的大小。
RLC电路微分方程的求解方法主要有两种:一种是采用数值方法,即通过电路的初始条件和外加电源的电压,使用数值积分的方法,求出RLC电路中电流的时变行为;另一种是采用解析方法,即通过对RLC电路微分方程进行求解,求出电路中电流的时变行为。
RLC电路微分方程可以被用来描述各种不同的电路系统,如滤波器、振荡器等,这些电路系统的特性和性能可以通过解决RLC电路微分方程来确定。
此外,RLC电路微分方程也可以用来研究复杂的电子系统,如模拟信号处理、数字信号处理、电磁场分析以及电磁兼容性等,从而提高电子系统的性能和可靠性。
和谐与统一的美——浅谈微分方程的解与电路的响应11123766 齐梦雨前言:如果说数学和物理解释了世界,机械和电气点亮了世界,那么通信则像一扇窗一样呈现了世界。
建立在数学和物理学基础上的通信技术,像一阵光,以难以置信的速度发展着,前进着,它让从前的世界变成了另一个世界,它让未来变得更加难以预见,值得期待。
如果说17世纪和18世纪是数学和物理学的世纪,那么21世纪乃至可以预见的未来,将会是通信的世纪,信息时代将会是通信技术的时代。
任何前沿科技都是建立在理论基础上的,通信技术也不例外。
最基础的通信技术和数学中的微分方程密切相关。
本文我们将会看到,通信技术在工程中的应用,是如何建立在数学基础之上的,而我们也将看到,他们之间“无意”中产生的惊人的一致性和相互契合。
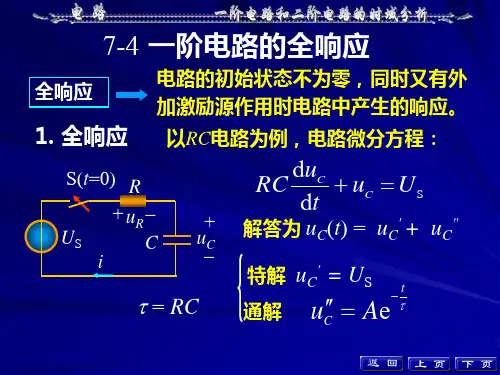
关键词:一阶电路二阶电路电路的激励与响应零状态零输入一阶微分方程二阶微分方程微分方程的通解与特解一、电路响应的数学理论基础首先,我们先看两个简单的电路图:I、II在通信技术中,这是两个最简单最基础的电路图,其中第一个称作RC 电路(电阻+电容),第二个称为RL 电路(电阻+电感)。
在第一个电路中,0 ,i ≥=+t U u dt du RC C C (α) 其中Ui 为输入电压。
其中i =dtdu C C而第二个电路中,0 ,0u iL ≥=+t dt d R L (β)其中Ui 为输入电压。
其中L U i =dtd L而一个最简单也是最基础的问题,就是求电路的响应。
如果抽象成数学问题的话,就是求这两个微分方程的解。
所以,必须掌握一阶微分方程的求解方法。
下面简单介绍一下一阶微分方程的解法:一、关于第二个式子:(1)变量分离方程)()(y g x f dx dy⋅=,或0)()()()(2121=+dy y N x N dx y M x M分离变量即可求解.(2)可化为变量分离方程的类型令 xyu =,可化为变量分离的方程 xuu g dx du -=)( 求解.(3)形如:.222111 分三种情况进行求解方程 C y b x a C y b x a dx dy ++++=当 0,21=C C 时,可化为齐次方程求解. 当 21,C C 不全为零时,但212121c ck b b a a ≠==,我们令 y b x a u 22+=,可将方程化为变量分离方程212222c u c ku b a dx dyb a dx du +++=+= 求解.当21,C C 不全为零时,但2121b b a a ≠,令变换 ⎩⎨⎧+=+=00y Y y x X x其中0x ,0y 是待定常数(即两直线的交点),可将方程化为关于X 与Y 的齐次方程)(2211XYg Y b X a Y b X a dX dY =++= 求解,最后代回原变量即可得原方程的解. 二、关于第一个式子:此即一阶线性微分方程,0)()()(=++x c y x b dxdyx a , )()(x Q y x P dxdy+=, 非齐次线性方程)()(x Q y x P dxdy+=用常数变易法求解. ⎰+⎰⎰=-))(()()(c dx e x Q e y dx x P dxx P 为非齐次线性方程)()(x Q y x P dxdy+=通解公式。
振荡电路微分方程
振荡电路是指能够产生持续振荡的电路,如LC振荡器或RC振荡器。
其中,微分方程用于描述振荡电路中电压或电流随时间变化的关系。
以简单的LC振荡器为例,其中包含一个电感L和一个电容C。
假设电感L的电流为I(t),电容C的电压为V(t)。
根据基尔霍夫电压定律和欧姆定律,可以得到以下微分方程:L * d^2(I(t))/dt^2 + (1/C) * I(t) = 0
这是一个二阶常微分方程,描述了电感电流对时间的二阶导数和电容电压的关系。
该方程表示了电感感应的自感和电容的贮能之间的交互作用。
对于其他类型的振荡电路,如RC振荡器,也可以得到相应的微分方程,但具体形式会根据电路的结构和元件的特性而有所不同。
微分方程是分析和研究振荡电路行为的重要工具。
通过求解微分方程,可以获得电路中电压、电流随时间的变化规律,进而了解振荡频率、幅值等重要的振荡特性。
二阶电路微分方案二阶电路微分方程是描述二阶电路响应的微分方程。
在电路分析中,通过建立微分方程可以解决电路中电流、电压等物理量的变化问题。
二阶电路是指电路中包含两个电感元件或两个电容元件的电路。
在二阶电路中,我们可以通过Kirchhoff定律建立微分方程。
根据Kirchhoff第二定律,电路中的电压和电流满足以下关系:在电感元件上的电压等于电感元件的自感系数乘以电流的导数,而在电容元件上的电压等于电容元件的容值乘以电压的导数。
根据这两个关系,我们可以建立二阶电路的微分方程。
假设我们有一个包含电感元件和电容元件的二阶电路。
设电感元件的自感系数为L,电容元件的容值为C。
根据Kirchhoff定律,我们可以得到以下微分方程:L * di/dt + R * di/dt + 1/C * ∫i(t) dt = V(t)其中,i(t)是电路中的电流,V(t)是电路中的电压,R是电路中的电阻。
这个微分方程描述了电路中电流的变化情况。
为了求解这个微分方程,我们可以使用一些常用的技巧。
例如,可以使用Laplace变换将微分方程转化为代数方程。
另外,也可以使用欧拉公式将微分方程转化为复数形式进行求解。
这些方法可以根据具体的问题选择使用。
在实际应用中,二阶电路微分方程可以用于分析电路中的振荡、滤波等问题。
例如,在无线通信系统中,二阶电路微分方程可以用于分析电路中的振荡器。
在音频系统中,二阶电路微分方程可以用于分析电路中的滤波器。
二阶电路微分方程是描述二阶电路响应的重要方程。
通过建立微分方程,我们可以解决电路中电流、电压等物理量的变化问题。
在实际应用中,二阶电路微分方程可以用于分析电路中的振荡、滤波等问题,具有重要的意义。