材料力学(机械工业出版社)知识小结:第一章 轴向拉伸和压缩
- 格式:doc
- 大小:3.26 MB
- 文档页数:6





材料力学 - 轴向拉伸和压缩材料力学是研究材料性质和行为的学科,包括弹性、塑性、疲劳、断裂等方面。
在材料力学中,轴向拉伸和压缩是重要的力学测试方法。
轴向拉伸测试轴向拉伸测试是材料测试中最常用的测试方法之一。
该测试方法涉及将试验样品拉伸至破裂点,并测量在拉伸过程中的应力和应变。
在这种测试中,试验样品的截面积比长度更重要,因为应力是由试样的横截面积决定的。
实验过程首先,通过切割样品制备试样。
样品应该是长条状,尺寸应该足够大,能够容纳拉伸机的夹具和测量设备。
然后将样品置于拉伸机上,将试样夹具固定在机器的上部,并将另一个夹具固定在机器的下部。
然后将机器调整到适当的测试条件,比如设置测试速度、卸载条件等。
开始拉伸后,由于拉伸过程会导致不均匀应变,需要使用应变计进行应变测量。
最后,测试结果应该包括应力 - 应变曲线和破坏点。
结果解释轴向拉伸测试的结果由两种性质构成:杨氏模量和屈服强度。
杨氏模量衡量材料的弹性变形特性,而屈服强度则衡量材料开始塑性变形的能力。
在拉伸试验中,将出现线性区域,在该区域,样品的杨氏模量可由应力-应变曲线的斜率计算。
当样品的应变超过线性区域后,就会进入塑性区域,此时材料会表现出不可逆的形变特性。
轴向压缩测试轴向压缩测试是一种用于测量材料在压缩负载下的应变和应力的测试方法。
在这种测试中,材料试件放置在压力夹具之间,并受到垂直于试件轴向的载荷。
压缩测试与轴向拉伸测试非常相似,但它们的结果不同。
由于材料的差异,它们所能承受的压缩力和拉伸力也会存在一定的不同。
实验过程样品制备和夹具的选择与轴向拉伸测试类似,但是在拉伸试验机与压缩机之间存在差异。
进行轴向压缩测试时,需要将夹具安装在垂直于轴向的方向上,并将试件放置在夹具内。
与轴向拉伸测试相同,需要记录测试过程中的应变和应力变化。
结果解释与轴向拉伸测试一样,轴向压缩测试的结果也由杨氏模量和屈服强度构成。
杨氏模量是指在材料的弹性变形区域中,材料的应力与应变的比例系数。
第一章轴向拉伸和压缩
1–1轴向拉压的概念及实例
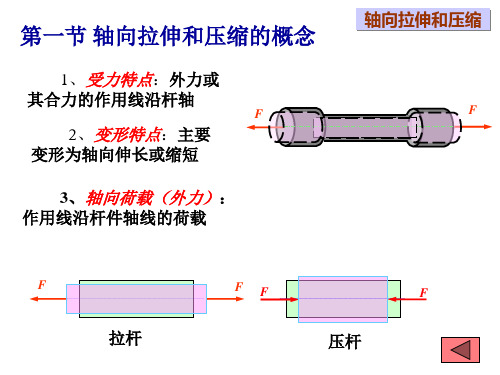
一、概念
轴向拉压的外力特点:外力的合力作用线与杆的轴线重合。
轴向拉压的变形特点:杆的变形主要是轴向伸缩,伴随横向缩扩。
轴向拉伸,对应的力称为拉力。
轴向压缩,对应的力称为压力。
二、工程实例
1–2轴力及轴力图
一、轴力 拉压杆外力作用所引起的内力系的合力是沿轴线方向的一个力,故称为轴力,用N 表示。
2.轴力——轴向拉压杆的内力,用N 表示。
3.轴力的正负规定:
N 与外法线同向,为正轴力(拉力)
N 与外法线反向,为负轴力(压力)
三、轴力图——N (x )的图象表示。
意义:①反映出轴力与横截面位置变化关系,较直观;
②确定出最大轴力的数值及其所在横截面的位置,即确定危险截面位置,为强度计算提供依据。
1–3截面上的应力及强度条件
一、拉(压)杆横截面上的应力
1.变形规律试验及平面假设:
平面假设:原为平面的横截面在变形后仍为平面。
纵向纤维变形相同。
自:平面为平面 均匀材料、均匀变形,内力当然均匀分布。
2.拉伸应力:A
x N )( =σ 轴力引起的正应力——σ:在横截面上均布。
3.危险截面及最大工作应力: 危险截面:内力最大的面,截面尺寸最小的面。
危险点:应力最大的点。
))
()(max( max x A x N =σ 4.强度设计准则(Strength Design ):
保证构件不发生强度破坏并有一定安全余量的条件准则。
[] ))
()(max( max σσ≤=x A x N 其中:[σ]—构件的许用应力,σmax --危险点的最大工作应力。
自:工作应力应小于许用应力
关于许用应力--[σ]:[]n jx σσ=
极限应力:{}b s jx σσσσ,,2.0=材料特性,由试验确定;
安全系数:n>1 综合因素,考虑:材料、受力、工况、安全重要性、计算模型等等 依强度准则可进行三种强度计算:
①校核强度:[] max σσ≤ ②设计截面尺寸:]
[max min σN A ≥ ③许可载荷: []; max σA N ≤[])(i N f P =
5.公式的应用条件:
直杆、杆的截面无突变、截面到载荷作用点有一定的距离。
6.Saint-Venant 原理:
离开载荷作用处一定距离,应力分布与大小不受外载荷作用方式的影响。
7.应力集中(Stress Concentration ):
由于截面尺寸急剧变化而引起的局部应力增大的现象。
应力集中因数 不同性质的材料对应力集中的敏感程度不同
1.脆性材料
σmax 达到强度极限,此位置开裂,所以脆性材料构件对应力集中很敏感。
2.塑性材料
应力集中对塑性材料在静载作用下的强度影响不大,因为σmax 达到屈服极限,应力不再增加,未达到屈服极限区域可继续承担加大的载荷,应力分布趋于平均。
在静载荷情况下,不需考虑应力集中的影响;但在交变应力情况下,必须考虑应力集中对塑性材料的影响。
二、拉(压)杆斜截面上的应力
由平衡方程:Pa =P 则:α
ααA P p = Aa :斜截面面积;P a :斜截面上内力。
由几何关系:ααααcos cos A A A A =⇒=
代入上式,得: ασααααcos cos 0=⋅==A
P A P p 斜截面上全应力:ασαcos 0=p
分解:ασασαα20cos cos ==p ασαασαταα2sin 2sin cos sin 0
0===p
当α = 0°时, )(0max σσα=(横截面上存在最大正应力)
max m K σσ=
当α = 90°时,0)(min =ασ(纵截面上正应力等于零)
当α = ± 45°时,2||0
max στα=(45°斜截面上剪应力达到最大)
当α = 0,90°时,0||min =ατ(纵截面上剪应力等于零)
事实上,通过受力物体内任一点处所取的相互垂直的两个截面上,剪应力总是绝对值相等而正负号相反的。
上述结论称为剪应力互等定理
1-5材料在拉伸和压缩时的力学性能
力学性能:材料在外力作用下表现的有关强度、变形方面的特性。
一、试验条件及试验仪器
1、试验条件:常温(20℃);静载(极其缓慢地加载);标准试件。
2、试验仪器:万能材料试验机;变形仪(常用引伸仪)。
二、低碳钢试件的拉伸图(P -- ⎢L 图)
EA PL L =∆E
EA P L L σε==∆= 三、低碳钢试件的应力--应变曲线(σ --ε 图)
(一)低碳钢拉伸的弹性阶段 (oe 段)
1、op --比例段: σp --比例极限
E σ
ε=αtg =E
2、pe --曲线段:σe --弹性极限
)(n f εσ=
(二)低碳钢拉伸的屈服(流动)阶段 (es 段)
es --屈服段:σs ---屈服极限
滑移线:
三)、低碳钢拉伸的强化阶段(sb段)
1、σb---强度极限
2、卸载定律:
3、冷作硬化:
4、冷拉时效:
(四)、低碳钢拉伸的颈缩(断裂)阶段(bf 段)
1、延伸率:δ
2、面缩率:ψ
3、脆性、塑性及相对性为界以005=δ
四、其它材料拉伸时的机械性能
五、无明显屈服现象的塑性材料
名义屈服应力:σ0.2,即此类材料的失效应力。
64图
六、铸铁拉伸时的机械性能
σbL ---铸铁拉伸强度极限(失效应力)
割线斜率 ; tg α=E 64图
七、材料压缩时的机械性能
σby ---铸铁压缩强度极限;
σby ≈(4~6)σbL
10000100L L L δ-=⨯01000
100A A A ψ-=⨯
1-4拉压杆的变形弹性定律
一、拉压杆的变形及应变(自:没有太大用)
1、杆的纵向总变形:
2、线应变:单位长度的线变形。
3、平均线应变:
4、x 点处的纵向线应变:x
x x ∆∆=→∆d lim 0ε 5、杆的横向变形:ac c a ac -''=∆
6、x 点处的横向线应变:ac
ac ∆='ε 7、泊松比(或横向变形系数)
二、拉压杆的弹性定律
1、等内力拉压杆的弹性定律
“E ”称为材料的弹性模量。
“EA ”称为杆的抗拉压刚度。
2、变内力拉压杆的弹性定律 )
(d )()d (x EA x x N x =∆,⎰⎰=∆=∆L L x EA dx x N dx L )()()( 3、单向应力状态下的弹性定律
1)()(1)d (σεE
x A x N E dx x ==∆= 1:σεE =即
小变形放大图与结构节点位移的求法。
1、怎样画小变形放大图?
a.求各杆的变形量△Li ,如图1;
b.变形图严格画法,图中弧线;
c.变形图近似画法,图中弧之切线。
2、写出图2中B 点位移与两杆变形间的关系
1-6 拉压杆的弹性应变能
一、弹性应变能:杆件发生弹性变形,外力功转变为变形能贮存于杆内,这种能成为应变能(Strain Energy )用“U ”表示。
二、拉压杆的应变能计算:不计能量损耗时,外力功等于应变能。
内力为段常量时∑==n
i i i i i A E L N U 122
三、 拉压杆的比能u :
1L L L
∆=-1L L L L L ε-∆== εμε
'=: εμε'=-或PL NL L EA EA
∆==
单位体积内的应变能。
能量法:利用应变能的概念解决与结构物或构件的弹性变形有关的问题,这种方法称为能量法。
1-7 拉压超静定问题及其处理方法
一、超静定问题及其处理方法
1、超静定问题:单凭静力平衡方程不能确定出全部未知力(外力、内力、应力)的问题。
2、超静定问题的处理方法:平衡方程、变形协调方程、物理方程相结合,进行求解。
3、超静定问题的处理方法步骤:
a.平衡方程;
b.几何方程——变形协调方程;
c.物理方程——弹性定律;
d.补充方程:由几何方程和物理方程得;
e.解由平衡方程和补充方程组成的方程组。
二、装配应力——预应力
1、静定结构无装配应力。
2、静不定结构存在装配应力。
三 、应力温度
1、静定结构无温度应力。
2、静不定结构存在温度应力。
d 1()(d )1d 2d 2
U N x x u V A x σε∆===。