材料力学第二章轴向拉伸和压缩汇编
- 格式:ppt
- 大小:2.88 MB
- 文档页数:5






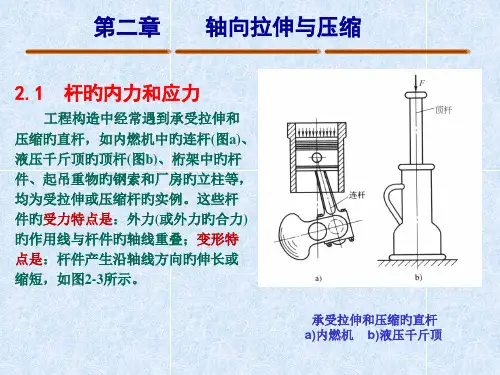
第2章 拉伸、压缩与剪切1、轴向拉伸与压缩概念:作用于杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短。
2、直杆轴向拉伸或压缩时横截面上的内力与应力内力:把拉伸时的轴力(轴力背向截面)为正,压缩时轴力(轴力指向截面)为负。
应力:平面假设(变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线。
)规定:拉应力为正,压应力为负。
AF A dA F N A N =⇒==⎰σσσ 式中N F 为轴力,A 为横截面面积,σ为正应力。
3、直杆轴向拉伸或压缩时斜截面上的应力ασσα2cos = αστα2sin 2= 式中ασ和ατ分别为斜截面的正应力和切应力,σ为横截面的正应力,α为斜截面与横截面的夹角。
4、材料拉伸时的力学性能 应变:ll ∆=ε l ∆为伸长量,l 为原始长度。
(1)弹性阶段:应力σ与应变ε成正比,即εσE =。
其中E 为与材料有关的比例常数,为弹性模量。
直线部分的最高点a 所对应的应力p σ为比例极限。
b 点所对应的应力e σ为弹性极限。
(2)屈服阶段:通常把下屈服极限称为屈服极限或屈服点,用s σ表示。
其是衡量材料强度的重要指标。
(3)强化阶段:强化阶段中的最高点e 所对应的应力b σ是材料能承受的最大应力,称为强度极限。
其是衡量材料强度的另一重要指标。
(4)局部变形阶段:某一局部的横向尺寸急剧缩小,形成缩颈现象。
伸长率:%1001⨯-=ll l δ 塑性材料:%5>δ 脆性材料:%5<δ 断面收缩率:%1001⨯-=A A A ψ A 为原始横截面积,1A 为最小横截面积 5、材料压缩时的力学性能低碳钢压缩时的弹性模量E 和屈服极限s σ与拉伸时相同。
但是得不到强度极限。
铸铁的抗压强度极限比抗拉极限高5~4倍。
6、失效、安全因数和强度计算脆性材料断裂时的应力是强度极限b σ,塑性材料屈服时的应力是屈服极限s σ,这二者是构件失效时的极限应力。



第2章拉伸、压缩与剪切§2-1 轴向拉伸与压缩的概念和实例ACF以轴向拉压为主要变形的杆件,称为拉压杆或轴向承载杆。
§2-2 轴向拉伸或压缩时横截面上的内力和应力F N以1-1截面的右段为研究对象:F N沿轴线方向,所以称为轴力。
F N+直观反映轴力与截面位置变化关系;确定出最大轴力的数值及其所在位置,即确定危险截面位置,为强度计算提供依据。
F N 1A B CF AF B F C F D O OA 段内力F N 1:设截面如图=X 01=−+−+N A B C D F F F F F 05841=−+−+N F F F F FF N 21=∴A B C D F AF BF CF DF N 2F N 3D F DF N 4A B C F AF B F C F D O :段内力:0=−D C F 03=−−D C F F F ,F N 4= FB C D F B F C F D C D F CF D F N 2= –3F ,F N 4= FA B CF A F B F C F D O2F3F 5FF2、变形规律:横向线——仍为平行的直线,且间距增大。
纵向线——仍为平行的直线,且间距减小。
3、平面假设:变形前的横截面,变形后仍为平面且各横截面沿杆轴线作相对平移。
轴向拉压杆横截面上正应力的计算公式σA or =σANor =σAC 45°12B45°AC45°12B 1NF y45°§2-3 直杆轴向拉伸或压缩时斜截面上的应力ασααcos cos cos ==A F A F αp ααxF N F N α§2-4 材料拉伸时的力学性能常温、静载两个塑性指标:%100%5>δ为塑性材料§2-5 材料压缩时的力学性能σbL,铸铁抗压性能远远大于抗拉性§2-7 失效、安全因素和强度计算§2-8 轴向拉伸或压缩时变形(胡克定律的另一种表达方式)1L 1a a1b伸长为正,缩短为负。