表3-6 HL140型水轮机等效率曲线计算表
- 格式:doc
- 大小:70.50 KB
- 文档页数:2


(一)水轮机型号的选择根据题目条件已知要用HL120-38和HL100-40型水轮机进行选择,对比计算分别如下: (二)水轮机主要参数的计算HL120-38型水轮机方案主要参数的计算1、转轮直径的计算1D =式中:'3112500;240;380/0.38/r r N kW H m Q L s m s====同时在附表1中查得水轮机模型在限制工况的效率=88.4%M η,由此可初步假定水轮机在该工况的效率为90.4%将以上各值代入上式得10.999D m == 选用与之接近而偏大的标准直径1 1.00D m =。
2、效率修正值的计算由附表一查得水轮机模型在最优工况下的max =90.5%M η,模型转轮直径10.38M D m =,则原型水轮机的最高效率max η可依下式计算,即max max =1M ηη-(1-1(10.93593.5%=--== 考虑到制造工艺水平的情况取11%ε=;由于水轮机所应用的蜗壳和尾水管的型式与模型基本相似,故认为20ε=,则效率修正值η∆为:max max 10.9350.9050.010.02M ηηηε∆=--=--=由此求出水轮机在限制工况的效率为:0.8840.020.904M ηηη=+∆=+=(与原来假定的数值相同)1、 转速的计算1n =式中'''10101M n n n =+∆有附表一查得在最优工况下的'1062.5/min M n r =,同时由于'1'10110.0160.03M n n n ∆====<所以'1n ∆可以忽略不计,则以'1062.5n =代入上式得:973.3/min n r ==选用与之接近而偏大的标准同步转速1000/min n r =。
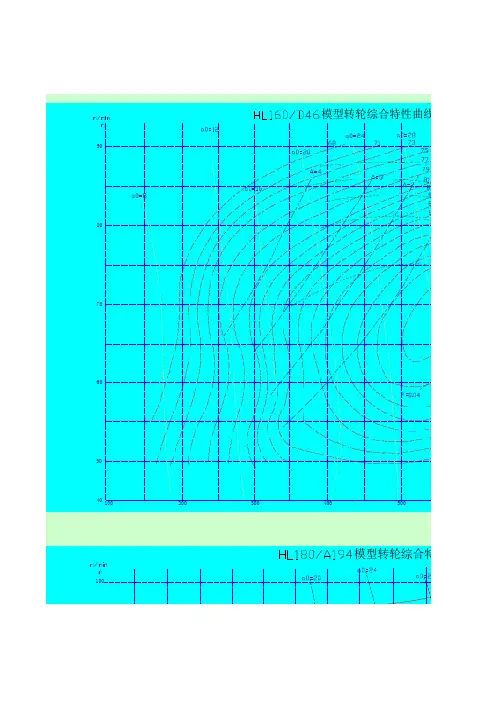
2、 工作范围的验算在选定的1 1.00D m =、1000/min n r =的情况下,水轮机的'1max Q 和各种特征水头下相应的'1n 值分别为:'31max 3232221125000.3790.38/9.8112400.9049.81rrN Q m s D H η===<⨯⨯⨯/ 则水轮机的最大引用流量max Q 为:'23max 1max 1= 1.0/s Q Q D ⨯对'1n 值:在设计水头240r H m =时'164.5/min r n r === 在最大水头max 245H m =时'1min 63.9/min n r === 在最小水头min 235H m =时'1max 65.2/min n r === 在HL120型水轮机的模型综合特性曲线图上,分别画出'1max 379/,Q L s ='1min 63.9/min n r =和'1m 65.2/min ax n r =的直线,如图所示。


船舶下水曲线计算第一篇:船舶下水曲线计算下水曲线计算一.下水时的主要数据船厂L=33.6m 下水重量Wc=130t 重心位置:11.5站处前支架位置:18站重心距前支架:10.92m 龙骨坡度=滑道坡度:3°=0.0523 rad 下水前尾部距离滑道末端15m 二.下水计算1.第二阶段:船体尾部接触水面到船尾开始上浮为止首吃水:dF=dA-L*0.0523=-1.757+0.0523x 尾吃水:dA=0.0523x 重心到滑道末端距离:Sg=x-(15+11.5*1.68)浮心到前支架距离:lb=18*1.68-Xb’ 浮心到滑道末端距离SB=x-(15+Xb’)Xb’为浮心到尾垂线距离利用不同滑行距离的收尾吃水,结合邦戎曲线和辛普森计算第一法,可计算得到每一水线下的浮力和浮心纵向位置。
下水第二阶段计算表如下从图中可得出结论(1)在x1=34.65m处船尾开始上浮(2)船尾上浮时前支架受力R=65.4t(3)第二阶段中Mv>Mw,故不会发生尾落现象2.第三阶段:自船尾开始上浮至前支点离开滑道船尾上浮后,前支点滑动,船体绕前支点转动,故收尾吃水不确定,采用如下方法确定某一下滑时刻的排水:对于某一行程假设一尾吃水,分别算该吃水下排水和矩,利用图形确定真实尾吃水。
辅助表格和辅助曲线如图。
图中可得M’w与M’v相交是排水量wv=61.19t 同理,43m,46m时可得排水量分别为68.76t,70.51t,即可做出尾上浮之后的曲线。
从图中可知,前支架完全离开滑道末端后,重力依旧大于浮力,因此会出现较为严重的首落。
二.曲线分析此下水情况下,会出现严重的首落,并且Mv与Mw交点与X1距离很近,实际工程中极容易发生尾落,因此可加大滑道入水部分长度,即,采用更高的水位。
备注:美观起见,下水曲线的绘制采取了如下比例下滑距离X100 重力对前支点矩X1 浮力对前支点矩X1 重量对滑道末端矩X0.2 浮力对滑道末端矩X0.2 重力X10 浮力X10 X1=34.65 X2=45.24第二篇:船舶下水方法船舶下水分重力式下水、漂浮式下水和机械化下水重力式下水适合绝大多数船舶。
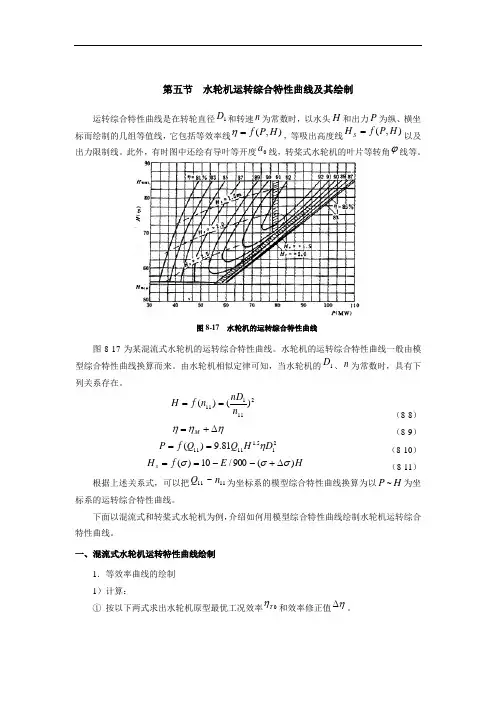
第五节 水轮机运转综合特性曲线及其绘制运转综合特性曲线是在转轮直径1D 和转速n 为常数时,以水头H 和出力P 为纵、横坐标而绘制的几组等值线,它包括等效率线),(H P f =η,等吸出高度线),(H P f H S =以及出力限制线。
此外,有时图中还绘有导叶等开度0a 线,转桨式水轮机的叶片等转角ϕ线等。
图8-17 水轮机的运转综合特性曲线图8-17为某混流式水轮机的运转综合特性曲线。
水轮机的运转综合特性曲线一般由模型综合特性曲线换算而来。
由水轮机相似定律可知,当水轮机的1D 、n 为常数时,具有下列关系存在。
211111)()(n nD n f H == (8-8)ηηη∆+=M (8-9) 215.1111181.9)(D H Q Q f P η== (8-10)H E f H s )(900/10)(σσσ∆+--== (8-11)根据上述关系式,可以把1111~n Q 为坐标系的模型综合特性曲线换算为以P ~H 为坐标系的运转综合特性曲线。
下面以混流式和转桨式水轮机为例,介绍如何用模型综合特性曲线绘制水轮机运转综合特性曲线。
一、混流式水轮机运转特性曲线绘制1.等效率曲线的绘制 1)计算:① 按以下两式求出水轮机原型最优工况效率0T η和效率修正值η∆。
11500)1(1D D MM T ηη--= (8-12)00M T ηηη-=∆ (8-13)为简化计算,其他工况的效率修正值也采用η∆。
② 求水轮机的最优单位转速011n 和单位转速修正值11n ∆。
③ 在最小水头min H 和最大水头max H 范围内进行分段,一般可取4~5个水头,其中包括min H 、r H 和max H ,并分别计算各水头对应应的单位转速11n 。
④ 求各选取水头相应的模型单位转速M n 11111111111n HnD n n n M ∆-=∆-= (8-14)⑤ 在模型综合特性曲线图上作各M n 11的水平线,得到与模型综合特性曲线等效率曲线交点的坐标值M Q 11和M η。

第四章 水轮机的特性曲线与选型第一节 水轮机的相似律一、水轮机的相似条件在进行模型试验时,模型与原型水轮机之间应满足的条件称为水轮机的相似条件。
模型和原型水轮机之间应满足几何相似、运动相似和动力相似三个相似条件。
1.几何相似(必要非充分)(同轮系)几何相似是指两个水轮机的过流部件形状相同(即过流部件几何形状的所有对应角相等),尺寸大小成比例。
即:===mmma ab b D D 000011式中 :01b D 、、0a ——水轮机的转轮直径、导叶高度、导叶开度。
满足几何相似的一系列大小不同的水轮机,称为同轮系(或同型号)水轮机。
只有同轮系的水轮机才能建立起运动相似或动力相似。
2.运动相似(等角工作状态)运动相似是指同一轮系的水轮机,水流在过流通道中对应点的同名流速方向相同,大小成比例,即相应点的速度三角形相似。
即两水轮机运动相似就称此两水轮机为等角工作状态。
3.动力相似动力相似是指同一轮系水轮机在等角工作状态下,水流在过流部件对应点的作用力(惯性力、重力、粘滞力、摩擦力等),同名力的方向相同,大小成比例。
二、轮机的相似律在满足相似条件的基础上原型与模型水轮机各参数之间的相互关系称为水轮机的相似律,也称为水轮机的相似公式。
1.转速相似律s m sm mH D H D n nηη11=s H D n η11∝2.流量相似律sm m msvmm vH D H D Q Q ηηηη2121=s VH D Q ηη21∝式中:v Q η—有效流量。
称为水轮机的流量相似律,亦称为流量方程式。
在应用中,直径m D 1、1D 、水头m H 、H 为定值,若效率vm η、sm η、v η、s η为已知时,则可由测得的m Q 求得原型水轮机的流量Q 。
3.出力相似律()()jmsm m m j s mH D H D N N ηηηη23212321=2321s H D N η∝称为水轮机的出力相似律,亦称出力方程式。


水电站作业水轮机型号及主要参数的选择:已知某水电站最大水头H max=245m,加权平均水头H av=242.5m,设计水头H r=240m,最小水头H min=235m,水轮机的额定出力为12500kw,水电站的海拔高程为2030m,最大允许吸出高Hs≥-4.0m。
要求:1、选择两种机型(HL120-38,HL100-40)进行选择。
2、对选择的机型进一步绘制其运转特性曲线,`(一)水轮机型号的选择根据题目条件已知要用HL120-38和HL100-40型水轮机进行选择,对比计算分别如下: (二)水轮机主要参数的计算HL120-38型水轮机方案主要参数的计算1、转轮直径的计算1D =式中:'3112500;240;380/0.38/r r N kW H m Q L s m s====同时在附表1中查得水轮机模型在限制工况的效率=88.4%M η,由此可初步假定水轮机在该工况的效率为90.4%将以上各值代入上式得10.999D m ==选用与之接近而偏大的标准直径1 1.00D m =。
2、效率修正值的计算由附表一查得水轮机模型在最优工况下的max =90.5%M η,模型转轮直径10.38M D m =,则原型水轮机的最高效率max η可依下式计算,即max max =1M ηη-(1-1(10.93593.5%=--== 考虑到制造工艺水平的情况取11%ε=;由于水轮机所应用的蜗壳和尾水管的型式与模型基本相似,故认为20ε=,则效率修正值η∆为:max max 10.9350.9050.010.02M ηηηε∆=--=--=由此求出水轮机在限制工况的效率为:0.8840.020.904M ηηη=+∆=+=(与原来假定的数值相同)3、 转速的计算1n =式中'''10101M n n n =+∆有附表一查得在最优工况下的'1062.5/min M n r =,同时由于'1'10110.0160.03M n n n ∆====<所以'1n ∆可以忽略不计,则以'1062.5n =代入上式得:973.3/min n r ==选用与之接近而偏大的标准同步转速1000/min n r =。
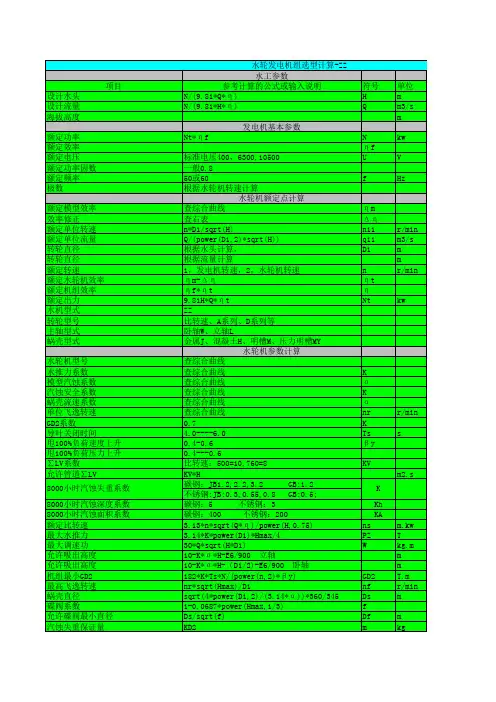

水轮机型号选择根据已知的水能参数初选水轮机型号最大工作水头:H max=Z上max-Z 下min-△h=609.86-573.12-1.732=35 m 最小工作水头:H min=Z 上min-Z 下max-△h=607.78-574.27-1.732=31.77m平均水头:1 1H a= (H max+H min)= X (35.85+31.35)=33.4 m2 2查水电站机电设备手册根据我国小型反击式水轮机适应范围参考表初选水轮机型号。
初选水轮机型号:HL240-LJ-140水轮机类型混流式转轮型号HL240最大水头35m最小水头31.77m设计水头33m出力3400kw校核机组的稳定性水轮机主要参数的计算:HL240-LJ-140型水轮机方案主要参数的计算转轮直径计算Nr=3400/0.95=3368.42kw Hr=33.4mD i=,——Nr—(1-3).9.81Q i Hr 2M式中:Nr-为水轮机的额定出力(kw)D 1 -为水轮机的转轮直径(mn M-为水轮机的效率Hr-为设计水头(m)Q 1'--为水轮机的单位流量(m/s)由水力机械课本附表1中查得Q'=12.4 L/s=1.24m3/s,同时在附表1中查得水轮机模型在限制工况下的效率 n 沪90.4%,由此可初步假定水轮机在该工况的效率为92.0%将 Nr=3400kw, Q i '=1.24 m 3/s, Hr=33.4m,n M =92%#3368.429.81 1.24 33.4320.92选择与之接近而偏大的标准直径 D=1.40m 效率的修正值计算由水力机械课本附表1查得水轮机模型在最优工况下的效率 型转轮直径Di M =0.46m,则原型水轮机的最高效率n max ,即:式中:n max --为原型水轮机的最高效率n Mma --为水轮机模型在最优工况下的效率D 1M --为模型转轮直径 (m D 1 --为原型转轮直径(m将 n Mma =91.0% , Di M =0.46m, D 1=1.4m 带入得:n Mma =1- ( 1- n max ) 5 nD 1=92.8%考虑到制造工艺水平的情况取 & 1=1%由于水轮机所应用的蜗壳和尾水管的型式与模型基本相似,故认为& 2=0,则效率修正值△ n 为:△ n = n ma - n Mmax - £ 1式中:△ n --为效率修正值n max --为原型水轮机的最咼效率 n Mma --为水轮机模型在最优工况下的效率 将 n max=0.928, n Mmax=0.91 £ 1= 0.01 带入上式得:= 1.12mn Mma =89.6%,模n ma =1- (1-4)D 1M =1- (1-0.91 )0.46 1.4(1- n Mma )D 1 MD 1△ n = n max-n Max- & 1=0.928-0・91-0.01=0・008由此求得水轮机在限制工况的效率为:n =n M +^ n =0.904+0.008=0.912 (与原来假定的数值相近) 转速的计算n 。
水电站出力不足的原因分析及解决办法Cause Analysis and Solution to Output Deficiency of a Hydropower Station黄少敏Huang Shaoming(福建水利电力职业技术学院福建永安366000)(Fujian Institute of Hydraulic and Electric Technology, Yong’an, 366000)【摘要】本文是按照运行中的一座水电站出现出力不足的现象,针对该水电站出力不足现象的原因进行分析,并提出适合实际需要的解决办法。
【Abstract】Based on the output deficiency phenomena of a hydropower station observed during operation, t he underlying reasons for output deficiency of the station are analyzed in this paper, and a practical solution is suggested to deal with this problem。
【关键词】水电站;出力不足;原因分析;解决办法;【Keywords】Hydropower Station;Output deficiency;Cause analysis;Solution;永安亿泉发电有限公司位于文川溪中上游河段,是永安境内文川溪梯级工程中,装机规模最大、具有调节库容的龙头电站,能对下游各梯级电站起调节作用。
坝址上游流域面积为541平方千米,水库总库容为×108 m3。
水电站正常蓄水位为m,死水位为m,设计洪水位为m,校核洪水位为m;调洪库容为×106 m3,调节库容×106 m3。
水电站装设两台2×5000 KW的立式水轮发电机组,连年平均年发电量为×107kwh,年利用小时数为4130h,连年平均年利用小时数为3560h;保证出力为9800 KW,水轮机型号为HL250—LJ—140,额定转速为375 r/min,单机额定流量为s,最大水头,额定水头为m,最小水头m;发电机型号为SF5000-16/3250,额定容量为5000 KW,额定转速为375转/分。
课程设计任务书学院专业班课程名称题目任务起止日期:年月日~年月日学生姓名学号指导教师年月日教研室主任年月日审查院长年月日批准一、课程设计的目的和任务1、目的:通过水轮机的课程设计,将各种水轮机的性能参数整理并绘制成不同形式的曲线,它是与水轮机课程教学相辅助的一个理论学习的环节,也是课程教学中一个必不可少的环节。
通过水轮机课本章节的相关理论知识的学习后,再通过课程设计的环节以达到巩固和加强理论知识的目的,进一步培养学生独立思考、严谨工作的能力;此外,通过课程设计更进一步掌握造型、设计、参数等程序内容,提高了学生查阅资料和动手实践的能力。
2、课程设计的任务:通过所给的原始资料,根据要求明确水轮机的基本工作参数(包括水头H、流量Q、转速n、效率 、出力P、吸出高度H S、转轮直径D、水轮机型号、机组台数、装置方式等),整理并绘制成不同形式的曲线,即获得水轮机的特性曲线图。
二、电站基本参数G水电站具有防洪,灌溉,发电,养殖等功能。
水电站厂房为坝后式,水电站装机容量为7MW,厂房所在平均地面高程440.0m。
水位:正常蓄水位为470.00m.死水位:459.00m。
距厂房下游100m处水位流量关系见下表格三、水电站水头范围:H=39M,H min=28M,H av=33Mmax水轮机的简介水轮机是一种将河流中蕴藏的水能转换成旋转机械能的原动机,当水流流过水轮机时,通过主轴带动发电机,将旋转机械能转换成电能。
与发电机连接成的整体称为水轮发电机组,它是水电站的主要设备部分。
水电站是借助水工建筑物和机电设备将水能转换成为电能的企业,在未来,水能资源的开发和利用将成为资源开发利用的主导能源,所以,水轮机的设计开发对我国水能资源的开发起到很大的推进作用。
水轮机大致分为两大类:反击式水轮机和冲击式水轮机;反击式水轮机:转轮利用水流的压力能和动能做工的水轮机称为反击式水轮机。
其特征是:压力水流充满水轮机的整个流道,水流流经转轮叶片时,受叶片的作用面改变压力、流速的大小和方向,同时水流在转轮叶片正反面产生压力差,对转轮产生反作用力,形成旋转力矩使转轮旋转。