2018届高中数学苏教版 直线、平面垂直的判定及其性质 单元测试 Word版 含答案

直线与平面垂直的判定及其性质测试题(答案)直线与平面垂直的判定与性质一、选择题1．两异面直线在平面α内的射影（）A．相交直线 B．平行直线C．一条直线—个点 D．以上三种情况均有可能2．若两直线a与b异面，则过a且与b垂直的平面（）A．有且只有—个 B．可能存在也可能不存在C．有无数多个 D．—定不存在3．在空间，下列哪些命题是正确的（）①平行于同一条直线的两条直线互相平行；②垂直于同一条直线的两条直线互相平行；③平行于同一个平面的两条直线互相平行；④垂直于同—个平面的两条直线互相平行．A．仅②不正确 B．仅①、④正确 C．仅①正确 D．四个命题都正确4．若平面α的斜线l在α上的射影为l′，直线b∥α，且b⊥l′，则b与l（）A．必相交 B．必为异面直线 C．垂直 D．无法确定5．下列命题①平面的每条斜线都垂直于这个平面内的无数条直线；②若一条直线垂直于平面的斜线，则此直线必垂直于斜线在此平面内的射影；③若平面的两条斜线段相等，则它们在同一平面内的射影也相等；④若一条线段在平面外并且不垂直于这个平面，则它的射影长一定小于线段的长．其中，正确的命题有（）A．1个 B．2个 C．3个 n 4个6．在下列四个命题中，假命题为（）A．如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直B．垂直于三角形两边的直线必垂直于第三边C．过点A垂直于直线a的所有直线都在过点A垂直于a的平面内D．如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面7．已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD内，若P到这四边形各边的距离相等，那么这个四边形是（）A．圆内接四边形 B．矩形 C．圆外切四边形 D．平行四边形8．在△ABC中，AB＝AC＝5，BC＝6，PA⊥平面ABC，PA＝8，则P到BC 的距离等于（）A．5 B．25 C．35 D．45二、填空题9．AB是平面α的斜线段，其长为a，它在平面α内的射影A′B的长为b，则垂线A′A_________．10．如果直线l、m与平面α、β、γ满足：l＝β∩γ，l⊥α，α和m⊥γ，现给出以下四个结论：①α∥γ且l⊥m；②αγ且m∥β③αβ且l⊥m；④αγ且l⊥m；其中正确的为“________”．（写出序号即可）11．在空间四面体的四个面中，为直角三角形的最多有____________个．12．如图，正方形ABCD，P是正方形平面外的一点，且PA⊥平面ABCD 则在△PAB、△PBC、△PCD、△PAD、△PAC及△PBD中，为直角三角形有_________个．13．给出以下四个命题（1）两条平行直线在同一平面内的射影一定是平行直线；（2）两条相交直线在同一平面内的射影一定是相交直线；（3）两条异面直线在同一平面内的射影—定是两条相交直线；（4）一个锐角在平面内的射影一定是锐角．其中假命题的共有_________个．14．若一个直角在平面α内的射影是一个角，则该角最大为___________．三、解答题15．已知直线a∥平面α,直线b⊥平面α，求证：a⊥b．16．如图，在长方体AC1中，已知AB＝BC＝a，BB1＝b（b＞a），连结BC1，过Bl作B1⊥BC1交CC1于E，交BC1于Q，求证：AC⊥平面EBlD117．如图在△ABC中，已知∠ABC＝90°，SA⊥△ABC所在平面，又点A 在SC和SB上的射影分别是P、Q．求证：PQ⊥SC．18．已知在如图中，∠BAC在平面α内，点α，PE⊥AB，PF⊥AC，PO⊥α，垂足分别是E、F、O，PE＝PF，求证：∠BAO＝∠CAO，19．已知：点P与直线a，试证；过点P与a垂直的直线共面．20．四面体ABCD的棱AB⊥CD的充要条件是AC2＋BD2＝AD2＋BC2．四、思考题对于一个三角形，它的三条高线总相交于—点，而对于一个四面体，它的四条高线是否总相交于一点呢?若不总相交于一点，则怎样的四面体其四条高线才相交于一点呢?这是一个美丽而非凡的问题，请读者进行研究拓展．参考答案一、选择题1．D 2．B 3．B 4．C 5．A 6．A 7．C 8．D二、填空题9．a－b 10．③、④ 11．4 12．5 13．4 14．180°三、解答题 2215．证明：设β为过a的平面，且α∩β＝l．∵a∥α，∴a∥l．∵b⊥l，∴b⊥a．16．证明：∵AB⊥面B1C，BC1为AC1在平面B1C上的射影，且B1E⊥BC1，∴由三垂线定理知B1E⊥AC1．又∵AA1⊥面A1C1，AB＝BC，A1C1⊥B1D1，A1C1是AC1在面A1C1上的射影∴由三垂线定理得AC1⊥B1D1．又∵B1E∩B1D1＝B1，∴AC1⊥平面EB1D1．17．证明：∵SA⊥面ABC，面ABC，∴SA⊥BC．又∵AB⊥BC且SA∩AB＝A，∴BC⊥面SAB，面SAB．∴BC⊥AQ，又AQ⊥SB，BC∩SB＝B．∵AQ⊥面SBC．∴PQ是斜线AP在平面SBC上的射影，又∵AQ⊥SC，∴由三垂线定理的逆定理可得PQ⊥SC．18．证明：∵PO⊥α，PE＝PF，∴OE＝OF，又∵PE⊥AB、PF⊥AC，∴OE⊥AB、OF⊥AC．故Rt△AOE≌Rt△AOF，∴∠BAO＝∠CAO．19．证明：如图，在点P和直线a所在的平面β内，过点P作直线a 的垂线b，设垂足为A．设过点P与β垂直的直线为c，则必有c⊥a，再设由b、c确定的平面为α，则必有a⊥α．设l是过点P与a垂直的直线，下证：α．若α，设由l与c确定的平面为α′，则由a⊥l，a⊥c，l∩c＝P，∴a⊥α′，这样平面α与α′都是过点P与直线a垂直的平面．这是一个错误的结论，因此，假设不成立，故必有α，也就是说过点P与a垂直的直线均在平面α内，于是本题获证．20．证明：先证必要性：过B作CD的垂线，垂足E，连AE，∵CD⊥AB，∴CD⊥平面ABE，∴CD⊥AE．∴AC2＝AE2＋CE2、BD2＝BE2＋DE2；又有AD2＝AE2＋DE2、BC2＝BE2＋CE2．∴AC2＋BD2＝AE2＋BE2＋CE2＋DE2，而AD2＋BC2＝AE2＋BE2＋CE2＋DE2．∴AC2＋BD2＝AD2＋BC2．再证充分性：过A点作CD的垂线，垂足设为F，于是有：AD2＝AF2＋DF2、BC2＝BE2＋CE2；AC2＝AF2＋CF2、BD2＝BE2＋DE2；∵AD2＋BC2＝AC2＋BD2；∴AF2＋DF2＋BE2＋CE2＝AF2＋CF2＋BE2＋DE2∴DF2＋CE2＝CF2＋DE2，∴DF2―CF2＝DE2―CE2，∴（DF＋CF）（DF－CF）＝（DE＋CE）（DE－CE），∴DF－CF＝DE－CE．∴DF＋CE＝DE＋CF．∴E、F只能重合于一点，故有CD⊥平面ABE，∴CD⊥AB．四、思考题我们称：三对对棱分别互相垂直的四面体为对棱垂直的四面体．可以证明：对棱垂直的四面体的四条高线相交于一点，反过来，若一个四面体，若它的四条高线相交于一点，则该四面体一定是对棱垂直的四面体．。

温馨提示：此题库为Word 版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，关闭Word 文档返回原板块。

考点36 直线、平面垂直的判定及其性质一、选择题1.(2016·新课标全国Ⅱ高考理科·T4)已知m,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m,l ⊥n,l ⊄α,l ⊄β,则 ( ) A.α∥β且l ∥α B.α⊥β且l ⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l【解题指南】结合已知的线面关系,画出图形,分析推断得正确结论. 【解析】选D 因为m,n 为异面直线,所以过空间内一点P ,作//,//m m n n '',则,l m l n ''⊥⊥,即l 垂直于m '与n '确定的平面γ,又m ⊥平面α,n ⊥平面β,所以m '⊥平面α,n '⊥平面β,所以平面γ既垂直平面α,又垂直平面β,所以α与β相交,且交线垂直于平面γ,故交线平行于l ,选D.2.(2016·浙江高考文科·T4)设m,n 是两条不同的直线,α,β是两个不同的平面 ( )A.若m ∥α,n ∥α,则m ∥nB.若m ∥α,m ∥β,则α∥βC.若m ∥n,m ⊥α,则n ⊥αD.若m ∥α,α⊥β,则m ⊥β 【解题指南】根据线、面平行、垂直的定义与性质判断.【解析】选C. A 选项中m 与n 还有可能相交或异面;B 选项中α与β还有可能相交;D 选项中m 与β还有可能平行或m ⊂β.3. （2016·山东高考理科·Ｔ4）已知三棱柱ABC-A 1B 1C 1的侧棱与底面垂直,体积为49,底面积是边长为3的正三角形，若P 为底面A 1B 1C 1的中心,则PA 与平面ABC 所成角的大小为 ( ) A.125π B.3π C.4π D.6π【解题指南】本题考查直线与平面所成的角，注意线面角的做法：垂-连-证-求.【解析】选 B. 取正三角形ABC 的中心O ，连结OP ,则PAO ∠是PA 与平面ABC 所成的角.322AD ==,2231332AO AD ==⨯=.三棱柱的体积为211924AA ⨯=,解得1AA =1OP AA ==所以tan OPPAO OA∠==3PAO π∠=.4. （2016·大纲版全国卷高考文科·Ｔ11）与（2016·大纲版全国卷高考理科·Ｔ10）相同已知正四棱柱1111112,ABCD A B C D AA AB CD BDC -=中，则与平面所成角的正弦值等于（ ）A.23B.3 C.3D.13【解题指南】利用体积相等法求出三棱锥1BDC C -的高为h 即可确定CD 与平面1BDC 所成角的正弦值.【解析】选A.如图，设a AB =，则a AA 21=，三棱锥1BDC C -的高为h ，CD 与平面1BDC 所成的角为α.因为BD C C BD C C V V --=11，即a a ah a 22131223221312⨯⨯=⨯⨯⨯，解得a h 32=.所以32sin ==CD h α. 5.(2016·浙江高考理科·T10)在空间中,过点A 作平面π的垂线,垂足为B,记B=f π(A).设α,β是两个不同的平面,对空间任意一点P ,Q 1=f β[f α(P)],Q 2=f α[f β(P)],恒有PQ 1=PQ 2,则 ( ) A.平面α与平面β垂直B.平面α与平面β所成的(锐)二面角为45°C.平面α与平面β平行D.平面α与平面β所成的(锐)二面角为60°【解题指南】充分理解题意,依据立体几何中的面面之间的位置关系判断.【解析】选A.由于P 是空间任意一点,不妨设P ∈α,如图所示,则Q 1=f β[f α(P)]=f β(P),Q 2=f α[f β(P)]=f α(Q 1),又PQ 1=PQ 2,显然B,C,D 不满足,故选A. 二、解答题6. （2016·重庆高考文科·Ｔ19）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，PA =2BC CD ==，3ACB ACD π∠=∠=．（Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）若侧棱PC 上的点F 满足7PF FC =，求三棱锥P BDF -的体积． 【解题指南】直接利用线面垂直的判定定理证明BD ⊥平面PAC ,通过转化可求解三棱锥的体积.【解析】（Ⅰ）证明:因CD BC =,即BCD ∆为等腰三角形,又ACD ACB ∠=∠,故AC BD ⊥.因为PA ⊥底面ABCD ，所以BD PA ⊥.从而BD 与平面PAC 内两条相交直线AC PA ,都垂直,所以BD ⊥平面PAC . （Ⅱ）三棱锥BCD P -的底面BCD 的面积.332sin 2221sin 21=∙∙∙=∠∙∙=∆πBCD CD BC S BCD由PA ⊥底面ABCD ，得.23233131=∙∙=∙=∆-PA S V BCD BCD P由FC PF 7=,得三棱锥BCD F -的高为PA 81,故.4132813318131=∙∙∙=∙=∆-PA S V BCD BCD F所以.47412=-=-=---BCD F BCD P BDF P V V V7.（2016·广东高考文科·Ｔ18）如图①，在边长为1的等边∆ABC 中，,D E 分别是,AB AC 边上的点，AD AE =，F 是BC 的中点，AF 与DE 交于点G ，将ABF ∆沿AF 折起，得到如图②所示的三棱锥A BCF -，其中BC =．① ② (1) 证明：DE //平面BCF ； (2) 证明：CF ⊥平面ABF ；(3) 当23AD =时，求三棱锥F DEG -的体积F DEG V -．【解题指南】本题以折叠问题为背景，考查线面平行与垂直的证明及空间几何体体积的求法，对于立体几何中的折叠问题要注意折叠前后变与不变量.【解析】（1）在等边ABC ∆中，AD AE =，所以AD AEDB EC =, 在折叠后的三棱锥A BCF -中也成立，所以//DE BC .因为DE ⊄平面BCF ，BC ⊂平面BCF ，所以//DE 平面BCF ； （2）在等边∆ABC 中，F 是BC 的中点，所以AF BC ⊥①，12BF CF ==.因为在三棱锥A BCF -中，2BC =，所以222,BC BF CF CF BF =+⊥② 因为BF CF F ⋂=，所以CF ⊥平面ABF ；（3）由（1）可知//GE CF ，结合（2）可得GE ⊥平面DFG .111111132323323324F DEG E DFGV V DG FG GE --⎛==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎝⎭. 8. （2016·辽宁高考文科·Ｔ18）如图， AB 是圆O 的直径，PA 垂直圆O 所在的平面，C 是圆O 上的点.()I 求证：平面PAC ⊥平面PBC ;()II 设Q 为PA 的中点, G 为AOC △的重心,求证: QG ∥平面PBC .【解题指南】利用条件证明线线垂直，进而证明线面垂直；借助线线平行去证明线面平行,再由面面平行的性质得到线面平行。

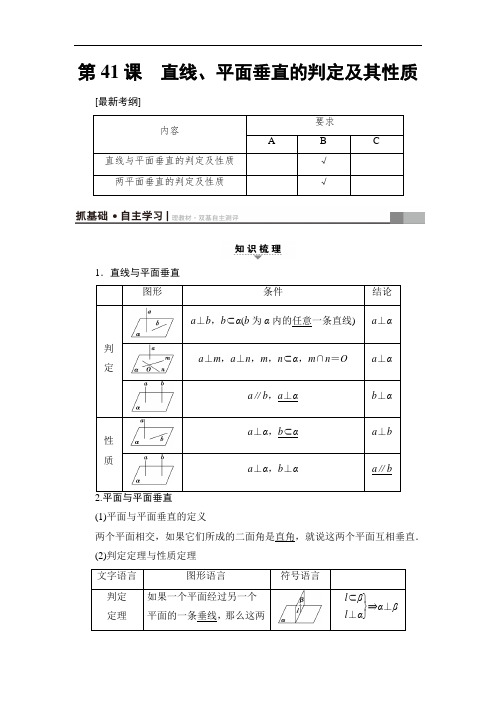
第41课 直线、平面垂直的判定及其性质[最新考纲]1．直线与平面垂直(1)平面与平面垂直的定义两个平面相交，如果它们所成的二面角是直角，就说这两个平面互相垂直． (2)判定定理与性质定理1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)直线l与平面α内的无数条直线都垂直，则l⊥α.()(2)垂直于同一个平面的两平面平行．()(3)若两条直线与一个平面所成的角相等，则这两条直线平行．()(4)若两个平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．()[答案](1)×(2)×(3)×(4)×2．(2017·南京模拟)设l，m是两条不同的直线，α是一个平面，有下列四个命题：(1)若l⊥α，m⊂α，则l⊥m；(2)若l⊥α，l∥m，则m⊥α；(3)若l∥α，m⊂α，则l∥m；(4)若l∥α，m∥α，则l∥m，则其中正确的命题是____________．(填序号)(1)(2)[∵l⊥α，m⊂a，∴l⊥m，故(1)正确；若l⊥α，l∥m，由线面垂直的第二判定定理，我们可得m⊥α，故(2)正确；若l∥α，m⊂α，则l与m可能平行也可能垂直，故(3)错误；若l∥α，m∥α，则l与m可能平行也可能垂直也可能异面，故(4)错误．] 3．如图41-1，已知P A⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．图41-14[∵P A⊥平面ABC，∴P A⊥AB，P A⊥AC，P A⊥BC，则△P AB，△P AC为直角三角形．由BC⊥AC，且AC∩P A＝A，∴BC⊥平面P AC，从而BC⊥PC.∴△ABC，△PBC也是直角三角形．]4．(教材改编)在三棱锥P-ABC中，点P在平面ABC中的射影为点O，(1)若P A＝PB＝PC，则点O是△ABC的____________心．(2)若P A⊥PB，PB⊥PC，PC⊥P A，则点O是△ABC的____________心．(1)外心(2)垂心[∵PO⊥平面ABC，且P A＝PB＝PC，∴OA＝OB＝OC，∴O是△ABC的外心．(2)∵P A⊥PB，P A⊥PC，PB∩PC＝P，∴P A⊥平面PBC，∴P A⊥BC，又PO⊥BC∴BC⊥平面P AO∴AO⊥BC，同理BO⊥AC，CO⊥AB，∴O是△ABC的垂心．]5．边长为a的正方形ABCD沿对角线BD折成直二面角，则折叠后AC的长为________．a[如图所示，取BD的中点O，连结A′O，CO，则∠A′OC是二面角A′-BD-C的平面角．即∠A′OC＝90°，又A′O＝CO＝22a，∴A′C＝a22＋a22＝a，即折叠后AC的长(A′C)为a.]上一点，且AD＝13DB，点C为圆O上一点，且BC＝3AC，PD⊥平面ABC，PD＝DB.图41-2求证：P A⊥CD. 【导学号：62172224】[证明]因为AB为圆O的直径，所以AC⊥CB，在Rt△ABC中，由3AC ＝BC，得∠ABC＝30°.设AD＝1，由3AD＝DB，得DB＝3，BC＝23，由余弦定理得CD2＝DB2＋BC2－2DB·BC cos 30°＝3，所以CD2＋DB2＝BC2，即CD⊥AO.因为PD⊥平面ABC，CD⊂平面ABC，所以PD⊥CD，由PD∩AO＝D，得CD⊥平面P AB，又P A⊂平面P AB，所以P A⊥CD.[规律方法] 1.证明直线和平面垂直的常用方法有：(1)判定定理；(2)垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；(3)面面平行的性质(a⊥α，α∥β⇒a⊥β)；(4)面面垂直的性质．2．证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．[变式训练1] 如图41-3，在三棱锥A -BCD 中，AB ⊥平面BCD ，CD ⊥BD .图41-3(1)求证：CD ⊥平面ABD ；(2)若AB ＝BD ＝CD ＝1，M 为AD 中点，求三棱锥A -MBC 的体积． [解] (1)证明：因为AB ⊥平面BCD ，CD ⊂平面BCD ， 所以AB ⊥CD .又因为CD ⊥BD ，AB ∩BD ＝B ， AB ⊂平面ABD ，BD ⊂平面ABD ， 所以CD ⊥平面ABD .(2)由AB ⊥平面BCD ，得AB ⊥BD . 又AB ＝BD ＝1，所以S △ABD ＝12×12＝12.因为M 是AD 的中点，所以S △ABM ＝12S △ABD ＝14. 根据(1)知，CD ⊥平面ABD ， 则三棱锥C -ABM 的高h ＝CD ＝1， 故三棱锥V A -MBC ＝V C -ABM＝13S △ABM ·h ＝112.如图41-4，三棱台DEF -ABC 中，AB ＝2DE ，G ，H 分别为AC ，BC的中点．图41-4(1)求证：BD∥平面FGH；(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH.[证明](1)如图所示，连结DG，CD，设CD∩GF＝M，连结MH.在三棱台DEF-ABC中，AB＝2DE，G为AC的中点，可得DF∥GC，DF＝GC，所以四边形DFCG为平行四边形．则M为CD的中点，又H为BC的中点，所以HM∥BD，由于HM⊂平面FGH，BD⊄平面FGH，故BD∥平面FGH.(2)连结HE.因为G，H分别为AC，BC的中点，所以GH∥AB.由AB⊥BC，得GH⊥BC.又H为BC的中点，所以EF∥HC，EF＝HC，因此四边形EFCH是平行四边形，所以CF∥HE.由于CF⊥BC，所以HE⊥BC.又HE，GH⊂平面EGH，HE∩GH＝H.所以BC ⊥平面EGH . 又BC ⊂平面BCD ， 所以平面BCD ⊥平面EGH .[规律方法] 1.面面垂直的证明的两种思路：(1)用面面垂直的判定定理，即先证明其中一个平面经过另一个平面的一条垂线；(2)用面面垂直的定义，即证明两个平面所成的二面角是直二面角，把证明面面垂直的问题转化为证明平面角为直角的问题．2．垂直问题的转化关系：线线垂直 判定性质线面垂直 判定性质面面判定性质垂直[变式训练2] 如图41-5，在三棱锥P -ABC 中，平面P AB ⊥平面ABC ，P A ⊥PB ，M ，N 分别为AB ，P A 的中点．图41-5(1)求证：PB ∥平面MNC ；(2)若AC ＝BC ，求证：P A ⊥平面MNC . 【导学号：62172225】 [证明] (1)因为M ，N 分别为AB ，P A 的中点，所以MN ∥PB ， 又因为MN ⊂平面MNC ，PB ⊄平面MNC ， 所以PB ∥平面MNC .(2)因为P A ⊥PB ，MN ∥PB ，所以P A ⊥MN . 因为AC ＝BC ，AM ＝BM ，所以CM ⊥AB . 因为平面P AB ⊥平面ABC ，CM ⊂平面ABC ，平面P AB ∩平面ABC ＝AB . 所以CM ⊥平面P AB .因为P A ⊂平面P AB ，所以CM ⊥P A . 又MN ∩CM ＝M ，所以P A ⊥平面MNC .☞角度1多面体中平行与垂直关系的证明(2016·江苏高考)如图41-6，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.图41-6求证：(1)直线DE∥平面A1C1F；(2)平面B1DE⊥平面A1C1F.[证明](1)在直三棱柱ABC-A1B1C1中，A1C1∥AC.在△ABC中，因为D，E分别为AB，BC的中点，所以DE∥AC，于是DE∥A1C1.又因为DE⊄平面A1C1F，A1C1⊂平面A1C1F，所以直线DE∥平面A1C1F.(2)在直三棱柱ABC-A1B1C1中，A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.又因为A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1，所以A1C1⊥B1D.又因为B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE，所以平面B1DE⊥平面A1C1F.[规律方法] 1.三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化．2．垂直与平行结合问题，求解时应注意平行、垂直的性质及判定的综合应用．☞角度2平行垂直中探索开放问题如图①所示，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图②所示．①②图41-7(1)求证：A1F⊥BE；(2)线段A1B上是否存在点Q，使A1C⊥平面DEQ？并说明理由．[证明](1)由已知，得AC⊥BC，且DE∥BC.所以DE⊥AC，则DE⊥DC，DE⊥DA1，因为DC∩DA1＝D，所以DE⊥平面A1DC.由于A1F⊂平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，CD∩DE＝D，所以A1F⊥平面BCDE，又BE⊂平面BCDE，所以A1F⊥BE.(2)线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：如图，分别取A1C，A1B的中点P，Q，连结PQ，则PQ∥BC.又因为DE∥BC，则DE∥PQ.所以平面DEQ即为平面DEQP.由(1)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点，所以A1C⊥DP.又DP∩DE＝D，所以A1C⊥平面DEQP.从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.[规律方法] 1.对命题条件探索性的主要途径：(1)先猜后证，即先观察与尝试给出条件再证明；(2)先通过命题成立的必要条件探索出命题成立的条件，再证明充分性．2．平行(垂直)中点的位置探索性问题：一般是先根据条件猜测点的位置再给出证明，探索点存在问题，点多为中点或三等分点中某一个，也可以根据相似知识建点．[思想与方法]1．证明线面垂直的方法：(1)线面垂直的定义：a 与α内任一直线都垂直⇒a ⊥α；(2)判定定理1：⎭⎬⎫m ，n ⊂α，m ∩n ＝A l ⊥m ，l ⊥n ⇒l ⊥α； (3)判定定理2：a ∥b ，a ⊥α⇒b ⊥α；(4)面面垂直的性质：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β.2．证明面面垂直的方法．(1)利用定义：两个平面相交，所成的二面角是直二面角；(2)判定定理：a ⊂α，a ⊥β⇒α⊥β.3．转化思想：垂直关系的转化 线线垂直面面判定性质垂直[易错与防范]1．在解决直线与平面垂直的问题过程中，要注意直线与平面垂直的定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化．2．面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可．课时分层训练(四十一)A 组 基础达标(建议用时：30分钟)一、填空题1．已知m 和n 是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m ⊥β的是____________．(填序号) 【导学号：62172226】①α⊥β且m ⊂α；②α⊥β且m ∥α；③m ∥n 且n ⊥β；④m ⊥n 且α∥β.③ [由线线平行性质的传递性和线面垂直的判定定理，可知③正确．]2．(2017·徐州模拟)设l是直线，α，β是两个不同的平面，则下列说法正确的是____________．(填序号)①若l∥α，l∥β，则α∥β；②若l∥α，l⊥β，则α⊥β；③若α⊥β，l⊥α，则l∥β；④若α⊥β，l∥α，则l⊥β.②[①中，α∥β或α与β相交，不正确．②中，过直线l作平面γ，设α∩γ＝l′，则l′∥l，由l⊥β，知l′⊥β，从而α⊥β，②正确．③中，l∥β或l⊂β，③不正确．④中，l与β的位置关系不确定．]3．如图41-8，在正四面体P-ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论不成立．．．的是____________．(填序号)图41-8①BC∥平面PDF；②DF⊥平面P AE；③平面PDF⊥平面P AE；④平面PDE⊥平面ABC.④[因为BC∥DF，DF⊂平面PDF，BC⊄平面PDF，所以BC∥平面PDF，故①正确．在正四面体中，AE⊥BC，PE⊥BC，DF∥BC，所以BC⊥平面P AE，则DF⊥平面P AE，从而平面PDF⊥平面P AE.因此②③均正确．]4．设m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是____________．(填序号)①若m⊥n，n∥α，则m⊥α；②若m∥β，β⊥α，则m⊥α；③若m⊥β，n⊥β，n⊥α，则m⊥α；④若m⊥n，n⊥β，β⊥α，则m⊥α.③[①中，由m⊥n，n∥α可得m∥α或m与α相交或m⊥α，错误；②中，由m∥β，β⊥α可得m∥α或m与α相交或m⊂α，错误；③中，由m⊥β，n⊥β可得m∥n，又n⊥α，所以m⊥α，正确；④中，由m⊥n，n⊥β，β⊥α可得m∥α或m与α相交或m⊂α，错误．]5．如图41-9，在三棱锥D-ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列命题中正确的是________．(填序号)图41-9①平面ABC⊥平面ABD；②平面ABD⊥平面BCD；③平面ABC⊥平面BDE，且平面ACD⊥平面BDE；④平面ABC⊥平面ACD，且平面ACD⊥平面BDE.③[因为AB＝CB，且E是AC的中点，所以BE⊥AC，同理有DE⊥AC，于是AC⊥平面BDE.因为AC⊂平面ABC，所以平面ABC⊥平面BDE.又AC⊂平面ACD，所以平面ACD⊥平面BDE.]6．如图41-10所示，在四棱锥P-ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可) 【导学号：62172227】图41-10DM⊥PC(或BM⊥PC等)[由定理可知，BD⊥PC.∴当DM⊥PC(或BM⊥PC)时，有PC⊥平面MBD.又PC⊂平面PCD，∴平面MBD⊥平面PCD.]7．(2016·全国卷Ⅱ)α，β是两个平面，m，n是两条直线，有下列四个命题：①如果m⊥n，m⊥α，n∥β，那么α⊥β；②如果m⊥α，n∥α，那么m⊥n；③如果α∥β，m⊂α，那么m∥β；④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________．(填写所有正确命题的编号)②③④[对于①，α，β可以平行，也可以相交但不垂直，故错误．对于②，由线面平行的性质定理知存在直线l⊂α，n∥l，又m⊥α，所以m ⊥l，所以m⊥n，故正确．对于③，因为α∥β，所以α，β没有公共点．又m⊂α，所以m，β没有公共点，由线面平行的定义可知m∥β，故正确．对于④，因为m∥n，所以m与α所成的角和n与α所成的角相等．因为α∥β，所以n与α所成的角和n与β所成的角相等，所以m与α所成的角和n与β所成的角相等，故正确．]8．如图41-11，在三棱柱ABC-A1B1C1中，各棱长都相等，侧棱垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是________．图41-11π3[取BC的中点E，连接AE，DE，则AE⊥平面BB1C1C.所以∠ADE为直线AD与平面BB1C1C所成的角．设三棱柱的所有棱长为a，在Rt△AED中，AE ＝32a ，DE ＝a 2.所以tan ∠ADE ＝AE DE ＝3，则∠ADE ＝π3.故AD 与平面BB 1C 1C 所成的角为π3.]9.如图41-12，直三棱柱ABC －A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E .要使AB 1⊥平面C 1DF ，则线段B 1F 的长为____________．图41-1212[设B 1F ＝x ， 因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可得A 1B 1＝2，设Rt △AA 1B 1斜边AB 1上的高为h ，则DE ＝12h .由面积相等得2×2＝h 22＋(2)2，所以h ＝233，DE ＝33.在Rt △DB 1E 中，B 1E ＝⎝ ⎛⎭⎪⎫222－⎝ ⎛⎭⎪⎫332＝66. 由面积相等得66×x 2＋⎝ ⎛⎭⎪⎫222＝22x ， 得x ＝12.]10.(2017·南京模拟)如图41-13，P A ⊥圆O 所在的平面，AB 是圆O 的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.图41-13其中正确结论的序号是____________. 【导学号：62172228】①②③[由题意知P A⊥平面ABC，∴P A⊥BC.又AC⊥BC，且P A∩AC＝A，∴BC⊥平面P AC，∴BC⊥AF.∵AF⊥PC，且BC∩PC＝C，∴AF⊥平面PBC，∴AF⊥PB，又AE⊥PB，AE∩AF＝A，∴PB⊥平面AEF，∴PB⊥EF，故①②③正确．]11．(2017·盐城模拟)如图41-14，在直三棱柱ABC－A1B1C1中，已知AC⊥BC，BC＝CC1.设AB1的中点为D，B1C∩BC1＝E，求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.图41-14[证明](1)由题意知，E为B1C的中点，又D为AB1的中点，因此DE∥AC.因为DE⊄平面AA1C1C，AC⊂平面AA1C1C，所以DE∥平面AA1C1C.(2)因为棱柱ABC－A1B1C1是直三棱柱，所以CC1⊥平面ABC.因为AC⊂平面ABC，所以AC⊥CC1.因为AC⊥BC，CC1⊂平面BCC1B1，BC⊂平面BCC1B1，BC∩CC1＝C，所以AC⊥平面BCC1B1.因为BC1⊂平面BCC1B1，所以BC1⊥AC.因为BC＝CC1，所以矩形BCC1B1是正方形，因此BC1⊥B1C.因为AC，B1C⊂平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.因为AB1⊂平面B1AC，所以BC1⊥AB1.12．(2016·苏州期末)如图41-15，在直四棱柱ABCD-A1B1C1D1中，E，F分别是AB，BC的中点，A1C1与B1D1交于点O.(1)求证：A1，C1，F，E四点共面；(2)若底面ABCD是菱形，且OD⊥A1E，求证：OD⊥平面A1C1FE.【导学号：62172229】图41-15[证明](1)连结AC，因为E，F分别是AB，BC的中点，所以EF是△ABC的中位线，所以EF∥AC.由直棱柱知AA1綊CC1，所以四边形AA1C1C为平行四边形，所以AC∥A1C1.所以EF∥A1C1，故A1，C1，F，E四点共面．(2)连结BD，因为直棱柱中DD1⊥平面A1B1C1D1，A1C1⊂平面A1B1C1D1，所以DD1⊥A1C1.因为底面A1B1C1D1是棱形，所以A1C1⊥B1D1.又DD1∩B1D1＝D1，所以A1C1⊥平面BB1D1D.因为OD⊂平面BB1D1D，所以OD⊥A1C1.又OD⊥A1E，A1C1∩A1E＝A1，A1C1⊂平面A1C1FE，A1E⊂平面A1C1FE，所以OD⊥平面A1C1FE.B组能力提升(建议用时：15分钟)1．如图41-16，在正方形ABCD中，E，F分别是BC，CD的中点，沿AE，AF，EF把正方形折成一个四面体，使B，C，D三点重合，重合后的点记为P，P点在△AEF内的射影为O，则下列说法正确的是____________．(填序号)图41-16①O是△AEF的垂心；③O是△AEF的内心；③O是△AEF的外心；④O是△AEF的重心．①[由题意可知P A，PE，PF两两垂直，所以P A⊥平面PEF，从而P A⊥EF，而PO⊥平面AEF，则PO⊥EF，因为PO∩P A＝P，所以EF⊥平面P AO，所以EF⊥AO，同理可知AE⊥FO，AF⊥EO，所以O为△AEF的垂心．]2．如图41-17，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，底面是以∠ABC为直角的等腰直角三角形，AC＝2a，BB1＝3a，D是A1C1的中点，点F 在线段AA1上，当AF＝________时，CF⊥平面B1DF.图41-17a或2a[∵B1D⊥平面A1ACC1，∴CF⊥B1D.为了使CF⊥平面B1DF，只要使CF⊥DF(或CF⊥B1F)．设AF ＝x ，则CD 2＝DF 2＋FC 2，∴x 2－3ax ＋2a 2＝0，∴x ＝a 或x ＝2a .]3．(2016·四川高考)如图41-18，在四棱锥P -ABCD 中，P A ⊥CD ，AD ∥BC ，∠ADC ＝∠P AB ＝90°，BC ＝CD ＝12AD .图41-18(1)在平面P AD 内找一点M ，使得直线CM ∥平面P AB ，并说明理由；(2)证明：平面P AB ⊥平面PBD .[解] (1)取棱AD 的中点M (M ∈平面P AD )，点M 即为所求的一个点．理由如下：连结CM ，因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM .所以四边形AMCB 是平行四边形，所以CM ∥AB .又AB ⊂平面P AB ，CM ⊄平面P AB ，所以CM ∥平面P AB .(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点)(2)证明：由已知，P A ⊥AB ，P A ⊥CD ，因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交，所以P A ⊥平面ABCD ，所以P A ⊥BD .因为AD ∥BC ，BC ＝12AD ，M 为AD 的中点，连结BM ，所以BC ∥MD ，且BC ＝MD ，所以四边形BCDM 是平行四边形，所以BM ＝CD ＝12AD ，所以BD ⊥AB .又AB∩AP＝A，所以BD⊥平面P AB.又BD⊂平面PBD，所以平面P AB⊥平面PBD.4．⊙O的直径AB＝4，点C，D为⊙O上两点，且∠CAB＝45°，F为BC的中点．沿直径AB折起，使两个半圆所在平面互相垂直(如图①)．①②图41-19(1)求证：OF∥平面ACD；(2)在AD上是否存在点E，使得平面OCE⊥平面ACD？若存在，试指出点E的位置；若不存在，请说明理由．[解](1)证明：由∠CAB＝45°，知∠COB＝90°，又因为F为的中点，所以∠FOB＝45°，因此OF∥AC，又AC⊂平面ACD，OF⊄平面ACD，所以OF∥平面ACD.(2)存在，E为AD中点，因为OA＝OD，所以OE⊥AD.又OC⊥AB且两半圆所在平面互相垂直．所以OC⊥平面OAD.又AD⊂平面OAD，所以AD⊥OC，由于OE，OC是平面OCE内的两条相交直线，所以AD⊥平面OCE.又AD⊂平面ACD，所以平面OCE⊥平面ACD.。

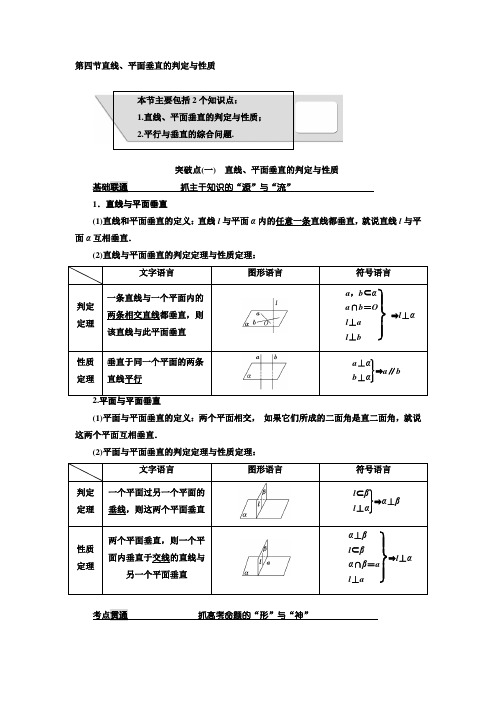
第四节直线、平面垂直的判定与性质本节主要包括2个知识点：1.直线、平面垂直的判定与性质；2.平行与垂直的综合问题.突破点(一)直线、平面垂直的判定与性质1．直线与平面垂直(1)直线和平面垂直的定义：直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直．(2)直线与平面垂直的判定定理与性质定理：(1)平面与平面垂直的定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．(2)平面与平面垂直的判定定理与性质定理：直线与平面垂直的判定与性质[例1]如图所示，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.[证明](1)在四棱锥P-ABCD中，∵PA⊥底面ABCD，CD⊂平面ABCD，∴PA⊥CD.∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC.而AE⊂平面PAC，∴CD⊥AE.(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC.由(1)知AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.而PD⊂平面PCD，∴AE⊥PD.∵PA⊥底面ABCD，∴PA⊥AB.又∵AB⊥AD且PA∩AD＝A，∴AB⊥平面PAD，而PD⊂平面PAD，∴AB⊥PD.又∵AB∩AE＝A，∴PD⊥平面ABE.[方法技巧]证明直线与平面垂直的方法(1)定义法：若一条直线垂直于一个平面内的任意一条直线，则这条直线垂直于这个平面(不常用)；(2)判定定理(常用方法)；(3)若两条平行直线中的一条垂直于一个平面，则另一条也垂直于这个平面(客观题常用)；(4)若一条直线垂直于两个平行平面中的一个平面，则它必垂直于另一个平面(客观题常用)；(5)若两平面垂直，则在一个平面内垂直于交线的直线必垂直于另一个平面(常用方法); (6)若两相交平面同时垂直于第三个平面，则这两个平面的交线垂直于第三个平面(客观题常用)．平面与平面垂直的判定与性质[例2] 如图，四棱锥P -ABCD 中，AB ⊥AC ，AB ⊥PA ，AB∥CD ，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．求证：(1)CE ∥平面PAD ； (2)平面EFG ⊥平面EMN .[证明] (1)法一：如图，取PA 的中点H ，连接EH ，DH .因为E 为PB 的中点， 所以EH ∥AB ，EH ＝12AB .又AB ∥CD ，CD ＝12AB ，所以EH ∥CD ，EH ＝CD ， 因此四边形DCEH 是平行四边形． 所以CE ∥DH .又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD . 法二：如图，连接CF . 因为F 为AB 的中点，所以AF ＝12AB .又CD ＝12AB ，所以AF ＝CD . 又AF ∥CD ，所以四边形AFCD 为平行四边形． 因此CF ∥AD .又CF ⊄平面PAD ，AD ⊂平面PAD ， 所以CF ∥平面PAD .因为E ，F 分别为PB ，AB 的中点，所以EF ∥PA . 又EF ⊄平面PAD ，PA ⊂平面PAD ， 所以EF ∥平面PAD .因为CF ∩EF ＝F ，故平面CEF ∥平面PAD . 又CE ⊂平面CEF ， 所以CE ∥平面PAD .(2)因为E ，F 分别为PB ，AB 的中点， 所以EF ∥PA .又AB ⊥PA ，所以AB ⊥EF . 同理可证AB ⊥FG .又EF ∩FG ＝F ，EF ⊂平面EFG ，FG ⊂平面EFG ， 因此AB ⊥平面EFG .又M ，N 分别为PD ，PC 的中点， 所以MN ∥CD .又AB ∥CD ，所以MN ∥AB ，所以MN ⊥平面EFG . 又MN ⊂平面EMN ， 所以平面EFG ⊥平面EMN .[方法技巧]证明面面垂直的方法(1)利用面面垂直的定义(不常用)；(2)可以考虑证线面垂直，即设法先找到其中一个平面的一条垂线，再证这条垂线在另一个平面内或与另一个平面内的一条直线平行(常用方法)．能力练通 抓应用体验的“得”与“失”1．[考点一]如图，在四棱锥P -ABCD 中，底面ABCD 为菱形，PB ⊥平面ABCD .(1)若AC ＝6，BD ＝8，PB ＝3，求三棱锥A -PBC 的体积； (2)若点E 是DP 的中点，证明：BD ⊥平面ACE . 解：(1)∵四边形ABCD 为菱形， ∴BD 与AC 相互垂直平分，∴底面ABCD 的面积S 菱形ABCD ＝12×6×8＝24，∴S △ABC ＝12S 菱形ABCD ＝12.又PB ⊥平面ABCD ，且PB ＝3，∴三棱锥A -PBC 的体积V A -PBC ＝V P -ABC＝13×PB ×S △ABC ＝12. (2)证明：如图，设BD 与AC 相交于点O ，连接OE ，∵O 为BD 的中点，E 是DP 的中点， ∴OE ∥PB .又PB ⊥平面ABCD ， ∴OE ⊥平面ABCD . ∵BD ⊂平面ABCD ， ∴OE ⊥BD ， 由(1)知AC ⊥BD ，又AC∩OE＝O，∴BD⊥平面ACE.2．[考点一、二]如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD.E和F分别是CD和PC的中点．求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.(2)因为AB∥CD，CD＝2AB，E为CD的中点，所以AB∥DE，且AB＝DE.所以平面ABED为平行四边形．所以BE∥AD.又因为BE⊄平面PAD，AD⊂平面PAD，所以BE∥平面PAD.(3)因为AB⊥AD，而且平面ABED为平行四边形，所以BE⊥CD，AD⊥CD.由(1)知PA⊥底面ABCD，所以PA⊥CD.又PA∩AD＝A，所以CD⊥平面PAD.又PD⊂平面PAD，所以CD⊥PD.因为E和F分别是CD和PC的中点，所以PD∥EF.所以CD⊥EF.又EF∩BE＝E，所以CD⊥平面BEF.因为CD⊂平面PCD，所以平面BEF ⊥平面PCD .突破点(二) 平行与垂直的综合问题1．平行关系之间的转化在证明线面、面面平行时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向是由题目的具体条件而定的，不可过于“模式化”．2．垂直关系之间的转化在证明线面垂直、面面垂直时，一定要注意判定定理成立的条件．同时抓住线线、线面、面面垂直的转化关系，即：在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若这样的直线在图中不存在，则可通过作辅助线来解决.[例1] (2016·江苏高考)如图，在直三棱柱ABC -A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且B 1D ⊥A 1F ，A 1C 1⊥A 1B 1.求证：(1)直线DE ∥平面A 1C 1F ； (2)平面B 1DE ⊥平面A 1C 1F .[证明] (1)在直三棱柱ABC -A 1B 1C 1中，A 1C 1∥AC .在△ABC中，因为D，E分别为AB，BC的中点，所以DE∥AC，于是DE∥A1C1.又因为DE⊄平面A1C1F，A1C1⊂平面A1C1F，所以直线DE∥平面A1C1F.(2)在直三棱柱ABC-A1B1C1中，A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.又因为A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1，所以A1C1⊥B1D.又因为B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE，所以平面B1DE⊥平面A1C1F.[例2](2016·北京高考)如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面PAC；(2)求证：平面PAB⊥平面PAC；(3)设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．[解](1)证明：因为PC⊥平面ABCD，所以PC⊥DC.又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面PAC.(2)证明：因为AB∥DC，DC⊥AC，所以AB⊥AC.因为PC⊥平面ABCD，所以PC⊥AB.又因为PC∩AC＝C，所以AB⊥平面PAC.又AB⊂平面PAB，所以平面PAB⊥平面PAC.(3)棱PB上存在点F，使得PA∥平面CEF.理由如下：取PB的中点F，连接EF，CE，CF，如图所示．因为E为AB的中点，所以EF∥PA.又因为PA⊄平面CEF，且EF⊂平面CEF，所以PA∥平面CEF.[方法技巧]平行与垂直关系中探索性问题的类型及解题策略(1)对命题条件的探索①先猜后证，即先观察并尝试给出条件，再给出证明；②先通过命题成立的必要条件探索出命题成立的条件，再证明条件的充分性；③把几何问题转化为代数问题，探索出命题成立的条件．(2)对命题结论的探索①探索结论是什么，常从条件出发，探索出要求的结论是什么；②探索结论是否存在，常先假设结论存在，再在这个假设下进行推理论证，寻找与条件相符或矛盾的结论，相符则存在，矛盾则不存在．平行与垂直关系中的折叠问题[例3]＝60°，点E，F分别是边CD，CB的中点，AC∩EF＝O.沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2的五棱锥P-ABFED，且PB＝10.(1)求证：BD⊥平面POA；(2)求四棱锥P-BFED的体积．[解](1)证明：∵点E，F分别是边CD，CB的中点，∴BD∥EF.∵ABCD是菱形，∴BD⊥AC，∴EF⊥AC，∴翻折后EF⊥AO，EF⊥PO，∵AO⊂平面POA，PO⊂平面POA，AO∩PO＝O，∴EF⊥平面POA，∴BD⊥平面POA.(2)如图，设AO∩BD＝H，连接BO，∵ABCD是菱形，∴AB＝AD.∵∠DAB＝60°，∴△ABD为等边三角形，∴BD＝4，BH＝2，HA＝23，HO＝PO＝ 3.在Rt△BHO中，BO＝BH2＋HO2＝7，在△PBO中，BO2＋PO2＝10＝PB2，∴PO⊥BO.∵PO⊥EF，EF∩BO＝O，EF⊂平面BFED，BO⊂平面BFED，∴PO⊥平面BFED，又梯形BFED的面积为S＝12(EF＋BD)·HO＝33，∴四棱锥P-BFED的体积V＝13S·PO＝13×33×3＝3.[方法技巧]求解折叠问题的关键及注意事项求解平面图形翻折问题的关键是弄清原有的性质变化与否，即翻折后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化．应注意：(1)点的变化，点与点的重合及点的位置变化；(2)线的变化，翻折前后，若线始终在同一平面内，则它们的位置关系不发生变化，若线与线由在一个平面内转变为不在同一个平面内，应注意其位置关系的变化；(3)长度、角度等几何度量的变化．能力练通抓应用体验的“得”与“失”1．[考点一]如图，在三棱柱ABC-A1B1C1中，AB⊥平面BB1C1C，BB1＝2BC，D，E，F分别是CC1，A1C1，B1C1的中点，G在BB1上，且BG＝3GB1.求证：(1)B1D⊥平面ABD；(2)平面GEF∥平面ABD.证明：(1)取BB1的中点为M，连接MD，如图所示．因为BB1＝2BC，且四边形BB1C1C为平行四边形，所以四边形CDMB和四边形DMB1C1均为菱形．故∠CDB＝∠BDM，∠MDB1＝∠B1DC1，所以∠BDM＋∠MDB1＝90°，即BD⊥B1D.又AB⊥平面BB1C1C，B1D⊂平面BB1C1C，所以AB⊥B1D.又AB∩BD＝B，所以B1D⊥平面ABD.(2)连接MC1，可知G为MB1的中点，又F为B1C1的中点，所以GF∥MC1.又MB綊C1D，所以四边形BMC1D为平行四边形，所以MC1∥BD，故GF∥BD.又BD⊂平面ABD，所以GF∥平面ABD.又EF∥A1B1，A1B1∥AB，AB⊂平面ABD，所以EF ∥平面ABD .又EF ∩GF ＝F ，故平面GEF ∥平面ABD .2．[考点一、二]如图，已知三棱柱ABC -A ′B ′C ′的侧棱垂直于底面，AB ＝AC ，∠BAC ＝90°，点M ，N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面AA ′C ′C ；(2)设AB ＝λAA ′，当λ为何值时，CN ⊥平面A ′MN ，试证明你的结论．解：(1)证明：如图，取A ′B ′的中点E ，连接ME ，NE .因为M ，N 分别为A ′B 和B ′C ′的中点，所以NE ∥A ′C ′，ME ∥AA ′.又A ′C ′⊂平面AA ′C ′C ，A ′A ⊂平面AA ′C ′C ，所以ME ∥平面AA ′C ′C ，NE ∥平面AA ′C ′C ，所以平面MNE ∥平面AA ′C ′C ， 因为MN ⊂平面MNE ，所以MN ∥平面AA ′C ′C .(2)连接BN ，设AA ′＝a ，则AB ＝λAA ′＝λa ，由题意知BC ＝2λa ，CN ＝BN ＝a 2＋12λ2a 2， 因为三棱柱ABC -A ′B ′C ′的侧棱垂直于底面，所以平面A ′B ′C ′⊥平面BB ′C ′C ，因为AB ＝AC ，点N 是B ′C ′的中点，所以A ′B ′＝A ′C ′，A ′N ⊥B ′C ′，所以A ′N ⊥平面BB ′C ′C ，所以CN ⊥A ′N ，要使CN ⊥平面A ′MN ，只需CN ⊥BN 即可，所以CN 2＋BN 2＝BC 2，即2⎝⎛⎭⎫a 2＋12λ2a 2＝2λ2a 2， 解得λ＝2，故当λ＝2时，CN ⊥平面A ′MN .3．[考点一、三]如图所示，在矩形ABCD 中，AB ＝3，BC ＝4，E ，F 分别在线段BC ，AD 上，EF ∥AB ，将矩形ABEF 沿EF 折起，记折起后的矩形为MNEF ，且平面MNEF ⊥平面ECDF .(1)求证：NC∥平面MFD；(2)若EC＝3，求证：ND⊥FC；(3)求四面体N-EFD体积的最大值．解：(1)证明：∵平行四边形MNEF和EFDC都是矩形，∴MN∥EF，EF∥CD，MN＝EF＝CD，∴MN∥CD.∴四边形MNCD是平行四边形．∴NC∥MD.∵NC⊄平面MFD，MD⊂平面MFD，∴NC∥平面MFD.(2)证明：连接ED，交FC于点O，如图所示．∵平面MNEF⊥平面ECDF，且NE⊥EF，平面MNEF∩平面ECDF＝EF，NE⊂平面MNEF，∴NE⊥平面ECDF.∵FC⊂平面ECDF，∴FC⊥NE.∵EC＝CD，∴四边形ECDF为正方形，∴FC⊥ED.又∵ED∩NE＝E，ED，NE⊂平面NED，∴FC⊥平面NED.∵ND⊂平面NED，∴ND⊥FC.(3)设NE＝x，则FD＝EC＝4－x，其中0<x<4，由(2)得NE⊥平面FEC，∴四面体N-EFD的体积为V N-FED＝13S△EFD·NE＝12x(4－x)．∴V N-FED≤12⎣⎢⎡⎦⎥⎤x＋(4－x)22＝2，当且仅当x＝4－x，即x＝2时，四面体N-EFD的体积最大，最大值为2.[全国卷5年真题集中演练——明规律]1．(2016·全国乙卷)如图，已知正三棱锥P-ABC的侧面是直角三角形，PA＝6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G.(1)证明：G是AB的中点；(2)在图中作出点E在平面PAC内的正投影F(说明作法及理由)，并求四面体PDEF的体积．解：(1)证明：因为P在平面ABC内的正投影为D，所以AB⊥PD.因为D在平面PAB内的正投影为E，所以AB⊥DE.因为PD∩DE＝D，所以AB⊥平面PED，故AB⊥PG.又由已知可得，PA＝PB，所以G是AB的中点．(2)如图，在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影．理由如下：由已知可得PB⊥PA，PB⊥PC，又EF∥PB，所以EF⊥PA，EF⊥PC.又PA∩PC＝P，因此EF⊥平面PAC，即点F为E在平面PAC内的正投影．连接CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心．由(1)知，G是AB的中点，所以D在CG上，故CD＝23CG.由题设可得PC⊥平面PAB，DE⊥平面PAB，所以DE∥PC，因此PE＝23PG，DE＝13PC.由已知，正三棱锥的侧面是直角三角形且PA＝6，可得DE＝2，PE＝2 2. 在等腰直角三角形EFP中，可得EF＝PF＝2，所以四面体PDEF 的体积V ＝13S △PEF ·|DE |＝13×12×2×2×2＝43. 2．(2015·新课标全国卷Ⅰ)如图，四边形ABCD 为菱形，G 为AC 与BD 的交点，BE ⊥平面ABCD .(1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC ，三棱锥E -ACD 的体积为63，求该三棱锥的侧面积．解：(1)证明：因为四边形ABCD 为菱形，所以AC ⊥BD .因为BE ⊥平面ABCD ，所以AC ⊥BE .故AC ⊥平面BED .又AC ⊂平面AEC ，所以平面AEC ⊥平面BED .(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝32x ，GB ＝GD ＝x 2. 因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x . 由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x . 由已知得，三棱锥E -ACD 的体积V 三棱锥E -ACD ＝13×12·AC ·GD ·BE ＝624x 3＝63， 故x ＝2.从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为 5.故三棱锥E -ACD 的侧面积为3＋2 5.3．(2014·新课标全国卷Ⅰ)如图，三棱柱ABC -A1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C .(1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABC -A 1B 1C 1的高．解：(1)证明：如图，连接BC 1，则O 为B 1C 与BC 1的交点．因为侧面BB1C 1C 为菱形，所以B 1C ⊥BC 1.又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ，故B 1C ⊥平面ABO .由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)作OD ⊥BC ，垂足为D ，连接AD .作OH ⊥AD ，垂足为H .由于BC ⊥AO ，BC ⊥OD ，故BC ⊥平面AOD ，所以OH ⊥BC .又OH ⊥AD ，所以OH ⊥平面ABC .因为∠CBB 1＝60°，所以△CBB 1为等边三角形，又BC ＝1，可得OD ＝34. 由于AC ⊥AB 1，所以OA ＝12B 1C ＝12. 由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114. 又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217. 故三棱柱ABC -A 1B 1C 1的高为217. 4．(2012·新课标全国卷)如图，三棱柱ABC -A1B 1C 1中，侧棱垂直底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点． (1)证明：平面BDC 1⊥平面BDC ；(2)平面BDC 1分此棱柱为两部分，求这两部分体积的比．解：(1)证明：由题设知BC ⊥CC 1，BC ⊥AC ，CC 1∩AC ＝C ，所以BC ⊥平面ACC 1A 1. 又DC 1⊂平面ACC 1A 1，所以DC 1⊥BC .由题设知∠A 1DC 1＝∠ADC ＝45°，所以∠CDC 1＝90°，即DC 1⊥DC .又DC ∩BC ＝C ，所以DC 1⊥平面BDC .又DC 1⊂平面BDC 1，故平面BDC 1⊥平面BDC .(2)设棱锥B-DACC1的体积为V1，AC＝1.由题意得V1＝13×1＋22×1×1＝12.又三棱柱ABC-A1B1C1的体积V＝1，所以(V－V1)∶V1＝1∶1.故平面BDC1分此棱柱所得两部分体积的比为1∶1.[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是() A．若m⊂β，α⊥β，则m⊥αB．若α∩γ＝m，β∩γ＝n，m∥n，则α∥βC．若m⊥β，m∥α，则α⊥βD．若α⊥γ，α⊥β，则β⊥γ解析：选C A中m与α的位置关系不确定，故错误；B中α，β可能平行或相交，故错误；由面面垂直的判定定理可知C正确；D中β，γ平行或相交，故错误．2.如图，在Rt△ABC中，∠ABC＝90°，P为△ABC所在平面外一点，PA⊥平面ABC，则四面体P -ABC中共有直角三角形个数为()A．4 B．3C．2 D．1解析：选A由PA⊥平面ABC可得△PAC，△PAB是直角三角形，且PA⊥BC.又∠ABC＝90°，即AB⊥BC，所以△ABC是直角三角形，且BC⊥平面PAB，又PB⊂平面PAB，所以BC⊥PB，即△PBC为直角三角形，故四面体P -ABC中共有4个直角三角形．3．如图，PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中正确的结论有________．解析：①AE⊂平面PAC，BC⊥AC，BC⊥PA⇒AE⊥BC，故①正确；②AE⊥PC，AE⊥BC，PB⊂平面PBC⇒AE⊥PB，AF⊥PB，EF⊂平面AEF⇒EF⊥PB，故②正确；③AF⊥PB，若AF⊥BC⇒AF⊥平面PBC，则AF∥AE与已知矛盾，故③错误；由①可知④正确．答案：①②④4．设a，b为不重合的两条直线，α，β为不重合的两个平面，给出下列命题：①若a∥α且b∥α，则a∥b；②若α⊥β，则一定存在平面γ，使得γ⊥α，γ⊥β；③若α⊥β，则一定存在直线l，使得l⊥α，l∥β.上面命题中，所有真命题的序号是________．解析：①中a与b可能相交或异面，故①是假命题．②中存在γ，使得γ与α，β都垂直，故②是真命题．③中只需直线l⊥α且l⊄β就可以，故③是真命题．答案：②③[练常考题点——检验高考能力]一、选择题1．设a，b是两条不同的直线，α，β是两个不同的平面，则能得出a⊥b的是() A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β解析：选C对于C项，由α∥β，a⊂α可得a∥β，又b⊥β，得a⊥b，故选C.2.如图，O是正方体ABCD-A1B1C1D1的底面ABCD的中心，则下列直线中与B1O垂直的是()A．A1D B．AA1C．A1D1D．A1C1解析：选D连接B1D1(图略)，则A1C1⊥B1D1，根据正方体特征可得BB1⊥A1C1，故A1C1⊥平面BB1D1D，B1O⊂平面BB1D1D，所以B1O⊥A1C1.3.如图，在斜三棱柱ABC-A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部解析：选A连接AC1(图略)，由AC⊥AB，AC⊥BC1，得AC⊥平面ABC1.∵AC⊂平面ABC，∴平面ABC1⊥平面ABC.∴C1在平面ABC上的射影H必在两平面的交线AB上．4．设a，b，c是空间的三条直线，α，β是空间的两个平面，则下列命题中，逆命题不成立的是( )A ．当c ⊥α时，若c ⊥β，则α∥βB ．当b ⊂α时，若b ⊥β，则α⊥βC ．当b ⊂α，且c 是a 在α内的射影时，若b ⊥c ，则a ⊥bD ．当b ⊂α，且c ⊄α时，若c ∥α，则b ∥c解析：选B A 的逆命题为：当c ⊥α时，若α∥β，则c ⊥β.由线面垂直的性质知c ⊥β，故A 正确；B 的逆命题为：当b ⊂α时，若α⊥β，则b ⊥β，显然错误，故B 错误；C 的逆命题为：当b ⊂α，且c 是a 在α内的射影时，若a ⊥b ，则b ⊥c .由三垂线逆定理知b ⊥c ，故C 正确；D 的逆命题为：当b ⊂α，且c ⊄α时，若b ∥c ，则c ∥α.由线面平行判定定理可得c ∥α，故D 正确．5．如图所示，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°.将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A -BCD ，则在三棱锥A -BCD 中，下列结论正确的是( )A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABC解析：选D ∵在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，∴BD ⊥CD .又平面ABD ⊥平面BCD ，且平面ABD ∩平面BCD ＝BD ，故CD ⊥平面ABD ，则CD ⊥AB .又AD ⊥AB ，AD ∩CD ＝D ，AD ⊂平面ADC ，CD ⊂平面ADC ，故AB ⊥平面ADC .又AB ⊂平面ABC ，∴平面ADC ⊥平面ABC .6.如图，直三棱柱ABC -A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E .要使AB 1⊥平面C 1DF ，则线段B 1F 的长为( )A.12 B ．1 C.32D ．2 解析：选A 设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可得A 1B 1＝2，设Rt △AA 1B 1斜边AB 1上的高为h ，则DE ＝12h . 又2×2＝h 22＋(2)2，所以h ＝233，DE ＝33.在Rt △DB 1E 中，B 1E ＝ ⎝⎛⎭⎫222－⎝⎛⎭⎫332＝66. 由面积相等得66× x 2＋⎝⎛⎭⎫222＝22x ，得x ＝12. 二、填空题 7.如图，在三棱锥D -ABC 中，若AB ＝CB ，AD ＝CD ，E 是AC 的中点，则下列命题中正确的有________(写出全部正确命题的序号)．①平面ABC ⊥平面ABD ；②平面ABD ⊥平面BCD ；③平面ABC ⊥平面BDE ，且平面ACD ⊥平面BDE ；④平面ABC ⊥平面ACD ，且平面ACD ⊥平面BDE .解析：由AB ＝CB ，AD ＝CD 知AC ⊥DE ，AC ⊥BE ，从而AC ⊥平面BDE ，所以平面ABC ⊥平面BDE ，且平面ACD ⊥平面BDE ，故③正确．答案：③8.如图所示，在四棱锥P -ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)解析：如图，连接AC ，BD ，则AC ⊥BD ，∵PA ⊥底面ABCD ，∴PA⊥BD .又PA ∩AC ＝A ，∴BD ⊥平面PAC ，∴BD ⊥PC ，∴当DM ⊥PC (或BM ⊥PC )时，即有PC ⊥平面MBD .而PC ⊂平面PCD ，∴平面MBD ⊥平面PCD .答案：DM ⊥PC (或BM ⊥PC 等)9．设l ，m ，n 为三条不同的直线，α为一个平面，给出下列命题：①若l ⊥α，则l 与α相交；②若m ⊂α，n ⊂α，l ⊥m ，l ⊥n ，则l ⊥α；③若l ∥m ，m ∥n ，l ⊥α，则n ⊥α；④若l ∥m ，m ⊥α，n ⊥α，则l ∥n .其中正确命题的序号为________．解析：①显然正确；对于②，只有当m ，n 相交时，才有l ⊥α，故②错误；对于③，由l ∥m ，m ∥n ，得l ∥n ，由l ⊥α，得n ⊥α，故③正确；对于④，由l ∥m ，m ⊥α，得l ⊥α，再由n ⊥α，得l ∥n ，故④正确．答案：①③④10．(2016·兰州质检)如图，在直角梯形ABCD 中，BC ⊥DC ，AE ⊥DC ，且E 为CD 的中点，M ，N 分别是AD ，BE 的中点，将三角形ADE 沿AE 折起，则下列说法正确的是________．(写出所有正确说法的序号)①不论D 折至何位置(不在平面ABC 内)，都有MN ∥平面DEC ；②不论D 折至何位置(不在平面ABC 内)，都有MN ⊥AE ；③不论D 折至何位置(不在平面ABC 内)，都有MN ∥AB ；④在折起过程中，一定存在某个位置，使EC ⊥AD .解析：由已知，在未折叠的原梯形中，AB ∥DE ，BE ∥AD ，所以四边形ABED 为平行四边形，所以BE ＝AD ，折叠后如图所示．①过点M 作MP ∥DE ，交AE 于点P ，连接NP .因为M ，N 分别是AD ，BE 的中点，所以点P 为AE 的中点，故NP ∥EC .又MP ∩NP ＝P ，DE ∩CE ＝E ，所以平面MNP ∥平面DEC ，故MN ∥平面DEC ，①正确；②由已知，AE ⊥ED ，AE ⊥EC ，所以AE ⊥MP ，AE ⊥NP ，又MP ∩NP ＝P ，所以AE ⊥平面MNP ，又MN ⊂平面MNP ，所以MN ⊥AE ，②正确；③假设MN ∥AB ，则MN 与AB 确定平面MNBA ，从而BE ⊂平面MNBA ，AD ⊂平面MNBA ，与BE 和AD 是异面直线矛盾，③错误；④当EC ⊥ED 时，EC ⊥AD .因为EC ⊥EA ，EC ⊥ED ，EA ∩ED ＝E ，所以EC ⊥平面AED ，AD ⊂平面AED ，所以EC ⊥AD ，④正确．答案：①②④三、解答题11.如图，四棱锥P -ABCD 中， AP ⊥平面PCD ，AD ∥BC ，AB ＝BC ＝12AD ，E ，F 分别为线段AD ，PC 的中点．求证： (1)AP ∥平面BEF ；(2)BE ⊥平面PAC .证明：(1)设AC ∩BE ＝O ，连接OF ，EC ，如图所示．由于E 为AD 的中点，AB ＝BC ＝12AD ，AD ∥BC ，所以AE ∥BC ，AE ＝AB ＝BC ，因此四边形ABCE 为菱形，所以O 为AC 的中点．又F 为PC 的中点，因此在△PAC 中，可得AP ∥OF .又OF ⊂平面BEF ，AP ⊄平面BEF .所以AP ∥平面BEF .(2)由题意知ED ∥BC ，ED ＝BC .所以四边形BCDE 为平行四边形，因此BE ∥CD .又AP ⊥平面PCD ，所以AP ⊥CD ，因此AP ⊥BE .因为四边形ABCE 为菱形，所以BE ⊥AC .又AP ∩AC ＝A ，AP ，AC ⊂平面PAC ，所以BE ⊥平面PAC .12.如图所示，已知长方体ABCD -A 1B 1C 1D 1，点O 1为B 1D 1的中点．(1)求证：AB 1∥平面A 1O 1D ；(2)若AB ＝23AA 1，在线段BB 1上是否存在点E 使得A 1C ⊥AE ？若存在，求出BEBB 1；若不存在，说明理由． 解： (1)证明：如图1所示，连接AD 1交A 1D 于点G ，∴G 为AD 1的中点，连接O 1G ，在△AB 1D 1中，∵O 1为B 1D 1的中点，∴O 1G ∥AB 1.∵O 1G ⊂平面A 1O 1D ，且AB 1⊄平面A 1O 1D ，∴AB 1∥平面A 1O 1D .(2)若在线段BB 1上存在点E 使得A 1C ⊥AE ，连接A 1B 交AE 于点M ，如图2所示． ∵BC ⊥平面ABB 1A 1，AE ⊂平面ABB 1A 1，∴BC ⊥AE .又∵A 1C ∩BC ＝C ，且A 1C ，BC ⊂平面A 1BC ，∴AE ⊥平面A 1BC .∵A 1B ⊂平面A 1BC ，∴AE ⊥A 1B .在△AMB 和△ABE 中，∠BAM ＋∠ABM ＝90°，∠BAM ＋∠BEA ＝90°，∴∠ABM ＝∠BEA .∴Rt △ABE ∽Rt △A 1AB ，∴BE AB ＝AB AA 1. ∵AB ＝23AA 1，∴BE ＝23AB ＝49BB 1， 即在线段BB 1上存在点E 使得A 1C ⊥AE ，此时BE BB 1＝49.。

学业分层测评(七)(建议用时：45分钟)[学业达标]一、填空题1．下列语句中正确的是________．(填序号)①l⊥α⇒l与α相交；②m⊂α，n⊂α，l⊥m，l⊥n⇒l⊥α；③l∥m，m∥n，l⊥α⇒n⊥α.【解析】①正确，由线面垂直的定义可知；②不正确，没有明确直线m，n的情况；③正确，∵l∥m，m∥n，∴l∥n，又l⊥α，∴n⊥α.【答案】①③2．已知PA垂直平行四边形ABCD所在平面，若PC⊥BD，则平行四边形ABCD 一定是________．【解析】如图，∵PA⊥平面ABCD，∴PA⊥BD.∵PC⊥BD，且PA∩PC＝P，∴BD⊥平面PAC，∴AC⊥BD.【答案】菱形3．已知△ABC在平面α内，∠A＝90°，DA⊥平面α，则AC与BD的位置关系是________．【解析】∵DA⊥α，∴DA⊥AC.又AC⊥AB，AB∩DA＝A，∴AC⊥平面ABD，∴AC⊥BD.【答案】垂直4．如图1­2­66，在正三棱柱ABC­A1B1C1中，侧棱长为2，底面三角形的边长为1，则BC1与侧面ACC1A1所成的角的大小是________．图1­2­66【解析】取AC的中点D，连结DB，C1D，则可证得∠BC1D即为BC1与侧面ACC1A1所成的角，在△ABC中，易得BD＝32.在△DCC1中，易得DC1＝32，在Rt△BC1D中，tan∠BC1D＝BDDC1＝33，即∠BC1D＝30°.【答案】30°5．对于四面体A­BCD，给出下列四个命题：①若AB＝AC，BD＝CD，则BC⊥AD；②若AB＝CD，AC＝BD，则BC⊥AD；③若AB⊥AC，BD⊥CD，则BC⊥AD；④若AB⊥CD，BD⊥AC，则BC⊥AD.其中真命题的序号是________. 【导学号：60420025】【解析】对于命题①，取BC的中点E，连结AE，DE，则BC⊥AE，BC⊥DE，且AE∩DE＝E，∴BC⊥平面ADE.∵AD⊂平面ADE，∴BC⊥AD.对于④，过A向平面BCD作垂线AO，如图所示．连结BO与CD交于E，则CD⊥BE，同理CF⊥BD，∴O为△BCD的重心，连结DO，则BC⊥DO，BC⊥AO，且AO∩DO＝O，∴BC⊥平面AOD，∴BC⊥AD.【答案】①④6．在△ABC中，AB＝AC＝5，BC＝6，PA⊥平面ABC，PA＝8，则P到BC的距离是__________．【解析】如图所示，作PD⊥BC于D，连结AD.∵PA⊥△ABC，∴PA⊥BC，且PA∩PD＝P，∴BC⊥平面PAD，∴AD⊥BC.在△ACD中，AC＝5，CD＝3，∴AD＝4，在Rt△PAD中，PA＝8，AD＝4，∴PD＝82＋42＝4 5.【答案】4 57．如图1­2­67，直三棱柱ABC­A1B1C1中，∠ABC＝90°，M为线段BB1上的一动点，则直线AM与直线BC的位置关系为__________．图1­2­67【解析】∵AA1⊥平面ABC，∴BC⊥AA1，∵∠ABC＝90°，∴BC⊥AB，又AB∩AA1＝A，∴BC⊥平面AA1B1B，又AM⊂平面AA1B1B，∴AM⊥BC.【答案】垂直8．如图1­2­68所示，已知矩形ABCD中，AB＝1，BC＝a，PA⊥平面ABCD，若在BC上只有一个点Q满足PQ⊥QD，则a的值等于________．图1­2­68【解析】∵PA⊥平面ABCD，∴PA⊥QD.又∵PQ⊥QD，且PA∩PQ＝P，∴QD⊥平面PAQ，∴AQ⊥QD，即Q在以AD为直径的圆上，当圆与BC相切时，点Q只有一个，故BC＝2AB＝2.【答案】 2二、解答题9.如图1­2­69，在四棱锥P­ABCD中，PD⊥平面ABCD，AD⊥CD，DB平分∠ADC，E为PC的中点，AD＝CD.图1­2­69(1)证明：PA∥平面BDE；(2)证明：AC⊥平面PBD.【证明】(1)设AC∩BD＝H，连结EH，在△ADC中，因为AD＝CD，且DB平分∠ADC，所以H为AC的中点，又由题设，E为PC的中点，故EH∥PA，又EH⊂平面BDE，且PA⊄平面BDE，所以PA∥平面BDE.(2)因为PD⊥平面ABCD，AC⊂平面ABCD，所以PD⊥AC.由(1)可得，DB⊥AC，又PD∩DB＝D，故AC⊥平面PBD.10．如图1­2­70，已知矩形ABCD，SA⊥平面AC，AE⊥SB于点E，EF⊥SC 于点F.图1­2­70(1)求证：AF⊥SC；(2)若平面AEF交SD于点G，求证：AG⊥SD.【证明】(1)∵SA⊥平面AC，BC⊂平面AC，∴SA⊥BC.∵四边形ABCD为矩形，∴AB⊥BC.又AB∩SA＝A，∴BC⊥平面SAB，∴BC⊥AE，又SB⊥AE，SB∩BC＝B，∴AE⊥平面SBC，∴AE⊥SC.又EF⊥SC，EF∩AE＝E，∴SC⊥平面AEF.又AF⊂平面AEF，∴AF⊥SC.(2)∵SA⊥平面AC，∴SA⊥DC.又AD⊥DC，SA∩AD＝A，∴DC⊥平面SAD，∴DC⊥AG.又由(1)有SC⊥平面AEF，AG⊂平面AEF，∴SC⊥AG，又SC∩DC＝C，∴AG⊥平面SDC，∴AG⊥SD.[能力提升]1．如图1­2­71所示，PA⊥平面ABC，M，N分别为PC，AB的中点，使得MN ⊥AC的一个条件为__________．图1­2­71【解析】取AC中点Q，连结MQ，NQ，则MQ∥AP，NQ∥BC，由已知条件易得MQ⊥AC，若AC⊥BC，则NQ⊥AC，所以AC⊥平面MNQ，所以AC⊥MN.【答案】AC⊥BC2．如图1­2­72，在四棱锥P­ABCD中，PA⊥底面ABCD，底面是边长为2的菱形，且∠ABC＝45°，PA＝AB，则直线AP与平面PBC所成角的正切值为________．图1­2­72【解析】 作AE ⊥BC 于点E ，则BC ⊥平面PAE ，可知点A 在平面PBC 上的射影在直线PE 上，故∠APE 为所求的角．AE ＝AB sin 45°＝2，∴tan ∠APE ＝AE PA ＝22.【答案】223．已知平面α∩平面β＝l ，EA ⊥α于A ，EB ⊥β于B ，a ⊂α，a ⊥AB ，则直线a 与l 的位置关系是________. 【导学号：60420026】【解析】 由EA ⊥α，EB ⊥β知l ⊥EA ，l ⊥EB ， 从而l ⊥平面EAB ， 而a ⊥AB ，a ⊥EA ， ∴a ⊥平面EAB ，∴l ∥a . 【答案】 平行4．如图1­2­73，在四棱锥P ­ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC ＝60°，PA ＝AB ＝BC ，E 是PC 的中点．图1­2­73(1)证明：CD⊥AE；(2)证明：PD⊥平面ABE.【证明】(1)在四棱锥P­ABCD中，因PA⊥底面ABCD，CD⊂平面ABCD，故PA⊥CD. 又∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC.而AE⊂平面PAC，∴CD⊥AE.(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA. 又∵E是PC的中点，∴AE⊥PC.由(1)知，AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.而PD⊂平面PCD，∴AE⊥PD.∵PA⊥底面ABCD，∴PA⊥AB.又∵AB⊥AD，PA∩AD＝A，AB⊥平面PAD.又∵PD⊂平面PAD，∴AB⊥PD.又∵AB∩AE＝A，∴PD⊥平面ABE.。

直线、平面垂直的判定及其性质【课前回顾】1．直线与平面垂直(1)直线和平面垂直的定义：直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直．(2)直线与平面垂直的判定定理及性质定理：．平面与平面垂直的判定定理与性质定理21．若l，m是两条不同的直线，m垂直于平面α，则“l⊥m”是“l∥α”的() A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选B∵m⊥α，若l∥α，则必有l⊥m，即l∥α⇒l⊥m.但l⊥m⇒/ l∥α，∵l⊥m 时，l可能在α内．故“l⊥m”是“l∥α”的必要不充分条件．2．设α，β是两个不同的平面，l ，m 是两条不同的直线，且l ⊂α，m ⊂β( ) A ．若l ⊥β，则α⊥β B ．若α⊥β，则l ⊥m C ．若l ∥β，则α∥βD ．若α∥β，则l ∥m解析：选A ∵l ⊥β，l ⊂α，∴α⊥β(面面垂直的判定定理)，故A 正确．3．设m ，n 表示两条不同的直线，α，β表示两个不同的平面，下列命题为真命题的是( )A ．若m ⊥α，α⊥β，则m ∥βB ．若m ∥α，m ⊥β，则α⊥βC ．若m ⊥n ，m ⊥α，则n ∥αD ．若m ∥α，n ∥β，α⊥β，则m ⊥n解析：选B 对于A ，m 可以在β内，故A 错；对于C ，n 可以在α内，故C 错误；对于D ，m 与n 可以平行，故D 错．4．已知PD 垂直于正方形ABCD 所在的平面，连接PB ，PC ，PA ，AC ，BD ，则一定互相垂直的平面有________对．解析：由于PD ⊥平面ABCD ，故平面PAD ⊥平面ABCD ，平面PDB⊥平面ABCD ，平面PDC ⊥平面ABCD ，平面PDA ⊥平面PDC ，平面PAC ⊥平面PDB ，平面PAB ⊥平面PAD, 平面PBC ⊥平面PDC ，共7对．答案：7考点一 直线与平面垂直的判定与性质角度(一) 证明直线与平面垂直 证明线面垂直的4种方法(1)线面垂直的判定定理：l ⊥a ，l ⊥b ，a ⊂α，b ⊂α，a ∩b ＝P ⇒l ⊥α. (2)面面垂直的性质定理：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β. (3)性质：①a ∥b ，b ⊥α⇒a ⊥α，②α∥β，a ⊥β⇒a ⊥α. (4)α⊥γ，β⊥γ，α∩β＝l ⇒l ⊥γ.(客观题可用)1．如图所示，在四棱锥P -ABCD 中，AB ⊥平面PAD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点，且DF ＝12AB ，PH 为△PAD 中AD 边上的高．求证： (1)PH ⊥平面ABCD ； (2)EF ⊥平面PAB . [学审题]①想到AB 与平面PAD 内所有的直线垂直；②想到△PAD 为等腰三角形，可取PA 的中点得垂线；③可证PH 与平面ABCD 内的两条相交直线垂直；④可利用线面垂直的判定定理证明，也可以转化为与EF 平行的某条直线与平面PAB 垂直的证明．证明：(1)因为AB ⊥平面PAD ，PH ⊂平面PAD ， 所以PH ⊥AB .因为PH 为△PAD 中AD 边上的高，所以PH ⊥AD . 因为AB ∩AD ＝A ，AB ⊂平面ABCD ，AD ⊂平面ABCD ， 所以PH ⊥平面ABCD .(2)如图，取PA 的中点M ，连接MD ，ME . 因为E 是PB 的中点， 所以ME 綊12AB .又因为DF 綊12AB ，所以ME 綊DF ，所以四边形MDFE 是平行四边形，所以EF ∥MD . 因为PD ＝AD ，所以MD ⊥PA . 因为AB ⊥平面PAD ，所以MD ⊥AB . 因为PA ∩AB ＝A ，所以MD ⊥平面PAB ， 所以EF ⊥平面PAB .角度(二) 利用线面垂直的性质证明线线垂直 证明线线垂直的4种方法(1)以算代证法：先平移到相交位置，再证明所构成的三角形的三边满足勾股定理． (2)利用线面垂直的性质：a ⊥α，b ⊂α⇒a ⊥b . (3)三垂线定理(垂影⇒垂斜)及其逆定理(垂斜⇒垂影)． (4)a ∥b ，b ⊥c ⇒a ⊥c .2.(2017·江苏高考)如图，在三棱锥A -BCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD .求证：(1)EF ∥平面ABC ； (2)AD ⊥AC .证明：(1)在平面ABD 内，因为AB ⊥AD ，EF ⊥AD ， 所以EF ∥AB .又因为EF ⊄平面ABC ，AB ⊂平面ABC ，所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD.因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.【针对训练】1.如图，S是Rt△ABC所在平面外一点，且SA＝SB＝SC，D为斜边AC的中点．(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC.证明：(1)如图所示，取AB的中点E，连接SE，DE，在Rt△ABC中，D，E分别为AC，AB的中点．∴DE∥BC，∴DE⊥AB，∵SA＝SB，∴SE⊥AB.又SE∩DE＝E，∴AB⊥平面SDE.又SD⊂平面SDE，∴AB⊥SD.在△SAC中，∵SA＝SC，D为AC的中点，∴SD⊥AC.又AC∩AB＝A，∴SD⊥平面ABC.(2)由于AB＝BC，则BD⊥AC，由(1)可知，SD⊥平面ABC，又BD⊂平面ABC，∴SD⊥BD，又SD∩AC＝D，∴BD⊥平面SAC.2.如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.证明：(1)在四棱锥P-ABCD中，∵PA⊥平面ABCD，CD⊂平面ABCD，∴PA⊥CD.∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC.而AE⊂平面PAC，∴CD⊥AE.(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC.由(1)知AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.而PD⊂平面PCD，∴AE⊥PD.∵PA⊥平面ABCD，∴PA⊥AB.又∵AB⊥AD且PA∩AD＝A，∴AB⊥平面PAD，而PD⊂平面PAD，∴AB⊥PD.又∵AB∩AE＝A，∴PD⊥平面ABE.考点二面面垂直的判定与性质1．证明面面垂直的2种方法(1)定义法：利用面面垂直的定义，即判定两平面所成的二面角为直二面角，将证明面面垂直问题转化为证明平面角为直角的问题．(2)定理法：利用面面垂直的判定定理，即证明其中一个平面经过另一个平面的一条垂线，把问题转化成证明线线垂直加以解决．2．三种垂直关系的转化线线垂直判定性质线面垂直判定性质面面垂直【典型例题】如图，四棱锥P-ABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．求证：(1)CE∥平面PAD；(2)平面EFG⊥平面EMN.[学审题]①想到线面垂直的判定，可证线面垂直；或想到转化为证与其中一直线的平行线垂直；②想到平行公理，可转化为一直线与另一直线的平行线平行；③想到连中点得三角形中位线，可证线线平行；④要证CE∥平面PAD想到证CE与平面PAD中的一条直线平行，或证CE所在平面与平面PAD平行；⑤要证平面EFG⊥平面EMN想到证其中一平面内的直线与另一平面垂直．证明：(1)法一：如图，取PA的中点H，连接EH，DH.因为E 为PB 的中点， 所以EH ∥AB ，EH ＝12AB .又AB ∥CD ，CD ＝12AB ，所以EH ∥CD ，EH ＝CD ， 因此四边形DCEH 是平行四边形． 所以CE ∥DH .又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD . 法二：如图，连接CF .因为F 为AB 的中点， 所以AF ＝12AB .又CD ＝12AB ，所以AF ＝CD .又AF ∥CD ，所以四边形AFCD 为平行四边形．因此CF ∥AD . 又CF ⊄平面PAD ，AD ⊂平面PAD ， 所以CF ∥平面PAD .因为E ，F 分别为PB ，AB 的中点， 所以EF ∥PA .又EF ⊄平面PAD ，PA ⊂平面PAD ， 所以EF ∥平面PAD .因为CF ∩EF ＝F ，故平面CEF ∥平面PAD . 又CE ⊂平面CEF ，所以CE ∥平面PAD . (2)因为E ，F 分别为PB ，AB 的中点， 所以EF ∥PA .又AB ⊥PA ，所以AB ⊥EF . 同理可证AB ⊥FG .又EF ∩FG ＝F ，EF ⊂平面EFG ，FG ⊂平面EFG ， 因此AB ⊥平面EFG .又M ，N 分别为PD ，PC 的中点， 所以MN ∥CD .又AB ∥CD ，所以MN ∥AB ，所以MN⊥平面EFG.又MN⊂平面EMN，所以平面EFG⊥平面EMN.【针对训练】(2017·北京高考)如图，在三棱锥P-ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点．(1)求证：PA⊥BD；(2)求证：平面BDE⊥平面PAC；(3)当PA∥平面BDE时，求三棱锥E-BCD的体积．解：(1)证明：因为PA⊥AB，PA⊥BC，AB∩BC＝B，所以PA⊥平面ABC.又因为BD⊂平面ABC，所以PA⊥BD.(2)证明：因为AB＝BC，D为AC的中点，所以BD⊥AC.由(1)知，PA⊥BD，又AC∩PA＝A，所以BD⊥平面PAC.因为BD⊂平面BDE，所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE，平面PAC∩平面BDE＝DE，所以PA∥DE.因为D为AC的中点，所以DE＝12PA＝1，BD＝DC＝ 2.由(1)知，PA⊥平面ABC，所以DE⊥平面ABC.所以三棱锥E-BCD的体积V＝16BD·DC·DE＝13.考点三平面图形的翻折问题平面图形翻折为空间图形问题的解题关键是看翻折前后线面位置关系的变化，根据翻折的过程找到翻折前后线线位置关系中没有变化的量和发生变化的量，这些不变的和变化的量反映了翻折后的空间图形的结构特征．解决此类问题的步骤为：【典型例题】(2018·广州综合测试)如图1，在边长为1的等边三角形ABC 中，D ，E 分别是AB ，AC 边上的点，AD ＝AE ，F 是BC 的中点，AF 与DE 交于点G ，将△ABF 沿AF 折起，得到如图2所示的三棱锥A -BCF ，其中BC ＝22.(1)求证：DE ∥平面BCF ； (2)求证：CF ⊥平面ABF ；(3)当AD ＝23时，求三棱锥F -DEG 的体积．[学审题]解：(1)所以AD AB ＝AEAC，所以DE ∥BC .因为DE ⊄平面BCF ，BC ⊂平面BCF ， 所以DE ∥平面BCF .(2)证明：在折叠前的图形中， 因为△ABC 为等边三角形，BF ＝CF ，所以AF ⊥BC ，则在折叠后的图形中，AF ⊥BF ，AF ⊥CF . 又BF ＝CF ＝12，BC ＝22，所以BC 2＝BF 2＋CF 2，所以BF ⊥CF .又BF ∩AF ＝F ，BF ⊂平面ABF ，AF ⊂平面ABF ， 所以CF ⊥平面ABF .(3)由(1)知，平面DEG ∥平面BCF ， 由(2)知，AF ⊥BF ，AF ⊥CF ， 又BF ∩CF ＝F ，所以AF ⊥平面BCF ， 所以AF ⊥平面DEG ，即GF ⊥平面DEG . 在折叠前的图形中，AB ＝1，BF ＝CF ＝12，AF ＝32.由AD ＝23，知AD AB ＝23，又DG ∥BF ，所以DG BF ＝AG AF ＝AD AB ＝23，所以DG ＝EG ＝23×12＝13，AG ＝23×32＝33，所以FG ＝AF －AG ＝36. 故三棱锥F ­DEG 的体积V ＝13S △DEG ·FG ＝13×12×⎝⎛⎭⎫132×36＝3324.【针对训练】1．(2018·合肥二检)如图1，在平面五边形ABCDE 中，AB ∥CE ，且AE ＝2，∠AEC ＝60°，CD ＝ED ＝7，cos ∠EDC ＝57.将△CDE 沿CE 折起，使点D 到P 的位置，且AP＝3，得到如图2所示的四棱锥P -ABCE .(1)求证：AP ⊥平面ABCE ；(2)记平面PAB 与平面PCE 相交于直线l ，求证：AB ∥l . 证明：(1)在△CDE 中，∵CD ＝ED ＝7，cos ∠EDC ＝57，由余弦定理得CE ＝2.连接AC ，∵AE ＝2，∠AEC ＝60°， ∴AC ＝2. 又AP ＝3，∴在△PAE 中，PA 2＋AE 2＝PE 2， 即AP ⊥AE . 同理，AP ⊥AC .∵AC ∩AE ＝A ，AC ⊂平面ABCE ，AE ⊂平面ABCE ， ∴AP ⊥平面ABCE .(2)∵AB ∥CE ，且CE ⊂平面PCE ，AB ⊄平面PCE ， ∴AB ∥平面PCE .又平面PAB ∩平面PCE ＝l ，∴AB ∥l .2．如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝90°，AB ＝BC ＝12AD ＝a ，E是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图2中△A 1BE 的位置，得到四棱锥A 1-BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1-BCDE 的体积为362，求a 的值． 解：(1)证明：在图1中，连接EC (图略)，因为AB ＝BC ＝12AD ＝a ，∠BAD ＝90°，AD ∥BC ，E 是AD 的中点，所以四边形ABCE 为正方形， 所以BE ⊥AC ，即在图2中，BE ⊥A 1O ，BE ⊥OC ， 又A 1O ∩OC ＝O ，从而BE ⊥平面A 1OC ， 又CD ∥BE ，所以CD ⊥平面A 1OC . (2)由已知，平面A 1BE ⊥平面BCDE ， 且平面A 1BE ∩平面BCDE ＝BE ， 又由(1)可知A 1O ⊥BE ， 所以A 1O ⊥平面BCDE ，即A1O是四棱锥A1-BCDE的高，由图1知，A1O＝22AB＝22a，平行四边形BCDE的面积S＝BC·AB＝a2，从而四棱锥A1-BCDE的体积V＝13×S×A1O＝13×a2×22a＝26a3，由26a3＝362，解得a＝6.【课后演练】1．设α，β为两个不同的平面，直线l⊂α，则“l⊥β”是“α⊥β”成立的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解析：选A依题意，由l⊥β，l⊂α可以推出α⊥β；反过来，由α⊥β，l⊂α不能推出l⊥β.因此“l⊥β”是“α⊥β”成立的充分不必要条件，故选A.2．设α为平面，a，b为两条不同的直线，则下列叙述正确的是()A．若a∥α，b∥α，则a∥b B．若a⊥α，a∥b，则b⊥αC．若a⊥α，a⊥b，则b∥αD．若a∥α，a⊥b，则b⊥α解析：选B若a∥α，b∥α，则a与b相交、平行或异面，故A错误；易知B正确；若a⊥α，a⊥b，则b∥α或b⊂α，故C错误；若a∥α，a⊥b，则b∥α或b⊂α或b与α相交，故D错误．3．(2018·广州一模)设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是()A．若m⊂β，α⊥β，则m⊥αB．若m⊥α，m∥n，n∥β，则α⊥βC．若m⊥n，m⊂α，n⊂β，则α⊥βD．若α∥β，m⊂α，n⊂β，则m∥n解析：选B A中m与α的位置关系不能确定，故A错误；∵m⊥α，m∥n，∴n⊥α，又∵n∥β，∴α⊥β，故B正确；若m⊥n，m⊂α，n⊂β，则α与β的位置关系不确定，故C错误；若α∥β，m⊂α，n⊂β，则m与n平行或异面，故D错误．选B.4．(2018·天津模拟)设l是直线，α，β是两个不同的平面，则下列说法正确的是() A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l∥βD．若α⊥β，l∥α，则l⊥β解析：选B对于A，若l∥α，l∥β，则α∥β或α与β相交，故A错；易知B正确；对于C，若α⊥β，l⊥α，则l∥β或l⊂β，故C错；对于D，若α⊥β，l∥α，则l与β的位置关系不确定，故D错．选B.5.如图，在三棱锥D-ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列命题中正确的是()A．平面ABC⊥平面ABDB．平面ABD⊥平面BCDC．平面ABC⊥平面BDE，且平面ACD⊥平面BDED．平面ABC⊥平面ACD，且平面ACD⊥平面BDE解析：选C因为AB＝CB，且E是AC的中点，所以BE⊥AC，同理，DE⊥AC，由于DE∩BE＝E，于是AC⊥平面BDE.因为AC⊂平面ABC，所以平面ABC⊥平面BDE.又AC⊂平面ACD，所以平面ACD⊥平面BDE.故选C.6.(2018·广州模拟)如图是一个几何体的平面展开图，其中四边形ABCD为正方形，E，F分别为PA，PD的中点，在此几何体中，给出下面四个结论：①直线BE与直线CF异面；②直线BE与直线AF异面；③直线EF∥平面PBC；④平面BCE⊥平面PAD.其中正确结论的个数是()A．1 B．2C．3 D．4解析：选B画出该几何体，如图所示，①因为E，F分别是PA，PD的中点，所以EF∥AD，所以EF∥BC，直线BE与直线CF是共面直线，故①不正确；②直线BE与直线AF满足异面直线的定义，故②正确；③由E，F分别是PA，PD的中点，可知EF∥AD，所以EF∥BC，因为EF⊄平面PBC，BC⊂平面PBC，所以直线EF∥平面PBC，故③正确；④因为BE与PA的关系不能确定，所以不能判定平面BCE⊥平面PAD，故④不正确．所以正确结论的个数是2.7.如图，已知∠BAC＝90°，PC⊥平面ABC，则在△ABC，△PAC的边所在的直线中，与PC垂直的直线有____________；与AP垂直的直线有________．解析：∵PC⊥平面ABC，∴PC垂直于直线AB，BC，AC.∵AB⊥AC，AB⊥PC，AC∩PC＝C，∴AB⊥平面PAC，又∵AP⊂平面PAC，∴AB⊥AP，与AP垂直的直线是AB.答案：AB，BC，AC AB8．若α，β是两个相交平面，m为一条直线，则下列命题中，所有真命题的序号为________．①若m⊥α，则在β内一定不存在与m平行的直线；②若m⊥α，则在β内一定存在无数条直线与m垂直；③若m⊂α，则在β内不一定存在与m垂直的直线；④若m⊂α，则在β内一定存在与m垂直的直线．解析：对于①，若m⊥α，如果α，β互相垂直，则在平面β内存在与m平行的直线，故①错误；对于②，若m⊥α，则m垂直于平面α内的所有直线，故在平面β内一定存在无数条直线与m垂直，故②正确；对于③④，若m⊂α，则在平面β内一定存在与m垂直的直线，故③错误，④正确．答案：②④9．在直三棱柱ABC-A1B1C1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α.有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE.其中正确命题的序号是________．∥平面α，平面α∩平面AA1B1B＝EH，解析：如图所示，因为AA所以AA1∥EH.同理AA1∥GF，所以EH∥GF，又ABC-A1B1C1是直三棱柱，易知EH＝GF＝AA1，所以四边形EFGH是平行四边形，故①正确；若平面α∥平面BB1C1C，由平面α∩平面A1B1C1＝GH，平面BCC1B1∩平面A1B1C1＝B1C1，知GH∥B1C1，而GH∥B1C1不一定成立，故②错误；由AA1⊥平面BCFE，结合AA1∥EH知EH⊥平面BCFE，又EH⊂平面α，所以平面α⊥平面BCFE，故③正确．答案：①③10．(2018·武汉调研)在矩形ABCD中，AB<BC，现将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折的过程中，给出下列结论：①存在某个位置，使得直线AC与直线BD垂直；②存在某个位置，使得直线AB与直线CD垂直；③存在某个位置，使得直线AD与直线BC垂直．其中正确结论的序号是________．解析：①假设AC 与BD 垂直，过点A 作AE ⊥BD 于E ，连接CE .则 ⎭⎪⎬⎪⎫AE ⊥BD AC ⊥BD AE ∩AC ＝A ⇒BD ⊥平面AEC ⇒BD ⊥CE ，而在平面BCD 中，EC 与BD 不垂直，故假设不成立，①错误．②假设AB ⊥CD ，∵AB ⊥AD ，AD ∩CD ＝D ，∴AB ⊥平面ACD ，∴AB ⊥AC ，由AB <BC 可知，存在这样的等腰直角三角形，使AB ⊥CD ，故假设成立，②正确．③假设AD ⊥BC ，∵DC ⊥BC ，∴BC ⊥平面ADC ，∴BC ⊥AC ，即△ABC 为直角三角形，且AB 为斜边，而AB <BC ，故矛盾，假设不成立，③错误．答案：②11.如图，在斜三棱柱ABC -A 1B 1C 1中，∠BAC ＝90°，BC 1⊥AC ，则C 1在底面ABC 上的射影H 必在( )A ．直线AB 上B ．直线BC 上C ．直线AC 上D ．△ABC 内部解析：选A 连接AC 1(图略)，由AC ⊥AB ，AC ⊥BC 1，AB ∩BC 1＝B ，得AC ⊥平面ABC 1.∵AC ⊂平面ABC ，∴平面ABC 1⊥平面ABC .∴C 1在平面ABC 上的射影H 必在两平面的交线AB 上．12．如图所示，在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°.将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A -BCD ，则在三棱锥A -BCD 中，下列结论正确的是()A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABC解析：选D ∵在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，∴BD ⊥CD .又平面ABD ⊥平面BCD ，且平面ABD ∩平面BCD ＝BD ，故CD ⊥平面ABD ，则CD ⊥AB .又AD ⊥AB ，AD ∩CD ＝D ，AD ⊂平面ADC ，CD ⊂平面ADC ，故AB ⊥平面ADC . 又AB ⊂平面ABC ，∴平面ADC ⊥平面ABC .13.如图，在直三棱柱ABC -A1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E .要使AB 1⊥平面C 1DF ，则线段B 1F 的长为( )A.12B ．1 C.32 D ．2解析：选A 设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可得A 1B 1＝2，设Rt △AA 1B 1斜边AB 1上的高为h ，则DE ＝12h . 又2×2＝h 22＋(2)2，所以h ＝233，DE ＝33. 在Rt △DB 1E 中，B 1E ＝ ⎝⎛⎭⎫222－⎝⎛⎭⎫332＝66. 由面积相等得66× x 2＋⎝⎛⎭⎫222＝22x ，解得x ＝12.14.如图所示，在四棱锥P -ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足______时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)解析：连接AC ，则AC ⊥BD ，∵PA ⊥底面ABCD ，∴PA ⊥BD .又PA ∩AC ＝A ，∴BD ⊥平面PAC ，∴BD ⊥PC .∴当DM ⊥PC (或BM ⊥PC )时，即有PC ⊥平面MBD .而PC ⊂平面PCD ，∴平面MBD ⊥平面PCD .答案：DM ⊥PC (或BM ⊥PC )15．(2018·兰州实战考试)α，β是两平面，AB ，CD 是两条线段，已知α∩β＝EF ，AB ⊥α于B ，CD ⊥α于D ，若增加一个条件，就能得出BD ⊥EF .现有下列条件：①AC ⊥β；②AC 与α，β所成的角相等；③AC 与CD 在β内的射影在同一条直线上；④AC ∥EF .其中能成为增加条件的序号是________．解析：由题意得，AB ∥CD ，∴A ，B ，C ，D 四点共面．①中，∵AC ⊥β，EF ⊂β，∴AC ⊥EF ，又∵AB ⊥α，EF ⊂α，∴AB ⊥EF ，∵AB ∩AC ＝A ，∴EF ⊥平面ABCD ，又∵BD ⊂平面ABCD ，∴BD ⊥EF ，故①正确；②不能得到BD ⊥EF ，故②错误；③中，由AC 与CD 在β内的射影在同一条直线上可知平面ABCD ⊥β，又AB ⊥α，AB ⊂平面ABCD ，∴平面ABCD ⊥α.∵平面ABCD ⊥α，平面ABCD ⊥β，α∩β＝EF ，∴EF ⊥平面ABCD ，又BD ⊂平面ABCD ，∴BD ⊥EF ，故③正确；④中，由①知，若BD ⊥EF ，则EF ⊥平面ABCD ，则EF ⊥AC ，故④错误，故填①③. 答案：①③16．(2017·全国卷Ⅰ)如图，在四棱锥P -ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面PAB ⊥平面PAD ；(2)若PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P -ABCD的体积为83，求该四棱锥的侧面积． 解：(1)证明：由∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD .因为AB ∥CD ，所以AB ⊥PD .又AP ∩PD ＝P ，所以AB ⊥平面PAD .又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD .(2)如图所示，在平面PAD 内作PE ⊥AD ，垂足为E .由(1)知，AB ⊥平面PAD ，故AB ⊥PE ，可得PE ⊥平面ABCD .设AB ＝x ，则由已知可得AD ＝2x ，PE ＝22x . 故四棱锥P -ABCD 的体积V P -ABCD ＝13AB ·AD ·PE ＝13x 3.由题设得13x 3＝83，故x ＝2. 从而PA ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝22，PB ＝PC ＝2 2.可得四棱锥P -ABCD 的侧面积为12PA ·PD ＋12PA ·AB ＋12PD ·DC ＋12BC 2sin 60°＝6＋2 3. 17．(2017·山东高考)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1-B 1CD 1后得到的几何体如图所示．四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，A 1E ⊥平面ABCD .(1)证明：A 1O ∥平面B 1CD 1；(2)设M 是OD 的中点，证明：平面A 1EM ⊥平面B 1CD 1.证明：(1)取B 1D 1的中点O 1，连接CO 1，A 1O 1，因为ABCD -A 1B 1C 1D 1是四棱柱，所以A 1O 1∥OC ，A 1O 1＝OC ，因此四边形A 1OCO 1为平行四边形，所以A 1O ∥O 1C ，因为O 1C ⊂平面B 1CD 1，A 1O ⊄平面B 1CD 1，所以A 1O ∥平面B 1CD 1.(2)因为E ，M 分别为AD ，OD 的中点，所以EM ∥AO .因为AO ⊥BD ，所以EM ⊥BD .又A 1E ⊥平面ABCD ，BD ⊂平面ABCD ，所以A 1E ⊥BD ，因为B 1D 1∥BD ，所以EM ⊥B 1D 1，A 1E ⊥B 1D 1，又A 1E ⊂平面A 1EM ，EM ⊂平面A 1EM ，A 1E ∩EM ＝E ，所以B 1D 1⊥平面A 1EM ，又B1D1⊂平面B1CD1，所以平面A1EM⊥平面B1CD1.。

《直线与平面的垂直的判定、性质》单元测试卷一、 选择题1.如果直线l 和平面α内的无数条直线都垂直,那么( )A.α⊥lB.l 与α相交C.α⊄lD.l 与α的关系不确定2.如图，PA ⊥平面ABC ，△ABC 中，BC ⊥AC ，则图中直角三角形的个数是（ ）。

A.4 B.3 C.2 D.13.两条异面直线在同一平面内的射影是( ).A.两条平行直线B.两条相交直线C.一个点和一条直线D.以上都有可能4.已知Rt △ABC 中，∠C=90°,点P 在平面ABC 外，且PA=PB=PC, PO ⊥平面ABC 于点O ，则O 是（ ）A.AC 边的中点B.BC 边的中点C.AB 边的中点D.以上都有可能5.a,b 表示两条直线，α表示平面，给出以下命题，其中正确的命题是（ ） ①a ⊥α,b ∥α⇒a ⊥b ②a ⊥α, a ⊥b ⇒ b ∥α③a ∥α, a ⊥b ⇒ b ⊥α ④a ⊥α,b ∥a ⇒b ⊥αA.①②B.②③C.③④D.①④6.已知P 是平面四边形ABCD 所在平面外一点，且P 到这个四边形各边的距离相等，那么这个四边形一定是（ ）。

A.圆内接四边形B.矩形C.圆外切四边形D.平行四边形7.正方体ABCD-A 1B 1C 1D 1中，E 为A 1C 1的中点，则直线CE 垂直于（ ）。

A.ACB.BDC.A 1D 1D.AA 18.下列命题中真命题是（ ）。

A.和平面的斜线垂直的直线也和这条斜线的射影垂直B.和斜线的射影垂直的直线也和斜线垂直C.如果两条直线垂直于同一个平面，那么这两条直线平行D.和斜线的射影不垂直的直线也和斜线不垂直9.从平面α外一点P 作与α相交的直线，使得P 与交点的距离为1，则满足条件的直线条数一定不可能是（ ）.A.0B.1C.2D.无数个10.已知PA ⊥平面ABCD ，四边形ABCD 是矩形，并且PA=6,AB=3,AD=4，则P 到BD 的距离是（ ）. A.5296 B.296 C.53 D.132 11. Rt △ABC 的斜边AB 在平面α内，直角顶点C 在平面α外，C 在α上的射影为D （不在AB 上），则△ABD 是（ ）。

2.3 直线与平面垂直的判定及其性质（满分150分 时间 120分钟）班级：__________ 姓名：__________ 成绩：__________一、 选择题（每题5分，共12题，共60分）1. 已知直线a ，b 和平面α，有以下四个命题：若a α//，a b //，则b α//； 若a α⊂，b A α= ，则a 与b 异面；若a b //，b α⊥，则a α⊥； 若a b ⊥，a α⊥，则b α//．其中真命题的个数是（ ）Ａ．0 Ｂ．1 Ｃ．2 Ｄ．32. 已知直线l α⊥平面，有以下几个判断：①若m l ⊥，则m α//；②若m α⊥，则m l //；③若m α//，则m l ⊥；④若m l //，则m α⊥．上述判断中正确的是（ ）Ａ．①②③ Ｂ．②③④ Ｃ．①③④ Ｄ．①②④3. 已知两个平面垂直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线．②一个平面内的已知直线必垂直于另一个平面的无数条直线．③一个平面内的任一条直线必垂直于另一个平面．④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面．其中正确的个数是（ ）A ．３ Ｂ．２ Ｃ．１ Ｄ．０4. 在正方形ABCD 中，E ，F 分别是AB 及BC 的中点，M 是EF 的中点，沿DE ，DF 及EF 把DAE △，DFC △，EBF △折起使A ，B ，C 三点重合，重合后的点记作P ，那么在四面体P DEF -中必有（ ）Ａ．DP ⊥面PEF Ｂ．DM ⊥面PEF Ｃ．PM ⊥面DEF Ｄ．PF ⊥面DEF5. 直线a 不垂直于平面α，则α内与a 垂直的直线有（ ）Ａ．0条 Ｂ．1条 Ｃ．无数条 Ｄ．α内所有直线6. 已知三条直线m ，n ，l ，三个平面α，β，γ．下面四个命题中，正确的是（ ）Ａ．αγαββγ⊥⎫⇒⎬⊥⎭// Ｂ．m l l m ββ⎫⇒⊥⎬⊥⎭// Ｃ．m m n γ⎫⇒⎬//// Ｄ．m m n γ⊥⎫⇒⎬//7. 在空间四边形ABCD 中，若AB BC =，AD CD =，E 为对角线AC 的中点，下列判断正确的是（ ）Ａ．平面ABD ⊥平面BDC Ｂ．平面ABC ⊥平面ABDＣ．平面ABC ⊥平面ADC Ｄ．平面ABC ⊥平面BED8. α，β，γ，ω是四个不同平面，若αγ⊥，βγ⊥，αω⊥，βω⊥，则（ ）Ａ．αβ//且γω// Ｂ．αβ//或γω//Ｃ．这四个平面中可能任意两个都不平行 Ｄ．这四个平面中至多有一对平面平行9. 设a ，b 是异面直线，下列命题正确的是（ ）Ａ．过不在a ，b 上的一点P 一定可以作一条直线和a ，b 都相交Ｂ．过不在a ，b 上的一点P 一定可以作一个平面和a ，b 垂直Ｃ．过a 一定可以作一个平面与b 垂直Ｄ．过a 一定可以作一个平面与b 平行10. 设平面α⊥平面β，且l αβ= ，直线a α⊂，直线b β⊂，且a 不与l 垂直，b 不与l 垂直，那么a 与b （ ）Ａ．可能垂直，不可能平行Ｂ．可能平行，不可能垂直 Ｃ．可能垂直，也可能平行 Ｄ．不可能垂直，也不能垂直二 填空题11已知直线a ，b 和平面α，且a b ⊥，a α⊥，则b 与α的位置关系是___________．12. αβ，是两个不同的平面，m n ，是平面α及β之外的两条不同的直线，给出四个论断： m n ⊥①；αβ⊥②；n β⊥③；m α⊥④．以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题__________．13. 设O 为平行四边形ABCD 对角线的交点，P 为平面AC 外一点且有PA PC =，PB PD =，则PO 与平面ABCD 的关系是_____________．14. 设三棱锥P ABC -的顶点P 在底面ABC 内射影O （在ABC △内部，即过P 作PO ⊥底面ABC ，交于O ），且到三个侧面的距离相等，则O 是ABC △的______心.15. 如图所示，AB 是圆O 的直径，C 是异于A ，B 两点的圆周上的任意一点，PA 垂直于圆O 所在的平面，则PAB △，PAC △， ABC △，PBC △中，直角三角形的个数是_________．三 解答题16已知平面α，β，γ满足αγ⊥，βγ⊥，l αβ= ，求证：l⊥17. 如图，已知平面α，β，直线a 满足αβ⊥，a β⊥，a α⊄，试判断直线a 与平面α的位置关系并证明．18. 如图所示，ABCD 为正方形，SA ⊥平面ABCD ，过A 且垂直于SC 的平面分别交SB ，SC ，SD 于E ，F ，G ．求证：AE SB AG SD ⊥⊥，．19. 如图所示，四棱锥P ABCD -的底面是正方形，PA ⊥底面ABCD ，AE PD ⊥，EF CD //，AM EF =．求证：MF 是异面直线AB 与PC 的公垂线．α βb aP20. 如图，直角ABC △所在平面外一点S ，且SA SB SC ==，点D 为斜边AC 的中点．(1)求证：SD ⊥平面ABC ；(2)若AB BC =，求证：BD ⊥面SAC ．21. 如图所示，平面α⊥平面β，l αβ= ，在l 上取线段4AB =，AC ，BD 分别在平面α和平面β内，且AC AB ⊥，DB AB ⊥，3AC =，12BD =，求CD 长．A答 案一 选择题BBBAC;DDBDB二 填空题11.αα⊂b b 或//12.（2）（3）（4）⇒（1）或（1）（3）（4）⇒（2）13.垂直14.内心15.4三 解答题16解：在平面γ内做两条相交直线分别垂直于平面α，β与平面γ的交线，再利用面面垂直的性质定理证直线l γ⊥平面．17解：在α内作垂直于α与β交线的直线b ，因为αβ⊥，所以b β⊥．因为a β⊥，所以a b //．又因为a α⊄，所以a α//．即直线a 与平面α平行．18答案：证明：∵SA ⊥平面ABCD ，SA BC ⊥∴．又AB BC ⊥，∴BC SAB ⊥平面．AE SAB ⊂平面∵，BC AE ⊥∴，SC AEFG ⊥平面∵，SC AE AE SBC ⊥⊥平面，∴，AE SB ⊥∴．同理AG SD ⊥．19答案：证明：PA ⊥∵底面，PA AB ⊥∴．已知AB AD ⊥，AB ⊥∴面PAD ．BA AE ⊥∴．又AM CD EF ////，且AM EF =．AEFM ∴是矩形，AM MF ⊥∴．又AE PD ⊥∵，AE CD ⊥，AE ⊥∴平面PCD ．又MF AE //，MF ⊥∴平面PCD ．MF PC ⊥∴．∴MF 是异面直线AB 与PC 的公垂线．20答案：证明：（１）SA SC =∵，D 为AC 的中点，SD AC ⊥∴．连结BD ．在ABC Rt △中，则AD DC BD ==．ADS BDS ∴△≌△，SD BD ⊥∴．又AC BD D = ，SD ⊥∴面ABC ．（２）BA BC =∵，D 为AC 的中点，BD AC ⊥∴．又由（１）知SD ⊥面ABC ， SD BD ⊥∴．于是BD 垂直于平面SAC 内的两条相交直线．∴BD ⊥面SAC ．21答案：解：连结BC ．AC AB ⊥∵，AC β⊥∴，AC BD ⊥．BD AB ⊥∵，BD α⊥∴，BD BC ⊥．CBD ∴△是直角三角形．在BAC Rt △中，BC =5==，在C BD R t △中，13CD ==．CD ∴长为13．。

课题∶直线、平面垂直的判定与性质学习探究归结：一、双基自测1.判断正误：(1)一条直线垂直于一个平面内的无数条直线就垂直于这个平面（）(2)若a∥b,a⊥α,则b⊥α（）(3)若平面α⊥β，α∩β=a，b⊥a则b⊥β（）2.设m,n是两条不同的直线,α,β,γ是三个不同的平面.有下列四个命题:①若平面α⊥β，b∥α则b⊥β②若m⊥α,m∥β,则α⊥β③若n⊥α,n⊥β,m⊥α,则m⊥β④若α⊥γ,β⊥γ, α∩β=a,则a⊥γ.其中错误命题的序号是( ) (A)①④ (B)① (C)③④ (D) ②③三、典型例题例1.如图，P 为△ABC 所在平面外一点，PA ⊥平面 ABC，∠ABC＝90°，AE⊥PB 于 E. 求证：(1)BC⊥平面 PAB；(2)AE⊥平面 PBC.归结：证明线面垂直的方法：（1）（2）变式在例1中，三棱锥P-ABC的四个面中，相互垂直的平面有几对?例2. （2013年山东高考题）CBAPECBAP如图，四棱锥P-ABCD中，AB⊥AC，AB⊥PA，AB∥CD， E、F、G、M、N分别为PB、AB、BC、PD、PC的中点求证：平面EFG⊥平面EMN归结：证明面面垂直的方法：（1）（2）变式（2015年山东高考题）如图，三棱台DEF—ABC中，AB=2DE，G，H分别为AC，BC的中点，CF⊥BC，AB⊥BC.求证：平面BCD⊥平面EGH四、检测：CDFABEGH1. 设l，m， n为直线，期中m，n在平面α内，则“l⊥α”是“l⊥m且l⊥n”得（）(A)充分不必要条件 (B)必要不充分条件(C)充分必要条件 (D) 既不充分也不必要条件2 已知平面α、β和直线m，给出条件：①m∥α；②m⊥α；③m α；④α⊥β；⑤α∥β.（1）当满足条件_____________时, m∥β;（2）当满足条件_____________时, m⊥β.3.在四棱锥P-ABCD中，三角形PBC为正三角形，AB⊥平面 PBC，AB ∥CD，AB= CD，E为PD中点.求证：AE⊥平面 PDC五、总结六、作业布置课后完成新学案96-99页的相关题目ECPD BA2 1。