九年级数学上册24.4解直角三角形3学案无答案新版华东师大版

第3课时 解直角三角形的应用(二)学前温故如图，在进行测量时，从下向上看，视线与水平线的夹角叫做______；从上往下看，视线与水平线的夹角叫做______．新课早知1．坡面的铅垂高度(h )和水平宽度(l )的比叫做坡面的坡度(i )，即______；若坡角为α，则有tan α＝______，即坡度越大，坡面越陡．2．如图，AB 为斜坡，D 是斜坡上一点，斜坡AB 的坡度为i ，坡角为α，AC ⊥BM 于C ，DE ⊥BM 于E ，下列式子：①i ＝AC ∶AB ；②i ＝(AC －DE )∶EC ；③i ＝tan α＝DE BE；④AC ＝i ·B C ．其中正确的有( )．A ．1个B ．2个C ．3个D ．4个3．如图是一水库大坝横截面的一部分，坝高h ＝6 m ，迎水斜坡AB ＝10 m ，斜坡的坡角为α，则tan α的值为( )．A ．35B ．45C ．43D ．344．如图，水库堤坝的横断面成梯形ABCD ，DC ∥AB ，迎水坡AD 长为DC 长为2米，背水坡BC 长也为2米，又测得∠DAB ＝30°，∠CBA ＝60°，求下底AB 的长．答案：学前温故仰角 俯角新课早知1．i ＝h∶l4．解：过D 、C 分别作DE⊥AB 于E ，CF⊥AB 于F ，在Rt△ADE 中，∠A＝30°，AD ＝23(米)，∴DE＝ADsin 30°＝3(米)，AE ＝ADcos 30°＝3(米)．在Rt△CBF 中，BF ＝BCcos 60°＝1(米)，∴AB＝AE ＋EF ＋BF ＝3＋2＋1＝6(米)．答：下底的长为6米．坡度、坡角问题【例题】 如图，拦水坝的横断面为梯形ABCD ，坝高23米，坝面宽BC ＝6米，根据条件求：(1)斜坡AB 的坡角α；(2)坝底宽AD 和斜坡AB 的长(精确到)．分析：过B 、C 分别作梯形的高，将梯形分割为两个直角三角形和一个矩形，结合坡度即可求解．解：分别过B 、C 两点作BE ⊥AD 于E ，CF ⊥AD 于F ，则四边形BCFE 为矩形．∴BE ＝CF ，BC ＝EF .(1)在Rt△BAE 中，i ＝1∶3，tan α＝BE AE ＝13≈0.333 33.∴α≈18°26′. (2)在Rt△ABE 中，i ＝1∶3，BE ＝23米，∴AE ＝3BE ＝3×23＝69(米)．在Rt△CDF 中，i ＝1∶2.5，CF ＝BE ＝23米，∴DF ＝2.5×23＝57.5(米)．∴AD ＝AE ＋EF ＋FD ＝AE ＋BC ＋FD ＝69＋6＋57.5＝132.5(米)，AB ＝AE 2＋BE 2＝692＋232＝ 5 290≈72.7(米)．答：坡角α为18°26′，坝底AD 为，斜坡AB 约为．点拨：梯形的问题，首先应作辅助线构造直角三角形，再结合条件，利用三角函数解直角三角形．1．如图，斜坡AB 的坡度i ＝3∶1，那么tan B 的值为( )．A ．32B ．33C ．3D ．122．有一拦水坝的横断面是等腰梯形，它的上底长为6米，下底长为10米，高为23米，那么拦水坝斜坡的坡度和坡角分别是( )．A ．33，60° B．3，30° C．3，60° D．33，30° 3．一段公路水平方向每前进100米，竖直方向就升高4米，则路面坡度为__________，路面水平的倾斜角约为__________．4．如图，在坡屋顶的设计图中，AB ＝AC ，屋顶的宽l 为10米，坡角α为35°，则坡屋顶的高度h 为__________米．(结果精确到)5．(2010某某某某中考)如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌C D ．小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°，沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°.已知山坡AB 的坡度i ＝1∶3，AB ＝10米，AE ＝15米，求这块宣传牌CD 的高度．(测角器的高度忽略不计，结果精确到．参考数据：2≈1.414，3≈1.732)答案：1．C 2.C 3.1∶25 2°17′4．3.5 由题意，得tan 35°＝h l 2， ∴h＝l 2tan 35°＝5tan 35°≈3.5(米)． 5．解：作BF⊥DE 于点F ，BG⊥AE 于点G.在Rt△ADE 中，∵tan∠DAE＝DE AE， ∴DE＝AE·tan∠DAE＝153(米)．∵山坡AB 的坡度i ＝1∶3，AB ＝10米，∴BG＝5米，AG ＝53米．∴EF＝BG ＝5米，BF ＝AG ＋AE ＝53＋15(米)．∵∠CBF＝45°，∴CF＝BF ＝53＋15(米)．∴CD＝CF ＋EF －DE ＝20－103≈20－10×1.732＝2.68≈2.7(米)．答：这块宣传牌CD 的高度约为．。

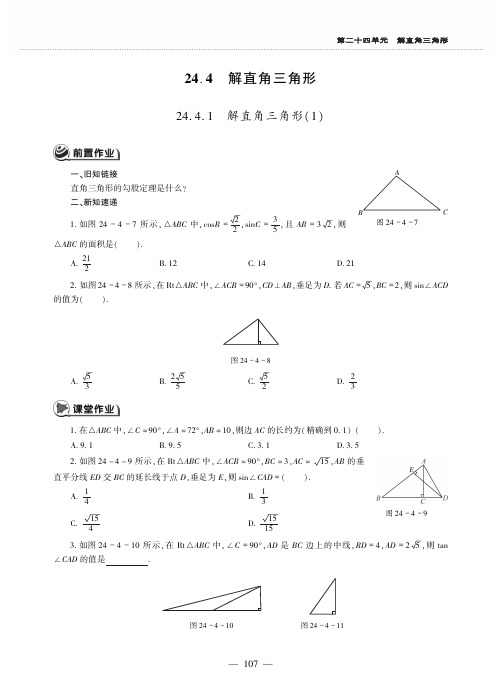
第二十四单元㊀解直角三角形２４．４㊀解直角三角形２４．４．１㊀解直角三角形（１）图２４－４－７一㊁旧知链接直角三角形的勾股定理是什么？二㊁新知速递１．如图２４－４－７所示，әＡＢＣ中，ｃｏｓＢ＝２２，ｓｉｎＣ＝３５，且ＡＢ＝３２，则әＡＢＣ的面积是（㊀㊀）．㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ ２１２Ｂ １２Ｃ １４Ｄ ２１２．如图２４－４－８所示，在ＲｔәＡＢＣ中，øＡＣＢ＝９０ʎ，ＣＤʅＡＢ，垂足为Ｄ．若ＡＣ＝５，ＢＣ＝２，则ｓｉｎøＡＣＤ的值为（㊀㊀）．ＡＣＢＤ图２４－４－８Ａ ５３Ｂ ２５５Ｃ５２Ｄ ２３㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀１．在әＡＢＣ中，øＣ＝９０ʎ，øＡ＝７２ʎ，ＡＢ＝１０，则边ＡＣ的长约为（精确到０．１）（㊀㊀）．Ａ ９．１Ｂ ９．５Ｃ．３．１Ｄ ３．５图２４－４－９２．如图２４－４－９所示，在ＲｔәＡＢＣ中，øＡＣＢ＝９０ʎ，ＢＣ＝３，ＡＣ＝１５，ＡＢ的垂直平分线ＥＤ交ＢＣ的延长线于点Ｄ，垂足为Ｅ，则ｓｉｎøＣＡＤ＝（㊀㊀）．Ａ１４Ｂ １３Ｃ １５４Ｄ １５１５３．如图２４－４－１０所示，在ＲｔәＡＢＣ中，øＣ＝９０ʎ，ＡＤ是ＢＣ边上的中线，ＢＤ＝４，ＡＤ＝２５，则ｔａｎøＣＡＤ的值是㊀㊀㊀㊀㊀．ＡＣＢＤ图２４－４－１０㊀㊀㊀㊀ＡＣＢ图２４－４－１１４．如图２４－４－１１所示，әＡＢＣ中，ÐＣ＝９０°，ＢＣ＝４ｃｍ，ｔａｎＢ＝３２，则әＡＢＣ的面积是㊀㊀㊀㊀ｃｍ２．５．已知：正方形ＡＢＣＤ的边长为２，点Ｐ是直线ＣＤ上一点，若ＤＰ＝１，则ｔａｎøＢＰＣ的值是㊀㊀㊀㊀．６．如图２４－４－１２所示在一次课外实践活动中，同学们要测量某公园人工湖两侧Ａ，Ｂ两个凉亭之间的距离．现测得ＡＣ＝３０ｍ，ＢＣ＝７０ｍ，øＣＡＢ＝１２０ʎ，请计算Ａ㊁Ｂ两个凉亭之间的距离．图２４－４－１２基础训练１．（２０１４㊃连云港）如图２４－４－１３所示，若әＡＢＣ和әＤＥＦ的面积分别为Ｓ１㊁Ｓ２，则（㊀㊀）．ＦＥＡＣＢＤ５８８５４０°１４０°图２４－４－１３㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ Ｓ１＞Ｓ２Ｂ Ｓ１＝Ｓ２Ｃ Ｓ１＜Ｓ２Ｄ Ｓ１ȡＳ２２．如图２４－４－１４所示，在把易拉罐中的水倒入一个圆水杯的过程中，若水杯中的水在点Ｐ与易拉罐刚好接触，则此时水杯中的水深为（㊀㊀）．１图２４－４－１４Ａ ２ｃｍＢ．４ｃｍＣ．６ｃｍＤ．８ｃｍ３．如图２４－４－１５所示，在әＡＢＣ中，ＡＢ＝１６，ＡＣ＝９１，ＢＣ＝５３，则øＢ＝㊀㊀㊀㊀㊀．ＡＣＢ图２４－４－１５㊀㊀㊀图２４－４－１６４．如图２４－４－１６，机器人从Ａ点，沿着西南方向，行了４２个单位，到达Ｂ点后观察到原点Ｏ在它的南偏东６０ʎ的方向上，则原来Ａ的坐标为㊀㊀㊀㊀㊀㊀㊀㊀．（结果保留根号）５．如图２４－４－１７所示，在ＲｔәＡＢＣ中，øＡ＝９０ʎ，ＡＤʅＢＣ，垂足为Ｄ，øＢ＝６０ʎ，ＡＤ＝３，求ＢＣ的长．ＡＢＣＤ图２４－４－１７第二十四单元㊀解直角三角形６．如图２４－４－１８所示，一艘海轮位于灯塔Ｐ的北偏东６０ʎ方向上，它沿正南方向航行７０海里，到达位于灯塔Ｐ的南偏东３０ʎ方向的Ｂ处，问：此时海轮距离灯塔Ｐ多远？图２４－４－１８７．在锐角三角形ＡＢＣ中，øＣ＝４５ʎ，ＡＣ＝６，ＡＢ＝２，求这个三角形的未知的边和未知的角？提高练习８．（２０１４浙江省杭州）如图２４－４－１９所示，已知ＡＤ／／ＢＣ，ＡＢʅＡＤ，点Ｅ，点Ｆ分别在射线ＡＤ，射线ＢＣ上，若点Ｅ与点Ｂ关于ＡＣ对称，点Ｅ与点Ｆ关于ＢＤ对称，ＡＣ与ＢＤ相交于点Ｇ．则（㊀㊀）．图２４－４－１９Ａ １＋ｔａｎøＡＤＢ＝２Ｂ ２ＢＣ＝５ＣＦＣ øＡＥＢ＋２２ʎ＝øＤＥＦＤ ４ｃｏｓøＡＧＢ＝６发散思维９．（２０１４㊃南昌）在ＲｔәＡＢＣ中，øＡ＝９０ʎ，有一个锐角为６０ʎ，ＢＣ＝６．若点Ｐ在直线ＡＣ上（不与点Ａ，Ｃ重合），且øＡＢＰ＝３０ʎ，则ＣＰ的长为㊀㊀㊀㊀㊀．ＤＢＣＡ图２４－４－２０１０．（２０１４㊃大庆）如图２４－４－２０所示，等腰әＡＢＣ中，ＡＢ＝ＡＣ，øＢＡＣ＝３６ʎ，ＢＣ＝１，点Ｄ在边ＡＣ上且ＢＤ平分øＡＢＣ，设ＣＤ＝ｘ．（１）求证：әＡＢＣʐәＢＣＤ；（２）求ｘ的值；（３）求ｃｏｓ３６ʎ－ｃｏｓ７２ʎ的值．２４．４．２㊀解直角三角形（２）一㊁旧知链接解直角三角形常常用到的方法是什么？二㊁新知速递１．如图２４－４－２９所示，从热气球Ｃ上测定建筑物Ａ㊁Ｂ底部的俯角分别为３０ʎ和６０ʎ，如果这时气球的高度ＣＤ为１５０米，且点Ａ㊁Ｄ㊁Ｂ在同一直线上，建筑物Ａ㊁Ｂ间的距离为（㊀㊀）．图２４－４－２９Ａ １５０３米Ｂ １８０３米Ｃ ２００３米Ｄ ２２０３米２．如图２４－４－３０所示，在高楼前Ｄ点测得楼顶的仰角为３０ʎ，向高楼前进６０米到Ｃ点，又测得仰角为４５ʎ，则该高楼的高度大约为（㊀㊀）米．ＢＣＡＤ３０°４５°图２４－４－３０Ａ ８２Ｂ １６３Ｃ ５２Ｄ ３０１．如图２４－４－３１所示，两建筑物的水平距离为ａ米，从Ａ测得Ｄ点的俯角为α，测得Ｃ点的俯角为β，则较低建筑物ＣＤ的高为（㊀㊀）．图２４－４－３１㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ ａ米Ｂ ａｔａｎα米Ｃ ａｔａｎβＤ ａ（ｔａｎβ－ｔａｎα）米２．如图２４－４－３２所示，小河对岸有一座塔ＡＢ．分别在点Ｄ㊁Ｃ处测得塔尖点Ａ处的仰角为ø１＝３０ʎ㊁ø２＝４５ʎ，且ＣＤ＝１２米．则塔的高度ＡＢ约为㊀㊀㊀㊀㊀㊀㊀米．（精确到０．１米）图２４－４－３２第二十四单元㊀解直角三角形３．（２０１０㊃潼南）如图２４－４－３３所示，小明在家里楼顶上的点Ａ处，测量建在与小明家楼房同一水平线上相邻的电梯楼的高，在点Ａ处看电梯楼顶部点Ｂ处的仰角为６０ʎ，在点Ａ处看这栋电梯楼底部点Ｃ处的俯角为４５ʎ，两栋楼之间的距离为３０ｍ，则电梯楼的高ＢＣ为㊀㊀㊀㊀㊀㊀㊀米（精确到０．１）．（参考数据：２ʈ１．４１４，３ʈ１．７３２）ＢＣＡ６０°４５°图２４－４－３２４．目前世界上最高的电视塔是广州新电视塔．如图２４－４－３４所示，新电视塔高ＡＢ为６１０米，远处有一栋大楼，某人在楼底Ｃ处测得塔顶Ｂ的仰角为４５ʎ，在楼顶Ｄ处测得塔顶Ｂ的仰角为３９ʎ．（１）求大楼与电视塔之间的距离ＡＣ；（２）求大楼的高度ＣＤ（精确到１米）．ＢＥＤＣＡ３９°４５°图２４－４－３４５．在一个阳光明媚㊁清风徐来的周末，小明和小强一起到郊外放风筝﹒他们把风筝放飞后，将两个风筝的引线一端都固定在地面上的Ｃ处（见图２４－４－３５）．现已知风筝Ａ的引线（线段ＡＣ）长２０ｍ，风筝Ｂ的引线（线段ＢＣ）长２４ｍ，在Ｃ处测得风筝Ａ的仰角为６０ʎ，风筝Ｂ的仰角为４５ʎ．（１）试通过计算，比较风筝Ａ与风筝Ｂ谁离地面更高？（２）求风筝Ａ与风筝Ｂ的水平距离．（精确到０．０１ｍ；参考数据：ｓｉｎ４５ʎʈ０．７０７，ｃｏｓ４５ʎʈ０．７０７，ｔａｎ４５ʎ＝１，ｓｉｎ６０ʎʈ０．８６６，ｃｏｓ６０ʎ＝０．５，ｔａｎ６０ʎʈ１．７３２）ＥＤＣＡ６０°４５°Ｂ图２４－４－３５视线视线铅垂线水平线１２３４图２４－４－３６基础训练１．如图２４－４－３６所示，下列角中为俯角的是（㊀㊀）．㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ ø１Ｂ ø２Ｃ ø３Ｄ ø４㊀㊀２．如图２４－４－３７所示，某地修建高速公路，要从Ｂ地向Ｃ地修一座隧道（Ｂ㊁Ｃ在同一水平面上）．为了测量Ｂ㊁Ｃ两地之间的距离，某工程师乘坐热气球从Ｃ地出发，垂直上升１００ｍ到达Ａ处，在Ａ处观察Ｂ地的俯角为３０ʎ，则Ｂ㊁Ｃ两地之间的距离为（㊀㊀）．３０°ＡＣＢ图２４－４－３７Ａ １００３Ｂ ５０２Ｃ ５０３Ｄ １００３３３．某中学升国旗时，李蕊同学站在离旗杆底部１２ｍ处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰巧为４５ʎ，若她的双眼离地面１．３ｍ，则旗杆高度为㊀㊀㊀㊀㊀ｍ．４．在地面上一点，测得一电视塔尖的仰角为４５ʎ，沿水平方向，再向塔底前进ａｍ，又测得塔尖的仰角为６０ʎ，那么电视塔的高为㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ｍ．５．如图２４－４－３８所示，为了测量电线杆的高度ＡＢ，在离电线杆２２．７米的Ｃ处，用１．２０米的测角仪ＣＤ测得电线杆顶端Ｂ的仰角ａ＝２２ʎ，求电线杆ＡＢ的高度．ＡＥＤＣＢ图２４－４－３８６．如图２４－４－３９所示，从相距１００ｍ的Ａ，Ｂ两点观测建筑物ＣＤ，用测角仪测得建筑物顶点Ｃ的仰角分别为６０ʎ和４５ʎ，求Ａ，Ｂ两点到建筑物底端Ｄ的距离分别为多少米？ＡＥＤＤ′ＦＣＢ６０°４５°图２４－４－３９７．如图２４－４－４０所示，甲㊁乙两楼相距８０ｍ，从乙楼底Ｄ望甲楼顶Ａ的仰角为４５ʎ，从甲楼顶Ａ望乙楼顶Ｃ的俯角为３０ʎ，求甲㊁乙两楼的高（精确到１ｍ）．ＡＤＣＢ３０°甲乙４５°图２４－４－４０第二十四单元㊀解直角三角形提高练习８．如图２４－４－４１所示，某侦察机在空中Ａ处发现敌方地面目标Ｂ，此时从飞机上看目标Ｂ的俯角为α，已知飞行高度ＡＣ＝４５００米，ｔａｎα＝５６，则飞机到目标Ｂ的水平距离ＢＣ为（㊀㊀）．图２４－４－４１Ａ ５４００５米Ｂ ５４００３米Ｃ．５６００５米Ｄ．５６００３米９．如图２４－４－４２所示，小明发现在教学楼走廊上有一拖把以１５ʎ的倾斜角斜靠在栏杆上，严重影响了同学们的行走安全．他自觉地将拖把挪动位置，使其的倾斜角为７５ʎ，如果拖把的总长为１．８０ｍ，则小明拓宽了行路通道多少米？（结果保留小数点后两位数字，参考数据：ｓｉｎ１５ʎʈ０．２６，ｃｏｓ１５ʎʈ０．９７）７５°１５°图２４－４－４２发散思维１０．如图２４－４－４３所示，Ａ㊁Ｂ是两幢地平高度相等㊁隔岸相望的建筑物，Ｂ楼不能到达，由于建筑物密集，在Ａ楼的周围没有开阔地带，为测量Ｂ楼的高度，只能充分利用Ａ楼的空间，Ａ楼的各层都可到达且能看见Ｂ楼，现仅有测量工具为皮尺和测角器（皮尺可用于测量长度，测角器可以测量仰角㊁俯角或两视线的夹角）．ＡＢ图２４－４－４３（１）你设计一个测量Ｂ楼高度的方法，要求写出测量步骤和必需的测量数据（用字母表示），并画出测量图形．（２）用你测量的数据（用字母表示）写出计算Ｂ楼高度的表达式．２４．４．３㊀解直角三角形（３）一㊁旧知链接解直角三角形用到的关系式是什么？二㊁新知速递１．河堤的横断面如图２４－４－５３所示，堤高ＢＣ是５米，迎水斜坡ＡＢ的长是１３米，那么斜坡ＡＢ的坡度ｉ是（㊀㊀）．ＡＣＢ图２４－４－５３㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ １ʒ３Ｂ １ʒ２．６Ｃ １ʒ２．４Ｄ １ʒ２２．如图２４－４－５４所示，一水库迎水坡ＡＢ的坡度ｉ＝１︰３，则该坡的坡角α＝㊀㊀㊀㊀．图２４－４－５４１．如图２４－４－５５所示，水库大坝的横断面为梯形，坝顶宽为６米，坝高为２４米，斜坡ＡＢ的坡角为４５ʎ，斜坡ＣＤ的坡度为ｉ＝１ʒ２，则坝底ＡＤ的长为（㊀㊀）．ＡＢＣＤ图２４－４－５５Ａ ４２米Ｂ （３０＋２４３）米Ｃ ７８米Ｄ （３０＋８３）米２．如图２４－４－５６所示，梯形护坡石坝的斜坡ＡＢ的坡度ｉ＝１ʒ３，坝高ＢＣ＝２米，则斜坡ＡＢ的长为㊀㊀㊀㊀㊀米．ＡＣＢ图２４－４－５６３．小明要在坡度为３４的山坡上植树，要想保证水平株距为５ｍ，则相邻两株树植树地点的高度差应为㊀㊀㊀㊀㊀ｍ．４．有一拦水坝的横断面是等腰梯形，它的上底长为６米，下底长为１０米，高为２３米，那么此拦水坝斜第二十四单元㊀解直角三角形坡的坡度为㊀㊀㊀㊀㊀，坡角为㊀㊀㊀㊀㊀．５．如图２４－４－５７所示，在一滑梯侧面示意图中，ＢＤ／／ＡＦ，ＢＣʅＡＦ于点Ｃ，ＤＥʅＡＦ于点Ｅ．ＢＣ＝１．８ｍ，ＢＤ＝０．５ｍ，øＡ＝４５ʎ，øＦ＝２９ʎ．（１）求滑道ＤＦ的长（精确到０．１ｍ）；（２）求踏梯ＡＢ底端Ａ与滑道ＤＦ底端Ｆ的距离ＡＦ（精确到０．１ｍ）．（参考数据：ｓｉｎ２９ʎʈ０．４８，ｃｏｓ２９ʎʈ０．８７，ｔａｎ２９ʎʈ０．５５）ＣＡＥＢＤ图２４－４－５７基础训练１．如图２４－４－５８所示，已知在ＲｔәＡＢＣ中，øＣ＝９０ʎ，ＡＣ＝４，ｔａｎＡ＝１２，则ＡＢ的长是（㊀㊀）．图２４－４－５８Ａ ２Ｂ ８Ｃ ２５Ｄ ４５２．如图２４－４－５９所示，小明去爬山，在山脚看山顶角度为３０ʎ，小明在坡比为５ʒ１２的山坡上走１３００米，此时小明看山顶的角度为６０ʎ，求山高（㊀㊀）．图２４－４－５９Ａ ６００－２５０５Ｂ ６００３－２５０Ｃ ３５０＋３５０３Ｄ ５００３３．某人沿着一山坡向上走了４００米，其铅直高度上升了２００米，则山坡与水平面所成的锐角是㊀㊀㊀㊀㊀．４．如图２４－４－６０所示，沿ＡＣ方向开山修渠，为加快施工进度，要在小山的另一边同时施工．从ＡＣ上的一点Ｂ取øＡＢＤ＝１４０ʎ，ＢＤ＝５２０ｍ，øＤ＝５０ʎ，那么开挖点Ｅ离Ｄ㊀㊀㊀㊀㊀ｍ，正好能使Ａ，Ｃ，Ｅ成直线（精确到０．１ｍ）．ＡＢＣＥＤ１４０°５０°图２４－４－６０５．某商场为方便顾客使用购物车，准备将滚动电梯的坡面坡度由１ʒ１．８改为１ʒ２．４（见图２４－４－６１）．如果改动后电梯的坡面长为１３米，求改动后电梯水平宽度增加部分ＢＣ的长．图２４－４－６１６．某武警部队探测队参加一次地质灾害抢险工作，探测出某建筑物下面有生命迹象，为了准确测出生命迹象所在的深度，他们在生命迹象上方建筑物的一侧地面上相距５米的Ａ㊁Ｂ处，用仪器探测生命迹象Ｃ，已知探测线与地面的夹角分别是３０ʎ和６０ʎ（见图２４－４－６２），则该生命迹象所在位置的深度（结果可以带根号）为多少米？ＡＢＣ３０°６０°图２４－４－６２７．如图２４－４－６３所示，某防洪指挥部发现长江边一处长６００米，高１０米，背水坡的坡角为４５ʎ的防洪大堤（横断面为梯形ＡＢＣＤ）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：沿背水坡面用土石进行加固，并使上底加宽２米，加固后背水坡ＥＦ的坡比ｉ＝１ʒ３．（１）求加固后坝底增加的宽度ＡＦ；（结果保留根号）（２）求完成这项工程需要土石多少立方米？（结果取３ʈ１．７３２）ＡＣＢＦＥｉ＝１：Ｄ４５°３图２４－４－６３提高练习图２４－４－６４８．图２４－４－６４是某水库大坝横断面示意图．其中ＡＢ㊁ＣＤ分别表示水库上下底面的水平线，øＡＢＣ＝１２０ʎ，ＢＣ的长是５０ｍ，则水库大坝的高度ｈ是（㊀㊀）．㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Ａ ２５３ｍＢ ２５ｍＣ ２５２ｍＤ ５０３３ｍ第二十四单元㊀解直角三角形发散思维９．如图２４－４－６５，测量底部不能直接到达的建筑物ＭＮ的高度，其测量的一般步骤是：图２４－４－６５（１）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀；（２）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀；（３）㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀．１０．如图２４－４－６６所示，某大楼的顶部树有一块广告牌ＣＤ，小李在山坡的坡脚Ａ处测得广告牌底部Ｄ的仰角为６０ʎ．沿坡面ＡＢ向上走到Ｂ处测得广告牌顶部Ｃ的仰角为４５ʎ，已知山坡ＡＢ的坡度ｉ＝１ʒ３，ＡＢ＝１０米，ＡＥ＝１５米．（ｉ＝１ʒ３是指坡面的铅直高度ＢＨ与水平宽度ＡＨ的比）（１）求点Ｂ距水平面ＡＥ的高度ＢＨ；（２）求广告牌ＣＤ的高度．（测角器的高度忽略不计，结果精确到０．１米．参考数据：２ʈ１．４１４，３ʈ１．７３２）ＡＥＨＣＢＤ６０°４５°图２４－４－６６７１１。

24.4.3 解直角三角形【学习目标】1．掌握坡角与坡度概念, 能利用解直角三角形解决有关实际问题。

2．由实际问题转化为几何问题时,学会自己画图,建立模型.【学习重难点】掌握坡角与坡度概念, 能利用解直角三角形解决有关实际问题。

【学习过程】一、课前准备1.计算: ︒︒+︒+︒60cot 60tan 30cos 30sin 2222 2．如图，两建筑物的水平距离BC 为24米，从点A 测得点D 的俯角α＝30°，测得点C 的俯角β＝60°，求AB 和CD 两座建筑物的高．（结果保留根号）二、学习新知自主学习：1.坡面的铅垂高度（h ）和水平长度（l ）的比叫做坡面的坡度（或坡比），记作i ，即=i ．(坡度通常写成1∶m 的形式，如i ＝1∶6．)2.坡面与水平面的夹角叫做坡角，记作α，有tan α＝ ．3.坡度越大，坡角α就越 ，坡面就越 ．图25.3.5图25.3.6实例分析：例1如图25．3．6，一段路基的横断面是梯形，高为4．2米，上底的宽是12．51米，路基的坡面与地面的倾角分别是32°和28°．求路基下底的宽．（精确到0．1米）解：【随堂练习】1. 如果a ∠是等腰直角三角形的一个锐角，则tan α的值是 。

2.如图，坡角为30的斜坡上两树间的水平距离AC 为2m ，则两树间的坡面距离AB 为（ ）A ．4m BC．m 3 D．3. 如图，为了绿化荒山，某地打算从位于山脚下的机井房沿着山坡铺设水管，在山坡上修建一座扬水站，对坡面的绿地进行喷灌。

现测得斜坡与水平面所成角的度数是30°，为使出水口的高度为35m ，那么需要准备的水管的长为（ ） A.17.5m B.35m C.335m D.70m4.如图，一架梯子斜靠在墙上，若梯子到墙的距离AC =3米，3cos 4BAC ∠=，则梯子AB 的长度为 米．5.在Rt ABC △中，90C ∠=，:3:4BC AC =，则cos A = ．【中考连线】河堤横断面如图所示，堤高BC=6米，迎水坡AB 的坡比为1：，则AB 的长为（ ）A ．12B ．4米C ．5米D ．6米【参考答案】随堂练习1、12、B 3、D 4、4 5、中考连线A。

解直角三角形（3）【学习目标】1.了解常用的测量名词的意义，会用解直角三角形的有关知识解某些简单的实际问题；2.能根据测量术语绘出示意图，学会把实际问题转化为数学问题的方法；3.认识数学与生活生产的联系，养成应用数学的意识。

【重点】用解直角三角形的有关知识解决实际问题. 【难点】用解直角三角形的有关知识解决实际问题。

【使用说明与学法指导】先预习课本P115—P116，了解坡角、坡度等名词的实际意义，能够根据实际情境，画出图形，解决问题，再针对预习案二次阅读教材，疑惑随时记录在课本或预习案上，准备课上讨论质疑；预 习 案一、预习导学：1.了解测量名词:坡度、坡角如图所示， 叫做坡度，记作 ，通常写成 的形式。

角叫做坡角。

2. 坡度、坡角问题（1）如图所示，请写出坡度与坡角的关系。

小结：坡度越大， 。

（2）如图，沿坡角为30°的山坡植树，要求相邻两棵树间的水平距离AC 为2m ，求相邻两棵树的斜坡距离AB 约为多少米？（精确到0.1m ）【预习自测】1.某斜坡的坡度为3=i ，则该斜坡的坡角为 度。

2.王英同学沿坡度为33:1=i 的山路行了40m,则王英升高了 m. 二、我的疑惑合作探究探究一：如图，一段河坝的断面为梯形ABCD ，试根据图中数据，求出坡角α和坝底宽AD ．（i ＝CE ∶ED ，单位米，结果保留根号）小结：探究二：一水库大坝的横断面为梯形ABCD ，坝顶宽6．2米，坝高23．5米，斜坡 AB 的坡度1i ＝1∶3，斜坡CD 的坡度2i ＝1∶2．5．求：（1）斜坡AB 与坝底AD 的长度；（精确到0．1米） （2）斜坡CD 的坡角α．（精确到1°）我本节课的收获与反思：单元过关测试小组： 姓名： 评价：一、选择题（每小题3分，共21分） 1．计算sin45°的结果等于………………………（ ） A ．B ．1C ．D ．2．如图，在Rt△ABC 中，CD 是斜边AB 上的中线，已知CD ＝2， AC ＝3，则sinB 的值是……………………………………………（ ） A ．B ．C ．D ．3．如果∠A 是锐角，sinA ＝cos60°，那么∠A 的度数是…（ ）A ．30°B ．45°C ．60°D ．不存在4．在Rt△ABC 中，∠ACB＝Rt∠，BC ＝1，AB ＝2，则下列结论正确的是……（ ） A ．sinA ＝B ．tanA ＝C ．cosB ＝D ．tanB ＝5．河堤横断面如图所示，堤高BC ＝5米，迎水坡AB 的坡比 是1:(坡比是坡面的铅直高度BC 与水平宽度AC 之比)，则AC 的长是（） A ．5米 B ．10米 C ．15米 D ．10米6．边长为2的菱形，一个内角为120°，则较长的对角线长为（ ） A 、2B 、C 、2D 、17.如图，在直角坐标系中，将矩形OABC 沿OB 对折，使点A 落在A 1处，已知OA ＝，AB ＝1，则点A 1的坐标是…………………（ ） A ．（，） B ．（，3） C ．（，） D ．（，）二、填空题（每小题4分，共40分） 8．计算：2sin30°＝ . 9．在Rt△ABC 中，∠C＝90°，sinA ＝，则∠A＝ ．10．在Rt△ABC 中，∠C＝90°，当a ＝12时，b ＝5时，sinA ＝ ． 11．已知Rt△ABC,AD 是斜边BC 上的高,∠B＝2∠C, AB ＝6cm, 则CD 的长为 cm. 12．如图，在平面直角坐标系中，已知点A(3，０)，点B(0，－4)， 则cos∠OAB＝ ．13．如果方程x 2－4x ＋3＝0的两个根分别是Rt△ABC 的两条边，□B C□ ABCD△ABC 最小的角为A ，那么tanA 的值为 ．14．如图，已知在直角三角形ABC 中，∠C＝90°，AC ＝5，AB ＝10，则∠B＝ 度 15．如图，从点C 测得树的顶端的仰角为33°，BC ＝20米，则树高AB≈ 米（结果精确到0.1米）.16．如图，一架梯子斜靠在墙上，若梯子到墙的距离AC ＝3米，cos∠BAC＝，则梯子AB 的长度为 米．17．如图，某河道要建造一座公路桥，要求桥面离地面高度AC 为3米，引桥的坡角∠ABC 为15°，引桥的水平距离BC 的长是__________米（精确到0.1米）．三、解答题（共89分） 18．（9分）计算：tan60°－cos45°＋19．（9分）计算：4cos30°sin60°＋(－2)－1－(－2008)°20．（9分）如图，有一个坡角为28°的斜坡AB ，若坡面的铅垂高度AC 为10米，求坡面AB 的长度.（结果精确到0.1米）21．（9分）在菱形ABCD 中，AE⊥BC 于E 点，CE ＝2，sinB ＝，求菱形ABCD 的面积．ABC（第14题）AC22．（9分）如图，在梯形ABCD 中，AD∥BC，AC⊥AB，AD ＝CD ，cos∠DCA＝ ，BC ＝10，求AB 的长.23．（9分）如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB 、CD 分别表示一楼、二楼地面的水平线，∠ABC＝152°，BC ＝9m ，求乘电梯从点B 到点C 上升的高度CE ．（精确到0.1m ）24．（9分）如图，在矩形ABCD 中，E 是BC 边上的点，AE （1）求证：△ABE≌△DFA；（2）如果AD ＝10，AB ＝6，求sin∠EDF 的值．BACD25．（13分）如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端B，梯子与地面所成的角∠BAC 一般要满足50°≤∠BAC≤75°.现有一个长4m的梯子，问：（1）安全使用这个梯子时，梯子顶端距离地面的最大高度BC约为多少m？（结果精确到0.1m）；（2）当梯子底端与墙面的距离AC等于2.8m时，梯子与地面所成的角∠BAC约为多少度（精确到1°）？这时人是否能够安全使用这个梯子？26．（13分）如图，已知一次函数y＝kx＋b的图象经过A(－2，－1)，B(1，3)两点，并且交x轴于点C，交y轴于点D，（1）求该一次函数的解析式；（2）求tan∠OCD的值；（3）求证：∠AOB＝135°．一1－7 BCADAAA二、8、1 9、45°10、11、9 12、13、或14、30°15、13 16、4 17、11.218、4 19、120、AB≈21.3m21、在Rt△ABE中，sinB＝，∴AE＝5x，AB＝13x，BE＝12x．又∵四边形ABCD是菱形，∴AB＝BC，即13x＝12x＋2，∴x＝2．∴AB＝26，AE＝10，S菱形ABCD＝26×10＝260．22、由∠ACB＝∠CAD＝∠DCA可知cos∠ACB＝cos∠DCA＝，∴＝，AC＝8 ∴AB ＝6 23、CE≈4.2m24、（1）证明：在矩形ABCD中，BC＝AD，AD∥BC，∠B＝90°∴∠DAF＝∠AEB，QDF⊥AE，AE＝BC ∴∠AFD＝90°＝∠B AE＝AD ∴△ABE≌△DFA （2）解：由（1）知△ABE ≌△DFA ∴AB＝DF＝6 在直角△ADF中，AF＝＝＝8 ∴EF＝AE－AF＝AD －AF＝2 在直角△DFE中，DE＝＝＝2．∴sin∠EDF＝＝＝．25、⑴3.9m ⑵约46°，不能安全使用26、⑴y＝x＋⑵⑶延长AO到A'，使OA'＝OA，则A'（2，1）易求OA'＝，OB＝，A'B＝，∴OA'2＋A'B 2＝OB2∴∠OA'B ＝90°，∴∠BOA'＝45°∴∠AOB＝135°。

测量【学习目标】1．复习巩固相似三角形知识，掌握测量方法；2．通过测量旗杆高度的活动，巩固相似三角形有关知识，累积数学活动经验，使学生初步学会数学建模的方法；3．通过运用相似以及已学过的知识探索解三角形的方法，体验教学研究和发现的过程，逐渐培养学生用数学说理的习惯，激起学生学习后续内容的积极性．【学习重点】掌握测量方法．【学习难点】理解并掌握测量方法．情景导入生成问题问题：1.复习相似三角形的主要性质．2．当你走进学校，仰头望着操场旗杆上高高飘扬的五星红旗时，你也许想知道操场旗杆有多高？我们知道可以利用相似三角形的对应边，首先请同学量出太阳下自己的影子长度，旗杆的影子长度，再根据自己的身高，计算出旗杆的高度．如果在阴天，你一个人能测量出旗杆的高度吗？自学互研生成能力知识模块测量物体的高度或宽度阅读教材P99～P101的内容．问题：如下图所示，站在离旗杆BE底部10米处的D点，目测旗杆的顶部，视线AB与水平线的夹角∠BAC＝34°，并已知目高AD为1米．现在请你按1∶500的比例将△ABC画在纸上，并记为△A1B1C1，用刻度尺量出纸上B1C1的长度，便可以算出旗杆的实际高度．你知道计算的方法吗？解：∵△ABC∽△A1B1C1，∴AC∶A1C1＝BC∶B1C1＝500∶1，∴只要用刻度尺量出纸上B1C1的长度，就可以计算出BC 的长度，加上AD长即为旗杆的高度．若量得B1C1＝a cm，则BC＝500a cm＝5a m.故旗杆高(1＋5a)m.范例：小兵身高160cm ，他的影子长度是100cm ，如果同时，他朋友的影子比他的影子短5cm ，那么他的朋友有多高？解：设他朋友身高为x cm ，则160100＝x 100－5，解得：x ＝152.答：他朋友身高为152cm . 仿例1：小明想知道学校旗杆的高度，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，求旗杆的高度．解：设旗杆的高度为x m ，则x 2＋52＝(x ＋1)2，解得x ＝12.答：旗杆的高度为12m .仿例2：如图，小明站在C 处看甲乙两楼楼顶上的点A 和点E ，点C 、E 、A 在同一条直线上，点B 、D 分别在点E 、A 的正下方，且点D 、B 、C 在同一条直线上，点B 、C 相距20米，点D 、C 相距40米，乙楼高BE 为15米，求甲楼AD 的高．(小明的身高忽略不计)解：由题意知BC ＝20，CD ＝40，△CBE ∽△CDA.∴CB CD ＝BE AD 即2040＝15AD， ∴AD ＝30(米)．答：甲楼AD 高30米．交流展示 生成新知1．将阅读教材时“生成的问题”和通过“自主探究、合作探究”得出的“结论”展示在各小组的小黑板上．并将疑难问题也板演到黑板上，再一次通过小组间就上述疑难问题相互释疑．2．各小组由组长统一分配展示任务，由代表将“问题和结论”展示在黑板上，通过交流“生成新知”．知识模块 测量物体的高度或宽度范例：(方法二)160x ＝100100－5，解得x ＝152 检测反馈 达成目标1．某同学的身高为1.6米，某一时刻他在阳光下的影长为1.2米，与他相邻的一棵树的影长为3.6米，则这棵树的高度为( B )A ．5.3米B ．4.8米C ．4.0米D ．2.7米2．垂直于地面的竹杆的影长为12米，其顶端到其影子顶端的距离为13米，如果此时测得某小树的影长为6米，则树高为__2.5__米．3．如图，一条河的两岸有一段是平行的，两岸岸边各有一排树，每排树相邻两棵的间距都是10米，在这岸离开岸边16米的A处看对岸，看到对岸两棵树B、C的树干恰好被这岸两棵树D、E的树干遮住，这岸的两棵树D、E之间有一棵树，B、C 之间有四棵树，求河C、D的宽．解：CD＝24米．4．如图，在距离旗杆AB 18米的地面上平放着一面镜子E，人退后到距离镜子2.1米的D处，在镜子里恰好看见旗杆顶，若人眼距地面1.4米，求旗杆高．解：AB＝12米课后反思查漏补缺1．收获：________________________________________________________________________2．存在困惑：______________________________________________________________________。

24.4 解直角三角形（ 3）教课目标： 弄清铅垂高度、水平长度、坡高（或坡比） 、坡角等看法；教课要点： 理解坡度和坡角的看法教课难点： 利用坡度和坡角等条件，解决有关的实质问题教课过程：一、复习发问：什么叫仰角、俯角？二、坡度、坡角的看法几个看法： 1、铅垂高度 h2、水平长度l3、坡度（坡比） i : 坡面的铅垂高度 h 和水平长度 l 的比h 1 1itanll mh4、坡角：坡面与水平面的夹角. h tanil明显，坡度 i 越大，坡角就越大，坡面就越陡。

练习： 1、沿山坡行进 10 米，相应高升5 米，则山坡坡度1，坡角 3 0°，32、若一斜坡的坡面的余弦为3 10，则坡度 i 1 ，1033、堤坝横断面是等腰梯形， （以下列图）DC若 AB=10，CD=4，高 h=4，则坡度 i = 4，AD= 5①3AB1EF，则 h 2，②若 AB=10， CD=4 ， i5例 1、书 P115 例 4例 2、如图，水库堤坝的横断面成梯形ABCD ，DC ∥AB ，迎水坡 AD 长为2 3 米，上底 DC 长为2 米，背水坡 BC 长也为 2 米，又测得∠ DAB=30°，∠ CBA=60°，求下底AB 的长 .解：过 D 、 C 分别作 DE ⊥AB 于 E ， CF ⊥ AB 于 F ，DC在直角△ ADE 中，∠ A=30°， AD=23∴ DE=AD sin30 °= 3 ，AE=AD cos30°=3.30A°E60F °B在直角△ CBF 中， BF=BC cos60°=1∴ AB=AE+EF+BF=3+2+1=6答：下底的长为 6 米。

思虑：延长两腰或平移一腰能求出下底的长吗？说明：以上解法表现了“转变”思想，把梯形的有关问题转变成解直角三角形可多角度的解析，增添辅助线，灵巧、合适地构造直角三角形，使解法合理化。

24.4解直角三角形(1)【学习目标】使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、解决问题的能力．渗透数形结合的数学思想，培养学生良好的学习习惯．【学习重点】直角三角形的解法．【学习难点】三角函数在解直角三角形中的灵活运用【课标要求】能利用三角函数的知识解决实际问题【知识回顾】1．在三角形中共有几个元素？2．直角三角形ABC中，∠C=90°，a、b、c、∠A、∠B这五个元素间有哪些等量关系呢？(1)边角之间关系(2)三边之间关系(3)锐角之间关系【自主学习】1、如图所示，一棵大树在一次强烈的地震中于离地面10米处折断倒下，树顶落在离树根24米处．大树在折断之前高多少？【例题学习】2、一个公共房屋门前的台阶共高出地面1．2米．台阶被拆除后，换成供轮椅行走的斜坡．根据这个城市的规定，轮椅行走斜坡的倾斜角不得超过9°．从斜坡的起点至楼门的最短的水平距离该是多少？（sin9°≈0.16，cos9°≈0.99，tan9°≈0.16，精确到0．1米）【巩固训练】3、如图，从点C测得树的顶角为33º，BC＝20米，则树高AB多少米？（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65，结果精确到0.1米）4、小明放一个线长为125米的风筝，他的风筝线与水平地面构成39°角．他的风筝有多高？（sin39°≈0.63，cos39°≈0.78，tan39°≈0.81，精确到1米）【归纳小结】【作业】1、在△ABC中，∠C=90°，AC=6，BC=8，那么sinA=________．2、在△ABC中，∠C=90°，sinA=35，则cosA的值是（）A．35B．45C．916.2525D3、如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB．CD分别表示一楼．二楼地面的水平线，∠ABC=150°，BC的长是8 m，则乘电梯从点B到点C上升的高度h是（）Am B．4 m C． m D．8 m4、某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（）A．8米B．C米D米5、在平静的湖面上，有一枝红莲，高出水面1米，阵风吹来，红莲被风吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，问这里水深多少？6、如图，在一棵树的10米高B处有两只猴子，一只猴子爬下树走到离树20米处的池塘A处．另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，求这棵树的高度．7、若河岸的两边平行，河宽为900米，一只船由河岸的A处沿直线方向开往对岸的B处，AB与河岸的夹角是600，船的速度为5米/秒，求船从A到B处约需时间几分。

九年级数学上册第24章解直角三角形24.4解直角三角形第1课时解直角三角形及其简单应用教案新版华东师大版12第1课时 解直角三角形及其简单应用1．理解解直角三角形的意义和条件，能根据元素间的关系，选择适当的关系式，求出所有未知元素；(重点)2．能够把实际问题转化为数学问题，建立数学模型，并运用解直角三角形求解，通过生活中的实际问题体会锐角三角函数在解题过程中的作用．(难点)一、情境导入世界遗产意大利比萨斜塔在1350年落成时就已倾斜．设塔顶中心点为B, 塔身中心线与垂直中心线夹角为∠A ，过点B 向垂直中心线引垂线，垂足为点C .在Rt △ABC 中，∠C ＝90°，BC ＝5.2m ，AB ＝54.5m ，求∠A 的度数．在上述的Rt △ABC 中，你还能求其他未知的边和角吗？二、合作探究探究点一：解直角三角形【类型一】 利用解直角三角形求边或角已知在Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 的对边分别为a ，b ，c ，按下列条件解直角三角形．(1)若a ＝36，∠B ＝30°，求∠A 的度数和边b 、c 的长；(2)若a ＝62，b ＝66，求∠A 、∠B 的度数和边c 的长． 解析：(1)已知直角边和一个锐角，解直角三角形；(2)已知两条直角边，解直角三角形． 解：(1)在Rt △ABC 中，∵∠B ＝30°，a ＝36，∴∠A ＝90°－∠B ＝60°，∵cos B ＝ac，即c ＝acos B＝3632＝243，∴b ＝sin B ·c ＝12×243＝123；(2)在Rt △ABC 中，∵a ＝62，b ＝66，∴tan A ＝ab ＝33，∴∠A ＝30°，∴∠B ＝60°，∴c ＝2a ＝12 2.方法总结：解直角三角形时应求出所有未知元素，解题时尽可能地选择包含所求元素与两个已知元素的关系式求解．【类型二】 构造直角三角形解决长度问题一副直角三角板如图放置，点C 在FD 的延长线上，AB ∥CF ，∠F ＝∠ACB ＝90°，∠E ＝30°，∠A ＝45°，AC ＝122，试求CD 的长．解析：过点B 作BM ⊥FD 于点M ，求出BM 与CM 的长度，然后在△EFD 中可求出∠EDF ＝60°，利用解直角三角形解答即可．解：过点B 作BM ⊥FD 于点M ，在△ACB 中，∠ACB ＝90°，∠A ＝45°，AC ＝122，∴BC ＝AC ＝12 2.∵AB ∥CF ，∴BM ＝sin45°BC ＝122×22＝12，CM ＝BM ＝12.在△EFD 中，∠F ＝90°，∠E ＝30°，∴∠EDF ＝60°，∴MD ＝BMtan60°＝43，∴CD ＝CM －MD ＝12－4 3.方法总结：解答此类题目的关键是根据题意构造直角三角形，然后利用所学的三角函数的关系进行解答．【类型三】 运用解直角三角形解决面积问题如图，在△ABC 中，已知∠C ＝90°，sin A ＝37，D 为边AC 上一点，∠BDC ＝45°，DC ＝6.求△ABC 的面积．解析：首先利用正弦的定义设BC ＝3k ，AB ＝7k ，利用BC ＝CD ＝3k ＝6，求得k 值，从而求得AB 的长，然后利用勾股定理求得AC 的长，再进一步求解．解：∵∠C ＝90°，∴在Rt △ABC 中，sin A ＝BC AB ＝37，设BC ＝3k ，则AB ＝7k (k ＞0)，在Rt △BCD 中，∵∠BCD ＝90°，∴∠BDC ＝45°，∴∠CBD ＝∠BDC ＝45°，∴BC ＝CD ＝3k ＝6，∴k ＝2，∴AB ＝14.在Rt △ABC 中，AC ＝AB 2－BC 2＝142－62＝410，∴S △ABC ＝12AC ·BC ＝12×410×6＝1210.所以△ABC 的面积是1210.方法总结：若已知条件中有线段的比或可利用的三角函数，可设出一个辅助未知数，列方程解答．探究点二：解直角三角形的简单应用 【类型一】 求河的宽度根据网上消息，益阳市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥．如图，新大桥的两端位于A 、B 两点，小张为了测量A 、B 之间的河宽，在垂直于新大桥AB 的直线型道路l 上测得如下数据：∠BDA ＝76.1°，∠BCA ＝68.2°，CD ＝82米．求AB 的长(精确到0.1米)．参考数据：sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.0；sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.5.解析：设AD ＝x m ，则AC ＝(x ＋82)m.在Rt △ABC 中，根据三角函数得到AB ＝2.5(x ＋82)m ，在Rt △ABD 中，根据三角函数得到AB ＝4x ，依此得到关于x 的方程，进一步即可求解．解：设AD ＝x m ，则AC ＝(x ＋82)m.在Rt △ABC 中，tan ∠BCA ＝AB AC，∴AB ＝AC ·tan ∠BCA ＝2.5(x ＋82)．在Rt △ABD 中，tan ∠BDA ＝AB AD，∴AB ＝AD ·tan ∠BDA ＝4x ，∴2.5(x ＋82)＝4x ，解得x ＝4103.∴AB ＝4x ＝4×4103≈546.7m.答：AB 的长约为546.7m.方法总结：解题的关键在于构造出直角三角形，通过测量角的度数和测量边的长度，计算出所要求的物体的高度或长度．【类型二】 求不可到达的两点的高度如图，放置在水平桌面上的台灯的灯臂AB 长为30cm ，灯罩BC 长为20cm ，底座厚度为2cm ，灯臂与底座构成的∠BAD ＝60°.使用发现，光线最佳时灯罩BC 与水平线所成的角为30°，此时灯罩顶端C 到桌面的高度CE 是多少(结果精确到0.1cm ，参考数据：3≈1.732)?解析：首先过点B 作BF ⊥CD 于点F ，作BG ⊥AD 于点G ，进而求出FC 的长，再求出BG 的长，即可得出答案．解：过点B 作BF ⊥CD 于点F ，作BG ⊥AD 于点G ，∴四边形BFDG 是矩形，∴BG ＝FD .在Rt △BCF 中，∠CBF ＝30°，∴CF ＝BC ·sin30°＝20×12＝10cm.在Rt △ABG 中，∵∠BAG ＝60°，∴BG ＝AB ·sin60°＝30×32＝153cm ，∴CE ＝CF ＋FD ＋DE ＝10＋153＋2＝12＋153≈38.0(cm)．答：此时灯罩顶端C 到桌面的高度CE 约是38.0cm.方法总结：将实际问题抽象为数学问题，画出平面图形，构造出直角三角形转化为解直角三角形问题．三、板书设计1．解直角三角形的基本类型及其解法；2．解直角三角形的简单应用.本节课为了充分发挥学生的主观能动性，可引导学生通过小组讨论，大胆地发表意见，提高学生学习数学的兴趣．能够使学生自己构造实际问题中的直角三角形模型，并通过解直角三角形解决实际问题.。

DC第七讲 解直角三角形授课班级： 课程类型：□复习 □预习 □习题 上课日期： 年 月 日重点：三角函数的含义 难点：三角函数的计算考点一、直角三角形的性质1、直角三角形的两个锐角互余：可表示如下：∠C=90° ∠A+∠B=90°2、在直角三角形中，30°角所对的直角边等于斜边的一半。

3、直角三角形斜边上的中线等于斜边的一半4、勾股定理： 如果直角三角形的两直角边长分别为a ，b ，斜边长为c ，那么a 2＋b 2＝c 2. 即直角三角形两直角边的平方和等于斜边的平方ABCa b c弦股勾勾：直角三角形较短的直角边 股：直角三角形较长的直角边 弦：斜边勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a 2＋b 2＝c 2，那么这个三角形是直角三角形。

Type 1直角三角形的性质[例1] 在 直角三角形ABC 中，∠ACB=90度，CD 是AB 边上中线，若CD=5cm,则AB=_____，三角形ABC 的面积=____________[变式] 在直角三角形ABC 中，∠ACB=90度，CD 是AB 边上中线，图中有__________个等腰三角形.[例2] 如图，在△ABC 中，∠B=∠C ，D 、E 分别是BC 、AC 的中点，AB=6，求DE 的长。

[变式1]如图，在锐角三角形ABC 中，AD ⊥BC 于D,E 、F 、G 分别是AC 、AB 、BC 的中点。

求证：四边形OEFG 是等腰梯形。

[变式2] 如图所示，BD 、CE 是三角形ABC 的两条高，M 、N 分别是BC 、DE 的中点 求证：MN ⊥DE考点二、锐角三角函数的概念 1、如图，在△ABC 中，∠C=90°①锐角A 的对边与斜边的比叫做∠A 的正弦，记为sinA ，即c asin =∠=斜边的对边A A②锐角A 的邻边与斜边的比叫做∠A 的余弦，记为cosA ，即c bcos =∠=斜边的邻边A A③锐角A 的对边与邻边的比叫做∠A 的正切，记为tanA ，即b atan =∠∠=的邻边的对边A A A④锐角A 的邻边与对边的比叫做∠A 的余切，记为cotA ，即abcot =∠∠=的对边的邻边A A A2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值（1）互余关系：sinA=cos(90°—A)，cosA=sin(90°—A) ；（2）平方关系：1cos sin 22=+A A （3）倒数关系：tanA ∙tan(90°—A)=1 （4）商（弦切）关系：tanA=AAcos sin 5、锐角三角函数的增减性当角度在0°~90°之间变化时，（1）正弦值随着角度的增大（或减小）而增大（或减小）；（2）余弦值随着角度的增大（或减小）而减小（或增大）；（3）正切值随着角度的增大（或减小）而增大（或减小）；（4）余切值随着角度的增大（或减小）而减小（或增大） ype 2 锐角三角函数求值问题[例1] 如图所示，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝5，求∠A ，∠B 的正弦、余弦、正切值．[变式1]（1）在Rt △ABC 中，∠C 为直角，a=1，b=2，则cosA=________ ，tanA=_________． （2）在Rt △ABC 中，∠C 为直角， ∠A=300，b=4，则a=__________，c=__________．[变式2] 在△ABC 中，∠C 为直角，∠A 、∠B 、∠C 所对的边分别是a 、b 、c ，已知b=3， c=14．求∠A 的四个三角函数． [例2][变式]Type 3 特殊的锐角三角函数计算[例4] （1）11(1|1sin 30|2-⎛⎫--+ ⎪⎝⎭° （2）(tan 45π︒︒-+[变式]（1）︒-++︒-︒30sin 1160sin 260sin 2（2）︒-+-︒30sin 1)160(cos 2Type 5 锐角三角函数的关系 [例5] 已知求锐角．[变式]若∠A 为锐角，且tan 2A+2tanA-3=0，则∠A=______度．[例6]已知α为锐角，tan α=2，求aa aa sin 2cos 5cos 3sin -+[变式1] 已知α为锐角，tan α=31 ，求aa a sin 1cos tan ++BEDC BA[变式2]已知α为锐角，且1sin cos 5αα-=，求sin cos αα+的值．Type 6 综合问题[例1] 如图，在矩形ABCD 中，DE ⊥AC 于E ，设ADE α∠=，且35cos α=，AB=4，则AD 的长为多少？[变式1] △ABC 中，∠C=90°，D 为BC 中点，DE ⊥AB 于E ，tanB=21，AE=7，求DE 长。