37正多边形课件-浙江省嘉兴市秀洲区高照实验学校浙教版九年级上册数学(共19张PPT)

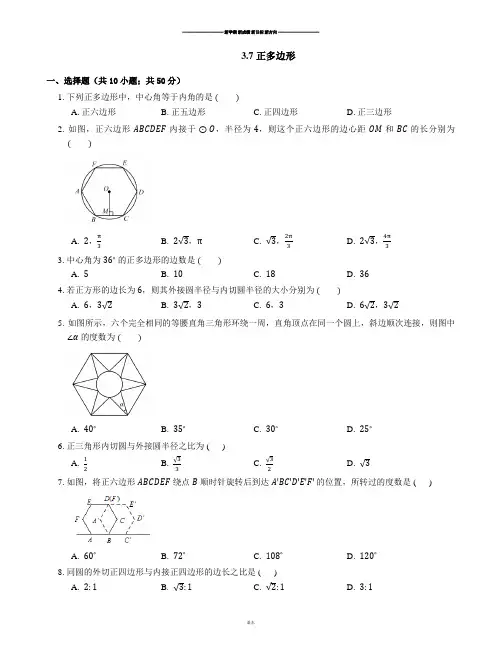
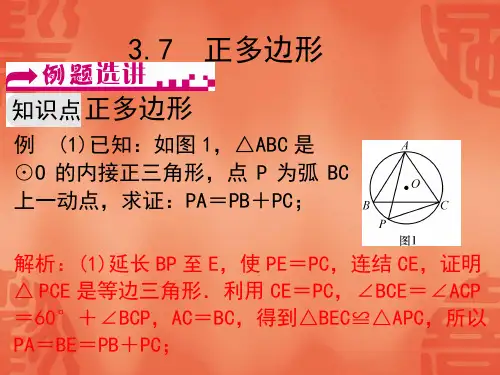
3.7 正多边形一、选择题（共10小题；共50分）1. 下列正多边形中，中心角等于内角的是( )A. 正六边形B. 正五边形C. 正四边形D. 正三边形2. 如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM和BC的长分别为( )A. 2，π3B. 2√3，π C. √3，2π3D. 2√3，4π33. 中心角为36∘的正多边形的边数是( )A. 5B. 10C. 18D. 364. 若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为( )A. 6，3√2B. 3√2，3C. 6，3D. 6√2，3√25. 如图所示，六个完全相同的等腰直角三角形环绕一周，直角顶点在同一个圆上，斜边顺次连接，则图中∠α的度数为( )A. 40∘B. 35∘C. 30∘D. 25∘6. 正三角形内切圆与外接圆半径之比为 ( )A. 12B. √33C. √32D. √37. 如图，将正六边形ABCDEF绕点B顺时针旋转后到达AʹBCʹDʹEʹFʹ的位置，所转过的度数是 ( )A. 60∘B. 72∘C. 108∘D. 120∘8. 同圆的外切正四边形与内接正四边形的边长之比是 ( )A. 2:1B. √3:1C. √2:1D. 3:19. 如右图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，EF则的GH 值为 ( ) .C. √3D. 2A. √2B. 3210. 如图所示，有一个边长为1的正六边形ABCDEF，其中C，D坐标分别为(1,0)和(2,0)，若在无滑动的情况下，将这个正六边形沿着x轴向右滚动，则在滚动过程中，这个正六边形的顶点A，B，C，D，E，F中，会过点(2014,2)的是( )A. 点BB. 点CC. 点DD. 点E二、填空题（共10小题；共50分）11. 一个正多边形的叫做这个正多边形的中心；叫做正多边形的半径；正多边形每一边所对的叫做正多边形的中心角；中心到正多边形的一边的叫做正多边形的边心距．12. 已知正n边形的一个外角与一个内角之比为1:3，则n等于．13. 已知一个圆的半径为5 cm，则它的内接正六边形的边长为．14. 如图所示，若干全等正五边形排成环状．如图所示的是前3个正五边形，要完成这一圆环还需个正五边形．15. 半径为2的圆的内接正方形的面积是．16. 已知正六边形的边心距为√3，则它的周长是．17. 已知⊙O的周长等于6π cm，则它的内接正六边形ABCDEF的边长为 cm．18. 已知正六边形ABCDEF的边心距为√3 cm，则正六边形的半径为cm．19. 如图，正六边形ABCDEF的边长为4，两顶点A，B分别在x轴和y轴上运动，则顶点D到原点O的距离的最大值和最小值的乘积为．20. 粉笔是校园中最常见的必备品．图 1 是一盒刚打开的六角形粉笔，总支数为50支．图 2 是它的横截面（矩形ABCD），已知每支粉笔的直径为12 mm，由此估算矩形ABCD的周长约为mm．（√3≈1.73，结果精确到1 mm）三、解答题（共5小题；共65分）21. 画一个边长为1cm的正六边形．22. 已知圆内接正三角形边心距为2 cm，求它的边长．23. 已知⊙O和⊙O上一点A．Ⅰ作⊙O的内接正方形ABCD和内接正六边形AEFCGH；Ⅱ在（1）题的作图中，若点E在AD上，求证：DE是⊙O内接正十二边形的一边．24. 已知：如图，正八边形A1A2A3A4A5A6A7A8内接于半径为R的⊙O．Ⅰ求A1A3的长；Ⅱ求四边形A1A2A3O的面积；Ⅲ求此正八边形的面积S．25. 如图，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N．Ⅰ ①求∠MPN的度数；②求证：PM+PN=3a；Ⅱ如图，点O是AD的中点，连接OM，ON，求证：OM=ON；Ⅲ如图，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形?并说明理由．答案第一部分1. C2. D3. B4. B5. C6. A7. A8. C9. C 10. B第二部分11. 外接圆的圆心；外接圆的半径；圆心角；距离12. 813. 5 cm14. 715. 816. 1217. 3 cm18. 219. 4820. 300第三部分21.如图所示，以1 cm为半径作一个⊙O，由于正六边形的半径等于边长，所以在圆上依次截取等于1 cm的弦，就可以将圆6等分，顺次连接各分点即可．22. 如图：连接OB，过O点作OD⊥BC于点D .在Rt△OBD中，=60∘∵∠BOD=360∘6∵BD=OD⋅tan60∘=2√3∴BC=2BD=4√3∴三角形的边长为4√3 cm．23. （1）作法：①作直径AC；②作直径BD⊥AC；③依次连接A、B、C、D四点，四边形ABCD即为⊙O的内接正方形；④分别以A、C为圆心，以OA长为半径作弧，交⊙O于E、H、F、G；⑤顺次连接A、E、F、C、G、H各点．六边形AEFCGH即为⊙O的内接正六边形．（2）连接OE、DE．∵∠AOD=360∘4=90∘，∠AOE=360∘6=60∘，∴∠DOE=∠AOD−∠AOE=90∘−60∘=30∘．∴DE为⊙O的内接正十二边形的一边．24. （1）∵正八边形A1A2A3A4A5A6A7A8，∴OA3=OA1，∠A3OA1=90∘．∵⊙O的半径为R．∴A1A3=√2R（2）在四边形A1A2A3O中，∵OA2⊥A1A3．∴S四边形A1A2A3O =12×OA2×A1A3=12×R×√2R=√22R2．（3）由（2）可得四边形A1A2A3O的面积为√22R2．∴正八边形的面积S=4S四边形A1A2A3O =4×√22R2=2√2R2．25. （1）① ∵四边形ABCDEF是正六边形，∴∠A=∠B=∠C=∠D=∠E=∠F=120∘．∴PM∥AB，PN∥CD，∴∠BPM=60∘，∠NPC=60∘，∴∠MPN=180∘−∠BPM−∠NPC=180∘−60∘−60∘=60∘．②如图，作AG⊥MP交MP于点G，BH⊥MP于点H，CL⊥PN于点L，DK⊥PN于点K，MP+PN= MG+GH+HP+PL+LK+KN．∵正六边形ABCDEF中，PM∥AB，作PN∥CD，∴∠AMG=∠BPH=∠CPL=∠DNK=60∘，∴GM=12AM，HL=12BP，PL=12PM，NK=12ND，∵AM=BP，PC=DN，∴MG+HP+PL+KN=a，GH=LK=a，∴MP+PN=MG+GH+HP+PL+LK+KN=3a．（2）如图，连接OE．∵四边形ABCDEF是正六边形，AB∥MP，PN∥DC，易证AM=BP=EN．∵∠MAO=∠NOE=60∘，OA=OE，在△ONE和△OMA中，{OA=OE,∠MAO=∠NEO, AM=NE,∴△OMA≌△ONE(SAS)．∴OM=ON．（3）四边形MONG是菱形．如图，连接OE．由（2）得△OMA≌△ONE．∴∠MOA=∠EON．∵EF∥AO，AF∥OE，∴四边形AOEF是平行四边形，∴∠AFE=∠AOE=120∘，∴∠MON=120∘，∴∠GON=60∘．∵∠GOE=60∘−∠EON，∠DON=60∘−∠EON，∴∠GOE=∠DON．∵OD=OE，∠ODN=∠OEG，在△GOE和∠NOD中，{∠GOE=∠DON, OE=OD,∠OEG=∠ODN,∴△GOE≌△NOD(ASA)，∴ON=OG．∵∠GON=60∘，∴△ONG是等边三角形，∴ON=NG．∵OM=ON=OG，∠MOG=60∘，∴△MOG是等边三角形，∴MG=GO=MO，∴MO=ON=NG=MG，∴四边形MONG是菱形．初中数学试卷鼎尚图文**整理制作。

浙教版九年级上册第三章圆的基本性质《3.7正多边形》《3.7正多边形》《正多边形》是新教材九年级（上）第三章的内容。

学生已经学习了圆的性质和与圆有关的三种位置关系，这些知识都将为本节的学习起着铺垫作用。

本节内容正多边形和圆也是今后进一步研究圆的性质的基础，在教才中有着承上启下的重要地位。

在当今的改革大潮中，我们应以《新课标》的眼光来重新审视它。

《新课标》对数学学习内容的要求是：现实的、有意义的、富有挑战性的。

数学作为一种普遍适用的技术，要有助于人们收集信息、描述信息，建立数学模型，进而解决问题，直接为社会创造价值。

本节课从定性、定量的两个角度去探讨，挖掘蕴涵的数学知识，把感性认识转化成理性认识，具体到抽象，让学生主动参与，亲身体验知识的发生与发展的过程。

利用正多边形和圆的位置关系探究数量关系，把形的问题转化成了数的问题，体现了数形结合的思想。

【知识与能力目标】了解正多边形和圆的有关概念；理解并掌握正多边形半径、中心角、弦心距、边长之间的关系，会应用多边形和圆的有关知识解决实际问题．【过程与方法目标】学生在探讨正多边形和圆的关系的学习过程中，体会到要善于发现问题，解决问题，发展学生的观察、比较、分析、概括及归纳的逻辑思维能力。

【情感态度价值观目标】通过本节知识的学习，体验数学与生活的紧密相连，感受圆的对称美，正多边形与圆的和谐美，从而更加热爱生活，珍爱生命。

【教学重点】讲清正多边形和圆中心正多边形半径、中心角、弦心距、边长之间的关系．【教学难点】通过例题使学生理解四者：正多边形半径、中心角、弦心距、边长之间的关系教师准备：圆规，三角尺，PPT课件，多媒体学生准备：圆规，三角尺，练习本教学过程（一）、创设情景，导入新课本节课开始，让他们观察美丽的图案，欣赏生活中正多边形形状的物体，让学生感受到数学来源于生活，并从生活中感受到数学美。

同时，提出本节课要研究的问题：正多边形和圆有什么关系？你能借助圆做出一个正多边形吗？然后引导学生观思考这个问题。

3．7 正多边形1．正多边形的中心角(即正多边形的相邻两个顶点与它的中心的连线的夹角)与该正多边形一个内角的关系是(B )A ．互余B ．互补C ．互余或互补D ．不能确定2．如果一个正多边形绕着它的中心旋转60°后，能与原正多边形重合，那么这个正多边形(C )A ．是轴对称图形，但不是中心对称图形B ．是中心对称图形，但不是轴对称图形C ．既是轴对称图形，又是中心对称图形D ．既不是轴对称图形，也不是中心对称图形3．正多边形的一个内角的度数不可能是(A )A ．80°B ．135°C ．144°D ．150°4．有一个边长为50 cm 的正方形洞口，要用一个圆盖去盖住这个洞口，那么圆盖的直径至少应为(C ) A ．50 cm B ．25 2 cmC ．50 2 cmD ．50 3 cm 5．已知正多边形的每一个外角都是72°，那么这个正多边形的内角和等于540°．6．已知正多边形的内角和等于1440°，那么这个正多边形的边数为__10__．7．一个正多边形的一个内角的度数比相邻外角的6倍还多12°，求这个正多边形的内角和．【解】 设这个正多边形的一个外角的度数为x ，根据题意，得180°－x ＝6x ＋12°，解得x ＝24°.∴这个正多边形的边数＝360°÷24°＝15，∴这个正多边形的内角和＝(15－2)×180°＝2340°.8．如图①，圆内接正五边形的中心角∠AOB ＝72°，∠ACB ＝36°；如图②，圆内接正六边形的中心角∠AOB ＝60°，∠ACB ＝30°．(第8题)探究：如图③，圆内接正n 边形的中心角∠AOB ＝360°n ，∠ACB ＝180°n(用含n 的代数式表示)． 9．若用一种正多边形瓷砖铺满地面，则这样的正多边形可以是(A )A ．正三角形或正方形或正六边形B ．正三角形或正方形或正五边形C ．正三角形或正方形或正五边形或正六边形D ．正三角形或正方形或正六边形或正八边形【解】 ∵用一种正多边形镶嵌，只有正三角形、正方形、正六边形这三种正多边形能镶嵌成一个平面图案，∴若用一种正多边形瓷砖铺满地面，则这样的正多边形只能是正三角形或正方形或正六边形．(第10题)10．如图，已知正六边形的外接圆的半径是2，则正六边形的周长是(C )A ．4B ．6C ．12D ．24【解】 ∵正六边形的边长等于其外接圆的半径，∴正六边形的周长＝2×6＝12.11．一个正多边形的所有对角线都相等，则这个正多边形的内角和为360°或540°．【解】 ∵一个正多边形的所有对角线都相等，∴该正多边形为正方形或正五边形，∴这个正多边形的内角和为(4－2)×180°＝360°或(5－2)×180°＝540°.(第12题)12．如图，△ABC 内接于⊙O ，AB ＝AC ，∠BAC ＝36°，AB ，AC 的中垂线分别交⊙O 于点E ，F .求证：五边形AEBCF 是⊙O 的内接正五边形．【解】 连结OB ，OC .∵OE ，OF 分别垂直平分AB ，AC ，∴AE ＝BE ，AF ＝CF ，∴AE ︵＝BE ︵，AF ︵＝CF ︵.∵AB ＝AC ，∴AB ︵＝AC ︵，∴AE ︵＝BE ︵＝12AB ︵＝12AC ︵＝AF ︵＝CF ︵. ∵∠BAC ＝36°，∴∠BOC ＝72°.∴AE ︵＋BE ︵＋AF ︵＋CF ︵＝360°－72°＝288°，∴AE ︵＝BE ︵＝AF ︵＝CF ︵＝288°÷4＝72°＝BC ︵，∴AE ＝BE ＝AF ＝CF ＝BC ，∴五边形AEBCF 为⊙O 的内接正五边形．13．如图①②③，正三角形ABC 、正方形ABCD 、正五边形ABCDE 分别是⊙O 的内接三角形、内接四边形、内接五边形，点M ，N 分别从点B ，C 开始，以相同的速度在⊙O 上逆时针运动．(第13题)(1)在图①中，求∠APB 的度数；(2)在图②中，∠APB 的度数是90°；在图③中，∠APB 的度数是72°．(3)根据前面的探索，你能否将本题推广到一般的正n 边形的情况？若能，写出推广问题和结论；若不能，请说明理由．【解】 (1)∵点M ，N 分别从点B ，C 开始，以相同的速度在⊙O 上逆时针运动，∴∠BAM ＝∠CBN .∴∠APN ＝∠ABN ＋∠BAM ＝∠ABN ＋∠CBN ＝∠ABC ＝60°，∴∠APB ＝120°.(2)同理(1)可得，图②中，∠APB ＝90°；图③中，∠APB ＝72°.(第13题解)(3)能．问题：如解图，正n 边形ABCDE …是⊙O 的内接正n 边形，点M ，N 分别从点B ，C 开始，以相同的速度在⊙O 上逆时针运动，求∠APB 的度数．结论：∠APB ＝360°n. 证明：∵点M ，N 分别从点B ，C 开始，以相同的速度在⊙O 上逆时针运动，∴∠BAM ＝∠CBN .∴∠APN ＝∠BAM ＋∠ABN ＝∠CBN ＋∠ABN ＝∠ABC ＝（n －2）×180°n ＝180°－360°n. ∴∠APB ＝180°－∠APN ＝360°n .初中数学试卷。