当前位置：文档之家 › 第三章 多组分系统

第三章 多组分系统

  • 格式：ppt
  • 大小：1.85 MB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

大学物理化学 第三章 多组分系统热力学习指导及习题解答

大学物理化学 第三章 多组分系统热力学习指导及习题解答
证明： RT d ln f =Vmdp
RT Vm p A Bp
积分区间为 0 到 p,
RT
p
d ln
f=
（p RT
A Bp)dp
0
0p
RT p d ln（ f ）= （p A Bp)dp Ap 1 Bp2
0
p0
2
因为
lim ln( f ) 0 p0 p
则有
RT ln（ f ）=Ap 1 Bp2
为两相中物质的量浓度，K 为分配系数。
萃取量
W萃取
=W
1
KV1 KV2 V2
n
二、 疑难解析
1. 证明在很稀的稀溶液中，物质的量分数 xB 、质量摩尔浓度 mB 、物质的量浓度 cB 、质量分数 wB
之间的关系： xB
mBM A
MA
cB
MA MB
wB 。
证明：
xB
nA
nB nB
nB nA
）pdT
-S
l A,m
dT
RT xA
dxA
-S（mg A）dT
-
RT xA
dxA =
S（mg A）-S
l A,m
dT
Δvap Hm (A) T
dT
-
xA 1
dxA = xA
Tb Tb*
Δvap Hm (A) R
dT T2
若温度变化不大， ΔvapHm 可视为常数
- ln
xA =
Δvap Hm (A) R
真实溶液中溶剂的化学势 μA μ*A(T, p) RT ln γx xA =μ*A(T, p) RT ln aA,x
真实溶液中溶质 B μB μB* (T, p) RT ln γx xB =μ*A(T, p) RT ln aB,x

第三章 多组分精馏和特殊精馏(化工分离过程)

第三章 多组分精馏和特殊精馏(化工分离过程)

3.1.3 最少理论板数（Nm）和组分分配
全回流对应最少理论板数，但全回流下无产品采出， 因此正常生产中不会采用全回流。 什么时候采用全回流呢？
1、开车时，先全回流，待操作稳定后出料。 2、在实验室设备中，研究传质影响因素。 3、工程设计中，必须知道最少板数。
最少理论板数的计算
Fenske（芬斯克）方程推导前提： 1、塔顶采用全凝器，（若采用分凝器，则分凝器为第1块塔板） 2、所有板都是理论板。
一、关键组分（Key Components）
Na=串级数(2)＋分配器(1)＋侧线采出
F
(0)＋传热单元(2) = 5
已被指定的可调变量： （1）进料位置；（2）回流比； （3）全凝器饱和液体回流或冷凝 器的传热面积或馏出液温度。
余下的2个可调设 计变量往往用来指 定组分在馏出液和 釜液中的浓度。
两组分精馏 指定馏出液中一个组分的浓度，就确定了馏 出液的全部组成；指定釜液中一个组分的浓 度，也就确定了釜液的全部组成。
下面通过实例分别对二组分精馏和多组分精馏过 程分析进行比较。
二组分精馏实例：苯－甲苯
图3-1 二组分精馏流率、温度、浓度分布
三组分精馏实例：苯(LK)－甲苯(HK)－异丙苯
图3-2 三组分精馏流量分布 图3-3 三组分精馏温度分布
四组分精馏实例：苯－甲苯(LK)－二甲苯(HK)-异丙苯
图3-6 四组分精馏液相组成分布
⎜⎜⎝⎛
yA yB
⎟⎟⎠⎞ 2
= ⎜⎜⎝⎛
xA xB
⎟⎟⎠⎞1
代入（3-2）式：
⎜⎜⎝⎛
yA yB
⎟⎟⎠⎞1
= α1 ⎜⎜⎝⎛
xA xB
⎟⎟⎠⎞1
=
⎜⎜⎝⎛

化工分离过程(第7讲)(3.2多组分精馏过程分析)

化工分离过程(第7讲)(3.2多组分精馏过程分析)

x1
y2 y 1
* TB
1.0 B7
3.2.1 多组分精馏过程分析
精馏是多次简单蒸馏的组合。
精馏塔底部是加热区，
温度最高；塔顶温度最低。
精馏结果，塔顶冷凝收 集的是低沸点组分，高沸 点组分则留在塔底。
8
3.2.1 多组分精馏过程分析
1 从塔的中间O点进料； 2 组分B的液、汽相组 成分别为 x3 和 y3； 3 每层塔板都经历部分 汽化和部分冷凝过程；T
4
3.2.1 多组分精馏过程分析

简单蒸馏以及二组分精馏的原理图 关键组分(Key Components) 清晰分割 多组分精馏过程的复杂性
二组分精馏实例：苯－甲苯 三组分精馏实例：苯(LK)－甲苯(HK)－异丙苯 四组分精馏实例：苯－甲苯(LK)－二甲苯(HK)-异丙苯

多组分精馏与二组分精馏在浓度分布上的区别
22
3.2.1 多组分精馏过程分析
2、关键组分
①若无LNK：HK分别在二段出现两个最高点，LK 表现像LNK。 （图3-7） ②若无HNK：LK分别在二段出现两个最高点，HK 表现像HNK。 （图3-8） ③有LNK、HNK，且都不同时出现在顶、釜时： LK在精馏段出现一个最大值，然后降到所规定的浓度； HK在提馏段出现一个最大值，然后降到所规定的浓度。 （图3-9）

甲苯为LK，二甲苯为HK，两 者的浓度分布曲线变化规律相 同，方向相反。 在 塔 底 处 ， 主 要 分 离 HK 和 HNK，所以此处HK浓度向上 增大；同理，在塔顶处，主要 分离LK和LNK，所以此处LK 浓度向上减小。


图3-9 苯－甲苯(LK)－二甲苯(HK)-异丙 苯液相浓度分布
苯为LNK，在进料板以下浓度 快速减小，最终全部进入塔顶； 异丙苯为HNK，在进料板以上 浓度快速减小，最终全部进入 21 塔釜。

第三章 多组分系统热力学习题解08-9-2稿

第三章 多组分系统热力学习题解08-9-2稿

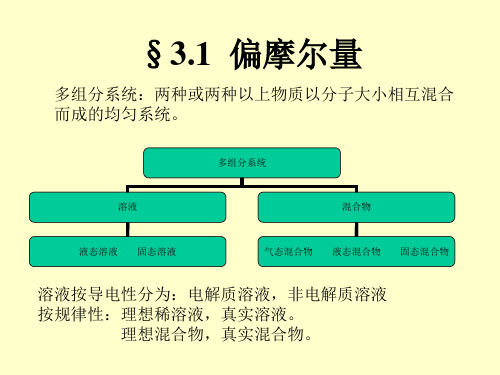
第三章 多组分系统热力学一、基本内容前面讨论的系统一般为纯组分或组成不变的均相封闭系统，只需要两个物理量，如温度和压力，就能确定系统的热力学性质。

而对组成可变的多组分均相系统（如均相化学反应）或多组分多相系统（如二元液态混合物与其气相或固相的平衡），系统的热力学容量性质除与温度和压力有关外，还与系统的组成或物质的量有关。

为此，在讨论多组分系统的热力学、相平衡和化学平衡之前，首先要掌握偏摩尔量、化学势的概念以及由此而引出的一系列定律和公式。

（一） 偏摩尔量1. 定义系统中任一组分B 的偏摩尔量Z B 被定义为CB B T p n Z Z n ⎛⎫∂= ⎪∂⎝⎭，， 其物理意义是等温等压及除B 组分外，其余各组分的量均保持不变的情况下，在无限大量系统中，加入1mol B 组分所引起系统某热力学容量性质Z (V 、U 、H 、S 、A 、G )的改变。

由此可见，Z B 是温度、压力、各组分的物质的量的函数，即 'B B c B (,,,)(,,)Z f T p n n Z f T p C ==或式中C 表示系统的组成。

2. 偏摩尔量的集合公式等温、等压、定浓下，系统的热力学容量性质Z 与各组分的偏摩尔量Z B 之间有加和关系，称为偏摩尔量的集合公式。

即B B B=1kZ n Z =∑(二) 化学势1. 定义任何均相多组分系统的热力学容量性质均可表示为其特征变量与其组成的函数，因此CC1B B 1B B (,,,,)(,,,,)k S V n k S p nU U f S V n n n H H f S p n n n μμ⎛⎫∂=⋅⋅⋅=⎪∂⎝⎭⎛⎫∂=⋅⋅⋅=⎪∂⎝⎭，，，，定义：化学势定义：化学势CC1B B 1B B (,,,,)(,,,,)k T V n k T p nA A f T V n n n G G f T V n n n μμ⎛⎫∂=⋅⋅⋅=⎪∂⎝⎭⎛⎫∂=⋅⋅⋅=⎪∂⎝⎭，，，，定义：化学势定义：化学势用热力学的四个基本方程可以证明C C C CB B B B B S V n S p n T V n T p n U H A G n n n n μ⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂====⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭，，，，，，，， 由定义式可知组分B 的化学势就是此组分的偏摩尔吉布斯自由能。

物理化学简明教程(第四版)第三章 化学势

物理化学简明教程(第四版)第三章 化学势
pB pB* xB
• 体积具有加和性和没有热效应，即
mixV 0， mixH 0
（3）理想液态混合物中物质的化学势
• 当此液态混合物与蒸气相达成平衡时，
B (l) B (g)
• 假定蒸气均遵守理想气体定律，
B (g)
B
(g)
RT
ln
pB p
• 因为 B (sln) B (g)
故
B (sln)
•
=[µB()－µB()] dnB
• 当系统达成平衡时，dG = 0，因此
•
µB()= µB()
（2）化学势在多相平衡中的应用
• 这就是说，多组分系统多相平衡的条件 为：“除系统中各相的温度和压力必须
相同以外，各物质在ห้องสมุดไป่ตู้相中的化学势亦 必须相等”。即
•
µB()= µB()=…=µB()
• 若化学势不相等，物质必然要从化学势 较大的相向化学势较小的相转移。
§3.1 偏摩尔量
多组分系统：两种或两种以上物质以分子大小相互混合 而成的均匀系统。
多组分系统
溶液
混合物
液态溶液 固态溶液
气态混合物 液态混合物 固态混合物
溶液按导电性分为：电解质溶液，非电解质溶液 按规律性：理想稀溶液，真实溶液。
理想混合物，真实混合物。
（1）偏摩尔量的定义
（以偏摩尔体积为例）我们知道，对纯物质来讲， 系统的广度量性质具有严格的加和性。
（3）理想液态混合物中物质的化学势
• 例题2 25℃时，将1mol纯态苯加入大量 的、苯的物质的量分数为0.200的苯和甲 苯的混合物中。求算此过程的ΔG。
• 解 此过程的
G GB Gm* ,B
• 因为

第三章_多组分系统热力学要点

第三章_多组分系统热力学要点
p
第三章 多组分系统热力学及其在溶液中的应用
p/Pa
p = kx,B xB 服从Henry定律
R
p
W 纯B
纯溶剂
p gh h
pP
稀溶液
pB = pB* xB
实际曲线
A
xA xB
B
A*
A
半透膜
§1 引言 § 2 多组分系统的组成表示法 § 3 多组分体系中物质的偏摩尔量和化学势 § 4 稀溶液中的两个经验定律 § 5 气体混合物中各组分的化学势 § 6 理想溶液的定义、通性及各组分的化学势 § 7 稀溶液中各组分的化学势 § 8 稀溶液的依数性
S(T) S(0) Tf Cp(固)dT melt H
0T
Tf
+
Tb Tf
CpT(液)dT

T
Cp
(气) dT
vapH Tb
T Tb
从图解积分求熵值
图中阴影下的面积加上两个相变熵即为所求的值。
如果以S为纵坐标，T为横坐标，所求得的熵值 等于S-T图上阴影下的面积再加上两个相变时的熵 变。
AB def
A n B T , p,nC(CB)
GB def
G n B T , p,nC(CB)
ZB (ZB,m)代表偏摩尔量,Zm*(B) 代表B的摩尔量。
由曲线的斜率可求得 mB= 0.2mol·kg-1溶液中, Mg2SO4的偏摩尔体积VBm.
由于混合后水分子和酒精分子之间的引力大于混合前水分子 之间或酒精分子间的引力，使分子可以靠得更近，总体积缩小。
例外情况：冰醋酸和二硫化碳，混合后体积增大。
因为混合后醋酸分子和二硫化碳分子的分子间的引力 小于混合前各自分子间的引力，使分子间的距离增大， 总体积增大。

物理化学：第三章 多组分系统


dU TdS - pdV BdnB
B
B
U nB
S ,V ,nj B
二、广义化学势和热力学基本公式
同样的方法，按H=f(S,p,n1,n2……)，F=f(T,V,n1,n2……) 及H、F的定义进行处理，可得化学势的另一些表示式：
B
U nB
S ,V ,nj B
H nB
S , p ,nj B
二广义化学势和热力学基本公式对于组成可变的系统四个热力学基本公式为???bbbddddnvpstu??bbbddddnpvsth????bbbddddnvptsf???bbbddddnpvtsg三温度压力对化学势的影响bbbbb????????????????????????????????????????????????????????????????????????????????????????????????????jiijinptntntnptntpgnngppvpgt????????????????????代入上式得压力对化学势的影响
(与等温、等压下某均相体系任一容量性质的全微分比较)
得 dX = n1dX1,m n2dX2,m … nidXi,m=0
吉布斯—杜亥姆公式
nBdXB,m =0
B
当一个组分的偏摩尔量增加时，另一个组分的偏摩尔量必将
减少，其变化是以此消彼长的方式进行。偏摩尔量之间是具
有一定联系的。某一偏摩尔量的变化可从其它偏摩尔量的变化
B
三、温度、压力对化学势的影响
B
p
T ,ni
p
G nB
T
,
p
,n
j
B
T
,ni
nB
G p
T ,ni T , p ,nj B

第三章 多组分系统热力学

第三章 多组分系统热力学一、选择题1．1 mol A 与n mol B 组成的溶液，体积为0.65dm 3，当x B = 0.8时，A 的偏摩尔体积 V A = 0.090dm 3·mol -1，那么B 的偏摩尔V B 为： ( )(A) 0.140 dm 3·mol -1 ； (B) 0.072 dm 3·mol -1 ；(C) 0.028 dm 3·mol -1 ； (D) 0.010 dm 3·mol -1 。

2．注脚“1”代表298K 、p 的O 2，注脚“2”代表298K 、2p 的H 2，那么： ( )(A) 2121，μμμμ≠≠； (B) 因为21μμ≠，1μ与2μ大小无法比较 ；(C) 2121，μμμμ=>；(D) 2121，μμμμ<<。

3．气体B 的化学势表达式：()()B B B ln ln g g x RT p p RT +⎪⎪⎭⎫⎝⎛+=μμ，那么：⑴上式表 明气体B 在混合理想气体中的化学势；⑵()()g g B B μμμ-=∆体现在该条件下做非 体积功的本领；⑶μB (g)是表明做非体积功的本领；⑷μB (g)是气体B 的偏摩尔Gibbs 自由能。

上述四条中正确的是： ( )(A) ⑴⑵⑶ ； (B) ⑵⑶⑷ ； (C) ⑴⑶⑷ ； (D) ⑴⑵⑷ 。

4．373K 、p 时H 2O(g) 的化学势为μ1；373K 、0.5p 时H 2O(g) 的化学势μ2，那么： ①21μμ=；②μ2 - μ1 = RT ln2；③μ2 - μ1 = -RT ln2；④μ2 = μ1 – RT ln0.5。

以上四条中 正确的是： ( )(A) ①② ； (B) ①③ ； (C) ③④ ； (D) ②④5．对于A 、B 两种实际气体处于相同的对比状态，对此理解中，下列何者正确：( )(A) A 、B 两种气体处于相同的状态 ； (B) A 、B 两种气体的压力相等 ；(C) A 、B 两种气体的对比参数π、τ相等 ； (D) A 、B 两种气体的临界压力相等 。

物理化学第三章-2019-3-28

偏摩尔焓
HB (H / n )B T , p,nC' nB
VB=加1mol B 的体积增量
恒T, p 偏摩尔量VB的意义
多组分系统
1.偏摩尔量的含义是：在等温、等压条件下，在大 量的定组成系统中，加入单位物质的量的B物质所 引起广度性质的变化值。
或在等温、等压、保持B物质以外的所有组分 的物质的量不变的有限系统中，改变 dnB 所引起广 度性质的变化值。
多组分系统
4. 理想气体纯态化学势公式的推导
过程：B(1mol, T, p$): m$(T) →B(1mol, T, p ): m*(T, p)
1mol
dG = V dp
dGm = Vm dp
m = Gm VmRT/p
dm =(RT/p) dp
对过程积分
∫ ∫ m*(T, p)
p
m$（T） dm = p$ RTdlnp
若溶剂和溶质很难区分时可认为是混合物
乙醇
+水
溶液
甲苯 +水
混合物
多组分系统
混合物系统组成的表示方法
1. 物质的量分数 - 摩尔分数xB
物质B的物质的量与系统总的物质的量之比。
xB = nB/SAnA
SBxB = 1
气相常用y, 液相或固相用x。
2. 物质B的质量分数 wB 物质B的质量与系统的总质量之比。
关系式
dX (X / T ) p, nB , nC , ... dT (X / p)T , nB , nC , ... dp X BdnB
B
恒T, p
dX XBdnB
B
同时按比例加入各组分(即XB不变)时有
X
X = 0 dX =XBnB +XCnC +...

第3章 多组分系统的热力学,逸度和活度

第3章 多组分系统的热力学，逸度和活度
3.1 引言
I.
多组分系统的热力学
3.2 偏摩尔量 3.3 化学势与热力学基本方程 3.4 平衡判据与平衡条件 3.5 相律
返回首页
II. 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13
逸度、活度和混合性质 化学势与逸度 逸度和逸度因子的求取 拉乌尔定律和亨利定律 理想混合物和理想稀溶液 化学势与活度（1） 活度和活度因子的求取 化学势与活度（2） 混合性质与超额函数
2.组成可变的多相多组分系统 多相系统的广延性质
X X ( 1 ) X ( 2 ) X ( ) X ( )
dX dX
(1)

dX
( 2)
dX
1 ( )
dX ( )
1

热力学基本方程
dU TdS pdV
返回章首
I. 多组分系统的热力学
3.2 偏摩尔量
1.偏摩尔量的定义与物理意义
根据关于状态函数的基本假定，对于均相 多组分系统的广延性质X，可写出
X X (T , p, n1 , n2 , , nK )
K
X X dX dT dp T p p ,n j T ,n j
51.823 0.2788nB / mol cm 3 mol -1
A
返回章首
V nAVA nBVB
VA V nBVB / nA M A / m A V nBVB 18.0152 / 1 10 3 1002.935 51.832nB / mol 0.1394nB / mol
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1000 n1 55.5087 mol 18.0152
V2,m=b+2cn2=51.832+20.1394×1.000=52.111 cm3· mol-1 V1,m=(a-cn22)/n1=(1002.935-0.139412)/55.5087=18.0656 cm3· mol-1
其物质的量和偏摩尔 体积分别为 n1 ,V1 和 n2 ,V2 ，则体系的总体积为：
V n1V1 n2V2
X nB X B,m
B 1
i
如二组分溶液的体积
U nBU B
B
U UB ( )T , p ,nc ( c B) nB H HB ( )T , p ,nc ( c B) nB F A AB ( )T , p ,nc ( c B) F nB S SB ( )T , p , nc ( c B) nB G GB ( )T , p ,nc ( c B) nB
第三章 多组分系统热力学
Thermodynamics of the solution
第一节 多组分系统和组成表示法
一、多组分均相系统分类
1. 混合物：在热力学中，任何组分可按同样的方法来处理的均 相系统； 2. 溶液：在热力学中，各组分不能用同样的方法来处理 含量较多的组分称为溶剂 其他组分称为溶质 3. 稀溶液：溶质摩尔分数的总和远小于1 稀溶液有依数性质 有溶质和溶剂之分为溶液，否则为混合物
化学势是状态函数，是强度量，由于其绝对值不可知， 因此不同物质的化学势大小不能比较。 同偏摩尔量一样，没有体系的化学势可言。 化学势在判断相变和化学变化的方向和限度方面有重 要作用。
二、广义化学势和热力学基本公式
G=f(T, p, n1, n2…)
G G G G dG dp dn1 dn2 dT T p ,ni p T ,ni n1 T , p ,n j 1 n2 T , p ,n j 2
一、化学势的定义
广义定义：
保持特征变量和除B以外其它组分不变，某热力学函数随其 物质的量 n 的变化率称为化学势。
U H B ( )S ,V ,ncn(c(jB) ( ) S , p ,nn B) (j B) c (c nB nB A F G ( )T ,V ,nn )T , p ,nn (j B) ( B) (j B) c (c c (c nB nB
V = n1V1,m n2V2,m
H nB H B
B
A nB F AB F
B
S nB S B
B
G nB GB
B
= B
二、偏摩尔量的集合公式
例3-2 298K有摩尔分数为0.40的甲醇水溶液，若往大量的此种 溶液中加1 mol的水，溶液体积增加17.35 cm3；若往大量的 此种溶液中加1 mol的甲醇，溶液体积增加39.01 cm3。试计 算将0.4 mol 的甲醇及0.6 mol 的水混合成溶液时，体积为若 干？已知25C时甲醇和水的密度分别为0.7911 g· cm3和 0.9971 g· cm3。
1
根据偏摩尔量集合公式： V=n1V1,m+n2V2,m 则H2O的偏摩尔体积： V1,m=(V-n2V2,m)/n1= [(a+bn2+cn22)- n2(b+2cn2)] /n1 即 V1,m =(a-cn22)/n1
例3-3 298K，100kPa下，HAc(2) 溶于1kg H2O(1)中所形成溶液 的体积V与HAc量n2的关系如下： V=1002.935+51.832n2+0.1394n22 cm3，试将HAc和H2O的偏摩 尔体积表示为n2函数，并求n2=1.000 mol时HAc和H2O的偏摩 尔体积。 V1,m =(a-cn22)/n1 当 V2,m=b+2cn2 n2=1.000mol时
j j j j
狭义定义：
B
偏摩尔吉布斯能GB,m称为化学势
B GB,m n B T , p ,n B
j
G
保持温度、压力和除B以外的其它组分不变，体系的 Gibbs自由能随 nB的变化率称为化学势，所以狭义化 学势指的是偏摩尔Gibbs自由能。（其它三个化学势 不是偏摩尔量）
二、偏摩尔量的集合公式
、k个组分组成，则体 设一个均相体系由1、2、 系任一容量性质Z应是T，p及各组分物质的量的函数， 即： X Z Z X (T , p, n1 , n2 , , nk )
在等温、等压条件下： Z X X
Z X dZ ( )T , p ,n2 ,,nk dn1 ( )T , p ,n1 ,n3 ,,nk dn2 n1 n2
X B,m
X 为B物质的偏摩尔量 n B T , p ,n j B
偏摩尔量的物理意义可理解为： 在等温等压条件下，在一定浓度的有限量溶液中，加入dnB 的B物质所引起系统广度性质X随该组分的量的变化率， 或在等温等压条件下，往一定浓度的大量溶液中加入1 molB 物质所引起系统广度性质X的变化量。 各种偏摩尔量 p 78
例3-3 298K，100kPa下，HAc(2) 溶于1kg H2O(1)中所形成溶液 的体积V与HAc量n2的关系如下： V=1002.935+51.832n2+0.1394n22 cm3，试将HAc和H2O的偏摩 尔体积表示为n2函数，并求n2=1.000 mol时HAc和H2O的偏摩 尔体积。 解：设a=1002.935，b=51.832，c=0.1394，则V=a+bn2+cn22 V b 2cn2 HAc的偏摩尔体积 V2,m n 2 T , p ,n
第二节 偏摩尔量
单组分体系的摩尔热力学函数值
体系的状态函数中V，U，H，S，A，G等是广度性 质，与物质的量有关。设由物质B组成的单组分体 系的物质的量为 nB ，则各摩尔热力学函数值的定义 式分别为：
摩尔体积（molar volume）
V
* m,B
V nB U nB
摩尔热力学能（molar thermodynamic energy）
* U m, B
单组分体系的摩尔热力学函数值
摩尔焓（molar enthalpy） 摩尔熵（molar entropy）
H
* m,B * S m, B
H nB S nB
摩尔Helmholz自由能（molar Helmholz free energy） F A * F Am,B nB 摩尔Gibbs 自由能（molar Gibbs free energy） G * Gm,B nB 这些摩尔热力学函数值都是强度性质。
B=1 k
在保持偏摩尔量不变的情况下，对上式积分
Z X Z1 dn1 X Z2 dn2 X Zk dnk X 0 0 0
n1 n2 nk
偏摩尔量的集合公式
n1X Z1 n2X Z2 nkX Zk
X XB Z= nB Z
B=1
k
这就是偏摩尔量的集合公式，说明体系的总的容 量性质等于各组分偏摩尔量的加和。
U dU TdS pdV dnB n B B S ,V ,n j B
G=UpVTS 可得 dU=dGpdVVdpTdSSdT
dU TdS - pdV BdnB
B
U B n B S ,V ,n j B
得 dX = n1dX1,m n2dX2,m … nidXi,m=0 吉布斯—杜亥姆公式
n dX
B B
B,m
=0
当一个组分的偏摩尔量增加时，另一个组分的偏摩尔量必将 减少，其变化是以此消彼长的方式进行。偏摩尔量之间是具
有一定联系的。某一偏摩尔量的变化可从其它偏摩尔量的变化
中求得。
第三节 化学势
集合公式 X= n1X1,m+ n2X2,m + … niXi,m
全微分
dX = n1dX1,m+ X1,mdn1 n2dX2,mX2,mdn2 … nidXi,m Xi,mdni
因 dX = X1,mdn1 X2,mdn2 … Xi,mdni
(与等温、等压下某均相体系任一容量性质的全微分比较)
X Z = ( )T , p ,nc ( c B) B=1 nB
k
X Z + ( )T , p ,n1 ,,nk-1 dnk nk
偏摩尔量的集合公式
按偏摩尔量定义, Z X X
ZB ( nB )T , p ,nc ( c B)
则
dZ Z1dn1 X Z 2 dn2 X Z k dnk X X =X Z B dnB
解：设有1kg溶液
0.12 1000 nB 0.7064 mol 169.87 (1 0.12) 1000 nA 48.85 mol 18.015 nB 0.7064 xB 0.01426 nB nA 0.7064 48.85
nB 0.7064 cB 0.7827 mol dm - 3 V 1 / 1.108 nB 0.7064 mB 0.8028 mol kg -1 m (A) 1 (1 0.12)
多组分体系的偏摩尔热力学函数值
使用偏摩尔量时应注意： 1.偏摩尔量的含义是：在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下，改变 dnB 所引起广度性质Z的变化值，或在等温、等压条件 下，在大量的定组成体系中加入单位物质的量的B 物质所引起广度性质Z的变化值。 2.只有广度性质才有偏摩尔量，而偏摩尔量是强度 性质。 3.纯物质的偏摩尔量就是它的摩尔量。 4.任何偏摩尔量都是T，p和组成的函数。 5.指某种物质在某一特定相态，整个体系无偏摩尔量。