多组分系统热力学小结

第四章 多组分系统热力学
前面所讨论的是：单组分单相（两相）系统或多 组分组成恒定的系统。 但常见系统绝大部分是：多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外，还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为：单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ，单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变，某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言，本身是强度量；
3 偏摩尔量与浓度有关，与系统的总量无关。
4 偏摩尔量 X B ( nX，B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下，于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积：
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B

Vm*,B Vm*,C Vm*,B xC
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势

第四章多组分系统热力学主要公式及其适用条件基本概念1. 溶剂和溶质如果组成溶液的物质有不同的状态，通常将液态物质称为溶剂，气态或固态物质称为溶质。

如果都是液态，则把含量多的一种称为溶剂，含量少的称为溶质。

2. 溶液广义地说，两种或两种以上物质彼此以分子或离子状态均匀混合所形成的体系称为溶液。

溶液以物态可分为气态溶液、固态溶液和液态溶液。

根据溶液中溶质的导电性又可分为电解质溶液和非电解质溶液。

3. 混合物多组分均匀体系中，溶剂和溶质不加区分，各组分均可选用相同的标准态，使用相同的经验定律，这种体系称为混合物，也可分为气态混合物、液态混合物和固态混合物。

1. 偏摩尔量的定义偏摩尔量的物理意义：在定温定压条件下，往无限大的系统中（可以看作其浓度不变）加入1 mol 物质B 所引起的系统中某个（容量性质的）热力学量X 的变化。

几点注意事项:只有在定温和定压条件下才有偏摩尔量。

只有广度性质才有偏摩尔量，而偏摩尔量是强度性质。

纯物质的偏摩尔量就是它的摩尔量。

任何偏摩尔量都是T，p和组成的函数。

化学势定义保持温度、压力和除B以外的其它组分不变，体系的G自由能随nB的变化率称为化学势，所以化学势就是偏摩尔G自由能。

化学势在判断相变和化学变化的方向和限度方面有重要作用。

化学势的物理意义：是决定物质传递方向和限度的强度因素。

多相和多组分体系的热力学基本方程多组分系统多相平衡的条件为：除系统中各相的温度和压力必须相同以外，各物质在各相中的化学势必须相等。

如果某物质在各相中的化学势不等，则该物质必然从化学势较大的相向化学势较小的相转移。

由于考虑了系统中各组分物质的量的变化对热力学状态函数的影响。

因此该方程不仅能应用于封闭系统，也能应用于开放系统。

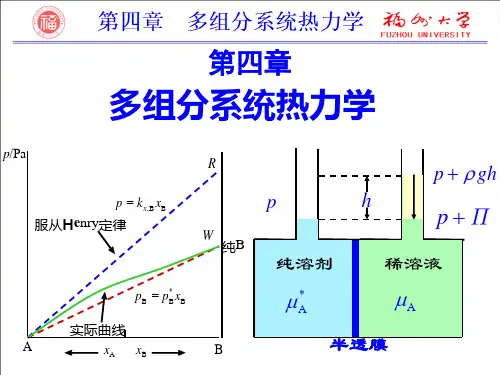
拉乌尔定律和亨利定律乌拉尔定义：一定温度时，溶液中溶剂的蒸气压pA与溶剂在溶液中的物质的量分数xA成正比，其比例系数是纯溶剂在该温度时的蒸气压pA*。

拉乌尔定律只适用于稀溶液中的溶剂1. 在稀溶液中，溶剂分子之间的引力受溶质分子的影响很小，即溶剂分子周围的环境与纯溶剂几乎相同。

H2
( p p* H 2 O ) 0.40 (105.4 7.33) 0.40kPa 39.23kPa
p N2 p p * H 2 O p H 2 (105.4 7.33 39.23) kPa 58.84kPa
M H 2 2.0158, x H2 pH2 k x,H2 M N 2 28.0134 mH2 / M H 2 m H 2O / M H 2O m H 2 / M H 2 m N 2 / M N 2 mH 2 / M H 2 m H 2O / M H 2O
* p甲苯 y苯
p p
* 苯
* 甲苯
y苯 p y苯
* 苯

38.7 0.3 0.142 ； x甲苯 1 x苯 0.858 100 38.7 0.3 100 0.3
4-6 在 18℃，气体的压力为 101.325kPa 下，1dm3 的水中能 溶解 O20.045g，能溶解 N20.02g。现 1dm3 将被 202.65kPa 空气饱 和了的水溶液加热沸腾，赶出所溶解 O2 的和 N2，并干燥之，求此 干燥气体在 101.325kPa、18℃下的体积及组成。设空气为理想 气体混合物，其组成（体积百分数）为： (O 解： M
x 2 d 2 RTdx2 x1 d 1 x 2 d 2
x 1 d 1 RTdx 2 RTd (1 x1 ) RTdx1
d1 RTdx1 / x1

1

1
d 1 RT d ln x1
x1 1
x1
1 1 RT ln x1 1 ( pg ) RT ln( p1* / p ) RT ln x1 1 1 ( pg ) RT ln( p1 / p )

体系中的组分对某热力学性质的贡献.
三.
化学势
• 定义: 偏摩尔吉布斯自由能为化学势 (chemical potential)
•
i=(G/ni)T,p,n(j≠i) (5)
• i : i物质的化学势. • 化学势也是一种偏摩尔量, 因为G的偏摩 尔量在化学中特别重要, 在计算中常常出 现, 故人们特意定义它为化学势.
(1)
•求Z的全微分: • dZ=(Z/T)dT+(Z/p)dp+∑(Z/ni)T,p,n(j≠i)dni •对于恒温, 恒压过程, 上式变为: •
Z dZ dni i ni T , p ,n ji
dT=0 dp=0
• 定义: •
Zi,m= (Z/ni)T,p,n(j≠i)
=TdS－pdV+∑idni
• 比较(7)式和上式, 可得:
•
i=(U/ni)S,V,n(j≠i)
• 上式也是化学势的定义式, 与(5)是等价的.
• 多组分体系的Gibbs关系式 :
• (适用于达力平衡, 热平衡,只作体积
功的均相体系) • dU=TdS－pdV+∑idni (8)
•
• •
dH=TdS+Vdp+∑idni
dF=－SdT－pdV+∑idni dG=－SdT+Vdp+∑idni (11)
(9)
(10)
• 化学势的四个等价的定义式: •
• • •
i=(U/ni)S,V,n(j≠i) (12)
i=(H/ni)S,p,n(j≠i) (13) i=(F/ni)T,V,n(j≠i) (14) i=(G/ni)T,p,n(j≠i) (15)

在25℃时，CH4(g)的溶解度在水和苯中的亨 利系数分别为k1和k2，且k1 > k2，则在相同的
平衡分压p(CH4)下，CH4(g)在水中的溶解度
（ ）在苯中的溶解度。
• A. >
B. <
C. =
D. 无法比较
理想液态混合Βιβλιοθήκη 的混合性质 (1)ΔmixH = 0 (2) ΔmixV = 0 (3) ΔmixS = -R(nBlnxB + nClnxC)>0 (4) ΔmixG = RT(nBlnxB + nClnxC)<0
例：0.01 mol· -1的尿素溶液 (CO(NH2)2)、0.01 mol· -1 L L 的CaCl2溶液和0.01 mol· -1的NaCl溶液同时放到冰箱 L 里，令冰箱从0 oC起缓慢降温，则以下说法正确的为 ： ( ) A) 尿素最早结冰 B) CaCl2和尿素同时结冰 C) NaCl最晚结冰 D) 三种溶液同时结冰 例：伤口上撒盐为什么会疼？往水蛭身上撒盐为什 么会令其死亡？
多组分系统热力学总结
化学势：偏摩尔吉布斯函数
是温度、压力以及组成的函数
298K、101.325kPa下，将50ml与100ml浓度均为 1mol· -3 萘的苯溶液混合，混合液的化学势μ为： dm
• • • •
(A) μ = μ1 + μ2 ； (B) μ = μ1 + 2μ2 ； (C) μ = μ1 = μ2 ； (D) μ = ⅓μ1 + ⅔μ2 。
在恒温密封容器中有A、B两杯稀盐水溶液，盐的 浓度分别为cA和cB(cA > cB)，放置足够长的时间后： (A) A杯盐的浓度降低，B杯盐的浓度增加 ； (B) A杯液体量减少，B杯液体量增加 ； (C) A杯盐的浓度增加，B杯盐的浓度降低 ； (D) A、B两杯中盐的浓度会同时增大 。

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B，C形成真实液态混合物： 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时，两组分的偏摩尔体积可用下法表示： 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线，此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB，VC。
B
系统中各广度量的偏摩尔量： 对于多组分系统中的组分B，有： 偏摩尔体积： VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能： UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓： HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵： SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数：AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数： GB=(ƽG/ƽnB)T,p,n
C
几点说明： (1)偏摩尔量为两个广度性质之比，所以为强度 性质； (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下，偏导数式的下标为T，p 时才是偏摩尔量； (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中，偏摩尔量不同； (4)若系统为单组分系统，则该组分的偏摩尔量 与该组分的摩尔量相等，即： XB=X*B，m
C
=VB (数学知识：二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势，用符号μB表示：
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质，其化学势等于它的摩尔吉布斯函 数。

多组分系统热力学小结1. 引言多组分系统热力学研究了由多个组分组成的热力学系统的性质和行为。

在这篇文档中，我们将总结多组分系统热力学的一些重要概念和理论，并讨论其在应用中的一些关键应用。

2. 多组分系统的基本概念在多组分系统中，每个组分都有自己的化学组成和性质。

这些组分可以是单一物质或混合物。

多组分系统研究的核心是了解混合物内各组分的相互作用和行为。

多组分系统中的组分可以通过化学势来描述。

化学势是衡量组分在系统中存在的倾向的度量。

对于一个多组分系统，其总能量和组分的化学势之间存在一定的关系，这在热力学理论中被称为Gibbs-Duhem方程。

3. 多组分系统的相平衡在多组分系统中，相平衡是重要的概念。

相平衡指的是不同组分之间达到了平衡状态，可以通过化学势来描述。

当系统达到相平衡时，每个组分的化学势相等。

根据Gibbs相律，对于多组分系统，相平衡条件可以表示为：$\\sum_i \\mu_i dx_i=0$，其中$\\mu_i$表示第i个组分的化学势。

这个方程表明，在相平衡条件下，各组分的化学势满足一定的平衡关系。

4. 多组分系统的热力学性质多组分系统的热力学性质包括混合熵、混合焓和混合自由能等。

这些性质可以通过计算混合物的热力学函数来获得。

4.1 混合熵混合熵指的是混合物的熵减去各组分的熵的总和。

根据熵的定义，混合熵可以通过计算每个组分的摩尔熵和摩尔分数来求得。

4.2 混合焓混合焓指的是混合物的焓减去各组分的焓的总和。

根据焓的定义，混合焓可以通过计算每个组分的摩尔焓和摩尔分数来求得。

4.3 混合自由能混合自由能指的是混合物的自由能减去各组分的自由能的总和。

根据自由能的定义，混合自由能可以通过计算每个组分的摩尔自由能和摩尔分数来求得。

5. 多组分系统的关键应用多组分系统热力学在很多领域中有着重要的应用，以下是其中几个典型的应用：5.1 相平衡计算根据相平衡条件的方程，可以使用多组分系统热力学的理论和方法来计算系统中各相的成分和分布。

V dp n B T ,nB ,nC ... B
dnB T , p ,nC
dp VBdnB B T ,nB ,nC ...
等T，等p:
dV VBdnB
B
等T，等p:
V nBVB
是孤立的，它们的关系是在等温、
x d
B
B
0
xAdA xBdB 0
系统中其它偏摩尔量均可通过化学势、化学势的 偏导数或它们的组合表示：
B VB p T B AB B pVB B p p T
B SB T p
溶液中任意组分B的 偏摩尔体积 m3mol1
(1) 物理意义： 在恒温、恒压、保持B物质以外的所有组分物质的 量不变的条件下，改变dnB引起广度性质X的质的量的B物质所引起广度性质X的变化值。
定义：
V VB n B
以化学变化为例： 封闭系统： A A BB Y Y Z Z
等T，等p，W’ = 0，系统内发生微量发应（d） 对于参加反应的每个组分，有：
dGi SidT Vidp idni idni i id
对于整个系统，有：
dG ( Y Yd Z Zd ) ( A Ad B Bd )
* V V (3) 当xB→1， B m,B
∴ 在稀溶液中 VA V
* m,A
* 对纯物质 VB Vm,B
6．偏摩尔量集合公式
V f (T , p, nB ,)
V V dV dT p T p ,nB ,nC ...
V V dT p T p ,nB ,nC ...

第三章 多组分系统热力学§ 引言基本概念 1、多组分系统两种或两种以上的物质（或称为组分）所形成的系统称为多组分系统。

多组分系统可以是均相的，也可以是多相的。

它（如：多组分单相系统）的热力学性质，则不仅由系统的温度、压力所决定，还与系统的相的组成有关。

2、混合物（mixture ）多组分均匀系统中，各组分均可选用相同的方法处理，有相同的标准态，遵守相同的经验定律，这种系统称为混合物。

混合物有气相、液相和固相之分。

3、溶液（solution ）含有一种以上组分的液体相或固体相称之为溶液。

溶液有液态溶液和固态溶液之分，但没有气态溶液。

4、溶剂（solvent ）和溶质（solute ）如果组成溶液的物质有不同的状态，通常将液态物质称为溶剂，气态或固态物质称为溶质。

如果都具有相同状态，则把含量多的一种称为溶剂，含量少的称为溶质。

溶剂和溶质要用不同方法处理，他们的标准态、化学势的表示式不同，服从不同的经验定律。

溶质有电解质和非电解质之分，本章主要讨论非电介质所形成的溶液。

如果在溶液中含溶质很少，这种溶液称为稀溶液，常用符号“∞”表示。

多种气体混合在一起，因混合非常均匀，称为气态混合物，而不作为气态溶液处理。

多组分系统的组成表示法 1、B 的质量浓度B def(B)m Vρ 即用B 的质量m B 除以混合物的体积V 。

B ρ的单位是： kg ·m —3。

2、B 的质量分数BAAdef(B)m w m ∑ 即B 的质量m B 与混合物的质量之比。

w B 的单位为1。

3、B 的浓度B Bdefn c V即B 的物质的量与混合物体积V 的比值。

c B 常用单位是mol ·L —1。

4、B 的摩尔分数B BAAdefn x n ∑ B 的物质的量与混合物总的物质的量之比称为溶质B 的摩尔分数，又称为物质的量分数。

摩尔分数的单位为1。

气态混合物中摩尔分数常用y B 表示。

第二章 多组分系统热力学
含两个或两个以上组分的系统称为多组分系统。 含两个或两个以上组分的系统称为多组分系统。 多组分系统 均相(单相 非均相(多相 多组分系统可以是均相 单相) 也可以是非均相 多相)的 多组分系统可以是均相 单相 ，也可以是非均相 多相 的。 多组分均相系统又可以区分为混合物 溶液。 混合物和 多组分均相系统又可以区分为混合物和溶液。并以不同的方法 加以研究： 加以研究： 混合物：混合物中的各组分不分为溶剂 溶质， 溶剂及 混合物：混合物中的各组分不分为溶剂及溶质，对各组分 均选用同样的标准态 标准态； 均选用同样的标准态； 溶液：溶液中的各组分区分为溶剂 溶质， 溶剂及 溶液：溶液中的各组分区分为溶剂及溶质，并选用不同的 标准态加以研究。 标准态加以研究。 气态混合物 液态溶液 混合物 液态混合物 溶液 固态溶液（固溶体） 固态溶液（固溶体） 固态混合物
(2-18)
可得： 又µB=GB=HB－TSB ，可得： HB = µB+TSB 有
µ B 1 ∂µ B ∂(µ B / T ) =− 2 + ( ) p ,n ∂T T ∂T T p ,n
=−
2) 化学势与压力的关系
µB
T
2
HB −S + =− 2 T T
(2-19)
∂µ B ( ) T ,n = VB ∂p
X = ∫ dX = ∑ ∫0 X B dn B = ∑ n B X B
X
nB
0
(2-7)
3 吉布斯 杜哈姆公式 吉布斯–杜哈姆公式 在温度、压力下， 微分， 在温度、压力下，对(2-7)微分，得： 微分
B
B
2 偏摩尔量集合公式 由X＝ f (T，p，nA，nB，……)，当温度、压力一定时，对 ＝ ， ，当温度、压力一定时， 一微小变化， 一微小变化，

多组分系统热力学及其在溶液中的应用2在前面的讨论中,我们所涉及到的系统均为纯物质系统或组成恒定的系统。

但在实际上常见的却是多组分系统或变速成系统。

本章将就多组分系统的热力学问题进行讨论。

在正式讨论之前,先将多组分系统进行分类:①按研究的方法分:多组分系统可有单相和多相之分。

本章将讨论多组分系统单相系统。

多组分单相系统由两种或两种以上的物质以分子大小相互均匀混合而成的均匀系统当对均匀系统中各组分现用相同的标准和同样方法研究时,称之为混合物;当对均匀系统中各组分加以区别,选用不同的标准和不同的方法(例如:将系统中的组分分为溶剂(A)和溶质(B))研究时,称之为溶液。

②按聚集状态分:分为气态溶液或混合物、液态溶液或混合物、固态溶液或混合物本章讨论的对象主要是液态系统,包括液态溶液和液态混合物。

③按导电性能分:对于溶液中溶质,按其导电性能可分为电解质溶液和非电解质溶液,本能力讨论非电解质溶液。

④按规律性分:理想混合物理想稀溶液混合物｛溶液｛真实混合物真实溶液本章讨论的主要对象为混合物和稀溶液,适当介绍一些真实溶液。

1.物质B的物质的量分数(物质B的摩尔分数):某BnB某B＝────∑B某B＝1∑BnB2.物质B的物质的质量分数:WBmBWB＝────∑BWB＝1∑BmB3.物质B的量浓度:CB／mol·m-3nBcB＝───V4.物质B的质量摩尔浓度:mB／mol·kg-1nBmB＝───W剂1.拉乌尔定律在一定温度下,纯液体A有一定的蒸汽压p某A,若向液体A加入溶质B,实验表明这是溶剂A的蒸汽压会下降。

法国化学家拉乌尔归纳多次的实验结果得出如下结论:“定温下稀溶液内溶剂的蒸汽压等于同温度下纯溶剂的蒸汽压乘它在溶液内的摩尔分数”。

即pA＝p某A某A推导:设溶液由二个组分构成:A-溶剂B-溶质向溶剂A加入溶质B由实验知pA＜p某A即Δp＝(p某A-pA)＞0且某B↑→Δp↑所以Δp∝某B由于构成稀溶液,加入的溶质较少,溶剂A分子电动势受力环境没有什么改变,只是单位体积溶液中A分子的数量减少了,使气相中ρA下降,而导致pA亦下降,也就是说加入B的数量越多,ρA下降越多,pA的下降也越大,这样,Δp仅与加入溶质B的数量有关,而与其本性无关了。

多组分系统热力学小结[5篇范文]第一篇：多组分系统热力学小结多组分系统热力学小结一、重要概念混合物（各组分标准态相同）与溶液（分溶剂和溶质，标准态不同），组成表示：物质B的摩尔分数xB、质量分数wB、（物质的量）浓度cB、质量摩尔浓度bB，理想稀溶液，理想液态混合物，偏摩尔量，化学势，稀溶液的依数性，逸度与逸度系数，活度与活度系数二、重要定理与公式 1．稀溶液的性质（1）拉乌尔定律：稀溶液的溶剂：pA=pA*xA（2）亨利定律：稀溶液的溶质：pB=kx.B xB , pB=B , pB=kb.BbB（3）Nernst分配定律:（4）依数性：溶剂蒸气压降低：∆pA=pA*xB凝固点降低: ∆Tf=KfbB沸点升高: ∆Tb=KbbB渗透压: ∏B=cBRT 2．理想混合物定义：任一组分在全部组成范围内符合拉乌尔定律的液态混合物。

性质：dp=0, dT=0 混合(1)∆mixV=0(2)∆mixH=0(3)∆mixS=-nR∑xBlnxB(4) ∆mixG=∆mixH-T∆mixS=nRT∑xBlnxB 3．偏摩尔量定义：XB=(X/nB)T,p,nc≠nB性质：恒温恒压下：4．化学势（1）定义：μB=GB=(G/nB)T,p,nc'≠nB自发：朝化学势小的方向（3）化学势的表达式理想气体：μB=μB*(T,p,yc)=μB(T)+RTln(pyB/p)实际气体：μB=μB*(T,p,yc)=μB(T)+RTln(pB/p)逸度 :有效压力逸度系数: ϕB= /pB=理想液态混合物：μB=μB*+RTln(xB)真实液态混合物：μB=μB*+RTln(αB)活度α=fBxB在常压下，压力影响可忽略不计，故μB=μBθ+RTln(αB)若气相为理想气体，则活度的计算式：/pyBαB=pB/pB*fB=αB/xB=pB/pB* xB稀溶液：溶剂或溶质：μA=μA+RTln(xA)真实溶液溶剂：μA=μA+RTln(αA)溶质：采用质量摩尔浓度时：μB=μB，b+RTln(αb，B)采用浓度时μB=μc，B+RTln(αc，B)5.多组分系统的热力学基本方程三、常见的计算题型1．根据稀溶液的性质作依数性等方面的计算2．在相平衡一章中常用拉乌尔定律和亨利定律。

溶液组成的表示
在液态的非电解质溶液中，溶质B的浓度表 示法主要有如下四种：
1.物质的量分数 2.质量摩尔浓度 3.物质的量浓度 4.质量分数
溶液组成的表示
1.物质的量分数 xB (mole fraction)
xB def
nB n(总）
溶质B的物质的量与溶液中总的物质的量之比 称为溶质B的物质的量分数，又称为摩尔分数，单 位为1。
2.只有广度性质才有偏摩尔量，而偏摩尔量是强度 性质。
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T，p和组成的函数。
5.指体系某相中某种物质，整个体系无偏摩尔量。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成，则体
系任一容量性质Z应是T，p及各组分物质的量的函数，
即：
Z Z (T , p, n1, n2 , , nk )
第四章 多组分系统热力学
引言：
前几章介绍了简单系统发生PVT变化、相变化、 和化学变化时W、Q、 U、 H、 S、 A、 G的
计算。所谓简单系统是指由组成不变的系统。但常见 系统多数为多组分、组成发生变化的系统。
多组分系统可为单相或多相。若它为多相的，则 可将它分为几个单相系统。多组分单相系统由两种或 两种以上物质以分子 大小均匀混合组成。
V
V n B
T ,P ,nC
V* m ,B
V* m ,C VC
VB
nB xC = 0 xC
xC = 1
Gibbs-Duhem公式
如果在溶Байду номын сангаас中不按比例地添加各组分，则溶液浓 度会发生改变，这时各组分的物质的量和偏摩尔量均 会改变。
根据集合公式 Z n1Z1 n2Z2 nk Zk

第四章 多组分系统热力学 主要内容1.混合物和溶液（1）多组分系统的分类含一个以上组分的系统称为多组分系统。

多组分系统可以是均相（单相）的，也可以是非均相（多相）的。

将多组分均相系统区分为混合物和溶液,并以不同的方法加以研究：（Ⅰ）混合物：各组分均选用同样的标准态和方法处理；（Ⅱ）溶液：组分要区分为溶剂及溶质，对溶剂及溶质则选用不同的标准态和方法加以研究。

（2）混合物及溶液的分类混合物有气态混合物液态混合物和固态混合物；溶液亦有气态溶液液态溶液和固态溶液。

按溶液中溶质的导电性能来区分，溶液又分为电解质溶液和非电解质溶液（分子溶液）。

2.拉乌尔定律与亨利定律拉乌尔定律与亨利定律是稀溶液中两个重要的经验规律。

（1）拉乌尔定律平衡时，稀溶液中溶剂A 在气相中的蒸气分压A p 等于纯溶剂在同一温度下的饱和蒸气压与该溶液中溶剂的摩尔分数A x 的乘积。

这就是拉乌尔定律。

用数学式表达拉乌尔定律为 A *A Ax p p = （2）亨利定律一定温度下，微溶气体B 在溶剂A 中的溶解度B x 与该气体在气相中的分压B p 成正比。

也可表述为：一定温度下，稀溶液中挥发性溶质B 在平衡气相中的分压力B p 与该溶质B 在平衡液相中的摩尔分数B x 成正比。

这就是亨利定律。

用数学式表达亨利定律为： B B ,B x k p x =B ,x k 、B ,b k 为以不同组成标度表示的亨利系数，其单位分别为Pa ，Pa·kg·mol -1。

应用亨利定律时，要注意其不同表达式所对应的亨利系数及其单位。

还要注意亨利定律适用于稀溶液中的溶质分子同气相同种分子相平衡，即亨利定律适用于稀溶液中的溶质在液相及气相中具有相同分子形态的场合。

3.偏摩尔量（1）偏摩尔量的定义设X 代表V ,U ,H,S ,A ,G 这些广度性质，则对多组份系统（混合物或溶液）即 X =f (T ,p ,n A ,n B ,…)定义 ()B C C,,,B B def ≠⎪⎪⎭⎫ ⎝⎛∂∂n p T n X X式中，X Ｂ称为广度性质X （X=V ,U ,H ,S ,A ,G 等）的偏摩尔量，它们分别为只有系统的广延量才具有偏摩尔量，偏摩尔量是强度量。

多组分系统热力学及其在溶液中的应用概念及公式总结(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第四章多组分系统热力学及其在溶液中的应用一.多组分系统的组成表示法1.混合物中任一组分B的表示法：（1）B的质量浓度： B的质量浓度=B密度（2）B的质量分数：（3）B的浓度：（4）B的摩尔分数：（单位为1）2.溶液中任一组分B的表示法：（1）溶质B的质量摩尔浓度或：（2）溶质B的摩尔比：（单位为1）二、偏摩尔量1.系统的任一种容量性质Z除了与温度、压力有关外，还与系统中各组分的数量即物质的量有关。

2.偏摩尔量的Gibbs自由能：【只有广度性质才有偏摩尔量，偏微商外的下角标均为，，即只有在等温等压，除B以外的其他组分的量保持不变时，某广度性质对组分B 的物质的量的偏微分才称为偏摩尔量又称为化学势】3.偏摩尔量的加和公式：例：在298K和大气压力下，含甲醇（B）的摩尔分数X为的水溶液的密度为Bdm3 ,甲醇的偏摩尔体积，试求该溶液中水的偏摩尔体积：三、化学势（化学势是状态函数，是强度量，绝对值不可知，因此不同物质的化学势大小不能进行比较）1.热力学能：狭义化学势是指偏摩尔Gibbs自由能：2.化学势在相平衡中的应用：化学式与温度、压力的关系：化学式与压力的关系：化学式与温度的关系：四、气体混合物中各组分的化学式：对于理想气体混合物的分子模型和纯理想气体是相同的，即分子自身的体积相对容器体积而言可以忽略不计，分子间的相互作用能极小也可以忽略不计。

因此，把几组纯组分的理想气体混合变成混合气体时，混合热等于零，并在宏观上遵守如下的状态方程：也满足道尔顿分压定律：混合气体平衡后有：混合气体的化学势：五、稀溶液中的两个经验定律1.拉乌尔定律：（溶剂）（如果溶剂和溶质分子间的相互作用的差异可以忽略不计，而且当溶质和溶剂形成溶液时，，相当于形成了液体混合物，则由于在纯溶剂中加入溶质后减少了溶液单位体积和单位表面上溶剂分子的数目，因而也减少了单位时间内可能离开液相表面而进入气相的溶剂分子数目，以致溶剂与其蒸汽在较低的蒸汽压力下即可达到平衡，所以溶液中溶剂的蒸气压较纯溶剂的蒸气压较低）2.亨利定律：（溶质）、、六、理想液态混合物：（当各组分混合时，没有焓变和体积的变化，即、）1理想液态混合物中任一组分的化学势：设温度T时，当理想液态混合物与其蒸汽达平衡时，理想液态混合物中任一组分B与气相中该组分的化学势相等，即.=1 , 故在温度T，压力P时，对于纯的液相B，XB七、稀溶液的依数性：（取决于所含溶质分子的数目，而与溶质本性无关）1. 凝固点降低：固态纯溶剂与溶液成平衡时的温度称为溶液的凝固点。

A
l
O
g T
(
Gm
*
B
p
)T Vm
*
1 3
373.15K
1 2 3 4
16
4.5 混合气体中组元的化学势
纯理想气体的化学势
理想气相混合物中各组分的化学势
实际气体中组分的化学势
17
纯理想气体的化学势
只有一种理想气体，
G ( )T ( )T , p p p nB T

18
p (T , p) (T , p ) RT ln p
纯理想气体的化学势
p (T , p) (T , p ) RT ln p p i i ( g ) RT ln p

这是理想气体化学势的表达式。 μi(g)是温度为T，压力为标准压力时理想气体 i 的 化学势，这个状态就是气体的标准态。
22
气体中组分的化学势小结
纯理想气体
* p B B* B ( g ) RT ln p
pB 混合理想气体 B B ( g ) RT ln p

fB 混合实际气体 B B ( g ) RT ln p

作业2-3 简要论述多组分系统中的相平衡条件和化学反应平衡条件 作业2-4 理想气体混合物和实际气体混合气的化学势的区别和联系是什么
G ( )T , p n B G ( )T nB p T , p
V Vm nB T , p
(dG SdT Vdp)
p



dμ Vmdp p
p

p
RT dp p
p (T , p) (T , p ) RT ln p