初一几何探究题
- 格式:doc
- 大小:133.00 KB
- 文档页数:3

中考数学复习《几何探究型问题》经典题型及测试题(含答案)题型解读1.考查类型:①动点探究题;②平移、旋转、折叠探究题;③图形形状变化探究题.2.考查内容:①多与特殊四边形的性质、三角形全等、相似的判定和性质有关;②涉及平移、旋转或折叠的相关性质;③多与二次函数的性质有关.3.备考指导:在做此类题型时,要观察题中已知条件,并结合题设,联系相关的知识解题,对结果猜想题根据前面问题大胆猜想,往往是解题的突破口.类型一动点探究题1.如图,在Rt△ABC中,∠ACB=90°,AC=5 cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2 cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒3 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.2.如图①,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于点E、F.(1)如图②,当顶点G运动到与点A重合时,求证:EC+CF=BC;(2)知识探究:①如图③,当顶点G运动到AC中点时,探究线段EC、CF与BC的数量关系;②在顶点G 的运动过程中,若ACCG =t ,请直接写出线段EC 、CF 与BC 的数量关系(不需要写出证明过程);(3)问题解决:如图④,已知菱形边长为8,BG =7,CF =65,当t >2时,求EC 的长度.图①3.已知:如图,在矩形ABCD 中,AB =6 cm ,BC =8 cm .对角线AC ,BD 交于点O ,点P 从点A 出发,沿AD 方向匀速运动,速度为1 cm /s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1 cm /s ;当一个点停止运动时,另一个点也停止运动.连接PO 并延长,交BC 于点E ,过点Q 作QF∥AC,交BD 于点F.设运动时间为t(s )(0<t<6),解答下列问题: (1)当t 为何值时,△AOP 是等腰三角形?(2)设五边形OECQF 的面积为S(cm 2),试确定S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使S 五边形OECQF ∶S △ACD =9∶16?若存在,求出t 的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t ,使OD 平分∠COP?若存在,求出t 值;若不存在,请说明理由.4.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF. (1)观察猜想如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:____________. ②BC ,CD ,CF 之间的数量关系为:____________(将结论直接写在横线上). (2)数学思考如图②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明. (3)拓展延伸如图③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =22,CD =14BC ,请求出GE 的长.类型二 平移、旋转、折叠探究题5.如图①,△ABC 是等腰直角三角形,∠BAC =90°,AB =AC ,四边形ADEF 是正方形,点B 、C 分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H.①求证:BD⊥CF;②当AB=2,AD=32时,求线段DH的长.图①图②图③6.在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.(1)如图,当α=60°时,延长BE交AD于点F.①求证:△ABD是等边三角形;②求证:BF⊥AD,AF=DF;③请直接..写出BE的长;(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接..写出BE+CE的值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.7.已知矩形ABCD中AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(1)如图①,已知折痕与边BC交于点O,连接AP、OP、OA,若△OCP与△PDA的面积比为1∶ 4,求边CD 的长;(2)如图②,在(1)的条件下擦去AO、OP,连接BP,动点M在线段AP上(点M不与点P、A重合),动点N 在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明变化规律,若不变,求出线段EF的长度.图①图②8.问题情境在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图①,将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.操作发现(1)将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图②所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________;(2)创新小组将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图③所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形.请你证明这个结论;实践探究(3)缜密小组在创新小组发现结论的基础上,量得图③中BC=13 cm,AC=10 cm,然后提出一个问题:将△AC′D沿着射线DB方向平移a cm,得到△A′C″D′,连接BD′,CC″,使四边形BCC″D′恰好为正方形,求a的值.请你解答此问题;(4)请你参照以上操作,将图①中的△ACD在同一平面内进行一次平移,得到△A′C′D,在图④中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.9.如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;②求EF的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AFBF的值.10.如图①,矩形ABCD 中,AB =2,BC =5,BP =1,∠MPN =90°,将∠MPN 绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB(或AD)于点E ,PN 交边AD(或CD)于点F ,当PN 旋转至PC 处时,∠MPN 的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D , 此时,△ABP________△PCD(填“≌”或“∽”);(2)类比探究:如图③,在旋转过程中,PEPF 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE =t ,△EPF 的面积为S ,试确定S 关于t 的函数关系式;当S =4.2时,求所对应的t 值.11.如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).(1)计算矩形EFGH的面积;(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为316时,求矩形平移的距离;(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.类型三图形形状变化探究题12.如图①,②,③分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.(1)在图①中,求证:△ABE≌△ADC.图①(2)由(1)证得△ABE≌△ADC,由此可推得在图①中∠BOC=120°,请你探索在图②中∠BOC的度数,并说明理由或写出证明过程.图②(3)填空:在上述(1)(2)的基础上可得在图③中∠BOC=________(填写度数).图③图④(4)由此推广到一般情形(如图④),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想∠BOC的度数为____________________(用含n的式子表示).13.阅读理解:我们知道,四边形具有不稳定性,容易变形.如图①,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把1sinα的值叫做这个平行四边形的变形度.(1)若矩形发生形变后的平行四边形有一个内角是120°,则这个平行四边形的变形度是________;猜想证明:(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2,1sinα之间的数量关系,并说明理由;拓展探究:(3)如图②,在矩形ABCD中,E是AD边上的一点,且AB2=AE·AD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4m(m>0),平行四边形A1B1C1D1的面积为2m(m>0),试求∠A1E1B1+∠A1D1B1的度数.14.已知AC ,EC 分别为四边形ABCD 和EFCG 的对角线,点E 在△ABC 内,∠CAE +∠CBE=90°. (1)如图①,当四边形ABCD 和EFCG 均为正方形时,连接BF. ①求证:△CAE∽△CBF; ②若BE =1,AE =2,求CE 的长;(2)如图②,当四边形ABCD 和EFCG 均为矩形,且AB BC =EFFC =k 时,若BE =1,AE =2,CE =3,求k 的值;(3)如图③,当四边形ABCD 和EFCG 均为菱形,且∠DAB =∠GEF=45°时,设BE =m ,AE =n ,CE =p ,试探究m ,n ,p 三者之间满足的等量关系(直接写出结果,不必写出解答过程).15.已知点O 是△ABC 内任意一点,连接OA 并延长到E ,使得AE =OA ,以OB ,OC 为邻边作▱OBFC ,连接OF ,与BC 交于点H ,再连接EF.(1)如图①,若△ABC 为等边三角形,求证:①EF⊥BC; ②EF =3BC ;(2)如图②,若△ABC 为等腰直角三角形(BC 为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;(3)如图③,若△ABC 是等腰三角形,且AB =AC =kBC ,请你直接写出EF 与BC 之间的数量关系.类型一 动点探究题1. 解:(1)根据题意BM =2t ,BN =BC -3t ,而BC =5×tan 60°=5 3.∴当BM =BN 时,2t =53-3t ,解得t =103-15. (2)分类讨论:①当∠BMN =∠ACB =90°时,如解图①, △NBM ∽△ABC ,cos B =cos 30°=BM BN ,∴2t 53-3t =32,解得t =157.②当∠BNM =∠ACB =90°时,如解图②, △MBN ∽△ABC ,cos B =cos 30°=BNBM, ∴53-3t 2t =32,解得t =52. 因此当运动时间是157秒或52秒时,△MBN 与△ABC 相似.第1题解图(3)由于△ABC 面积是定值,∴当四边形ACNM 面积最小时,△MBN 面积最大, 而△MBN 的面积是S =12BM ×BN ×sin B=12×2t ×(53-3t)×12=-32t 2+532t , 由于a =-32<0, ∴当t =-5322×(-32)=52时,△MBN 面积最大,最大值是-32×(52)2+532×52=2538, 因此四边形ACNM 面积最小值是12×5×53-2538=7538.2. (1)证明:∵四边形ABCD 是菱形,∠BAD =120°,∴∠BAC =60°,∠B =∠ACF =60°,AB =BC , ∴AB =AC ,∵∠BAE +∠EAC =∠EAC +∠CAF =60°, ∴∠BAE =∠CAF , 在△BAE 和△CAF 中, ⎩⎪⎨⎪⎧∠BAE =∠CAF AB =AC ∠B =∠ACF, ∴△BAE ≌△CAF(ASA ), ∴BE =CF ,∴EC +CF =EC +BE =BC ,即EC +CF =BC ;(2)解:①线段EC ,CF 与BC 的数量关系为: EC +CF =12BC.理由如下:如解图①,过点A 作AE′∥EG ,AF ′∥GF ,分别交BC 、CD 于E′、F′.第2题解图①类比(1)可得:E′C +CF′=BC , ∵G 为AC 中点,AE ′∥EG , ∴CE CE′=CG AC =12, ∴CE =12CE′,同理可得:CF =12CF′,∴CE +CF =12CE′+12CF′=12(CE′+CF′)=12BC ,即CE +CF =12BC ;②CE +CF =1tBC ;【解法提示】类比(1)可得:E′C +CF′=BC , ∵AE ′∥EG ,ACCG =t ,∴CE CE′=CG AC =1t,∴CE =1tCE′,同理可得:CF =1tCF′,∴CE +CF =1t CE′+1t CF′=1t (CE′+CF′)=1t BC ,即CE +CF =1tBC.(3)解:如解图②,连接BD 与AC 交于点H.第2题解图②在Rt △ABH 中,∵AB =8,∠BAC =60°, ∴BH =AB·sin 60°=8×32=43, AH =CH =AB·cos 60°=8×12=4,∴GH =BG 2-BH 2=72-(43)2=1, ∴CG =4-1=3, ∴CG AC =38, ∴t =83(t >2),由(2)②得:CE +CF =1t BC ,∴CE =1t BC -CF =38×8-65=95.∴EC 的长度为95.3. 解:(1)分三种情况: ①若AP =AO ,在矩形ABCD 中,∵AB =6,BC =8, ∴AC =10,第3题解图①∴AO =CO =5,∴AP =5, ∴t =5,②若AP =PO =t , 在矩形ABCD 中, ∵AD ∥BC ,∴∠PAO =∠OCE ,∠APO =∠OEC , 又∵OA =OC ,∴△APO ≌△CEO ,∴PO =OE =t.如解图①,作AG ∥PE 交BC 于点G ,则四边形APEG 是平行四边形, ∴AG =PE =2t ,GE =AP =t. 又∵EC =AP =t ,∴BG =8-2t.在Rt △ABG 中,根据勾股定理知62+(8-2t)2=(2t)2, 解得t =258.第3题解图②③若OP =AO =5,则t =0或t =8,不合题意,舍去. 综上可知,当t =5或t =258时,△AOP 是等腰三角形.(2)如解图②,作OM ⊥BC ,垂足是M ,作ON ⊥CD ,垂足是N. 则OM =12AB =3,ON =12BC =4,∴S △OEC =12·CE·OM =12·t·3=32t ,S △OCD =12·CD·ON =12·6·4=12.∵QF ∥AC ,∴△DFQ ∽△DOC , ∴S △DFQ S △DOC =(DQ DC)2,即S △DFQ 12=(t 6)2,∴S △DFQ =13t 2,∴S 四边形OFQC =12-13t 2,∴S 五边形OECQF =S 四边形OFQC +S △OEC =12-13t 2+32t ,即S =-13t 2+32t +12(0<t <6).(3)存在.理由如下:要使S 五边形OECQF :S △ACD =9∶16,即(-13t 2+32t +12)∶(12×6×8)=9∶16,解得t 1=3,t 2=1.5,两个解都符合题意,∴存在两个t 值,使S 五边形OECQF ∶S △ACD =9∶16,此时t 1=3,t 2=1.5; (4)存在.理由如下:如解图③,作DI ⊥OP ,垂足是I ,DJ ⊥OC ,垂足是J ,第3题解图③作AG ∥PE 交BC 于点G.∵S △OCD =12·OC·DJ =12·5·DJ ,且由(2)知,S △OCD =12,∴DJ =245.∵OD 平分∠POC ,DI ⊥OP ,DJ ⊥OC , ∴DI =DJ =245=4.8.∵AG ∥PE ,∴∠DPI =∠DAG .∵AD ∥BC ,∴∠DAG =∠AGB ,∴∠DPI =∠AGB , ∴Rt △ABG ∽Rt △DIP.由(1)知,在Rt △ABG 中,BG =8-2t , ∴AB DI =BG IP ,∴64.8=8-2t IP, ∴IP =45(8-2t).在Rt △DPI 中,根据勾股定理得 (245)2+[45(8-2t)]2=(8-t)2, 解得t =11239.(t =0不合题意,舍去)4. (1)解:①BC ⊥CF ;②BC =CD +CF. 【解法提示】①∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF , 又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°,∴∠BCF =90°,即BC ⊥CF ; ②∵△ABD ≌△ACF , ∴BD =CF , ∵BC =CD +BD , ∴BC =CD +CF.(2)解:结论①仍然成立,②不成立. ①证明:∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF ,∴∠ACF =∠ABD =180°-45°=135°, ∵∠ACB =45°, ∴∠BCF =90°,即BC ⊥CF ; ②结论为:BC =CD -CF. 证明:∵△ABD ≌△ACF , ∴BD =CF ,∵BC =CD -BD ,∴BC =CD -CF.(3)解:如解图,过点E 作EM ⊥CF 于M ,作EN ⊥BD 于点N ,过点A 作AH ⊥BD 于点H. ∵AB =AC =22,第4题解图∴BC =4,AH =12BC =2,∵CD =14BC ,∴CD =1,∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°, ∴∠BCF =90°,∴CN =ME ,CM =EN , ∴∠AGC =∠ABC =45°, ∴CG =BC =4,∵∠ADE =90°,∴∠ADH +∠EDN =∠EDN +∠DEN =90°, ∴∠ADH =∠DEN ,又∵∠AHC =∠DNE =90°,AD =DE , ∴△AHD ≌△DNE ,∴DN =AH =2,EN =DH =3, ∴CM =EN =3,ME =CN =3, 则GM =CG -CM =4-3=1, ∴EG =EM 2+GM 2=10.类型二 平移、旋转、折叠探究题5. (1)解:BD =CF 成立.理由如下:∵AC =AB ,∠CAF =∠BAD =θ,AF =AD , ∴△ACF ≌△ABD ,∴CF =BD.(2)①证明:由(1)得,△ACF ≌△ABD , ∴∠HFN =∠ADN , 在△HFN 与△ADN 中,∵∠HFN =∠ADN ,∠HNF =∠AND , ∴∠NHF =∠NAD =90°,第5题解图∴HD ⊥HF ,即BD ⊥CF.②解:如解图,连接DF ,延长AB ,与DF 交于点M , 在△MAD 中,∵∠MAD =∠MDA =45°, ∴∠BMD =90°.在Rt △BMD 与Rt △FHD 中, ∵∠MDB =∠HDF ,∴△BMD ∽△FHD.∵AB =2,AD =32,四边形ADEF 是正方形, ∴MA =MD =322=3,∴MB =MA -AB =3-2=1,BD =MB 2+MD 2=12+32=10, 又∵MD HD =BD FD ,即3HD =106,∴DH =9105.6. (1)①证明:∵△ABC 绕点A 顺时针方向旋转60°得到△ADE , ∴AB =AD ,∠BAD =60°, ∴△ABD 是等边三角形;②证明:由①得△ABD 是等边三角形, ∴AB =BD ,∵△ABC绕点A顺时针方向旋转60°得到△ADE,∴AC=AE,BC=DE,又∵AC=BC,∴EA=ED,∴点B,E在AD的中垂线上,∴BE是AD的中垂线,∵点F在BE的延长线上,∴BF⊥AD,AF=DF;③解:BE的长为33-4;【解法提示】由②知AF=12AD=12AB=3,AE=AC=5,BF⊥AD,由勾股定理得EF=AE2-AF2=4.在等边△ABD中,AB=6,BF⊥AD,∴BF=32AB=33,∴BE=33-4.(2)解:BE+CE的值为13;第6题解图【解法提示】如解图,∵∠DAG=∠ACB,∴∠DAB=2∠CAB.∵∠DAE=∠CAB,∴∠BAE=∠CAB,∴∠BAE=∠CBA,∴AE∥BC,∵AE=AC=BC,∴四边形ACBE是菱形,∴CE 垂直平分AB ,BE =AC =5.设CE 交AB 于M ,则CM ⊥AB ,CM =EM ,AM =BM , ∴在Rt △ACM 中,AC =5,AM =3, 由勾股定理得CM =4, ∴CE =8, ∴CE +BE =13.7. 解:(1)由矩形性质与折叠可知,∠APO =∠B =∠C =∠D =90°, ∴∠CPO +∠DPA =∠DPA +∠DAP =90°, ∴∠DAP =∠CPO , ∴△OCP ∽△PDA , ∴S △OCP S △PDA =(CP DA)2,即14=(CP8)2,∴CP =4,设CD =x ,则DP =x -4,AP =AB =CD =x , ∵AP 2-DP 2=AD 2, ∴x 2-(x -4)2=82, 解得x =10, 故CD =10. (2)第7题解图线段EF 的长度始终不发生变化,为2 5.证明:如解图,过点N 作NG ⊥PB ,与PB 的延长线相交于点G , ∵AB =AP ,∴∠APB =∠ABP =∠GBN , 在△PME 和△BNG 中, ⎩⎪⎨⎪⎧∠MEP =∠NGB =90°∠MPE =∠NBG MP =NB, ∴△PME ≌△BNG(AAS ), ∴ME =NG ,PE =BG , 在△FME 和△FNG 中, ⎩⎪⎨⎪⎧∠MEF =∠NGF ∠MFE =∠NFG ME =NG,∴△FME ≌△FNG(AAS ), ∴EF =GF , ∴EF =12EG ,∵BP =BE +EP =BE +GB =EG , ∴EF =12BP ,∵BP =BC 2+CP 2=82+42=45, ∴EF =12BP =2 5.8. (1)解:菱形.(2)证明:如解图①,作AE ⊥CC′于点E , 由旋转得AC′=AC ,∴∠CAE =∠C′AE =12α=∠BAC ,第8题解图①∵四边形ABCD 是菱形, ∴BA =BC ,BC =DC′, ∴∠BCA =∠BAC , ∴∠CAE =∠BCA , ∴AE ∥BC , 同理AE ∥DC′, ∴BC ∥DC ′,∴四边形BCC′D 是平行四边形, 又∵AE ∥BC ,∠CEA =90°, ∴∠BCC ′=180°-∠CEA =90°,∴四边形BCC′D 是矩形.(3)解:如解图①,过点B 作BF ⊥AC 于点F , ∵BA =BC ,∴CF =AF =12AC =12×10=5.在Rt △BCF 中,BF =BC 2-CF 2=132-52=12. 在△ACE 和△CBF 中,∵∠CAE =∠BCF ,∠CEA =∠BFC =90°, ∴△ACE ∽△CBF , ∴CE BF =AC BC ,即CE 12=1013, 解得CE =12013.∵AC =AC′,AE ⊥CC ′, ∴CC ′=2CE =2×12013=24013.当四边形BCC″D′恰好为正方形时,分两种情况: ①点C″在边CC′上,a =CC′-13=24013-13=7113,②点C″在边C′C 的延长线上,a =CC′+13=24013+13=40913.综上所述,a 的值为7113或40913.第8题解图②(4)解:答案不唯一,例:画出正确图形如解图②所示.平移及构图方法:将△ACD 沿着射线CA 方向平移,平移距离为12AC 的长度,得到△A ′C ′D ,连接A′B ,DC.结论:四边形A′BCD 是平行四边形.9. 解:(1)∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF , ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF ,∴S 四边形ECBF =3S △AEF .∵S △ACB =S △AEF +S 四边形ECBF ,∴S △ACB =S △AEF +3S △AEF =4S △AEF , ∴S △AEF S △ACB =14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC , ∴S △AEF S △ABC =(AE AB )2, ∴(AE AB )2=14. 在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB =42+32=5, ∴(AE 5)2=14,∴AE =52.(2)第9题解图①①四边形AEMF 是菱形.证明:如解图①,∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA ,∴∠CEM =∠EMF , ∴∠CAB =∠CEM , ∴EM ∥AF ,∴四边形AEMF 是平行四边形. 又∵AE =ME ,∴四边形AEMF 是菱形.②如解图①,连接AM ,AM 与EF 交于点O ,设AE =x ,则ME =AE =x ,EC =4-x. ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴△ECM ∽△ACB. ∴EC AC =EMAB , ∵AB =5,AC =4, ∴4-x 4=x5, 解得x =209,∴AE =ME =209,EC =169.在Rt △ECM 中,∵∠ECM =90°,∴CM 2=EM 2-EC 2, 即CM =EM 2-EC 2=(209)2-(169)2=43. ∵四边形AEMF 是菱形,∴OE =OF ,OA =OM ,AM ⊥EF , ∴S 菱形AEMF =4S △AOE =2OE·AO. 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠MAC , ∴OE AO =CM AC. ∵CM =43,AC =4,∴AO =3OE ,∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE·CM ,∴6OE 2=209×43,∴OE =2109,∴EF =4109. (3)如解图②,第9题解图②过点F 作FH ⊥CB 于点H ,在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH , ∴EC NC =FH NH, ∵NC =1,EC =47,∴FH NH =47, 设FH =x ,则NH =74x ,∴CH =NH -NC =74x -1.∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x.在Rt △BHF 和Rt △BCA 中,∵tan ∠FBH =tan ∠ABC , ∴HF BH =CA BC , ∴x4-74x =43, 解得x =85,∴HF =85.∵∠B =∠B ,∠BHF =∠BCA =90°, ∴△BHF ∽△BCA , ∴HF CA =BFBA,即HF·BA =CA·BF , ∴85×5=4BF ,∴BF =2,∴AF =AB -BF =3, ∴AF BF =32. 10. 解:(1)△ABP ∽△PCD. 【解法提示】∵∠MPN =90°, ∴∠APB +∠DPC =90°, ∵∠B =90°,∴∠APB +∠BAP =90°, ∴∠DPC =∠BAP , 又∵∠B =∠C =90°, ∴△ABP ∽△PCD.(2)在旋转过程中,PEPF 的值为定值.如解图,过点F 作FG ⊥BC ,垂足为G.第10题解图类比(1)可得:△EBP ∽△PGF , ∴EP PF =PB FG, ∵∠A =∠B =∠FGB =90°, ∴四边形ABGF 是矩形, ∴FG =AB =2, ∵BP =1, ∴PE PF =12, 即在旋转过程中,PE PF 的值为定值12.(3)由(2)知△EBP ∽△PGF , ∴EB PG =BP GF =12, 又∵AE =t , ∴BE =2-t ,∴PG =2(2-t)=4-2t ,∴AF =BG =BP +PG =1+(4-2t)=5-2t ,∴S =S 矩形ABGF -S △AEF -S △BEP -S △PFG=2(5-2t)-12t(5-2t)-12×1×(2-t)-12×2×(4-2t)=t 2-4t +5,即S =t 2-4t +5(0≤t ≤2), 当S =4.2时,4.2=t 2-4t +5,解得:t 1=2-455,t 2=2+455(不合题意,舍去).∴t 的值是2-455.11. 解:(1)如解图①,在△ABC 中, ∵∠ACB =90°,∠B =30°,AC =1, ∴AB =2,又∵D 是AB 的中点,第11题解图①∴AD =1,CD =12AB =1,又∵EF 是△ACD 的中位线,∴EF =DF =12,在△ACD 中,AD =CD ,∠A =60°,∴△ACD 为等边三角形, ∴∠ADC =60°, 在△FGD 中,GF =DF·sin 60°=34, ∴矩形EFGH 的面积S =EF·GF =12×34=38.(2)如解图②,设矩形移动的距离为x ,则0<x ≤12,①当矩形与△CBD 重叠部分为三角形时,则0<x ≤14,重叠部分的面积S =12x·3x =316,第11题解图②∴x =24>14(舍去), ②当矩形与△CBD 重叠部分为直角梯形时,则14<x ≤12,重叠部分的面积S =34x -12×14×34=316, ∴x =38,即矩形移动的距离为38时,矩形与△CBD 重叠部分的面积是316.第11题解图③(3)如解图③,作H 2Q ⊥AB 于Q , 设DQ =m ,则H 2Q =3m , 又DG 1=14,H 2G 1=12,在Rt △H 2QG 1中, (3m)2+(m +14)2=(12)2,解得m 1=-1+1316,m 2=-1-1316<0(舍去),∴cos α=QG 1F 1G 1=-1+1316+1412=3+138.类型三 图形形状变化探究题12. (1)证明:∵△ABD 、△ACE 是等边三角形, ∴AB =AD ,AC =AE ,∠CAE =∠DAB =60°,∴∠CAE +∠BAC =∠DAB +∠BAC ,即∠BAE =∠DAC , 在△ABE 和△ADC 中, ⎩⎪⎨⎪⎧AB =AD ∠BAE =∠DAC AE =AC, ∴△ABE ≌△ADC(SAS ). (2)解:∠BOC =90°.理由如下: 由(1)得△ABE ≌△ADC ,∴∠EBA =∠CDA.∵∠FBA +∠FDA =180°,∴∠FBA -∠EBA +∠FDA +∠CDA =180°, 即∠FBO +∠FDO =180°.在四边形FBOD 中,∠F =90°, ∴∠DOB =360°-∠F -(∠FBO +∠FDO)=90°, ∴∠BOC =90°. (3)解:72°.【解法提示】∠BOC =180°-108°=72°.(4)解:180°-180°·(n -2)n.【解法提示】由(3)可知,∠BOC 度数应为180°减去正多边形内角度数. 13. 解:(1)233.【解法提示】sin 120°=32,故这个平行四边形的变形度是233. (2)1sin α=S 1S 2,理由如下: 如解图,设矩形的长和宽分别为a ,b ,其变形后的平行四边形的高为h ,第13题解图则S 1=ab ,S 2=ah ,sin α=hb ,∴S 1S 2=ab ah =b h , 又∵1sin α=b h ,∴1sin α=S 1S 2. (3)由AB 2=AE·AD ,可得A 1B 21=A 1E 1·A 1D 1,即A 1B 1A 1D 1=A 1E 1A 1B 1. 又∵∠B 1A 1E 1=∠D 1A 1B 1, ∴△B 1A 1E 1∽△D 1A 1B 1, ∴∠A 1B 1E 1=∠A 1D 1B 1, ∵A 1D 1∥B 1C 1,∴∠A 1E 1B 1=∠C 1B 1E 1,∴∠A 1E 1B 1+∠A 1D 1B 1=∠C 1B 1E 1+∠A 1B 1E 1=∠A 1B 1C 1. 由(2)结论1sin α=S 1S 2,可得1sin ∠A 1B 1C 1=4m2m =2,∴sin ∠A 1B 1C 1=12,∴∠A 1B 1C 1=30°,∴∠A 1E 1B 1+∠A 1D 1B 1=30°. 14. (1)①证明:如解图①, ∵∠ACE +∠ECB =45°,∠BCF +∠ECB =45°,第14题解图①∴∠ACE =∠BCF ,又∵四边形ABCD 和EFCG 是正方形, ∴AC BC =CECF=2, ∴△CAE ∽△CBF.②解:∵AE BF =ACBC =2,AE =2,∴BF =AE2=2, 由△CAE ∽△CBF 可得∠CAE =∠CBF , 又∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°,即∠EBF =90°,第14题解图②由CE 2=2EF 2=2(BE 2+BF 2)=6, 解得CE = 6.(2)解:连接BF ,如解图②,同(1)证△CAE ∽△CBF ,可得∠EBF =90°,AC BC =AE BF, 由AB BC =EFFC=k ,可得BC ∶AB ∶AC =1∶k ∶k 2+1, CF ∶EF ∶EC =1∶k ∶k 2+1,∴CE EF =ACAB =k 2+1k ,AE BF =AC BC=k 2+1, ∴EF =kCE k 2+1,EF 2=k 2CE 2k 2+1,BF =AE k 2+1,BF 2=AE 2k 2+1,∴CE 2=k 2+1k 2×EF 2=k 2+1k2(BE 2+BF 2), ∴32=k 2+1k 2(12+22k 2+1), 解得k =104. (3)解:p 2-n 2=(2+2)m 2.【解法提示】如解图③,连接BF ,同(1)证△CAE ∽△CBF ,可得∠EBF =90°, 过点C 作CH ⊥AB 交AB 延长线于点H , 类比第(2)问得AB 2∶BC 2∶AC 2=1∶1∶(2+2),第14题解图③EF 2∶FC 2∶EC 2=1∶1∶(2+2), ∴p 2=(2+2)EF 2=(2+2)(BE 2+BF 2)=(2+2)(m 2+n 22+2)=(2+2)m 2+n 2,∴p 2-n 2=(2+2)m 2.15. 证明:(1)①连接AH ,如解图①. 第15题解图①∵四边形OBFC 是平行四边形, ∴BH =HC =12BC ,OH =HF ,∵△ABC 是等边三角形, ∴AB =BC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2, ∴AH =BC 2-(12BC )2=32BC ,∵OA =AE ,OH =HF ,∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC.②由①得AH =32BC ,∵AH =12EF∴32BC =12EF ,∴EF =3BC.(2)EF ⊥AB 仍然成立,EF =BC.第15题解图②【解法提示】如解图②,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰直角三角形,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(2BH)2-BH2=BH2,∴AH=BH=12BC,∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,EF=2AH=BC.第15题解图③(3)EF=4k2-1 BC.【解法提示】如解图③,连接AH,∵四边形OBFC是平行四边形,∴BH=HC=12BC,OH=HF,∵△ABC是等腰三角形,AB=kBC,∴AH⊥BC,在Rt△ABH中,AH2=AB2-BH2=(kBC)2-(12=(k2-14)BC2,2BC)∴AH=12-1 BC,24k∵OA=AE,OH=HF,∴AH是△OEF的中位线,∴AH=12EF,AH∥EF,∴EF⊥BC,12-1 BC=12EF,24k∴EF=4k2-1 BC.。
1、己知:如图,AB//CD,试解决下歹恫题: (1) Zl + Z2= __________ ; (2) Zl + Z2+Z3= ____________ ; (3) Zl + Z2+Z3+Z4= _______________ ;(4) 试探究Z1 + Z2+ Z3+ Z4+... + Zn= ________________________2、直线AC 〃BD,连结AB,直线AC, BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不 属于任何部分.当动点P 落在某个部分时,连结PA, PB,构成ZPAC, ZAPB, ZPBD 三个角.(提示:有公 共端点的两条重合的射线所纽成的角是0。
角・)(1) 当动点P 落在第①部分时,求证:ZAPB =ZPAC +ZPBD ;(2) 当动点P 落在第②部分时,ZAPB 二ZPAC +ZPBD 是否成立(直接回答成立或不成立)?(3) 当动点P 在第③部分时,全面探究ZPAC, ZAPB, ZPBDZ 间的关系,并写出动点P 的具体位置和相应的结论.选择其中一种结论加以证明.3、(1)如图,点C 在线段AB 上,AC = 8 cm, CB = 6 cm,点M 、N 分别是AC 、BC 的中点,求线段MN的长;③明理由。
(3)若C在线段AB的延长线上,且满足AC —BC二bcm, M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由。
I 2 丄 2 」A M C N B解:7 a//bZ1 =(又V Z3 = 60°Z4=(Z1 =(又T Z2 = 120°AZ1 + Z2=( ):A〃m (5、如图,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点.(1)用1个单位长度表示1cm,请你在数轴上表示出A、B、C三点的位置;(2)把点C到点A的距离记为CA,贝IJCA二 ____________ cm.(3)若点B以每秒2cm的速度向左移动,同吋A、C点分別以每秒lcm、4cm的速度向右移动.设移动吋间为t 秒,试探索:CA-AB的值是否会随着t的变化而改变?请说明理由.4、, 如图,直线Q // b ,Z3 = 60°, Z2 = 120% 说明:I //m.请在下面的说理中的箱号內填空)(()()或写理由.6、如%1是一副三角尺拼成的图案,三角尺的3个角的顶点是久C、B,记作〃三角尺奴心";三角尺的3个角的顶点是E、B、D,记作〃三角尺EBD”,且ZACB=ZEBD=90o, ZA=30°, ZABC=60°, ZE=ZEDB=45°.(1)图1中ZEBC= ;(2)如图1,二角尺BED不动,将三角尺ABC绕点B顺时针或逆时针旋转a度((f<a<90。

纯几何探究(二)1、(2009东营)已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG .(1)求证:EG =CG ;(2)将图①中△BEF 绕B 点逆时针旋转45º,如图②所示,取DF 中点G ,连接EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?.1.(本题满分10分)解:(1)证明:在Rt △FCD 中, ∵G 为DF 的中点,∴ CG= FD .………………1分 同理,在Rt △DEF 中, EG= FD . ………………2分 ∴ CG=EG .…………………3分(2)(1)中结论仍然成立,即EG=CG .…………………………4分 证法一:连接AG ,过G 点作MN ⊥AD 于M ,与EF 的延长线交于N 点. 在△DAG 与△DCG 中,∵ AD=CD ,∠ADG=∠CDG ,DG=DG , ∴ △DAG ≌△DCG .∴ AG=CG .………………………5分 在△DMG 与△FNG 中,D图①D图②图③∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴MG=NG在矩形AENM中,AM=EN.……………6分在Rt△AMG 与Rt△ENG中,∵AM=EN,MG=NG,∴△AMG≌△ENG.∴AG=EG.∴EG=CG.……………………………8分证法二:延长CG至M,使MG=CG,连接MF,ME,EC,……………………4分在△DCG 与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG ≌△FMG.∴MF=CD,∠FMG=∠DCG.∴MF∥CD∥AB.………………………5分∴.在Rt△MFE 与Rt△CBE中,∵MF=CB,EF=BE,∴△MFE ≌△CBE.∴.…………………………………………………6分∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°.…………7分∴△MEC为直角三角形.∵MG = CG,∴EG= MC.∴.………………………………8分(3)(1)中的结论仍然成立,即EG=CG.其他的结论还有:EG⊥CG.……10分2、(2009年常德市)如图9,若△ABC 和△ADE 为等边三角形,M ,N 分别EB ,CD 的中点,易证:CD=BE ,△AMN 是等边三角形.(1)当把△ADE 绕A 点旋转到图10的位置时,CD=BE 是否仍然成立?若成立请证明,若不成立请说明理由;(4分)(2)当△ADE 绕A 点旋转到图11的位置时,△AMN 是否还是等边三角形?若是,请给出证明,并求出当AB =2AD 时,△ADE 与△ABC 及△AMN 的面积之比;若不是,请说明理由.(6分)2.解:(1)CD =BE .理由如下: ··········································· 1分 ∵△ABC 和△ADE 为等边三角形∴AB=AC ,AE=AD ,∠BAC=∠EAD =60o ∵∠BAE =∠BAC -∠EAC =60o -∠EAC , ∠DAC =∠DAE -∠EAC =60o -∠EAC ,∴∠BAE=∠DAC , ∴△ABE ≌ △ACD ·············································3分 ∴CD=BE ···································································· 4分 (2)△AMN 是等边三角形.理由如下: ···························· 5分 ∵△ABE ≌ △ACD , ∴∠ABE =∠ACD . ∵M 、N 分别是BE 、CD 的中点, ∴BM =1122BE CD CN == ∵AB=AC ,∠ABE=∠ACD , ∴△ABM ≌ △ACN . ∴AM=AN ,∠MAB=∠NAC . ······································ 6分 ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC =60o∴△AMN 是等边三角形. ·············································· 7分设AD=a ,则AB=2a .∵AD=AE=DE ,AB=AC , ∴CE=DE .∵△ADE 为等边三角形, ∴∠DEC=120 o , ∠ADE=60o ,∴∠EDC =∠ECD =30o , ∴∠ADC =90o . ······················································· 8分 ∴在Rt △ADC 中,AD=a ,∠ACD =30 o , ∴ CD.图9 图10 图11图10CNDA ME图11CND AME∵N 为DC 中点,∴DN =,∴AN . ···························· 9分 ∵△ADE ,△ABC ,△AMN 为等边三角形,∴S △ADE ∶S △ABC ∶ S △AMN 7:16:447:4:1)27(:)2(:222===a a a ······························ 10分解法二:△AMN 是等边三角形.理由如下: ········································································· 5分∵△ABE ≌ △ACD ,M 、N 分别是BE 、CN 的中点,∴AM=AN ,NC=MB . ∵AB=AC ,∴△ABM ≌ △ACN ,∴∠MAB=∠NAC , ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC =60o∴△AMN 是等边三角形 ···································································································· 7分 设AD=a ,则AD =AE =DE = a ,AB =BC =AC =2a 易证BE ⊥AC ,∴BE =a a a AE AB 3)2(2222=-=-,∴EM =∴a a a AE EM AM 27)23(2222=+=+= ∵△ADE ,△ABC ,△AMN 为等边三角形∴S △ADE ∶S △ABC ∶ S △AMN 7:16:447:4:1)27(:)2(:222===a a a ·································· 10分3、(2009年宁德市)如图(1),已知正方形ABCD 在直线MN 的上方,BC 在直线MN上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG . (1)连接GD ,求证:△ADG ≌△ABE ; (2)连接FC ,观察并猜测∠FCN 的度数,并说明理由; (3)如图(2),将图(1)中正方形ABCD 改为矩形ABCD ,AB =a ,BC =b (a 、b 为常数),E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请用含a 、b 的代数式表示tan ∠FCN 的值;若∠FCN 的大小发生改变,请举例说明.N M B E C D F G图(1)图(2)M B E A C DF G N3.(本题满分13分)解:(1)∵四边形ABCD 和四边形AEFG 是正方形∴AB =AD ,AE =AG ,∠BAD =∠EAG =90º∴∠BAE +∠EAD =∠DAG +∠EAD ∴∠BAE =∠DAG∴△ BAE ≌△DAG …………4分(2)∠FCN =45º …………5分理由是:作FH ⊥MN 于H ∵∠AEF =∠ABE =90º ∴∠BAE +∠AEB =90º,∠FEH +∠AEB =90º ∴∠FEH =∠BAE又∵AE =EF ,∠EHF =∠EBA =90º∴△EFH ≌△ABE …………7分 ∴FH =BE ,EH =AB =BC ,∴CH =BE =FH∵∠FHC =90º,∴∠FCH =45º …………8分 (3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,…………9分 理由是:作FH ⊥MN 于H 由已知可得∠EAG =∠BAD =∠AEF =90º 结合(1)(2)得∠FEH =∠BAE =∠DAG又∵G 在射线CD 上∠GDA =∠EHF =∠EBA =90º∴△EFH ≌△GAD ,△EFH ∽△ABE ……11分∴EH =AD =BC =b ,∴CH =BE ,∴EH AB =FH BE =FH CH ∴在Rt △FEH 中,tan ∠FCN =FH CH =EH AB =ba…………13分∴当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =ba4.(2009年莆田)已知:等边ABC △的边长为a . 探究(1):如图1,过等边ABC △的顶点A B C 、、依次作AB BC CA 、、的垂线围成MNG △,求证:MNG △是等边三角形且.MN =;探究(2):在等边ABC △内取一点O ,过点O 分别作OD AB OE BC OF CA ⊥⊥⊥、、,垂足分别为点D E F 、、.①如图2,若点O 是ABC △的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.2OD OE OF a ++=;结论2.32AD BE CF a ++=; ②如图3,若点O 是等边ABC △内任意一点,则上述结论12、是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.M B E A C N DF G 图(1) HM B E A C N D F G 图(2)H4.证明:如图1,ABC △为等边三角形60ABC ∴∠=°BC MN BA MG ⊥⊥ ,∴90CBM BAM ∠=∠=°9030ABM ABC ∴∠=∠=︒°- ····················································· 1分 9060M ABM ∴∠=︒∠=︒- ·························································· 2分 同理:60N G ∠=∠=︒ MNG ∴△为等边三角形.··········································································································· 3分 在Rt ABM △中,sin sin 60AB a BM M ===︒在Rt BCN △中,tan tan 60BC a BN N ===︒ ···································································· 4分MN BM BN ∴=+= ····················································································································· 5分 (2)②:结论1成立.证明;方法一:如图2,连接AO BO CO 、、 由ABC AOB BOC AOC S S S S =++△△△△=()12a OD OE OF ++ ··············· 7分 作AH BC ⊥,垂足为H ,则sin sin 602AH AC ACB a a =∠=⨯︒=11222ABC S BC AH a ∴==△·· ()1122a OD OE OF a ∴++= NMAGC BAF CBDA F CB D(图1)(图2) (图3)O AF CB D(图4)O O N MAGC B(图1) A FCBD(图2)O2OD OE OF ∴++=··········································································································· 8分 方法二:如图3,过点O 作GH BC ∥,分别交AB AC 、于点G H 、,过点 H 作HM BC ⊥于点M , 6060DGO B OHF C ∴∠=∠=∠=∠=°,° AGH ∴△是等边三角形 GH AH ∴= ·········································································· 6分 OE BC ⊥ OE HM ∴∥∴四边形OEMH 是矩形 HM OE ∴= ············································································ 7分 在Rt ODG △中,sin sin 60OD OG DGO OG =∠=︒=·· 在Rt OFH △中,sin sin 602OF OH OHF OH =∠=︒=·· 在Rt HMC △中,sin sin 602HM HC C HC HC ==︒=··OD OE OF OD HM OF HC ∴++=++=+)GH HC AC =+== ···························· 8分 (2)②:结论2成立.证明:方法一:如图4,过顶点A B C 、、依次作边AB BC CA 、、的垂线围成MNG △,由(1)得M N G △为等边三角形且MN = ··················································· 9分 过点O 分别作OD MN '⊥于D ',OE NG '⊥于NG 于点E OF MG ''⊥,于点F '由结论1得:32OD OE OF MN a '+'+'=== ········································································ 10分 又OD AB AB MG OF MG ⊥⊥'⊥ ,,90ADO DAF OF A ∴∠=∠'=∠'=︒ ∴四边形ADOF '为矩形 OF ∴'=AD同理:OD BE '=,OE CF '= ··································································································· 11分A F CEBD(图4)O F 'D 'MGNE 'AF CBD (图3)OHG2方法二:(同结论1方法二的辅助线) 在Rt OFH △中,tan 3OF FH OHF ==∠在Rt HMC △中,sin HM HC C == ··························· 9分CF HC FH ∴=+=同理:AD BE =+=, ··················································· 10分 AD BE CF ∴+++)OD OE OF ++ ················································································································ 11分 由结论1得:OD OE OF ++=32AD BE CF a ∴++== ························································································· 12分 方法三:如图5,连接OA OB OC 、、,根据勾股定理得:22222BE OE OB BD OD +==+① 22222CF OF OC CE OE +==+②22222AD OD AO AF OF +==+③ ························································································· 9分①+②+③得:222222BE CF AD BD CE AF ++=++ ··················································································· 10分 ()()()222222BE CF AD a AD a BE a CF ∴++=-+-+-222222222a AD a AD a BE a BE a CF a CF =-++-++-+ ············································ 11分整理得:()223a AD BE CF a ++=A FC BD(图5)OAF CBD(图3)OHG25.(2009 黑龙江大兴安岭)已知:在ABC ∆中,AC BC >,动点D 绕ABC ∆的顶点A 逆时针旋转,且BC AD =,连结DC .过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N .(1)如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、HF ,根据三角形中位线定理和平行线的性质,可得结论BNE AMF ∠=∠(不需证明).(2)当点D 旋转到图2或图3中的位置时,AMF ∠与BNE ∠有何数量关系?请分别写出猜想,并任选一种情况证明.5. 图2:ENB AMF ∠=∠…………………………2分图3:︒=∠+∠180ENB AMF …………………………2分 证明:如图2,取AC 的中点H ,连结HE 、HF …………1分 ∵F 是DC 的中点,H 是AC 的中点,∴AD HF //,AD HF 21=, ∴HFE AMF ∠=∠.………………….1分 同理,CB HE //,CB HE 21=, ∴HEF ENB ∠=∠.…………………………. 1分 ∵BC AD =, ∴HE HF =,图2图3图1AD∴HFE HEF ∠=∠∴AMF ENB ∠=∠.………………… 1分证明图3的过程与证明图2过程给分相同.6.(2009年上海市)已知∠ABC=90°,AB=2,BC=3,AD ∥BC ,P 为线段BD 上的动点,点Q 在射线AB 上,且满足ABADPC PQ =(如图1所示). (1)当AD=2,且点Q 与点B 重合时(如图2所示),求线段PC 的长; (2)在图中,联结AP .当32AD =,且点Q 在线段AB 上时,设点B Q 、之间的距离为x ,APQ PBCS y S =△△,其中APQ S △表示△APQ 的面积,PBC S △表示PBC △的面积,求y 关于x 的函数解析式,并写出函数定义域;(3)当AD AB <,且点Q 在线段AB 的延长线上时(如图3所示),求QPC ∠的大小.解:(1)AD=2,且Q 点与B 点重合,根据题意,∠PBC=∠PDA ,因为∠A=90。

纯几何探究(一)1. (2008年广东省中山市)(本题满分9分)(1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连结AC 和BD ,相交于点E ,连结BC . 求∠AEB 的大小;(2)如图8,ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点O旋转(ΔOAB 和ΔOCD 不能重叠),求∠AEB 的大小. 1.解:(1)如图7.∵ △BOC 和△ABO 都是等边三角形, 且点O 是线段AD 的中点,∴ OD=OC=OB=OA,∠1=∠2=60°, ……1分 ∴ ∠4=∠5.又∵∠4+∠5=∠2=60°,∴ ∠4=30°.…………………………2分 同理,∠6=30°.…………………………3分 ∵ ∠AEB=∠4+∠6,∴ ∠AEB=60°.………………………4分(2)如图8. ∵ △BOC 和△ABO 都是等边三角形,∴ OD=OC, OB=OA,∠1=∠2=60°,………5分又∵OD=OA, ∴ OD =OB ,OA =OC ,∴ ∠4=∠5,∠6=∠7. …………………6分 ∵ ∠DOB=∠1+∠3, ∠AOC=∠2+∠3, ∴∠DOB=∠AOC. …………………………………7分 ∵ ∠4+∠5+∠DOB=180°, ∠6+∠7+∠AOC=180°, ∴ 2∠5=2∠6,∴ ∠5=∠6.………………………………………………8分 又∵ ∠AEB=∠8-∠5, ∠8=∠2+∠6, ∴ ∠AEB =∠2+∠5-∠5=∠2,∴ ∠AEB =60°.…………………………………………9分C B OD 图7 A B O D CE 图8图88765421E OD CBA32.(2008年湖北省鞥仙桃市潜江市江汉油田)小华将一张矩形纸片(如图1)沿对角线CA 剪开,得到两张三角形纸片(如图2),其中α=∠ACB ,然后将这两张三角形纸片按如图3所示的位置摆放,∆EFD 纸片的直角顶点D 落在∆ACB 纸片的斜边AC 上,直角边DF 落在AC 所在的直线上.(1) 若ED 与BC 相交于点G ,取AG 的中点M ,连接MB 、MD ,当∆EFD 纸片沿CA 方向平移时(如图3),请你观察、测量MB 、MD 的长度,猜想并写出MB 与MD 的数量关系,然后证明你的猜想;(2) 在(1)的条件下,求出BMD ∠的大小(用含α的式子表示),并说明当45=α°时, BMD ∆是什么三角形?(3) 在图3的基础上,将∆EFD 纸片绕点C 逆时针旋转一定的角度(旋转角度小于90°),此时CGD ∆变成CHD ∆,同样取AH 的中点M ,连接MB 、MD (如图4),请继续探究MB 与MD 的数量关系和BMD ∠的大小,直接写出你的猜想,不需要证明,并说明α为何值时,BMD ∆为等边三角形.2. (10分)解:(1)MB =MD ………………………………………………………(1分) 证明:∵AG 的中点为M ∴在ABG Rt ∆中, AG MB 21= 在ADG Rt ∆中,AG MD 21=∴MB =MD ………………………………………………(3分)(2)∵BAM ABM BAM BMG ∠=∠+∠=∠2同理DAM ADM DAM DMG ∠=∠+∠=∠2 ∴BMD ∠=DAM BAM ∠+∠22=BAC ∠2 而α-=∠090BAC∴α21800-=∠BMD …………………………………………(6分)∴当045=α时,090=∠BMD ,此时BMD ∆为等腰直角三角形.…(8分) (3)当CGD ∆绕点C 逆时针旋转一定的角度,仍然存在MB =MD , α21800-=∠BMD ………………………………………………(9分)A B A BCD EF 图1图2 A BCDEFGM 图3ABCDEFMH图4故当060=α时,BMD ∆为等边三角形.…………………………(10分) 3.(2008年义乌市)如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系;②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中正方形改为矩形(如图4—6),且AB=a ,BC=b ,CE=ka , CG=kb (a ≠b ,k >0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由. (3)在第(2)题图5中,连结DG 、BE ,且a =3,b =2,k =12,求22BE DG +的值. 3.解:(1)①,BG DE BG DE =⊥ ……………………………2分 ②,BG DE BG DE =⊥仍然成立 ……………………………1分在图(2)中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴ BC CD =,CG CE =, 090BCD ECG ∠=∠=∴BCG DCE ∠=∠……………………………………………1分∴BCG DCE ∆≅∆ (SAS )…………………………………1分∴BG DE = CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ ………………………………………………1分(2)BG DE ⊥成立,BG DE =不成立 …………………………………2分简要说明如下∵四边形ABCD 、四边形CEFG 都是矩形,且AB a =,BC b =,CG kb =,CE ka =(a b ≠,0k >)∴BC CG bDC CE a==,090BCD ECG ∠=∠= ∴BCG DCE ∠=∠∴BCG DCE ∆∆ ……………………………………1分∴CBG CDE ∠=∠又∵BHC DHO ∠=∠ 090CBG BHC ∠+∠= ∴090CDE DHO ∠+∠= ∴090DOH ∠=∴BG DE ⊥ …………………………………………1分(3)∵BG DE ⊥ ∴22222222BE DG OB OE OG OD BD GE +=+++=+ 又∵3a =,2b =,k =12∴ 222222365231()24BD GE +=+++= …………………………1分 ∴22654BE DG +=……………………………………………………1分 4. (2008盐城)如图甲,在△ABC 中,∠ACB 为锐角.点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .解答下列问题:(1)如果AB=AC ,∠BAC=90º.①当点D 在线段BC 上时(与点B 不重合),如图乙,线段CF 、BD 之间的位置关系为 ▲ ,数量关系为 ▲ . ②当点D 在线段BC 的延长线上时,如图丙,①中的结论是否仍然成立,为什么?(2)如果AB ≠AC ,∠BAC ≠90º,点D 在线段BC 上运动.试探究:当△ABC 满足一个什么条件时,CF ⊥BC (点C 、F 重合除外)?画出相应图形,并说明理由.(画图不写作法)(3)若AC=BC=3,在(2)的条件下,设正方形ADEF 的边DE 与线段CF 相交于点P ,求线段CP 长的最大值.4.(1)①CF 与BD 位置关系是 垂 直、数量关系是相 等; ②当点D 在BC 的延长线上时①的结论仍成立. 由正方形ADEF 得 AD=AF ,∠DAF=90º.∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC, 又AB=AC ,∴△DAB≌△FAC , ∴CF=BD ∠ACF=∠ABD.∵∠BAC=90º, AB=AC ,∴∠ABC=45º,∴∠ACF=45º, ∴∠BCF=∠ACB+∠ACF= 90º.即 CF⊥BD (2)画图正确当∠BCA=45º时,CF⊥BD(如图丁).理由是:过点A 作AG⊥AC 交BC 于点G ,∴AC=AG 可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º ∠BCF=∠ACB+∠ACF= 90º. 即CF⊥BD (3)当具备∠BCA=45º时,过点A 作AQ⊥BC 交BC 的延长线于点Q ,(如图戊) ∵DE 与CF 交于点P 时, ∴此时点D 位于线段CQ 上,∵∠BCA=45º,可求出AQ= CQ=4.设CD=x ,∴ DQ=4—x ,容易说明△AQD∽△DCP,∴CP CD DQ AQ= , ∴44CP xx =-,221(2)144x CP x x ∴=-+=--+.∵0<x ≤3 ∴当x=2时,CP 有最大值1.5.(2008年泰安市)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .A B C D EF 第28题图 图甲 图乙 F EAF E D C B A 图丙 图丁GABCDEF图戊 PQ AB CD E F(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:DC BE ⊥. 6.(本小题满分9分)(1)解:图2中ABE ACD △≌△ ···················································································· 1分 证明如下:ABC △与AED △均为等腰直角三角形AB AC ∴=,AE AD =,90BAC EAD ∠=∠= ···························································· 3分 BAC CAE EAD CAE ∴∠+∠=∠+∠即BAE CAD ∠=∠ ················································································································ 4分ABE ACD ∴△≌△ ·············································································································· 6分 (2)证明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠= ·········································································································· 7分 又45ACB ∠=90BCD ACB ACD ∴∠=∠+∠=DC BE ∴⊥ ··························································································································· 9分 6.(9分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC 中,AB =AC ,P 是△ABC 内部任意一点,将AP 绕A 顺时针旋转至AQ ,使∠QAP =∠BAC ,连接BQ 、CP ,则BQ =CP .”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ ≌△ACP ,从而证得BQ =CP 之后,将点P 移到等腰三角形ABC 之外,原题中的条件不变,发现“BQ =CP ”仍然成立,请你就图②给出证明.图1图2(第22题)图①QPBAAQBPC图②证明:∵∠QAP =∠BAC∴∠QAP +∠PAB =∠PAB +∠BAC即∠QAB =∠PAC 4分 在△ABQ 和△ACP 中 AQ =AP∠QAB =∠PAC AB =AC 6.(本题10分)(2008年武汉市)正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC 上一动点,过点P 作PF ⊥CD 于点F 。

初一数学《相交线与平行线》及探究题、答案解析知识要点:1. 两条直线的位置关系(1)在同一平面内,两条直线的位置关系有两种:相交与平行. (2)平行线:在同一平面内,不相交的两条直线叫平行线. 2. 几种特殊关系的角(1)余角和补角:如果两个角的和是直角,称这两个角互为余角.如果两个角的和是平角,称这两个角互为补角.(2)对顶角:①定义:一个角的两边分别是另一个角两边的反向延长线,这两个角叫对顶角. ②性质:对顶角相等.(3)同位角、内错角、同旁内角两条直线分别与第三条直线相交,构成八个角.①在两条直线之间并且在第三条直线的两旁的两个角叫做内错角. ②在两条直线的同一侧并且在第三条直线同旁的两个角叫做同位角. ③在两条直线之间并且在第三条直线同旁的两个角叫做同旁内角. 3. 主要的结论 (1)垂线①过一点有且只有一条直线与已知直线垂直.②直线外一点与直线上各点连结的所有线段中,垂线段最短.简称:垂线段最短. (24. 几个概念(1)垂线段:过直线外一点,作已知直线的垂线,这点和垂足之间的线段. (2)点到直线的距离:从直线外一点到这条直线的垂线段的长度. 5. 几个基本图形(1)相交线型.①一般型(如图①);②特殊型(垂直,如图②).(2)三线八角.①一般型(如图①);②特殊型(平行,如图②).ABC DOABCDO ①②重点难点:重点有两个:一方面要掌握关于相交线和平行线的一些基本事实,另一方面学会借助三角尺上的直角或量角器画已知直线的垂线,用移动三角尺的方法画平行线.难点是是利用对顶角的性质、平行线的特征、两直线平行的条件等进行推理和计算.考点分析:考查(1)对顶角的性质;(2)平行线的识别方法;(3)平行线的特征,其中依据平行线的识别与特征解决一类与平行线有关的几何问题是历届中考命题的重要考点.常见题型有填空题、选择题和解答题,单纯考查一个知识点的题目并不难,属于中低档题,将平行线的特征与其他知识综合起来考查的题目难度较大,属高档题.【典型例题】1. 如图所示,已知FC ∥AB ∥DE ,∠α∶∠D ∶∠B =2∶3∶4,求∠α、∠D 、∠B 的度数.2. 如图所示,直线a ∥b ,则∠A =__________.3.如图1,直线MN 与直线AB 、CD 分别交于点E 、F ,∠1与∠2互补. (1)试判断直线AB 与直线CD 的位置关系,并说明理由;A BCDEFAB CDEF①②ABC DEF12αABCEa b28°50°(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.4.已知,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图①,求证:OB∥AC.(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA度数等于.(在横线上填上答案即可).5.如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.(1)请在图中找出与∠AOC相等的角,并说明理由;(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.6.已知E,F分别是AB、CD上的动点,P也为一动点.(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.7.已知:∠A=(90+x)°,∠B=(90﹣x)°,∠CED=90°,射线EF∥AC,2∠C﹣∠D=m.(1)判断AC与BD的位置关系,并说明理由.(2)如图1,当m=30°时,求∠C、∠D的度数.(3)如图2,求∠C、∠D的度数(用含m的代数式表示).8.(1)如图(1),EF⊥GF,垂足为F,∠AEF=150°,∠DGF=60°.试判断AB和CD的位置关系,并说明理由.(2)如图(2),AB∥DE,∠ABC=70°,∠CDE=147°,∠C=.(直接给出答案)(3)如图(3),CD∥BE,则∠2+∠3﹣∠1=.(直接给出答案)(4)如图(4),AB∥CD,∠ABE=∠DCF,求证:BE∥CF.9.如图1,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠DCE﹣∠HAE=90°.(1)求证:BH∥CD.(2)如图2:直线AF交DC于F,AM平分∠EAF,AN平分∠BAE.试探究∠MAN,∠AFG的数量关系.10.平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等,如图,一束光线m先射到平面镜a上,被平面镜a反射到平面镜b上,又被平面镜b反射出光线n.(1)若m∥n,且∠1=50°,则∠2=°,∠3=°;(2)若m∥n,且∠1=40°,则∠3=°;(3)根据(1)、(2)猜想:当两平面镜a、b的夹角∠3是多少度时,总有m∥n?试证明你的猜想.初一数学相交线和平行线探究题1.AB∥CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.2.已知:如图①、②,解答下面各题:(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF 的度数。

几何图形操作探究型问题★1.已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.(1)如图①,若点D是AC的中点,连接PC.①求BP,BD的长;②求证:四边形BCPD是平行四边形;(2)如图②,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.第1题图解:(1)①在Rt△ABC中,AC=4,BC=2,∴BA=AC2+BC2=42+22=25,又∵点D是AC的中点,∴AD=CD=2,在Rt△BCD中,由勾股定理得:BD=BC2+CD2=22+22=22,由翻折可知,BP=BA=25;②证明:∵△BCD是等腰直角三角形,∴∠BDC=45°,∴∠ADB=∠BDP=135°,∴∠PDC=135°-45°=90°,∴∠BCD=∠PDC=90°,∴DP∥BC,∵DP=AD=BC=2,∴四边形BCPD是平行四边形;(2)如解图,连接P A ,分别过点D 作DN ⊥AB 于点N ,过点P 作PE ⊥AC 于点E ,延长BD 交P A 于点M ,则△ABP 为等腰三角形,BM ⊥AP .第1题解图设BD =AD =x ,则CD =4-x ,在Rt △BDC 中,由勾股定理得:BD 2=CD 2+BC 2, ∴x 2=(4-x )2+22, ∴x =52,∵BD =AD ,DN ⊥AB , ∴BN =AN =12AB =5,在Rt △BDN 中,DN =BD 2-BN 2=(52)2-(5)2=52, 由△BDN ∽△BAM ,可得DN AM =BDAB ,∴52AM =5225, ∴AM =2, ∴AP =2AM =4,由△ADM ∽△APE ,可得AM AE =ADAP ,∴2AE =524, ∴AE =165,∴EC =AC -AE =4-165=45,易证四边形PECH 是矩形, ∴PH =EC =45.★2.如图,正方形ABCD 的边长为1,点E 为边AB 上一动点,连接CE 并将其绕点C 顺时针旋转90°得到CF ,连接DF ,以CE 、CF 为邻边作矩形CFGE ,GE 与AD 、AC 分别交于点H 、M ,GF 交CD 延长线于点N .(1)证明:点A 、D 、F 在同一条直线上;(2)随着点E 的移动,线段DH 是否有最小值?若有,求出最小值;若没有,请说明理由; (3)连接EF 、MN ,当MN ∥EF 时,求AE 的长.第2题图(1)证明:由旋转可知∠ECF =90°, ∵四边形ABCD 是正方形, ∴CD =CB ,∠ADC =∠BCD =90°,∵∠BCE +∠DCE =∠BCD =90°,∠DCF +∠DCE =∠ECF =90°, ∴∠DCF =∠BCE , 在△CDF 与△CBE 中, ⎩⎪⎨⎪⎧CF =CE ∠DCF =∠BCE CD =CB, ∴△CDF ≌△CBE , ∴∠CDF =∠B =90°,∴∠ADF =∠CDF +∠CDA =180°, ∴点A 、D 、F 在同一条直线上;(2)解:DH 有最小值,设BE =x ,则AE =1-x , 由(1)得DF =BE =x , 易证∠DCF =∠AEH ,∴tan ∠DCF =tan ∠AEH =DF CD =AH AE ,∴11x AH x=-, 解得AH =x -x 2,∴DH =1-AH =(x -12)2+34,∴当x =12时,DH 有最小值,且DH 最小=34;(3)解:如解图,过点E 作EP ⊥AC 于点P.第2题解图易证四边形CFGE 为正方形. ∵EF ∥MN , ∴FN FG =EM EG , ∵FG =EG , ∴FN =EM ,在△CFN 和△CEM 中,⎩⎪⎨⎪⎧FN =EM ∠CFN =∠CEM CF =CE, ∴△CFN ≌△CEM , ∴∠FCN =∠ECM , 由(1)得∠FCN =∠ECB , ∴∠ECM =∠ECB , ∴EP =EB ,∴sin ∠EAP =EP AE =EBAE=1x x =-,解得x =11+2,则AE =1-x =21+2=2- 2.★3.如图①,四边形ABCD 的对角线AC ,BD 相交于点O ,OB =OD ,OC =OA +AB ,AD =m ,BC =n ,∠ABD +∠ADB =∠ACB .(1)填空:∠BAD 与∠ACB 的数量关系为______; (2)求mn的值;(3)将△ACD 沿CD 翻折,得到△A ′CD (如图②),连接BA ′,与CD 相交于点P .若CD =5+12,求PC 的长.第3题图解:(1)∠ACB +∠BAD =180°;【解法提示】∵在△ABD 中,由三角形内角和得∠ABD +∠ADB +∠BAD =180°, ∵∠ABD +∠ADB =∠ACB ,∴∠ACB +∠BAD =180°. (2)如解图①,过点B 作BE ∥AD ,交AC 于点E ,第3题解图①∴∠ADO =∠EBO ,∠DAO =∠BEO , ∵OB =OD , ∴△ADO ≌△EBO , ∴BE =AD =m ,OE =OA , ∵OC =OA +AB , ∴CE =AB .∵∠ABO +∠ADO =∠ACB ,∠ABO +∠EBO =∠ABE , ∴∠ABE =∠ACB , ∵∠BAE =∠CAB , ∴△BAE ∽△CAB , ∴AB AC =AE AB =BE BC, ∴AB 2=AC ·AE =(2OA +AB )·2OA ,即4OA 2+2OA ·AB -AB 2=0,解得OA =5-14AB ,∴m n =AD BC =BE BC =AB AC =2AB OA AB =AB 5-12AB +AB =25+1=5-12; (3)如解图②,过点D 作DG ∥AB 交AC 于G ,同理可得△DOG ≌△BOA ,第3题解图②∴DG =AB ,OG =OA , ∴CG =AB , ∴∠GCD =∠GDC ,∵∠ADG =∠ADO +∠ODG =∠ADO +∠ABO =∠ACB , ∴∠ADC =∠ADG +∠GDC =∠ACB +∠GCD =∠BCD . 由折叠可知∠A ′DC =∠ADC =∠BCD , ∴A ′D ∥BC , ∴△A ′DP ∽△BCP , ∴A ′D BC =DP CP =5+12-CP CP , 由(2)知AD BC =A′D BC =m n =5-12,即5+12-CP CP =5-12,解得CP =1.★4.如图,在矩形ABCD 中,点E 是BC 的中点,把△ABE 沿着AE 折叠得到△AFE ,AF 的延长线交CD 于G ,连接CF . (1)证明:AE ∥FC ;(2)猜想线段CF ,EF ,AE 之间的数量关系,证明你的猜想; (3)若AB =9,AD =6,求CF 的长.第4题图解:(1)由折叠得,EF =EB ,∠FEA =∠BEA , ∵点E 是BC 中点,∴EB =EC =EF ,∴∠EFC =∠ECF , ∵∠BEF =∠BEA +∠FEA =∠ECF +∠EFC . ∴∠ECF =∠BEA ,∴AE ∥FC ; (2)EF 2=12AE ·CF , 理由如下:如解图,取AE 中点O ,连接O B ,第4题解图在矩形ABCD 中,∠ABC =90°, ∴O E =O B =12AE , ∴∠O EB =∠O BE , 由(1)得:EF =EB ,∠ECF =∠BEA =∠EFC =∠O BE , ∴△EFC ∽△O EB ,2,1·2EF CFOE EBEF AE CF∴=∴=(3)在矩形ABCD 中,BC =AD =6,∠ABC =90°, ∴BE =EF =EC =3, 由勾股定理得:()22122132AE EF AE CF CF =∴⨯∴由得:=,=,★5.如图,将一张矩形纸片ABCD 沿直线MN 折叠,使点C 落在A 处,点D 落在E 处,直线MN 交BC 于点M ,交AD 于点N .(1)求证:CM =CN ;(2)若△CMN 的面积与△CDN 的面积比为3∶1,求MNDN的值.第5题图(1)证明:由折叠的性质可得:∠ENM =∠DNM , 即∠ENA +∠ANM =∠DNC +∠CNM , ∵∠ENA =∠DNC , ∴∠ANM =∠CNM , ∵四边形ABCD 是矩形, ∴AD ∥BC , ∴∠ANM =∠CMN , ∴∠CMN =∠CNM , ∴CM =CN ;(2)解:如解图,过点N 作NH ⊥BC 于点H ,则四边形NHCD 是矩形, ∴HC =DN ,NH =DC ,∵△CMN 的面积与△CDN 的面积比为3∶1,CMN CDNS S=12MC ·NH 12ND ·NH =MC ND =3, ∴MC =3ND =3HC ,设DN =x ,则HC =x ,MH =2x , ∴CM =3x =CN , 在Rt △CDN 中, DC =CN 2-DN 2=22x ,∴HN =22x , 在Rt △MNH 中, MN =MH 2+HN 2=23x ,∴MN DN =23x x=2 3.第5题解图★6.如图①,将一张矩形纸片ABCD 沿着对角线BD 向上折叠,顶点C 落到点E 处,BE 交AD 于点F . (1)求证:△BDF 是等腰三角形;(2)如图②,过点D 作DG ∥BE ,交BC 于点G ,连接FG 交BD 于点O . ①判断四边形BFDG 的形状,并说明理由; ②若AB =6,AD =8,求FG 的长.第6题图(1)证明:由折叠的性质可得,∠DBC =∠DBF , ∵四边形ABCD 是矩形, ∴AD ∥BC , ∴∠ADB =∠DBC , ∴∠DBF =∠ADB ,∴△BDF 是等腰三角形; (2)解:①四边形BFDG 是菱形. 理由:∵四边形ABCD 是矩形, ∴AD ∥BC ,即DF ∥BG , ∵DG ∥BF ,∴四边形BFDG 是平行四边形, ∵BF =DF ,∴平行四边形BFDG 是菱形;②∵矩形ABCD 中AB =6,AD =8,∠A =90°, ∴BD =AB 2+AD 2=10,∵四边形BFDG 是菱形,∴BD ⊥GF ,GF =2OF ,BD =2OD , ∴OD =5,∴tan ∠ADB =OF OD =AB AD ,∴OF =154,∴FG =152.★7.如图,正方形ABCD 的边长是16,点E 在边AB 上,AE =3,动点F 在边BC 上,且不与点B ,C 重合,将△EBF 沿EF 折叠,得到△EB ′F .(1)当∠BEF =45°时,求证:CF =AE ; (2)当B ′D =B ′C 时,求BF 的长; (3)求△CB ′F 周长的最小值.第7题图(1)证明:如解图①,当∠BEF =45°时,易知四边形BEB ′F 是正方形,∴BF=BE,∵AB=BC,∴CF=AE;(2)解:如解图②,作B′N⊥BC于点N,NB′的延长线交AD于点M,作EG⊥MN于点G,则四边形MNCD、四边形AEGM 都是矩形.第7题解图①第7题解图②∵B′D=B′C,∴∠B′DC=∠B′CD,∵∠ADC=∠BCD=90°,∴∠B′DM=∠B′CN,∵∠B′MD=∠B′NC=90°,∴△B′MD≌△B′NC(AAS),∴B′M=B′N=8,∵AE=MG=3,∴GB′=5,在Rt△EGB′中,EG=EB′2-GB′2=132-52=12,∵∠EB′G+∠FB′N=90°,∠FB′N+∠B′FN=90°,∴∠EB′G=∠B′FN,∵∠EGB′=∠FNB′=90°,∴△EGB′∽△B′NF,∴EG B′N =EB′FB′,∴12 8=13 B′F,∴BF=B′F=263;(3)解:如解图③,以E为圆心,EB为半径画圆,连接EC,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,第7题解图③∴EC=162+132=517,∵△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,∴欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,∵CB′+EB′≥EC,∴当E、B′、C共线时,CB′的值最小,CB′最小值是为517-13.∴△CFB′的周长的最小值为3+517.★8.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E为边AD上一点,将△ABE沿直线BE折叠,使A点落在四边形对角线BD上的P点处,EP的延长线交直线BC于点F.设AD=a,AB=b,BC=c.(1)若∠ABE=30°,AE=3,请写出BE的长度;(2)求证:△ABP∽△BFE;(3)当四边形EFCD为平行四边形时,试求出a,b,c的数量之间的关系式.第8题图(1)解:BE=6;【解法提示】∵AB⊥BC,AD∥BC,∴BA⊥AD,在Rt△ABE中,∠ABE=30°,AE=3,∴BE=2AE=6;(2)证明:∵AD∥BC,∴∠AEB=∠EBF,由折叠得△EAB≌△EPB,∴∠AEB=∠BEP,∴∠EBF=∠BEF,∴FE =FB ,∴△FEB 为等腰三角形, ∵∠ABP +∠PBF =90°, ∠PBF +∠EFB =90°, ∴∠ABP =∠EFB ,在等腰△ABP 和等腰△FEB 中, ∠BAP =12(180°-∠ABP ),∠FBE =12(180°-∠EFB ),∴∠BAP =∠FBE , ∴△ABP ∽△BFE ;(3)解:∵四边形EFCD 为平行四边形, ∴EF ∥DC ,∴∠EFB =∠C ,∠ADB =∠DBC , ∵∠ABD =∠EFB , ∴∠ABD =∠C , ∴△ABD ∽△DCB , ∴AD DB =DB CB , 即a a 2+b2=a 2+b 2c, ∴a 2+b 2=ac .★9.已知边长为3的正方形ABCD 中,点E 在射线BC 上,且BE =2CE ,连接AE 交射线DC 于点F ,若△ABE 沿直线AE 翻折,点B 落在点B 1处.(1)如图,若点E 在线段BC 上,求CF 的长; (2)求sin ∠DAB 1的值;(3)如果题设中“BE =2CE ”改为“BECE =x ”,其他条件都不变,试求△ABE 翻折后与正方形ABCD 公共部分的面积y 与x 的关系式及自变量x 的取值范围(只要写出结论,不需写出解题过程).第9题图 备用图解:(1)∵AB ∥DF ,∴∠BAF =∠F ,∠B =∠BCF =90°, ∴△ABE ∽△FCE , ∴AB FC =BE CE, ∵BE =2CE ,AB =3, ∴3CF =2CE CE . ∴CF =32;(2)①若点E 在线段BC 上,如解图①,设直线AB 1与DC 相交于点M .第9题解图①由题意翻折得:∠1=∠2. ∵AB ∥DF , ∴∠1=∠F , ∴∠2=∠F , ∴AM =MF .设DM =x ,则CM =3-x , 又∵CF =32,∴AM =MF =92-x ,在Rt △ADM 中,AD 2+DM 2=AM 2, ∴32+x 2=(92-x )2,解得x =54,∴DM =54,AM =134,∴sin ∠DAB 1=DM AM =513;②若点E 在边BC 的延长线上,如解图②,设直线AB 1与CD 的延长线交于点N .第9题解图②同理可得:AN =NF . ∵BE =2CE , ∴BC =CE =AD . ∵AD ∥BE , ∴AD CE =DF FC , ∴DF =FC =32,设DN =x ,则AN =NF =x +32.在Rt △ADN 中,AD 2+DN 2=AN 2, ∴32+x 2=(x +32)2,∴x =94.∴DN =94,AN =154,sin ∠DAB 1=DN AN =35,综上:当点E 在线段BC 上时,sin ∠DAB 1=513,当点E 在BC 的延长线上时,sin ∠DAB 1=35;(3)若点E 在线段BC 上,y =9x2x +2,x 的取值范围为0<x <1; 若点E 在边BC 的延长线上,y =9x -92x,x 的取值范围为1<x .★10.如图所示,在Rt △ABC 中,∠A =90°,AB =6,AC =8,D 、E 分别是边AB ,AC 的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ ⊥BC 于点Q ,过点Q 作QR ∥BA 交AC 于R ,当点Q 与点C 重合时,点P 停止运动,设BQ =x ,QR =y .(1)填空:BC =________,sin B =________,点D 到BC 的距离DH =________; (2)求y 关于x 的函数关系式(不要求写出自变量的取值范围);(3)是否存在点P ,使△PQR 为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.第10题图 备用图解:(1)10;45;125;【解法提示】在Rt △ABC 中,AB =6,AC =8,∠A =90°, ∴由勾股定理得BC =AB 2+AC 2=10;sin B =AC BC =810=45;∵D 是AB 的中点,∴BD =3, ∴DH =BD ·sin B =3×45=125.(2)∵QR ∥AB , ∴△CQR ∽△CBA ,∴QR BA =CQCB ,即10610y x -=, 解得y =-35x +6;(3)存在,分三种情况:①当PQ =PR 时,如解图①,过点P 作P M ⊥QR 于点M ,则QM =RM ,第10题解图①∵∠1+∠2=90°,∠C +∠2=90°, ∴∠1=∠C ,∴cos ∠1=cos C =810=45,∴QM QP =45, ∴12(-35x +6)125=45,∴x =185;②当PQ =RQ 时,如解图②,-35x +6=125,∴x =6;第10题解图②③当PR =QR 时,如解图③,则R 为PQ 中垂线上的点,于是点R 为EC 的中点,第10题解图③∴CR =12CE =14AC =2,∵tan C =QR CR =BA CA =68,即-35x +62=68,∴x =152,综上所述,当x 为185或6或152时,△PQR 为等腰三角形.。
1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例1. 已知:如图1求证:DE = 分析:由∆ABC 连结CD ,易得CD = 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆A D E CDFDE DF说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线。
显然,在等腰直角三角形中,更应该连结CD ,因为CD 既是斜边上的中线,又是底边上的中线。
本题亦可延长ED 到G ,使DG =DE ,连结BG ,证∆EFG 是等腰直角三角形。
有兴趣的同学不妨一试。
例2. 已知:如图2所示,AB =CD ,AD =BC ,AE =CF 。
求证:∠E =∠FAB CD BC AD AC CA ABC CDA SSS B DAB CD AE CF BE DF===∴≅∴∠=∠==∴=,,,∆∆()在∆BCE 和∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意:(1)制造的全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到的两个全等三角形。
2、证明直线平行或垂直在两条直线的位置关系中,平行与垂直是两种特殊的位置。
证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明。
证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。
初一几何题题库初一的几何学习,是同学们打开数学世界新大门的重要一步。
为了帮助大家更好地掌握这部分知识,下面为大家整理了一系列具有代表性的初一几何题。
一、直线、射线和线段相关题目1、已知线段 AB 的长度为 10cm,点 C 在线段 AB 上,且 AC =6cm,求线段 BC 的长度。
这道题主要考查线段的加减法。
因为点 C 在线段 AB 上,所以 BC= AB AC = 10 6 = 4cm。
2、已知直线 l 上有 A、B、C 三点,其中 AB = 5cm,BC = 3cm,求 AC 的长度。
这道题需要分两种情况讨论。
当点 C 在线段 AB 上时,AC = AB BC = 5 3 = 2cm;当点 C 在线段 AB 的延长线上时,AC = AB + BC = 5 + 3 = 8cm。
二、角的相关题目1、已知∠AOB = 60°,∠BOC = 20°,求∠AOC 的度数。
这道题同样需要分情况讨论。
当 OC 在∠AOB 内部时,∠AOC =∠AOB ∠BOC = 60° 20°= 40°;当 OC 在∠AOB 外部时,∠AOC=∠AOB +∠BOC = 60°+ 20°= 80°。
2、如图,∠AOC 和∠BOD 都是直角,∠COD = 30°,求∠AOB的度数。
因为∠AOC =∠BOD = 90°,又因为∠COD = 30°,所以∠AOB=∠AOC +∠BOD ∠COD = 90°+ 90° 30°= 150°。
三、平行线相关题目1、如图,直线 a∥b,∠1 = 50°,求∠2 的度数。
因为 a∥b,所以∠1 =∠3(同位角相等),又因为∠2 +∠3 =180°(邻补角互补),所以∠2 = 180° 50°= 130°。
七年级数学几何图形初步难题精选(含解析答案)1.美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部分困成一个立体模型,然后放在桌而上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是D2.《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它奠左了现代数学的基础•它是下列哪位数学家的著作()A.欧几里得B.杨辉C.费马D.刘徽 3•如图,在直角梯形ABCD中,AD//BC, ZABC=90。
,丄DC, BD=DC, CE 平分/BCD,交 AB 于点E,交BD于点H, EN//DC交BD于点、N,下列结论:①BH=DH;②CH=(A/2+1)EH:③护廻=学.其中正确的是()S QH ECA __________ DA.①②③B.只有②(③C.只有②D.只有③4•如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个而涂有颜色,下列图形中,是该几何体的表而展开图的是()6•图1所示的正方体木块棱长为6 cm 船其相邻三个而的对角线(图中虚线)剪掉一角,得到如图2的几何 体,一只蚂蚁沿着图2的几何体表而从顶点A 爬行到顶点B 的最短距离为 _________ c m.&如图,n+1个上底、两腰长皆为1, P 阿“凡而积为» 四边形PN 斟汕的而积为亠,…,四边形屮的面积记为» 通过逐一计9•有一张矩形纸片ABCD.按下而步骤进行折叠:第一步:如图①,将矩形纸片ABCD 折叠,使点B, D 重合,点C 落在点C ,处,得折痕EF :第二步:如图②,将五边形AEFCD 折叠,使CF 重合,得折痕DG,再打开:第三步:如图③,进一步折叠,使AE, CF 均落在DG 上,点A, U 落在点/V 处,点E, F 落在点E 处, 得折痕MN, QP.n> 下底长为2的等腰梯形的下底均在同一直线上,设四边形A. B. D.A. AB. BC.CD. D图1图3图2 7•如图1罔2,图3,用一种大小相等的正多边形密铺成一个“环二我们称之为环形密铺,但图4,图5不是我(1) 请写出图①中一组相等的线段 _________ (写出一组即可);(2) 若这样折岀的五边形DMNPQ(如图③)恰好是一个正五边形,当AB=a, AD=b, DM=m 时,有下列 结论: (X)a 2—b 2=2cih tan 18°; (2)w=-/a 2 + b 2 tan 18°;③b=m+a tan 18°: ④b=^n+m tan 18°其中,正确结论的序号是 _____ (把你认为正确结论的序号都填上).■10.—个圆柱形的蛋糕,将它截三刀,能截出六块、七块或八块吗?若能,画出示意图:若不能,请说 明理由.11•图①的正方体切去一块,得到图②迴的几何体.① ② ③ ④ ⑤(1)所得几何体各有多少个而?多少条棱?多少个顶点? (2)举例说明其他形状的几何体也切去一块,所得到的几何体的而数、棱数和顶点数各是多少? (3) 若而数记为「棱数记为e,顶点数记为-则f f v f e 应满足什么关系?12.有一副直角三角板,其中一个三角板的内角是45。
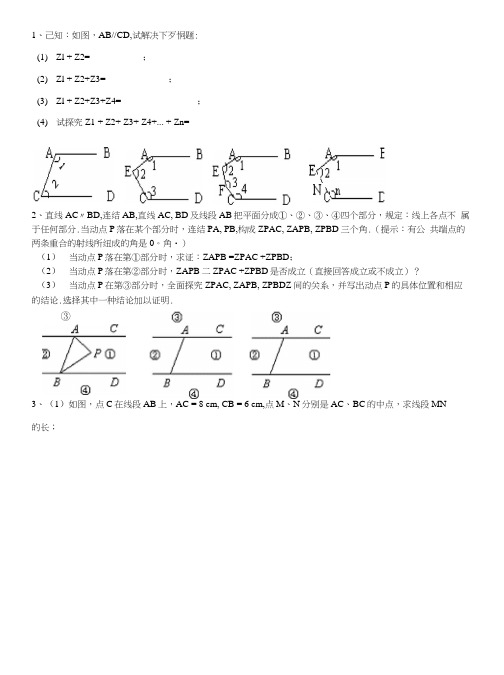
1、已知:如图,AB//CD,试解决下列问题:
(1)∠1+∠2=___ ___;
(2)∠1+∠2+∠3=___ __;
(3)∠1+∠2+∠3+∠4=_ __ __;
(4)试探究∠1+∠2+∠3+∠4+…+∠n=;
2、直线AC∥BD,连结AB,直线AC,BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角.)
(1)当动点P落在第①部分时,求证:∠APB =∠PAC +∠PBD;
(2)当动点P落在第②部分时,∠APB =∠PAC +∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
3、(1)如图,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点,求线段MN
的长;
M N
C
A B
(2)若C 为线段AB 上任一点,满足AC + CB = a cm ,其它条件不变,你能猜想MN 的长度吗?并说明理由。
(3)若C 在线段AB 的延长线上,且满足AC BC = b cm ,M 、N 分别为AC 、BC 的中点,你能猜想MN 的长度吗?请画出图形,并说明理由。
4、
5、如图,一个点从数轴上的原点开始,先向左移动2cm 到达A 点,再向左移动3cm 到达B 点,然后向右移动9cm 到达C 点.
(1)用1个单位长度表示1cm ,请你在数轴上表示出A 、B 、C 三点的位置;
(2)把点C 到点A 的距离记为CA ,则CA= _________ cm .
(3)若点B 以每秒2cm 的速度向左移动,同时A 、C 点分别以每秒1cm 、4cm 的速度向右移动.设移动时间为t 秒,试探索:CA ﹣AB 的值是否会随着t 的变化而改变?请说明理由.
A B C M N A B C M N
6、。