用尺规作三角形

尺规作三角形的方法
嘿，你知道不？尺规作三角形那可老神奇啦！先来说说步骤哈。

首先确定一条线段当三角形的一边，这就好比盖房子先打下一根坚实的柱子。

然后用圆规以线段的一个端点为圆心，任意长度为半径画弧。

接着以另一个端点为圆心，同样长度为半径画弧，两弧交点一确定，连接起来，这三角形的另外两条边不就有啦？这过程中，可得小心圆规别扎到手哇！那可是疼得要命呢！
说到安全性和稳定性，只要你操作得当，那是稳稳当当的。

圆规和直尺又不是啥危险物品，不像刀子啥的让人提心吊胆。

只要你不瞎折腾，能出啥事儿呢？
这尺规作三角形有啥用呢？在学习几何的时候，那可太有用啦！可以帮助你更好地理解三角形的性质。

就好比你有了一把神奇的钥匙，能打开几何世界的大门。

它的优势也不少呢，简单易操作，不用啥高科技设备。

你想想，要是没有圆规和直尺，那可咋整？
给你举个实际案例哈。

老师在课堂上让同学们用尺规作三角形，大家都做得可认真啦！不一会儿，一个个漂亮的三角形就出现在纸上。

这效果，那叫一个棒！
尺规作三角形就是这么牛！简单又实用，安全又稳定。

你还等啥，赶紧试试吧！。

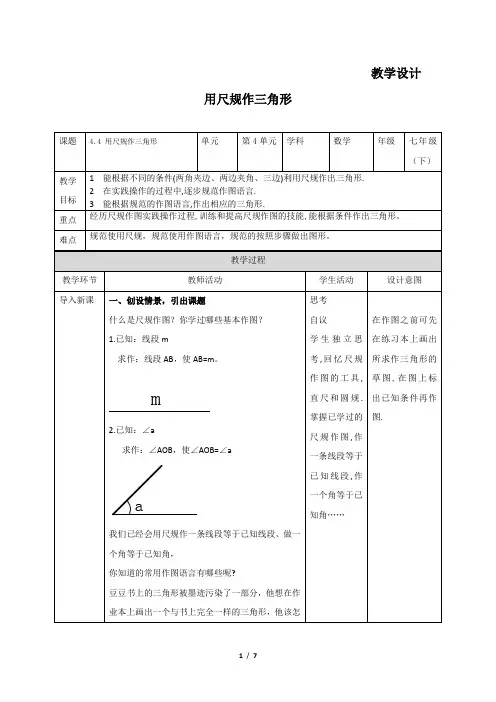
教学设计用尺规作三角形么办？边和角是三角形的基本元素，那么你能利用尺规做一个三角形与已知三角形全等吗？【做一做】已知三角形的两边及其夹角，求作这个三角形．已知：线段a, c, ∠α.a c求作：△ABC，使BC=a AB=c, ∠ABC=∠α.作法：（1）作一条线段BC=a；（2）以B为顶点，以BC为一边作∠DBC=∠α；（3）在射线BD上截取线段BA=c；（4）连接AC，△ABC就是所求作的三角形.将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？回顾刚才作三角形的顺序还有没有其他的作法？还有没有其他的作法？作法：____________________________________________ _____________________________________________________________________ ________________________________________________________________________ ____________________________将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？二、提炼概念利用尺规作三角形，有三种基本类型：(1)已知三角形的两边及其夹角，求作符合要求的三角形，其作图依据是“____SAS____”；(2)已知三角形的两角及其夹边，求作符合要求的三角形，其作图依据是“____ASA____”；(3)已知三角形的三边，求作符合要求的三角形，其作图依据是“___SSS_____”．三、典例精讲例已知三角形的两角及其夹边，求作这个三角形. 已知：∠α，∠β，线段c(如图).αβ求作：△ABC，使∠A＝∠α，∠B＝∠β，AB＝c.请按照给出的作法作出相应的图形.作法与示范(1)作∠DAF=∠α；(2)在射线AF上截取线段AB=c；(3)以B为顶点，以BA为一边，作∠ABE=∠β，BE 交AD于点C．△ABC就是所求作的三角形．【小组讨论】将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？试一试.已知三角形的三条边，求作这个三角形.已知：线段a，b，c (如图).a b c求作：△ABC，使AB＝c，AC＝b，BC＝a. (1)请写出作法并作出相应的图形.作法与示范(1)作一条线段BC=a；(2)分别以B，C为圆心，以c，b为半径画弧，两弧交于A点；(3)连接AB,AC,△ABC就是所求作的三角形.【小组讨论】将你所作的三角形与同伴作出的三角形进行比较，它们全等吗？为什么？课堂检测四、巩固训练1.利用基本作图方法，不能作出唯一三角形的是(C)A．已知两边及其夹角B．已知两角及其夹边C．已知两边及一边的对角D．已知三边2.如图，用尺规作出∠OBF＝∠AOB，作图痕迹弧线MN是（）A．以点B为圆心，OD长为半径的弧B．以点B为圆心，DC长为半径的弧C．以点E为圆心，OD长为半径的弧D．以点E为圆心，DC长为半径的弧D3.你能用尺规作一个直角三角形，使其两条直角边分别等于已知线段a，b吗？并写出作法。

用尺规作图画三角形的方法
三角形是一种常见的几何图形，它可以用来表达各种概念，可以用来构建形状、结构和物理实体，也可以被用来展示统计数据。

用尺规作图画三角形的方法可以用来创建几何图形，并且可以判断几何图形的性质，以及三角形的一些属性。

用尺规画三角形可以分为三步：
1.使用尺规以中心点为中心画一个圆，圆的半径就确定了三角形的高度，然后以圆为中心画出三条射线，假设射线A、B、C，A-C为60度，B-A为90度，C-B为90度，就已经完成了三角形的基本形状。

2.然后使用尺规根据基准线给每条射线依次画出三条边，射线A-B-C的边长分别为a、b、c，可以用任意一条边的长度表示三角形的边平行四边形的长度，例如a=5cm，b=3cm，c=4cm，那么三角形的面积就等于a*b/2，也就是5*3/2=7.5cm。

3.接下来就是要判断三角形的形状，如果a=b=c，则为等边三角形，如果a=b≠c，则为等腰三角形，如果a≠b≠c，则为一般三角形。

用尺规作图画三角形的方法很容易操作，先画一个圆，再画三条射线，然后再以基准线给每条射线依次画出三条边，并且判断出三角形的形状，就可以得出其边长及面积了。

加入现在要求我们在一个长方形的基准线上画一个三角形，那么我们首先要做的就是把长方形分成六段，每段的边长不一定相等，接着在六段上画出相应的射线，然后下一步就是给每个射线依次画出三条边，可以用任意一条边的长度表示三角形的边长，最后根据三个边
的长度来判断出三角形的形状。

以上就是用尺规作图画三角形的方法，只要熟悉其原理以及相应的步骤，就可以很快的将相应的几何图形画出来，掌握了这个方法，就可以轻松的创建几何图形，判断几何图形的性质，从而更好的展示统计数据。

尺规作全等三角形的方法嘿，咱今儿个就来讲讲尺规作全等三角形的方法哟！你想想看，三角形那可是几何世界里的大主角之一呀！全等三角形就像是一对双胞胎，长得一模一样呢。

那怎么用尺规把它们给作出来呢？先来说说第一种方法哈。

咱先画一条线段，这就好比是给三角形打底呀。

然后呢，用圆规以这条线段的一个端点为圆心，以另外一个已知长度为半径画弧，哎呀呀，这弧画出来可漂亮啦，就像一道弯弯的彩虹。

再在另一个端点也这么来一下，这两条弧的交点一确定，嘿，三角形的一个角不就出来啦！接下来顺着把其他边一连接，一个全等三角形就搞定啦，是不是很神奇呀！还有一种方法也很有意思呢。

咱先确定一个角，就像给三角形安个漂亮的帽子。

然后用圆规在这个角的两边上分别截取相等的线段，这就好比给帽子配上合适的飘带呀。

再把这两个截点连接起来，哇塞，又一个全等三角形闪亮登场啦！这尺规作全等三角形呀，就像是在玩一个神奇的拼图游戏。

你得细心，得耐心，还得有点小技巧呢。

就好像你要给三角形穿上最合适的衣服，每一个步骤都不能马虎。

你说要是没掌握好方法，那作出来的三角形可就不“全等”啦，那不就闹笑话了嘛！所以呀，咱得好好琢磨琢磨这其中的门道。

你再想想，生活中不也有很多像这样需要我们精心去“制作”的东西吗？就像我们对待一件心爱的物品，要用心去呵护，去打造。

尺规作全等三角形也是这样，需要我们用认真的态度去对待它。

总之呢，尺规作全等三角形的方法可多着呢，每一种都有它的独特之处。

只要我们用心去学，去练，就一定能掌握好这门有趣的技能。

到时候呀，我们就能像个小魔法师一样，用尺规变出一个个漂亮的全等三角形啦！怎么样，是不是迫不及待想去试试啦？那就赶紧行动起来吧！。