奥数专题:棋盘上能放多少麦粒?
- 格式:pptx
- 大小:2.05 MB
- 文档页数:15

24道经典名题1.不说话的学术报告1903年10月,在美国纽约的一次数学学术会议上,请科尔教授作学术报告。
他走到黑板前,没说话,用粉笔写出2^67-1,这个数是合数而不是质数。
接着他又写出两组数字,用竖式连乘,两种计算结果相同。
回到座位上,全体会员以暴风雨般的掌声表示祝贺。
证明了2自乘67次再减去1,这个数是合数,而不是两百年一直被人怀疑的质数。
有人问他论证这个问题,用了多长时间,他说:“三年内的全部星期天”。
请你很快回答出他至少用了多少天?2.国王的重赏传说,印度的舍罕国王打算重赏国际象棋的发明人——大臣西萨·班·达依尔。
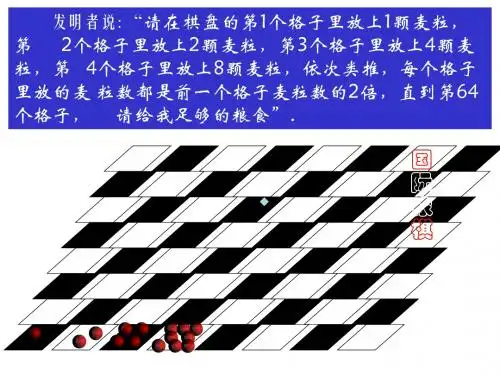
这位聪明的大臣跪在国王面敢说:“陛下,请你在这张棋盘的第一个小格内,赏给我一粒麦子,在第二个小格内给两粒,在第三个小格内给四粒,照这样下去,每一小格内都比前一小格加一倍。
陛下啊,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧?”国王说:“你的要求不高,会如愿以偿的”。
说着,他下令把一袋麦子拿到宝座前,计算麦粒的工作开始了。
……还没到第二十小格,袋子已经空了,一袋又一袋的麦子被扛到国王面前来。
但是,麦粒数一格接一格地增长得那样迅速,很快看出,即使拿出来全印度的粮食,国王也兑现不了他对象棋发明人许下的语言。
算算看,国王应给象棋发明人多少粒麦子?3.王子的数学题传说从前有一位王子,有一天,他把几位妹妹召集起来,出了一道数学题考她们。
题目是:我有金、银两个手饰箱,箱内分别装自若干件手饰,如果把金箱中25%的手饰送给第一个算对这个题目的人,把银箱中20%的手饰送给第二个算对这个题目的人。
然后我再从金箱中拿出5件送给第三个算对这个题目的人,再从银箱中拿出4件送给第四个算对这个题目的人,最后我金箱中剩下的比分掉的多10件手饰,银箱中剩下的与分掉的比是2∶1,请问谁能算出我的金箱、银箱中原来各有多少件手饰?4.公主出题古时候,传说捷克的公主柳布莎出过这样一道有趣的题:“一只篮子中有若干李子,取它的一半又一个给第一个人,再取其余一半又一个给第二人,又取最后所余的一半又三个给第三个人,那么篮内的李子就没有剩余,篮中原有李子多少个?”5.哥德巴赫猜想哥德巴赫是二百多年前德国的数学家。

按上图棋盘中目前的局势,双方的将(帅)均无法移动,双方的士(仕)也无法移动,底炮也不能在横线底线兵(卒)只能横向移动。
谁先移动底线兵移出,从而出现移兵(卒)方自己必输的态势。
因而只有底炮、中炮和边卒(兵)可以在纵线上移动,兵(卒)只能8步。
实际上现在的问题是:乙先走,轮流走完这三对子的我们把乙的获胜策略及甲的各种走法列于下表(其中,甲、…”分别表示中路炮进2步、相位炮进7格,则第7列只有第8格可以放后,那么第列第1格,如下图。
著名的数学家高斯曾经给出76种不同解法,条线(如下左图),在棋盘上组成许多大小不同的正方形,那么,在棋盘中可以找到的方格图,共有324个小方格,391个交叉点。
本例属于图形计数问题,只要做到有序思考,结合以前学习的计数的有关知识,应该有较多解法。
:我们把小正方形放在大正方形的左上角,则小正方形的右边线与大正方形的第则又可出现一个小正方形,顺次向右移动个小正方形。
同样,将左上角小正方形再每次向下移动一格,个小正方形。
现在的问题是,能否经若干次翻动,使得剩下的这34个1×2的方格正面向上。
.下图是一盘未下完的中国象棋残局,各子走法必须遵照中国象棋的规则,若现在轮到黑方走棋,请你判断这黑方只有两个“炮”可以前进,其他棋子受到制约都不能移动。
红方也只有两个炮可以移动,但由于两红炮与两黑炮间隔相同,那么不论黑炮如何移动,红方只要在保持两红炮与两黑炮间隔相同的前提下,相应移动红炮,最终黑方将被逼得无棋可走而失败。
因此利用中国象棋比赛规则,红方有获胜的策略。
.在一个国际象棋的棋盘上,规定有一个棋子可在方格之间走动,每步走一方格,或水平方向或垂直方向(不个“后”能够控制整个棋盘。
个“后”控制整个棋盘。
实际上,在国际象棋棋盘上,至少要放5个“后”才能控制整个棋盘,少于的放法并不只有上面这一种,请你试一试其它的放法。
.在国际象棋棋盘上,最少要用多少个下面的“L”形(如下图)当我们把类),总之一个形骨牌将盖住个。

国际象棋棋盘上放⽶粒国际象棋棋盘上放⽶粒,数⽬是天数的平⽅。
这个关于关于平⽅的故事⼤家帮忙回忆⼀下第⼀个:我朋友的记忆⼀国家被围困,⼀能⼈帮国王让敌⼈退兵。
国王提出奖励,他说你每天给我在国际象棋棋盘上⽅⼀些⽶粒,数⽬是天数的平⽅,直到棋盘的格⼦被放满。
第⼀个格放1粒,第2个格放2的平⽅2x2=4粒。
第3个格放3的平⽅3x3=9粒。
以此类推。
第⼆个:我的记忆是2个商⼈和国王做交易。
他们说我每天给你10万两黄⾦,你每天给我在国际象棋棋盘的格⼦上⽅些⽶粒,数⽬是2的当天天数次⽅。
就是说第⼀天21(代表2的⼀次⽅)是2粒;第2天22是4粒;第3天23是8粒,以此类推。
该故事应该是什么版本?⼤家都说说⾃⼰的记忆或知道⽐较详细和确凿的版本吧。
还有,就是我很想知道这种交易到最后能收⼊多少粒⽶。
我觉得第⼀个开始肯定⽐第⼆个快。
但第2个都后⾯就⽐第1个快多了吧。
有⼈能否写个程序让我们能⽅便地查出⽅法⼀和⼆任意⼀天该天是多少粒⽶,该天总共收⼊了多少粒⽶。
算出多少粒⽶,下⼀步就是⼤家算算多少粒⽶是⼀⽄。
我们算算收⼊了多少⽄。
wow~好多⼤⽶啊~~!:)这个是从⼀个地⽅复制过来的.因为看了⼀本书叫<⾃动百万富翁>,⾥⾯讲到了复利的神奇,这可以作为⼀个左证的.这也激起了我理财的信念.只是去银⾏问了下,并不理想,哎!现在真的很想多赚些钱,但不知道怎么去赚?这段时间⾥,看了⼀些这⽅⾯的书籍,也了解了⼀些股票和基⾦⽅⾯的事情当然只限于粗浅的⽅⾯.现在的情形也不是很乐观的.在2个朋友从盘锦⾛了之后,⽇⼦变得更加的平淡与⽆味.真的不知道在这上⾯说点什么也是应该的.胡乱的拼凑,只有这么说,也只能这么做了.。

小学数学数学故事宰相的麦子
宰相的麦子
相传古代印度国王舍罕要褒赏他的聪明能干的宰相达依尔(国际象棋发明者),问他需要什么达依尔回答说:“国王只要在国际象棋棋盘的棋盘第一格子上放一粒麦子,第二个格子上放二粒,第三个格子里放四粒,以后按此比例每一格加一倍,一直放到第64格(国际像棋盘是8*8=64格),我就感恩不尽,其它我什么也不要了。
”国王想:“这有多少!还不容易!”让人扛来一袋小麦,但不到一会儿全用没了,再来一袋很快又没有了,结果全印度的粮食都用完还不够。
国王奇怪,怎么也算不清这笔账。
现在我们用电子计算机来算一下。
求需要多少体积的小麦:1立方米约有1.42*10^8(10的8次方)颗。

棋盘上的数学同学们,听说过国际象棋吗?国际象棋起源于印度,它的棋盘是正方形的,由8行8列颜色一深一浅、交错排列的64个小方格组成(如右图)。
国际象棋和它的发明人——印度人西萨·班·达依尔还有一段有趣的故事呢!读一读棋盘上的麦粒西萨·班·达依尔是古印度舍罕王的宰相。
一次,舍罕王觉得自己王宫里的所有游戏都玩腻了,于是,他下令说,如果谁能发明一种使他开心的游戏,谁就将得到很多的赏赐。
达依尔知道了这个消息,便把自己发明的国际象棋奉献给了舍罕王。
舍罕王觉得这种游戏很有趣,非常高兴,就打算重赏达依尔。
舍罕王问达依尔:“你的发明给我带来了很多欢乐,你要什么赏赐,我就给你什么赏赐!”达依尔不慌不忙地说:“陛下,请你在这张棋盘的第一个小格里,赏给我1粒麦子,在第二格里赏2粒,照这样下去,每一格里的麦子都比前一格加一倍。
直到把棋盘的64个格子都摆满,您把这些麦子赏给我就够了。
”舍罕王对达依尔的要求既奇怪,又高兴:“达依尔,你的要求也太少了,我会让你满足的!”于是舍罕王命令侍臣,把这些麦子如数付给达依尔。
数麦粒的工作开始了,第一格放1粒,第二格放2粒,第三格放4粒,可还没放到20格,一袋的麦子已经空了。
接着一袋又一袋的麦子被扛上来,一袋又一袋的麦子被数尽,依旧无法达到达依尔的要求。
而舍罕王也惊得目瞪口呆,因为他发现:达依尔的要求竟是无法兑现的!??做一做让我们一起来动手做一做吧!这是为什么呢?图画不好,本意想画成两次对折状。
我们研究所要借助的材料是一张普通的白 纸。
如图,对折1次,纸有几层?对折2次, 纸有几层? 对折3次呢?1. 随着对折次数的不断增加,你发现纸的层数变化有什么规律吗?2. 这些层数与2又有什么特殊的联系呢?○ 小 贴 士 ○4可以写成2×2,两个2相乘可以在2 的右上角写一个2,即22,读作2的平方,或 2的2次方。
通常,几个2连乘,就可以在2的右上角写 几,读的时候就读作2的几次方。

棋盘麦粒问题,也叫“麦子数问题”,是一个古老的数学问题,传说是古印度一位聪明的大臣向国王提出的。
问题的具体描述是:在一个棋盘上放入一粒麦子,接着在第二格里放入两粒麦子,第三格里放入四粒麦子,第四格里放入八粒麦子……如此类推,直到放满64 格,问最后棋盘上共放了多少粒麦子?
这个问题可以用指数函数和求和公式来计算。
首先,第n 格放的麦子数量为2^(n-1)。
也就是说,第一格放的是2^(1-1)=1 粒麦子,第二格放的是2^(2-1)=2 粒麦子,第三格放的是2^(3-1)=4 粒麦子,以此类推。
其次,总共放的麦子数就是每一格放的麦子数之和。
因此,可以使用求和公式来计算:
总共放的麦子数= 1 + 2 + 4 + 8 + ... + 2^(n-1)
其中n=64,因为棋盘共有64 格。
这是一个等比数列,公比为2。
因此,可以使用等比数列求和公式来计算:
总共放的麦子数= (1 - 2^n) / (1 - 2) = 2^n - 1
将n=64 代入公式,得到:
总共放的麦子数= 2^64 - 1 = 18,446,744,073,709,551,615
因此,如果在棋盘上按照上述规律放麦子,最后总共会放下18,446,744,073,709,551,615 粒麦子。
这个数字非常大,相当于全球人口数量的数倍。

棋盘上的麦粒问题(数学文化)(学习版)编制人:__________________审核人:__________________审批人:__________________编制学校:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的教学资料,如数学资料、英语资料、语文资料、历史资料、地理资料、生物资料、物理资料、政治资料、美术资料、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of teaching materials, such as mathematics materials, English materials, Chinese materials, historical materials, geographic materials, biological materials, physical materials, political materials, art materials, other materials, etc. Please pay attention to the data format and writing method!棋盘上的麦粒问题(数学文化)学习数学是为了探索宇宙的奥秘。

棋盘麦粒问题
闲暇时间,给学生听了个数学家的故事,讲的是欧拉的故事,里面提到了棋盘麦粒问题。
故事讲完了,我在群里发信息,到底是多少小麦?真的有那么多吗?
然后我一个一个地发加法竖式,
……
一直发到8192.严格来说,过万的数,学生还没学过。
8192粒小麦了,
其实,麦子很小,8192粒也没多少。
1000粒小麦大约40克,8192粒大约250克,放到矿泉水瓶里,半瓶。
不过没关系,我们刚写到这儿
啊!
再往下加就过万了……
然后,我就不再发竖式了。
等了一会儿,我说,想知道最后有多少吗?想知道就别等着我。
然后,就有学生往下算起来了。
我说,老师,就像阶梯,你们可以踩上去,走到更远的地方……
下课过了一会儿,已经有十几位数出现了。
我说,这个其实,工作量很大。
我估计一直不停的话,得算五六个小时。
要有心理准备。
所以,吃饭,睡觉,别耽误,劳逸结合。


棋盘上的麦粒(印度)古时候,印度有个国王很爱玩。
一天,他对大臣们说,希望得到一种玩不腻的玩意儿,谁能贡献给他,将有重赏。
不久,有个聪明的大臣向他献上一种棋子,棋盘上有64个格子,棋子上刻着“皇帝”、“皇后”、“车”、“马”、“炮”等字。
下这种棋子,是玩一种变化无穷的游戏,确实让人百玩不厌。
国王就对那个聪明的大臣说:“我要重赏你。
说吧,你要什么,我都能满足你。
”那个大臣说:“我只要些麦粒。
”“麦粒?哈,你要多少呢?”“国王陛下,你在第一格棋盘上放1粒,第二格上放2粒,第三格上放4粒,第四格上放8粒……照这样放下去,把64格棋盘都放满就行了。
”国王想:这能要多少呢?最多几百斤吧。
小意思,就对管粮食的大臣说:“你去拿几麻袋的麦子赏给他吧。
”管粮食的大臣计算了一下,忽然大惊失色,忙向国王报告道:“照这样的计算,把我们全国所有的粮食全给他,还差得远呢!”说完把计算题列给国王看——322463++++21+22=18,446,774,073,709,551,615(颗麦粒)1立方米麦粒大约有1500万粒,那么照这样计算,得给那位大臣12000亿立方米,这些麦子比全世界2000年生产的麦子的总和还多。
国王脸色铁青,忙问管粮食的大臣说:“那怎么办?要是给他吧,我将永远欠他的债;要是不给他吧,我不就成了说话不算数的小人了吗?请你给想想办法吧。
”管粮食的大臣想了想说:“办法只有一个,你应该说话算话,才能让全国人民相信您是位好国王。
”“可是我没有那么多的麦子呀。
”“请您下令打开粮仓,然后请献棋的大臣自己一粒一粒地数出那些麦子就行了。
”。
【知识与方法】有序的排成一列的数,称为数列。
一些数列中数的排列是很有规律的,通过对这些规律的学习以及推导,我们可以进行相关的计算。
在数列中,所有的排列的数都称为“项”,排在首位的数叫“首项”,一般用字母a1表示;排在第n位的一般用a n ;数列里面数的个数我们说项数。
一般的,在一个有限数列里面(项数确定),我们把最后的那个项叫做末项。
例1:已知数列1、4、7、10、13、16、19、22、25……试求出第2008项,即a2008=?分析:这是一个等差数列。
很明显,我们能够发现后一项总比前一项多3。
数列有这样的规律:a2=a1+3, a3=a2+3, a4=a3+3……即每相邻的两个项之间的差距都是 3.我们把这个差叫做“公差”,习惯上我们用d表示。
如果我们每一项都用a1与d来表示,我们可以有以下的规律:a2=a1+d,a3=a2+d=a1+2d,a4=a3+d=a1+3d,……a n=a n-1+d=a1+(n-1)d……①①式我们通常说成是等差数列的通项公式,就是由a1来表示数列中其它项a n的表示公式。
根据通项公式我们可以很快地求出等差数列中任何一项是多少。
解:根据 an =a1+(n-1)× d已知原数列 a1=1,d=3,n=2008,所以 a2008=1+(2008-1)×3=6022习题1:已知数列2、4、6、8、10……,试求出第2010项是多少?习题2:已知数列1、3、5、7、9……,试求出第2009项是多少?例2:已知一个数列,相邻的两项的差为4,且后一项比前一项大。
第10项为41,试写出这个等差数列。
习题3:一个等差数列,相邻的两项差为3,第10项为35,求这个等差数列。
习题4:一个等差数列,前项比后项大5,第11项为47,求这个等差数列的第1000项是多少?例3:已知一个数列,1、2、3、5、8、13、21……,求它的第20项。
分析:这个数列是一种十分有名的数列,叫做“斐波那契数列”。
棋盘上的麦粒古时候,印度有个国王很爱玩.一天,他对大臣们说,希望得到一种玩不腻的玩意儿,谁能贡献给他,将有重赏.不久,有个聪明的大臣向他献上一种棋子,棋盘上有64个格子,棋子上刻着“皇帝”、“皇后”、“车”、“马”、“炮”等字.下这种棋子,是玩一种变化无穷的游戏,确实让人百玩不厌.国王就对那个聪明的大臣说:“我要重赏你.说吧,你要什么,我都能满足你.”那个大臣说:“我只要些麦粒.”“麦粒?哈,你要多少呢?”“国王陛下,你在第一格棋盘上放1粒,第二格上放2粒,第三格上放4粒,第四格上放8粒……照这样放下去,把64格棋盘都放满就行了.”国王想:这能要多少呢?最多几百斤吧.小意思,就对管粮食的大臣说:“你去拿几麻袋的麦子赏给他吧.”管粮食的大臣计算了一下,忽然大惊失色,忙向国王报告道:“照这样的计算,把我们全国所有的粮食全给他,还差得远呢!”说完把计算题列给国王看,得数等于18,446,774,073,709,551,615(颗麦粒)1立方米麦粒大约有1500万粒,那么照这样计算,得给那位大臣12000亿立方米,这些麦子比全世界2000年生产的麦子的总和还多.国王脸色铁青,忙问管粮食的大臣说:“那怎么办?要是给他吧,我将永远欠他的债;要是不给他吧,我不就成了说话不算数的小人了吗?请你给想想办法吧.”管粮食的大臣想了想说:“办法只有一个,你应该说话算话,才能让全国人民相信您是位好国王.”“可是我没有那么多的麦子呀.”“请您下令打开粮仓,然后请献棋的大臣自己一粒一粒地数出那些麦子就行了.“那么要数多长时间呢?”管粮食的大臣计算了一下说:“假设每秒钟能数2粒麦子的话,每天他数上12小时,是43200多秒,数上10年才能数出20立方米,要数完那个数目将需要2900亿年呢.他能活多少年呢?再说枯燥的生活能折磨人,他这样下去岂不要短寿?因此我想,他的本意并不是想要得到那些不可能得到的麦粒,他只是试试我国有没有比他更聪明的人罢了.”国王大喜,夸奖道:“看来,至少你比他还要聪明呢!智慧人物治理国家,国家才能兴旺发达.我决定提拔你俩当我的左右宰相!”启示:这则故事让我们明白了滴水穿石的启示,积小成多,即使一滴雨水,也能成就大海.再弱小的事物当初总是被世人讥笑,但是只要它不断积聚力量,总有一天会强大的.而从弱小变为强大的过程也许很难被人察觉,当你能看见它时,它一定到了一个令人难以置信的地步.因此,我们平时应该从小事做起、从身边事做起,踏踏实实,争取每天都有新进步,这样积少成多,将来就会有大成功.麦粒的颗数求:1+2+22+23+24+…+263的值.如何求它的值呢?1+2+22+23+24+25+26+27+28+…+262+263=21-1+22-1+23-1+…+263-1+264-1=1×(1−264)1−2=264-1=18446744073709551615。
龙源期刊网 棋盘上的麦子作者:来源:《小天使·五年级数学人教版》2010年第09期2000多年前的印度,有一位叫舍罕王的国王,酷爱玩游戏。
有一天,舍罕王觉得自己王宫里的所有游戏都玩腻了,于是,他下令说,如果谁能发明一种使他开心的游戏,谁就能得到很多的赏赐。
这时,舍罕王的宰相达依尔知道了这个消息,便把自己发明的国际象棋奉献给了舍罕王。
舍罕王觉得这种游戏很有趣,非常高兴,就打算重赏达依尔。
舍罕王问达依尔:“你的发明给我带来了很多快乐,你要什么赏赐,我就给你什么赏赐!”达依尔故作惶恐地说:“陛下,请您在这张棋盘的第一个小格里,赏给我1粒麦子,在第二格里赏2粒,照这样下去,每一格里的麦子都比前一格加一倍。
直到把棋盘的64个格子都摆满,您把这些麦子赏给我就够了。
”舍罕王对达依尔的要求既奇怪,又高兴:“达依尔,你的要求也太少了,我会让你满足的!”于是舍罕王命令侍臣,把这些麦子如数付给达依尔。
数麦粒的工作开始了,第一格放1粒,第二格放2粒,第三格放4粒……可还没放到第20格,一袋麦子已经空了。
接着,一袋又一袋的麦子被扛来,一袋又一袋的麦子被数尽,依旧无法达到达依尔的要求,把64个棋盘格填满。
实际上,这时棋盘上已经放不下这些麦子了。
而舍罕王也惊得目瞪口呆,因为他发现:达依尔的要求是远远不能兑现的。
小朋友们,你们知道这是为什么吗?原来,把64格里的麦粒数依次记下来,就是:1,2,2×2,2×2×2,2×2×2×2,…,一直到把2乘上63次。
在数学上,这样的一列数叫做“等比数列”(这个我们以后才会学到哦)。
它的和究竟是多少呢?是18446744073709551615。
而这些麦粒是多少呢?大约是140万亿公斤。
这么多的麦子,全世界大约要两千年才能生产出来呢。
如果造一个高4米,宽10米的仓库来放这些麦子,那么仓库的长度将能够从地球修到太阳,再从太阳修回来。
第四讲计算综合一看完前面的故事,同学们可能有些疑问,真的需要那么多麦子吗?同学们可以试着算一算:从第一个棋盘开始,需要的麦子数分别为:1粒、2粒、4粒、8粒、16粒、32粒、64粒、128粒、256粒、512粒、1024粒、2048粒、……写到这里,同学们可以看出,开始的时候麦粒数量并不大,但越到后面数量越多,最终会达到全世界都无法承受的程度.我们的直觉往往是正确的,但有的时候我们也会被直觉所欺骗.麦粒数量形成的这串数列,就叫做等比数列.等比数列就是按照相同的倍数增加(或减少)的数列,例如“麦粒数列”就是按照2倍的速度增加的,这个相同的倍数就是公比,“麦粒数列”的公比就是2.同等差数列一样,等比数列同样有首项,末项及项数,同学们可以想一想如何通过首项和公比将等比数列的每一项都表示出来.等差数列求和是利用“倒序相加”或“配对求和”的方法,那么等比数列如何求和呢?我们来看一个例题.例题1.计算:(1)1248163264128256++++++++;(2)2618541624861458++++++.分析:这是一个等比数列求和的问题.如果一个一个的计算会有点复杂,那么该如何简便地算出数列的和呢?练习1.(1)3456789++++++;2222222(2)2373333++++.(836561=)有关等比数列的知识,同学们到中学以后还会继续学习,在这里只需掌握简单的等比数列求和即可.下面我们看一些技巧性比较强的分数计算的题目,首先我们先来看一个整体约分的题目.例题2.计算:123246481271421 13526104122072135⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯.分析:注意到246⨯⨯是123⨯⨯的32倍,4812⨯⨯是123⨯⨯的34倍,71421⨯⨯是123⨯⨯的37倍,那么可以把123⨯⨯都提出来.分母也可以同样处理.练习2.计算:234468691281216 345681091215121620⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯.除了整体约分,有时候我们也可以对计算中的某些数进行适当的拆分,从而避免很多冗繁的计算.使得计算过程呈现出“四两拨千斤”的效果.例题3.计算:113114115 151617 131414151516⨯+⨯+⨯.分析:把算式里的某些数适当拆分,可以简化计算的过程.练习3.计算:115116117 333537 151616171718⨯+⨯+⨯.例题4.计算:201111 20112011227201262013÷+÷+.分析:利用前面两道题目用过的技巧,就可以解决这道题目了.练习4.计算:19811 19819864919917200÷+÷+.例题5.定义新运算a bΩ为a与b之间(包含a,b)所有与a奇偶性相同的自然数的平均数,例如:()714791113410Ω=+++÷=,()18101816141210514Ω=++++÷=.(1)计算:1019Ω;(2)在算式()199980ΩΩ=的方框中填入恰当的自然数后可使等式成立,请问:所填的数是什么?分析:根据题意,可知a bΩ是公差为2的等差数列的平均数.想一下,等差数列的平均数有什么简便算法吗?最后我们来看一下数列数表的问题,数列数表的问题一般难度比较大,需要我们仔细观察,寻找规律.例题6.观察数列11212312341223334444,,,,,,,,,,的规律,求:(1)150是数列中第几项?(2)数列中第100个分数是多少?分析:观察数列,你找到什么规律了吗?又如何来利用这些规律呢?心算能力超强的数学家“欧拉进行计算看起来毫不费劲儿,就像人进行呼吸,像鹰在风中盘旋一样.”(数学家阿拉戈语)欧拉是历史上最多产的数学家,写下了浩如烟海的书籍和论文.他心算能力极强,如果你问他前一百个质数中任何一个数的六次方,他都可以瞬间告诉你结果.有一次欧拉的两个学生算无穷级数求和,算到第17项时两人在小数点后第50位数字上发生争执,欧拉这时进行心算,迅速给出了正确答案.莱昂哈德·欧拉(Leonhard Euler)约翰·冯·诺依曼(John Von Neumann)(1707年4月15日~1783年9月18日)(1903年12月28日~1957年2月8日)约翰·冯·诺依曼,被誉为“现代电子计算机之父”,也是公认的数学天才.据说:六岁时他能心算八位数乘除法,八岁时掌握微积分,十二岁就读懂领会了波莱尔的大作《函数论》要义.有一次,美国物理学家塞格雷(诺贝尔奖获得者)和同事(也是个诺贝尔奖牛人)为一个积分问题奋斗了一个下午,却毫无进展.这时他们从开着的门缝中看到冯·诺依曼正沿着走廊朝他们的办公室走来,于是他们问冯·诺依曼:“您能帮我们解决这个积分问题吗?”困扰他们的积分问题就写在移动黑板上,冯·诺依曼走到门口,看了一眼黑板,立即给出了答案(大概花了3秒钟).1. 计算:212222++2. 计算:361224384+++++.3. 计算:111112252711121213⨯+⨯. 4. 计算:12324651015125241051025⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯. 5. 数列23、25、45、27、47、67、29、…中,第100项是多少?100105是数列的第几项?第四讲 计算综合一例题1. 答案:(1)511;(2)2186详解:(1)设1248163264128256S =++++++++,2248163264128256512S =++++++++,二式相减得5121511S =-=.(2)设261458S =+++,36184374S =+++,两式相减得2437424372S =-=,2186S =.例题2. 答案:25 详解:整体约分,原式333333123123212341237135135212341237⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯ 33333312312471351247⨯⨯⨯+++=⨯⨯⨯+++()()25=.例题3. 答案:45 详解:11311411514+115+116+1131414151516=⨯+⨯+⨯原式()()()131413141514151615=14++15++16+141314151415161516⨯⨯⨯⨯⨯⨯=13+1+14+1+15+1=45例题4. 答案:146详解:171=11+(21+)7+201262013÷÷原式201217=++217+7201320136÷÷1=46.例题5. 答案:(1)14;(2)101或100详解:(1)10191018214Ω=+÷=();(2)199********Ω=+÷=();方框里有两种填法,80259101⨯-=或者80260=100⨯-.例题6. 答案:(1)1226;(2)914详解:(1)150是()1494921=1226+⨯÷+项.(2)因为()11313291+⨯÷=,114是第92个数.那么第100个数就是从114开始数的第9个,是914.练习1. 答案:(1)1016;(2)3279简答:(1)原式932221016=⨯-=;(2)原式83332792-==.练习2. 答案:25简答:原式23423455⨯⨯==⨯⨯.练习3. 答案:99 简答:原式115116117321341361151616171718⎛⎫⎛⎫⎛⎫=+⨯++⨯++⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 30132134199=+++++=.练习4. 答案:2817简答:原式11119921211631978199172002001720017⎛⎫=÷++÷+=+++= ⎪⎝⎭.作业1. 答案:8190 简答:原式.作业2. 答案:765简答:原式38423765=⨯-=.作业3. 答案:48 简答:原式1111122412612212414811121213⎛⎫⎛⎫=+⨯++⨯=+++= ⎪ ⎪⎝⎭⎝⎭. 作业4. 答案:35 简答:原式12331255⨯⨯==⨯⨯. 作业5. 答案:1829,第1376项 简答:把数列改写成一个三角形的数表,然后再做就可以了.122228190=⨯-=。
关于棋盘麦粒的传说
关于棋盘麦粒的传说
在印度,有一个古老的传说:当时舍罕王打算重赏国际象棋的发明人宰相西萨·班·达依尔。
宰相请舍罕王在棋盘的第一个小格内赏给他一粒麦子,在第二个格子内赏给他2粒麦子,第三个格赏给他2×2=4粒麦子,……照此下去,每一格内的麦子都比前一小格的加一倍。
舍罕王认为这样摆满棋盘上所有64格的麦粒也不过一小袋,就答应了宰相的要求。
可是当宫廷数学家计算了这个数目之后,才发现整个国家仓库里的所有麦子全部给宰相还相差很多,甚至在全世界的土地上也不可能收获这么多的麦子。
这是怎么回事呢?实际上这是一个等比数列也称几何级数求前64项和的问题。
根据等比数列求前几项和的公式:。
其中a1是等比数列{an}的第一项,q是公比,n为项数。
而在该题中,a1=1,q=2,n=64,则:
这个数字是非常大的。
可见,古印度在很早以前就有了几何级数的思想。
在我国2000多年前的《易经》和《九章算术》等著作中,都包含了等比数列的内容。
这个数到底多大?
这个数到底有多大?
据说,国际象棋是古代印度宰相沙伊尔发明的,国王舍罕要奖励这个聪明的宰相,就问沙伊尔要什么样的奖励。
沙伊尔说,棋盘有64个格子,给我第1个格子里放1粒麦子,第2个格子放2粒麦子,第3个格子放4粒麦子,第4个格子放8粒麦子,第5个格子放16粒麦子,第6 个格子放32粒麦子,以此类推,后面的格子;里放入的麦子个数,总是它相邻的前面的格子里的麦子数的2倍,直到放到第64个格子。
用数的幂表示,第1个格子是2的0次方,第2 个格子是2的1次方,第3个格子是2的2次方,……最后第64个格子是2的63次方。
把这些数相加,利用等比级数的公式,求出公比为2、首项为1的前64项的和,结果是:2的64次方减1,这就是在64个格子中放进去的麦子的总个数。
那么,这个数到底有多大呢?这个数可以近似为2的64次方,利用对数和反对数表,可以求出来。
根据小麦的千粒重,求得这些小麦的重量是2587亿吨。
2013年,全世界的小麦的产量为7.126亿吨,2587除以7.126,结果是363,就是说,这些麦子的总重量相当于全世界363年的产量!
由此可见,2的64次方,是一个很大的数字!不算不知道,一算吓一跳。
据传说,国王舍罕根本不可能满足沙伊尔的要求,干脆把沙伊尔杀了。