八年级数学《勾股定理》练习题含答案

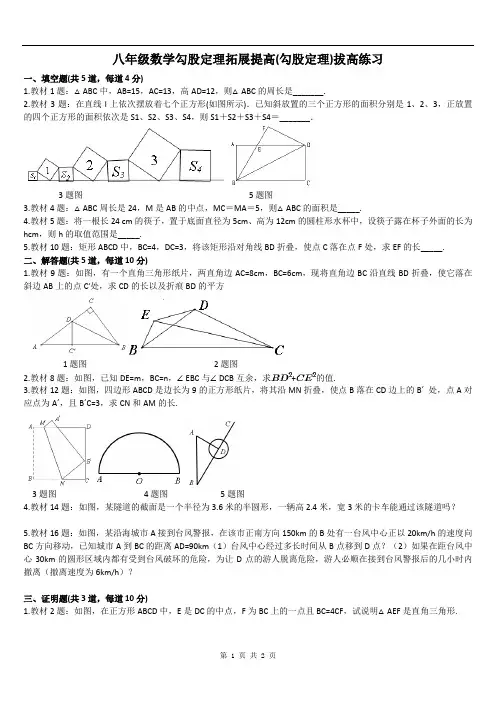
第 1 页 共 2 页 八年级数学勾股定理拓展提高(勾股定理)拔高练习

一、填空题(共5道，每道4分)

1.教材1题：△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长是_______.

2.教材3题：在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_______．

3题图 5题图

3.教材4题：△ABC周长是24，M是AB的中点，MC＝MA＝5，则△ABC的面积是_____.

4.教材5题：将一根长24 cm的筷子，置于底面直径为5cm、高为12cm的圆柱形水杯中，设筷子露在杯子外面的长为hcm，则h的取值范围是_____.

5.教材10题：矩形ABCD中，BC=4，DC=3，将该矩形沿对角线BD折叠，使点C落在点F处，求EF的长_____.

二、解答题(共5道，每道10分)

1.教材9题：如图，有一个直角三角形纸片，两直角边AC=8cm，BC=6cm，现将直角边BC沿直线BD折叠，使它落在斜边AB上的点C′处，求CD的长以及折痕BD的平方

1题图 2题图

2.教材8题：如图，已知DE=m，BC=n，∠EBC与∠DCB互余，求+的值.

3.教材12题：如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B´ 处，点A对应点为A´，且B´C=3，求CN和AM的长.

3题图 4题图 5题图

4.教材14题：如图，某隧道的截面是一个半径为3.6米的半圆形，一辆高2.4米，宽3米的卡车能通过该隧道吗？

5.教材16题：如图，某沿海城市A接到台风警报，在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动，已知城市A到BC的距离AD=90km（1）台风中心经过多长时间从B点移到D点？（2）如果在距台风中心30km的圆形区域内都有受到台风破坏的危险，为让D点的游人脱离危险，游人必顺在接到台风警报后的几小时内撤离（撤离速度为6km/h）？

1 八年级上北师大版第一章勾股定理测试

一、选择题（每小题3分，共30分）

1. 下列各组中，不能构成直角三角形的是 （ ）.

（A）9，12，15 （B）15，32，39 （C）16，30，32 （D）9，40，41

2. 如图1，直角三角形ABC的周长为24，且AB：BC=5：3，则AC= （ ）.

（A）6 （B）8 （C）10 （D）12

3. 已知：如图2，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3,则图中阴影部分的面积为 （ ）.

（A）9 （B）3 （C）49 （D）29

4. 如图3，在△ABC中，AD⊥BC与D，AB=17，BD=15，DC=6，则AC的长为（ ）.

（A）11 （B）10 （C）9 （D）8

5. 若三角形三边长为a、b、c，且满足等式abcba2)(22，则此三角形是（ ）.

（A）锐角三角形 （B）钝角三角形 （C）等腰直角三角形 （D）直角三角形

6. 直角三角形两直角边分别为5、12，则这个直角三角形斜边上的高为 （ ）.

（A）6 （B）8.5 （C）1320 （D）1360

7. 高为3，底边长为8的等腰三角形腰长为 （ ）.

（A）3 （B）4 （C）5 （D）6

一、选择题

1．已知：△ABC中，BD、CE分别是AC、AB边上的高，BQ＝AC，点F在CE的延长线上，CF＝AB，下列结论错误的是（ ）．

A．AF⊥AQ B．AF=AQ C．AF=AD D．FBAQ

2．△ABC的三边分别为,,abc，下列条件能推出△ABC是直角三角形的有（ ）

①222acb;②2()()0ababc;③ ∠A＝∠B∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤111,,345abc;⑥10,a 24,b 26c

A．2个 B．3个 C．4个 D．5个

3．如图，ABC中，有一点P在AC上移动．若56ABACBC，，则APBPCP的最小值为( )

A．8 B．8.8 C．9.8 D．10

4．如图，在ABC中，90A，6AB，8AC，ABC与ACB的平分线交于点O，过点O作ODAB于点D，若则AD的长为( )

A．2 B．2 C．3 D．4

5．棱长分别为86cmcm，的两个正方体如图放置，点A，B，E在同一直线上，顶点G在棱BC上，点P是棱11E F的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P，它爬行的最短距离是( )

A．(3510)cm

B．513cm C．277cm D．(2583)cm

6．以线段a、b、c 的长为边长能构成直角三角形的是（ ）

A．a=3，b=4，c=6 B．a=1，b=2，c=3

C．a=5，b=6，c=8 D．a=3，b=2，c=5

7．如图，已知数轴上点P表示的数为1，点A表示的数为1，过点A作直线l垂直于PA，在l上取点B，使1AB，以点P为圆心，以PB为半径作弧，弧与数轴的交点C所表示的数为（ ）

A．5 B．51 C．51 D．51

8．如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形，若直角三角形的两直角边长分别为5和3，则小正方形的面积为（ ）

勾股定理

练习题

温故而知新： 1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a2+b2=c2.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 （2013·安顺）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

米 米

米 米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

例2 （2013·衢州）如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

cm cm 2 cm 2 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

答案：D

小结：在直角三角形中，30°角所对的直角边等于斜边的一半，45°的直角三角形中，斜边是直角边的2倍.

八年级下《勾股定理》单元检测题含答案

《勾股定理》单元检测题

一、选择题（每小题只有一个正确答案）

1．设直角三角形的两条直角边分别为a和b，斜边长为c，已知1213bc，，则a=( )

A. 1 B. 5 C. 10 D. 25

2．在下列四组数中，不是勾股数的一组数是（ ）

A. 15817abc，， B. 91215abc，，

C. 72425abc，， D. 357abc，，

3．一个三角形的三边长为15，20，25，则此三角形最大边上的高为（ ）

A. 10 B. 12 C. 24 D. 48

4．如图，有一个由传感器控制的灯A装在门上方离地高4.5 m的墙上，任何东西只要移至距该灯5 m及5 m以内时，灯就会自动发光，请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光？（ ）

A. 4 m B. 3 m C. 5 m D. 7 m

5．下列选项中，不能用来证明勾股定理的是( )

A. B. C. D.

6．若直角三角形的三边长分别为ab、a、ab，且a、b都是正整数，则三角形其中一边的长可能为（ ）

A. 22 B. 32 C. 62 D. 82

7．如图，△ABC中，AC=3，BC= 5，AD⊥BC交BC于点D，AD=125，延长BC至E使得CE=BC，将△ABC沿AC翻折得到△AFC，连接EF，则线段EF的长为（ ）

A. 6

B. 8

C. 325 D. 323

8．如图,点P是平面坐标系中一点,则点P到原点的距离是（ ）

A. 3 B. 2 C. 7 D. 5

9．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2 ， 则该半圆的半径为（ ）

A. (4+5)cm

...

... 八年级数学勾股定理练习

1.填空题:

(1)在△ABC中,∠C=Rt∠.若a =2,b=3则c = 若a =5,c =13.则b = .若c=61,b=11.则a= .若a∶c =3∶5且c =20则b= .若∠A=60°且AC=7cm则AB=

cm，BC=

cm.

(2)直角三角形一条直角边与斜边分别为8cm和10cm.则斜边上的高等于 cm.

(3)在△ABC中，如果a∶b∶c =1∶∶2,那么∠A= °,∠B= °

∠C= °

(4)已知两条线段的长为5cm和12cm,当第三条线段的长为

cm时,这三条线段能组成一个直角三角形.

(5)等腰三角形的周长是20cm,底边上的高是6cm,则底边的长为

cm.

(6)△ABC中,∠C=90°,∠A=2∠B,则∠A= 度,∠B= 度

(7)△ABC中,∠C=90°,∠A比∠B大24°,则∠A= 度,∠B= 度.

(8)△ABC中,AB=AC,∠BAC=120°,AB=12cm,则BC边上的高AD=

cm.

(9)已知：△ABC中，∠ACB=90°，CD⊥AB于D，BC=,DB=2cm,则BC cm, AB= cm,

AC=

cm.°

(10)已知:如图,△ABD中,∠B=90°,∠D=15°,C是BD上一点,AC=CD=8cm,则AB= cm,

BC= cm.

2.选择题

(1)在下列长度的四组线段中,不能组成直角三角形的是( )

(A)3,3,3 (B)+1,－１,2

(C)8,15,17 (D)3.5,4.5,5.5 ...

... (2)下列命题中是假命题的是( )

八年级数学勾股定理拓展提高(勾股定理)拔高练习

一、填空题(共5道，每道4分)

1.教材1题：△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长是

_______.

2.教材3题：在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的

三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是

S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_______．

3题图 5题图

3.教材4题：△ABC周长是24，M是AB的中点，MC＝MA＝5，则△ABC的

面积是_____.

4.教材5题：将一根长24 cm的筷子，置于底面直径为5cm、高为12cm的

圆柱形水杯中，设筷子露在杯子外面的长为hcm，则h的取值范围是

_____.

5.教材10题：矩形ABCD中，BC=4，DC=3，将该矩形沿对角线BD折叠，

使点C落在点F处，求EF的长_____.

二、解答题(共5道，每道10分)

1.教材9题：如图，有一个直角三角形纸片，两直角边AC=8cm，

BC=6cm，现将直角边BC沿直线BD折叠，使它落在斜边AB上的点Cʹ处，

求CD的长以及折痕BD的平方

1题图 2题图

2.教材8题：如图，已知DE=m，BC=n，∠EBC与∠DCB互余，求+

的值.

3.教材12题：如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折

叠，使点B落在CD边上的B´ 处，点A对应点为A´，且B´C=3，求CN和AM的

长.

3题图 4题图 5题图

4.教材14题：如图，某隧道的截面是一个半径为3.6米的半圆形，一辆高

2.4米，宽3米的卡车能通过该隧道吗？

5.教材16题：如图，某沿海城市A接到台风警报，在该市正南方向150km

的B处有一台风中心正以20km/h的速度向BC方向移动，已知城市A到BC

的距离AD=90km（1）台风中心经过多长时间从B点移到D点？（2）如果

在距台风中心30km的圆形区域内都有受到台风破坏的危险，为让D点的

游人脱离危险，游人必顺在接到台风警报后的几小时内撤离（撤离速度

扬帆教育 伴你成长

1 勾股定理练习题：练习一：（基础）

1.等腰三角形的腰长为13，底边长为10，则顶角的平分线为＿＿.

2.一个三角形的三边之比为5∶12∶13，它的周长为60，则它的面积是＿＿＿.

3.已知a，b，c为△ABC三边，且满足(a2－b2)(a2+b2－c2)＝0，则它的形状为（ ）

A.直角三角形 B.等腰三角形

C.等腰直角三角形 D.等腰三角形或直角三角形

4.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程（ 取3）是（ ）.

（A）20cm （B）10cm （C）14cm （D）无法确定

5. 在Rt△ABC中，斜边AB=2，则AB2＋BC2＋AC2=____．

6．Rt△一直角边的长为11，另两边为自然数，则Rt△的周长为（ ）

A、121 B、120 C、132 D、不能确定

7．如图，正方形网格中的△ABC，若小方格边长为1，则△ABC是 （ ）

A.直角三角形 B.锐角三角形 C.钝角三角形 D.以上答案都不对

8．如果Rt△的两直角边长分别为n2－1，2n（n >1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、n2+1

9.在△ABC中,,90C若,7ba△ABC的面积等于6，则边长c=

10.如图△ABC中，BCBMACANBCACACB,,5,12,90则MN=

11.一个直角三角形的三边长的平方和为200，则斜边长为

12.若△ABC是直角三角形，两直角边都是6，在三角形斜边上有一点P，到两直角边的距离相等，则这个距离等于 A

B

ABC扬帆教育 伴你成长

2

13.如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？

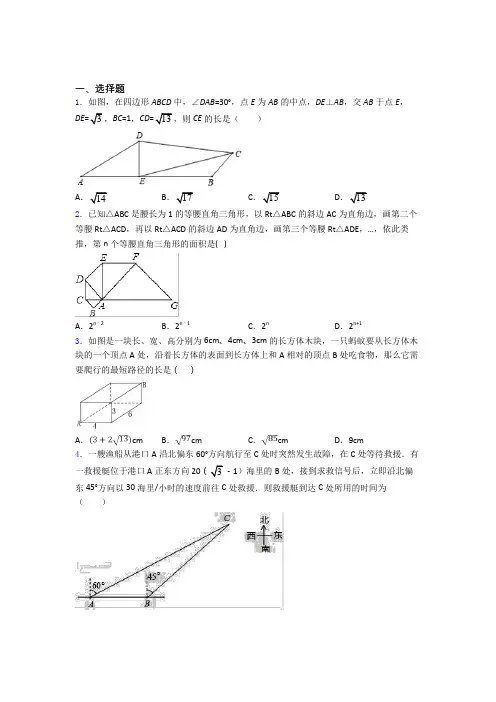
一、选择题

1．如图，在四边形ABCD中，∠DAB=30°，点E为AB的中点，DE⊥AB，交AB于点E，DE=3，BC=1，CD=13，则CE的长是（ ）

A．14 B．17 C．15 D．13

2．已知△ABC是腰长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的面积是( )

A．2n﹣2 B．2n﹣1 C．2n D．2n+1

3．如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）

A．cm B．cm C．cm D．9cm

4．一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障，在C处等待救援．有一救援艇位于港口A正东方向20（3﹣1）海里的B处，接到求救信号后，立即沿北偏东45°方向以30海里/小时的速度前往C处救援．则救援艇到达C处所用的时间为（ ）

A．33小时 B．23小时

C．223 小时 D．2323小时

5．在Rt△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，交AC于点D，若CD=1，则AB的长是（

）

A．2 B． 23 C． 43 D．4

6．A、B、C分别表示三个村庄，AB1700米，800BC米，AC1500米，某社区拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（ ）

A．AB的中点 B．BC的中点

C．AC的中点 D．C的平分线与AB的交点

7．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE=10，BE=24，则EF的长是（ ）

A．14 B．13 C．143 D．142

八年级数学勾股定理拓展提高勾股定理拔高练习

The pony was revised in January 2021 八年级数学勾股定理拓展提高(勾股定理)拔高练习

一、填空题(共5道，每道4分)

1.教材1题：△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长是_______.2.教材3题：在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_______．

3题图5题图

3.教材4题：△ABC周长是24，M是AB的中点，MC＝MA＝5，则△ABC的面积是_____.

4.教材5题：将一根长24cm的筷子，置于底面直径为5cm、高为12cm的圆柱形水杯中，设筷子露在杯子外面的长为hcm，则h的取值范围是_____.

5.教材10题：矩形ABCD中，BC=4，DC=3，将该矩形沿对角线BD折叠，使点C落在点F处，求EF的长_____.

二、解答题(共5道，每道10分) 1.教材9题：如图，有一个直角三角形纸片，两直角边AC=8cm，BC=6cm，现将直角边BC沿直线BD折叠，使它落在斜边AB上的点C′处，求CD的长以及折痕BD的平方

1题图2题图

2.教材8题：如图，已知DE=m，BC=n，∠EBC与∠DCB互余，求+的值.3.教材12题：如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，求CN和AM的长.

3题图4题图5题图

4.教材14题：如图，某隧道的截面是一个半径为3.6米的半圆形，一辆高2.4米，宽3米的卡车能通过该隧道吗5.教材16题：如图，某沿海城市A接到台风警报，在该市正南方向150km的B处有一台风中心正以20km/h的速度向BC方向移动，已知城市A到BC的距离AD=90km（1）台风中心经过多长时间从B点移到D点（2）如果在距台风中心30km的圆形区域内都有受到台风破坏的危险，为让D点的游人脱离危险，游人必顺在接到台风警报后的几小时内撤离（撤离速度为6km/h）

依提木孔乡中学 买买提依力·吾司曼

《勾股定理》练习题

一、选择题（12×3′=36′）

1．已知一个Rt△的两边长分别为3和4，则第三边长的平方是（ ）

A、25 B、14 C、7 D、7或25

2．下列各组数中，以a，b，c为边的三角形不是Rt△的是（ ）

A、a=1.5，b=2,c=3 B、a=7,b=24,c=25

C、a=6,b=8,c=10 D、a=3,b=4,c=5

3．若线段a，b，c组成Rt△，则它们的比为（ ）

A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7

4．Rt△一直角边的长为11，另两边为自然数，则Rt△的周长为（ ）

A、121 B、120 C、132 D、不能确定

5．如果Rt△两直角边的比为5∶12，则斜边上的高与斜边的比为（ ）

A、60∶13 B、5∶12 C、12∶13 D、60∶169

6．如果Rt△的两直角边长分别为n2－1，2n（n>1），那么它的斜边长是（ ）

A、2n B、n+1 C、n2－1 D、n2+1

7．已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（ ）

A、24cm2 B、36cm2 C、48cm2 D、60cm2

8．等腰三角形底边上的高为8，周长为32，则三角形的面积为（ ）

A、56 B、48 C、40 D、32

9．三角形的三边长为（a+b）2=c2+2ab,则这个三角形是( )

A. 等边三角形; B. 钝角三角形; C. 直角三角形; D. 锐角三角形.

10．某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要（ ）

一、选择题

1．如图：在△ABC中，∠B=45°，D是AB边上一点，连接CD，过A作AF⊥CD交CD于G，交BC于点F．已知AC=CD，CG=3，DG=1，则下列结论正确的是（ ）

①∠ACD=2∠FAB ②27ACDS ③272CF ④ AC=AF

A．①②③ B．①②③④ C．②③④ D．①③④

2．△ABC的三边分别为,,abc，下列条件能推出△ABC是直角三角形的有（ ）

①222acb;②2()()0ababc;③ ∠A＝∠B∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤111,,345abc;⑥10,a 24,b 26c

A．2个 B．3个 C．4个 D．5个

3．如图，已知1号、4号两个正方形的面积之和为7，2号、3号两个正方形的面积之和为4，则a、b、c三个正方形的面积之和为（ ）

A．11 B．15 C．10 D．22

4．如图，在△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH、BE与相交于点G，以下结论中正确的结论有（ ）

（1）△ABC是等腰三角形；（2）BF＝AC；（3）BH：BD：BC＝1：2：3；（4）GE2+CE2＝BG2．

A．1个 B．2个 C．3个 D．4个

5．如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（ ）

A．cm B．cm C．cm D．9cm

6．若△ABC中，AB=AC=25，BC=4，则△ABC的面积为（ ）

A．4 B．8 C．16 D．52

7．已知,,abc是ABC的三边，且满足222()()0ababc，则ABC是（ ）

A．直角三角形 B．等边三角形

13.11勾股定理的应用练习（1）

第1题. 如图，△ABC中，∠ACB=90º，CD为AB边上的高，若∠A=30º，AB=16，则BC=______，BD=______，CD=______．

答案：8，4，43．

第2题. 如图是一种“牛头形”图案，其作法是：从正方形1开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形2，以此类推，若正方形1的边长为64cm，则正方形7的边长为_________cm．

答案：8．

第3题. 甲、乙两人从同一地点出发，甲往东走了4km，乙往南走了3km，这时，甲、乙两人相距______．

答案：5km

第4题. 如果梯子底端离建筑物9m，那么15m长的梯子可达到建筑物的高度是______．

答案：12m

第5题. 如图，一扇宽为4米，高为3米的栅栏门，需要一根长______米的木条像图中那样固定．

答案：5

第6题. 一块土地的形状如图所示，90,20,15,7,BDABBCCD米米米求这块土地的面积?

答案：234平方米

第7题. 某菜农修建一个塑料大棚（如图），若棚宽a=4m，高b=3m，长d=35m，求覆盖在顶上的塑料薄膜的面积． A B C

D

4 4 3 3 2 2

1

3米

4米

A

B C D

a b c d

答案：175m2

第8题. 一游泳池长48cm，小方和小朱进行游泳比赛，从同一处出发，小方平均速度为3m/秒，小朱为3.1m/秒．但小朱一心想快，不看方向沿斜线游，而小方直游，俩人到达终点的位置相距14m．按各人的平均速度计算，谁先到达终点，为什么？

答案：小朱用16.13秒,小方用16秒,小方先到达终点

第9题. 如图，正方形ACDE的面积为25cm，测量出AB=12cm，BC=13cm，问E、A、B三点在一条直线上吗？为什么？

答案：在一条直线上，理由略

第10题. 从A到B有两种路线，一种走直线由A到B，另一种走折线，先从A直线到C，再由C直线到B，其中ACB成直角，已知A到C为600m，C到B为800m，问从A到B走直线比走折线少走多少米？

1 温故而知新：

1.勾股定理

直角三角形两条直角边a,b的平方和等于斜边c的平方，即a+b=c.

2.勾股定理的验证

勾股定理的证明方法很多，据说已有400余种，其证明的内涵极其丰富.常用的证法是面积割补法，如图所示.

3.直角三角形的性质

两锐角互余（角的关系）、勾股定理（边的关系），30°角所对的直角边等于斜边的一半（边角关系），这些性质在求线段的长度、证明线段倍分关系、证明线段平方关系等方面有广泛的应用.

例1 如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢,小鸟至少飞行（ ）

A.8米 B.10米

C.12米 D.14米

解析：小鸟飞行的最短路线如图所示为线段AB；过点A向10米高的树作垂线，垂足为C，则易知AC=8米，BC=10-4=6（米）；根据勾股定理可得

AB=22ACBC=2286=10（米）.

答案：B

小结：在解决实际问题时，往往根据题意把实际问题转化为数学问题，构造直角三角形利用勾股定理来解决.有时根据需要巧设未知数，借助勾股定理列方程求解，常可使问题简便.

2

例2

如图，将一个有45°角的三角板的直角顶点放在一张宽为3cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最大边的长为（ ）

A.3 cm B.6 cm

C.3 cm D.6 cm

解析：如图所示在图中标上字母，过点A作AD⊥BD，

垂足为D，则AD=3 cm；

因为∠ABD=30°，所以AB=2AD=6 cm；

又△ABC是等腰直角三角形，故BC=AB=6 cm，根据勾股定理可得AC=22ABBC=2266=62（cm）

答案：D

小结：在直角三角形中，30°角所对的直角边等于斜边的一半，45°的直角三角形中，斜边是直角边的2倍.

17.2勾股定理的逆定理

一、选择题（本大题共8小题；每小题3分，共24分）

（下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的，请把正确结论的代号填入题号后的括号内）

1．下列各组数中，以它们为边的三角形不是直角三角形的是（ ）

A．1.5，2，3 B. 7，24，25

C．6，8，10 D. 3，4，5

2．一个直角三角形，有两边长分别为6和8，下列说法正确的是（ ）

A. 第三边一定为10 B. 三角形的周长为25

C. 三角形的面积为48 D. 第三边可能为10

3．直角三角形的斜边为20cm，两条直角边之比为3∶4，那么这个直角三角形的周长为（ ）

A . 27cm B. 30cm C. 40cm D. 48cm

4．下列命题中是假命题的是( )

A. △ABC中,若∠B=∠C－∠A,则△ABC是直角三角形.

B. △ABC中,若a2=(b+c)(b－c),则△ABC是直角三角形.

C. △ABC中,若∠A∶∠B∶∠C=3∶4∶5则△ABC是直角三角形.

D. △ABC中,若a∶b∶c=5∶4∶3则△ABC是直角三角形.

5．若△ABC的三边a、b、c满足(a-b)(a2+b2-c2)=0，则△ABC是 ( )

A. 等腰三角形 B. 等边三角形

C. 等腰直角三角形 D. 等腰三角形或直角三角形

6．将直角三角形的三边扩大相同的倍数后，得到的三角形是（ ）

A 直角三角形 B 锐角三角形 C 钝角三角形 D 不能

2022-2023学年人教版八年级数学下册《17.1勾股定理》同步练习题（附答案）

一．选择题

1．已知直角三角形的两条边长分别是3和4，那么这个三角形的第三条边的长为（ ）

A．5 B．25 C． D．5或

2．△ABC中，AB＝20，AC＝13，高AD＝12，则△ABC的面积为（ ）

A．66 B．126 C．54或44 D．126或66

3．如图，Rt△ABC中，∠BAC＝90°，分别以边AB，CA，BC向外作正方形，正方形ABIH的面积为25，正方形BDEC的面积为169，则正方形ACFG的面积是（ ）

A．194 B．144 C．122 D．110

4．下面图形能够验证勾股定理的有（ ）

A．4个 B．3个 C．2个 D．1个

5．如图，我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形的面积为1，大正方形的面积为13，则直角三角形较短的直角边a与较长的直角边b的比的值是（ ）

A． B． C． D． 6．如图是一正方体的平面展开图，若AB＝6，则该正方体A、B两点间的距离为（ ）

A．2 B．3 C．4 D．6

7．如图，在△ABC中，∠C＝90°，分别以A、B为圆心画弧，所画的弧交于两点，再连接该两点所在直线交BC于点D，连接AD．若BD＝2，则AD的长为（ ）

A． B． C．1 D．2

8．如图，是我国古代著名的“赵爽弦图”的示意图，此图是由四个全等的直角三角形拼接而成，其中AE＝10，BE＝24，则EF的长是（ ）

A．14 B．13 C．14 D．14

9．如图，正方形ABCD的面积为15，Rt△BCE的斜边CE的长为8，则BE的长为（ ）

A．17 B．10 C．6 D．7

10．如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（ ）

A．1条 B．2条 C．3条 D．4条 二．填空题