求向量组的秩与极大无关组
- 格式:doc
- 大小:145.99 KB
- 文档页数:4


习题4.31.求下列向量组的秩与一个极大线性无关组: (1)[]12,1,3,1T α=-, []23,1,2,0Tα=-,[]31,3,4,2T α=-,[]44,3,1,1Tα=-.(2)[]11,1,1,1T α=, []21,1,1,1Tα=--, []31,1,1,1Tα=--,[]41,1,1,1Tα=---.(3)[]11,1,2,4T α=-, []20,3,1,2T α=,[]33,0,7,14Tα=,[]41,1,2,0T α=-,[]52,1,5,6Tα=.分析 向量组的秩等于该向量组构成的矩阵的秩, 所以求向量组的秩可以转化为求矩阵的秩. 先把向量构成矩阵通过矩阵的初等行变换成阶梯形, 通过阶梯形便可得到矩阵的秩, 它也就是该向量组的秩, 而阶梯形的阶梯头所在的列对应的向量便构成该向量组的一个极大线性无关组.解 (1) []123423141133113301123241000010210000αααα--⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=−−→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦, 所以该向量组的秩为2, 且1α, 2α为它的一个极大线性无关组.(2) []123411111111111101011111001111110001αααα--⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=−−→⎢⎥⎢⎥---⎢⎥⎢⎥--⎣⎦⎣⎦, 所以该向量组的秩为4, 且1α,2α,3α,4α为它的一个极大线性无关组.(3) []1234510312103121301101101217250001042140600000ααααα⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥=−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦, 所以该向量组的秩为3, 且1α,2α,4α为它的一个极大线性无关组.2.计算下列向量组的秩,并判断该向量组是否线性相关. (1)[]11,1,2,3,4T α=-,[]23,7,8,9,13Tα=-,[]31,3,0,3,3T α=----,[]41,9,6,3,6Tα=-.(2)[]11,3,2,1T β=--, []22,1,5,3T β=-,[]34,3,7,1Tβ=-, []41,11,8,3Tβ=---,[]52,12,30,6Tβ=-.解 (1) []123413111311173901122806000039330000413360000αααα--⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥=−−→⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦所以该向量组的秩为2, 小于向量的个数4, 所以线性相关.(2)[]123451241212412313111201548257830001111313600000βββββ----⎡⎤⎡⎤⎢⎥⎢⎥-----⎢⎥⎢⎥=−−→⎢⎥⎢⎥-⎢⎥⎢⎥--⎣⎦⎣⎦所以该向量组的秩为3, 小于向量的个数5, 所以线性相关.3.设[]11,2,1T α=-, []22,4,T αλ=, []31,,1Tαλ=.(1) λ取何值时1α,2α,3α线性相关? λ取何值时1α,2α,3α线性无关? 为什么? (2)λ取何值时3α能经1α,2α线性表示? 且写出表达式.解 (1)[]1231211212402211002αααλλλλ⎡⎤⎡⎤⎢⎥⎢⎥=−−→+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦当2λ≠且2λ≠-时, 矩阵的秩为3与向量个数相同, 所以此时该向量组线性无关.当2λ=或2λ=-时, 矩阵的秩为2小于向量个数, 所以此时向量组线性相关. (1) 当2λ=时, 秩([]12αα)=秩([]123ααα)=2, 此时3α能经1α,2α线性表示.表达式的系数为方程组[]123X ααα=的解, 而此时该方程组的解为120,1.2x x =⎧⎪⎨=⎪⎩所以表达式为3α=212α. 当2λ=-时, 秩([]12αα)=1, 秩([]123ααα)=2, 两者不相等, 所以不能线性表示.当2λ≠且2λ≠-时, 秩([]12αα)=2, 秩([]123ααα)=3, 两者不相等,所以不能线性表示.4.下述结论不正确的是( ),且说明理由.(A) 秩为4的4×5矩阵的行向量组必线性无关. (B) 可逆矩阵的行向量组和列向量组均线性无关. (C) 秩为r(r<n)的m ×n 矩阵的列向量组必线性相关. (D) 凡行向量组线性无关的矩阵必为可逆矩阵.解 (A) 正确. 如果行向量组线性相关则行向量组的秩必小于行向量的个数4, 即矩阵的行秩小于4, 而矩阵的行秩等于矩阵的秩, 因此矩阵的秩小于4, 这与矩阵的秩为4矛盾! 所以行向量组必线性无关.(B) 正确. 可逆矩阵必为满秩矩阵, 即n n ⨯的可逆矩阵的秩为n , 而矩阵的秩等于行秩和列秩, 所以矩阵的行秩=列秩=n , 因此行向量组的秩和所含向量个数相同, 据此可知该行向量组必线性无关; 同理列向量组也必线性无关.(C) 正确. 列向量组含有n 个向量, 又由于列向量组的秩(即列秩)等于矩阵的秩r , 而r<n , 即列向量组的秩小于向量组所含向量的个数, 据此列向量组必线性相关.(D) 设111001A ⎡⎤=⎢⎥⎣⎦, 易知该矩阵的行向量组线性无关, 但是它不是方阵, 所以不是可逆矩阵. 所以该选项不正确.综上所述应选D.。


求向量组的秩与极大无关组对于具体给出的向量组,求秩与极大无关组的常用方法如下。
方法1 将向量组排成矩阵:(列向量组时)或(行向量组时) (*)并求的秩,则即是该向量组的秩;再在原矩阵中找非零的阶子式,则包含的个列(或行)向量即是的列(或行)向量组的一个极大无关组.方法2 将列(或行)向量组排成矩阵如(*)式,并用初等行(或列)变换化为行(或列)阶梯形矩阵(或),则(或)中非零行(或列)的个数即等于向量组的秩,且是该向量组的一个极大无关组,其中是(或)中各非零行(或列)的第1个非零元素所在的列(或行).方法3 当向量组中向量个数较少时,也可采用逐个选录法:即在向量组中任取一个非零向量作为,再取一个与的对应分量不成比例的向量作为,又取一个不能由和线性表出的向量作为,继续进行下去便可求得向量组的极大无关组。
对于抽象的向量组,求秩与极大无关组常利用一些有关的结论,如“若向量组(Ⅰ)可由向量组(Ⅱ)线性表示,则(Ⅰ)的秩不超过(Ⅱ)的秩",“等价向量组有相同的秩”,“秩为的向量组中任意个线性无关的向量都是该向量组的极大无关组"等.例1 求向量组,,,,的秩与一个极大无关组。
解法1,所以向量组的秩为3;又中位于1,2,4行及1,2,4列的3阶子式故是向量组的一个极大无关组(可知;均可作为极大无关组)。
法2由于的第1,2,4个行向量构成的向量组线性无关,故是向量组的一个极大无关组.例2 求向量组,,,的秩和一个极大无关组。
解(1)当且时,,故向量组的秩为3,且是一个极大无关组;(2)当时,,故向量组的秩为3,且是一个极大无关组;(3) 当时,若,则,此时向量组的秩为2,且是一个极大无关组。
若,则,此时向量组的秩为3,且是一个极大无关组.例3 设向量组的秩为.又设,,求向量组的秩.解法1 由于,且所以故向量组与等价,从而的秩为.法2 将看做列向量,则有其中可求得,即可逆,从而可由线性表示,故这两个向量组等价,即它们有相同的秩。






求向量组的秩与极大无关组
对于具体给出的向量组,求秩与极大无关组的常用方法如下.
方法1 将向量组排成矩阵:
(列向量组时)或(行向量组时) (*)
并求的秩,则即是该向量组的秩;再在原矩阵中找非零的阶子式,
则包含的个列(或行)向量即是的列(或行)向量组的一个极大无关组.
方法2 将列(或行)向量组排成矩阵如(*)式,并用初等行(或列)变换化为行(或列)阶梯形矩阵(或),则(或)中非零行(或列)的个数即等于向量组的秩,且是该向量组的一个极大无关组,其中是(或)中各非零行(或列)的第1个非零元素所在的列(或行).
方法3 当向量组中向量个数较少时,也可采用逐个选录法:即在向量组中任取一个非零向量作为,再取一个与的对应分量不成比例的向量作为,
又取一个不能由和线性表出的向量作为,继续进行下去便可求得向量组的极大无关组.
对于抽象的向量组,求秩与极大无关组常利用一些有关的结论,如“若向量组(Ⅰ)可由向量组(Ⅱ)线性表示,则(Ⅰ)的秩不超过(Ⅱ)的秩”,“等价向量组有相同的秩”,“秩为的向量组中任意个线性无关的向量都是该向量组的极大无关组”等.
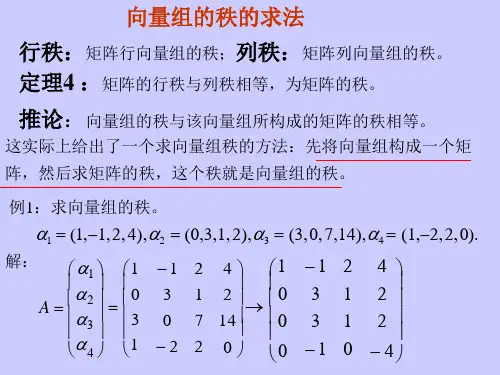
例1 求向量组,,,,
的秩与一个极大无关组.
解法1
,所以向量组的秩为3;又中位于1,2,4行及1,2,4列的3阶子式
故是向量组的一个极大无关组(可知;均可作为极大无关组).
法2
由于的第1,2,4个行向量构成的向量组线性无关,故是向量组的一个极大无关组.
例2 求向量组,,,的秩和一个极大无关组.
解
(1) 当且时,,故向量组的秩为3,且是一个极大无关组;
(2) 当时,,故向量组的秩为3,且是一个极大无关组;
(3) 当时,若,则,此时向量组的秩为2,且是
一个极大无关组.若,则,此时向量组的秩为3,且是一个极大无关组.
例3 设向量组的秩为.又设
,,
求向量组的秩.
解法1 由于,且
所以
故向量组与等价,从而的秩为.
法2 将看做列向量,则有
其中
可求得,即可逆,从而可由线性表示,故这两个向量组等价,即它们有相同的秩.
例4 设向量组(Ⅰ):和向量组(Ⅱ):的秩分别为和
,而向量组(Ⅲ):的秩为.证明:.
证若和中至少有一个为零,显然有,结论成立.若和都不为零,不妨设向量组(Ⅰ)的极大无关组为,向量组(Ⅱ)的极大无关组为,由于向量组可以由它的极大无关组线性表示,所以向量组(Ⅲ)可以由,线性表示,故
的秩。