当前位置：文档之家 › 西南交大 材料力学 龚晖 截面几何性质

西南交大 材料力学 龚晖 截面几何性质

  • 格式：ppt
  • 大小：409.00 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

材料力学第六章 截面的几何性质惯性矩

材料力学第六章 截面的几何性质惯性矩

IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的 y1dA (y a)2 dA A
y2dA 2a ydA a2 dA
I z1 z a2 A; y1 y b2 A;
2dA
A
(y2
A
z2 )dA
IZ
Iy.
Izy
z y dA;
A
五、平行移轴公式:
I z1 z a2 A; y1 y b2 A;
I z1y1 I zy abA;
返回 下一张 上一张 小结
六、主惯性轴和主惯性矩: 主惯性轴（主轴）—使 I zoyo 0 的这对正交坐标轴； 主惯性矩（主惯矩）—截面对主惯性轴的惯性矩； 形心主惯性轴（形心主轴）—通过形心的主惯性轴； 形心主惯性矩（形心主惯矩）—截面对形心主轴的惯性矩。
I z1y1 I zy abA;
注意: y、z轴必须是形心轴。
二、转轴公式:
Iz1
A y12dA
( y cos z sin)2 dA;
A
I z1
Iz
Iy 2
Iz
Iy 2
cos 2
I zy
sin 2;
I y1
Iz
2
Iy
Iz
2
Iy
cos 2
I zy
sin 2;
I z1y1
Iz
Iy 2
三、惯性积:
定义:平面图形内, 微面积dA与其两个坐 标z、y的乘积zydA在整个图形内的积分称为 该图形对z、y轴的惯性积。
Izy
z y dA;
A
特点: ①惯性积是截面对某两个正交

材料力学 截面的几何性质

材料力学 截面的几何性质
附
录
附录Ⅰ
§Ⅰ-1 §Ⅰ-2 §Ⅰ-3 §Ⅰ-4
截面的几何性质
截面的静矩和形心位置 惯性矩、惯性积和惯性半径 平行移轴公式 转轴公式 主惯性矩
静矩与形心
一、静矩的定义(与力矩类似)（也称面积矩或一次矩） 截面对z轴的静矩： y 截面对y轴的静矩：
Sz Sy
dS
A A
z

ydA
A
3
z 100
I
C
CI
a1 a2
I y I yI I yII 443 10 768 10
4
4
y
1211 104 mm 4
由于z轴是对称轴 ，故图形对两轴的惯性积为
140 103.3
CII
II
y
I yz 0
20
I z y 2 dA 2h y 2 bdy
3
附
录
组合截面形心
组合截面：如果截面的图形是由几个简单图形(如矩形、圆形 等）组成的，这种截面称为组合截面。 组合截面对X、Y轴静矩的计算：
S x Ai yci Ayc
i
n
S y Ai xci Axc
i
n
Ai——任一简单图形的面积； xci，yci——任一简单图形的形心坐标； n——全部简单图形的个数。 确定组合截面形心位置的公式：
C H/2
X
1 h 1 h yc 1 y1 ( y1 ) ( y1 ) 2 2 2 2
h 1 h S x Ayc 1 b( y 1 ) ( y 1 ) 2 2 2
b
b 2 2 (h 4y1 ) 8
例2、图形对 x 轴的静矩为

材料力学截面的几何性质

材料力学截面的几何性质
I z I zi
i
，I y I yi，
i
2 I y dA , 元面积对z轴的惯性矩就等于将各元 因 z
面积对z轴的惯性矩求和，因质量连续分布，求和则为积 分。
应用于圆环的情形,可看成两个圆形截面，
I I 1 I 2 I z I y 2I z 2I y，
定义：I A 2 dA
I zy A zydA ——平面图形对z,y轴的惯性积;
极惯性矩.
• 二、性质
1、 I z、I y 恒为正， I zy 可正、可负、也可以为零，其正 负值与坐标轴的位置有关。 2、单位：（长度）4；
例4-4 ： 计算直径为d的圆截面对形心轴z,y的惯性矩 和惯性积。 解：用平面极坐标 (r , ).
y
dy
R
o
y

sz A ydA y z dy
z
z
0 2 R sin cos d
3 2

dz
R3 3
y R

o
z
z
sz 4R 3 yc 2 A R 3 4
R3
z R cos y R sin dy R cosd
sz A zdA z y dz
270 50
S y zci Ai 0，（ z1 z2 0）；
i
y
s z yci Ai y1 A1 y2 A2 15 300 30
i
270 30 270 50 23.625 105 (mm) 2 , 2
• 4-2 惯性矩和惯性积
1 d 4 64
因坐标轴是对称轴，如对左右的 dA （如上图），

专题：简单截面的几何性质【工程力学西南交大4学分】

专题：简单截面的几何性质【工程力学西南交大4学分】

x
60 96 65 (77) 39.7(mm) 96 77
§ I－2 极惯性矩 · 惯性矩 · 惯性积
设任意形状截面如图所示。 1.极惯性矩（或截面二次极矩）
2 Ip d A A
d A 2 π d

d O
d
I p d A 2 (2 π d )
a
x xC b
y yC a
I x A y d A A y c a d A
2 2
y c d A 2a y c d A a
2 A
2
I xc 2 a A y c a 2 A I xc a 2 A
同理，有：

A


A
dA
O y dA
C
3. 静矩与形心坐标的关系
Sy x A
Sy A x
Sx y A
Sx A y
x
x
即：轴过形心
<==> xS该轴=0
结论（1）截面对某一轴的静面矩等于0，则该轴必须通过截面的形心。 （2）截面对过形心的坐标轴的静面矩等于0。 （3）对于具有对称轴的截面，截面对其对称轴的 静面矩必为零。
O
S d A
x
x
1、静矩不仅与平面图形的形状尺寸有关，还与 所选坐标的位置有关。 2、静矩的数值可正可负，也可以为零。 3、静矩的单位：mm3 或 m3
2.形心坐标公式（可由均质等厚薄板的重心坐标而得）
x

A
xd A A
y

A
y d A A
y
y
I x I xc a 2 A
I y I yc b 2 A

材料力学截面的几何性质课件

材料力学截面的几何性质课件
材料力学截面的几何 性质课件
目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后，与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状，截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标，对于承受弯矩的构件， 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标，对于承受剪力的构件 ，选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中，需要考虑梁的截面尺寸、材料类型和截面形式等 因素，以确保桥梁具有足够的强度和刚、单位等因素，以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦，计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩，找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数， 且各主轴与截面垂直，说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比，说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小，但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值，用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数，如圆截面为1 ，矩形截面为1.13，工字形截面为1.44等。

材料力学第四章截面的几何性质_2023年学习资料

材料力学第四章截面的几何性质_2023年学习资料

【例题2】试计算图示矩-形对其对称轴的惯性矩。-Z-解：-dz-I,=L z'dA-C-h-=fiz'bd -bh'-12-hb3-12=
【例题3】试计算图示-圆形对其形心轴的惯性-矩和极惯性矩。-解：-dp-Ip=∫pdA-=p2.2元pdp 元D4-32-I=I,+I-L,=L=-64
I,=∫zdA-4.组合截面的惯性矩和极惯性矩-I:=S y'dA-I,=SP'dA-i=1-I.-A2p-pi
§I.4平行移轴公式-已知：:-1-a b-a和b是截面的形心-在oyz坐标系中的坐标-求：I,LIz-0
ly-lye-C-b-y=y。+b-dA②-Z=Z。+a-c-I,=S z'dA-0-=∫z。+adA-zidA +2af z.dA +a'ldA-=I,,+2a.S,+a'A-=I,.+a2A-其中：S.=
讨论：主轴方向的惯性矩-I,+I21I、-I2-y1-cos 2a-Iy:sin 2a-二-I,-Iss131-sin 2a+Iy cos 2a-应²-dIx=0-得：-da-I,-I:sin2a+Ixcos2 =0-可见，使惯性矩取极值的轴即为主轴。
VI,-12+4I-3.主惯性矩-2a-I-I-定义：截面对主轴的惯性矩称为主惯性矩。-212-由：g2, -1,-1-得：c0s20,=-sin20。--21元-I,-1+4I-VI,-I2+4-将上式代入-Yo I,I:cos 20-In sin 2do-得主惯性矩的计算公式：
31-故过O点的任何一对正-交轴都是主轴，定理得证。-推论：-★-若通过截面某点有三根（或三根以上）的-对 轴，则通过该点的所有轴都是主轴。-★正多边形有无数对主形心轴。-Le-.C

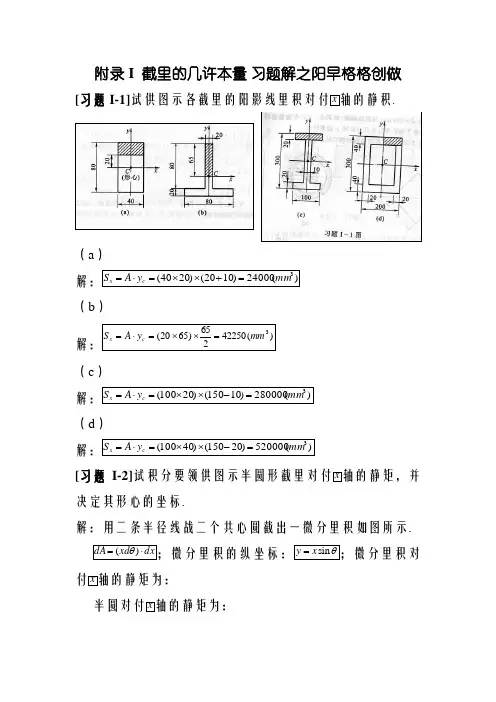
《材料力学》附录I截面的几何性质习题解

附录I 截里的几许本量 习题解之阳早格格创做[习题I-1]试供图示各截里的阳影线里积对付x 轴的静积.（a ）解：)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅= （b ） 解：)(42250265)6520(3mm y A S c x =⨯⨯=⋅=（c ）解：)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅= （d ）解：)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅= [习题I-2]x 轴的静矩，并决定其形心的坐标.解：用二条半径线战二个共心圆截出一微分里积如图所示.dx xd dA ⋅=)(θ；微分里积的纵坐标：θsin x y =；微分里积对付x 轴的静矩为：半圆对付x 轴的静矩为：[习题I-3]试决定图示各图形的形心位子. （a ） 解：(b) 解：(c) 解：[习题I-4]解：用二条半径线战二个共心圆截出一微分里积如图所示.为：[习题I-5].解：圆的圆程为：里积，微分里积为：[习题I-6] 试供图示正圆形对付其对付角线的惯性矩.解：正圆形四条边的曲线圆程如图所示（设火仄坐标轴为.[习题I-7] 试分别供图示环形战箱形截里对付其对付称轴x 的惯性矩. (a) 解：)(21177368])175150(1[17514.3641)1(64144424mm D I x =-⨯⨯=-=απ(b)[习题I-8]试供图示三角形截里对付通过顶面A 并仄止于底边BC 的轴的惯性矩.解：已知三角形截里对付以BC 边为轴的惯性矩是，利用仄止轴定理，可供得截里对付形心轴的惯性矩 所以再次应用仄止轴定理，得[习题I-9]试供图示的半圆形截里对付于轴的惯性矩，其中轴取半圆形的底边仄止，相距1 m. 解：已知半圆形截里对付其底边的惯性矩是，用仄止轴定理得截里对付形心轴的惯性矩 再用仄止轴定理，得截里对付轴的惯性矩[习题I-10] 试供图示拉拢截里对付于形心轴x 的惯性矩. 解：由于三圆曲径相等，并二二相切.它们的圆心形成一个边少为的等边三角形.该等边三角形的形心便是拉拢截里的形心，果此底下二个圆的圆心，到形心轴的距离是上头一个圆的圆心到轴的距离是d 632.利用仄止轴定理，得拉拢截里对付轴的惯性矩如下： [习题I-11]试供图示各拉拢截里对付其对付称轴的惯性矩. 解：（a ）22a 号工字钢对付其对付称轴的惯性矩是.利用仄止轴定理得拉拢截里对付轴的惯性矩（b ）等边角钢的截里积是，其形心距中边沿的距离是28.4 mm ，供得拉拢截里对付轴的惯性矩如下：习题I-11（b ）图图形 b h Ixc a A Ix中间矩形 10 600 180000000 0 6000 180000000 上矩形 250 10 20833 305 2500 232583333 下矩形 250 10 20833 305 2500 232583333 左上L 形 1795100 1926 143869495 左上L 形 1795100 1926 143869495 左下L 形 1795100 1926 143869495 左下L 形17951001926143869495 A a I I xc x 2+=1220644645[习题I-12]试供习题I-3a 图所示截里对付其火仄形心轴的惯性矩.闭于形心位子，可利 用该题的截止.解：形心轴位子及几许尺寸如图所示.惯性矩估计如下：试供图示各截里对付其形心轴x的惯性矩.习题I-13(a)图形bi hi Ai Yci AiYci Yc ai Ixc Ix(mm4)上矩形1000 100 100000 650 65000000 225 83333333 5145833333 下矩形300 600 180000 300 54000000 125 5400000000 8212500000 齐图280000 119000000 425习题I-13(c)图形bi hi r Ai Yci AiYci Yc Ixc(mm4) ai Ix(mm4)矩形2140 1150 2461000 575 1415075000 271222708333 159 333213698275 半圆790 -980333 335 -328692667 42750202791 399齐图1480667 1086382333 734半圆：π3/4ryc=半圆：ππ9/88/44rrIxc-=习题I-13(d)图形bi hi Ai Yci AiYci Yc ai Ixci Ix(mm4)从下往上2216 3520 8 28160 37475093 4924386131814 2520 23 57960 35941160 324821280 16 674 10784 367 3957728 0 408242699 408242699 2214 3080 711 2189880 32950307 333432587 449 4005 2893613 3427034 464367735习题I-13( b)图形bi hi Ai Yci AiYci Yc ai Ixc Ix(mm4)上图(3) 25 150 3750 275 1031250 148 7031250 89601489 中图(2) 200 150 30000 125 3750000 2 56250000 56328044 下图(1) 100 50 5000 25 125000 102 1041667 52667577 齐图38750 4906250 127 1985971105 123909 9127341 382 202330291 4[习题I-14] 正在曲径aD8=圆截里中，启了一个aa42⨯的矩形孔，如图所示.试供截里对付其火仄形心轴战横曲轴形心的惯性矩xI战y I.解：先供形心主轴的位子截里图形对付形心轴的静矩（里积矩）等于整：（y轴背下为正）（拉拢图形对付过圆心轴x1的惯性矩）（拉拢图形对付形心轴x的惯性矩）习题I-14b(a) h(a) r(a) Ai(a2) Yci(a) AiYci Yc(a) Ixc ai Ix(a4) 矩形4 2 -8.00 1 -8 2.667 1.1893 14.0圆 4 50.27 0 0 201.062 -0.1893 202.942.27 -8 -0.1893 188.9 [习题I-15]正圆形截里中启了一个曲径为mmd100=的半圆形孔，如图所示.试决定截里的形心位子，并估计对付火仄形心轴战横曲形心轴的惯性矩.解：习题I-15图形 bi hi rAiYci AiYciYcIxci ai Ix正圆形 200 20040000 100 4000000 133333333 2 133546801 半圆 50 -3927 79 -30936568597724 2860346 齐图360733690635 102130686455π34100r y c -=ππ98844r r I xc -⋅=A a I I xc x 2+=形心位子：X （0，102）.对付火仄形心轴的惯性矩：4130686455m m I x =.对付横曲形心轴的惯性矩：习题I-15图形 a r Iy （mm 4） 正圆形 200半圆 50 2454367齐图13087896681244r a I y ⋅-=π[习题I-16] 图示由二个a 20号槽钢组成的拉拢截里，若欲使截里对付二对付称轴的惯性矩x I 战y I 相等，则二槽钢的间距a 应为几？解：20a 号槽钢截里对付其自己的形心轴、的惯性矩是，；横截里积为；槽钢背到其形心轴的距离是.根据惯性矩定义战仄止轴定理，拉拢截里对付，轴的惯性矩分别是 ；若即等式二边共除以2，而后代进数据，得 于是所以，二槽钢相距[习题I-17] 试供图示截里的惯性积xy I解：设矩形的宽为b 下为h ，形心主惯性轴为c c y x 0，则由仄止移轴公式得：故，矩形截里对付其底边取左边所形成的坐标系的惯性积为：2241h b I xy =[习题I-18] 图示截里由二个mm mm mm 10125125⨯⨯的等边角钢及缀板（图中实线）拉拢而成.试供该截里的最大惯性矩max I 战最小惯性矩习题I-17 图形 b h Ixy 左矩形 10 100 250000 下矩形: 100 10 250000 沉复加的矩形 10102500齐图上图+下图-沉复图= 497500解：从图中可知，该截里的形心C位于二缀板共共的形心上.过C C.C后所得到的坐标系是截里的的二条对付称轴，也便是该截查型钢表得：12.5号等边角钢的参数如下：，，，角钢形心主惯性轴取截里形心主惯性轴之间的距离：（注：缀板用实线绘出，表示其里积可忽略没有计）[习题I-19].论断：1、过正圆形形心的一对付相互笔曲的轴，它们的惯性矩相等，它们的惯性积为整；2、过正圆形形心的一对付相互笔曲的轴，绕形心转化之后，惯性矩、惯性积脆持没有变.[习题I-20]决定图示截里的形心主惯性轴的位子，并供形心主惯性矩.（a ）解：截里的形心主惯性轴取横曲矩形的形心主惯性轴沉合.Ix Iy Ixy-259200000 Ix0= 704109187-259200000Iy0=54184146224)(2120xy y x yx y x I I I I I I I +-±+=(b)解：以20号槽钢（图I ）的下边沿为x 轴，左边沿为y 轴，修坐坐标系.8号槽钢编号为图II.则拉拢截里的形心估计如下：习题I-20(b) 少度单位:cm图形 Ai Xci Yci AiXci AiYci Xc Yc I 10 64 II 16 -15 齐图习题I-20（b ）图形 Ai iabiIxci' Iyci' Ixci Iyci Ixciyci' Ixciyci tan2a0a0Ix0Iy0I 1981 165 0 II齐2296249[习题21]试用近似法供习题I-4出的透彻值相比较.解：圆的圆程为：把y轴的半径10过仄分面，做x轴的仄止线.从下往上，每个分块的中面的y坐标取x坐标如下表所示.[习题I-22]（提示：最简朴的证法是利用惯性积的仄止移轴公式，并利用一对付相互笔曲的坐标轴中有一为截里的对付称轴时，其惯性积为整的特性.）解。

材料力学课件之截面几何性质


d
2 2
16 43 416 (5.53 2)2 12
4123 412 (10.57 6)2 12
2416.76mm4
y
C2 C
z
C1
646 （单位mm）
y1
y2
29
Ai yi Ai Ai zi Ai
Ai yi
A
Ai zi
A
o Z1
z
Z2
使用上述公式时，对于挖掉部分的面积应取负值。
6
例2 求图示矩形截面abcd 部分对z 轴的静矩。
y
C3
C1
C2
o 2
4
6
12
123
Ai 144 72 -16
yi 6 4 6
z
zi 6 16 4
（单位：cm）
解：
yC
404
402
(mm)
402 )
12
64
4
23034100.7mm4
17
截面图形的的几何性质------形心和惯性矩
1，简单截面
1、有对称轴的截面，记忆或直接判断 教材353页附录Ⅱ
2、型钢，查表。教材356页附录Ⅲ
2，组合截面，组合法。
§Ⅰ.5惯性矩和惯性积的转轴公式,主惯性轴
一：已知 Iy、Iz、Iyz、(逆时针为正)，求 Iy1、Iz1、Iy1z1
cos 2
0
C
z
方形截面
Iz'
Iz
Iy 2
Iz
Iy 2
cos 2
I yz sin 2
Iz
Iy 2
Iz
I
y'
Iz
2
其中：
I

材料力学课件第六章截面图形的几何性质


例6-1 求图示半径为r的半圆形对其直径轴x的静矩及其形心坐 标yC。 解：过圆心O作与x轴垂直的y轴，在距x任意高度y处取一个与x 轴平行的窄条， d A 2 r2 - y2 d y

所以 S x A y d A 0
r
2 3 y( 2 r - y ) d y r 3
2 2
y dA yC O C r
第6章 截面的几何性质
惯性矩与惯性积的移轴定理
y z1
z
已知： Iy，Iz，Iyz A dA
y
求： Iy1，Iz1，Iy1z1
I y 1 z1 d A
2 A
O a
y1
O´ b
z
I z1 y1 dA
2 A
I y1z1 y1 z1dA
A
y1=y＋a z1=z＋b
第6章 截面的几何性质
2 A
b 2 b 2
hb3 z hdz 12
2
惯性矩与惯性积的移轴定理
第6章 截面的几何性质
惯性矩与惯性积的移轴定理
惯性矩与惯性积的移轴定理
移轴定理（parallel-axis theorem）是指图形对于 互相平行轴的惯性矩、惯性积之间的关系。即通过已 知图形对于一对坐标的惯性矩、惯性积，求图形对另 一对坐标的惯性矩与惯性积。
Δ Pi y i P
于是有 同理有
yC
x xC
xi
§6-1 截面的静距与形心位置
工程中常遇到由基本图形构成的组合截面，例如下面 例题中所示的两种横截面。当对组合截面杆件计算在外力 作用下的应力和变形时需要求出它们对于形心轴x，y (本 节中的x轴就是以前我们所用的z轴) 的一些几何性质，例

材料力学 截面的几何性质


O1 O 2
O
x
O3
x 1
C
课堂练习
I.
&
任意图形，若对某一对正交坐标轴的惯性积为零， 则这一对坐标轴一定是该图形的（ ）。
B
A. 形心轴； B. 主轴 C. 主形心轴 D. 对称轴 在图示开口薄壁截面图形中，当（ 为一对主轴。
y
）时，y-z轴始终保持
A. y轴不动，x轴平移； B. x轴不动，y轴平移； C. x轴不动，y轴任意移动；
y b C 1x C 2x O a x
æ 1 öæ 2 ö æ 1 öæ h ö = ç bh ÷ç h ÷ + ç ah ÷ç ÷ è 2 øè 3 ø è 2 øè 3 ø
h 2 = (a + 2 b ) 6
形心位置
h
x = 0
h 2 (a + 2 b ) h a + 2 b S x y = = பைடு நூலகம்· = 6 A h 3 a + b (a + b ) 2
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
课堂练习
I.
&
在下列关于平面图形的结论中，（
）是错误的。
A.图形的对称轴必定通过形心； B.图形两个对称轴的交点必为形心； C.图形对对称轴的静矩为零； D.使静矩为零的轴必为对称轴。 在平面图形的几何性质中，（
y
dA y
ü2、惯性矩和极惯矩永远为正，
惯性积可能为正、为负、为零。
x 1
ü3、任何平面图形对于通过其形
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

d 4
128
d4
18
Iy
z
z0
C o
z1
y1 y
2）解法二
I z1 I y1 I z0 I y
I z0 I z1 I y1 I y 2I z1 I y
2 d 4
256
Iy

d 4
128
Iy
Iz

I z0
OC2
d2
16

d 4
附录 截面的几何性质
y
yy
O
§ -1 置
dA
C
x
z
x
截面的静矩和形心位
1. 静矩（或一次矩）
S y
zdA
A
Sz
ydA
A
(单位： m3 或mm3 。）
2. 形心坐标公式
z A z d A A Sy A
y A y d A A Sz A
Sy A z Sz A y
C zC o z0
yC y
解：1）解法一
I zC

I yC
I z0
a2 d 2 d 4
16 256
( 2d )2 d 2 3 16
d 4 d 4 256 36
I y I z I yC I zC
I z I yC I zC I y 2I zC I y
C
z
y b
y
z
z
d
解： I y I z I p
Iy Iz
Iy

Iz

Ip 2

πd 4 64
§-3 惯性矩和惯性积的平行移轴公式 •组合截面的惯性矩和惯性积
1.惯性矩和惯性积的平行移轴公式
y
Iz

bh3 12
h
C
z
Iz'

bh3 12
z’ b
y yc C
Iz Izc a2 A
zc
57.4104 mm4
3. 形心主轴的确定
1) 过同一点的轴系中，主矩是唯
A o
0
z0
一的；
2) 过不同点的轴系中，主轴和主
z
矩是不同的；
3) 较小的形心主矩是最小值，
y
y0
但较大的形心主矩不是最大值；
4) 截面有三根或以上的对称轴时，则 过形心的任一根轴均为形心主轴， 且惯性矩相等；
1.惯性矩和惯性积的转轴公式
y
Iz

bh3 12
h
C
z
Iz'

bh3 12
b
y
注意：1. 两个座标系的原点
必须重合；
2. 两轴惯性矩之和为常量
O
z
I y1 I z1 I y I z I p
I z1

Iz
Iy 2

Iz
Iy 2
cos 2
I yz
sin 2
I y1

Iz
2
y
dA
1.极惯性矩
Ip
2d A
A
2. 惯性矩
I y
z2d A
A
I z
y2d A
A
O
z
I p
2d A
A
(y2 z2)d A
A
z
IzIy
y
3. 惯性积
I yz
yz d A
A
1) 极惯性矩、惯性矩和惯性积均与所取的坐标系有关，
2) 惯性积可正可负
4）静矩为0的轴为截面的形心轴。
例 求图示T形截面的形心位置。
100 A1 A1
解：建立参考坐标系。
n
20
z z'
yC

Ai yCi
i 1 n
Ai

A1 yC1 A2 yC2 A1 A2
100
i 1
A2
A2 y A3 20
100 2010 100 20 70
z"
100 20 100 20
A1 yC1 A2 yC 2 A1 A2
14 3 a 3(8 )
a2 a ( a2 )(a 2a )

2
8
3
a2 ( a2 )
8
yC
a
C
z 3) 求IzC
A1 zC
I zC I zC 1 I zC 2
2a
3
y a
A2zz0C’
I zC 1

例：试计算截面的形心主惯性矩。
80 10
y C 120
解：1) 求形心坐标
Ⅰ
2) 求对自身形心轴
的惯性矩
C
zC 3) 由平行移轴公式
求对整个截面形
心轴的惯性矩
10 Ⅱ 4) 用转轴公式确定主轴位置
tan 20

2I yczc Izc I yc
1.093
20 227 .6 0 113 .8
a4 12

(a 2

yC
)2 a2
I zC 2

I zC' 2
(a
2a
3

yC )2
a2
8
I zC' 2

I z0
( 2a )2
3
a2
8
a4 ( 2a )2 a2 128 3 8
I xC

10 a4
3(8 )
§-4 惯性矩和惯性积的转轴公式 •截面的主惯性轴和主惯性矩

hb3 12
I yz 0
y和z中只要有一根轴是截面的对称轴，则Iyz=0
思考：O为直角三角形ABD斜边上的中点，y、z轴为
过点Ｏ且分别平行于两条直角边的两根轴，关于惯性
积Iyz= ______。
A
y
Iyz=
0
bO
z
Ba
D
y
bh3 I z 12
h
例：试计算图示圆截面对于其 形心轴的惯性矩。
128

Iy

(
2 2d )2 d 2 3 16

d 4
128
d4
18
Iy
z0 z1 A1 z
A2 C
y1
C’ o y
A3
3）解法三
I z I z1
I z0
I z01 I z0 2 I z0 3
d 4
128
d4
I z0 2 I y 128
d4
I z0 2 128 I y
302
100 20
=3.467 106 mm4
Iz =1.867 106+3.467 106 =5.334 106 mm4
补例1 求图示截面对其形心轴的惯性矩。
a
C
z A1
zC
解：1) 求Iy
I y I y1 I y2
a4 12
a4
128
2) 求yC
y
A2
a
yC

5) 正多边形任意一根形心轴均为形心 主轴；
6) 截面有两根互相垂直的对称轴，则 这两根轴即为形心主轴；
7) 截面只有一根对称轴时，该对称轴 是一根形心主轴，另一根形心主轴 与该轴垂直；
8) 无对称轴（例）；
补例2 直径为d的四分之一圆形，C是其形心，已知
z
Iy

(
2)d 4 256
，试求Iz。
zc
I y I yc b2 A 平行移轴公式
I yz I yczc abA
b O
z 注意：1. 两轴必须平行；
2. 两轴中必须有一轴为形心轴：
已知对形心轴的惯性矩和惯性积: Iz Izc a2 A 已知非形心轴的惯性矩和惯性积: Izc Iz a2 A
3. 在一组平行轴系中对形心轴的惯性矩最小；
= 40 mm
100 20 (10) 100 2050
yC '
100 20 100 20
= 20 mm
yC
"

100
120 (60) 100 120
(100 40) 100 40
2
(50)

2
=
-80
mm
d
o yC
z
yC

2d
3
y
Байду номын сангаас
§ I－2 极惯性矩 ·惯性矩 ·惯性积
(2) 主惯性矩:截面对于主惯性轴的惯性矩。
Iz0

Iz
Iy 2

1 2
Iz Iy
2

4I
2 yz
I y0

Iz
Iy 2

1 2
Iz Iy
2

4I
2 yz
极大值Imax 极小值Imin
(3) 形心主惯性轴：主惯性轴的原点与形心重合。
(4) 形心主惯性矩:截面对于形心主惯性轴的惯性矩。
Iy

Iz
Iy 2
cos 2

I yz
sin 2
I y1z1

Iz
2
Iy
sin 2

I yz
cos 2
2.截面的主惯性轴和主惯性矩 (1) 主惯性轴:截面对其惯性积为0的一对坐标轴。
I y1z1

Iz
Iy 2
sin 20