下载文档原格式
西南交《工程力学A》在线作业二
下列结论中正确的是( )
A:内力是应力的代数和
B:应力是内力的平均值
C:应力是内力的集度
D:内力必大于应力
答案：C
构件在外力作用下平衡时，可以利用( )
A:平衡条件求出所有未知力
B:平衡条件求出某些未知力
C:力系的简化求未知力
D:力系的合成或分解求未知力
答案：B
一空心钢轴和一实心铝轴的外径相同，比较两者的抗扭截面模量，可知( )。
A:空心钢轴的较大
B:实心铝轴的较大
C:其值一样大
D:其大小与轴的剪切弹性模量有关
答案：B
根据均匀性假设,可认为构件的( )在各点处相同。
A:应力
B:应变
C:材料的弹性常数
D:位移
答案：C
材料经过冷作硬化后,其( )
A:弹性模量提高,塑性降低
B:弹性模量降低,塑性提高
C:比例极限提高,塑性提高
D:比例极限提高,塑性降低
答案：D
下列说法正确的是（）。
A:内力随外力增大而增大。
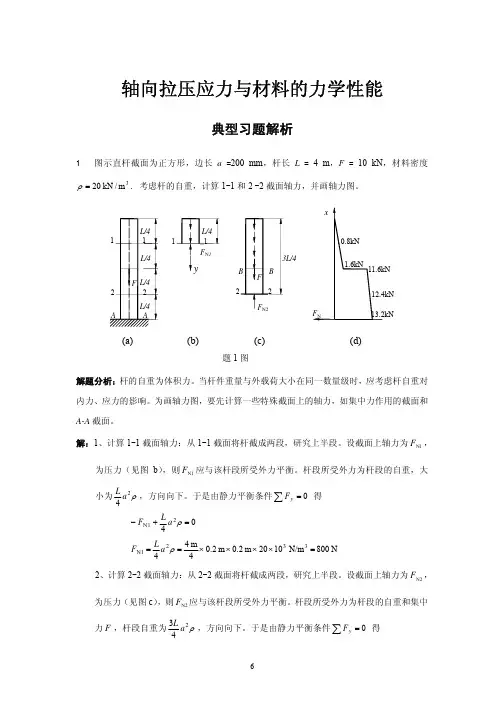
1、对于轴力图来说和剪力图、扭矩图类似也是会发生突变的，当某截面受到外力（一般都是指垂直于该截面的外力）作用是轴力图中会发生突变，轴力的代数和等于该外力的大小，并且当轴力图从左向右画时方向向左的集中力引起向上的突变，方向向右的集中力引起向下的突变。
2、当杆件受到拉压作用时，轴向伸长横向就压缩，轴向压缩横向就向四周膨胀，这变形规律适用于落在与轴线垂直的横截面内的所有线段，包括圆截面杆的直径、方形截面杆的边长和横截面的周长以及横截面上任意两点之间的距离，这两点之间的连线甚至可以跨过没有材料的空心区域。
例题：等直空心圆截面杆收到轴向拉伸作用，材料的受力在弹性范围内，则外径和内径都减小。
3、线应变的计算：变形的累加是有意义的，即一段杆件的总的变形量等于每个分段变形量的代数和；但是线应变指的是在一个很小的范围内杆件的变形程度，可以简单地将线应变理解成事属于某个截面的。
当一段杆件受力均匀时，这段杆件各个横截面上的线应变都是相等的，可以笼统地说这段杆件的线应变是多少，但是当杆件的轴力不同时，只能说两段杆件的线应变各是多少，而不能把两段杆件的线应变加起来。
把两段的线应变加起来是没有任何力学意义的。
就像一辆汽车行驶在路上，在第一段是一个速度，第二段是另外一个速度，把这两个速度加起来是没有什么意义的！！！注意：变形量是可以直接求代数和的，即为整段的变形量！！！在计算线应变时要注意，具体到哪一段，这一段的长度必须明确！！4、切应变：切应变是指直角的改变量，即受力前确定两条互相垂直的线段，受力后如果这两条线段的夹角发生变化，那么这两条线段在直角范围内的改变量就是切应变。
（注意受力前后的限制）5、传动轴计算中的注意点：由功率向力偶的转化公式必须熟练同时注意单位的限制；传动轴的转向和主动轮的转向相同，而从动轮的转向和主动轮（传动轴）的转向相反；6、在扭转问题中，扭转角是可以相加的，并且要求求某一段的扭转角是，当整段截面的扭矩不同时，必须分段求，再求代数和！！！另外在扭转的问题中I P 和W P （这两者是对整个截平面而言）与第四章中的梁的弯曲和扭转中的Iz和Wz （这两者是对截平面中的某一轴Z轴而言）的二倍关系！！！εσGγτ=与对比着运用!E=7、在求解梁的弯矩和剪力时，经常涉及到含中间绞的超静定问题，这就需要在中间绞上下手，一般来说是分两段，借助中间绞来求解各个约束力。
西交《材料力学》在线作业一、单选题（共 30 道试题，共 60 分。
）1. 厚壁玻璃杯倒入开水发生破裂时，裂纹起始于（）。
A. 内壁；B. 外壁；C. 壁厚的中间；D. 整个壁厚。
正确答案：B2. 阶梯圆轴的最大切应力发生在（）。
、A. 扭矩最大截面；B. 直径最小的截面；C. 单位长度扭转角最大的截面；D. 不能确定。
正确答案：D3. 应用叠加原理求梁横截面的挠度、转角时，需要满足的条件有（）。
、A. 梁必须是等截面的；B. 梁必须是静定的；C. 变形必须是小变形；D. 梁的弯曲必须是平面弯曲。
正确答案：C4. 梁在某一段内作用有向下的分布力时,则在该段内M图是一条()。
A. 上凸曲线；B. 下凸曲线；C. 带有拐点的曲线；D. 斜直线。
正确答案：A5. 应用叠加原理求梁横截面的挠度、转角时，需要满足的条件有（）。
A. 梁必须是等截面的；B. 梁必须是静定的；C. 变形必须是小变形；D. 梁的弯曲必须是平面弯曲。
正确答案：C6. 非对称的薄壁截面梁承受横向力时，若要求梁只产生平面弯曲而不发生扭转，则横向力作用的条件是（）。
、A. 作用面与形心主惯性平面重合；B. 作用面与形心主惯性平面平行；C. 通过弯曲中心的任意平面；D. 通过弯曲中心，平行于主惯性平面。
正确答案：D7. 在以下措施中（）将会降低构件的持久极限。
A. 增加构件表面光洁度；B. 增加构件表面硬度；C. 加大构件的几何尺寸；D. 减缓构件的应力集中。
正确答案：C8. 滚珠轴承中，滚珠和外圆接触点处的应力状态是（）应力状态。
A. 单向；B. 二向；C. 三向；D. 纯剪切。
正确答案：C9. 材料的持久极限与试件的（）无关。
A. 材料；B. 变形形式；C. 循环特征；D. 最大应力。
正确答案：D10. 判断下列结论正确的是（）A. 杆件某截面上的内力是该截面上应力的代数和；B. 杆件某截面上的应力是该截面上内力的平均值；C. 应力是内力的集度；D. 内力必大于应力。
东北农业大学网络教育学院材料力学网上作业题（2015更新版）绪论一、名词解释1.强度2. 刚度3. 稳定性4. 变形5. 杆件6.板或壳7.块体二、简答题1．构件有哪些分类？2. 材料力学的研究对象是什么？3. 材料力学的任务是什么？4. 可变形固体有哪些基本假设？5. 杆件变形有哪些基本形式？6. 杆件的几何基本特征？7.载荷的分类？8. 设计构件时首先应考虑什么问题？设计过程中存在哪些矛盾？第一章轴向拉伸和压缩一、名词解释1.内力2. 轴力3.应力4.应变5.正应力6.切应力7.伸长率8.断面收缩率9. 许用应力 10.轴向拉伸 11.冷作硬化二、简答题1.杆件轴向拉伸或压缩时，外力特点是什么？2.杆件轴向拉伸或压缩时，变形特点是什么？3. 截面法求解杆件内力时，有哪些步骤？4.内力与应力有什么区别？5.极限应力与许用应力有什么区别？6.变形与应变有什么区别？7.什么是名义屈服应力？8.低碳钢和铸铁在轴向拉伸时，有什么样的力学特性？9.强度计算时，一般有哪学步骤？10.什么是胡克定律？11.表示材料的强度指标有哪些？12.表示材料的刚度指标有哪些？13.什么是泊松比？14. 表示材料的塑性指标有哪些？15.拉压杆横截面正应力公式适用范围是什么？16.直杆轴向拉伸或压缩变形时，在推导横截面正应力公式时，进行什么假设？三、计算题1. 试用截面法求下列各杆指定截面的轴力。
2. 试用截面法求下列各杆指定截面的轴力。
3. 试用截面法求下列各杆指定截面的轴力。
4. 试用截面法求下列各杆指定截面的轴力。
5. 试用截面法求下列各杆指定截面的轴力。
6. 试用截面法求下列各杆指定截面的轴力。
7 高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的小径d = 175 mm。
已知作用于拉杆上的静拉力F=850 kN，试计算大钟拉杆横截面上的最大静应力。
8 一桅杆起重机如图所示，起重杆AB为一钢管，其外径D = 20 mm，内径d≈18 mm；钢绳CB的横截面面积为10 mm2。
材料力学复习题（一）一、1． B 2． B 3． A 、C 4． D5． A 、B 、D 6． C 7． A 、B 8． A 、B 、D 二、3.43-=xy τMPa ，3.43-''y x τMPa ，50='y σMPa三、3.254=BC Cr FkN ，45][=F kN四、略， 五、1.14-=Hx σMPa ，6.0=Hxz τ MPa ，2.143=r σMPa六、EIQl Ql EIh v Cd 94)41811(33++=材料力学复习题（二）一、选择题1、D ；2、B ；3、D ；4、C ；5、D 。
二、填空1、3段；位移边界条件 0,0,0===D A A w w θ；光滑连续条件CD C BC C w w ,,=，CD C BC C ,,θθ=，BC B AB B w w ,,=。
2、h y c 32=3、连续性假设；均匀性假设；各向同性假设；线弹性；小变形。
4、< ；= 。
5、0.003；0.002；47.12kN 。
三、计算题1、图示为由五根直径50d mm =的圆形钢杆组成边长 为1a m =的正方形结构，材料为235Q 钢，比例极限aABC FaDF 题 3-1 图200p MPa σ=，屈服应力235s MPa σ=，弹性模量200E GPa =，中柔度杆的临界应力公式为304 1.12()cr MPa σλ=-。
试求该结构的许用载荷[]F 。
解：（1）求AB 、BD 和AD 杆的内力绘制节点A 和B 的受力图如图所示。
FF BAF DAA45ºF ABF BCF BDBAB 杆和AD 杆为受压杆，BD 杆受拉。
其内力分别为：2F F F AD AB ==，F F BD =（2）根据杆AB 和AD 的压杆稳定确定许可载荷圆杆4504mm d i ==，杆AB 和AD 的柔度均为805041000=⨯==mm i a μλ。
西南交《材料力学》在线作业二一、单选题（共 50 道试题，共 100 分。
）1. 在冲击应力和变形实用计算的能量法中，因为不计被冲击物的质量，所以计算结果与实际情况相比，（）. 冲击应力偏大，冲击变形偏小. 冲击应力偏小，冲击变形偏大. 冲击应力和变形均偏大. 冲击应力和变形均偏小正确答案：2. 若某低碳钢构件危险点的应力状态为近乎三向等值拉伸，进行强度校核时宜采用（）强度理论。
. 第一. 第二. 第三. 第四正确答案：3.在图示四个单元体的应力状态中，（）是正确的纯剪切状态。
. (). (). (). ()正确答案：4. 一内径为,外径为的空心圆轴,其扭转截面系数有四种答案:. W p = π 3 16 π 3 16. W p = π 3 32 π 3 32. W p = π( 4 4 ) 16. W p = π 4 32 π 4 32正确答案：5. 根据圆轴扭转的平面假设，可以认为圆轴扭转时其横截面（）。
. 形状尺寸不变，直径仍为直线. 形状尺寸改变，直径仍为直线. 形状尺寸不变，直径不保持直线. 形状尺寸改变，直径不保持直线正确答案：6. 用力法求解静不定问题的正则方程，实质上是（）. 静力平衡方程. 物理方程. 变形协调方程. 功的互等定理正确答案：7. 分析任意实心截面形状杆件的斜弯曲时，荷载分解的方向应当是一对（）. 任意正交坐标轴. 过形心的正交坐标轴. 过形心的水平与垂直正交坐标轴. 形心主惯性轴正确答案：8.与图示应力圆对应的是（）应力状态. 纯剪切.单向.二向.三向正确答案：9. 梁在集中力作用的截面处，（）。
. Q图有突变，M图光滑连续. Q图有突变，M图连续但不光滑. Ｍ图有突变，Ｑ图光滑连续. Ｍ图有突变，Q图连续但不光滑正确答案：10. 根据小变形条件，可以认为（）。
. 构件不变形. 构件不破坏. 构件仅发生弹性变形. 构件的变形远小于其原始尺寸正确答案：11. 剪应力互等定理是由单元体的（）导出的。
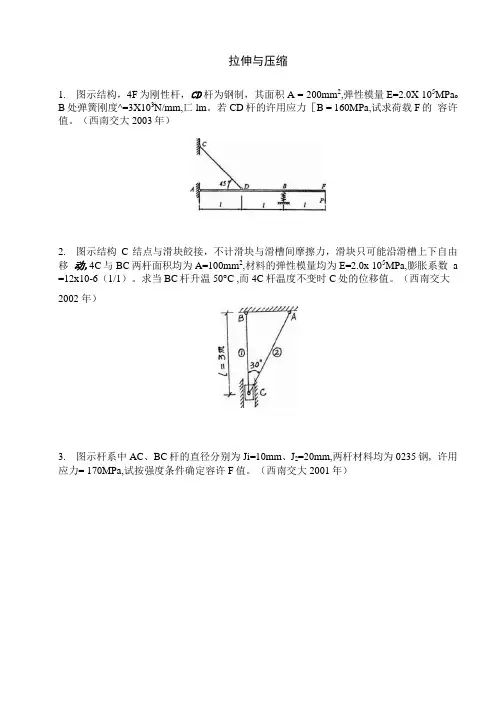
拉伸与压缩1.图示结构，4F为刚性杆，CD杆为钢制，其面积A = 200mm2,弹性模量E=2.0X 105MPa o B处弹簧刚度^=3X103N/mm,匸lm。
若CD杆的许用应力［B = 160MPa,试求荷载F的容许值。
（西南交大2003年）2.图示结构C结点与滑块餃接，不计滑块与滑槽间摩擦力，滑块只可能沿滑槽上下自由移动,4C与BC两杆面积均为A=100mm2,材料的弹性模量均为E=2.0x 105MPa,膨胀系数 a =12x10-6（1/1）。
求当BC杆升温50°C ,而4C杆温度不变时C处的位移值。
（西南交大2002 年）3.图示杆系中AC、BC杆的直径分别为Ji=10mm、J2=20mm,两杆材料均为0235钢, 许用应力= 170MPa,试按强度条件确定容许F值。
（西南交大2001年）4.图示两端固定的杆件，在距左端x处作用一轴向力F，杆横截面面积为4,材料的许用拉应力为［况，许用压应力为［创，且［创=3［5］。
求x为何值时F的许可值最大?其值［FUx 为多少？（西南交大1999年）X5.图示结构中①、②、③三杆的材料相同，弹性模量均为E，线膨胀系数均为a。
三杆的横截面面积分别为旳、A2、A3 ,各杆的长度如图所示。
横杆CD为钢杆。
受力如图所示, 各杆温度同时上升&°C。
求①、②、③三杆的轴力。
（西南交大1998年）6.图示结构中，BC为刚性梁，杆①、②、③的材料、横截面面积均相同，在横梁BC ± 作用一可沿横梁移动的载荷F,其活动范围为0 <x<2«o计算各杆的最大轴力值。
（西南交大1997年）p7、空心圆截面钢杆,其外径D=40mm,内径d=20mm,承受轴向拉力F=180kN,钢材的弹性常数E=2.0x 105MPa及v=0.3。
求m—m横截面上a、b两点的相对位移和b、c两点的相对位移。
（西南交大1991年）D8、AC及BC两钢杆的抗拉刚度为EA,在C点較接处受一铅垂向下的力F作用。
一、超静定结构的求解：
1、根据超静定的成因不同，列出的平衡方程和几何方程思路和方法也不同，要注意掌握其中的规律。
例如：
在本体中所补充的几何方程应该是{ EMBED Equation.KSEE3 \* MERGEFORMAT |C A ∆=∆如果补充的是由于结构的对称性会自动满足，还是无法求解。
所以对于有刚性构件的结构，几何方程应根据“变形协调”的思路去思考。
即寻找由刚性构件确定出来的变形规律。
2、对于一些题目来说涉及到斜变形，即：既有x 方向的变形又有y 方向的变形。
就要使用作图法来求解。
方法：以铰接点为圆心，以杆变形后的长度为半径，画圆弧，小变形可以以垂线（或者切线）代替圆弧。
3、温度变化在超静定中的应用
求解杆1、杆2的内力：
由于温度变化和受力是引起杆件变形的两种不同的物理因素，如果是静定结构，那么温度变化引起的杆件是不受任何约束的，而且只有上式的第一项，此时杆件不受力；但是对于超静定结构，温度变化引起的变形受到约束，杆件内产生了内力，内力对杆件的变形进行调整，因此，杆件的变形就要在上式的第一项的基础上加上杆件内力的影响。
其实，考虑的简单一点就是此时的结构是在温度变化和受力的两种因素的共同作用之下，因此变形的计算要同时考虑这两个因素的影响。
二、应力状态与强度理论
1、计算倾角截面上的正应力与切应力的公式的注意事项：
注意其中的的正负，绕轴线逆时针转动为正，顺时针为负。
2、主应力
对于平面单元体三个主应力必定是纯在一个主应力为零。
一定要给出三个，其下标1、2和3要按照数值的大小来排列，袋鼠值最大的主应力命名为第一主应力。
最大正应力作用的平面切应力一定为零。
而最大切应力作用的平面正应力一般不为零，除非应力圆的圆心正好与坐标原点。
根据切应力互等定理两个互相垂直的斜截面上的切应力大小相等符号相反，但是反过来并不一定成立。
两个在同一个应力圆的圆周上互相垂直的斜截面的正应力之和为定值
即：。
使用时要注意条件必须是位于同一应力园的圆周上，否则不一定成立。
对于纯剪单元体45度方向上快速求解其主应力的公式的使用
其对应的45度方向上的主应力为：
对应的公式为：
当应力为相反的方向时，相应的取负号
3、应力状态及应力圆
相应的应力圆
这表明这个单元体的所有斜截面都不会出现压应力，二只有拉应力和切应力的存在。
相应的应力圆
这表明这个单元体的所有斜截面上都不会出现拉应力，而只会存在只会有压应力和切应力存在。
相应的应力圆
由于这个单元体上下左右四个面上只有切应力、没有正应力，因此这种盈利状态又称为纯“剪应力状态”，丹药注意“纯剪应力状态”只是反映了单元体上作用的盈利特点，它不是除单向、平面和空间（三向）应力状态之外的第四种应力状态。
4、使用作图法求斜截面上的应力
注意：
1）、角度的起始位置时圆心与的连线，而不是轴
2）、旋转角度时应以应力圆的圆心C为中心，而不是以坐标原点O为中心，当坐标原点与应力圆的圆心非常接近时要非常的小心。
3）在应力圆上相对于起始点的旋转方向要和单元体上相对于起始面的旋转方向相同；
4）二倍角关系，应力圆上旋转角度应该是单元体上旋转的角度的两倍。
5）注意最大切应力可以应力圆上截取，即：纵坐标最大处，但由于作图的精度有限，所以最好还是利用公式计算：，但要注意其中的正负号的正确。
三、应力与应变的关系
1、根据应变效应可以知道，一个方向的正应力不仅在这个方向上引起线应变，而且还会在与这个方向垂直的方向引起线应变。
2、某一方向的线应变一定与两个互相垂直的方向上的主应力有关。
3、在强度理论中主应力的排序是非常的敏感的，排序出错，相应的强度理论也会出错。
4、一般说来，第一、二强度理论适用于脆性材料，而第三、四强度理论适用于
塑性材料，并且第三、四强度理论常用。
四、组合变形
1、一般说来，在压弯组合变形，中性轴会和惯性矩较小的主轴重合。
2、矩形截面的梁发生斜弯曲时，其中性轴不在于主轴重合如：
该横截面的主轴就不再是y轴，而是a-a轴。
3、当梁在两个互相垂直的平面内发生弯曲时弯曲平面和挠曲平面有如下关系：
两角度之间的关系为：
4、矩形截面的弯矩计算不可以用总弯矩来计算，应采取分解、分组、叠加的方法来来计算如：
则：
5、要正确的掌握概念，看清题目所给的信息，切不可想当然，死记公式。
如：
看清题目所给的信息，本题中所给的并不是a点的坐标，而是到x、y轴的距离，所以应该选A而不是B，所以应该题目所给的信息，切记想当然。
6、如图所示：
求解最大弯曲正应力的方法切不可使用
切记：
1）、圆是一个极对称图形，过形心的任意一根轴都是型心主轴，因此圆截面梁不会发生些弯曲。
2）、圆截面梁如果受到两个互相垂直的弯矩分量作用时，求截面内不在圆周上的点的最大主应力是可以采用先分解、分组、叠加的方法来求解。
求最大主应力是就不可以使用分解、分组、叠加的方法啦，应为坐标不是表示的那一点。
7、如图所示：
则矩形梁发生
注意规范的表达！
8、判断平面弯曲和斜弯曲的原则：外力的作用线是否平行于截面的型心主轴，如果平行则发生平面弯曲，否则发生斜弯曲。
判断是否发生扭转的原则：判断外力的作用线是否通过截面的弯曲中心，如果通过截面的弯曲中心，则不发生扭转，否则将发生扭转。
注意大多数的开口薄壁构件的弯曲中心是不和截面的型心从和的。
如：T形截面的弯曲中心在翼缘中心线和腹板中心线的交点处。
9、注意使用强度理论像第三强度理论的几种表达形式的使用条件，如
如果当截面上有轴力作用时，除非可以证明轴力引
起的正应力与弯矩引起的正应力相比可以忽略不计，否则是不可以用该种表达形式。
10、截面核心：
矩形的截面核心为一菱形其对角线为与之平行矩形边长的三分之一。
五、压杆稳定
1、在临界力作用下压杆仍可以保持直线平衡状态，只是失稳时直线平衡状态不再是压杆唯一的平衡状态，此时压杆还可以在微弯的状态下保持平衡状态。
2、由于正多边形（包括正方形）对其任意一根型心轴惯性矩横截面的都相等，所以正多边形过型心所有轴的强弱程度都相等，因此正多边形压杆失稳时其任意一根型心轴都可能成为中性轴。
3、当压杆的材料、长度及弯曲刚度均相同时，压杆临界力的大小就取决于约束条件，约束越强临界力就越大，反之亦反。
例如：
显然（4）的临界力最大。
（3）的临界力最小。
六、杆件连接
1、如果力F的作用线通过螺栓群的几何中心，则每根螺栓所承担的力相同且如图所示:
剪切面积为:
每个螺栓的挤压力与剪切力相同：
挤压面积为：
2、如图所示的安全联轴器，当安全销剪断时有：
要根据具体情况进行分析！
3、如图所示，其中D=4d，
支座的受剪面积为；
地基对基座的均布反力q；
基座受剪面上的剪应力的计算:由于基座中“挖去”一个“直径为d高度为t 的圆柱”后所剩部分的竖直方向的分力平衡，有：
注意其中的计算法则和技巧的运用！
4、如图所示，其中截面的宽度（垂直纸面）为b
通过去半边结构可以计算出每根钢板所受的力为
可以计算出剪切面积为bl；挤压面积为。
5、如图所示，在圆柱体中的剪切与挤压的计算：
（为夹接）
其中挤压力,挤压面积为圆柱体的直径和高度的乘积；而剪切力（若是
搭接则）,剪切面积为圆柱体的截面面积。
七、能量方法
1、图示杆件的刚度为EA，计算该杆的应变能：
则应变能为：在本题中
采用分段计算！
2、如图所示在悬臂梁1和2两个截面上收到集中力作用，设1和2 截面的绕度分别如图所示，求；
解：根据卡氏第二定理，令,;
则：
注意到第二个广义力与第二个绕度方向相反所以
3、如图所示，计算整体结构的应变能：
本结构为静定结构，易知BC杆的轴力为,则BC杆的应变能为，对于AB段为对称的结构可以去半边结构来计算；然后进行相加即可！
4、如图所示，求截面A的绕度和转角：
计算本题首先要区分同名荷载，对于A、B处可以都区分也可以只区分一个，对于所要求的可以同时求出转角和绕度！
本题也有要注意点：在求A截面的转角时需要加上一个虚拟的力矩;还有就是AB和BC杆的弯曲刚度不同！
5、如图所示，求C截面的相对转角：
对于本题，根据对陈性，可以去半边结构来进行计算，但是千万不可以想当然的认为A、B支座的水平反力为零！，并且在去半边结构进行计算A支座的水平反力时虚拟力矩必须参与计算！
八、动荷载
1、匀加速运动中的修正系数：当重物匀加速上升时，结果造成向上加速提升重物时需要大于重物重力的力；当重物匀加速下降时，结构造成重物向下匀加速运动时只需施加小于其重力的力即可。
2、如图所示：起重设备自重为Q,将重量为P的重物一匀加速a向上提升，求量的最大弯矩：
本题中梁的最大弯矩发生在跨中C截面处，但是要注意，由于起重设备有自重，
其引起的静弯矩是不可以修正的，而重物的提升过程中，其重力引起的静弯矩是要进行修正的。
3，如图所示，其中，求梁内最大的弯曲正应力。
首先这个题是一个超静定的题目，需要补充几何方程：
即：
然后在进行求解修正。
注意：对于这样的综合性的题目，特别注意步骤，步骤要完整，有了步骤就可以得分。
