工程问题中巧解交替合作

公务员行测考试工程问题示例工程问题在公务员考试行测中考核频率较高，但是难度并不大，大多数考生都是能够做出来的。

下面作者给大家带来关于公务员行测考试工程问题示例，期望会对大家的工作与学习有所帮助。

公务员行测考试工程问题示例对于这种问题常见的情形有两种，一种是显现的都是正效率，另一种是既有正效率也有负效率。

但不管哪种情形，最重要的就是要找到最小循环周期及一个循环周期的效率和。

常见题型1.正效率交替合作例1.一条公路需要铺设，甲单独铺设要20天完成，乙单独铺设要10天完成。

如果甲先铺1天，然后乙接替甲铺1天，再由甲接替乙铺1天……两人如此交替工作。

那么，铺完这条公路共用多少天?A.14B.16C.15D.13【答案】A，解析：设工作总量为20，则甲的工作效率为1，乙的工作效率为2，一个循环周期甲乙共完成工作量1+2=3。

20÷(2+1)=6……2，则经过6×2=12天后还剩下的工作量为2;第13天甲做1份，剩下1份的需要乙连续工作半天才能完成。

即在12天的基础上，还需要甲工作1天，乙工作半天才可以完成。

选项给出的都是整数天，所以乙最后工作的半天按一天来去运算。

故共用14天。

挑选A选项。

例2.单独完成某项工作，甲需要16小时，乙需要12小时，如果依照甲、乙、甲、乙、……的顺序轮番工作，每次1小时，那么完成这项工作需要多长时间?A.13小时40分钟B.13小时45分钟C.13小时50分钟D.14小时【答案】B，解析：设工作总量为48，甲效率为3，乙效率为4，一个循环周期甲乙共完成工作量3+4=7。

48÷7=6……6，则经过6×2=12小时后剩余工作量6，甲再做1小时完成3，乙还需要做全部完成，故完成这项工作共需要13小时45分钟。

挑选B选项。

2.正负效率交替合作例3.一个水池有一进水管A 和一出水管B,单开A需要4小时把空池注满,单开B需要6小时把一池水放空,依照AB循环,每次各开1个小时,经过量长时间空水池第一次注满?A.19B.17C.18D.20【答案】A，解析：设工作总量为12。

工程问题的巧妙解法
陈东明
【期刊名称】《数学小灵通：小学中高年级班》
【年(卷),期】2003(000)010
【摘要】工程问题的一般解法为分数求解法。

除这种解法外,这里向同学们介绍一种巧妙的解法——份数法。

例1.一项工程,由甲队独做要10天完成,由乙队独做要
8天完成。

两队合做多少天完成?[分析与解]把这项工程的工作总量看作(10×8)份。

则甲队每天的工作效率为8份,乙队每天的工作效率为10份。

【总页数】1页(P12)
【作者】陈东明
【作者单位】山东省济南市槐荫区腊山任庄小学
【正文语种】中文
【中图分类】G623.5
【相关文献】
1.共点力动态平衡问题的巧妙解法 [J], 周红霞;
2.一道经典解析几何问题的两种巧妙解法 [J], 张志华;武晓
3.一道经典解析几何问题的两种巧妙解法 [J], 张志华;武晓;
4.一类工程问题的巧妙解法 [J], 叶小飞;申生
5.巧妙利用图解法化解高中生物学部分疑难问题 [J], 刘建峰
因版权原因，仅展示原文概要，查看原文内容请购买。

18.工程问题知识要点梳理一、基本概念1．工程问题：做某件事，制造某种产品，完成某项任务或工程等，都叫做工程问题。

2．工程问题的三个基本量是工作效率、工作时间和工作总量。

（1）工作效率：单位时间内完成的工作量，它是衡量一个人工作快慢的量。

（2）工作时间：完成工作总量所需的时间。

（3）工作总量：完成一项工作的总量。

一般都是把工作总量看做单位“1”。

二、基本数量关系1．一般公式：工作总量＝工作效率×工作时间工作效率＝工作总量÷工作时间工作时间＝工作总量÷工作效率甲工效＋乙工效＝甲乙合作工效之和特别注意：工作量和工作效率都可以直接相加求和，但工作时间不能。

2．巧解工程问题：一般不知道工作总量的时候，我们常常用假设法求解。

我们把工作总量假设为单位“1”，这个巧解方法的公式有：（1）一般给出工作时间，工作效率＝1工作时间。

（2）一般给出工作效率1a，就可以知道工作时间为a。

三、基本方法算术方法、比例方法、方程方法。

考点精讲分析典例精讲考点1 简单的工程问题【例1】一件工作，甲单独10天完成，乙单独15天完成，甲乙合做（）天完成。

【精析】根据题意，把这件工作总量看作单位“1”，甲的工作效率是110，乙的工作效率是115，甲、乙的工作效率和是110+115，再用工作总量除以工作效率和就等于合作的工作时间。

【答案】 把这件工作总量看作单位“1”， 1÷(110+115)=1÷3+230=1÷16=6（天）【归纳总结】 此题主要考查工作时间、工作效率、工作总量三者之间的数量关系，要求甲乙合做需要多少天可以完成，应求出甲乙工作效率和。

考点2 合作工程问题【例2】 一件工作，甲、乙合作需4小时完成，甲、丙合作需5小时完成，乙、丙合作需6小时完成，乙单独做这件工作需多少个小时完成？【精析】 首先把这件工作看作单位“1”，根据工作效率＝工作量÷工作时间，分别求出甲乙、甲丙、乙丙的工作效率，再把它们求和，即可求出三人的工作效率之和的2倍，进而求出三人的工作效率之和是多少；然后用三人的工作效率之和减去甲丙的工作效率，求出乙的工作效率；最后根据工作时间＝工作量÷工作效率，用1除以乙的工作效率，求出乙单独做这件工作需多少个小时完成即可。

用比的知识巧解工程问题1、师徒二人加工一批零件，单独完成，师傅需15小时，徒弟需20小时。

已知师傅每小时比徒弟多加工80个零件。

这批零件共有多少个？2、师徒二人加工一批零件，单独完成，师傅需15小时，徒弟需20小时，若两人合作。

当完成任务时，师傅比徒弟多加工80个零件，这批零件共有多少个？3、加工一批零件，甲单独做需4天，乙单独做需5天，如果两人合做，那么完成任务时甲比乙多做了20个零件。

这批零件共有多少个？4、修一段路，甲独修需40天，乙独修需24天。

现在两人同时从两端开工，结果在距中点850米处相遇。

这段路全长多少米？5、快车从甲城到乙城，需20小时，慢车从乙城到甲城需30小时，两车同时从两城相对开出，相遇时慢车距甲城还有1080千米。

甲、乙两城相距多少千米？6、一列快车从甲站到乙站需5小时，一列慢车从乙站到甲站需8小时，快车先行2小时后，慢车才出发，两车相遇时，离两站中点84千米，甲、乙两站相距多少千米？7、客车和货车同时从甲、乙两地相向而行。

客车行完全程需10小时；货车行完全程需15小时。

两车在中途相遇后，客车又行了90千米。

这时客车行了全程的4/5，甲、乙两地的距离是多少千米？8、甲、乙两人同时开始加工一批零件，每人加工零件总数的一半。

甲完成任务的1/3时，乙加工了45个；甲完成任务的2/3时，乙完成了一半，这批零件共有多少个？9、一批零件，由师傅单独做，需5小时完成；由徒弟单独做，需7小时完成；两人合作，完成任务时师傅做的比总数的一半还多18个。

这批零件共有多少个？1 / 310、一批零件，甲独做比乙独做所需的时间多1/4，两人合作完成任务时，乙比甲多做80个零件，这批零件有多少个？11、东东放学回家需走10分，晶晶放学回家需走14分。

已知晶晶回家的路程比东东回家的路程多1/6，东东每分比晶晶多走12米。

晶晶回家的路程是多少千米？12、一个水池安装了甲、乙两条进水管，在同样的时间内，乙管的进水量是甲管的1.6倍，为了灌满空着的水池，开始由甲管灌入1/5池水，然后关闭甲管，打开乙管，由乙管单独灌满剩下的，共用12分15秒，甲管开了多少分钟？13、一件工作甲做6小时，乙做12小时可以完成。

巧妙解决工程问题在进行各类工程项目的过程中，难免会遇到各种问题和挑战。

这些问题可能会妨碍项目的进展，导致延误或超出预算。

然而，只要我们运用一些巧妙的方法和策略，就能够有效地解决工程问题，确保项目的顺利进行。

本文将针对工程问题的解决提供一些有用的建议和技巧。

第一，充分准备。

在开始任何工程项目之前，我们应该进行充分的准备工作。

这包括详细的计划和时间表，明确项目的目标和关键里程碑。

同时，还应该评估潜在的风险和问题，并制定相应的风险管理计划。

通过充分准备，我们可以尽早识别和预防潜在的问题，从而防患于未然。

第二，优化资源分配。

资源的合理分配和利用对于解决工程问题至关重要。

我们需要根据项目的需求和优先级，合理分配人力、物力和资金等资源。

同时，要注重资源的协调和整合，避免出现浪费或闲置的情况。

通过优化资源分配，可以最大限度地提高工程效率，解决问题时也能更加灵活和迅速。

第三，建立有效的沟通渠道。

在工程项目中，沟通是解决问题的关键。

我们应该建立起高效的沟通渠道，确保所有相关人员之间及时、准确地沟通信息和共享进展。

这可以帮助我们更好地协调和解决问题，避免信息不畅通导致的误解或错误。

因此，在工程项目中，建立良好的沟通渠道非常重要。

第四，保持灵活性和创新性。

工程项目往往是复杂和多变的，我们需要具备灵活性和创新性来应对问题和挑战。

当面临问题时，我们不要守旧和固执，而是应该积极寻找解决方案。

在解决问题的过程中，我们可以尝试新的方法或思路，从而在短时间内找到高效的解决方案。

第五，团队合作和协作。

在解决工程问题时，团队合作和协作是至关重要的。

我们应该建立一个团结合作的团队，鼓励成员之间的相互支持和协助。

每个人都应该肩负起自己的责任，积极参与问题的解决。

通过团队的力量，我们可以共同克服困难，找到最佳的解决方案。

总之，巧妙解决工程问题需要我们进行充分准备，优化资源分配，建立有效的沟通渠道，并保持灵活性和创新性。

此外，团队合作和协作也是解决问题的关键。

○叶小飞　申　生一类工程问题的巧妙解法 有一类较复杂的工程问题,若按一般的解题思路分析求解,有的比较麻烦,有的难以下手。

但如果能将题中条件摘录整理,写出关系式,再通过对比代换,不仅有助于探索解题途径,而且往往能得出简捷而巧妙的解法。

例1　修一条水渠,由甲队单独做,20天可以完成,若甲、乙两队合做,12天可以完成。

由乙队单独做,多少天可以完成?分析与解:将题中条件摘录整理写出下式:甲队12天工作量+乙队12天工作量=“1”①甲队12天工作量+甲队(20-12)天工作量=“1”②对比①、②两式可知,甲队(20-12)天工作量=乙队12天工作量,即甲队1天工作量=乙队112天工作量。

等量代换计算:由于甲队单独做需20天。

所以,由乙队单独做需112×20=30(天)。

例2　一项工程,甲队独做需30天完成,乙队独做需20天完成,两队合做若干天后,中间将乙队调出,所以整个工程经过18天才完成。

问乙队调出多少天?分析与解:由“甲队独做需30天完成,乙队独做需20天完成”可知,甲队1天工作量=乙队23天工作量。

将题中条件摘录整理写出以下关系式:甲队18天工作量+甲队(30-18)天工作量=“1”①甲队18天工作量+乙队?天工作量=“1”②对比①、②两式可知,乙队?天工作量=甲队12天工作量,而甲队1天工作量=乙队23天工作量。

等量代换计算得:23×12=8(天)(乙队做的天数),从而可求乙队调出的天数为:18-8=10(天)。

例3　某工程,甲、乙合作要12天完成,甲单独做要20天完成。

今甲、乙合作完成了工程的一半后,由甲单独做了4天,所剩下的工程由乙单独完成。

这项工程共需多少天完成?分析与解:将题中条件摘录整理,写出下式:甲12天工作量+乙12天工作量=“1”①甲12天工作量+甲(20-12)天工作量=“1”②对比①、②两式可知,乙12天工作量=甲8天工作量,即甲1天工作量=乙112天工作量。

事业单位：数量关系巧解工程类问题工程问题是考试的高频考点，为大家提供事业单位：数量关系巧解工程类问题，希望大家能好好掌握！事业单位：数量关系巧解工程类问题在数量关系的考查知识点中，有一类问题叫做工程问题，而恰恰工程问题又是考试的高频考点，自己查看历年考真题，不难发现几乎每年都会有那么一道工程类问题。

其实工程问题的解题方法很简单，大家只要记住我们今天提到的一些规律和特征，工程问题就是送分题啦!一、工程问题的解题公式工作总量=工作效率×工作时间字母表示：W=Pt二、工程问题的解题原则(一)已知各部分单独完成时间，设工作总量为各个时间的最小公倍数。

【例题1】一项工程甲单独做需要20小时，乙单独做需要24小时，丙单独做需要30小时，若甲先做了三分之一，剩下的工作由乙丙合作还需要多少小时才能完成?【解析】由于一直甲乙丙各部分单独完成时间，所以根据上述解题原则一，设工作总量为20、24、30的最小公倍数为120，所以甲的效率P甲=6，P乙=5，P丙=4，甲先做了三分之一就是30。

剩余工作量为90，交给乙丙合作，t=90÷(5+4)=10天。

(二)已知各部分效率比，设效率比为特殊值。

【例题2】一项工程甲乙丙单独做的效率如下：甲每天的工作效率等于乙丙二人每天效率和，丙的工作效率相当于甲乙每天工作效率的五分之一，如果三人合作只需12天便可完成工程，则乙单独完成工程需要多少天?【解析】题干条件中给了甲乙丙的三者效率间的关系，我们可以试着将甲乙丙的效率比找出来，P甲：P乙：P丙=3:2:1，所以我们就设P甲=3，P乙=2，P丙=1，工作总量=(3+2+1)×12=72，如果由乙单独做的话，t=72÷2=36天。

(三)当部分数较多且效率相等时，设各部分单位效率为1。

【例题3】有5台型号相同的收割机收割一片小麦，若同时投入工作至收割完毕需要24小时，若他们每隔2小时投入一台工作，每台都工作到收割完毕，则用这种方法需要多少小时?【解析】根据已知条件判断有5个部分，且每个收割机的工作效率相等，所以设每台收割机每小时的工作效率为1，工作总量=5×1×24=120，按照每隔2小时投入一台，可以分析出第一台从开始到结束一直做了t小时，第二台做了t-2小时，第三台做了t-4小时，第四台做了t-6小时，第五台做了t-8小时，则120=t+t-2+t-4+t-6+t-8，解得t=28小时，即需要28小时才能收割完毕。

如何巧妙协商施工中的工期问题在建筑工程领域，工期问题是一个经常会遇到的挑战。

合理安排和妥善协商工期，对项目的进展和质量至关重要。

本文将介绍一些巧妙的方法，帮助各方在施工中有效地协商和解决工期问题。

1. 提前沟通和规划在项目启动前，各方应提前进行沟通和规划，明确工期目标和预期时间节点。

要在项目计划中考虑到各项工程的复杂性和可能的延迟因素，确保计划合理可行，以避免后期紧急调整。

2. 深入了解工程情况在协商过程中，各方应事先了解项目现场情况和施工过程中可能遇到的问题。

通过对设计图纸、材料选择、施工方法等细节的深入了解，可以帮助各方更准确地评估所需时间，并提前预防潜在的延误问题。

3. 分阶段工期协商合理划分工程施工的不同阶段，并与各方协商确定每个阶段的工期目标。

通过将工期分解成更小的任务，可以更好地评估每个阶段的时间需求，并提前预警和解决潜在的延迟隐患。

4. 引入合理的工期保留在工期计划中，应该合理留出一定的保留时间，以应对突发状况和预期之外的延误。

这样可以在项目运行过程中灵活应对变化，并减少对整体工期的影响。

5. 进行实时监控和沟通在施工过程中，各方应保持实时监控项目进展，及时发现工期偏差和潜在的延误情况。

通过及时的沟通和信息共享，可以快速采取措施，解决问题，并确保项目按时完成。

6. 寻求各方合作与妥协当工期问题出现时，各方应以合作和妥协的态度解决问题。

通过协商找到双方都能接受的解决方案，例如增加人力、调整施工顺序、优化施工方法等，以减少延误和影响。

7. 留有协商空间在合同中应明确规定工期协商的方式和权力，确保各方在合理的范围内能够就工期问题进行协商和调整。

这样可以为解决潜在的工期冲突提供一定的灵活性和流程，避免纠纷的发生。

8. 寻求专业咨询和支持如果工期问题无法通过协商解决，各方可以寻求专业咨询和支持，如请工期管理专家、法律顾问等提供专业意见和辅助服务，以确保协商结果的合理性和有效性。

结论：巧妙协商施工中的工期问题对于项目的成功和顺利进行至关重要。

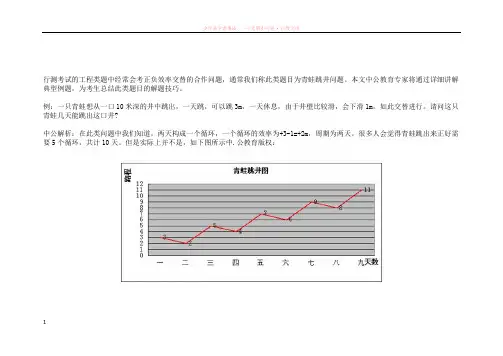
行测考试的工程类题中经常会考正负效率交替的合作问题，通常我们称此类题目为青蛙跳井问题。

本文中公教育专家将通过详细讲解典型例题，为考生总结此类题目的解题技巧。

例：一只青蛙想从一口10米深的井中跳出，一天跳，可以跳3m，一天休息，由于井壁比较滑，会下滑1m，如此交替进行。

请问这只青蛙几天能跳出这口井?中公解析：在此类问题中我们知道，两天构成一个循环，一个循环的效率为+3-1=+2m，周期为两天。

很多人会觉得青蛙跳出来正好需要5个循环，共计10天。

但是实际上并不是，如下图所示中.公教育版权：1从图中可以看出，实际在8天多，青蛙就已经跳出这口井了。

所以在做题过程中要树立一种预留思想。

当青蛙经过几个整循环后只要大于10-3=7m，青蛙就能跳出去，所以我们要把3m作为预留量。

首先我们要判断有多少个整循环和剩余的量，不管是均为正效率的交替合作，还是正负交替的交替合作，主要的关键在于剥离整循环和剩余量。

可得：2×[N]≥10-3，[N]=4注：[N]为能取的最小整数即经过4个整循环，剩余量10-4×2=2m剩余量时间：2/3天，整循环时间：4×2=8天共计：8+2/3=8.67天判断有几个整循环的关键在于找预留量，实际上预留量为一个循环效率能达到的最大值，我们把这个值叫做循环效率最大增量，比如说下面这几组效率能达到循环效率最大增量为：+3 +5 -7 +9 循环效率最大增量+10+12 -7 +6 - 7 循环效率最大增量+12注：循环效率最大增量就是从第一个数字开始加，不一定全部加完，能加出的最大值中.公教育版权。

综上所述，青蛙跳井问题的解题方法为：(1)找一个循环量的效率和，同时计算出循环周期2(2)找循环效率最大增量作为预留量(3)找整循环：循环量×[N]≥总量-最大增量,[ N]为满足不等式的最小正整数(4) 计算整循环时间=[N]x周期(5)计算剩余量=总量-循环量×[N](6)计算剩余量时间(7)计算总时间中公教育专家提醒考生，解决青蛙跳井问题，要掌握以上方法，并加以练习，便可快速正确的解答此类问题。

行测备考：巧解工程问题之交替合作在考场上人与人拉开差距的除了平常的知识点的积累，还有面对考试题型能够有一个更好的解答思路，下面为你精心准备了“行测备考：巧解工程问题之交替合作”，持续关注本站将可以持续获取的考试资讯！行测备考：巧解工程问题之交替合作行测数量关系是很多考生在考试过程中比较难啃的骨头。

但是如果我们全部放弃的话，又很可惜，所以数量关系，我们可以挑一类题型去做。

在数量关系中，有一类题型是工程问题，几乎每年都会涉及到，而且题型特征很明显，所以在遇到这种问题的时候，可以提前挑选出来，先把这部分分值拿到。

今天就带着大家一起来探讨一下工程问题中的交替合作问题。

【例1】一项工程，甲单独做要 6 小时完成，乙单独做要 10 小时完成。

如果按甲、乙、甲、乙……的顺序交替工作，每次 1 小时，那么完成该工程需要多少小时?A.7 小时B.7 小时 20 分钟C.8 小时D.8 小时 30 分钟【解析】设工作总量W=30，那么甲的效率为5，乙的效率为3，甲、乙、甲、乙......交替工作，每次1个小时，很明显，这是一个循环周期问题，一个循环周期完成的工作量W循=5+3=8，求完成该工程用了几个小时，其实就是求需要几个周期，周期数N=30/8=3......6，周期数为3，一个周期2个小时，也就是需要T1=3*2h=6h。

剩余工作量为6，要想完成该工程，还需要完成这6个工作量，也是甲先干，甲一个小时干了5，T2=2h。

还剩下1个工作量需要乙干，乙一个小时干3，因此还需要T3=1/3h=20分钟，因此一共需要6h+1h+20分钟=7个小时20分钟，选择B。

【例2】完成某项工作，甲需要 18 天，乙需要 15 天，丙需要 12 天，丁需要 9 天。

现按甲、乙、丙、丁的顺序轮班工作，每次轮班的工作时间为一天，则完成该项工作当天是( )在轮班。

A.甲B.乙C.丙D.丁【解析】设工作总量W=180，那么甲的效率为10，乙的效率为12，丙的效率为15，丁的效率为20，按照甲乙丙丁的顺序轮班工作，这是一个周期循环工作，一个循环周期内完成工作量为W 循=10+12+15+20=57，那么周期数N=180/57=3...9,剩余工作量W 剩=9，接着甲一个小时干10，在甲工作的这一个小时内，就完成了全部的工作，因此完成的时候，甲在轮班，选择A。

第9讲 巧解工程问题（一）工程问题是将一般的工作问题量化，换句话说就是从分率的角度研究工作总量，工作时间、工作效率三者之间的关系。

它的特点是将工作总量看作单位“1”，用分率表示工作效率，对所做工作的数量进行分析运算。

工作问题的三个基本数量关系式是：工作效率×工作时间＝工作总量工作总量÷工作时间＝工作效率工作总量÷工作效率＝工作时间一、常规工程问题，从条件入手例1、一项工作甲做10天可以完成，乙做5天可以完成。

现在甲先做了2天。

余下的工作由乙继续完成。

问：乙需要做几天可以完成全部工作？分析与解：甲做了2天，完成的工作量是102=51。

乙还需要完成的工作量是1-51=54。

乙每天能完成的工作量（工作效率）是51，完成余下54工作量所需的时间是： 54÷51=4（天） 答：乙需要四天完成剩下的工作。

做一做：一项工作，甲做9天可以完成，乙做六天可以完成。

现在甲先做了3天，剩下的工作由乙继续完成。

问：乙需要做几天才能完成剩下的这部分工作？例2、一项工程，甲、乙合做需6天完成，乙、丙两人合做需9天完成，甲、丙两人合做需15天完成。

问：甲、乙、丙三人合做需多少天完成？分析与解 先求出三人合做一天完成这项工程的几分之几，再求三人合做这项工程需要多少天完成。

1÷［（61+91+151）÷2］=53125（天） 答：甲、乙、丙三人合做需要53125天。

做一做：一项工作，甲、乙两人合做8天完成，乙、丙两人合做9天完成，丙、甲两人合做18天完成。

那么，丙一个人来做，需要多少天完成这项工作？例3、制作一批零件，由师、徒两人合做8天可完成，由师傅单独做12天可完成。

现在先由做了若干天后，再由师傅继续做，全部完成共用了15天。

求师、徒两人各工作了多少天。

分析与解 先求出徒弟的工作效率为：81-121=241。

借助假设法，可求出师傅工作的天数：（1-241×15）÷（121-241）=249÷241=9（天） 所以，徒弟做的天数为15-9=6（天）。

遂宁南山国际学校冬令营
小学六年级数学思维拓展训练之
巧解工程问题
姓名：分数：
〖方法和技巧〗
工程问题是研究工作效率、工作时间和工作总量之间关系的应用题，在分数的工作问题中，一般把工作总量设为“1”，在单位时间内完成的工作量称为工作效率，工程问题的基本数量关系式有：工作总量÷工作时间＝工作效率
工作总量÷工作效率＝工作时间
工作效率×工作时间＝工作总量
【例1】单独完成某项工程，甲、乙、丙三人分别需10小时、15小时、20小时，开始三人一起干，后因工作需要，甲中途调走了，结果共用了6小时完成这项工作，问：甲实际工作了多少小时？〖举一反三〗
甲、乙合做一件工作要15天才能完成，现在甲、乙合做10天后，再由乙独做6天，还剩下这件工作的1
10。

甲单独完成这件工作要多少天？
【例2】一件工程，甲、乙合做需6天完成，乙、丙合做需9天完成，甲、丙合做需15天完成。

现在甲、乙、丙三人合做需多少天完成？
〖举一反三〗
1.某工程，甲队单独做24天完成，乙队单独做30天完成。

甲、乙两队合做8天后，余下的工作由丙队单独做，又做了6天才完成。

问：这项工程由丙队单独做需几天完成？
好问的人，只做了几分钟的愚人；耻于发问的人，终身为愚人。

骄傲使人落后，谦虚使人进步。

2015山西公务员行测技巧：巧解工程中的多者合作问题在公务员行测考试中，工程问题已经越来越多地成为考试的重点，而在工程问题中，多者合作问题是出题人最为青睐的问题。

多者合作问题是指多人完成一项或者是多项工作，出题时问题问的最多的是求工作时间。

对于多者合作问题，经过中公教育的专家深入研究，发现解多者合作问题最主要的方法是特值法和方程法。

特值法就是在多者合作问题中通过通过设工程量或者工作效率为特值得方法解题，方程法就是运用工程问题中的等量关系：工程量=工作效率*工作时间去解题。

下面我们就通过两个例题来具体看看特值法和方程法在多者合作问题中的运用。

例1. 一项工程，甲一人做完需30天，甲、乙合作完成需18天，乙、丙合作完成需15天。

甲、乙、丙三人共同完成该工程需：A.8 天B.9 天C.10 天D.12 天答案：【C】。

解析：此题是一个典型的多者合作问题，可以特值工程总量为90，那么甲的效率为3，甲与乙的效率和为5，乙与丙的效率和为6，甲，乙，丙三人的效率和为9，则三人共同完成该工程需10天。

例2.某市有甲，乙，丙三个工程队，工作效率比为3:4:5。

甲队单独完成A工程需要25天，丙队单独完成B工程需要9天。

现由甲队负责B工程，乙队负责A工程，而丙队先帮甲队工作若干天后去帮助乙队工作。

如希望两个工程同时开工同时竣工，则丙队要帮乙队工作多少天?A.6B.7C.8D.9答案：【B】。

解析：此题需要用特值法和方程法，首先可以特值甲，乙，丙的效率分别为3,4,5。

则A工程的工程总量为75，B工程的工程总量为45。

再用方程法，设丙队帮乙队的工作时间为x,帮甲队的工作时间为y,则有方程组3*(x+y)+5*y=45, 4*(x+y)+5*x=75。

解得x=7。

从以上两题不难看出，多者合作问题中的方程法是比较简单的，主要是要学会特值法的运用。

在运用特值法时，广大考生的难点也是不知道特值法如何运用，到底是什么样的题目设工程总量为特值，什么样的题目设工作效率为特值。

第十一章工程问题知识要点工程问题是研究工作效率、工作时间和工作总量之间相互关系的一类分数应用题。

这种类型的应用题，工作总量不再是具体的数量，经常用单位“1”来表示，工作效率用分率来表示。

解答此类问题，主要利用三个量之间的关系解题。

工作总量＝工作效率×工作时间工作时间＝工作总量÷工作效率工作效率＝工作总量÷工作时间典例巧解例1 一项工程，甲单独做需12天完成，乙单独做需9天完成。

如果甲先单独做若干天后，乙接着单独做，共用10天完成。

甲做了几天？点拨这类工程应用题，我们可以根据题中的已知条件和数量间的关系列方程解答。

除了方程方法外，还可以用假设法解答此题。

解法一设甲做了x天，那么乙做了(10－x)天。

1 12x＋19×(10—x)＝1 112x＋109－19x＝1136x＝19x＝4答：甲做了4天。

解法二假设这10天全部是乙做的，由于乙比甲做得快，则应超过工作总量“1”。

超过的工作量是怎样造成的呢？这是因为把这10天全都看成是乙做的。

乙每天的工作效率比甲每天的工作效率多19－112＝136，多少天才做了超过的工作量呢？列式为：(19×10－1)÷(19＝112)＝19÷136＝4(天)答：甲做了4天。

例2 加工一批零件，甲、乙合作24天可以完成。

现在由甲先做16天，然后乙再做12天，还剩下这批零件的40%没有完成。

已知甲每天比乙多加工4个零件，求这批零件共多少个。

点拨甲、乙合作的效率和为124，甲先做16天，然后乙再做12天，可理解为甲、乙合作12天后，甲再单独做16－12＝4(天)，这样甲4天完成的工作量为1－40%－124×12＝110，于是，可以求出甲的工作效率为110÷4＝140，乙的工作效率为124－140＝160，从而求出4个零件占这批零件总数的140－160＝1120。

问题易解。

解甲的工作效率：(1－40%－124×12)÷(16－12)＝110÷4＝1 40这批零件总数：4÷[140－(124－140)]＝4÷1 120＝480(个)答：这批零件共有480个。