江苏省盐城市文峰中学高中数学 第二章 第15课时 圆与圆的位置关系教案 苏教版必修2

2.2. 圆与圆的位置关系-苏教版必修2教案教学目标1.能够正确地解释水平直径、垂直直径、切线、点与圆的位置关系以及圆与圆的位置关系。

2.能够运用相关的知识解决问题。

3.能够在实际情境中运用圆与圆的位置关系的知识。

教学重难点1.教学重点：圆与圆的位置关系。

2.教学难点：运用相关知识解决问题。

教学过程一、导入请同学们思考以下问题：•圆的定义是什么？•圆各部分的名称有哪些？•圆的相关术语有哪些？二、讲解1.圆的各部分名称：圆心、直径、半径、弧、圆周、弦、切线等。

2.圆的相关术语：–水平直径：过圆心的一条水平线段，它将圆分成上下两部分。

–垂直直径：过圆心的一条垂直线段，它将圆分成左右两部分。

–切线：只与圆相交于圆上某一点的直线。

–点与圆的位置关系：1.在圆内：点到圆心的距离小于圆的半径。

2.在圆上：点到圆心的距离等于圆的半径。

3.在圆外：点到圆心的距离大于圆的半径。

3.圆与圆的位置关系：•几何实体的位置关系包括重合、相离和相交。

–重合：两个圆的圆心重合且半径相等。

–相离：两个圆没有任何交点。

–相交：两个圆有交点。

•外离：两个圆的圆心间距离大于两个圆的半径之和。

•相切外离：两个圆的圆心间距离等于两个圆的半径之和。

•相离相交：两个圆的圆心间距离小于两个圆的半径之和。

•外切相交：两个圆的圆心间距离等于两个圆的半径之差。

•相切内含：一个圆完全在另一个圆内部，且两个圆的圆心相切。

•内含相交：两个圆的圆心间距离小于两个圆的半径之差，且一个圆完全在另一个圆内部。

三、练习练习1：判断以下每一对圆的位置关系。

1.O1(0,0)，r1 = 2，O2(11,0)，r2 = 4。

2.O1(-2,0)，r1 = 3，O2(5,0)，r2 = 9。

3.O1(−3,−2)，r1 = 5，O2(3,2)，r2 = 5。

练习2：两个相切的圆的半径分别为r，R(r<R)，它们的切点与第一个圆心连线的长度为ℎ，第二个圆心与切点连线的长度为d，试证明：d+ℎ=R−r。

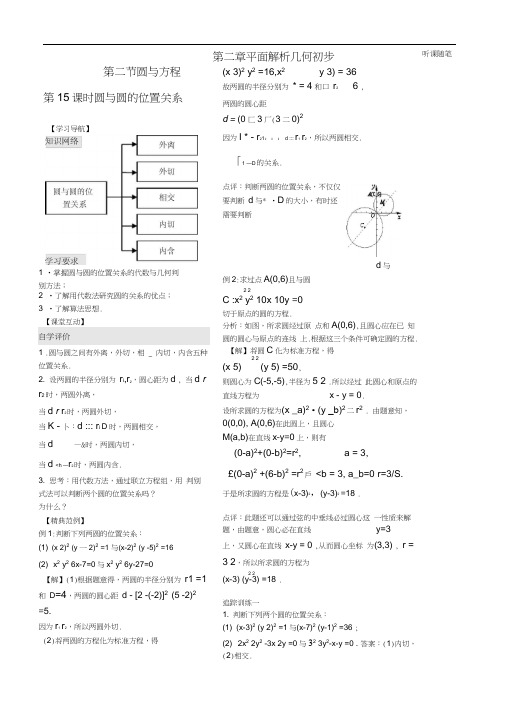
第二节圆与方程第15课时圆与圆的位置关系1 •掌握圆与圆的位置关系的代数与几何判别方法；2 •了解用代数法研究圆的关系的优点；3 •了解算法思想.自学评价1 .圆与圆之间有外离，外切，相 _ 内切，内含五种位置关系.2. 设两圆的半径分别为r i,r2，圆心距为d , 当d r r2时，两圆外离，当d r r2时，两圆外切，当K - 卜：d ::: r i D时，两圆相交，当d —&时，两圆内切，当d <h —r2时，两圆内含.3. 思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？【精典范例】例1:判断下列两圆的位置关系：(1) (x 2)2(y 一2)2=1 与(x-2)2(y -5)2=16(2) x2 y2 6x-7=0与x2 y2 6y-27=0【解】(1)根据题意得，两圆的半径分别为r1 =1和D=4，两圆的圆心距d - [2 -(-2)]2(5 -2)2=5.因为r1r2，所以两圆外切.(2)将两圆的方程化为标准方程，得(x 3)2 y2 =16,x2y 3) = 36故两圆的半径分别为* = 4和口r2 6 ,两圆的圆心距d = (0 匚3厂(3二0)2因为I * - r21：：： d ::: r1r2，所以两圆相交.点评：判断两圆的位置关系，不仅仅要判断d与* •D的大小，有时还需要判断d与例2:求过点A(0,6)且与圆2 2C :x2 y2 10x 10y =0切于原点的圆的方程.分析：如图，所求圆经过原点和A(0,6),且圆心应在已知圆的圆心与原点的连线上.根据这三个条件可确定圆的方程.【解】将圆C化为标准方程，得2 2(x 5) (y 5) =50,则圆心为C(-5,-5),半径为5 2 .所以经过此圆心和原点的直线方程为x - y = 0.设所求圆的方程为(x _a)2• (y _b)2二r2. 由题意知，0(0,0), A(0,6)在此圆上，且圆心M(a,b)在直线x-y=0上，则有(0-a)2+(0-b)2=r2, a = 3,£(0-a)2 +(6-b)2 =r2戶<b = 3, a_b=0 r=3/S.于是所求圆的方程是(x-3)2，(y-3)2=18 .点评：此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线y=3上，又圆心在直线x-y = 0 ,从而圆心坐标为(3,3) , r =3 2，所以所求圆的方程为2 2(x-3) (y-3) =18 .追踪训练一1. 判断下列两个圆的位置关系：(1) (x-3)2 (y 2)2 =1与(x-7)2 (y-1)2 =36 ;(2) 2x2 2y2 -3x 2y =0与32 3y2-x-y =0 . 答案：(1)内切，(2)相交.第二章平面解析几何初步听课随笔「1 —D的关系.【学习导航】2. 若圆x2• y2= m 与圆x2■ y2，6x-8yT1=0相交，求实数m的取值范围. 答案：1 ：：：m <121 .例 3: 已 知 圆 2 2G : x y 2x _6y 1=0 , 圆2 2C 2: x y -4x • 2y -1仁0 ,求两圆的公共弦所在的直线方程及公共弦长.分析：因两圆的交点坐标同时满足两个圆方 程，联立方程组，消去 x 2项、y 2项，即得 两圆的两个交点所在的直线方程， 利用勾股 定理可求出两圆公共弦长.【解】设两圆交点为Ad ,,%)、B(x 2,y 2), 则A B两点坐标满足方程组-2 2 x y 2x -6y 1 =0, (1)2 2， x y -4x 2y -11 =0, (2)(1)一(2)得 3x —4y 6 =0 .因为，A B 两点坐标都满足此方程，所以，3x - 4y • 6 =0即为两圆公共弦所在所以，所求圆方程为(x —1)2・(y ・7)2 =89 , 2 2 2 2 2 即 x y —x 7y 一32 = 0 (法二)设所求圆的方程为 2 2 2 2 x y 6 x4 . - ( x y 6 y2即8 ) 2 2 6 6■ 4 28■ x y x y 0 . 1 + & 1 + 扎 1 + k 故此圆的圆心为(一丄，二竺),它在直线 1+扎1+扎 x-y-4=0 上，所以 一 3—-4 = 0, 1 +人1 +九 所以，--7 . 所以所求圆方程为 x 2 • y 2 _x • 7y-32 = 0 点评：“解法二”中设出的经过两已知圆交点的 圆方程叫做经过两已知圆的圆系方程.的直线方程.易知圆G 的圆心(-1,3)，半径r =3 . 又G 到直线的距离为99 .所以,524点评：本题较为复杂，要讨论的情况比较多, 解题过程中要注重分析.思维点拔： 解题时要充分利用两圆位置关系的几何性质. 追踪训练二 1 .一个圆经过圆 G :x 2 • y 2-8x-9 = 0和圆 C 2 ：x 2 • y 2 -8y • 15 = 0的两个交点，且圆心 在直线2x-y-1=0上，求该圆的方程. 2 2 10 14 答案：x y x y-12 = 0. 3 3 2 .已知一个圆经过直线2x y ^0与圆 x 2 y 2 2x -4y • 1 = 0的两个交点，并且有 最小面积，求此圆的方程.例5 :求过两圆x 2 • y 2 • 6x - 4 = 0和 x 2 y 2 6y -28 =0的交点，且圆心在直 线x - y -4 =0上的圆的方程.分析：所求圆圆心是两已知圆连心线和已知 直线的交点，再利用弦心距、弦长、半径之 间的关系求圆半径【解】(法一)可求得两圆连心线所在直线 的方程为x y 3 0.1x —y —4=0, 1 7由 得圆心(丄，-上).x y 3 = 0, 2 2 利用弦心距、弦长、半径之间的关系可求得 公共弦长d 二・.50 , 所以，圆半径 听课随笔 | -1 3 -4 3 6| .32 (4)2 两圆的公共弦长为答案：(x 1■一)2 . (y _6)5 5。

第二章 平面解析几何初步第二节 圆与方程第15课时 圆与圆的位置关系2．了解用代数法研究圆的关系的优点；3．了解算法思想．【课堂互动】自学评价1．圆与圆之间有外离，外切，相交，内切，内含五种位置关系．2.设两圆的半径分别为12,r r ，圆心距为d ，当12d r r >+时，两圆外离，当12d r r =+时，两圆外切，当1212||r r d r r -<<+时，两圆相交，当12d r r =-时，两圆内切，当12d r r <-时，两圆内含．3.思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？【精典范例】例1：判断下列两圆的位置关系：2222(1)(2)(2)1(2)(5)16x y x y ++-=-+-=与222226706270x y x x y y ++-=++-=（）与【解】（1）根据题意得，两圆的半径分别为1214r r ==和，两圆的圆心距5.d ==因为 12d r r =+，所以两圆外切．听课随笔（2）将两圆的方程化为标准方程，得2222(3)16,(3)36x y x y ++=++=．故两圆的半径分别为1246r r ==和，两圆的圆心距d ==．因为1212||r r d r r -<<+，所以两圆相交．点评：判断两圆的位置关系，不仅仅要判断d 与12r r +的大小，有时还需要判断d 与12r r -的关系．例2：求过点(0,6)A 且与圆22:10100C x y x y +++=切于原点的圆的方程．点和(0,6)A ，且圆心应在已知圆的圆心与原分析：如图，所求圆经过原点的连线上．根据这三个条件可确定圆的方程． 【解】将圆C 化为标准方程，得22(5)(5)50x y +++=，则圆心为(5,5)C --，半径为0x y -=． 设所求圆的方程为222()()x a y b r -+-=．由题意知，(0,0),(0,6)O A 在此圆上，且圆心(,)M a b 在直线0x y -=上，则有222222(0)(0),3,(0)(6),3,0a b r a a b r b a b r ⎧-+-=⎧=⎪⎪-+-=⇒=⎨⎨⎪⎪-==⎩⎩于是所求圆的方程是22(3)(3)18x y -+-=．点评：此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线3y =上，又圆心在直线0x y -=，从而圆心坐标为(3,3)，r =，所以所求圆的方程为22(3)(3)18x y -+-=．追踪训练一1.判断下列两个圆的位置关系：2222(1)(3)(2)1(7)(1)36x y x y -++=-+-=与；2222(2)2232030x y x y x y x y +-+=+--=与3．答案：（1）内切，（2）相交．2. 若圆22x y m +=与圆2268x y x y ++- 110-=相交，求实数m 的取值范围．答案：1121m <<．【选修延伸】一、两圆公共弦长及公共弦所在直线方程例3: 已知圆221:2610C x y x y ++-+=，圆222:42110C x y x y +-+-=，求两圆的公共弦所在的直线方程及公共弦长．分析：因两圆的交点坐标同时满足两个圆方程，联立方程组，消去2x 项、2y 项，即得两圆的两个交点所在的直线方程，利用勾股定理可求出两圆公共弦长．【解】设两圆交点为11(,)A x y 、22(,)B x y ，则A B 、两点坐标满足方程组22222610,(1)42110,(2)x y x y x y x y ⎧++-+=⎪⎨+-+-=⎪⎩，(1)(2)-得3460x y -+=． 因为，A B 、两点坐标都满足此方程，所以，3460x y -+=即为两圆公共弦所在的直线方程．易知圆1C 的圆心(1,3)-，半径3r =．又1C 到直线的距离为95d ==．所以，245AB ===．即两圆的公共弦长为245．点评:本题较为复杂，要讨论的情况比较多，解题过程中要 注重分析．例5：求过两圆22640x y x ++-=和 226280x y y ++-=的交点，且圆心在直线40x y --=上的圆的方程．分析：所求圆圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径【解】（法一）可求得两圆连心线所在直线的方程为30x y ++=． 由40,30,x y x y --=⎧⎨++=⎩得圆心17(,)22-．利用弦心距、弦长、半径之间的关系可求得公共弦长d =， 所以，圆半径22289()22d r =+=⎝⎭． 所以，所求圆方程为221789()()222x y -++=， 即227320x y x y +-+-=（法二）设所求圆的方程为222264(628)0x y x x y y λ++-+++-=即22664280111x y x y λλλλλ++++-=+++． 故此圆的圆心为33(,)11λλλ--++，它在直线40x y --=上， 所以334011λλλ--+-=++，所以7λ=-．所以所求圆方程为227320x y x y +-+-= 点评:“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程．思维点拔：解题时要充分利用两圆位置关系的几何性质．追踪训练二听课随笔1．一个圆经过圆221:890C x y x +--=和圆222:8150C x y y +-+=的两个交点，且圆心在直线210x y --=上，求该圆的方程． 答案：22101412033x y x y +---=． 2．已知一个圆经过直线240x y ++=与圆222410x y x y ++-+=的两个交点，并且有最小面积，求此圆的方程． 答案：221364()()555x y ++-=．。

223 圆与圆的位置关系教学目标：1 •理解圆与圆的位置关系；2 •利用平面直角坐标系中两点间的距离公式求两圆的圆心距；3 •会用圆心距与两圆半径之间的大小关系判断两圆的位置关系.教材分析及教材内容的定位：本节教材是本单元的最后一节，从知识结构来看，它是直线与圆位置关系的延续，从解决问题的思想方法来看，它反映了事物内部的量变与质变. 通过这些对学生进行辩证唯物主义世界观的教育.所以这一节无论从知识性还是思想性来讲，在几何教学中都占有重要的地位.教学重点：两圆位置关系的判定.教学难点：通过两圆方程联立方程组的解来判断圆与圆的位置关系.教学方法：导学点拨法、电脑、投影.教学过程：一、问题情境1. 情境：古希腊哲学家芝诺的学生问他：“老师，难道你也有不懂的地方吗？”芝诺风趣的打了一个比方：“如果有小圆代表你学到的知识，用大圆代表我学到的知识，那么大圆的面积是多一些，但两圆之外的空白，都是我们的无知面，圆越大，其圆周接触的无知面就越多”请你谈谈其中的道理；2. 问题1:直线与圆的位置关系的几何特征是通过公共点来刻化的，请同学们猜想一下：圆与圆的位置关系按公共点分类能划分为哪几类？问题2:圆与圆的位置关系有几种情况?问题3:(师指出圆与圆的五种位置关系的名称之后提问)你能给这五种位置关系分别下一个准确的定义吗？二、学生活动1. 回顾知识点互相交流；2. 在教师引导下，阅读教科书；3•禾U用类比方法，总结出判定圆与圆的位置关系的方法.4•学生动手在同一个直角坐标系中画出两个圆，观察并思考用数学语言发表自己的解题方法5•在教师的引导下总结判定两圆位置关系的方法一代数法与几何法三、建构数学1•弓I导学生自己总结给出判定圆与圆位置关系的步骤；2. 圆与圆之间有_ ,_____ , , ,五种位置关系.3. 判断圆与圆的位置关系有两种方法：(1)几何方法：2 2 2 2 2 2两圆(x aj (y bi) r i(口0)与(x a?) (y b?) D(D 0)圆心距d =d r i b两圆d r i b两圆r i r2d r i r2两圆d r i D两圆0 d »r2两圆d 0时两圆为___________________________________ .2 2x y D i x E i y 0(2)代数方法：方程组x2y2D2x E2y F20有两组不同实数解__________________________________ ；有两组相同实数解__________________________________ ；无实数解__________________________________________4. 两圆的公切线条数.当两圆内切时有 _______ 条公切线；当两圆外切时有_____________ 条公切线；相交时有________ 条公切线；相离时有_________ 条公切线；内含时_________ 公切线.四、数学运用1. 例题.例1判断下列两圆的位置关系，并说明它们有几条公切线.(1)(x 2)2 (y 2)2 1 与(x 2)2(y 5)2 16(2) x2y26x 7 0与x2y26y 27 0例2求过点A(0,6)且与圆C ：x2y210x 10y 0切于原点的圆的方程.例 3 已知圆C：x2+ y2+ 4x + y+ 1 = 0 和圆0： x2+ y2+ 2x + 2y+ 1 = 0.(1)判断两圆的位置关系，若两圆相交，求公共弦AB所在直线的方程及公共弦的长；(2)试求两圆的公切线方程.2•练习.2 2 2 2(1)两圆x + y + 4x—4y + 7= 0和x + y - 4x —10y + 13= 0的公切线的条数为 .(2)若半径为1的动圆与圆x + y = 4相切，则动圆圆心的坐标满足的关系是_ .(3)圆x2+ y2= 1上动点A到圆(x —3)2+ (y —4) 2= 1上动点B间距离的最大值和最小值分另寸为_______ .(4)若两圆x2+ y2= 9与x2+ y2—8x + 6y —8a—25 = 0只有惟一的一个公共点，求实数a的值.(5)求与圆C： x2+ y2—4x —2y — 4 = 0相外切，与直线y= 0相切且半径为4的圆方程.(6)已知O C1：x2+ y2+ 6x — 4 = 0 和O C2: x2+ y2+ 6y—28 = 0 相交于A, B两点.求圆心在直线x—y—4= 0上，且经过A, B两点的圆C方程.五、要点归纳与方法小结本节课学习了以下内容：1. 圆与圆的五种位置关系；2. 圆与圆的位置关系的判定：(1)几何方法；(2)代数方法；3. 一个思想：数形结合思想方法.。

适用学科 适用区域 知识点 教学目标 教学重点 教学难点【教学建议】高中数学 苏教版区域 圆和圆的位置关系的判定 掌握圆和圆的五种位置关系 判定两圆位置关系 根据两圆位置关系求参数适用年级 课时时长（分钟）高二 2 课时在学习了“直线和圆”之后，再来学习本节内容，学生会有一种熟悉的感觉，如在研究 两个圆的位置关系时，通过画图就可以得到。

而在解题方法上，依然可以采用数形结合的方 法，而有的问题则必须通过代数方法才可以获得准确的解，所以对不同的题目要判断用什么 方法是最佳的。

对于五种关系的代数判断方法，也应该让学生在理解的基础上去记忆对应的 代数形式。

【知识导图】教学过程一、导入两个圆的位置关系有外离、外切、相交、内切、内含 如何判断圆与圆的位置关系 方法一（几何法）：设两圆连心的距离为 d ，两圆的半径为 R、r，则 ①两圆外离  d>R+r 没有公共点 ②两圆外切  d=R+r 有唯一的公共点 ③两圆相交  R-r<d<R+r(R≥r)  有两个公共点 ④两圆内切  d=R-r (R>r)  有唯一的公共点 ⑤两圆内含  d<R-r (R>r)  没有公共点二、知识讲解1.两个圆的位置关系有外离、外切、相交、内切、内含 考点 1 圆和圆的位置关系的判定 2.如何判断圆与圆的位置关系 方法一（几何法）：设两圆连心的距离为 d ，两圆的半径为 R、r，则 ①两圆外离  d>R+r 没有公共点  ②两圆外切 d=R+r 有唯一的公共点 ③两圆相交  R-r<d<R+r(R≥r)  有两个公共点 ④两圆内切  d=R-r (R>r)  有唯一的公共点 ⑤两圆内含  d<R-r (R>r)  没有公共点第 1 页 一个变元的二次方程，判别式 方法二（方程法）：将圆与圆的方程联立成方程组  为△，则 △<0 方程组无解  圆和圆无公共点（相离或内含） △=0 方程组仅有一解  圆和圆相切（内切或外切）； △>0 方程组有两组不同解  圆和圆相交消元两个圆的方程作差，即可得它们公共弦所在的直线方程考点 2相交弦方程三 、例题精析 类型一 两圆相切及其应用如图， 在平面直角坐标系 xOy 中， 已知以 M 为圆心的圆 M：x  y 12x 14y  60  0 .2 2例题 1及其上一点 A2， 4 ．设圆 N 与 x 轴相切，与圆 M 外切，且圆心 N 在直线 x  6 上，求圆 N 的标准方程。

第二章平面解析几何初步听课随笔第二节圆与方程第15课时圆与圆的位置关系【学习导航】知识网络学习要求1．掌握圆与圆的位置关系的代数与几何判别方法；2．了解用代数法研究圆的关系的优点；3．了解算法思想．【课堂互动】自学评价1．圆与圆之间有外离，外切，相交，内切，内含五种位置关系．2.设两圆的半径分别为，圆心距为，当时，两圆外离，当时，两圆外切，当时，两圆相交，当时，两圆内切，当时，两圆内含．3.思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？【精典范例】例1：判断下列两圆的位置关系：【解】（1）根据题意得，两圆的半径分别为，两圆的圆心距因为，所以两圆外切．（2）将两圆的方程化为标准方程，得．故两圆的半径分别为，两圆的圆心距．因为，所以两圆相交．点评：判断两圆的位置关系，不仅仅要判断与的大小，有时还需要判断与的关系．例2：求过点且与圆切于原点的圆的方程．分析：如图，所求圆经过原点和，且圆心应在已知圆的圆心与原点的连线上．根据这三个条件可确定圆的方程．【解】将圆化为标准方程，得，则圆心为，半径为．所以经过此圆心和原点的直线方程为．设所求圆的方程为．由题意知，在此圆上，且圆心在直线上，则有于是所求圆的方程是．点评：此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线上，又圆心在直线，从而圆心坐标为，，所以所求圆的方程为．追踪训练一1.判断下列两个圆的位置关系：；．答案：（1）内切，（2）相交．2.若圆与圆相交，求实数的取值范围．答案：．【选修延伸】一、两圆公共弦长及公共弦所在直线方程例3: 已知圆，圆，求两圆的公共弦所在的直线方程及公共弦长．分析：因两圆的交点坐标同时满足两个圆方程，联立方程组，消去项、项，即得两圆的两个交点所在的直线方程，利用勾股定理可求出两圆公共弦长．【解】设两圆交点为、，则两点坐标满足方程组，得．因为，两点坐标都满足此方程，所以，即为两圆公共弦所在的直线方程．易知圆的圆心，半径．又到直线的距离为．所以，．即两圆的公共弦长为．点评:本题较为复杂，要讨论的情况比较多，解题过程中要注重分析．例5：求过两圆的交点，且圆心在直线上的圆的方程．分析：所求圆圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径【解】（法一）可求得两圆连心线所在直线的方程为．由得圆心．利用弦心距、弦长、半径之间的关系可求得公共弦长，所以，圆半径．即（法二）设所求圆的方程为即．故此圆的圆心为，它在直线上，所以所求圆方程为点评:思维点拔：追踪训练二1答案：．2答案：．。

第二章 平面解析几何初步第二节 圆与方程第15课时 圆与圆的位置关系【学习导航】学习要求1．掌握圆与圆的位置关系的代数与几何判别方法；2．了解用代数法研究圆的关系的优点；3．了解算法思想．【课堂互动】自学评价1．圆与圆之间有外离，外切，相交,内切，内含五种位置关系．2。

设两圆的半径分别为12,r r ，圆心距为d ，当12d r r >+时,两圆外离，当12d r r =+时,两圆外切，当1212||r r d r r -<<+时,两圆相交，当12d r r =-时，两圆内切， 当12d r r <-时,两圆内含． 3。

思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？【精典范例】例1：判断下列两圆的位置关系：2222(1)(2)(2)1(2)(5)16x y x y ++-=-+-=与 222226706270x y x x y y ++-=++-=（）与 【解】（1)根据题意得,两圆的半径分别为1214r r ==和，两圆的圆心距 22[2(2)](52) 5.d =--+-=因为 12d r r =+，所以两圆外切．(2)将两圆的方程化为标准方程，得2222(3)16,(3)36x y x y ++=++=． 故两圆的半径分别为1246r r ==和,两圆的圆心距 22(03)(30)32d =-+-= ．因为1212||r r d r r -<<+，所以两圆相交．点评：判断两圆的位置关系,不仅仅要判断d 与12r r +的大小，有时还需要判断d 与12r r -的关系．例2:求过点(0,6)A 且与圆22:10100C x y x y +++=切于原点的圆的方程．分析:如图，所求圆经过原点和(0,6)A ，且圆心应在已知圆的圆心与原点的连线上．根据这三个条件可确定圆的方程．【解】将圆C 化为标准方程，得22(5)(5)50x y +++=,则圆心为(5,5)C --，半径为52．所以经过此圆心和原点的直线方程为0x y -=．设所求圆的方程为222()()x a y b r -+-=．由题意知,(0,0),(0,6)O A 在此圆上，且圆心(,)M a b 在直线0x y -=上，则有 222222(0)(0),3,(0)(6),3,03 2.a b r a a b r b a b r ⎧-+-=⎧=⎪⎪-+-=⇒=⎨⎨⎪⎪-==⎩⎩于是所求圆的方程是22(3)(3)18x y -+-=．点评:此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线3y =上，又圆心在直线0x y -=，从而圆心坐标为(3,3)，r =，所以所求圆的方程为22(3)(3)18x y -+-=．追踪训练一1.判断下列两个圆的位置关系:2222(1)(3)(2)1(7)(1)36x y x y -++=-+-=与；2222(2)2232030x y x y x y x y +-+=+--=与3． 答案：（1）内切,(2）相交．2. 若圆22x y m +=与圆2268x y x y ++-110-=相交,求实数m 的取值范围．答案：1121m <<． 【选修延伸】一、两圆公共弦长及公共弦所在直线方程例3: 已知圆221:2610C x y x y ++-+=，圆222:42110C x y x y +-+-=，求两圆的公共弦所在的直线方程及公共弦长．分析:因两圆的交点坐标同时满足两个圆方程，联立方程组，消去2x 项、2y 项，即得两圆的两个交点所在的直线方程,利用勾股定理可求出两圆公共弦长．【解】设两圆交点为11(,)A x y 、22(,)B x y ，则A B 、两点坐标满足方程组 22222610,(1)42110,(2)x y x y x y x y ⎧++-+=⎪⎨+-+-=⎪⎩，(1)(2)-得3460x y -+=．因为，A B 、两点坐标都满足此方程,所以，3460x y -+=即为两圆公共弦所在的直线方程．易知圆1C 的圆心(1,3)-，半径3r =．又1C 到直线的距离为95d==．所以,245AB===．即两圆的公共弦长为245．点评:本题较为复杂，要讨论的情况比较多,解题过程中要注重分析．例5:求过两圆22640x y x++-=和226280x y y++-=的交点,且圆心在直线40x y--=上的圆的方程．分析：所求圆圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径【解】(法一）可求得两圆连心线所在直线的方程为30x y++=．由40,30,x yx y--=⎧⎨++=⎩得圆心17(,)22-．利用弦心距、弦长、半径之间的关系可求得公共弦长d=所以，圆半径22217|()4|89()22dr⎛⎫--+⎪=+=．所以,所求圆方程为221789()()222x y-++=，即227320x y x y+-+-=（法二）设所求圆的方程为222264(628)0x y x x y yλ++-+++-=即2266428111x y x yλλλλλ++++-=+++．故此圆的圆心为33(,)11λλλ--++，它在直线40x y--=上，所以334011λλλ--+-=++,所以7λ=-．所以所求圆方程为227320x y x y+-+-=点评：“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程．思维点拔：解题时要充分利用两圆位置关系的几何性质．追踪训练二1．一个圆经过圆221:890C x y x +--=和圆222:8150C x yy +-+=的两个交点，且圆心在直线210x y --=上，求该圆的方程．答案:22101412033x y x y +---=． 2．已知一个圆经过直线240x y ++=与圆222410xy x y ++-+=的两个交点,并且有最小面积，求此圆的方程． 答案：221364()()555x y ++-=．第15课 圆与圆的位置关系分层训练 1． 圆222220x y x y +-+-=与圆22x y +68240x y ---=的位置关系是 （ ）()A 相离 ()B 相交 ()C 外切 ()D 内切2． 两圆1C ：224470x y x y ++-+=，2C ：22410130x y x y +--+=的公切线有（ ）()A 2条 ()B 3条 ()C 4条 ()D 0条3．已知半径为1的动圆与圆22(5)(7)16x y -++=相切,则动圆圆心的轨迹方程（动圆圆心坐标所满足的关系式)为（ ） ()A 22(5)(7)25x y -++=()B 22(5)(7)17x y -++=或22(5)(7)15x y -++=()C 22(5)(7)9x y -++=()D 22(5)(7)25x y -++=或22(5)(7)9x y -++= 4．若圆222()()1x a y b b -+-=+始终平分圆22(1)(1)4x y +++=的圆周，则,a b 应满足的关系式为 ( ）()A 22250a a b +++= ()B 22230a a b ---=()C 222210a b a +++=()D 22322210a b a b ++++= 5．若圆224x y +=和圆22(2)(2)4x y ++-=关于直线l 对称，则l 的方程为 ．6．圆224410x y x y ++--=与圆222130x y x ++-=相交于,P Q 两点，则直线PQ 的方程为 ，公共弦PQ 的长为 ．7．已知动圆0264222=-+--+m my mx y x 恒过一个定点,这个定点的坐标是______ ．8．求经过点(4,1)A -,且与圆22:2650C x y x y ++-+=相切于点(1,2)B 的圆的方程．9．求与两条平行直线210x y +-=和2x y + 50-=相切,且圆心在直线310x y ++=上的圆的方程．拓展研究10．已知圆221:2280C x y x y +++-=与圆222:210240C x y x y +-+-=相交于,A B 两点．(1）求直线AB 的方程;（2）求经过,A B 两点且面积最小的圆的方程；(3)求圆心在直线y x =-上，且经过,A B 两点的圆的方程．11．若两圆2216xy +=及222(4)(3)x y r -++=在交点处的切线互相垂直,求实数r的值．。

2.2.3 圆与圆的位置关系从容说课在掌握了圆的方程后，结合已学过的知识可以直接研究两圆的位置关系.从某种意义上讲本课是前面所学知识的收尾，教材中对圆与圆的位置关系的判定只要求从几何的角度加以分析，教学中注意难度不能提高.教学重点判定两圆位置的基本方法.教学难点带字母问题的两圆的位置关系的研究.教具准备多媒体、三角板、圆规.课时安排1课时三维目标一、知识与技能1.掌握研究两圆位置的基本方法.2.了解用代数法研究圆的关系的优点.3.了解算法思想.二、过程与方法师生共同探究.三、情感态度与价值观增加对解析法研究几何问题的了解，对笛卡儿创造解析法作用有一个更深刻的理解.教学过程导入新课师平面几何中研究两圆的位置关系有几种情形？生两圆的位置关系有：外离、外切、相交、内切、内含.师对！一般我们通过下列几步来研究.这五种关系可以通过下面的步骤来判断：第一步:计算两圆的半径r1、r2；第二步:计算两圆的圆心距d;第三步:根据d与r1、r2之间的关系，判断两圆的位置关系,外离:d>r1+r2外切:d=r1+r2相交:|r1-r2|<d<r1+r2内切:d=|r1-r2|内含:d<|r1-r2|推进新课当给出两个圆的方程时我们可以研究两圆的位置关系，我们一起来看例题.【例1】判断下列两圆的位置关系：(1)(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16;(2)x2+y2+6x-7=0与x2+y2+6y-27=0.解:(1)根据题意,得两个圆的半径分别为r 1=1和r 2=4，两圆的圆心距d=22)25()]2(2[-+--=5.因为d=r 1+r 2,所以两圆外切.(2)将两圆的方程化为标准方程，得(x +3)2+y 2=16，x 2+(y +3)2=36,故两圆的半径分别为r 1=4和r 2=6.两圆的圆心距d=23)03()30(22=-+-，因为|r 1-r 2|<d<r 1+r 2,所以两圆相交.【例2】求过点(0，6)且与圆C:x 2+y 2+10x +10y =0切于原点的圆的方程.分析：所求圆经过原点和(0，6)，且圆心应在已知圆的圆心与原点的连线上，根据这三个条件可确定圆的方程.解:将圆C 化为标准方程，得(x +5)2+(y +5)2=50,则圆心坐标为(－5，－5)，半径为52，所以经过此圆心和原点的直线方程为x －y ＝0.设所求圆的方程为(x -a )2+(y -b )2=r 2,由题意知(0，0)、(0，6)在此圆上，且圆心(a ，b )在直线x －y ＝0上，则有⎪⎩⎪⎨⎧===⇒⎪⎩⎪⎨⎧=-=-+-=-+-,23,3,30)6(0)0()0(22222r b a b a r b a r b a ）（于是所求圆的方程是(x -3)2+(y -3)2=18. 【例3】已知两圆(x -2)2+y 2=4与(x -4)2+y 2=1，(1)判断两圆的位置关系； (2)求两圆的公切线方程.分析：可根据公切线同时与两圆相切求其方程.解:(1)根据题意，两圆半径分别为r 1=2,r 2=1，圆心距d=2， ∵r 1-r 2<d<r 1+r 2， ∴两圆相交.(2)由(1)知，两圆相交，因此有两条公切线，由题意知，公切线斜率必定存在，可设为k.设公切线方程为y =k x +b ，即k x -y +b =0，由⎪⎪⎩⎪⎪⎨⎧=++=++,114,21222k b k k b k解得⎪⎩⎪⎨⎧-==32,33b k 或⎪⎩⎪⎨⎧=-=32,33b k ∴两圆的公切线方程为y =33x -23或y =-33x +23.【例4】(课本第108页习题第6题)已知一个圆经过直线l ：2x +y +4=0与圆C ：x 2+y 2+2x -4y +1=0的两个交点，并且有最小面积，求此圆的方程.分析：圆有最小面积，只要半径最小即可，而当所求圆以圆C 截直线所得线段为直径时，圆半径最小.解:由⎩⎨⎧=+-++=++0142,04222y x y x y x 得两交点分别为A(-52,511)、B(-3,2)， 当所求圆以AB 为直径时，圆面积最小，此时圆方程为(x +513)2+(y -56)2=54. 【例5】求过两圆x 2+y 2-6x -4=0和x 2+y 2+6y -28=0的交点，且圆心在直线x -y -4=0上的圆的方程.分析一：所求圆的圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径.解法一:由⎪⎩⎪⎨⎧=-++=--+0286,0462222y y x x y x 两方程相减得两圆的公共弦所在直线方程为x -y +4=0.又可求得两圆连心线所在直线方程为x +y +3=0，由⎩⎨⎧=++=--03,04y x y x 得圆心为(27,21-).利用弦心距、弦长、半径之间的关系可求得公共弦长d=50，∴圆半径r 2=(2d )2+(2)427(21+--)2=289. ∴所求圆方程为(x -21)2+(y +27)2=289，即x 2+y 2-x +2y -32=0. 分析二：过已知两交点的圆方程可设为x 2+y 2-6x -4+λ(x 2+y 2+6y -28)=0,再确定λ的值即可得圆的方程.解法二:设所求圆的方程为x 2+y 2-6x -4+λ(x 2+y 2+6y -28)=0，即x 2+y 2+λλλλλ++-+++12841616y =0， 圆心为(λλλ+-+-13,13)，它在直线x -y -4=0上， ∴λλλ+++-1313-4=0， ∴λ=-7.∴所求圆的方程为x 2+y 2-x +2y -32=0.点评:解法二中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程. 课堂小结研究两圆的位置关系通过圆心距来处理，要注意内切、外切之分,以及内含与外离之别. 布置作业P 107练习1、2. 板书设计2.2.3 圆与圆的位置关系圆与圆的位置关系：图形及关系…… 例1 例2例3 课堂小结 例4 布置作业 例5活动与探究运用“点圆法”巧求圆方程在求解有关圆方程问题时，往往要建立方程组，借助于解方程的方法进行求解，但由于参数较多，从而容易造成“入手容易”“答对困难”的局面.其主要原因是同学们盲目运算，以致运算量大，这样不仅影响了解题速度，也极容易出错.因而，尽量减少运算量是快速、准确解答此类问题的关键.为此，本文将介绍运用“点圆法”巧求圆方程，供同学们借鉴与参考，从而启迪思维，提高解题能力.【例1】有一圆与直线4x －3y +6=0相切于点A(3，6)，且经过点B(5，2)，求此圆的方程.解:将点A 表示成“点圆”形式(x －3)2+(y －6)2=0，设所求圆的方程为(x －3)2+(y －6)2+λ(4x －3y +6)=0，将点B(5，2)代入上述圆方程得λ=－1.所以满足条件的圆方程为(x －3)2+(y －6)2－(4x －3y +6)=0，即x 2+y 2－10x －9y +39=0为所求圆的方程.【例2】求经过点M(4，－1)，且与圆x 2+y 2+2x －6y +5=0相切于点N(1，2)的圆方程.解:将点N(1，2)表示成“点圆”形式，(x －1)2+(y －2)2=0.设所求的圆方程为(x －1)2+(y －2)2+λ(x 2+y 2+2x －6y +5)=0，将点M(4，－1)代入上式得18+36λ=0,即λ=－21. 所以满足条件的圆方程为(x －1)2+(y －2)2－21(x 2+y 2+2x －6y +5)=0，即(x －3)2+(y －1)2=5为所求圆的方程.【例3】求与直线4x －3y +25=0相切于点(－4，3)，且半径为5的圆方程.解:将切点(－4，3)表示成“点圆”形式，(x +4)2+(y －3)2=0.设所求圆的方程为(x +4)2+(y －3)2+λ(4x －3y +25)=0,即［x +(4+2λ)］2+［y -(3+23λ)］2=425λ2. ∵此圆半径为5， ∴425λ2=25，即λ=±2. 故所求圆的方程为(x +8)2+(y －6)2=25或x 2+y 2=25. 习题详解课本第107页习题2.2(2)习题解答： 1.(1)由题意,直线过圆心(1,-2),k=213142=++-.(2)设直线l 的方程为y ＋4＝k(x ＋3),即k x -y +3k-4=0, 由题意,得14322+-++k k k =2.解得k=0或k=43.(3)设直线l 的方程为y ＋4＝k(x ＋3),由题意,得14322+-++k k k =122-,解得k=13518±. 2.设直线方程为y ＋1＝k(x ＋1),即k x -y +k-1=0.圆心坐标为(1,－3),半径为2,故1132+-++k k k ＜2,得k<0,即斜率的取值范围为(－∞,0).3.设圆的方程为(x -a )2+(y -b )2=13,则⎪⎩⎪⎨⎧=-+=-+-,13131032,13)2()2(22b a b a解得⎩⎨⎧==5,4b a 或⎩⎨⎧-==.1,0b a故所求圆的方程为(x -4)2+(y -5)2=13或x 2+(y +1)2=13. 4.所求圆的半径为r 1=2234+-1=4或r 2=2234++1=6,故圆C 的方程为(x +4)2+(y -3)2＝16或(x +4)2+(y -3)2＝36.5.设所求圆的方程为x 2+(y -b )2=r 2,则⎪⎪⎩⎪⎪⎨⎧=--=+-,5124,5123r b r b 解得⎪⎩⎪⎨⎧==512,0r b 或⎪⎩⎪⎨⎧=-=.584,24r b 故所求圆的方程为x 2+y 2=25144或x 2+(y -24)2=257056. 6.略 7.略. 8.略备课资料备选练习或例题1.圆x 2+y 2-2x +2y -2=0与圆x 2+y 2-6x -8y -24=0的位置关系是() A.相离 B.相交 C.外切 D.内切2.两圆C 1：x 2+y 2+4x -4y +7=0，C 2：x 2+y 2-4x -10y +13=0的公切线有() A.2条 B.3条 C.4条 D.0条3.若圆(x -a )2+(y -b )2=b 2+1始终平分圆(x +1)2+(y +1)2=4的圆周，则a 、b 应满足的关系式为()A.a 2+2a +2b +5=0B.a 2-2a -2b -3=0 C.a 2+2b 2+2a +1=0 D.3a 2+2b 2+2a +2b +1=04.圆x 2+y 2=5和圆x 2+y 2+2x -3=0的交点坐标为_________.5.圆x 2+y 2+4x -6y +4=0与圆x 2+y 2+2x -4y -4=0的公共弦所在的直线方程为_________.6.已知动圆x 2+y 2-2m x -4m y +6m-2=0恒过一个定点,这个定点的坐标是_________.7.一个圆经过圆C 1:x 2+y 2-8x -9=0和C 2:x 2+y 2-8y +15=0的两个交点，且圆心在直线2x -y -1=0上，求该圆的方程.8.已知圆C 经过点(4,1)，且和直线x +y -3=0相切，和圆(x -6)2+(y -5)2=8外切，圆心在直线2x -3y =0上，求圆C 的方程.参考答案： 1.B 2.B 3.A 4.(-1,±2) 5.x -y +4=0 6.(1,1)7.x 2+y 2-310x -314y -12=0. 8.(x -3)2+(y -2)2=2.。

2.2.圆与圆的位置关系-苏教版必修2教案一、学习目标1.掌握两个圆的位置关系词汇和概念。

2.学会判定两个圆的位置关系。

3.能够通过绘制图形解决实际问题。

二、学习重点1.圆与圆的位置关系的词汇和概念。

2.判定两个圆的位置关系的方法。

三、学习难点1.对于某些特殊情况的位置关系需要特别注意。

2.准确绘制图形、建立坐标系。

四、学习内容1. 圆与圆的位置关系概述在平面直角坐标系中，两个圆的位置关系有七种，分别为：1.相离；2.外切；3.相交；4.内含；5.内切；6.同心；7.重合。

2. 判定两个圆的位置关系（1）相离：两个圆完全没有交点，则互为相离关系。

（2）外切：两个圆有且仅有一个交点，则互为外切关系。

（3）相交：两个圆有两个交点，则互为相交关系。

（4）内含：一个圆被另一个圆包含，则互为内含关系。

（5）内切：两个圆有且仅有一个交点，并且其中一个圆被另一个圆包含，则互为内切关系。

（6）同心：两个圆的圆心重合，则互为同心关系。

（7）重合：两个圆完全重合，则互为重合关系。

3. 应用在生活中，判定圆与圆的位置关系往往是为了解决某些问题，比如通过判定钢球的位置关系来预测钢球运动轨迹。

因此，我们需要能够通过绘制图形来解决实际问题。

五、课堂练习请完成如下题目：1.已知圆A正切于圆O，圆A的半径为3，圆O的半径为5，求OA的长度。

2.在平面直角坐标系中，有两个圆：圆A的圆心为(0,0)，半径为3，圆B与圆A相切于(2,0)，圆B是敞口向上的钟形，求圆B的方程。

3.在平面直角坐标系中，有两个圆：圆A的圆心为(-1,3)，半径为4，圆B的圆心为(3,2)，半径为5，求圆A和圆B的位置关系。

六、作业1.画出两个圆相切的示意图，标注关键信息。

2.解析题目：“在平面直角坐标系中，有两个圆：圆A的圆心为(1,2)，半径为4，圆B正切于圆A，求圆B的半径。

”3.预习下节课。

“2.3.直线与圆的位置关系”。

普通高中课程标准实验教科书—数学第一册[苏教版]第17课时圆与圆的位置关系教学目标（1）掌握圆与圆的位置关系的代数与几何判别方法；（2）了解用代数法研究圆的关系的优点；（3）了解算法思想．教学重难点理解圆与圆的位置关系，并掌握其判定方法教学过程一、问题情境1．情境：复习回顾：如何利用代数与几何方法判别直线与圆的位置关系？平面几何中，圆与圆的位置关系有哪几种呢？如何判断圆与圆之间的位置关系呢？二、学生活动分析、归纳圆与圆的位置关系，及其判断方法．三、建构数学1．判断两圆的位置关系的步骤：第一步：计算两圆的半径,R r；O O，即d；第二步：计算两圆的圆心距12第三步：根据d与,R r之间的关系，判断两圆的位置关系．2．两圆的位置关系：四、数学运用1．例题：例1．判断下列两圆的位置关系：2222与++-=-+-=(1)(2)(2)1(2)(5)16x y x y2222（）与++-=++-=26706270x y x x y y解：（1）根据题意得，两圆的半径分别为1214r r ==和，两圆的圆心距5.d ==因为 12d r r =+，所以两圆外切．（2）将两圆的方程化为标准方程，得2222(3)16,(3)36x y x y ++=++=． 故两圆的半径分别为1246r r ==和，两圆的圆心距d ==．因为1212||r r d r r -<<+，所以两圆相交．例2． 求过点(0,6)A 且与圆22:10100C x y x y +++=切于原点的圆的方程． 分析：如图，所求圆经过原点和(0,6)A ，且圆心应在已知圆的圆心与原点的连线上．根据这三个条件可确定圆的方程 ．解：将圆C 化为标准方程，得22(5)(5)50x y +++=， 则圆心为(5,5)C --，半径为和原点的直线方程为0x y -=．设所求圆的方程为222()()x a y b r -+-=． 由题意知，(0,0),(0,6)O A 在此圆上，且圆心(,)M a b 在直线0x y -=上，则有222222(0)(0),3,(0)(6),3,0a b r a a b r b a b r ⎧-+-=⎧=⎪⎪-+-=⇒=⎨⎨⎪⎪-==⎩⎩于是所求圆的方程是22(3)(3)18x y -+-=． 思考：本题还有其他解法吗？例3．已知圆221:2610C x y x y ++-+=，圆222:42110C x y x y +-+-=，求两圆的公共弦所在的直线方程及公共弦长．分析： 因两圆的交点坐标同时满足两个圆方程，联立方程组，消去2x 项、2y 项，即得两圆的两个交点所在的直线方程，利用勾股定理可求出两圆公共弦长．解：设两圆交点为11(,)A x y 、22(,)B x y ，则A B 、两点坐标满足方程组22222610,(1)42110,(2)x y x y x y x y ⎧++-+=⎪⎨+-+-=⎪⎩，(1)(2)-得3460x y -+=． 因为，A B 、两点坐标都满足此方程，所以，3460x y -+=即为两圆公共弦所在的直线方程． 易知圆1C 的圆心(1,3)-，半径3r =． 又1C到直线的距离为95d ==．所以，245AB ===．即两圆的公共弦长为245．例4．求过两圆22226406280x y x x y y ++-=++-=和的交点，且圆心在直线40x y --=上的圆的方程．分析一：所求圆圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径．解：（法一）可求得两圆连心线所在直线的方程为30x y ++=．由40,30,x y x y --=⎧⎨++=⎩得圆心17(,)22-．利用弦心距、弦长、半径之间的关系可求得公共弦长d =所以，圆半径22217|()4|89()22d r ⎛⎫--+ ⎪=+=． 所以，所求圆方程为221789()()222x y -++=，即227320x y x y +-+-=． （法二）设所求圆的方程为222264(628)0x y x x y y λ++-+++-=， 即22664280111x y x y λλλλλ++++-=+++． 故此圆的圆心为33(,)11λλλ--++，它在直线40x y --=上， 所以334011λλλ--+-=++，所以7λ=-． 所以所求圆方程为227320x y x y +-+-=．说明：“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程．2．练习：1．课本第107页练习第1、2题．2．已知圆2221:2450C x y mx y m +-++-=，圆2222:2230C x y x m y m ++-+-=，m为何值时，（1）圆1C 与圆2C 相外切；（2）圆1C 与圆2C 内含．五、回顾小结：掌握利用圆心距和半径之间的大小关系判定圆与圆的位置关系．六、课外作业：课本第107页习题2 .2(2) 第4、6题、第117页第14、19题．。