大学物理麦克斯韦电磁场理论汇总

麦克斯韦电磁场理论①几分立的带电体或电流，它们之间的一切电的及磁的作用都是通过它们之间的中间区域传递的，不论中间区域是真空还是实体物质。

②电能或磁能不仅存在于带电体、磁化体或带电流物体中，其大部分分布在周围的电磁场中。

③导体构成的电路若有中断处，电路中的传导电流将由电介质中的位移电流补偿贯通，即全电流连续。

且位移电流与其所产生的磁场的关系与传导电流的相同。

④磁通量既无始点又无终点，即不存在磁荷。

⑤光波也是电磁波。

麦克斯韦方程组有两种表达方式。

1. 积分形式的麦克斯韦方程组是描述电磁场在某一体积或某一面积内的数学模型。

表达式为：式①是由安培环路定律推广而得的全电流定律，其含义是：磁场强度H沿任意闭合曲线的线积分，等于穿过此曲线限定面积的全电流。

等号右边第一项是传导电流．第二项是位移电流。

式②是法拉第电磁感应定律的表达式，它说明电场强度E沿任意闭合曲线的线积分等于穿过由该曲线所限定面积的磁通对时间的变化率的负值。

这里提到的闭合曲线，并不一定要由导体构成，它可以是介质回路，甚至只是任意一个闭合轮廓。

式③表示磁通连续性原理，说明对于任意一个闭合曲面，有多少磁通进入盛然就有同样数量的磁通离开。

即B线是既无始端又无终端的；同时也说明并不存在与电荷相对应的磷荷。

式④是高斯定律的表达式，说明在时变的条件下，从任意一个闭合曲面出来的D的净通量，应等于该闭曲面所包围的体积内全部自由电荷之总和。

2. 微分形式的麦克斯韦方程组。

微分形式的麦克斯韦方程是对场中每一点而言的。

应用del算子，可以把它们写成式⑤是全电流定律的微分形式，它说明磁场强度H的旋度等于该点的全电流密度（传导电流密度J与位移电流密度之和），即磁场的涡旋源是全电流密度，位移电流与传导电流一样都能产生磁场。

式⑥是法拉第电磁感应定律的微分形式，说明电场强度E 的旋度等于该点磁通密度B的时间变化率的负值，即电场的涡旋源是磁通密度的时间变化率。

式⑦是磁通连续性原理的微分形式，说明磁通密度B的散度恒等于零，即B线是无始无终的。

麦克斯韦电磁理论一、电流密度电流密度⎪⎩⎪⎨⎧=⊥dS dI j j 大小：方向：沿电流方向SI ：2/m AdS j jdS jdS dI n ===⊥θcos S d j dI ⋅=⎰⎰⋅==SS d j dI I电流强度等于电流密度的通量二、位移电流 ⎰⋅=ΦSD S d DS D，2/m C ；D Φ，C 曲面固定，电场随时间变化⎰⎰⋅∂∂⋅=ΦS SD S d t D S d D dt d dt d曲面固定t D ∂∂ ：22//m A s m C =）（， 位移电流密度：t Dj D ∂∂=dtd D Φ：A s C =/， 位移电流：dt d I DD Φ=S d j I SD D⋅=⎰E D ε=，t D j D ∂∂= =t E ∂∂ ε，真空中，tD j D ∂∂= =t E∂∂0ε 位移电流的本质是变化的电场 三、静电场和稳恒磁场静电场， ⎰∑=⋅Sf q S d D 内）（1⎰=⋅Ll d E 01）（稳恒磁场， ⎰=⋅SS d B 01 ）（ ⎰∑=⋅LI l d H 内传）（1四、两个假说1、涡旋电场假说：变化的磁场产生涡旋电场S d t B dt d l d E S L m⋅∂∂-=Φ-=⋅⎰⎰）（2涡旋电力线的环绕方向 ∂与t B ∂∂/ 满足左手定则 2(E t B ∂/ ⎰=⋅SS d D 02）（2、位移电流假说⎰Φ==⋅L DD dt d I l d H ）（2⎰⋅∂∂=S S d tD)2(H 线的环绕方向t ∂与t D ∂∂/ 满足右手定则(Ht D ∂/⎰=⋅SS d B 02 ）（ 变化的电场产生磁场电荷→电场↓↑ 电磁场运动电荷→磁场五、麦克斯韦方程组的积分形式静电场： )1(E 、)1(D ， 传导电流的磁场：)1(B 、)1(H涡旋电场：)2(E 、)2(D ， 位移电流的磁场：)2(B 、)2(H )2()1(D D D +=，)2()1(E E E +=，)2()1(B B B +=，)2()1(H H H +=⎰∑⎰⎰=⋅+⋅=⋅Sf SSq S d D S d D S d D 内）（ )2(1电场的高斯定理⎰⎰⎰Φ-=⋅+⋅=⋅L m LL dtd l d E l d E l d E )2(1）（ 法拉第电磁感应定律⎰⎰⎰=⋅+⋅=⋅SSSS d B S d B S d B 0)2(1 ）（磁场的高斯定理 全内传）（I dt d I l d H l d H l d H D L LL =Φ+=⋅+⋅=⋅⎰∑⎰⎰ )2(1 全电流安培环路定律 D I I I +=∑内传全：全电流，不包括磁化电流∑⎰=⋅内f Sq S d Ddt d l d E m LΦ-=⋅⎰ 0=⋅⎰S S d Bdt d I l d H D LΦ+=⋅∑⎰内传 E D ε=，H B μ=，j洛仑兹力公式B V q E q F⨯+=变化的电磁场在空间传播⇒电磁波真空中电磁波的波速s m c /1031800⨯≈=με=真空光速光是电磁波，（麦克斯韦1865），1888，赫兹实验例：证明平板电容器充电过程中，两极板间的位移电流dtdUC ID = I 证明：t ，CU q =dt dU C dt dq I ==传 ⎰⋅=ΦSD S d DCU q S DS ====σdt d I D D Φ==传I dtdUC= 讨论：（1）q D =Φ：S 上没有电荷分布 （2）=D I 传I ，D I I I +=传全连续全电流永远是连续的传导电流传I 位移电流D I载流子定向移动形成的 变化的电场v nq j = tDj D ∂∂=⎰⋅=S S d j I 传=dt dq ， S d j I S D D ⋅=⎰dtd DΦ=焦耳热，焦耳定律 不产生焦耳热⎰∑=⋅L I l d H 内传）（ 1 ⎰Φ==⋅L DD dt d I l d H ）（2例：球形电容器与交流电源相连 t ωs i n 0求：（1）介质中的D j（2）通过半径为r 的 球面的D I（21R r R <<）解：（1）tDj D ∂∂= ，t CU CU q ωsin 0==r r r q D ⋅=24π=r r r t CU ⋅204sin πω，（122104R R R R C r -=επε） tD j D ∂∂= =r rr t CU ⋅204cos πωω （2）S d j I SD D⋅=⎰=dS j SD θcos ⎰=24r j D π=t CU ωωcos 0dtdU C dt dq I ==传=t CU ωωcos 0=D I例：圆片平板电容器t q q ωsin 0= 求：（1）板间D j 、D I（2）)(R r <处的 H 、B 、w解：（1）t D j D ∂∂=，20sin R t q S q D πωσ===，t D j D ∂∂==20cos Rtq πωω S d j I S D D⋅=⎰=dS j S D θcos ⎰=S j D =t q ωωcos 0（2）⎰=⋅L D I l d H ，22r j r H D ππ==22cos r R t q ππωω r R t q H 202c o s πωω=，r R tq H B 20002c o s πωωμμ== 200221212121H D H B E D w με+=⋅+⋅==)cos 41(sin 22220024022t r t R q ωωμεωεπ+ 例：q +以速率V 朝O 点运动 t 时刻q +与O 点相距x 求：（1）通过圆面的D I （2）圆周上的B +解：（1）⎰⋅=ΦSD S d D=⎰SdS D θcos =⎰++S ydy yx xy x q ππ2)(42222 =⎰+R y x ydyqx 02/322)(21=0)1(2122R yx qx +- =)1(2122Rx xq +-=Φ=Φ=dt dx dx d dt d I D D D 2/3222)(21R x R qV +，(dt dx V -=) （2）⎰=⋅L D I l d H ，=R H π22/3222)(21R x R qV +2/322)(4R x q V R H +=π，2/32200)(4R x q V RH B +==πμμ rR=αs i n，22R x r += 20s i n 4r qV B απμ=，304r r V q B⨯=πμ：运动电荷的磁场！例：电容器充电过程中（1）⎰⎰⋅>⋅21L L l d H l d H （2）⎰⎰⋅=⋅21L L l d H l d H（3）⎰⎰⋅<⋅21L L l d H l d H2L（4）01=⋅⎰L l d H例：在无自由电荷与传导电流的空间区域， 变化的电磁场遵循的规律？?=⋅⎰S S d D ，?=⋅⎰L l d E ，?=⋅⎰S S d B ，?=⋅⎰L l d H0=⋅⎰S S d D ，dt d l d E mL Φ-=⋅⎰ ，0=⋅⎰S S d B ，dt d l d H D L Φ=⋅⎰。

电磁场理论知识点总结1.麦克斯韦方程组：麦克斯韦方程组是电磁场理论的核心方程，它由四个方程组成，分别是高斯定律、法拉第电磁感应定律、安培环路定律和法拉第电磁感应定律的积分形式。

这些方程描述了电场和磁场随空间和时间的变化规律。

2.电场和磁场的相互作用：根据麦克斯韦方程组，电场和磁场相互作用，通过电场的变化会产生磁场，而通过磁场的变化会产生电场。

这种相互作用是电磁波传播的基础。

3.电磁波的传播：根据麦克斯韦方程组的解，电磁波以光速在真空中传播，它是由电场和磁场相互耦合而成的波动现象。

电磁波的传播速度不同于物质中的电磁波传播速度，它是真空中的最大可能速度。

4.电磁感应现象：根据法拉第电磁感应定律，当一个导体中的磁场发生变化时，会在导体中产生感应电流。

这个现象被广泛应用于发电机、变压器等电磁设备中。

5.静电场和静磁场：当电荷和电流都不随时间变化时，产生的电场和磁场称为静电场和静磁场。

在静电场中，电场符合高斯定律；在静磁场中，磁场符合安培环路定律。

静电场和静磁场的研究对于理解电磁场的基本性质和应用具有重要意义。

6.电磁辐射和辐射场：根据麦克斯韦方程组的解，加速的电荷会辐射出电磁波。

这种辐射就是电磁辐射，它是电磁波传播的一种形式。

辐射场是指由电磁辐射产生的电场和磁场。

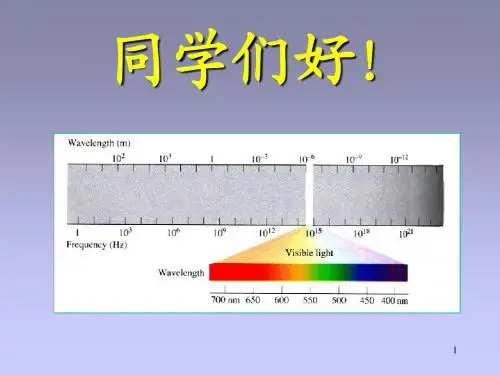
7.电磁波的频率和波长：电磁波的频率和波长是描述电磁波特性的两个重要参数。

频率指的是电磁波单位时间内振动的次数，单位是赫兹；波长指的是电磁波的一个完整振动周期所对应的空间距离，单位是米。

8.电磁场的能量和动量：根据电磁场的能量密度和动量密度的定义，可以推导出电磁场的能量和动量公式。

电磁场携带能量和动量，可以与物质相互作用，这是实现无线通信、光学传输等现代科技的基础。

9.电磁场的边界条件：电磁场在介质边界上的反射和折射现象可以通过电磁场的边界条件来描述。

边界条件包括麦克斯韦方程组的边界条件和介质的边界条件，它们确定了电磁场在边界上的行为和传播规律。

麦克斯韦电磁场理论简介麦克斯韦电磁场理论是描述电磁现象的最基本理论之一。

它由苏格兰物理学家詹姆斯·克拉克·麦克斯韦于19世纪提出，将电场和磁场统一到一个统一的理论框架中。

麦克斯韦方程组麦克斯韦电磁场理论的核心是麦克斯韦方程组，包括四个方程式：1.麦克斯韦第一方程（电场的高斯定理）：麦克斯韦第一方程麦克斯韦第一方程这个方程描述了电荷和电场的关系，其中Q是电荷，\Dot{D}是电通量密度，\Sigma是闭合曲面。

2.麦克斯韦第二方程（磁场的高斯定理）：麦克斯韦第二方程麦克斯韦第二方程这个方程表明，磁场没有单极子，磁通量密度\Bf通过任何闭合曲面总是为零。

3.麦克斯韦第三方程（电场的法拉第定律）：麦克斯韦第三方程麦克斯韦第三方程这个方程描述了变化的磁场产生的感应电场，\mathit{E}是电场强度，R是线路路径，\Phi是磁通量。

4.麦克斯韦第四方程（磁场的安培定律）：麦克斯韦第四方程麦克斯韦第四方程这个方程描述了电流和磁场之间的关系，\Bf是磁场强度，\Mob是电流密度。

这四个方程组成了麦克斯韦电磁场理论的基础，通过它们可以描述和预测电场和磁场的行为。

应用麦克斯韦电磁场理论在现代物理学和工程学中有广泛的应用。

以下是一些主要的应用领域：电磁波麦克斯韦电磁场理论预测了电磁波的存在和性质。

根据这个理论，电磁波是由振动的电场和磁场相互作用而产生的。

电磁波包括无线电波、微波、可见光、紫外线、X射线和γ射线等。

麦克斯韦电磁场理论的发现为广播、通信、雷达、光学和医学成像等领域的发展做出了重要贡献。

电磁感应麦克斯韦电磁场理论描述了磁场变化引起的感应电场。

这个现象被广泛应用在发电机、变压器和感应加热等领域。

根据麦克斯韦方程组，当磁场发生变化时，将产生感应电场。

这种感应电场可以被捕获和利用，用来产生电能或实现其他功能。

电磁场计算麦克斯韦电磁场理论为计算和模拟电磁场行为提供了有效的工具。

通过求解麦克斯韦方程组，可以准确地计算出电场和磁场在空间中的分布和变化。

l、麦克斯韦的理论要点一：变化的磁场产生电场演示实验装置如图所示，当穿过螺线管的磁场随时间变化时，上面的线圈中产生感应电动势，引起感应电流使灯泡发光．（1）线圈中产生感应电动势说明了什么？麦克斯韦认为变化的磁场在线圈中产生电场，正是这种电场（涡旋电场）在线圈中驱使自由电子做定向的移动，引起了感应电流．（2）如果用不导电的塑料线绕制线圈，线圈中还会有电流、电场吗？引导学生思考后回答，有电场、无电流．（3）想象线圈不存在时线圈所在处的空间还有电场吗？（有）（4）总结说明，麦克斯韦认为线圈只不过用来显示电场的存在，线圈不存在时，变化的磁场同样在周围空间产生电场，即这是一种普遍存在的现象，跟闭合电路是否存在无关．2、变化的电场产生磁场我们知道，电流周围存在着磁场，麦克斯韦研究了电现象和磁现象的相似和联系．经过反复思考提出一个假设，变化的电场产生磁场．这一点，我们从哲学上知道，事物之间是相互联系的，可以相互转化．比如根据麦克斯韦的理论，在给电容器充电的时候，不仅导体中电流要产生磁场，而且在电容器两极板问周期性变化着的电场周围也要产生磁场．3、电磁场、电磁波（l）概念麦克斯韦根据自己的理论进一步预言，如果在空间某域中有周期性变化的电场，那么，这个变化的电场就在它周围空间产生周期性变化的磁场，这个变化的磁场又在它周围空间产生新的周期性变化的电场……可见，变化的电场和变化的磁场是相互联系的，形成一个不可分离的统一体，这就是电磁场，这种变化的电场和变化的磁场总是交替产生，并且由发生的区域向周围空间传播．见课本图19—10，电磁场由发生区域向远处的传播就是电磁波．（2）电磁波的特点①是横波：用课本P270图19－10说明②是物质波，真空中也能传播，能独立存在（与机械波不同）③具有反射、折射、干涉、衍射等波的一切特性（1）波速公式（）电磁波在真空中速度等于光速．三、总结、扩展麦克斯韦的电磁场理论1、变化的磁场能够在周围空间产生电场，变化的电场能够在周围产生磁场．2、均匀变化的磁场，产生稳定的电场，均匀变化的电场，产生稳定的磁场．这里的“均匀变化”指在相等时间内磁感应强度（或电场强度）的变化量相等，或者说磁感应强度（或电场强度）对时间变化率一定．3、不均匀变化的磁场产生变化的电场，不均匀变化的电场产生变化的磁场4、振荡的（即周期性变化的）磁场产生同频率的振荡电场，振荡的电场产生同频率的振荡磁场．5、变化的电场和变化的磁场总是相互联系着，形成一个不可分离的统一体，这就是电磁场，向周围空间传播就是电磁波．。

大学物理电磁学基础知识点汇总一、电场1、库仑定律库仑定律描述了真空中两个静止点电荷之间的相互作用力与它们电荷量的乘积成正比，与它们之间距离的平方成反比，作用力的方向沿着它们的连线。

其表达式为：＄F ＝ k\frac{q_1q_2}｛r^2}＄，其中$k$为库仑常量，＄q_1$和$q_2$为两个点电荷的电荷量，＄r$为它们之间的距离。

2、电场强度电场强度是描述电场力的性质的物理量，定义为单位正电荷在电场中所受到的力。

其表达式为：＄E ＝＼frac{F}｛q}＄。

对于点电荷产生的电场，其电场强度的表达式为：＄E ＝ k\frac{q}｛r^2}＄，方向沿径向向外（正电荷）或向内（负电荷）。

3、电场线电场线是用来形象地描述电场的一种工具。

电场线的疏密表示电场强度的大小，电场线的切线方向表示电场强度的方向。

静电场的电场线不闭合，始于正电荷或无穷远，终于负电荷或无穷远。

4、电通量电通量是通过某一面积的电场线条数。

对于匀强电场，通过平面的电通量为：＄＼Phi ＝ ES\cos\theta$，其中$E$为电场强度，＄S$为平面面积，＄＼theta$为电场强度与平面法线的夹角。

5、高斯定理高斯定理表明，通过闭合曲面的电通量等于该闭合曲面所包围的电荷量的代数和除以$＼epsilon_0$。

即：＄＼oint_S E\cdot dS ＝＼frac{1}｛＼epsilon_0}＼sum q$。

高斯定理是求解具有对称性电场分布的重要工具。

二、电势1、电势电势是描述电场能的性质的物理量，定义为把单位正电荷从电场中某点移动到参考点（通常取无穷远处）时电场力所做的功。

某点的电势等于该点到参考点的电势差。

点电荷产生的电场中某点的电势为：＄V ＝ k\frac{q}｛r}＄。

2、等势面等势面是电势相等的点构成的面。

等势面与电场线垂直，沿电场线方向电势降低。

3、电势差电场中两点之间的电势之差称为电势差，也称为电压。

其表达式为：＄U_{AB} ＝ V_A V_B$。