(完整版)平面直角坐标系常见题型.docx

中考数学试题考点分类平面直角坐标系(含答案)————————————————————————————————作者：————————————————————————————————日期：平面直角坐标系考点1：特殊点坐标的特点1.在x轴上的点的_____坐标为__________,在y轴上的点的_____坐标为__________。

2．在第一象限内的点的横坐标为______，纵坐标为______.在第二象限内的点的横坐标为______，纵坐标为______.在第三象限内的点的横坐标为______，纵坐标为______.在第四象限内的点的横坐标为______，纵坐标为______.1.在平面直角坐标中，点M(－2，3)在（）A．第一象限B．第二象限C．第三象限D．第四象限2.在平面直角坐标系中，点（1，3）位于第________象限。

3.在平面直角坐标系中，点P(－2，2x＋1)所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限4.若点P（a，a－2）在第四象限，则a的取值范围是（）．A．－2＜a＜0 B．0＜a＜2 C．a＞2 D．a＜0考点2：轴对称的坐标1、关于x轴对称：两个点关于x轴对称，横坐标不变，纵坐标变相反。

即A（a，b）关于x轴对称的点的坐标为（____，____）。

2、关于y轴对称：两个点关于y轴对称，纵坐标不变，横坐标变相反。

即A（a，b）关于y轴对称的点的坐标为（____，____）。

3、关于原点对称：两个点关于原点对称，横坐标变相反，纵坐标变相反。

即A（a，b）关于原点对称的点的坐标为（____，____）。

1.点M（-2，1）关于x轴对称的点的坐标是（）．A．(-2，-1）B．(2，1）C．（2，-1）D．(1，-2）2.点P（－3,2）关于x轴对称的点P`的坐标是．3.在平面直角坐标系中，点A（2,3）与点B关于x轴对称，则点B的坐标为（）．A.（3, 2）B.（－2，－3）C.（－2, 3）D.(2,－3)4.平面直角坐标系中，与点（2，－3）关于原点中心对称的点是（）．A．（－3，2）B．（3，－2）C．（－2，3）D．（2，3）5.点P（1,2）关于原点的对称点P′的坐标为___________．6.如图，矩形OABC的顶点O为坐标原点，点A在x轴上，点B的坐标为(2，1).如果将矩形OABC绕点O旋转180°，旋转后的图形为矩形OA 1B1C1，那么点B1的坐标为( ).A. (2，1)B.(－2,l)C.(－2,－l)D.(2，－1)7.若点A（2，a）关于x轴的对称点是B（b，－3）则ab的值是.8.在平面直角坐标系中，点A（1，2）关于y轴对称的点为点B（a，2），则a＝．9.在平面直角坐标系中，点P（2，3）与点P (2a+b，a+2b)关于原点对称，则a－b的值为_________考点3：考平移后点的坐标1.将点（x，y）向右（或左）平移a个单位长度，可以得到对应点（____，____）（或（_____，____））；2.将点（x，y）向上（或下）平移b个单位长度，可以得到对应点（____，_____）（或（____，____））．1.在平面直角坐标系中，将点（－2，－3）向上平移3个单位，则平移后的点的坐标为_______．2.如图，在平面直角坐标系中，点P（－1，2）向右平移3个单位长度后的坐标是（）A.（2，2）B.（－4，2）C.（－1，5）D.（－1，－1）3.将点P（－2,1）先向左平移1个单位长度，再向上平移2个单位长度得到点P/,则点P/的坐标为。

初一数学平面直角坐标系30道必做题（含答案和解析及考点）1、如图是小刚画的一张脸，他对妹妹说“如果我用（1,3）表示左眼，用（3,3）表示右眼，那么嘴的位置可以表示成.答案：（2,1）.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.2、如图所示，小颖从家到达莲花中学要穿过一个居民小区，若小区的道路均是正南或正东方向，小颖走下面哪条线路不能到达学校（）.A.（0,4）（0,0）（4,0）B.（0,4）（4,4）（4,0）C.（0,4）（1,4）（1,1）（4,1）（4,0）D.（0,4）（3,4）（4,2）（4,0）答案：D.解析：（3,4）（4,2）所走路线为斜线，不符合题意，不能正常到达学校．考点：函数——平面直角坐标系.3、如图，围棋盘放置在某个平面直角坐标系内，白棋②的坐标为（-7,-4），白棋④的坐标为（-6,-8），那么，黑棋的坐标应该分别是．答案：（-6,-6），（-4,-7）.解析：黑棋①的坐标是（-6,-6），黑棋③的坐标是（-4,-7）.考点：函数——平面直角坐标系——点的位置与坐标.4、如果点A（x,y）在第三象限，则点B（-x,y-1）在（）．A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案: D.解析:∵点A（x,y）在第三象限，∴{x＜0y＜0.∴-x＞0，y-1＜0.∴点B（-x,y-1）在第四象限．考点：函数——平面直角坐标系——点的位置与坐标.5、如图的坐标平面上有P、Q两点，其坐标分别为（5,a）、（b,7）．根据图中P、Q两点的位置，判断点（）落在第象限．答案：四.解析：由图象可知，b＜5，a＜7.∴6-b＞0，a-10＜0.∴点（6-b,a-10）落在第四象限．考点：函数——平面直角坐标系——点的位置与坐标.6、已知A（-2,0），B（a,0）且AB=5，则B点坐标为．答案：（3,0）或（-7,0）.解析：由题知︱a+2︱=5，∴a=3或-7.∴B点坐标为（3,0）或（-7,0）.考点：函数——平面直角坐标系——坐标与距离.7、若点A（-2,n）在x轴上，则点B（n-1,n+1）在（）．A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案：B.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.8、点P（m+3,m+1）在直角坐标系的x轴上，则点P的坐标为（）．A.（1,-2）B.（2,0）C.（4,0）D.（0,-4）答案：B.解析：∵点P（m+3,m+1）在直角坐标系的轴上.∴m+1=0.∴m=-1.∴点P的坐标为（2,0）.考点：函数——平面直角坐标系——点的位置与坐标.9、已知点M（3a-8,a-1）．（1）若点M在第二象限，并且a为整数，则点M的坐标为．（2）若点N的坐标为（3,-6），并且直线MN∥x轴，则点M的坐标为．答案：（1）（-2,1）.（2）（-23,-6）.解析：（1）若点M在第二象限，3a＜0，a-1＞0.∴1＜a＜8，又a为整数.3∴a=2.∴M（-2,1）.（2）若点N的坐标为（3，-6），并且直线MN∥x轴.∴a-1=-6，即a=7.∴点M（-23,-6）.考点：函数——平面直角坐标系——点的位置与坐标.10、若点P（-1,a），Q（b,2），且PQ∥x轴，则a ，b .答案：a=2.b≠-1.解析：∵PQ∥x轴.∴PQ两点的纵坐标相同.∴a=2.又∵P、Q应为不重合的两点.∴b≠-1.考点：函数——平面直角坐标系——点的位置与坐标.11、点P（a,b）是平面直角坐标系内的点，请根据点的坐标判断点P的特征：（1）若a=b，则P点在.（2）若a+b=0，则P点在.答案：（1）一三象限坐标轴夹角平分线上.（2）二四象限坐标轴夹角平分线上.解析：（1）略.（2）略.考点：函数——平面直角坐标系——点的位置与坐标.12、若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是（）．A.（2,2）B.（-2,-2）C.（2,2）或（-2,-2）D.（2,-2）或（-2,2）答案：C.解析：略.考点：函数——平面直角坐标系——坐标与距离.13、已知点（3-2k2,4k-3）在第一象限的角平分线上，则k= ．答案：1.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.14、若点M（5-a，2a-6）在第四象限，且点M到x轴与y轴的距离相等，试求（a-2）2014-a-2015的值．答案：0.解析：由题意得，5-a+2a-6=0.解得a=1.所以，（a-2）2014-a-2015=（1-2）2014-1-2015=1-1=0.考点：函数——平面直角坐标系——坐标与距离.15、若点P位于y轴左方，距y轴3个单位长，位于x轴上方，距x轴四个单位长，则点P的坐标是．答案：（-3,4）.解析：略.考点：函数——平面直角坐标系——特殊点的坐标.16、在平面直角坐标系中，点P（-3,6）关于y轴的对称点的坐标为．答案：（3,6）.解析：根据关于谁对称，谁不变，可知，点P（-3,6）关于y轴的对称点的坐标为（3,6）. 考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.17、在平面直角坐标系中，点P（-1,2）关于y轴的对称点为.答案：（1,2）.解析：由关于谁对称谁不变，可知点P（-1,2）关于y轴的对称点为（1,2）.考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.18、在平面直角坐标系中，点P（-1,2）关于x轴的对称点在第象限．答案：三.解析：点P（-1,2）满足点在第二象限的条件．关于x轴的对称点的横坐标与P点的横坐标相同，是-2.纵坐标互为相反数，是-3.则P关于x 轴的对称点是（-2，-3），在第三象限．考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.19、平面直角坐标系中，将线段OA向左平移2个单位，平移后，点O 、A的对应点分别为点O1 、A1，则点O1 、A1的坐标分别是（）．A.（0,0），（1,4）B.（0,0），（3,4）C.（-2,0），（1,4）D.（-2,0），（-1,4）答案：D.解析：∵线段OA向左平移2个单位，点O（0,0），A（1,4）.∴点O1，A1的坐标分别是（-2,0），（-1,4）.考点：几何变换——图形的平移——坐标与图形变化：平移.20、已知三角形的三个顶点坐标分别是（-2,1），（2,3），（-3,-1），把△ABC运动到一个确定位置，在下列各点坐标中，（）是平移得到的．A.（0,3），（0,1），（-1,-1）B.（-3,2），（3,2），（-4,0）C.（1,-2），（3,2），（-1,-3）D.（-1,3），（3,5），（-2,1）答案：D.解析：由（-2,1）→（-1,3），（2,3）→（3,5），（-3,-1）→（-2,1）可以看作点向右平移1个单位长度，向上平移2个单位长度，而图形的平移是相同的，所以D对，A、B、C错．考点：函数——平面直角坐标系——点的位置与坐标.几何变换——图形的平移——点的平移.21、线段CD是由线段AB平移得到的，点A（-1,4）的对应点为，则点B（-4,-1）的对应点D坐标为（）.A.（2,9）B.（5,3）C.（1,2）D.（-9,-4）答案：C.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.22、已知点A（0,0），B（3,0），点C在y轴上，且△ABC的面积为6，则点C的坐标是．答案：（0,4）或（0，-4）.解析：由题意可知1AC·AB=6.2∴AC=4.∴点C的坐标是（0,4）或（0，-4）.考点：函数——平面直角坐标系——坐标与面积.23、如图所示，半圆AB平移到半圆CD的位置时所扫过的面积为（）．A.3B.3+πC.6D.6+π答案：C.解析：扫过面积即为矩形ABDC的面积.∴扫过面积=2×3=6.考点：函数——平面直角坐标系——坐标与面积.24、在正方形网格上有一个△ABC ，网格上最小正方形的边长为1．（1） 把△ABC 平移，使点A 移动到点A’的位置，画出平移后的△A’B’C’，写出结论：__________．（2）△A’B’C’的面积为__________．（3）若点A 的坐标是（-5,2），点C’为坐标是（0,-2），在图中画出平面直角坐标系，点B’的坐标是__________．答案：（1） 结论：A’B’∥AB （答案不唯一）．（2）△A’B’C’的面积是为5． （3）点B’的坐标是（-3,-3）.解析：（1）平移后的△A’B’C’如图所示，结论：A’B’∥AB （答案不唯一）．（2）观察图形可知，△A’B’C’内接在一个长为4，宽为3的长方形中.S △A’B’C’=4×3 −12×1×3−12×1×3−12×2×4=5. ∴△A’B’C’的面积是为5．（3）平面直角坐标系如图所示，点B’的坐标是（-3,-3）.考点：三角形——三角形基础——三角形面积及等积变换.几何变换——图形的平移——平移的性质——坐标与图形变化：平移——作图：平移变换.25、定义：f （a,b ）=（b,a ），g （m,n ）=（-m,-n ）.例如f （2,3）=（3,2），g （-1,-4）=（1,4）．则g[f （-5,6）] 等于 ． 答案：（-6,5）.解析：根据所给定义，g[f （-5,6）]=g （6,-5）=（-6,5）. 考点：式——探究规律——定义新运算.函数——平面直角坐标系.26、在平面直角坐标系中，对于平面内任一点（m ,n ），规定以下两种变换①f （m ,n ）=（m ,-n ），如f （2,1）=（2,-1）；②g （m ,n ）=（-m ,-n ），如g （2,1）=（-2,-1）.按照以上变换有：f[g （3,4）]=f （-3,-4）=（-3,4），那么g[f （-3,2）] 等于（ ）． A.（3,2） B.（3,-2） C.（-3,2） D.（-3,-2） 答案：A.解析：∵f （-3,2）=（-3,-2）.∴g[f （-3,2）]=g （-3,-2）=（3,2）. 考点：式——探究规律——定义新运算.27、观察下列有规律的点的坐标：A 1（1,1），A 2（2,-4），A 3（3,4），A 4（4,-2），A 5（5,7），A 6（6,−43），A 7（7,10），A 8（8,-1）依此规律，A 11的坐标为 ，A 12的坐标为 ． A.（12,16），（12,−23） B.（11,15），（11,−23）C.（11,16），（11,−23） D.（11,16），（12,−23）答案：D. 解析：略.考点：函数——平面直角坐标系——点的位置与坐标.28、如图，边长为1,2的长方形ABCD 以右下角的顶点为中心旋转90°，此时A 点的坐标为 ；依次旋转2011次，则顶点A 的坐标为 ． A.（3,3），（3027,0） B.（3,3），（3017,0） C.（3,2），（3027,0） D.（3,2），（3017,0） 答案：D. 解析：略.考点：式——探究规律.方程与不等式.函数——平面直角坐标系.29、一个粒子在第一象限内及x 轴、y 轴上运动，在第1min 内它从原点运动到（1,0），而后接着按如图所示方式在与x 轴、y 轴平行的方向上来回运动，且每分钟移动1个单位长度，那么，在2011min 后，求这个粒子所处的位置坐标．A.（41,13）B.（41,14）C.（44,13）D.（44,14） 答案：C.解析：弄清粒子的运动规律，并求出靠近2011min 后粒子所在的特殊点的坐标，最后确定所求点的坐标．对于这种运算数较大的题目，我们首先来寻找规律，先观察横坐标与纵坐标相同的点：（0,0），粒子运动了0min. （1,1），粒子运动了1×2=2（min ），向左运动． （2,2），粒子运动了2×3=6（min ），向下运动．（3,3），粒子运动了3×4=12（min），向左运动．（4,4），粒子运动了4×5=20（min），向下运动．……于是点（44,44）处粒子运动了44×45=1980（min）．这时粒子向下运动，从而在运动了2011后，粒子所在的位置是（44,44-31），即（44,13）.考点：函数——平面直角坐标系.30、在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图所示．①填写下列各点的坐标：A1（，），A3（，），A12（，）.②写出点A4n的坐标为（是正整数）.③指出蚂蚁从点A100到A101的运动方向为.A. ①（1,1），（1,0），（5,0）；②（2n，0）；③ 从下到上.B. ①（1,1），（1,0），（6,0）；②（2n，0）；③ 从上到下.C. ①（0,1），（1,0），（5,0）；②（2n，0）；③ 从上到下.D. ①（0,1），（1,0），（6,0）；②（2n，0）；③ 从下到上.答案：D.解析：略.考点：函数——平面直角坐标系——点的位置与坐标——坐标与距离.。

专题03 平面直角坐标系专题03 平面直角坐标系 (1)7.1 平面直角坐标系 (2)知识框架 (2)一、基础知识点 (2)知识点1 有序数对 (2)知识点2 平面直角坐标系 (2)知识点3 点的坐标特点 (3)二、典型题型 (6)题型1 有序数对 (6)题型2 平面直角坐标系的概念 (6)题型3 点的坐标的特征 (6)一、点的位置与坐标 (7)二、点的坐标与距离 (8)三、点的坐标与平行于坐标轴的直线（数形结合思想） (8)四、点的坐标与图形的面积 (9)（1）知坐标，求面积 (9)（2）知面积，求坐标（方程思想） (10)（3）分类讨论 (12)三、难点题型 (14)题型1 确定点所在的象限 (14)题型2 点到坐标轴的距离 (14)题型3 探究平面直角坐标系坐标的变化规律 (15)7.2 坐标系的简单运用 (17)知识框架 (17)一、基础知识点 (17)知识点1 用坐标表示地理位置 (17)知识点2 用坐标表示平移 (18)二、典型题型 (20)题型1 用坐标表示地理位置 (20)题型2 用坐标表示平移 (21)一、点的平移 (21)（1）已知点和平移方式，求对应点 (21)（2）已知点和对应点，求平移方式 (21)二、图形的平移 (22)三、难点题型 (23)题型1 动点问题 (23)7.1 平面直角坐标系知识框架{基础知识点{有序数对平面直角坐标系点的坐标的特点典型题型{ 有序数对平面直角坐标系的概念点的坐标的特征{ 点的位置与坐标点的坐标与距离点的坐标与平行于坐标轴的直线（数形结合思想）点的坐标与图形的面积{知坐标，求面积知面积，求坐标（方程思想）分类讨论难点题型{确定点所在的象限点到坐标轴的距离探究平面直角坐标系坐标的变化规律 一、基础知识点知识点1 有序数对1）我们把有顺序的两个数a 与b 组成的数对，用于表示平面中某一确定位置的，叫作有序数对，记作（a ，b ）注：①（a ，b ）与（b ，a ）表达的含义不同，注意有序数对的顺序②在表达有序数对时，一般行在前，列在后。

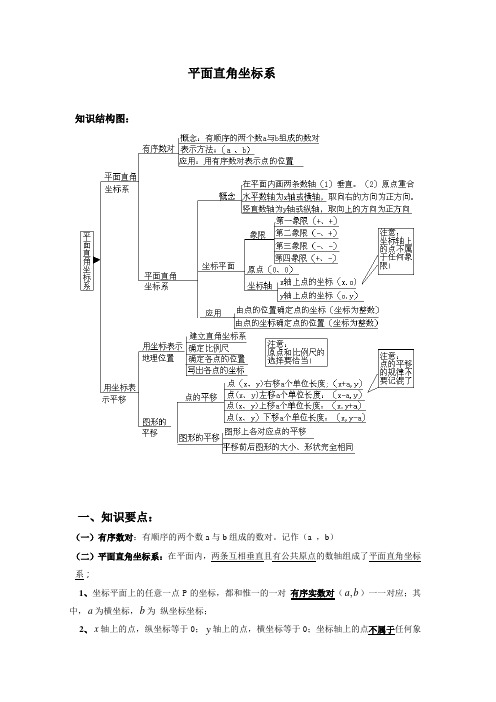
平面直角坐标系知识结构图：一、知识要点：（一）有序数对：有顺序的两个数a与b组成的数对。

记作（a ，b）（二）平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成了平面直角坐标系；a,）一一对应；其1、坐标平面上的任意一点P的坐标，都和惟一的一对有序实数对（b中，a为横坐标，b为纵坐标坐标；2、x轴上的点，纵坐标等于0；y轴上的点，横坐标等于0；坐标轴上的点不属于任何象限（三）四个象限的点的坐标具有如下特征：1、点P （y x ,）所在的象限 横、纵坐标x 、y 的取值的正负性；2、点P （y x ,）所在的数轴 横、纵坐标x 、y 中必有一数为零； （四）在平面直角坐标系中，已知点P ),(b a ，则 1、点P 到x 轴的距离为b ； 2、点P 到y 轴的距离为a ；3、点P 到原点O 的距离为PO ＝ 22b a +（五）平行直线上的点的坐标特征：1、在与x 轴平行的直线上， 所有点的纵坐标相等；点A 、B 的纵坐标都等于m ；2、在与y 轴平行的直线上，所有点的横坐标相等；点C 、D 的横坐标都等于n ；（六）对称点的坐标特征：1、点P ),(n m 关于x 轴的对称点为),(1n m P -， 即横坐标不变，纵坐标互为相反数；象限 横坐标x纵坐标y第一象限 正 正 第二象限 负 正 第三象限 负 负 第四象限正负P （b a ,）abxy OXYA BmXYC Dn2、点P ),(n m 关于y 轴的对称点为),(2n m P -， 即纵坐标不变，横坐标互为相反数；3、点P ),(n m 关于原点的对称点为),(3n m P --，即横、纵坐标都互为相反数；关于x 轴对称 关于y 轴对称 关于原点对称（七）两条坐标轴夹角平分线上的点的坐标的特征：1、若点P （n m ,）在第一、三象限的角平分线上，则n m =，即横、纵坐标相等；2、若点P （n m ,）在第二、四象限的角平分线上，则n m -=，即横、纵坐标互为相反数；在第一、三象限的角平分线上 在第二、四象限的角平分线上（八）利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下：1、建立坐标系，选择一个适当的参照点为原点，确定x 轴、y 轴的正方向；2、根据具体问题确定适当的比例尺，在坐标轴上标出单位长度；3、在坐标平面内画出这些点，写出各点的坐标和各个地点的名称。

【平面直角坐标系重点考点例析】考点一:平面直角坐标系中点的特征例1 在平面直角坐标系中,点P（m，m-2）在第一象限内，则m的取值范围是．思路分析：根据第一象限的点的坐标，横坐标为正，纵坐标为正，可得出m的范围．解:由第一象限点的坐标的特点可得:20 mm>⎧⎨->⎩,解得:m＞2．故答案为：m＞2．点评：此题考查了点的坐标的知识，属于基础题,解答本题的关键是掌握第一象限的点的坐标,横坐标为正,纵坐标为正．例1 如果m是任意实数，则点P（m-4，m+1)一定不在（）A．第一象限B．第二象限C．第三象限D．第四象限思路分析：求出点P的纵坐标一定大于横坐标,然后根据各象限的点的坐标特征解答．解：∵（m+1)-(m-4)=m+1-m+4=5，∴点P的纵坐标一定大于横坐标，∵第四象限的点的横坐标是正数，纵坐标是负数，∴第四象限的点的横坐标一定大于纵坐标，∴点P一定不在第四象限．故选D．点评：本题考查了点的坐标，记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是：第一象限（+，+）；第二象限（—，+）;第三象限(-,—)；第四象限(+，-）．例2 如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2012次相遇地点的坐标是（)A．（2,0) B．（﹣1，1）C．（﹣2，1）D．（﹣1，﹣1）分析：利用行程问题中的相遇问题，由于矩形的边长为4和2,物体乙是物体甲的速度的2倍，求得每一次相遇的地点,找出规律即可解答．解答：解：矩形的边长为4和2，因为物体乙是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1:2，由题意知：①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4，物体乙行的路程为12×=8,在BC边相遇；②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8，物体乙行的路程为12×2×=16,在DE边相遇;③第三次相遇物体甲与物体乙行的路程和为12×3，物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇；…此时甲乙回到原出发点,则每相遇三次，两点回到出发点,∵2012÷3=670…2，故两个物体运动后的第2012次相遇地点的是：第二次相遇地点,即物体甲行的路程为12×2×=8，物体乙行的路程为12×2×=16,在DE边相遇;此时相遇点的坐标为：（﹣1,﹣1)，故选：D．点评：此题主要考查了行程问题中的相遇问题及按比例分配的运用，通过计算发现规律就可以解决问题．例2 如图，动点P从(0，3)出发,沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时,点P的坐标为（）A．（1，4) B．（5，0）C．（6,4) D．（8,3)思路分析：根据反射角与入射角的定义作出图形，可知每6次反弹为一个循环组依次循环，用2013除以6，根据商和余数的情况确定所对应的点的坐标即可．解:如图，经过6次反弹后动点回到出发点（0，3）,∵2013÷6=335…3，∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,点P的坐标为（8，3）．故选D．点评：本题是对点的坐标的规律变化的考查了，作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键，也是本题的难点．对应训练2．如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2）,D（1，﹣2）．把一条长为2012个单位长度且没有弹性的细线（线的粗细忽略不计)的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是（）A ．（1，﹣1）B ． （﹣1，1）C ． （﹣1,﹣2）D ． (1，﹣2）分析： 根据点的坐标求出四边形ABCD 的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案．解答： 解：∵A(1，1）,B （﹣1,1)，C （﹣1，﹣2），D （1，﹣2），∴AB=1﹣（﹣1)=2，BC=1﹣（﹣2）=3，CD=1﹣（﹣1）=2，DA=1﹣(﹣2)=3, ∴绕四边形ABCD 一周的细线长度为2+3+2+3=10， 2012÷10=201…2,∴细线另一端在绕四边形第202圈的第2个单位长度的位置, 即点B 的位置,点的坐标为(﹣1，1）． 故选B ．点评： 本题利用点的坐标考查了数字变化规律，根据点的坐标求出四边形ABCD 一周的长度,从而确定2012个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键．例2 如图，在平面直角坐标系xOy 中，点P （-3，5）关于y 轴的对称点的坐标为（ ） A ．（—3，—5) B ．（3，5) C ．（3．—5） D ．(5，—3） 答：B考点二：函数的概念及函数自变量的取值范围 例3 在函数1x y x+=中，自变量x 的取值范围是 ． 思路分析:本题主要考查自变量的取值范围，函数关系中主要有二次根式和分式两部分．根据二次根式的意义,被开方数x+1≥0，根据分式有意义的条件，x≠0．就可以求出自变量x 的取值范围． 解：根据题意得：x+1≥0且x≠0 解得：x≥-1且x≠0． 例3 函数y=31x x +-中自变量x 的取值范围是（ ） 思路分析:根据被开方数大于等于0,分母不等于0列式计算即可得解． 解:根据题意得，x+3≥0且x —1≠0， 解得x≥—3且x≠1． 故选D ．点评：本题考查了函数自变量的范围，一般从三个方面考虑： （1)当函数表达式是整式时，自变量可取全体实数； (2)当函数表达式是分式时，考虑分式的分母不能为0； （3）当函数表达式是二次根式时，被开方数非负． 对应训练 3．函数2y x =+中自变量x 的取值范围是（ ）A ．x ＞—2B ．x≥2 C．x≠—2 D ．x≥-2 3．A考点三：函数图象的运用例4 一天晚饭后，小明陪妈妈从家里出去散步，如图描述了他们散步过程中离家的距离S （米）与散步时间t （分）之间的函数关系，下面的描述符合他们散步情景的是（ ）A ．从家出发,到了一家书店，看了一会儿书就回家了B ．从家出发，到了一家书店，看了一会儿书，继续向前走了一段，然后回家了C ．从家出发,一直散步（没有停留),然后回家了D ．从家出发，散了一会儿步，到了一家书店，看了一会儿书，继续向前走了一段,18分钟后开始返回思路分析：根据图象可知，有一段时间内时间在增加，而路程没有增加,意味着有停留,与x 轴平行后的函数图象表现为随时间的增多路程又在增加，由此即可作出判断．解:A 、从家出发，到了一家书店，看了一会儿书就回家了,图象为梯形，错误；B 、从家出发,到了一家书店，看了一会儿书，继续向前走了一段,然后回家了,描述不准确，错误；C 、从家出发，一直散步（没有停留），然后回家了，图形为上升和下降的两条折线，错误；D 、从家出发，散了一会儿步,到了一家书店，看了一会儿书,继续向前走了一段，18分钟后开始返回从家出发,符合图象的特点，正确． 故选D ．点评:考查了函数的图象，读懂图象是解决本题的关键．首先应理解函数图象的横轴和纵轴表示的量，再根据函数图象用排除法判断．例5 如图，ABCD 的边长为8，面积为32，四个全等的小平行四边形对称中心分别在ABCD 的顶点上,它们的各边与ABCD 的各边分别平行，且与ABCD 相似．若小平行四边形的一边长为x ，且0＜x≤8，阴影部分的面积的和为y ，则y 与x 之间的函数关系的大致图象是（ ）A ．B ．C ．D ．思路分析：根据平行四边形的中心对称性可知四块阴影部分的面正好等于一个小平行四边形的面积,再根据相似多边形面积的比等于相似比的平方列式求出y 与x 之间的函数关系式，然后根据二次函数图象解答． 解：∵四个全等的小平行四边形对称中心分别在ABCD 的顶点上，∴阴影部分的面积等于一个小平行四边形的面积， ∵小平行四边形与ABCD 相似,∴2()328y x =, 整理得212y x =,又0＜x≤8，纵观各选项，只有D 选项图象符合y 与x 之间的函数关系的大致图象． 故选D ．点评：本题考查了动点问题的函数图象，根据平行四边形的对称性与相似多边形的面积的比等于相似比的平方求出y与x的函数关系是解题的关键．例8已知一个矩形纸片OACB，将该纸片放置在平面直角坐标洗中,点A（11，0），点B（0，6），点P为BC 边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP=t．（Ⅰ）如图①，当∠BOP=30°时，求点P的坐标;(Ⅱ）如图②，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，若AQ=m，试用含有t 的式子表示m；（Ⅲ）在（Ⅱ）的条件下，当点C′恰好落在边OA上时，求点P的坐标(直接写出结果即可）．考点：翻折变换(折叠问题）;坐标与图形性质;全等三角形的判定与性质;勾股定理；相似三角形的判定与性质．分析：（Ⅰ）根据题意得,∠OBP=90°，OB=6,在Rt△OBP中，由∠BOP=30°，BP=t，得OP=2t，然后利用勾股定理，即可得方程，解此方程即可求得答案;（Ⅱ）由△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的，可知△OB′P≌△OBP,△QC′P≌△QCP，易证得△OBP∽△PCQ，然后由相似三角形的对应边成比例，即可求得答案；（Ⅲ）首先过点P作PE⊥OA于E,易证得△PC′E∽△C′QA，由勾股定理可求得C′Q的长,然后利用相似三角形的对应边成比例与m= 16t2-116t+6，即可求得t的值．点评:此题考查了折叠的性质、矩形的性质以及相似三角形的判定与性质等知识．此题难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想与方程思想的应用．对应训练4．甲、乙两队举行了一年一度的赛龙舟比赛，两队在比赛时的路程s（米）与时间t（分钟）之间的函数关系图象如图所示，请你根据图象判断,下列说法正确的是（）A．甲队率先到达终点B．甲队比乙队多走了200米路程C．乙队比甲队少用0。

人教版七年级下册数学第七章平面直角坐标系含答案一、单选题(共15题，共计45分)1、下列命题中：①若mn＝0，则点A(m,n)在原点处；②点(2,－m2)一定在第四象限；③已知点A(m,n)与点B(－m,n)，m，n均不为0，则直线AB平行x轴；④已知点A(2,－3)，AB//y轴，且AB=5，则B点的坐标为(2,4)；是真命题的有（）A.1个B.2个C.3个D.4个2、如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A.（3，2）B.（﹣3，2）C.（3，﹣2）D.（﹣3，﹣2）3、如果m是任意实数，则点P(m-4，m+1)一定不在（）A.第一象限B.第二象限C.第三象限D.第四象限4、以下是甲、乙、丙三人看地图时对四个坐标的描述：甲：从学校向北直走500米，再向东直走100米可到图书馆．乙：从学校向西直走300米，再向北直走200米可到邮局．丙：邮局在火车站西200米处．根据三人的描述，若从图书馆出发，判断下列哪一种走法，其终点是火车站（）A.向南直走300米，再向西直走200米B.向南直走300米，再向西直走100米C.向南直走700米，再向西直走200米D.向南直走700米，再向西直走600米5、安徽省蒙城县板桥中学办学特色好，“校园文化”建设，主体鲜明新颖：“国学引领，教老敬亲，家校一体，爱满乡村”．如图所示，若用“C4”表示“孝”，则“A5﹣B4﹣C3﹣C5”表示（）A.爱满乡村B.教老敬亲C.国学引领D.板桥中学6、下列哪个点位于平面直角坐标系的第二象限（）A.（2，3）B.（2，﹣3）C.（﹣2，3）D.（﹣2，﹣3）7、在平面直角坐标系中，已知线段AB的两个端点分别是A（4，﹣1），B （1，1）将线段AB平移后得到线段A′B′，若点A的坐标为（﹣2，2），则点B′的坐标为（）A.（﹣5，4）B.（4，3）C.（﹣1，﹣2）D.（﹣2，﹣1）8、已知点在第三象限，则点在（）A.第一象限B.第二象限C.第三象限D.第四象限9、平面直角坐标系中，将点A（﹣3，﹣5）向上平移4个单位，再向左平移3个单位到点B，则点B的坐标为（）A.（1，﹣8）B.（1，﹣2）C.（﹣6，﹣1）D.（0，﹣1）10、如右图，⊙M与x轴相切于原点，平行于y轴的直线交圆于P、Q两点，P 点在Q点的下方，若P点的坐标是（2，1），则圆心M的坐标是（）A.（0，3）B.（0，）C.（0，2）D.（0，）11、线段CD是由线段AB平移得到的，点A（﹣1，5）的对应点为C（4，8），则点B（﹣4，﹣2）的对应点D的坐标为（）A.（﹣9，﹣5）B.（﹣9，1）C.（1，﹣5）D.（1，1）12、直线y=﹣2x+m与直线y=2x﹣1的交点在第四象限，则m的取值范围是A.m＞﹣1B.m＜1C.﹣1＜m＜1D.﹣1≤m≤113、在平面直角坐标系xOy中，对于点P(x，y)，我们把P1(y-1，-x-1)叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，，这样依次得到各点.若A2020的坐标为(-3，2)，设A1(x，y)，则x+y 的值是（）A.-5B.-1C.3D.514、如图，一个粒子在第一象限内及x轴，y轴上运动，第一分钟内从原点运动到(1，0)，第二分钟从(1，0)运动到(1，1)，而后它接着按图中箭头所示的与x轴，y轴平行的方向来回运动，且每分钟移动1个长度单位．在第2020分钟时，这个粒子所在位置的坐标是( )A.(4，45)B.(45，4)C.(44，4)D.(4，44)15、如图，矩形OABC与矩形ODEF是位似图形，点O为位似中心，相似比为1：1.2，点B的坐标为（﹣3，2），则点E的坐标是（）A.（3.6，2.4）B.（﹣3，2.4）C.（﹣3.6，2）D.（﹣3.6，2.4）二、填空题(共10题，共计30分)16、已知直角坐标系内有四个点O(0,0),A(3,0),B(1,1),C(x,1),若以O,A,B,C 为顶点的四边形是平行四边形,则x=________.17、如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为________18、在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A′的坐标是（﹣1，1），现将△ABC平移，使点A变换为A′，点B′、C′分别是B、C的对应点，请画出平移后的△A′B′C′，并直接写出点B′、C′的坐标：B′（________）、C′（________）．19、如图，一甲虫从原点出发按图示方向作折线运动，第1次从原点到A1(1，0)，第2次运动到A2(1，1)，第3次运动到A3(－1，1)，第4次运动到A4(－1，－1)，第5次运动到A5(2，－1)……则第2020次运动到的点A2020的坐标是________．20、如图，在平面直角坐标系中有一菱形OABC且∠A=120°，点O、B在y轴上，OA=1，现在把菱形向右无滑动翻转，每次翻转60°，点B的落点依次为B 1、B2、B3…，连续翻转2017次，则B2017的坐标为________．21、已知点A（3a+5，a﹣3）在二、四象限的角平分线上，则a=________．22、已知点是直线上的一个动点，若点到两坐标轴的距离相等，则点的坐标是________.23、如图，在平面直角坐标系中，函数和的图象分别为直线，过上的点A1（1，）作x轴的垂线交于点A2，过点A2作y轴的垂线交于点A3，过点A3作x轴的垂线交于点A4…，一次进行下去，则点的横坐标为________ .24、在平面直角坐标系中，如果一个图形向右平移1个单位，再向上平移3个单位，称为一个变换，已知点A（1，-2），经过一个变换后对应点为A1，经过2个变换后对应点为A2，…经过n个变换后对应点为An，则用含n的代数式表示点An的坐标为________。

平面直角坐标系练习题1．已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）A．53°B．63°C．73°D．83°2．如图，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C 处，此时需把方向调整到与出发时一致，则方向的调整应是（）A．右转80° B．左转80° C．右转100°D．左转100°3．如图，给出以下条件：①∠1=∠2；②∠3=∠4；③AD∥BE，且∠D=∠B；④AD∥BE，且∠DCB=∠BAD；其中能推出AB∥DC的条件为（）A．①②B．②④ C．②③ D．②③④4．如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为．5．如图，在平面直角坐标系中，已知点A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一根长为2017个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在A处，并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上．则细线的另一端所在位置的点的坐标是．5．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是．7．如图，正方形A1A2A3A4，A5A6A7A8，A9A10A11A12，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4；A5，A6，A7，A8；A9，A10，A11，A12；…）正方形的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6，…，则顶点A2016的坐标为．8．如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为P n，则点P3的坐标是；点P2014的坐标是．9．如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2014OB2014，则点A2014的坐标为．10．如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013的直角顶点的坐标为．11．如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向持续地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为（用n表示）．12．如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2012个点的横坐标为．13．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）…根据这个规律探究可得，第88个点的坐标为．14．如图，A ，B 的坐标为（2，0），（0，1）若将线段AB 平移至A 1B 1，则a+b 的值为 ．15．如图，将直角△ABC 沿BC 方向平移得直角△DEF ，其中AB=8，BE=10，DM=4，则阴影部分的面积是 ． 16.如图在高为2米，水平距离为3米的楼梯的表面铺地毯，那么地毯长度至少需 米． 17．如图，将边长为12的正方形ABCD 沿其对角线AC 剪开，再把△ABC 沿着AD 方向向右平移，得到△A ′B ′C ′，当两个三角形重叠部分的面积为32时，它移动的距离AA ′等于 ．18．已知△ABC 面积为24，将△ABC 沿BC 的方向平移到△A ′B ′C ′的位置，使B ′和C 重合，连接AC ′交A ′C 于D ，则△C ′DC 的面积为 ．19．已知平面直角坐标系中A 、B 两点，根据条件求符合条件的点B 的坐标． （1）已知A （2，0），AB=4，点B 和点A 在同一坐标轴上，则点B 的坐标为： ； （2）已知A （0，0），AB=4，点B 和点A 在同一坐标轴上，则点B 的坐标为： ； 20.已知点A （m+2，3）和点B （m ﹣1，2m ﹣4），且AB ∥x 轴．则m 的值为 ；AB 的长为 ．21．若A （4，0），点B 是y 轴上一动点，点C 在x 轴上，AC=5．10ABC △S ，则点B 的坐标为 ．22.已知：在平面直角坐标系中，A （0，1），B （2，0），C （4，3）（1）求△ABC 的面积； （2）设点P 在x 轴上，且△ABP 与△ABC 的面积相等，求点P 的坐标． 23．如图，在长方形OABC 中，O 为平面直角坐标系的原点，点A 坐标为（a ，0），点C 的坐 标为（0，b ），且a 、b 满足+|b ﹣6|=0，点B 在第一象限内，点P 从原点出发，以每秒2个单位长度的速度沿着O ﹣C ﹣B ﹣A ﹣O 的线路移动．（1）a= ，b= ，点B 的坐标为 ；（2）当点P 移动4秒时，请指出点P 的位置，并求出点P 的坐标； （3）在移动过程中，当点P 到x 轴的距离为5个单位长度时，求点P 移动的时间．24．已知点M（3a+8，﹣1﹣a），分别根据以下条件求出点M的坐标．（1）点M在x轴上；（2）点M在一、三象限角平分线上；（3）点M在第四象限，并且a为最小自然数；（4）N点坐标为（﹣3，6），并且直线MN∥y轴．25.先阅读以下一段文字，再解答问题已知在平面内有两点P1（x1，y1），P2（x2，y2），其两点间的距离公式为P1P2=，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|（1）已知点A（2，4），B（﹣3，﹣8），试求A，B两点间的距离；（2）已知点A，B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为﹣1，试求A，B两点间的距离；（3）已知点A（0，6）B（﹣3，2），C（3，2），判断线段AB，BC，AC中哪两条是相等的？并说明理由．25．在平面直角坐标系中，以任意两点P（ x1，y1）、Q（x2，y2）为端点的线段的中点坐标为．（1）如图（1），C为线段AB中点，A点坐标为（0，4），B点坐标为（5，4），则点C的坐标为（2）如图（2），F为线段DE中点，D点坐标为（﹣4，﹣3），E点坐标为（1，﹣3）．则点F 的坐标为应用：（1）如图（3），矩形ONDF的对角线相交于点M，ON，OF分别在x轴和y轴上，O为坐标原点，点D的坐标为（4，3），则点M的坐标为；（2）在直角坐标系中．有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与A，B，C 构成平行四边形的顶点，求D的坐标．。

2、在平面直角坐标系中，点A(1,2a +3)在第一象限。

(1)若点A 到x 轴的距离与到y 轴的距离相等，求a 的值； (2)若点A 到x 轴的距离小于到y 轴的距离，求a 的取值范围。

3、如图所示,三角形ABC 中,任意一点P(a ,b )经平移后对应点1P (a −2,b +3),将∆ABC 作同样的平移得到111C B A ∆.求111C B A 的坐标。

4、如图,在平面直角坐标系中,已知点A(−5,0),B(3,0)，△ABC的面积为12，试确定点C的坐标特征。

5、△OAB的三个顶点坐标分别是O(0,0),A(2,0),B(0,4).(1)求△OAB的面积；(2)平移线段AB 得到线段CD,A 的对应点为点C(4,2)，连接OC 、OD ，求△OCD 的面积。

6、在平面直角坐标系中,△ABC 的三个顶点的位置如图所示,点A ′的坐标是(−2,2),现将△ABC 平移,使点A 变换为点A ′,点B ′、C ′分别是B. C 的对应点。

(1)请画出平移后的△A ′B ′C ′(不写画法)；(2)并直接写出点B ′、C ′的坐标：B ′(______)、C ′(______)；(3)若△ABC 内部一点P 的坐标为(a ,b ),则点P 的对应点P ′的坐标是(______). 7、如图,将△ABC 平移得到111C B A ∆,使1A 点坐标为(−1,4)，(1)在图中画出111C B A ∆；(2)直接写出另外两个点11C B 的坐标； (3)求111C B A ∆的面积。

坐标。

当s∆的面积.t3=时,求PDC(1)求三角形ABC 的面积；(2)如果三角形ABC 的纵坐标不变，横坐标增加3个单位长度，得到三角形111C B A ,试在图中画出三角形111C B A ,并求出111C B A 的坐标。

(3)三角形111C B A 与三角形ABC 的大小、形状有什么关系? 已知点A(-5,0),B(3,0).（1）在y 轴上找一点C,使之满足S △ABC =16,求点C 的坐标.（2）在坐标平面上找一点C,能满足S △ABC =16的点C 有多少个?这些点有什么规律?已知三角形ABC 在坐标系中的位置如图.(1)若三角形ABC中任意一点P(a，b)经平移后的对应点的坐标为P′(a+4，b-3)，求将三角形ABC作同样的平移得到三角形A′B′C′三点的坐标；(2)求△ABC的面积.在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A′的坐标是（﹣2，2），现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．（1）请画出平移后的像△A′B′C′（不写画法），并直接写出点B′、C′的坐标：B′_____、C′_____；（2）若△ABC内部一点P的坐标为（a，b），则点P的对应点P′的坐标是_____．已知：如图,A(0,3),B(2,4),C(3,0)，求四边形ABCO的面积。

位置与坐标知识点一确定位置1.平面内确定一个物体的位置需要2个数据。

2.平面内确定位置的几种方法:（1）行列定位法：在这种方法中常把平面分成若干行、列，然后利用行号和列号表示平面上点的位置，在此方法中，要牢记某点的位置需要两个互相独立的数据，两者缺一不可。

（2）方位角距离定位法：方位角和距离。

（3）经纬定位法：它也需要两个数据：经度和纬度。

（4）区域定位法：只描述某点所在的大致位置。

如“解放路22号”。

知识点二平面直角坐标系1.定义在平面内,两条互相_____且具有公共_____的数轴组成平面直角坐标系.其中水平方向的数轴叫____ 或______,向__ 为正方向；竖直方向的数轴叫_______或______，向____为正方向；两条数轴交点叫平面直角坐标系的_____.2.平面内点的坐标对于平面内任意一点P,过P分别向x轴、y 轴作垂线,x轴上的垂足对应的数a叫P的___ _坐标,y轴上的垂足对应的数b叫P的_______坐标。

有序数对(a,b),叫点P的坐标。

若P的坐标为(a,b)，则P到x轴距离为_______，到y轴距离为_______．注意：平面内点的坐标是有序实数对，（a，b）和（b，a）是两个不同点的坐标.3.平面直角坐标系内点的坐标特征:(1)坐标轴把平面分隔成四个象限。

根据点所在位置填表点的位置横坐标符号纵坐标符号第一象限第二象限第三象限第四象限(2)坐标轴上的点不属于任何象限，它们的坐标特征①在x轴上的点______坐标为0;②在y轴上的点______坐标为0 .(3)P(a,b)关于x轴、y轴、原点的对称点坐标特征①点P(a,b)关于x轴对称点P1_____________；②点 P(a,b)关于y轴对称点P2_____________；③点P(a,b)关于原点对称点P3____________．4.平行于x轴的直线上的点______坐标相同；平行于y轴的直线上的点_______坐标相同．知识点三轴对称与坐标变化(1)若两个图形关于x轴对称．则对应各点横坐标________，纵坐标互为___________．(2)若两个图形关于y轴对称，则对应各点纵坐标________，横坐标互为___________．(3)将一个图形向上(或向下)平移n(n>0)个单位,则图形上各点横坐标____，纵坐标加上(或减去)n个单位．(4)将一个图形向右(或向左)平移n(n>O)个单位,则图形上各点纵坐标____，横坐标加上(或减去)n个单位．（5）纵坐标不变，横坐标分别变为原来的a倍，则图形为原来横向伸长的a倍（a>1）或图形横向缩短为原来的a倍（0<a<1）。

第11章 平面直角坐标系一、选择题（共16小题）1．在平面直角坐标系中，已知点P 的坐标是（﹣1，﹣2），则点P 关于原点对称的点的坐标是（ ）A ．（﹣1，2）B ．（1，﹣2）C ．（1，2）D ．（2，1）2．△ABO 与△A 1B 1O 在平面直角坐标系中的位置如图所示，它们关于点O 成中心对称，其中点A （4，2），则点A 1的坐标是（ ）A ．（4，﹣2）B ．（﹣4，﹣2）C ．（﹣2，﹣3）D ．（﹣2，﹣4）3．在平面直角坐标系中，点P （﹣20，a ）与点Q （b ，13）关于原点对称，则a+b 的值为（ ）A ．33B ．﹣33C ．﹣7D ．74．在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（ ）A ．（4，﹣3）B ．（﹣4，3）C ．（0，﹣3）D ．（0，3）5．在平面直角坐标系中，若点P （m ，m ﹣n ）与点Q （﹣2，3）关于原点对称，则点M （m ，n ）在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．如图，在△ABO 中，AB ⊥OB ，OB=，AB=1．将△ABO 绕O 点旋转90°后得到△A 1B 1O ，则点A 1的坐标为（ ）A ．（﹣1，） B ．（﹣1，）或（1，﹣） C ．（﹣1，﹣） D ．（﹣1，﹣）或（﹣，﹣1）7．在平面直角坐标系中，把点P （﹣5，3）向右平移8个单位得到点P 1，再将点P 1绕原点旋转90°得到点P 2，则点P 2的坐标是（ ）A ．（3，﹣3）B ．（﹣3，3）C ．（3，3）或（﹣3，﹣3）D ．（3，﹣3）或（﹣3，3）8．如图，在平面直角坐标系中，点B 、C 、E 、在y 轴上，Rt △ABC 经过变换得到Rt △ODE ．若点C 的坐标为（0，1），AC=2，则这种变换可以是（ ）A ．△ABC 绕点C 顺时针旋转90°，再向下平移3B ．△ABC 绕点C 顺时针旋转90°，再向下平移1C ．△ABC 绕点C 逆时针旋转90°，再向下平移1D ．△ABC 绕点C 逆时针旋转90°，再向下平移39．如图，将斜边长为4的直角三角板放在直角坐标系xOy 中，两条直角边分别与坐标轴重合，P 为斜边的中点．现将此三角板绕点O 顺时针旋转120°后点P 的对应点的坐标是（ ）A ．（，1）B ．（1，﹣）C ．（2，﹣2）D ．（2，﹣2）10．在平面直角坐标系内，点P （﹣2，3）关于原点的对称点Q 的坐标为（ ）A ．（2，﹣3）B ．（2，3）C ．（3，﹣2）D ．（﹣2，﹣3）11．将点A （3，2）沿x 轴向左平移4个单位长度得到点A′，点A′关于y 轴对称的点的坐标是（ ）A ．（﹣3，2）B ．（﹣1，2）C ．（1，2）D ．（1，﹣2）12．将点P （﹣2，3）向右平移3个单位得到点P 1，点P 2与点P 1关于原点对称，则P 2的坐标是（ ）A ．（﹣5，﹣3）B ．（1，﹣3）C ．（﹣1，﹣3）D ．（5，﹣3）13．点A （3，﹣1）关于原点的对称点A′的坐标是（ ）A ．（﹣3，﹣1）B ．（3，1）C ．（﹣3，1）D ．（﹣1，3）14．在直角坐标系中，点B 的坐标为（3，1），则点B 关于原点成中心对称的点的坐标为（ ）A．（3，﹣1）B．（﹣3，1）C．（﹣1，﹣3） D．（﹣3，﹣1）15．在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（）A．（﹣2，1）B．（2，﹣1）C．（2，1） D．（﹣2，﹣1）16．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=（）A．﹣2 B．2 C．4 D．﹣4二、填空题（共12小题）17．若点（a，1）与（﹣2，b）关于原点对称，则a b= ．18．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为．19．已知A点的坐标为（﹣1，3），将A点绕坐标原点顺时针90°，则点A的对应点的坐标为．20．如图，△ABO中，AB⊥OB，AB=，OB=1，把△ABO绕点O旋转120°后，得到△A1B1O，则点A1的坐标为．21．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是．22．设点M（1，2）关于原点的对称点为M′，则M′的坐标为．23．已知点M（3，﹣2），将它先向左平移4个单位，再向上平移3个单位后得到点N，则点N的坐标是．24．点P（5，﹣3）关于原点的对称点的坐标为．25．在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是．26．已知点P（3，2），则点P关于y轴的对称点P1的坐标是，点P关于原点O的对称点P2的坐标是．27．在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是．28．若将等腰直角三角形AOB按如图所示放置，OB=2，则点A关于原点对称的点的坐标为．三、解答题（共2小题）29．在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．（1）点A关于原点O的对称点A′的坐标为，点B关于x轴的对称点B′的坐标为，点C 关于y轴的对称点C的坐标为．（2）求（1）中的△A′B′C′的面积．30．如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）（1）若点C与点A关于原点O对称，则点C的坐标为；（2）将点A向右平移5个单位得到点D，则点D的坐标为；（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．第11章平面直角坐标系参考答案与试题解析一、选择题（共16小题）1．在平面直角坐标系中，已知点P的坐标是（﹣1，﹣2），则点P关于原点对称的点的坐标是（）A．（﹣1，2）B．（1，﹣2）C．（1，2） D．（2，1）【考点】关于原点对称的点的坐标．【专题】压轴题．【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），据此即可求得点P关于原点的对称点的坐标．【解答】解：∵点P关于x轴的对称点坐标为（﹣1，﹣2），∴点P关于原点的对称点的坐标是（1，2）．故选：C．【点评】此题主要考查了关于原点对称点的坐标性质，这一类题目是需要识记的基础题，要熟悉关于原点对称点的横纵坐标变化规律．2．△ABO与△A1B1O在平面直角坐标系中的位置如图所示，它们关于点O成中心对称，其中点A（4，2），则点A1的坐标是（）A．（4，﹣2）B．（﹣4，﹣2） C．（﹣2，﹣3） D．（﹣2，﹣4）【考点】关于原点对称的点的坐标．【专题】几何图形问题．【分析】根据两个点关于原点对称时，它们的坐标符号相反可得答案．【解答】解：∵A和A1关于原点对称，A（4，2），∴点A1的坐标是（﹣4，﹣2），故选：B．【点评】此题主要考查了关于原点对称的点的坐标，关键是掌握点的坐标的变化规律．3．在平面直角坐标系中，点P（﹣20，a）与点Q（b，13）关于原点对称，则a+b的值为（）A．33 B．﹣33 C．﹣7 D．7【考点】关于原点对称的点的坐标．【分析】先根据关于原点对称的点的坐标特点：横坐标与纵坐标都互为相反数，求出a与b的值，再代入计算即可．【解答】解：∵点P（﹣20，a）与点Q（b，13）关于原点对称，∴a=﹣13，b=20，∴a+b=﹣13+20=7．故选：D．【点评】本题主要考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．4．在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（）A．（4，﹣3）B．（﹣4，3）C．（0，﹣3）D．（0，3）【考点】关于原点对称的点的坐标；坐标与图形变化-平移．【分析】根据关于原点的点的横坐标互为相反数，纵坐标互为相反数，可得关于原点的对称点，根据点的坐标向左平移减，可得答案．【解答】解：在直角坐标系中，将点（﹣2，3）关于原点的对称点是（2，﹣3），再向左平移2个单位长度得到的点的坐标是（0，﹣3），故选：C．【点评】本题考查了点的坐标，关于原点的点的横坐标互为相反数，纵坐标互为相反数；点的坐标向左平移减，向右平移加，向上平移加，向下平移减．5．（•贵港）在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】关于原点对称的点的坐标．【分析】根据平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，则m=2且n=﹣3，从而得出点M（m，n）所在的象限．【解答】解：根据平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，∴m=2且m ﹣n=﹣3，∴m=2，n=5∴点M （m ，n ）在第一象限，故选A ．【点评】本题考查了平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，该题比较简单．6．如图，在△ABO 中，AB ⊥OB ，OB=，AB=1．将△ABO 绕O 点旋转90°后得到△A 1B 1O ，则点A 1的坐标为（ ）A ．（﹣1，） B ．（﹣1，）或（1，﹣） C ．（﹣1，﹣） D ．（﹣1，﹣）或（﹣，﹣1）【考点】坐标与图形变化-旋转．【分析】需要分类讨论：在把△ABO 绕点O 顺时针旋转90°和逆时针旋转90°后得到△A 1B 1O 时点A 1的坐标．【解答】解：∵△ABO 中，AB ⊥OB ，OB=，AB=1，∴∠AOB=30°，当△ABO 绕点O 顺时针旋转90°后得到△A 1B 1O ，则易求A 1（1，﹣）； 当△ABO 绕点O 逆时针旋转90°后得到△A 1B 1O ，则易求A 1（﹣1，）．故选B ．【点评】本题考查了坐标与图形变化﹣旋转．解题时，注意分类讨论，以防错解．7．在平面直角坐标系中，把点P （﹣5，3）向右平移8个单位得到点P 1，再将点P 1绕原点旋转90°得到点P 2，则点P 2的坐标是（ ）A ．（3，﹣3）B ．（﹣3，3）C ．（3，3）或（﹣3，﹣3）D ．（3，﹣3）或（﹣3，3）【考点】坐标与图形变化-旋转；坐标与图形变化-平移．【专题】分类讨论．【分析】首先利用平移的性质得出点P1的坐标，再利用旋转的性质得出符合题意的答案．【解答】解：∵把点P（﹣5，3）向右平移8个单位得到点P1，∴点P1的坐标为：（3，3），如图所示：将点P1绕原点逆时针旋转90°得到点P2，则其坐标为：（﹣3，3），将点P1绕原点顺时针旋转90°得到点P3，则其坐标为：（3，﹣3），故符合题意的点的坐标为：（3，﹣3）或（﹣3，3）．故选：D．【点评】此题主要考查了坐标与图形的变化，正确利用图形分类讨论得出是解题关键．8．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C 的坐标为（0，1），AC=2，则这种变换可以是（）A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移3【考点】坐标与图形变化-旋转；坐标与图形变化-平移．【分析】观察图形可以看出，Rt△ABC通过变换得到Rt△ODE，应先旋转然后平移即可．【解答】解：根据图形可以看出，△ABC绕点C顺时针旋转90°，再向下平移3个单位可以得到△ODE．故选：A．【点评】本题考查的是坐标与图形变化旋转和平移的知识，掌握旋转和平移的概念和性质是解题的关键．9．如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（）A．（，1）B．（1，﹣） C．（2，﹣2）D．（2，﹣2）【考点】坐标与图形变化-旋转．【专题】计算题．【分析】根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD，连接OP，OQ，过Q作QM⊥y 轴，由旋转的性质得到∠POQ=120°，根据AP=BP=OP=2，得到∠AOP度数，进而求出∠MOQ度数为30°，在直角三角形OMQ中求出OM与MQ的长，即可确定出Q的坐标．【解答】解：根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD，连接OP，OQ，过Q作QM ⊥y轴，∴∠POQ=120°，∵AP=OP，∴∠BAO=∠POA=30°，∴∠MOQ=30°，在Rt△OMQ中，OQ=OP=2，∴MQ=1，OM=，则P的对应点Q的坐标为（1，﹣），故选B【点评】此题考查了坐标与图形变化﹣旋转，熟练掌握旋转的性质是解本题的关键．10．在平面直角坐标系内，点P （﹣2，3）关于原点的对称点Q 的坐标为（ ）A ．（2，﹣3）B ．（2，3）C ．（3，﹣2）D ．（﹣2，﹣3）【考点】关于原点对称的点的坐标．【专题】常规题型．【分析】平面直角坐标系中任意一点P （x ，y ），关于原点的对称点是（﹣x ，﹣y ）．【解答】解：根据中心对称的性质，得点P （﹣2，3）关于原点对称点P′的坐标是（2，﹣3）． 故选：A ．【点评】关于原点对称的点坐标的关系，是需要识记的基本问题．记忆方法是结合平面直角坐标系的图形记忆．11．将点A （3，2）沿x 轴向左平移4个单位长度得到点A′，点A′关于y 轴对称的点的坐标是（ ）A ．（﹣3，2）B ．（﹣1，2）C ．（1，2）D ．（1，﹣2）【考点】坐标与图形变化-平移；关于x 轴、y 轴对称的点的坐标．【分析】先利用平移中点的变化规律求出点A′的坐标，再根据关于y 轴对称的点的坐标特征即可求解．【解答】解：∵将点A （3，2）沿x 轴向左平移4个单位长度得到点A′，∴点A′的坐标为（﹣1，2），∴点A′关于y 轴对称的点的坐标是（1，2）．故选：C ．【点评】本题考查坐标与图形变化﹣平移及对称的性质；用到的知识点为：两点关于y 轴对称，纵坐标不变，横坐标互为相反数；左右平移只改变点的横坐标，右加左减．12．将点P （﹣2，3）向右平移3个单位得到点P 1，点P 2与点P 1关于原点对称，则P 2的坐标是（ ）A ．（﹣5，﹣3）B ．（1，﹣3）C ．（﹣1，﹣3）D ．（5，﹣3）【考点】关于原点对称的点的坐标；坐标与图形变化-平移．【分析】首先利用平移变化规律得出P 1（1，3），进而利用关于原点对称点的坐标性质得出P 2的坐标．【解答】解：∵点P （﹣2，3）向右平移3个单位得到点P 1，∴P 1（1，3），∵点P 2与点P 1关于原点对称，∴P 2的坐标是：（﹣1，﹣3）．故选：C ．【点评】此题主要考查了关于原点对称点的性质以及点的平移规律，正确把握坐标变化性质是解题关键．13．点A （3，﹣1）关于原点的对称点A′的坐标是（ ）A ．（﹣3，﹣1）B ．（3，1）C ．（﹣3，1）D ．（﹣1，3）【考点】关于原点对称的点的坐标．【分析】直接根据关于原点对称的点的坐标特点即可得出结论．【解答】解：∵两个点关于原点对称时，它们的坐标符号相反，∴点A （3，﹣1）关于原点的对称点A′的坐标是（﹣3，1）．故选C ．【点评】本题考查的是关于原点对称的点的坐标，熟知关于原点对称的点的坐标特点是解答此题的关键．14．在直角坐标系中，点B 的坐标为（3，1），则点B 关于原点成中心对称的点的坐标为（ ）A ．（3，﹣1）B ．（﹣3，1）C ．（﹣1，﹣3）D ．（﹣3，﹣1）【考点】关于原点对称的点的坐标．【分析】平面直角坐标系中任意一点P （x ，y ），关于原点的对称点是（﹣x ，﹣y ）．【解答】解：点（3，1）关于原点中心对称的点的坐标是（﹣3，﹣1），故选D．【点评】此题主要考查了关于原点对称的点坐标的关系，是需要识记的基本问题，记忆方法是结合平面直角坐标系的图形记忆．15．在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（）A．（﹣2，1）B．（2，﹣1）C．（2，1） D．（﹣2，﹣1）【考点】关于原点对称的点的坐标．【分析】关于原点的对称点，横纵坐标都变成原来相反数，据此求出点B的坐标．【解答】解：∵点A坐标为（﹣2，1），∴点B的坐标为（2，﹣1）．故选B．【点评】本题考查了关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y）．16．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=（）A．﹣2 B．2 C．4 D．﹣4【考点】关于原点对称的点的坐标；立方根；关于x轴、y轴对称的点的坐标．【专题】计算题．【分析】利用关于原点对称点的坐标性质得出P点坐标，进而利用关于x轴对称点的坐标性质得出P2坐标，进而得出答案．【解答】解：∵P点关于原点的对称点为P1（﹣3，﹣），∴P（3，），∵P点关于x轴的对称点为P2（a，b），∴P2（3，﹣），∴==﹣2．故选：A．【点评】此题主要考查了关于原点对称点的性质以及关于x轴对称点的性质，得出P点坐标是解题关键．二、填空题（共12小题）17．若点（a，1）与（﹣2，b）关于原点对称，则a b= ．【考点】关于原点对称的点的坐标．【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即：求关于原点的对称点，横纵坐标都变成相反数．记忆方法是结合平面直角坐标系的图形记忆．【解答】解：∵点（a，1）与（﹣2，b）关于原点对称，∴b=﹣1，a=2，∴a b=2﹣1=．故答案为：．【点评】此题考查了关于原点对称的点的坐标，这一类题目是需要识记的基础题，记忆时要结合平面直角坐标系．18．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为（﹣5，4）．【考点】坐标与图形变化-旋转．【分析】首先根据点A的坐标求出OA的长度，然后根据旋转变换只改变图形的位置，不改变图形的形状与大小，可得OA′=OA，据此求出点A′的坐标即可．【解答】解：如图，过点A作AC⊥y轴于点C，作AB⊥x轴于点B，过A′作A′E⊥y轴于点E，作A′D⊥x轴于点D，，∵点A（4，5），∴AC=4，AB=5，∵点A（4，5）绕原点逆时针旋转90°得到点A′，∴A′E=AB=5，A′D=AC=4，∴点A′的坐标是（﹣5，4）．故答案为：（﹣5，4）．【点评】此题主要考查了坐标与图形变换﹣旋转，要熟练掌握，解答此题的关键是要明确：旋转变换只改变图形的位置，不改变图形的形状与大小．19．已知A点的坐标为（﹣1，3），将A点绕坐标原点顺时针90°，则点A的对应点的坐标为（3，1）．【考点】坐标与图形变化-旋转．【分析】过A作AC⊥y轴于C，过A'作A'D⊥y轴于D，根据旋转求出∠A=∠A'OD，证△AC0≌△ODA'，推出A'D=OC=1，OD=CA=3，即可根据题意作出A点绕坐标原点顺时针90°后的点，然后写出坐标．【解答】解：过A作AC⊥y轴于C，过A'作A'D⊥y轴于D，∵∠AOA'=90°，∠ACO=90°，∴∠AOC+∠A'OD=90°，∠A+∠AOC=90°，∴∠A=∠A'OD，在△AC0和△ODA'中，，∴△AC0≌△ODA'（AAS），∴A'D=OC=1，OD=CA=3，∴A'的坐标是（3，1）．故答案为：（3，1）．【点评】本题主要考查对坐标与图形变换﹣旋转，全等三角形的性质和判定等知识点的理解和掌握，能正确画出图形并求出△AC0≌△ODA'是解此题的关键．20．如图，△ABO中，AB⊥OB，AB=，OB=1，把△ABO绕点O旋转120°后，得到△A1B1O，则点A1的坐标为（﹣2，0）或（1，﹣）．【考点】坐标与图形变化-旋转．【专题】压轴题；数形结合．【分析】在Rt△OAB中利用勾股定理计算出OA=2，则利用含30度的直角三角形三边的关系得∠A=30°，所以∠AOB=60°，然后分类讨论：当△ABO绕点O逆时针旋转120°后，点A的对应点A′落在x轴的负半轴上，如图，OA′=OA=2，易得A′的坐标为（﹣2，0）；当△ABO绕点O顺时针旋转120°后，点A的对应点A1落在第四象限，如图，则OA1=OA=2，∠AOA1=120°，∠BOA1=30°，利用三角函数可求出A1的纵坐标和横坐标．【解答】解：在Rt△OAB中，∵AB=，OB=1，∴OA==2，∴∠A=30°，∴∠AOB=60°，①当△ABO绕点O逆时针旋转120°后，点A的对应点A1落在x轴的负半轴上，如图，OA1=OA=2，此时A1的坐标为（﹣2，0）；②当△ABO 绕点O 顺时针旋转120°后，点A 的对应点A 1′落在第三象限，如图，则OA 1′=OA=2，∠AOA 1′=120°，∵∠AOB=60°，∴∠BOA 1′=60°，∴点A 1′的横坐标为OA 1′•cos60°=2×=1，纵坐标为OA 1′•sin60°=2×=， A 1′的坐标为（1，﹣）．综上所述，A 1的坐标为（﹣2，0）或（1，﹣）． 故答案为（﹣2，0）或（1，﹣）．【点评】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．21．如图，将线段AB 绕点O 顺时针旋转90°得到线段A′B′，那么A （﹣2，5）的对应点A′的坐标是 A′（5，2） ．【考点】坐标与图形变化-旋转．【分析】由线段AB 绕点O 顺时针旋转90°得到线段A′B′可以得出△ABO ≌△A′B′O′，∠AOA′=90°，作AC ⊥y 轴于C ，A′C′⊥x 轴于C′，就可以得出△ACO ≌△A′C′O，就可以得出AC=A′C′，CO=C′O，由A 的坐标就可以求出结论．【解答】解：∵线段AB 绕点O 顺时针旋转90°得到线段A′B′，∴△ABO ≌△A′B′O′，∠AOA′=90°，∴AO=A′O．作AC ⊥y 轴于C ，A′C′⊥x 轴于C′，∴∠ACO=∠A′C′O=90°．∵∠COC′=90°，∴∠AOA′﹣∠COA′=∠COC′﹣∠COA′，∴∠AOC=∠A′OC′．在△ACO和△A′C′O中，，∴△ACO≌△A′C′O（AAS），∴AC=A′C′，CO=C′O．∵A（﹣2，5），∴AC=2，CO=5，∴A′C′=2，OC′=5，∴A′（5，2）．故答案为：A′（5，2）．【点评】本题考查了旋转的性质的运用，全等三角形的判定及性质的运用，等式的性质的运用，点的坐标的运用，解答时证明三角形全等是关键．22．设点M（1，2）关于原点的对称点为M′，则M′的坐标为（﹣1，﹣2）．【考点】关于原点对称的点的坐标．【分析】根据关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反可直接得到答案．【解答】解：点M（1，2）关于原点的对称点M′的坐标为（﹣1，﹣2），故答案为：（﹣1，﹣2）．【点评】此题主要考查了关于原点对称的点的坐标特点，关键是熟练掌握点的坐标的变化规律．23．已知点M（3，﹣2），将它先向左平移4个单位，再向上平移3个单位后得到点N，则点N的坐标是（﹣1，1）．【考点】坐标与图形变化-平移．【分析】直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．【解答】解：原来点的横坐标是3，纵坐标是﹣2，向左平移4个单位，再向上平移3个单位得到新点的横坐标是3﹣4=﹣1，纵坐标为﹣2+3=1．则点N的坐标是（﹣1，1）．故答案填：（﹣1，1）．【点评】解题关键是要懂得左右平移点的纵坐标不变，而上下平移时点的横坐标不变，平移变换是中考的常考点，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．24．点P（5，﹣3）关于原点的对称点的坐标为（﹣5，3）．【考点】关于原点对称的点的坐标．【分析】两点关于原点对称，横坐标互为相反数，纵坐标互为相反数．【解答】解：∵5的相反数是﹣5，﹣3的相反数是3，∴点P（5，﹣3）关于原点的对称点的坐标为（﹣5，3），故答案为：（﹣5，3）．【点评】主要考查两点关于原点对称的坐标的特点：两点关于原点对称，两点的横坐标互为相反数，纵坐标互为相反数，用到的知识点为：a的相反数为﹣a．25．在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是（3，﹣2）．【考点】关于原点对称的点的坐标．【专题】数形结合．【分析】根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，即可得出答案．【解答】解：根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，∴点（﹣3，2）关于原点对称的点的坐标是（3，﹣2），故答案为（3，﹣2）．【点评】本题主要考查了平面直角坐标系内两点关于原点对称横纵坐标互为相反数，难度较小．26．已知点P（3，2），则点P关于y轴的对称点P的坐标是（﹣3，2），点P关于原点O的1的坐标是（﹣3，﹣2）．对称点P2【考点】关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．【分析】根据关于y轴对称的点的横坐标互为相反数，纵坐标相同；关于原点对称的点的横坐标与纵坐标都互为相反数解答．的坐标是（﹣3，2），【解答】解：点P（3，2）关于y轴的对称点P1的坐标是（﹣3，﹣2）．点P关于原点O的对称点P2故答案为：（﹣3，2）；（﹣3，﹣2）．【点评】本题考查了关于原点对称点点的坐标，关于y轴对称的点的坐标，熟记对称点的坐标特征是解题的关键．27．在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是（﹣5，3）．【考点】关于原点对称的点的坐标．【分析】根据关于坐标原点对称的点的横坐标与纵坐标都互为相反数解答．【解答】解：点P（5，﹣3）关于原点对称的点的坐标是（﹣5，3）．故答案为：（﹣5，3）．【点评】本题考查了关于原点对称的点的坐标，熟记关于坐标原点对称的点的横坐标与纵坐标都互为相反数是解题的关键．28．若将等腰直角三角形AOB按如图所示放置，OB=2，则点A关于原点对称的点的坐标为（﹣1，﹣1）．【考点】关于原点对称的点的坐标．【分析】过点A作AD⊥OB于点D，根据等腰直角三角形的性质求出OD及AD的长，故可得出A点坐标，再由关于原点对称的点的坐标特点即可得出结论．【解答】解：过点A作AD⊥OB于点D，∵△AOB是等腰直角三角形，OB=2，∴OD=AD=1，∴A（1，1），∴点A关于原点对称的点的坐标为（﹣1，﹣1）．故答案为（﹣1，﹣1）．【点评】本题考查的是关于原点对称的点的坐标特点，熟知等腰直角三角形的性质是解答此题的关键．三、解答题（共2小题）29．在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．（1）点A关于原点O的对称点A′的坐标为（1，﹣5），点B关于x轴的对称点B′的坐标为（4，﹣2），点C关于y轴的对称点C的坐标为（1，0）．（2）求（1）中的△A′B′C′的面积．【考点】关于原点对称的点的坐标；三角形的面积；关于x轴、y轴对称的点的坐标．【分析】（1）关于原点对称的两点的横、纵坐标都是互为相反数；关于x轴对称的两点的横坐标相同，纵坐标互为相反数；关于y轴对称的两点的横坐标互为相反数，纵坐标相同；（2）根据点A′（1，﹣5），B′（4，﹣2），C′（1，0）在平面直角坐标系中的位置，可以求得A′C′=5，B′D=3，所以由三角形的面积公式进行解答．【解答】解：（1）∵A（﹣1，5），∴点A关于原点O的对称点A′的坐标为（1，﹣5）．∵B（4，2），∴点B关于x轴的对称点B′的坐标为（4，﹣2）．∵C（﹣1，0），∴点C关于y轴的对称点C′的坐标为（1，0）．故答案为：（1，﹣5），（4，﹣2），（1，0）．（2）如图，∵A′（1，﹣5），B′（4，﹣2），C′（1，0）．∴A′C′=|﹣5﹣0|=5，B′D=|4﹣1|=3，=A′C′•B′D=×5×3=7.5，即（1）中的△A′B′C′的面积是7.5．∴S△A′B′C′【点评】本题考查了关于原点、x轴、y轴对称的点的坐标，三角形的面积．解答（2）题时，充分体现了“数形结合”数学思想的优势．30．如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）（1）若点C与点A关于原点O对称，则点C的坐标为（2，﹣2）；（2）将点A向右平移5个单位得到点D，则点D的坐标为（3，2）；（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．【考点】关于原点对称的点的坐标；坐标与图形变化-平移；概率公式．【分析】（1）根据关于原点的对称点，横纵坐标都互为相反数求解即可；（2）把点A的横坐标加5，纵坐标不变即可得到对应点D的坐标；（3）先找出在平行四边形内的所有整数点，再根据概率公式求解即可．【解答】解：（1）∵点C与点A（﹣2，2）关于原点O对称，∴点C的坐标为（2，﹣2）；（2）∵将点A向右平移5个单位得到点D，点D的坐标为（3，2）；（3）由图可知：A（﹣2，2），B（﹣3，﹣2），C（2，﹣2），D（3，2），∵在平行四边形ABCD内横、纵坐标均为整数的点有15个，其中横、纵坐标和为零的点有3个，即（﹣1，1），（0，0），（1，﹣1），∴P==．【点评】本题考查了关于原点对称的点的坐标，坐标与图形变化﹣平移，概率公式．难度适中，掌握规律是解题的关键．。