当前位置：文档之家 › 第10章 典型相关分析

第10章 典型相关分析

  • 格式：ppt
  • 大小：171.00 KB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

《SPSS统计分析》第10章 相关分析

《SPSS统计分析》第10章 相关分析

12.990 16.290 17.990 19.290
12.500 15.800 17.500 18.800
11.500 14.800 16.500 17.800
2.200 5.500 7.200 8.500
3.300 5.000 6.300
3.300
1.700 3.000
5.000 1.700
1.300
3.分析两个变量间线性关系的程度。往往因为第三个变量的作用，使相关系数不能真正反映两个 变量间的线性程度。 这是应该控制一个变量的变化求另两个变量间的相关系数，也就是说， 在第三个变量不变的情况下，两个变量的线性程度。
CORRELATIONS /VARIABLES=VCP with HEIGHT WEIGHT /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE .
6.300 3.000 1.300
1.800 1.500 3.200 4.500
2.700 6.000 7.700 9.000
5.000 8.300 10.000 11.300
12.000 15.300 17.000 18.300
9: 9 14.790 14.300 13.300
4.000 1.800 1.500 3.200 4.500
返回
典型相关分析
返回
典型相关分析概念
典型相关分析是用来描述两组随机变量间关 系的统计分析方法。
通过线性组合，可以将一组变量组合成一个 新的综合变量。虽然每组变量间的线性组合有无 数多个，但通过对其施加一些条件约束，能使其 具有确定性。
典型相关分析就是要找到使得这两个由线性 组合生成的变量之间的相关系数最大的系数。
学习通过编程解决偏相关问题

大数据解析与应用导论知到章节答案智慧树2023年浙江大学

大数据解析与应用导论知到章节答案智慧树2023年浙江大学

大数据解析与应用导论知到章节测试答案智慧树2023年最新浙江大学第一章测试1.下列属于多元统计方法的为（）参考答案:回归分析;主元分析2.多元统计分析的图表示法有（）参考答案:散布图矩阵;调和曲线图;轮廓图;雷达图3.完整的数据分析过程，包括数据采集、数据清洗和数据分析。

（）参考答案:对4.下列场景适用于回归分析的是 ( )参考答案:天气预报5.下面哪一句体现了主元分析的思想（）参考答案:牵牛要牵牛鼻子第二章测试1.一般常见的缺失值处理的方法有（）参考答案:回归填充法;最近邻插补填充法;插值填充;替换填充法2.一般常见的数据归一化的方法有（）参考答案:最小最大规范化;零均值规范化3.少量的异常值完全不会影响数据分析。

（）参考答案:错4.下列哪种方法不是数据填补的手段 ( )参考答案:均值标准化5.主成分分析的英文名是（）。

参考答案:Principal Component Analysis第三章测试1.下面哪个是SVM在实际生活中的应用（）参考答案:图片分类;邮件分类2.以下说法正确的有哪些（）参考答案:SVM是一种线性方法;软间隔的引入可以解决轻度线性不可分问题3.拉格朗日乘子法可用于线性可分SVM的模型求解。

（）参考答案:对4.SVM的中文全称叫什么？（）参考答案:支持向量机5.SVM算法的最小时间复杂度是O（n²），基于此，以下哪种规格的数据集并不适该算法？（）参考答案:大数据集第四章测试1.一元线性回归有哪些基本假定？（）参考答案:解释变量X是确定性变量，Y是随机变量；;随机误差项和解释变量X不相关；;随机误差项服从零均值、同方差的正态分布。

;随机误差项具有零均值、同方差和序列不相关的性质；2.最典型的两种拟合不佳的情况是（）。

参考答案:欠拟合;过拟合3.岭回归适用于样本很少，但变量很多的回归问题。

（）参考答案:对4.最小二乘方法的拟合程度衡量指标是（）。

参考答案:残差平方和5.关于最小二乘法，下列说法正确的是。

对应分析与典型相关分析

对应分析与典型相关分析

17
对应分析基本思想
v λ ... v λ 1m m 11 1 O M = ( λ1 v1 ,..., λm vm ), AR = M v λ L v p1 1 pm λm
u11 λ1 ... u1m λm AQ = M O M = ( λ1 u1,..., λm um ), un1 λ1 L unm λm
由于SR和 具有相同的非零特征值 具有相同的非零特征值， 由于 和SQ具有相同的非零特征值，而这些特征值又正好是各个 公共因子的方差，因此可以用相同的因子轴 相同的因子轴同时表示变量点和样品 公共因子的方差，因此可以用相同的因子轴同时表示变量点和样品 即把变量点和样品点同时反映在具有相同坐标轴的因子平面上， 点，即把变量点和样品点同时反映在具有相同坐标轴的因子平面上， 以便对变量点和样品点一起考虑进行分类。 以便对变量点和样品点一起考虑进行分类。
如果SR的特征值 如果 的特征值 λ i 对应的标准化特征向量为 vi ， 则SQ的特征值 λi 对应的标准化特征向量： 的特征值 对应的标准化特征向量： 1 ui = Zv i
λi
由此可以方便地由R型因子分析而得到 型因子分析的结果 由此可以方便地由 型因子分析而得到Q型因子分析的结果。由SR的特征值和 型因子分析而得到 型因子分析的结果。 的特征值和 特征向量即可以写出R型因子分析的因子载荷矩阵 记为AR） 型因子分析的因子载荷矩阵（ 特征向量即可以写出 型因子分析的因子载荷矩阵（记为 ）和Q型因子分析的 型因子分析的 因子载荷矩阵（记为AQ）： 因子载荷矩阵（记为 ）：
3
引例1. 引例1.
下表为2006年年底我国 个省市按照行业（这里仅列出12 年年底我国31个省市按照行业 这里仅列出12 下表为 年年底我国 个省市按照行业（ 个行业）城镇单位就业人数， 个行业）城镇单位就业人数，在一定程度上可以反映该地 区的经济结构。 区的经济结构。 我国地域辽阔，东西南北发展不平衡，是否按照地域划分 我国地域辽阔，东西南北发展不平衡，是否按照地域划分 就合理了呢？ 就合理了呢？ 自然地理位置对经济结构的影响固然重要，但是数据分析 自然地理位置对经济结构的影响固然重要，但是数据分析 显然更有说服力。 显然更有说服力。

第10章 典型相关分析

第10章 典型相关分析

X2
0.80 1.00 0.33 0.59 0.34
Y1
ቤተ መጻሕፍቲ ባይዱ
0.26 0.33 1.00 0.37 0.21
Y2
0.67 0.59 0.37 1.00 0.35
Y3
0.34 0.34 0.21 0.35 1.00
W V11ab111Y X 111ba22Y 11X 2 2 b3Y 13
(V1,W 1)?
V 1 X 1 2 X 2 p X p'X
和 W 1 Y 12 Y 2 q Y q'Y
之间有最大可能的相关,基于这个思想就产生了典型相关分析.
§10.1 总体典型相关
设 X(X1, ,Xp)'及 Y(Y1,,Yq)'为随机向量,我们用
X 和 Y 的线性组合 ' X 和 'Y 之间的相关性来研究两组随机变量
V2a12 X1a22 X2 ap2Xp W 2b1Y 21b2Y 22 bq2Yq
V2和W2与V1和W1相互独立,但V2和W2相关.如 此继续下去,直至进行到 r 步,两组变量的相关性 被提取完为止. R min(p,q),可以得到 r 组变量.
典型相关的数学描述
一般地,假设有一组变量X1,…,Xp与Y1,…,Yq ,我们要 研究这两组变量的相关关系,如何给两组变量之间的相
为了了解家庭的特征与其消费模式之间的关系。 调查了70个家庭的下面两组变量：
XX12： ：每 每年 年去 外餐 出馆 看就 电餐 影的 频率频 率 Y1：户主的年龄 Y2：家庭的年收入 Y3：户主受教育程度
分析两组变量之间的关系。
变量间的相关系数矩阵
X1
X2
Y1
Y2
Y3

应用多元统计分析.ppt

应用多元统计分析.ppt

多元统计分析研究 的对象就是多 维随机向量.
第一章
§1.1
绪
论
引言--多元分析的研究对象和内容
研究的内容既包括一元统计学中某 些方法的直接推广，也包括多个随机 变量特有的一些问题。
多元统计分析是一类范围很广 的理论和方法。
第一章
§1.1
绪
论
引言--多元分析的研究对象和内容
就以学生成绩为例，我们可以研究很多 问题：用各科成绩的总和作为综合指标来 比较学生学习成绩的好坏(如成绩好的与成 绩差的，又如文科成绩好的与理科成绩好 的）；研究各科成绩之间的关系（如物理 与数学成绩的关系，文科成绩与理科成绩 的关系）；……等等。所有这些都属于多 元统计分析的研究内容。
课程其它事项

教学软件: R 课程主页: 课程评估:

作业 : 期中 : 期末 :
10% 40% 50%

答疑时间: 周二 9:30—11:30
第一章
§1.1
绪
引 言
论
在实际问题中，很多随机现象涉及到 的变量不止一个，而经常是多个变量，而 且这些变量间又存在一定的联系。我们常 常需要处理多个变量的观测数据。例如考 察学生的学习情况时，就需了解学生在几 个主要科目的考试成绩。 下表给出从某年级随机抽取的12名学 生中5门主要课程期末考试成绩。
0 . 1025 X 0 . 2852 X 4 12 Z1是12个变量的线性组合，且系数都是正数， 数值有大有小。显然数值大的变量对综合指标 （主成分）的贡献大；数值小的变量对综合指 标（主成分）的贡献小。
教育学-主成分分析在学生学习成绩排序中的应用
12个原始变量（课程）提供的信息各为多少？用什 么量来表达？最经典的方法是用变量的方差Var(Xi)为 多少来表达。 如果某课程全班学生的成绩都差不多，比如都是80 分左右，则这门课程在学生成绩的排序中不起什么作 用。这反映在原始变量的线性组合Z1 （第一主成分） 上该变量对应的系数会很小（如0.1025). 如果另一门课程全班学生的成绩相差很大，有的 100分，有的只有30多分，则这门课程在学生成绩的 排序中起的作用很大。这反映在原始变量的线性组合 Z1 （第一主成分）上该变量对应的系数会很大（比如 0.4525).

生物统计学：第10章 多元线性回归分析及一元非线性回归分析

生物统计学：第10章 多元线性回归分析及一元非线性回归分析
的检验。在多元线性回归模拟中，随机误差是服从正 态分布的随即变量。因此，Y亦为独立正态随机变量。 在多元线性回归中，关于回归显著性检验的假设是：
H0 : 1 2 k 0 H A : 至少有一个i 0
拒绝H0意味着至少有一个自变量对因变量是有影 响的。
检验的程序与一元的情况基本相同，即用方差
胸围X2 186.0 186.0 193.0 193.0 172.0 188.0 187.0 175.0 175.0 185.0
体重Y 462.0 496.0 458.0 463.0 388.0 485.0 455.0 392.0 398.0 437.0
序号 体长X1 胸围X2 体重Y 11 138.0 172.0 378.0 12 142.5 192.0 446.0 13 141.5 180.0 396.0 14 149.0 183.0 426.0 15 154.2 193.0 506.0 16 152.0 187.0 457.0 17 158.0 190.0 506.0 18 146.8 189.0 455.0 19 147.3 183.0 478.0 20 151.3 191.0 454.0
R r Y•1,2,,k
yp yˆ p
,
p 1,2,, n
对复相关系数的显著性检验，相当于对整个回 归的方差分析。在做过方差分析之后，就不必再检 验复相关系数的显著性，也可以不做方差分析。
例10.1的RY·1，2为：
RY •1,2
24327 .8 0.9088 29457 .2
从附表（相关系数检验表）中查出，当独立
表示。同样在多元回归问题中，可以用复相关系数表 示。对于一个多元回归问题，Y与X1，X2，… ，Xk 的线性关系密切程度，可以用多元回归平方和与总平 方和的比来表示。因此复相关系数由下式给出，

典型相关分析

引言在一元统计分析中，用相关系数来衡量两个随机变量之间的线性相关关系；用复相关系数研究一个随机变量和多个随机变量的线性相关关系。

然而，这些统计方法在研究两组变量之间的相关关系时却无能为力。

比如要研究生理指标与训练指标的关系，居民生活环境与健康状况的关系，人口统计变量与消费变量（之间是否具有相关关系。

阅读能力变量（阅读速度、阅读才能）与数学运算能力变量（数学运算速度、数学运算才能）是否相关。

典型相关分析（Canonical Correlation ）是研究两组变量之间相关关系的一种多元统计方法。

它能够揭示出两组变量之间的内在联系。

1936年霍特林（Hotelling ）最早就“大学表现”和“入学前成绩”的关系、政府政策变量与经济目标变量的关系等问题进行了研究，提出了典型相关分析技术。

之后，Cooley 和Hohnes （1971），Tatsuoka （1971）及Mardia ，Kent 和Bibby （1979）等人对典型相关分析的应用进行了讨论，Kshirsagar （1972）则从理论上给出了最好的分析。

典型相关分析的目的是识别并量化两组变量之间的联系，将两组变量相关关系的分析，转化为一组变量的线性组合与另一组变量线性组合之间的相关关系分析。

目前，典型相关分析已被应用于心理学、市场营销等领域。

如用于研究个人性格与职业兴趣的关系，市场促销活动与消费者响应之间的关系等问题的分析研究。

第一章、典型相关的基本理论 1.1 典型相关分析的基本概念典型相关分析由Hotelling 提出，其基本思想和主成分分析非常相似。

首先在每组变量中找出变量的线性组合，使得两组的线性组合之间具有最大的相关系数。

然后选取和最初挑选的这对线性组合不相关的线性组合，使其配对，并选取相关系数最大的一对，如此继续下去，直到两组变量之间的相关性被提取完毕为此。

被选出的线性组合配对称为典型变量，它们的相关系数称为典型相关系数。

典型相关系数度量了这两组变量之间联系的强度。

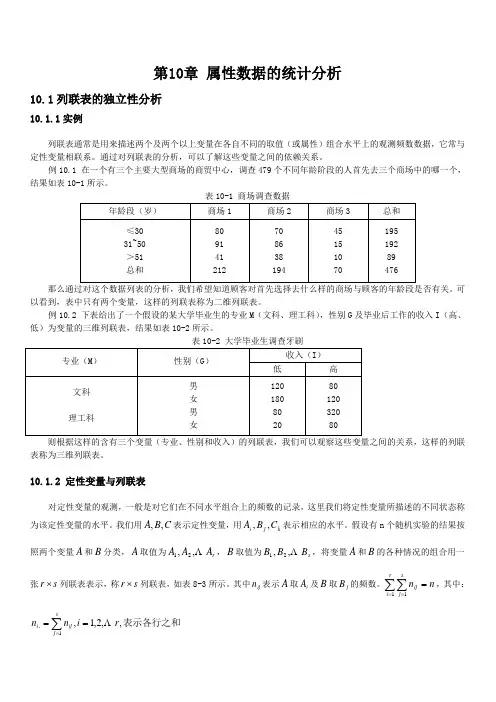
多元统计分析第十章 属性数据的统计分析

第10章 属性数据的统计分析10.1列联表的独立性分析10.1.1实例列联表通常是用来描述两个及两个以上变量在各自不同的取值（或属性）组合水平上的观测频数数据，它常与定性变量相联系。

通过对列联表的分析，可以了解这些变量之间的依赖关系。

例10.1 在一个有三个主要大型商场的商贸中心，调查479个不同年龄阶段的人首先去三个商场中的哪一个，结果如表10-1所示。

表10-1 商场调查数据那么通过对这个数据列表的分析，我们希望知道顾客对首先选择去什么样的商场与顾客的年龄段是否有关。

可以看到，表中只有两个变量，这样的列联表称为二维列联表。

例10.2 下表给出了一个假设的某大学毕业生的专业M （文科、理工科），性别G 及毕业后工作的收入I （高、低）为变量的三维列联表，结果如表10-2所示。

表10-2 大学毕业生调查牙刷则根据这样的含有三个变量（专业、性别和收入）的列联表，我们可以观察这些变量之间的关系，这样的列联表称为三维列联表。

10.1.2 定性变量与列联表对定性变量的观测，一般是对它们在不同水平组合上的频数的记录，这里我们将定性变量所描述的不同状态称为该定性变量的水平。

我们用C B A ,,表示定性变量，用k j i C B A ,,表示相应的水平。

假设有n 个随机实验的结果按照两个变量A 和B 分类，A 取值为r A A A ,,21，B 取值为s B B B ,,21，将变量A 和B 的各种情况的组合用一张s r 列联表表示，称s r 列联表，如表8-3所示。

其中ij n 表示A 取i A 及B 取j B 的频数。

r i sj ijn n11，其中：表示各行之和,,2,1,1.r i n n sj ij iri i sj j ri ij j n n n s j n n 1.1.1...,,,2,1,表示各列之和表10-3 变量频数表体表，但这样通常用起来不方便，所以一般是采用象例10.2的方式把三维列联表给出。

10章2节4C营销策略及案例分析

第十章市场营销组合策略4C策略的基本概念14Ps向4Cs的转变24C策略的相关分析3案例分析4随着市场竞争日趋激烈，媒介传播速度越来越快，4Ps理论越来越受到挑战。

1990年，美国学者罗伯特·劳特朋（Robert Lauterborn）教授在其《4P退休4C登场》(New Marketing Litany: Four Ps Passé: C-Words Take Over)专文中提出了与传统营销的4P 相对应的4Cs营销理论。

4C（Customer、Cost、Convenience、Communication）营销理论以消费者需求为导向，重新设定了市场营销组合的四个基本要素：瞄准消费者的需求和期望（Customer）。

基本概述：1970年，美国著名未来学家AlvinToHler在其著名的Futureshock中曾预言：“未来的社会将要提供的并不是有限的、标准化的商品，而是有史以来最大多样化的、非标准化的商品和服务。

”大规模定制作为一种现代生产和管理的模式，将大规模生产和定制生产两种生产模式结合起来，以低成本向多元化细分市场生产和销售满足客户个性化要求的产品和服务，最终形成“销售—生产—服务”一体化模式。

为了实现向客户提供低成本、高质量的个性化定制产品和服务的目标，必须迅速发现和准确捕捉细分市场中个性化客户需求信息，与客户直接进行交流。

传统的以推销为中心的市场营销方式已经不再适应大规模定制生产模式的要求。

大规模定制作为一种崭新的生产和管理模式必然要求有一种新的市场营销方式与之对应。

大规模定制营销需要以市场为起点，发现和挖掘客户的个性化需求，以此制定综合的市场营销组合策略，以实现顾客价值和企业效益的双赢。

4Cs ：指代Customer(顾客，主要指顾客的需求)、Cost(成本)、Convenience(便利)和Communication(沟通)。

Customer(顾客)：主要指顾客的需求。

医学统计学(高级篇)智慧树知到答案章节测试2023年山西医科大学

第一章测试1.四组均数比较的方差分析，其备择假设H1应为（）。

A:至少有两个样本均数不等B:C:D:各总体均数不全相等E:任两个总体均数间有差别答案:D2.随机区组设计的方差分析中，ν配伍等于（）。

A:ν总-ν处理-ν误差B:ν总-ν处理+ν误差C:ν总-ν误差D:ν总+ν处理+ν误差E:ν总-ν处理答案:A3.当自由度（ν1, ν2）及检验水准α都相同时，方差分析的界值比方差齐性检验的界值（）。

A:小B:不一定C:大D:相等答案:A4.完全随机设计方差分析的检验假设是（）。

A:各处理组样本均数相等B:各处理组样本均数不相等C:各处理组总体均数相等D:各处理组总体均数不相等答案:C5.关于方差分析，下列说法正确的是（）。

A:只要是定量资料，均能选用方差分析B:方差分析只能用于多组定量资料均数的比较C:只要各组例数相等，定量资料均数的比较可采用随机区组设计方差分析D:方差分析的基本思想是将数据均方与自由度进行分解E:方差分析可适用于多组正态且等方差的定量资料均数比较答案:E6.当组数等于2时，对于同一资料，方差分析结果与t检验结果相比（）。

A:方差分析结果更为准确B:t检验结果更为准确C:两者结果可能出现矛盾D:完全等价且答案:D7.完全随机设计、随机区组设计的SS和及自由度各分解为几部分（）。

A:2，2B:2，3C:2，4D:3，3答案:B8.完全随机设计方差分析中，组间均方主要反映（）。

A:处理因素的作用B:系统误差的影响C:抽样误差大小D:n个数据的离散程度E:随机误差的影响答案:A9.三组以上某实验室指标观测数据服从正态分布且满足参数检验的应用条件。

任两组分别进行多次t检验代替方差分析，将会（）。

A:使均数相差更为显著B:明显增大犯I型错误的概率C:使结论更加具体D:明显增大犯II型错误的概率E:使均数的代表性更好答案:B10.在完全随机设计的方差分析中，必然有（）。

A:MS组间＞ MS组内B:MS总 = MS组间 + MS组内C:SS总= SS组间 + SS组内D:MS组间＜ MS组内E:SS组内＜ SS组间答案:C第二章测试1.2×2析因试验设计表述正确的是（）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

令
V V
ar( X ) E[ X E( X )][X ar(Y ) E[Y E(Y )][Y
E(X E(Y )]T
)]T 11 22
Cov( X ,Y )
E[ X
E( X )][Y
E(Y )]T
12
Cov(Y , X ) E[Y E(Y )][X E( X )]T 21
• 则有
由上式可以看出，使U ,V 有最简单表示的约束为
aT 11 a 1, bT 22 b 1, (2) 这等价于规定Var(U ) Var(V ) 1. 于是典型相关分析即在约束条件（2）下，确定a和b, 使 （1）达到最大。这时称U ,V为典型变量。
如果只有一对U ,V还不足以反映X和Y之间的相关性， 可进一步构造与U，V互不相关的另外一对典型变量， 如此等等。具体的，各对典型变量的定义如下：
1 11
12
1 22
21 ,
B
1 22
21
1 11
12,如前所述，求解A和 B的特征根及其
相应的特征向量，即可得到所要求的典型相关变量
及其典型相关系数。
若样本数据矩阵已经标准化处理，此时样本的协差阵
就等于样本的相关系数矩阵
R
R11
R21
R12
R22
,由此
可得矩阵
A和B的样本估计 A
R 1 11
R12
R 1 22
R21,
B
R 1 22
R21
R 1 11
R12 ,
求解
A和
B的特征根及其相应的特征向量，
即可得到所要求的典型相关变量及其典型相关系数。
第四节 典型相关系数的显著性检验
在作两组变量X（1），X (2)的典型相关分析之前，
首先应检验两组变量是否相关，如果不相关，
即Cov( X（1），X (2) ) 0,则讨论两组变量的典型
变量的具体表达式和相应的典型相关系数。
为便于理解后述定理的内容，我们首先介正 定矩阵的平方根矩阵的概念及其简单性质。
设A为p阶对称正定矩阵，令P (e1, e2, , ep ), 其中ei (i 1,2, , p)为A的p个正交单位化特征向量，
i (i 1,2, , p)为相应的特征值，则i 0(i 1,2, , n)
由主成分分析思想启发，把两组随机变量之间的相 关关系转化为两个随机变量之间的相关关系来考虑。
• 采用主成分分析的方法，每组变量分别提取主成 分，再通过主成分之间的关系反映两组变量之间 的关系。 即考察一组变量的线性组合
Z a1X1 a2 X2 ap XP aT X
与另一组变量的线性组合
W b1Y1 b2Y2 bqYq bTY
a b
0 （3）
0
将上二式分别左乘aT与bT ,则得：
aT bT
12 21
b a
aT
v bT
11 22
a b
v
而（aT 12 b）T bT 12 a, 所以 v aT 12 b.
于是，解方程组（3）归结为解方程组：
-21a11a2212bb00(4)
为
了具体求解，以12
-1 22
左
个变量与多个变量间的相关关系。
• 现实中： 如鸡蛋、猪肉的价格（作为第一组 变量）和相应产品的销量（第二组变量）有相 关关系。如投资性变量（劳力投入、财力投入、 固定资产投资（用一种变量X1,X2….,XP 描述） 等）与国民收入（工农业收入、建筑业收入、 （用另一种变量Y1,Y2…YP描述）等）具有相 关关系。又如：在生物科学中，在研究某生物 种群状况（用一种变量X1,X2….,XP 描述）与 其生活环境（用另一种变量Y1,Y2…YP描述） 之间的相关关系。
乘（4）
中第二式并将
第一式代入，得（12
-1 22
21
-2
11 ）a
0,
(5)
以21 1-11 左乘（4）式第一式，并将第二式代入，得
（21 1-11 12 -2 22 ）b 0(6)
以 1-11
左乘（5）式，得1-11
12
-1 22
21
a
2a
0(7)
以 -212
左乘（6）式，得
-1 22
21 1-11
V
bTY
b1Y1
b2Y2
bqYq
下面计算U和V的相关系数。由于
V V
ar(U ) ar(V )
Var(aT X Var(bTY )
) aT 11 a bT 22 b
Cov(U ,V ) Cov(aT X ,bTY ) aT 12 b
则U和V的相关系数为
U ,V
aT 12 b
第10章 典型相关分析
• 典型相关分析着眼于识别和量化两组随机变量之 间的相关关系，它是两个随机变量之间的相关关 系在两组变量下的推广。
• 两个随机变量X，Y之间的相关关系可用它们的 相关系数来度量，其定义为
X ,Y
Cov( X ,Y ) Var( X )Var(Y )
但在许多实际问题中，需要研究多
11
1
1
（2）A2 A2 P2 PT P2 PT PPT A;
1
(3)(A2 )1
P
1 2
PT
,
其中-
1 2
1
（2）-1
diag(
1
,
1
,
1 2
,
1
),
通常记（A
12）1为A-
1
2；
p
（4）A
1 2
A
1 2

A1
总体的典型相关系数和典型变量的求法
在约束条件下：Var(U ) aT 11 a 1,Var(V ) bT 22 b 1
之下，寻求a和b使UV aT 12 b达到最大值，根据数学分析
中条件极值的求法，引入Lagrange乘数，可将问题转化为求：
（a, b）
aT
12
b
2
(aT
11
a
1)
v 2
(bT
22
b
1)
的极大值，其中，v是Lagrange乘数。
由极值的必要条件为：
a
b
12 b 11
21 a v 22
如何研究两组变量之间的相关关 系？
• 设两组变量用X1,X2….,XP以及Y1,Y2…YP表示。 分别研究Xi和Yj之间的相关关系，列出相关系数表。其
缺陷：虽然每个Xi和每个Yj之间的相关关系也反映了 两组变量间各对之间的联系，但不能反映这两组变量 整体之间的相关性。孤立地了解各对（ Xi ，Yj ）之间 的相关性无助于对于实际问题的全面分析和解决。另 外当两组变量较多时，处理较烦琐，不易抓住问题的 实质。
第三节 样本典型相关系数
• 一、样本典型相关变量及典型相关系数的 计算 在实际应用中，总体的协差阵通常是未知 的，往往需要从研究的总体中随机的抽取 一个样本，根据样本估计出总体的协差阵， 并在此基础上进行典型相关分析。
设X
X X
(1) (2)
服从正态分布N
p
q
(
,
),从该总体中抽取样本
容量为n的样本，得到下列数据矩阵：
变量归结为求A、B的特征根和特征向量。
典型变量具有如下性质： （1）V (Uk ) 1,V (Vk ) 1, k 1,2, , r
Cov(Ui ,U j ) 0, Cov(Vi ,Vj ) 0, i j
i 0,i j,i 1,2, , r
(2)Cov(Ui ,Vj ) 0,i j 0, j r
一般地，第k对（k p q）典型变量是Uk akT X和 Vk bkTY ,其中Uk ,Vk具有单位方差，且与前k 1对典型 变量中的每个Ui ,Vi (i 1,2, , k 1)均不相关，在此条件 下并使U k 和Vk的相关系数达到最大。 我们称第k对典型变量间的相关系数为第k个典型相关 系数。利用推导主成分类似的方法，可以给出各典型
X
(2) nq
样本均值向量X
X
(1)
,
其中X
(1)
X (2)
1 n
n a 1
X
(1) a
,
X
(2)
1 n
n a 1
X
(2) a
,
样本协差阵
11
21
12
，
22
其中kl
1 n 1
n
(X
j 1
(k) j
X
(k)
)(X
(l) j
X
T (l)
) ,k,l
1,2
由此可得矩阵A和B的样本估计 A
第一对典型变量是U1 a1T X和V1 b1TY , 其中U1和V1具有 单位方差且使U1和V1的相关系数达到最大。 第二对典型变量是U2 a2T X和V2 b2TY , 其中U2和V2具有 单位方差且使U 2，V2和U1，V1均不相关，即 Cov(U1,U2 ) Cov(U2 ,V1) Cov(V2 ,U1) Cov(V2 ,V1) 0 在上述约束条件下并使U 2和V2的相关系数达到最大。
12 T21 .进一步假定11 和22 是满秩阵（从而是
正定矩阵），令
11 21
12 22
，
这 是（X1, X 2 , , X p ,Y1,Y2 , ,Yq）T的协方差矩阵，
且不失一般性，可设p q.
为研究X和Y的相关关系，考虑两组变量的线性组合
U aT X a1X1 a2 X 2 ap X p
我们用通常符号12
22
2 p1
0表示（其余p
p1个
特征根为0），并称12
22
2 p1