下载文档原格式
spss相关性分析原理
SPSS相关性分析是一种统计方法，用于研究两个变量之间的
关系。
它通过计算变量间的相关系数来衡量它们之间的相关性强度和方向。
相关系数可以是皮尔逊相关系数（Pearson correlation coefficient）或斯皮尔曼等级相关系数（Spearman rank correlation coefficient）。
皮尔逊相关系数是用于度量两个连续变量之间线性相关的指标，它的取值范围从-1到1。
当相关系数为正时，表示变量之间存
在正相关关系；当相关系数为负时，表示变量之间存在负相关关系；当相关系数接近于0时，表示两个变量之间没有线性关系。
斯皮尔曼等级相关系数则用于度量两个有序变量之间的相关性，它将原始数据转换为变量的等级顺序，然后计算等级之间的相关系数。
它适用于非线性关系和存在异常值的情况。
在进行相关性分析之前，需要检查两个变量是否满足相关性分析的前提条件，如数据的正态性、线性关系和离群值的影响等。
如果数据不满足这些前提条件，可能需要进行数据转换或选择其他适当的分析方法。
相关性分析的结果通常用相关系数和p值来解释。
相关系数越接近于1或-1，则表示变量之间的相关性越强；p值则用于检
验相关系数是否显著，p值越小表示相关性越显著。
总体而言，相关性分析可以帮助研究者理解变量之间的关系，从而对研究对象或现象进行更深入的探索。
相关系数是衡量变量之间相关程度的度量，也是很多分析的中的当中环节，SPSS 做相关分析比较简单，主要是区别如何使用这些相关系数，如果不想定量的分析相关性的话，直接观察散点图也可以。
相关系数有一些需要注意的地方：1、两变量之间存在相关，仅意味着存在关联，并不意味着因果关系。
2、相关系数不能进行加减乘除运算，没有单位，不同的相关系数不可比较3、相关系数大小容易受到数据取值区间大小和数据个数大小的影响。
4、相关系数也需要进行检验确定其是否有统计学意义相关系数的假设检验中H0：相关系数=0，变量间没有相关性H1：相关系数≠0，变量间有相关性相关系数很多，我们一般根据变量的类型进行选择，我们知道变量类型由低级到高级可以分为定类、定序、定距、定比四种类型，而变量的数据类型则可以分为连续型或者离散型，注意不要混淆一、定距、定比变量，基本上也就是连续变量一般使用pearson相关系数，也称为积差相关系数，是一种线性相关系数，使用最为广泛，适用条件是两变量需要为线性关系，并且都来自正态分布总体，且要求成对出现二、定序、定距、定比变量一般使用spearman等级相关系数也称为秩相关系数，该系数利用了变量的次序信息，而且对原始数据没有过多要求，因此比pearson相关系数使用范围更广，它利用两变量的秩次大小作为分析依据，也可以认为是基于秩次的pearson相关系数，当数据不符合pearson相关系数的要求时，可以选择使用spearman相关系数，但是如果是定距或定比变量，还是建议用pearson相关系数，spearman 相关系数的效能略低。
三、只限定序变量1.Gamma相关系数2.Kendall等级相关系数，分为τ-a，τ-b，τ-c三种3.Somer's D相关系数四、定类变量定类变量的相关性大都是根据卡方值衍生而来1、person卡方实际上也就是卡方检验2.列联系数3.φ-Phi系数4.Cramer's V系数mbda（λ）系数6.Goodman and Kruskal的Tau-y系数五、二分类变量1.相对危险度RR值2.优势比OR值=========================================================熟悉了各种相关系数的情况之后，我们来看一下在SPSS中的操作1.分析—描述性统计—交叉表此过程一般用来分析列联表的，由于数据的组成大多是列联表形式，因此该过程包含了很多种相关系数2.分析—相关—双变量此分析为简单相关分析，是最常用的相关分析。
SPSS相关分析实例操作步骤-SPSS做相关分析SPSS（Statistical Product and Service Solutions）是目前在工业、商业、学术研究等领域中广泛应用的统计学软件包之一。
Correlation是SPSS的一个功能模块，可以用于分析两个或多个变量之间的关系。
下面是SPSS进行相关分析的具体步骤：1. 打开SPSS软件，选择“变量视图”（Variable View），输入相关的变量名，包括数字型变量和分类变量。
2. 进入“数据视图”（Data View），输入数据，并保存数据集。
3. 打开菜单栏中的“分析”（Analyze），选择“相关”（Correlate），再选择“双变量”（Bivariate）。
4. 在双变量窗口中，选择包含需要分析的变量的变量名，并将其移至右侧窗口中的变量框（Variables）。
5. 如果需要控制其他变量的影响，可以选择“控制变量”（Options）。
6. 点击“确定”（OK）按钮后，SPSS将输出结果，并将其显示在输出窗口中。
相关系数（Correlation Coefficient）介于-1和1之间，可以用来衡量两个变量之间的线性关系的强度。
7. 如果需要对结果进行图形化展示，可以选择“图”（Plots），并选择适当的图形类型。
需要注意的是，进行相关分析时需要确保变量之间存在线性关系。
如果变量之间存在非线性关系，建议使用其他统计方法进行分析。
同时，SPSS进行相关分析的结果只能描述变量之间的关系，不能用于说明因果关系。
以上是SPSS做相关分析的具体步骤，希望能对大家进行SPSS 数据分析有所帮助。
使用SPSS进行相关分析
介绍
SPSS是一种广泛使用的统计分析软件，可以帮助分析者完成复杂的数据分析
任务。
在这篇文档中，我们将介绍如何使用SPSS进行相关分析。
相关分析是一种
常用的统计分析方法，用于确定两个或更多变量之间的关系。
通过相关分析，我们可以识别出变量之间的相互依赖性，从而更好地理解数据。
本文将介绍如何使用SPSS进行相关分析，并且提供一些实践中可能遇到的问
题及相应的解决方案。
相关分析的基本概念
在进行相关分析之前，我们需要了解一些基本概念。
相关系数
相关系数是指两个变量之间的关系的统计测量量。
它的取值范围在-1到1之间。
相关系数为正数时，表示变量之间存在正相关关系；相关系数为负数时，表示变量之间存在负相关关系；相关系数为0时，表示变量之间不存在线性关系。
通常使
用皮尔逊相关系数来衡量两个连续变量之间的线性相关程度。
相关分析的假设
进行相关分析时，需要尝试验证一些假设。
这些假设包括：
•变量满足正态分布。
•两个变量之间的关系是线性的。
•变量的关系是稳定的。
如果这些假设不成立，相应的分析结果可能会产生误导。
使用SPSS进行相关分析
步骤1：导入数据
在进行相关分析之前，需要将数据导入SPSS中。
数据可以从数据库、Excel表
或纯文本文件中导入。
确保数据中包含需要进行相关分析的变量。
步骤2：打开相关分析界面
在SPSS主界面上方的菜单栏中选择。
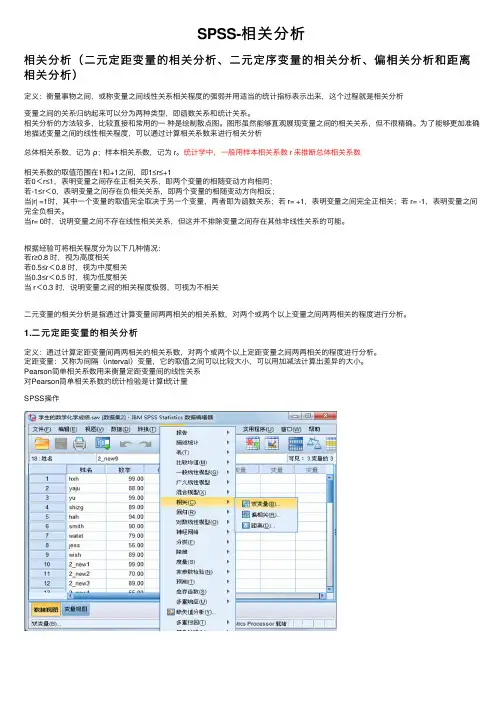
SPSS-相关分析相关分析（⼆元定距变量的相关分析、⼆元定序变量的相关分析、偏相关分析和距离相关分析）定义：衡量事物之间，或称变量之间线性关系相关程度的强弱并⽤适当的统计指标表⽰出来，这个过程就是相关分析变量之间的关系归纳起来可以分为两种类型，即函数关系和统计关系。
相关分析的⽅法较多，⽐较直接和常⽤的⼀种是绘制散点图。
图形虽然能够直观展现变量之间的相关关系，但不很精确。
为了能够更加准确地描述变量之间的线性相关程度，可以通过计算相关系数来进⾏相关分析总体相关系数，记为ρ；样本相关系数，记为 r。
统计学中，⼀般⽤样本相关系数 r 来推断总体相关系数相关系数的取值范围在1和+1之间，即1≤r≤+1若0＜r≤1，表明变量之间存在正相关关系，即两个变量的相随变动⽅向相同；若-1≤r＜0，表明变量之间存在负相关关系，即两个变量的相随变动⽅向相反；当|r| =1时，其中⼀个变量的取值完全取决于另⼀个变量，两者即为函数关系；若 r= +1，表明变量之间完全正相关；若 r= -1，表明变量之间完全负相关。
当r= 0时，说明变量之间不存在线性相关关系，但这并不排除变量之间存在其他⾮线性关系的可能。
根据经验可将相关程度分为以下⼏种情况：若r≥0.8 时，视为⾼度相关若0.5≤r＜0.8 时，视为中度相关当0.3≤r＜0.5 时，视为低度相关当 r＜0.3 时，说明变量之间的相关程度极弱，可视为不相关⼆元变量的相关分析是指通过计算变量间两两相关的相关系数，对两个或两个以上变量之间两两相关的程度进⾏分析。
1.⼆元定距变量的相关分析定义：通过计算定距变量间两两相关的相关系数，对两个或两个以上定距变量之间两两相关的程度进⾏分析。
定距变量：⼜称为间隔（interval）变量，它的取值之间可以⽐较⼤⼩，可以⽤加减法计算出差异的⼤⼩。
Pearson简单相关系数⽤来衡量定距变量间的线性关系对Pearson简单相关系数的统计检验是计算t统计量SPSS操作2.⼆元定序变量的相关分析定序变量：⼜称为有序（ordinal）变量、顺序变量，它取值的⼤⼩能够表⽰观测对象的某种顺序关系（等级、⽅位或⼤⼩等）Spearman和Kendall's tua-b等级相关系数⽤以衡量定序变量间的线性相关关系，它们利⽤的是⾮参数检验的⽅法。
SPSS中的相关分析及假设检验相关分析和假设检验是统计学中常用的方法。
在SPSS中，相关分析可以用来探究两个或多个变量之间的关系。
而假设检验可以用来验证研究者对一个或多个总体参数的假设。
相关分析是用来确定两个或多个变量之间的关系的统计方法。
SPSS 中可以通过选择菜单中的“相关”选项来进行相关分析。
在弹出的对话框中，用户可以选择要进行相关分析的变量，以及选择所需的统计指标。
最常用的统计指标是皮尔逊相关系数（Pearson correlation coefficient），可以用来度量两个连续变量之间的线性关系。
除了皮尔逊相关系数外，还可以选择斯皮尔曼等级相关系数（Spearman's rank correlation coefficient），用于度量两个有序变量之间的关联。
在进行相关分析时，我们还需要对相关系数进行显著性检验，以确定相关系数是否显著不为零。
SPSS会自动计算相关系数的显著性水平（p-value）。
p-value小于我们预先设定的显著性水平（通常为0.05），则可以拒绝原假设，认为相关系数显著不为零。
接下来，我们将介绍SPSS中常用假设检验的方法。
假设检验用于验证研究者对一个或多个总体参数的假设。
常用的假设检验方法包括单样本t检验、独立样本t检验、配对样本t检验和方差分析等。
单样本t检验用于检验一个总体均值是否等于一个给定的值。
SPSS 中可以通过选择菜单中的“分析”、“比较均值”、“单样本t检验”进行单样本t检验。
在弹出的对话框中，用户需要输入要进行检验的变量和给定的均值。
SPSS会给出t值、自由度和p值等统计结果。
如果p值小于我们设定的显著性水平，则可以拒绝原假设，认为总体均值与给定值存在显著差异。
独立样本t检验用于检验两个独立样本的均值是否相等。
SPSS中可以通过选择菜单中的“分析”、“比较均值”、“独立样本t检验”进行独立样本t检验。
在弹出的对话框中，用户需要输入两个独立样本的变量。
相关分析定义相关分析用于研究定量数据之间的关系情况，包括是否有关系，以及关系紧密程度等.此分析方法通常用于回归分析之前;相关分析与回归分析的逻辑关系为:先有相关关系，才有可能有回归关系。
分析过程相关分析使用相关系数表示分析项之间的关系。
1.在相关分析之前，SPSSAU建议可使用散点图直观查看数据之间的关系情况2.首先判断是否有关系(有*号则表示有关系，否则表示无关系)3.接着判断关系为正相关或者负相关(相关系数大于0为正相关，反之为负相关)4.最后判断关系紧密程度(通常相关系数大于则表示关系紧密);相关系数常见有两类，分别是Pearson和Spearman，默认使用Pearson相关系数。
除此之外，SPSSAU还提供Kendall相关系数。
三个相关系数的区别如下表格：如果多个量表题表示一个维度，可使用“生成变量”的平均值功能。
将多个量表题合并成一个整体维度。
分析结果格式1（当仅放入一个框中时）：* p< ** p<格式2（两个框均放置项时）：* p< ** p<*备注：通常情况下会使用格式1，如果希望格式2，则右侧两个框中均需要放置分析项。
单从相关分析方法角度看，其并不区分X和Y，但从实际意义上看，通常是研究X和Y的相关关系。
相关分析案例Contents1 背景 (4)2 理论 (4)3 操作 (5)4 SPSSAU输出结果 (7)5 文字分析 (8)6 剖析 (8)1背景研究“淘宝客服服务态度”，“淘宝商家服务质量”分别与“淘宝商家满意度”，“淘宝忠诚度”之间的关系情况，此句话中明显的可以看出“淘宝客服服务态度”，“淘宝商家服务质量”这两项为X；而“淘宝商家满意度”，“淘宝忠诚度”这两项为Y。
2理论相关分析是研究两个定量数据之间的相关关系情况，以及相关分析是研究有没有关系。
如果呈现出显著性（结果右上角有*号，此时说明有关系；反之则没有关系）；有了关系之后，关系的紧密程度直接看相关系数大小即可。
第10章相关分析 (225)1 双变量相关分析 (225)1.1 双变量相关分析的数据特征 (225)1.2 皮尔逊相关系数 (225)1.3 肯德尔相关系数 (228)1.4 例题3 (230)2 偏相关关系 (232)2.1 偏相关关系 (232)2.2 例题 (232)3 距离相关分析 (234)3.1 特征 (234)3.2 主要参数 (235)3.3 例题 (235)3.4 实例介绍 (237)第10章相关分析相关分析是研究变量之间关系密切程度的一种统计方法，包括双变量相关分析、偏相关分析和距离相关分析。
1 双变量相关分析1.1 双变量相关分析的数据特征当某一个事物存在着多个变量时，而各个变量之间呈数量关系时，可以用双变量相关分析来研究，并做出统计学推断。
双变量相关分析可以输出两两变量之间的相关系数，相关系数的种类有皮尔逊相关系数、肯德尔相关系数、斯皮尔曼等级相关系数等。
1.2 皮尔逊相关系数X和Y有线性函数关系，两变量间的相关系数是+1～-1，相关系数没有单位。
1.2.1 例题133名产妇进行产前检查，测定X1-X6六项指标，试计算X1-X4的皮尔逊相关系数。
1.2.2 SPSS过程Data，analyze，correlate，打开bivariate对话框，选择x1-x4→variables，选择pearson 相关系数，two-tail，flag significant correlations，打开options对话框，means and standard deviations，exclude case pairwirs，continue，ok.two-tail，双尾检验；Flag significant correlations：用星号显示有显著性相关的相关系数；Exclude case pairwirs：剔除有缺失值的配对变量；Cross-product deviations and covarances：显示每一对变量的离均差交叉积与协方差。
22533名产妇6项形态指标（只列出部分数据）X1 X2 X3 X4 X5 X623.00 27.00 17.00 8.50 9.30 1.4024.00 25.00 18.00 8.00 9.30 2.5521.00 23.00 16.50 7.00 8.70 2.6024.00 27.00 18.00 8.00 11.30 2.6023.00 26.00 18.00 6.50 10.70 2.6524.00 27.00 19.00 9.00 11.00 2.7024.00 25.00 17.50 7.00 9.30 2.7023.00 25.00 17.00 6.00 8.30 2.7524.00 26.00 17.00 8.00 8.70 2.8024.00 25.00 18.00 8.00 10.20 2.8022.00 24.00 17.50 7.00 10.70 2.90 1.2.3 SPSS主要对话框1.2.4 运行结果和分析226Descriptive StatisticsMean Std. Deviation NX1 23.6515 1.2021 33X2 25.9394 1.3155 33X3 17.5909 0.9799 33X4 7.8485 0.6433 33CorrelationsX1 X2 X3 X4X1 Pearson 1.000 0.796** 0.684** 0.283Sig. . 0.000 0.000 0.110Sum 46.242 40.303 25.795 7.008Covariance 1.445 1.259 0.806 0.219N 33 33 33 33X2 Pearson 0.796** 1.000 0.617** 0.441*Sig. 0.000 . 0.000 0.010Sum 55.379 25.432 11.947Covariance 1.259 1.731 0.795 0.373N 33 33 33 33X3 Pearson 0.684** 0.617** 1.000 0.171Sig. (2-tailed) 0.000 0.000 . 0.341Sum 25.795 25.432 30.727 3.455Covariance 0.806 0.795 0.960 0.108N 33 33 33 33X4 Pearson 0.283 0.441* 0.171 1.000S ig. (2-tailed) 0.110 .010 0.341 .Sum 7.008 11.947 3.455 13.242Covariance 0.219 0.373 0.108 0.414N 33 33 33 33** Correlation is significant at the 0.01 level (2-tailed).* Correlation is significant at the 0.05 level (2-tailed).上述第一个表是相关分析变量的描述统计量。
第二个表是描述两两变量之间的3个统计量，1，皮尔逊相关系数，2，双尾T检验227结果，3，观测量数。
1.3 肯德尔相关系数1.3.1 特征肯德尔相关系数是一种非参数测度，它是根据数据的秩，而不是根据实际数据计算的。
例如，不能计算宗教信仰与颜色之间的相关系数。
当资料不服从双变量正态分布或总体分布型未知或原始资料是用等级表示时易用肯德尔相关系数进行分析。
1.3.2 例题一些环状化合物的分子量与用药后大白鼠24小时胆汁排泄量。
试问分子量与大白鼠胆汁排泄量有无相关关系。
1.3.3 SPSS过程data大鼠胆汁排泄，Analyze，correlate，bivariate，选择value，excrete→variables，选择pearson，two-tail，flag significant correlations, 再选择Kendall's tau-b，open options 对话框，选择means and standard deviations, cross-product deviations and covarances，缺失值处理采用exclude case pairwirs，continue，ok。
1.3.4 结果和结果分析相关分析变量的描述统计量（Descriptive Statistics）228Mean Std. Deviation N分子量287.60 126.60 10排泄量64.70 34.08 10结果分析，9-3是；9-4，皮尔逊相关系数分析结果；肯德尔等级相关系数，tau-b=0.539,p<0.05。
说明value和excrete有等级相关关系。
皮尔逊相关系数（Correlations）分子量排泄量分子量Pearson 1.000 0.726Sig. . 0.017Sum 144256.40 28201.800Covariance 16028.489 3133.533N 10 10排泄量Pearson 0.726 1.000Sig. 0.017 .Sum of 28201.80 10452.10Covariance 3133.533 1161.344肯德尔等级相关系数（Correlations）分子量排泄量Kendall's tau_b 分子量Correlation 1.000 0.539*Sig. . 0.031N 10 10排泄量Correlation 0.539* 1.000Sig. 0.031 .2291.4 例题31.4.1 数据营养状况评价资料116名儿童的副食品供应与营养状况评价资料，试问副食品供应与营养状况有无相关关系。
副食品供应与营养状况评价资料见下表。
appraisefoodbad normal goodmuch 4 20 6little 7 38 411.4.2 SPSS数据food appraise frequence1.00 1.00 4.001.002.00 20.001.00 3.00 6.002.00 1.00 7.002.00 2.00 38.002.003.00 41.001.4.3 主要对话框data 营养状况评价，data，weight cases，打开加权对话框选择count→frequency，ok。
1.4.4 data 营养状况评价Analyze，correlate，bivariate，food,appraise→variables。
选择Kendall's tau-b/two-tail，230Spearman's rho，选择flag significant correlations。
open options对话框，选择means and standard deviations和cross-product deviations and covarancs，exclude case pairwise，continue ok。
1.4.5 SPSS结果Correlationsfood 评价Kendall's tau_b food Correlation Coefficient 1.000 0.229*Sig. (2-tailed) . 0.011N 116 116评价Correlation Coefficient 0.229* 1.000Sig. (2-tailed) 0.011 .N 116 116Spearman's rho food Correlation Coefficient 1.000 0.237*Sig. (2-tailed) . 0.010N 116 116评价Correlation Coefficient 0.237* 1.000Sig. (2-tailed) 0.010 .N 116 116* Correlation is significant at the0.05 level (2-tailed).结果分析，肯德尔等级相关系数，tau-b=0.229，p<0.05。
说明食品供应与营养状况有相关关系。
2312 偏相关关系2.1 偏相关关系用于计算在控制其他变量情况下，两变量之间的线性关系的偏相关系数，此模块还计算零阶相关系数（即简单相关系数，皮尔逊相关系数）矩阵，以及矩阵所产生的偏相关系数、自由度和显著性。
2.2 例题（1）data partial调查29名儿童身高(X1)，体重(X2)和肺活量(Y)，试计算简单相关关系，当体重X2被控制时，试计算身高X1和肺活量Y的偏相关系数。
