教案4轴向拉压杆的变形计算
- 格式:pdf
- 大小:333.90 KB
- 文档页数:6
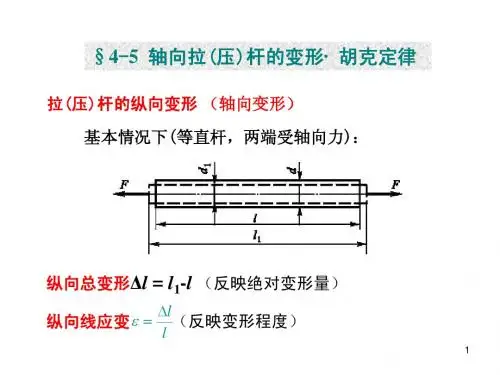

第4讲教学方案——拉压杆的变形与变形能1 / 7§2-8拉伸或压缩时的变形1.沿杆件轴线的轴向变形如图2-23,设等直杆的原长为l ,横截面面积为A 。
在轴向力P 作用下,长度由l 变为1l 。
杆件在轴线方向的伸长,即轴向变形为l l l -=∆1 (1)由于杆内各点轴向应力σ与轴向应变ε为均匀分布,所以一点轴向线应变即为杆件的伸长l ∆除以原长l : l l ∆=ε (2) 由εσE =得ll E A N ∆= 所以EAPl EA Nl l ==∆ (2-6) 式(2-6)表示:当应力不超过比例极限时,杆件的伸长l ∆与拉力P 和杆件的原长度l 成正比,与横截面面积A 成反比。
这是胡克定律的另一种表达形式。
式中EA 是材料弹性模量与拉压杆件横截面面积乘积,EA 越大,则变形越小,将EA 称为抗拉(压)刚度。
2.横向变形若在图2-23中,设变形前杆件的横向尺寸为b ,变形后相应尺寸变为1b ,则横向变形为 b b b -=∆1横向线应变可定义为bb ∆='ε 由实验证明,在弹性范围内3 / 7μεε=' (2-7) μ为杆的横向线应变与轴向线应变代数值之比。
由于μ为反映材料横向变形能力的材料弹性常数,为正值,所以,一般冠以负号εεμ'-=,称为泊松比或横向变形系数。
ε'与ε的关系为μεε-=' (2-8)3.变截面杆的伸长变形 ()()()x A x N x =σ例,变截面杆内应力相同,则杆截面面积按什么规律变化?()Adx A dA A γσσ+=+;dx A dA σγ= 积分:0ln C x A +=σγ;x e C A σγ0= 在0=x 处0A A =,所以:σP A C o ==0;x x e P e A A σγσγσ==0 即:A 按指数函数变化。
例2-6 图2-25所示为变截面杆,已知BD 段21=A cm 2,DA 段42=A cm 2,51=P kN ,102=P kN 。

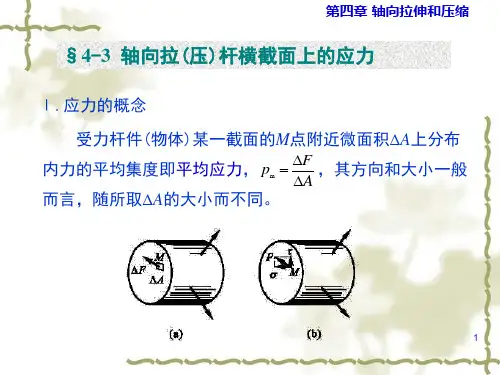






轴向拉压杆的变形的单元设计表1教案计划表2. 教学实施【步骤l 】复习巩固和引入新课⑵ 引入新课(案例): 1)怎么计算杆的轴向变形【步骤2】课程介绍及知识讲授(一)胡克定律对于轴向拉压杆,当材料在线性弹性范围内,根据胡克定律式(6-x )求杆的变形为EAlF l N =∆ (二)分段求杆的轴向总变形的方法对于轴力、横截面面积和弹性模量等沿杆轴线逐段变化的杆,要在截面变化处、轴力变化处、材料变化处分段。
杆的轴向总变形量l ∆为各段变形量i l ∆的代数和,即ini N i EA l F l l ∑∑=⎪⎭⎫⎝⎛=∆=∆1如图8-1所示阶梯形拉压杆,AB 段为铜材料,BCDE 为钢材。
若要计算阶梯形杆的轴向变形,要在材料变化点B 处,截面变化点C 处,轴力变化点D 处分段。
即分为AB 、BC 、CD 和DE 等4段。
分别计算各段变形。
最后求代数和。
图8-1【步骤3】例题讲解教学地点 教师任务 学生任务 教学条件 时间(分钟)多媒体教室给出例题听课,获取有关 知识和信息多媒体课件 背景资料10教学内容及要求:例题8-1短柱如例题8-1图所示,承受荷载kN F 5801=,kN F 6602=,其上部分长度m l 6.01=,截面为正方形(边长为70mm );下部分长度m l 7.02=,截面也为正方形(边长为120mm )。
设GPa E 200=,试求短柱顶面的位移。
解:先计算柱各段轴力。
上段:kN F F N 58011-=-=(压力) 下段:kN F F F N 1240212-=--=(压力) 短柱各段的轴向变形为mm EA l F l N 355.0701*******105802331111-=⨯⨯⨯⨯-==∆ mm EA l F l N 301.0120102007001012402332222-=⨯⨯⨯⨯-==∆ 短柱的总变形为mm mm mm l l l 656.0301.0355.021-=--=∆+∆=∆例题8-1图由于柱下部支座没有发生位移,柱被压缩了mm 656.0,所以,柱顶向下位移mm 656.0。
轴对称与轴对称图形-——说课稿连云港师范高等专科学校数学与应用数学系 09数教2一、说教材(一)教材的地位与作用今天我说课的内容是苏科版八年级上册第一章第一节的轴对称与轴对称图形。
“轴对称和轴对称图形”这一节是在学生小学学过对称的基础上,在学习等腰三角形的性质,以及线段垂直平分线的性质定理及逆定理前安排的一节内容。
它是前面所学知识在生活中的应用,也是后面学习中心对称的重要的基础知识。
通过本节课的教学,主要是训练学生初步的审美能力和初步的图案设计操作技能,拓展学生的想象能力。
因此,这一节课无论在知识上,还是对学生观察能力的培养上,都起着十分重要的作用。
(二)教学目标根据本课的具体情况,考虑到学生已有的认知结构和心理特征,我制订如下教学目标:1、经历观察生活中的轴对称现象和轴对称图形,探索它们的共同特征的活动过程,发展空间观念;2、能够认识轴对称和轴对称图形,并能找出对称轴;3、知道轴对称和轴对称图形的区别和联系;4、欣赏现实生活中的轴对称图形,体会轴对称在现实生活中的广泛应用和它的丰富的文化价值。
(三)教学重点、难点本着课程标准,我在认识了本节课教材在整个知识结构中所处的地位,考虑学生认知情况的基础上,我确立了如下教学重点、难点。
重点:轴对称与轴对称图形的概念及识别。
难点:轴对称与轴对称图形的区别和联系。
关键点:集会理解轴对称和轴对称图形的概念。
二、说教法根据本节教材内容和编排特点,为了更有效地突出重点,突破难点,按照学生的认知规律,遵循教师为主导,学生为主体,训练为主线的指导思想,采用观察发现法为主,直观演示法、设疑诱导法为辅。
教学中,教师精心设计一个又一个带有启发性和思考性的问题,创设问题情景,诱导学生思考、操作,教师适时地演示,并运用电教媒体化静为动,激发学生探求知识的欲望,逐步推导归纳得出结论,使学生始终处于主动探索问题的积极状态,从而培养思维能力。
三、说学法根据学法指导自主性和差异性原则,让学生在“观察一操作一概括一检验一应用”的学习过程中,自主参与知识的发生、发展、形成的过程,使学生掌握知识。