第四章 杆件的变形计算
- 格式:ppt
- 大小:2.90 MB
- 文档页数:48

理论力学中的杆件的变形分析杆件在力学中扮演着重要的角色,广泛应用于各种工程领域。
在理论力学中,对于杆件的变形进行分析是十分重要的,它能帮助工程师和设计师预测和评估结构的性能和可靠性。
本文将介绍杆件的变形分析的基本原理和方法。
1. 弹性变形杆件受到外力作用时,会发生弹性变形。
在弹性变形情况下,杆件会迅速恢复到未受力状态,且不会发生永久形变。
弹性变形是基于胡克定律,即应力与应变成正比。
根据胡克定律,可以得到杆件的弹性形变的方程。
2. 杆件的拉伸和压缩当杆件受到拉伸或压缩作用时,会发生轴向变形。
在理论力学中,我们可以使用材料力学的知识来分析杆件的轴向变形。
拉伸和压缩是杆件最常见的变形形式,例如,建筑物的柱子或者桥梁的支撑杆件都会经历拉伸或压缩。
3. 杆件的弯曲当杆件受到弯曲力矩作用时,会发生弯曲变形。
弯曲是指杆件在垂直于其长度方向上发生形状改变。
在理论力学中,我们可以使用梁的理论来分析杆件的弯曲变形。
通过应力和应变的关系以及几何形状的考虑,可以计算出杆件在弯曲过程中的变形情况。
4. 杆件的扭转当杆件受到扭矩作用时,会发生扭转变形。
扭转是指杆件在一个固定的截面上,某一段杆件相对于其他段发生旋转。
通过扭转变形分析,我们可以计算出杆件在扭转过程中的变形情况。
杆件的变形分析对于在工程设计过程中非常重要。
通过对杆件的变形情况进行准确的分析,可以帮助工程师和设计师了解结构的性能和可靠性。
此外,在设计过程中,合理地选择材料和截面形状也是非常关键的,因为不同的材料和截面形状会直接影响杆件的变形情况。
总之,理论力学中的杆件的变形分析是一个复杂但重要的领域。
它涉及到弹性变形、拉伸和压缩、弯曲和扭转等不同类型的变形。
通过对杆件变形进行准确的分析,可以帮助工程师预测结构的行为,并确保结构的性能和安全性。
对于工程设计和结构优化来说,杆件的变形分析是一项必不可少的工作。
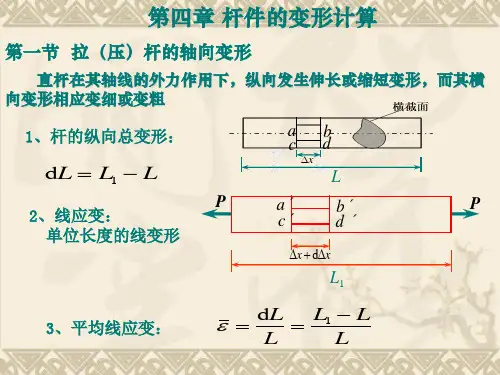


关于杆件变形能公式的推导杆件变形是指在受到外力作用下,杆件发生形变,这种形变可以用形变能来描述。
形变能是杆件弹性势能的一种表现形式,它是描述杆件形变程度的指标,与外力大小、杆件弹性系数、杆件长度和截面形状等相关。
要推导出杆件变形能公式,可以从杆件受力、应力、应变和势能等方面入手。
首先,杆件变形是由外力作用于杆件上引起的。
杆件在受力作用下会产生应力,应力是单位面积上的力。
杆件上的应变是指杆件在受力作用下,相应的长度变化。
根据胡克定律,应力与应变之间存在线性关系,可以表示为:σ=Eε其中,σ表示应力,E表示杨氏模量,ε表示应变。
接下来,考虑杆件的长度变化。
根据变形的几何关系,可知杆件长度的变化与应变之间存在关系。
设杆件在外力作用下发生的长度变化为ΔL,初始长度为L,变化后的长度为L',则有:ΔL=L'-L而杆件的应变ε可以表示为:ε=ΔL/L代入上述等式,可得:ΔL=εL将ε=σ/E代入,可以得到:PE=∫udV其中,V表示杆件的体积。
将杆件的应变ε替换进去,可以得到:PE=∫udV=∫σεdV=∫(σE)(ΔL/L)dV进一步展开,可以得到:PE = (∫ (σ E) ΔL dV) / L = (∫ (σ E) ΔL A dx) / L 其中,A表示杆件的截面积,x表示杆件的长度方向。
将ΔL=L'-L代入上式,可以得到:PE = (∫ (σ E) (L' - L) A dx) / L对式中的积分进行分解,可以得到:PE = ∫ (σ E A) (L' - L) dx / L再次代入ΔL=L'-L,可以得到:PE = ∫ (σ E A) ΔL dx / L由于σEA是常数,可以提到积分符号外,得到:PE = (σ E A) ∫ΔL dx / L杆件的长度与x成正比,对积分进行整理,可以得到:PE = (σ E A) ∫ L dx / L对上述积分进行求解,可以得到:因此,杆件的变形能可以表示为:PE=(σEA)L所以,杆件的变形能公式可以表达为:PE=Fδ其中,F表示外力,δ表示变形量。


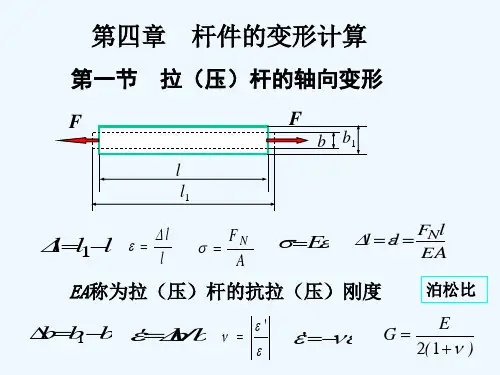
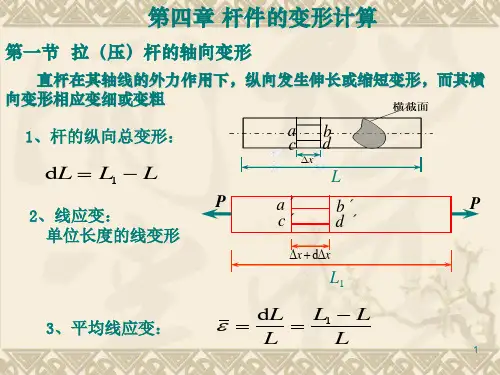

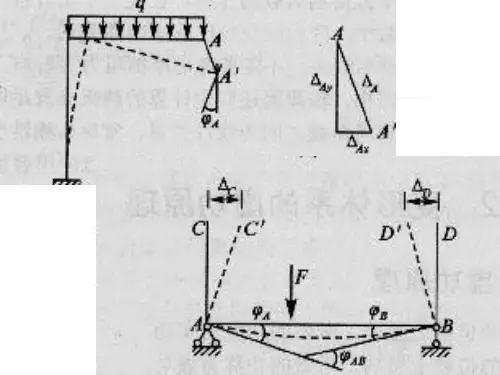

材料力学变形计算公式材料力学这门学科啊,可真是充满了各种奇妙的知识和计算公式。
其中,变形计算公式那可是相当重要的一部分。
先来说说什么是变形。
想象一下,你用力拉一根橡皮筋,它是不是变长了?这就是变形。
而材料力学里研究的变形,可比拉橡皮筋复杂得多。
咱们就拿一根钢梁来举例吧。
假设这根钢梁要承受很大的重量,那它会发生什么样的变形呢?这时候变形计算公式就派上用场啦。
比如说,拉伸或压缩变形的计算公式是ΔL = FL / (EA) 。
这里的ΔL 表示变形量,F 是所受的力,L 是杆件的长度,E 是材料的弹性模量,A 是杆件的横截面面积。
我记得有一次在工地上,看到工程师们在计算一个大型起重机的起重臂的变形量。
他们拿着各种测量工具,神情专注,一边测量一边在本子上记录数据。
然后就开始运用这些变形计算公式来计算,看起重臂是否能够承受预期的重量,并且保证在工作过程中不会发生过度的变形。
再来说说扭转变形的计算公式。
扭转角φ = TL / (GIp) ,其中 T 是扭矩,L 是杆件的长度,G 是材料的剪切模量,Ip 是极惯性矩。
弯曲变形的计算公式就更复杂一些啦。
比如简支梁受集中力作用时,最大挠度的计算公式是 Ymax = Fl³ / (48EI) 。
这些变形计算公式在实际工程中可太重要了。
就像建造高楼大厦,如果不精确计算建筑材料的变形,那可就危险啦。
咱们在学习这些公式的时候,可不能死记硬背,得理解每个参数的含义和它们之间的关系。
比如说弹性模量 E ,它反映了材料抵抗变形的能力,不同的材料 E 值可不一样。
而且,在实际应用中,还得考虑很多因素的影响。
比如温度的变化、材料的缺陷等等。
总之啊,材料力学的变形计算公式虽然看起来有点复杂,但只要咱们用心去学,结合实际去理解,就能掌握好它们,为解决实际问题提供有力的工具。
所以,小伙伴们,别害怕这些公式,加油去探索材料力学的奇妙世界吧!。
杆线变形计算公式杆线变形是指在外力作用下,杆件产生的形变现象。
在工程中,对于杆线的变形计算是非常重要的,可以帮助工程师们设计出更加稳固和安全的结构。
杆线的变形计算可以利用公式来进行,下面我们就来介绍一下杆线变形计算的公式及其应用。
杆线的变形计算公式一般可以分为静力学方法和弹性力学方法两种。
静力学方法主要是根据杆线的受力分析,利用受力平衡方程来推导出变形的计算公式;而弹性力学方法则是根据杆线的弹性变形特性,利用弹性力学理论来推导出变形的计算公式。
下面我们将分别介绍这两种方法的计算公式及其应用。
静力学方法的计算公式一般可以通过受力平衡方程来推导得出。
对于简单的杆线结构,可以利用受力平衡方程来推导出杆线的变形计算公式,例如对于受均匀分布载荷作用的杆线,可以利用受力平衡方程推导出杆线的变形计算公式为:δ = PL / AE。
其中,δ为杆线的变形量,P为作用在杆线上的力,L为杆线的长度,A为杆线的截面积,E为杆线的弹性模量。
这个公式适用于受均匀分布载荷作用的简单杆线结构,可以方便地计算出杆线的变形量。
对于复杂的杆线结构,静力学方法的计算公式可能会比较复杂,需要进行更加详细的受力分析来推导出变形的计算公式。
在实际工程中,可以利用有限元分析等方法来进行复杂杆线结构的变形计算,得到更加精确的结果。
弹性力学方法的计算公式则是根据杆线的弹性变形特性来推导得出。
对于弹性杆线结构,可以利用弹性力学理论来推导出变形的计算公式,例如对于受集中力作用的弹性杆线,可以利用弹性力学理论推导出杆线的变形计算公式为:δ = F L / AE。
其中,δ为杆线的变形量,F为作用在杆线上的力,L为杆线的长度,A为杆线的截面积,E为杆线的弹性模量。
这个公式适用于受集中力作用的弹性杆线结构,可以方便地计算出杆线的变形量。
对于复杂的弹性杆线结构,弹性力学方法的计算公式同样可能会比较复杂,需要进行更加详细的弹性变形分析来推导出变形的计算公式。
在实际工程中,可以利用有限元分析等方法来进行复杂弹性杆线结构的变形计算,得到更加精确的结果。