S门限模型的操作和结果详细解读

stata面板门限模型3200 conformability error1. 引言1.1 概述本文旨在介绍Stata面板门限模型以及涉及到的相关理论背景、数据与方法、结果与讨论以及结论和启示等部分。

通过对面板门限模型的详细解释与实例分析，我们将揭示其作为一种强大统计方法的应用潜力。

1.2 文章结构本文按照以下结构进行组织：首先，在第二部分中，我们将介绍面板数据分析和门限模型背后的基本理论，以帮助读者建立必要的知识框架。

接下来，在第三部分，我们将详细描述数据收集、描述统计和Stata数据准备步骤，并演示如何使用Stata软件实施面板门限模型。

然后，在第四部分中，我们将呈现并讨论面板门限模型的结果，并对敏感性分析和稳健性检验进行进一步探讨。

最后，在第五部分中，我们将总结研究发现并提供对相关政策和决策的启示和建议，并指出进一步研究的方向和可能性。

1.3 目的本篇文章旨在深入探讨Stata面板门限模型的应用和优势，并以一个具体案例来展示其在实际研究中的潜力和意义。

通过本文，读者将了解到如何使用Stata软件实施面板门限模型以及如何解释和分析其结果。

此外，我们还希望通过这篇文章向研究者、政策制定者和决策者们传递面板门限模型所揭示的经济现象和政策效果的重要信息，为相关领域的进一步研究提供有价值的启示和方向。

以上是关于文章“1. 引言”部分内容的详细描述。

2. 理论背景：2.1 面板数据分析：面板数据分析是一种经济学和社会科学研究中常用的方法。

与传统的截面数据（cross-sectional data）和时间序列数据（time series data）不同，面板数据由跨越时间和个体的观察值组成。

通过使用面板数据，我们可以同时考察个体间和时间间的变化，从而更全面地理解变量之间的关系。

2.2 门限模型介绍：门限模型（Threshold Model）是一种广泛应用于经济学和管理学领域的回归模型。

在门限模型中，变量之间的关系在特定阈值点上发生改变。

豪斯曼的门槛方法结果解读豪斯曼的门槛方法（Hausman's Threshold Method）是一种用于检测和处理回归模型中的异方差性（heteroscedasticity）的技术。

这种方法由美国经济学家James E. Hausman在1978年提出，旨在解决普通最小二乘法（OLS）在存在异方差性时估计的不准确性。

异方差性指的是在不同的观测值上，误差项的方差不同。

在回归分析中，如果误差项存在异方差性，那么普通最小二乘法的估计结果可能会产生偏误，因为OLS假设误差项具有恒定的方差。

豪斯曼的门槛方法通过引入一个门槛变量来解决这个问题，这个门槛变量通常是解释变量中的一个，用来划分观测值，使得在门槛的两侧，误差项的方差是恒定的。

豪斯曼的门槛方法的结果解读通常包括以下几个方面：1. 门槛效应的存在性：首先，需要判断门槛效应是否存在。

如果存在，这意味着解释变量中的一个或多个对误差项的方差有显著影响。

2. 门槛变量的选择：确定哪个解释变量作为门槛变量。

这通常是通过模型选择过程来确定的，比如使用似然比检验或沃尔德检验来选择最佳门槛变量。

3. 门槛值的确定：确定了门槛变量后，需要确定门槛值。

这通常是通过最大化似然函数或使用交叉验证来确定的最佳门槛值。

4. 回归结果的解读：在确定了门槛值后，需要对回归结果进行解读。

这包括估计系数的符号、大小和统计显著性，以及模型的拟合优度、预测能力等。

5. 异方差性的影响：豪斯曼的门槛方法可以帮助我们了解异方差性对回归估计的影响。

如果门槛方法显著改善了模型的估计，那么可以认为异方差性对原始的OLS估计有显著的影响。

6. 实证经济学的含义：豪斯曼的门槛方法不仅是一个统计技术，它还具有重要的实证经济学含义。

例如，门槛效应可能表明在不同的水平上，经济行为或政策的效果是不同的。

总之，豪斯曼的门槛方法的结果解读需要综合考虑统计显著性、经济意义以及模型的预测能力等多个方面，以得出合理的经济学结论。

门限自回归模型中门限和延时的小波识别一、门限自回归模型中门限和延时的小波识别1、门限自回归模型门限自回归模型(TAR，Threshold Autoregression Model)是一个简单的相关模型，用于描述变量X在被观测时间t和被观测时间t-1之间的相关性，该模型可以用来预测有限点Y的值，从而对潜在趋势顺利进行拟合。

TAR模型基于门限的概念，其制定的基本假设是：在某些观测时间，观测结果会根据其在上一个观测时间的结果而发生变化，也就是说，同一空间中观测值的变化率（SVR）实际上与前一观测结果相关。

2、门限与延时小波将小波分析应用于门限自回归模型中，可以获得较高的准确率，其原理是利用小波的平均稳定性、稳健性和多重尺度。

具体来说，通过在门限自回归模型中插入一个延时小波盒，可以使模型在噪声大的情况下更加稳健。

小波的重要特征之一就是其均衡性：即在一段时间内，对一个序列的值的平均值和标准差均比较稳定。

因而，如果要使用噪声大的序列进行模型拟合，那么我们就可以在自回归模型内部插入一个小波盒，这样就能够抵消噪声的影响，从而有效地提高模拟的准确性。

3、门限的特点延时小波的应用可以在门限自回归模型中得到实现，其基本特征就是门限的存在，它将模型中的延时项和自变量项划分开来，使得门限联合模型可以通过改变输入自变量来改变延时项的执行行为，从而更有效地拟合序列中的潜在趋势。

另外，研究发现，门限联合模型具有自回归要求得到无偏估计的优点，这使得该模型较其他有限自回归模型更容易拟合序列。

4、应用通过将门限自回归模型和延时小波应用于序列拟合，可以使得拟合的精度和稳健性大大增加。

为了更加准确地实现此目的，需要对门限和延时的许多参数进行有效的调整，以便更好地模拟数据的趋势。

如果正确地配置了这些参数，就可以有效地提供减小误差并实现稳健性的序列拟合效果。

因此，门限自回归模型和延时小波的结合，已经成为当前序列拟合的首选方法。

门限模型中的模型平均估计方法门限模型是广泛使用的技术，它可以用于处理两个群体之间的离散型数据。

门限模型不仅可以处理数据，还可以进行预测，分析和找出其中的规律。

为了更准确地预测结果，需要进行模型平均估计。

下面是10条关于门限模型中模型平均估计方法的详细描述：1. 了解模型平均估计的重要性门限模型中的模型平均估计是指使用多个模型来进行预测，并对这些模型的结果进行平均处理。

这个过程可以提高预测的准确性和稳定性。

2. 理解模型的不确定性在使用门限模型时，需要注意到模型的不确定性，这包括模型参数、数据和模型本身的不确定性。

处理这些不确定性的方法之一是模型平均估计。

3. 选择适合的模型集合模型平均估计需要选择合适的模型集合，这些模型应具有不同的参数和特征，以便在不同情况下提供更准确的预测。

4. 使用信息标准选择模型可以使用信息标准，如AIC和BIC，来选择候选模型，这些标准可以帮助确定哪些模型是最优的。

5. 对模型进行权值分配对于多个模型的情况，需要对这些模型进行权值分配，以反映每个模型在总体预测中的贡献。

这些权值可以基于似然函数或信息标准来计算。

6. 实施模型的组合方法模型平均估计需要实施模型的组合方法。

诸如简单平均、加权平均、贝叶斯模型平均等方法都可用于此目的。

7. 选择可行性的方法根据数据和模型的特征，可以选择不同的组合方法。

使用贝叶斯模型平均方法时需要先使用马尔科夫链蒙特卡罗（MCMC）技术进行后验分布估计。

8. 对预测进行评估完成模型平均估计后，需要对预测进行评估。

这可以通过预测准确性和稳定性的度量来完成。

9. 确认最终的预测结果通过选择可靠的模型集合、确保适当的权值分配和组合方法，以及评估预测的准确性和稳定性，可以提高最终的预测结果的可靠性。

10. 维护模型平均估计的透明度和可重复性为了确保模型平均估计的透明度和可重复性，在选择模型集合、权值分配和组合方法时应记录并报告相关的信息。

这将有助于其他人理解你的分析过程，并尝试复制你的结果。

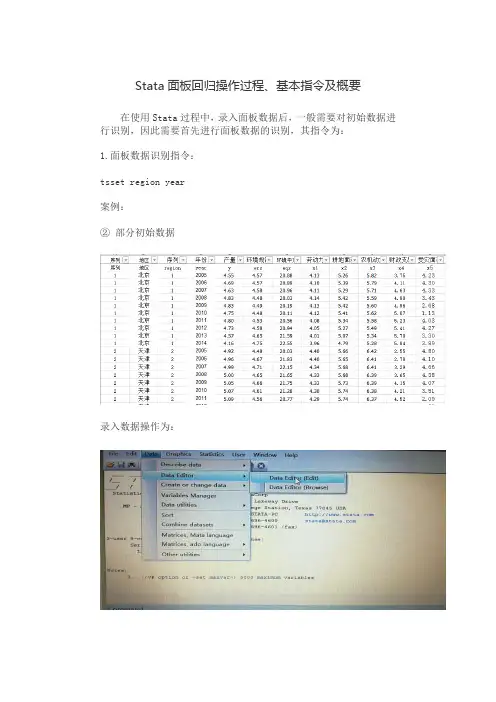
Stata面板回归操作过程、基本指令及概要在使用Stata过程中，录入面板数据后，一般需要对初始数据进行识别，因此需要首先进行面板数据的识别，其指令为：1.面板数据识别指令：tsset region year案例：②部分初始数据录入数据操作为：②将上述初始数据录入stata后（注意：录入数据及首行只能是英文字母或者数字，不能有汉字），显示如下：③输入指令tsset region year，显示如下结果. tsset region yearpanel variable: region (strongly balanced)time variable: year, 2005 to 2014delta: 1 unit2.面板数据固定效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe案例：录入数据，并进行面板数据识别之后，输入以上指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe其中，xtreg为面板回归指令，y为选取的因变量，ers、eqs、x1、x2、x3、x4、x5为自变量，末尾加fe表示为固定效应，如果末尾加re则是随机效应。

上述回归结果显示如下：3.面板数据随机效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,re4.hausman 检验指令：Hausman检验是固定效应或者随机效应回归之后，需要加入的一个检验，具体指令如下：qui xtreg y ers eqs x1 x2 x3 x4 x5,feest store fequi xtreg y ers eqs x1 x2 x3 x4 x5,feest store rehausman fe re5.门限回归指令使用门限（或者门槛）回归模型的，只需要在录入数据后，使用以下指令进行回归即可，xthreg为门限回归指令，y eqs x1 x2 x3 x4 x5分别为自变量和因变量，rx和qx括号中的分别为核心解释变量与门限变量，可以一致也可以不一致。

回顾 历 届 奥 运 会 的安 全 问题 ，曾频 频 发 生 自然 灾 害 和 人 为 事 故 。 １７ ９ ２年 慕 尼 黑 奥运 会 “ 九 月 流 血 事 件 ” 怖 组 织 “ 色 九 月 ” 以 色 黑 。 恐 黑 将 列 运 动 员 胁 迫 为 人质 ，造 成 １ 名 以 色 列 人 ， 名 德 国警 察 和 ５名恐 怖 １ １ 分 子 死 亡 ： ９ ６年 美 国 亚 特 兰 大 奥 运会 上，奥 林 匹克 公 园炸 弹爆 炸 造 １９ 成 １ 死亡，０ 人 １０多 人 受 伤 。 由 于 这 些 流 血 事 件 的发 生 及 严 峻 的 国 际 安 全形 势， 全 在 北 京 ２ ０ 安 ０ ８奥 运 会 的 举 办 中 显 得越 来 越重 要 。做好 奥
【 摘 要 】 如今 的 世界 ， 够 举 办 奥运 会 已 经成 为一 个 国 家的 国 际形 象和 综 合 国力 的 象征 。 全 问题 是 举 办 奥 运 会 的 生 命 线 ， 情报 信 息 在 能 安 而 是 奥 运 会 安 全 工 作 的 生 命 线 和 重要 警 务 资 源 ， 强情 报 信 息 工作 是 应 对 奥 运 期 间安 全 形 势 的 迫 切 需 要 。 运 会 已经 圆满 闭幕 ， 运 安 保 工 作 亦 加 奥 奥 圆满 完 成 ， 安 保 工 作 中 积 累 的 成 功 经验 为担 任 其 他 重 大活 动 安 保 工 作 任 务 的 有 关 单 位 提 供 了借 鉴 。 文 通 过 “ ” 曲线 建 立 了某 地 区刑 事 案 在 本 ｓ形 件 发 案 数 的 预 测 与控 制模 型 ． 据 模 型 分析 找 到 了控 制 刑 事 案 件 增 长 的时 间段 ， 当地 奥 运 安 保 工 作 提供 了参 考 ， 结 合 实 际给 全 运 会 、 根 给 并 国庆 、

SI
S
t
I
t
AI
At
I
t
IS
I
t
I
t
dR t
dt
I
RS
R
t
dAt
dt
S
t
At
AI
At I
t
模型的参数定义如下：
2) N：输入率，代表了网络中新计算机的进入；
3) ：非染病因素的死亡率；
4) SI ：易感计算机的感染率； 5) AI ：新病毒开始的解毒计算机的感染率； 6) ：感染计算机的移出率； 7)IS ：感染计算机的移出率； 8)RS : 由于一个操作的干预而移出的移出率； 9) ：易感计算机进入解毒类的移出率。此过程是在易感计算机和解毒类
“免疫”的结点或者死亡的结点，又以某一生还比率 μ 变成了易感染者，换言之部
分于感染而失去的结点在时间 t 时，又加入到易感染者行列，这就是 SIRS 模型
dI t I t S t I t
dt
dS t
dt
S
t
I
t
R
t
1.6
dR t I t R t
dt
其中的 μ 为消失（Removed）后结点的变为易感染者的生还率变量，其他的
dt
t0
大的条件：
S0I0
I0
0即
S0
。也就是说易感染的数目只有大于门限
值，病毒才可能流行，若
S0
，那么病毒是流行不起来的，而这一点与
Kermack-Mckendrick 的结论是一致的。
5.SAIR 模型
数学模型描述是：
dS t
dt
N
t
S
t

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：/~bhansen/progs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

03
空间滞后门限模型的应用
宏观经济领域
预测经济趋势
通过空间滞后门限模型，研究者 可以有效地预测经济趋势和未来 经济走向。这种模型能够考虑地 理位置和空间相关性的影响，从 而更准确地反映经济活动之间的 联系。
评估政策影响
空间滞后门限模型可以用于评估 政策对不同地区经济的影响。例 如，通过模型分析不同地区的税 收政策对经济发展的影响，有助 于政府制定更加科学合理的经济 政策。
门限模型的概念与类型
门限模型是一种非线性模型，其核心思想是将 变量间的关系划分为不同的阈值区间，每个区 间对应不同的模型形式。
研究现状评述
01
空间滞后门限模型的 应用范围
空间滞后门限模型广泛应用于地理学 、经济学、环境科学等领域，用于研 究空间自相关性和非线性关系。
02
当前研究的主要贡献
目前，已有大量文献对空间滞后门限 模型的理论基础、模型估计和检验方 法进行了深入研究，为该领域的发展 做出了重要贡献。
可解释性强
03
空间滞后模型的参数具有明确的经济学含义，便于解释和解读
。
空间滞后模型的重要性
处理空间自相关问题
在许多实际问题中，观测值之间可能存在空间自相关问题， 如相邻地区的经济指标可能相互影响。空间滞后模型为这类 问题提供了有效的解决方法。
提供政策启示
通过对空间滞后模型的分析，可以为政策制定提供有益的启 示，例如在制定区域经济发展政策时，需要考虑地区间的相 互影响。
拓展模型应用领域
空间滞后门限模型在经济学、 地理学等领域具有广泛的应用 前景，未来可以进一步拓展其
应用范围。
改进模型效率
目前空间滞后门限模型的估计 方法尚不够完善，未来可以进 一步改进模型的估计效率，提

s 曲线模型的饱和值是指S曲线模型在发展过程中达到的最大值或极限值。

S曲线模型是一个创新的元模型，此模型由一线、两点、三阶段组成，如同生命从诞生、成长、到衰败的过程。

其中一线指一条象征着连续性的“S形曲线”，曲线在开始的时候是呈下降趋势，因为此时的投入一般要高于产出，由下而上的翻转点被称为“破局点”，突破了“破局点”之后会产生自增长，从而实现连续性的上升，曲线一路向上发展，靠近上方时，增长速度开始放缓，由上向下的翻转点被称为“极限点”，也叫“失速点”，一旦过了“极限点”，便会快速向下坠落。

s曲线参数求解方法一、引言S曲线是一种在工程、科研等领域广泛应用的曲线类型，用以描述某一过程的发展变化。

准确地求解S曲线参数，对于过程的监控、预测和控制具有重要意义。

本文将介绍S曲线参数的定义及意义，并提出两种求解方法：数值积分法和解析法。

二、S曲线参数定义及意义1.拐点坐标S曲线的拐点坐标是指曲线在拐点处的横坐标和纵坐标。

拐点是曲线由上升转为下降或由下降转为上升的转折点，对于过程的监控具有实际意义。

2.曲线斜率S曲线的斜率表示曲线在某一段区间内的变化速率。

曲线斜率可以反映过程的加速或减速情况，对于过程的分析和控制具有重要参考价值。

3.曲线面积S曲线的面积表示曲线所围成的图形面积。

曲线面积在过程的量化和评估中具有实用价值，可以用于计算过程中的累积量、平均速率等。

三、S曲线参数求解方法1.数值积分法数值积分法是一种通过离散化求解曲线参数的方法。

基本原理是将S曲线划分为若干小段，计算每段弧长与对应横坐标的乘积，然后对所有乘积求和。

应用实例方面，如求解道路交通事故中车辆行驶轨迹的拐点坐标和曲线斜率等。

2.解析法解析法是通过建立数学模型，直接求解曲线参数的方法。

基本原理是根据S曲线的形状特征，设定相应的数学方程，然后求解方程组。

应用实例方面，如求解生长曲线、降解曲线等。

四、S曲线参数求解注意事项1.数据处理与分析在求解S曲线参数前，应对实验数据进行预处理，如去除异常值、平滑曲线等。

同时，应对数据进行详细分析，以确定合适的拟合方法和参数范围。

2.曲线拟合方法选择根据曲线特点和实际需求，选择合适的拟合方法。

如数值积分法适用于求解具有明显拐点和斜率的曲线，而解析法适用于求解形状较为复杂的曲线。

3.参数估计精度与稳定性在求解过程中，应关注参数估计的精度和稳定性。

可以通过调整拟合参数、增加数据点等方式提高估计精度。

同时，应检验曲线拟合的稳定性，避免因数据波动导致曲线形状发生较大变化。

五、结论与展望本文介绍了S曲线参数的定义及意义，并提出了两种求解方法：数值积分法和解析法。

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：/~bhansen/progs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

and uses the proof of the equality of
discretelogarithm to convincethe combinerit is valid.
Since,Wi is the base ATi is thesameas the discretelog of
VKi in the basedVK, namely thesecretkey SKi si.
x
ij
k
)
l 1
il il
i
j
(mod q)
il (mod il
q)
s=f(0)
重构 密钥恢复
l j
2023/12/26
6
Shamir门限方案
例k=3,n=5,q=19,s=11。随机选a1=2,a2=7 f(x)=7x2+2x＋11 mod 19。
计算f(1)=1,f(2)=5,f(3)=4,f(4)=17,f(5)=6 已知f(2),f(3),f(5),重构
si = s(mod mi) (i=1,…, N).（mi,si）为一子密钥.
密钥的恢复 当k个参与者提供子s 密s钥i1 (时mo，d可m建i1 )立方程组 s sik (mod mik )
由中国剩余定理可以求得s ≡ s’ mod N ’ ，N’为k 个m的乘积，s ≡ s’是唯一的
2023/12/26
此方法存在的欺骗问题包括在重建阶段的参与 者欺骗与分割阶段的分派者欺骗。
参与者欺骗是指参与者可能丢出假的子秘密， 使得只有他自己能解出共享的秘密，而其它人 无法解出该秘密。
分派者欺骗是指分派者可能把假的子秘密给参 与者，使得该参与者无法在日后重建共享的秘 密。

门限自回归模型建模步骤嘿，咱今儿个就来聊聊门限自回归模型建模那些事儿！你可别小瞧这门限自回归模型，它就像是一把神奇的钥匙，能打开好多复杂数据背后的秘密呢！首先呢，咱得搞清楚数据。

就好比你要去一个陌生的地方，得先知道路怎么走吧。

咱得好好观察这些数据，看看它们有啥特点，有啥规律。

这可不是随便看看就行的，得用心，就像挑礼物一样仔细。

然后呢，确定门限变量。

这就好比给数据分个类，把它们归到不同的“小组”里。

这可得有眼光，不能瞎分，不然模型可就建得乱七八糟啦。

接下来，估计模型参数。

这一步可重要啦，就像给房子打地基，得稳稳当当的。

可不能马虎，要反复调试，找到最合适的参数值。

再之后，就是检验模型啦。

这就像是给做好的衣服检查有没有线头一样，得看看模型是不是真的好用，能不能准确地描述数据。

哎呀呀，这每一步都不简单呢！就跟爬山似的，得一步一步地往上爬。

可不能嫌麻烦，不然怎么能看到山顶的美景呢？你想想，要是咱随随便便就把模型建了，那能靠谱吗？那不是自欺欺人嘛！咱得认真对待，就像对待自己最喜欢的东西一样。

而且啊，这建模的过程可不只是为了得到一个结果，更是让咱对这些数据有更深入的了解。

就像认识一个新朋友，越了解越觉得有意思。

你说，要是咱不认真建模，那不是浪费了这么好的方法吗？咱可不能干那种傻事儿！咱得好好利用门限自回归模型，让它为咱服务，帮咱解决问题。

总之呢，门限自回归模型建模可不是一朝一夕就能搞定的事儿，得有耐心，有细心，还得有智慧。

咱可不能怕困难，要勇往直前，相信自己一定能建好这个模型！加油吧！。

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen 的个人网站：/~bhansen/pr ogs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

shamir门限例题Shamir门限是一种密码学算法，用于将秘密信息分割成多个部分，并要求达到一定的门限值才能将信息恢复出来。

这种算法常用于保护敏感信息，确保即使部分秘密泄露，也无法完全获取原始信息。

为了更好地回答你的问题，我将给出一个Shamir门限的例题，并从多个角度进行详细解答。

假设有一个秘密信息，需要将它分割成5个部分，并设置门限值为3。

也就是说，只有当至少有3个部分合并才能恢复出原始信息。

现在，让我们来解答以下问题：1. 如何使用Shamir门限算法将秘密信息分割成5个部分？2. 如果只有2个部分被泄露，是否能够恢复出原始信息？3. 如果有3个部分被泄露，是否能够恢复出原始信息？4. 如果有4个部分被泄露，是否能够恢复出原始信息？5. 如果只有1个部分被泄露，是否能够恢复出原始信息？现在，让我从多个角度回答这些问题。

首先，使用Shamir门限算法将秘密信息分割成5个部分的步骤如下：1. 选择一个大于秘密信息的素数p作为有限域的模数。

2. 随机选择一个非零常数a作为多项式的常数项。

3. 构建一个次数为门限值减1的多项式f(x)，其中f(0)为秘密信息。

4. 选择4个非零随机数作为多项式f(x)的系数，并计算出多项式的其他点值。

5. 将多项式的点值分别作为分割后的部分。

对于第二个问题，如果只有2个部分被泄露，无法恢复出原始信息。

因为门限值为3，至少需要3个部分才能进行恢复。

对于第三个问题，如果有3个部分被泄露，可以恢复出原始信息。

因为门限值为3，当有3个部分时，可以通过插值多项式的方式计算出原始信息。

对于第四个问题，如果有4个部分被泄露，同样可以恢复出原始信息。

因为门限值为3，只要还有一个未泄露的部分，就可以通过插值多项式的方式计算出原始信息。

对于最后一个问题，如果只有1个部分被泄露，同样无法恢复出原始信息。

因为门限值为3，至少需要3个部分才能进行恢复。

综上所述，Shamir门限算法可以将秘密信息分割成多个部分，并通过门限值的设定来保护信息的安全。

门限回归方法门限回归方法是一种统计分析方法，主要用于研究两个变量之间的关系，并确定门限值。

门限值是一个非常重要的参数，可以用来确定变量之间的非线性关系，并确定变量之间的阈值。

门限回归方法在机器学习、数据挖掘、医学、生物学等领域都有广泛的应用。

门限回归方法是一种非参数方法，其基本思想是将自变量分为两个或多个组，并对每个组进行线性回归分析。

然后，根据每个组的回归方程和统计检验结果，确定门限值。

门限值可以是一个具体的数值，也可以是一个变量的范围。

通常，门限值表示数据分布的变化点，也可以解释为数据进入一个新的状态。

门限回归方法的基本步骤如下：1.将自变量分为两个或多个组。

2.对每个组进行线性回归分析。

3.根据每个组的回归方程和统计检验结果，确定门限值。

4.根据门限值给出变量之间的非线性关系。

门限回归方法的具体应用比较广泛，下面介绍一些典型的应用场景。

1.风险控制门限回归方法可以用于风险控制领域。

例如，在股票交易中，门限回归模型可以用来确定买入和卖出的时机。

根据股票的历史数据，可以确定股票价格和时间的门限值，并根据门限值进行预测和决策。

2.医学研究门限回归方法可以用于医学研究中。

例如，根据患者的症状和治疗结果，可以确定治疗时间和治疗剂量的门限值，并根据门限值调整治疗方案。

门限回归方法可以用于生物学研究中。

例如，在研究基因表达时，可以根据基因表达水平和相关的生物学特征，确定基因表达的门限值，并进一步研究基因表达和生物学特征之间的关系。

4.机器学习门限回归方法可以用于机器学习领域。

例如，在图像处理中，可以根据像素值和像素位置，确定图像处理的门限值，并实现图像分类和图像特征提取。