S门限模型的操作和结果详细解读

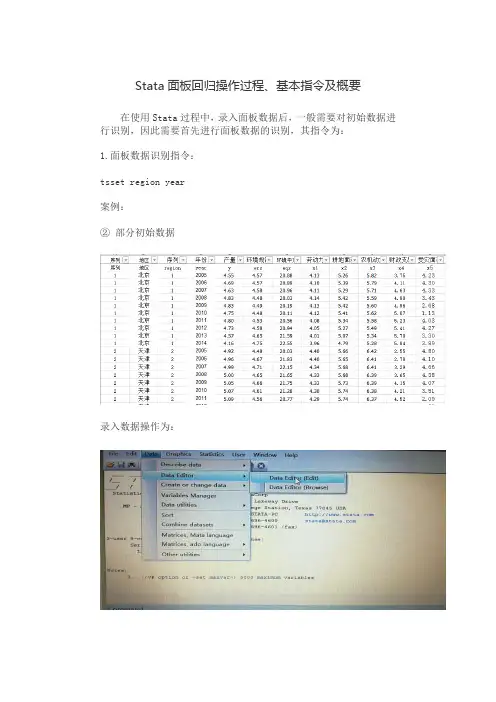
Stata面板回归操作过程、基本指令及概要在使用Stata过程中，录入面板数据后，一般需要对初始数据进行识别，因此需要首先进行面板数据的识别，其指令为：1.面板数据识别指令：tsset region year案例：②部分初始数据录入数据操作为：②将上述初始数据录入stata后（注意：录入数据及首行只能是英文字母或者数字，不能有汉字），显示如下：③输入指令tsset region year，显示如下结果. tsset region yearpanel variable: region (strongly balanced)time variable: year, 2005 to 2014delta: 1 unit2.面板数据固定效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe案例：录入数据，并进行面板数据识别之后，输入以上指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe其中，xtreg为面板回归指令，y为选取的因变量，ers、eqs、x1、x2、x3、x4、x5为自变量，末尾加fe表示为固定效应，如果末尾加re则是随机效应。

上述回归结果显示如下：3.面板数据随机效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,re4.hausman 检验指令：Hausman检验是固定效应或者随机效应回归之后，需要加入的一个检验，具体指令如下：qui xtreg y ers eqs x1 x2 x3 x4 x5,feest store fequi xtreg y ers eqs x1 x2 x3 x4 x5,feest store rehausman fe re5.门限回归指令使用门限（或者门槛）回归模型的，只需要在录入数据后，使用以下指令进行回归即可，xthreg为门限回归指令，y eqs x1 x2 x3 x4 x5分别为自变量和因变量，rx和qx括号中的分别为核心解释变量与门限变量，可以一致也可以不一致。

简述s型曲线的计算过程S型曲线，也称为S形增长曲线或S型增长模型，是一种常见的数学模型，用于描述某个变量随时间逐渐增长，并最终趋于稳定的过程。

它的名称来源于它所呈现的曲线形状，曲线起初缓慢增长，然后迅速增加，最后再度减缓趋于平缓。

S型曲线在经济学、生物学、市场营销等领域具有广泛应用，可以帮助我们更好地了解一些复杂的变量增长过程。

S型曲线可以用一个数学函数来描述，其中最常用的是 logistic 方程。

logistic 方程可以用以下公式表示：y = L / (1 + e^(-k(x-x0)))在这个公式中，y 是变量的值，L 是曲线的顶点值，k 是增长的速度，x0 是曲线的中点，e 是自然对数的底数。

公式中的变量 x 表示时间。

首先，我们需要确定数值 L、k 和 x0 的值。

这些值可以通过研究或实验数据来获得，也可以通过拟合曲线来估计。

L 表示曲线所能达到的最高值，k 表示增长速度的快慢，x0 表示曲线的中点位置。

这些值的确定将直接影响到曲线的形状和趋势。

接下来，我们可以使用计算机软件或计算器来计算每个时间点的变量值。

以 Excel 为例，我们可以依次输入时间点的值（x 值），然后使用 logistic 方程来计算对应的 y 值。

例如，假设我们选定的时间点为0、1、2、3、4、5，那么我们需要在Excel 中创建一个包含这些时间点的列。

接着，在某个单元格中输入 logistic 方程的公式，并将 L、k和 x0 的值替换到公式中相应的位置。

然后，使用填充函数将这个公式应用到时间点列中的每个单元格，即可得到每个时间点对应的变量值。

在计算过程中，我们可以发现，随着时间的增长，曲线的增长速度逐渐加快，直到达到拐点后开始减缓，最终趋于稳定。

这反映了变量在逐渐接近其最大值时的变化过程。

计算得到的变量值可以进一步用于分析和预测。

我们可以绘制S型曲线图来观察曲线的形状和变化趋势。

通过观察曲线的拐点，可以推断变量增长的临界点或分水岭。

s型控制曲线S型控制曲线（S曲线）是一种常用的管理工具，它通过图形化展示目标的变化趋势，帮助我们更好地理解和掌握问题的发展进程。

本文将从定义、应用领域、特点以及使用方法等方面详细介绍S型控制曲线，希望读者通过本文的阅读能够对S型控制曲线有更深入的了解。

首先，我们来定义一下S型控制曲线。

S型控制曲线是一种呈S形状的曲线，它图形化地展示了目标在不同阶段的增长或变化趋势。

S型控制曲线由三个阶段组成，分别是起始阶段、增长阶段和平稳阶段。

起始阶段是指目标在初始阶段变化缓慢，增长较慢；增长阶段是指目标增长速度加快，快速增长；平稳阶段是指目标增长达到饱和状态，增长速度趋于稳定。

S型控制曲线在各个领域都有广泛的应用。

在市场营销中，S型控制曲线可以用来分析产品销售的趋势，帮助企业预测和制定销售策略。

在项目管理中，S型控制曲线可以用于项目的进度控制和资源分配，帮助项目团队及时调整工作计划，确保项目按时完成。

在人力资源管理中，S型控制曲线可以用来评估员工的绩效变化，制定员工激励和晋升计划。

S型控制曲线具有一些明显的特点。

首先，曲线形状稳定，能够准确反映目标的增长趋势。

其次，曲线具有延迟效应，即目标在起始阶段增长缓慢，然后在增长阶段迅速加速，最后在平稳阶段趋于稳定。

最后，曲线的拐点位置可以用来预测目标的最终状态，帮助我们制定相应的策略和措施。

那么，如何使用S型控制曲线呢？首先，我们需要明确目标和可量化的指标。

其次，根据目标的特性和实际情况选择合适的S型控制曲线模型。

然后，收集相关数据并进行分析，画出S型控制曲线。

最后，根据曲线的变化趋势制定相应的战略和措施，以实现目标的快速增长和稳定发展。

综上所述，S型控制曲线是一种重要的管理工具，它能够帮助我们更好地理解和掌握目标的发展过程。

通过对S型控制曲线的应用，我们可以预测趋势、制定策略、实现目标。

希望读者通过本文的阅读，对S型控制曲线有更深入的认识，并将其应用于实际工作中，取得更好的管理效果。

SI
S
t
I
t
AI
At
I
t
IS
I
t
I
t
dR t
dt
I
RS
R
t
dAt
dt
S
t
At
AI
At I
t
模型的参数定义如下：
2) N：输入率，代表了网络中新计算机的进入；
3) ：非染病因素的死亡率；
4) SI ：易感计算机的感染率； 5) AI ：新病毒开始的解毒计算机的感染率； 6) ：感染计算机的移出率； 7)IS ：感染计算机的移出率； 8)RS : 由于一个操作的干预而移出的移出率； 9) ：易感计算机进入解毒类的移出率。此过程是在易感计算机和解毒类
“免疫”的结点或者死亡的结点，又以某一生还比率 μ 变成了易感染者，换言之部
分于感染而失去的结点在时间 t 时，又加入到易感染者行列，这就是 SIRS 模型
dI t I t S t I t
dt
dS t
dt
S
t
I
t
R
t
1.6
dR t I t R t
dt
其中的 μ 为消失（Removed）后结点的变为易感染者的生还率变量，其他的
dt
t0
大的条件：
S0I0
I0
0即
S0
。也就是说易感染的数目只有大于门限
值，病毒才可能流行，若
S0
，那么病毒是流行不起来的，而这一点与
Kermack-Mckendrick 的结论是一致的。
5.SAIR 模型
数学模型描述是：
dS t
dt
N
t
S
t

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：/~bhansen/progs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

S门限模型的操作和结果详细解读文件编码（008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256）一、门限面板模型概览？如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

？一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

？门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

？汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：。

？Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

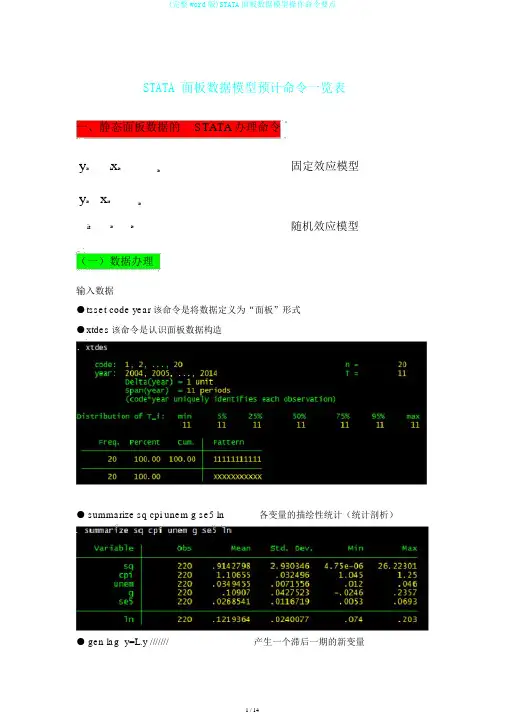
STATA 面板数据模型预计命令一览表一、静态面板数据的STATA办理命令y it i x it it固定效应模型y it x it itit it it随机效应模型（一）数据办理输入数据●tsset code year该命令是将数据定义为“面板”形式●xtdes该命令是认识面板数据构造● summarize sq cpi unem g se5 ln各变量的描绘性统计（统计剖析）● gen lag_y=L.y ///////产生一个滞后一期的新变量gen F_y=F.y ///////产生一个超前项的新变量gen D_y=D.y ///////产生一个一阶差分的新变量gen D2_y=D2.y ///////产生一个二阶差分的新变量（二）模型的挑选和查验●1、查验个体效应（混淆效应仍是固定效应）（原假定：使用 OLS 混淆模型）●xtreg sq cpi unem g se5 ln,fe关于固定效应模型而言，回归纳果中最后一行报告的 F 统计量便在于查验所有的个体效应整体上明显。

在我们这个例子中发现 F 统计量的概率为 0.0000 ，查验结果表示固定效应模型优于混淆 OLS模型。

● 2、查验时间效应（混淆效应仍是随机效应）（查验方法：LM统计量）（原假定：使用OLS混淆模型）●qui xtreg sq cpi unem g se5( 加上“ qui ”以后第一幅图将不会体现) ln,re xttest0能够看出， LM查验获取的 P 值为 0.0000 ，表示随机效应特别明显。

可见，随机效应模型也优于混淆 OLS模型。

● 3、查验固定效应模型or 随机效应模型（查验方法：Hausman查验）原假定：使用随机效应模型（个体效应与解说变量没关）经过上边剖析，能够发现当模型加入了个体效应的时候，将明显优于截距项为常数假定条件下的混淆 OLS模型。

可是没法明确划分 FE or RE 的好坏，这需要进行接下来的查验，以下：Step1 ：预计固定效应模型，储存预计结果Step2 ：预计随机效应模型，储存预计结果Step3 ：进行 Hausman查验●qui xtreg sq cpi unem g se5ln,fe est store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe(或许更优的是hausman fe,sigmamore/ sigmaless)能够看出， hausman查验的 P 值为 0.0000 ，拒绝了原假定，以为随机效应模型的基本假定得不到知足。

03
空间滞后门限模型的应用
宏观经济领域
预测经济趋势
通过空间滞后门限模型，研究者 可以有效地预测经济趋势和未来 经济走向。这种模型能够考虑地 理位置和空间相关性的影响，从 而更准确地反映经济活动之间的 联系。
评估政策影响
空间滞后门限模型可以用于评估 政策对不同地区经济的影响。例 如，通过模型分析不同地区的税 收政策对经济发展的影响，有助 于政府制定更加科学合理的经济 政策。
门限模型的概念与类型
门限模型是一种非线性模型，其核心思想是将 变量间的关系划分为不同的阈值区间，每个区 间对应不同的模型形式。
研究现状评述
01
空间滞后门限模型的 应用范围
空间滞后门限模型广泛应用于地理学 、经济学、环境科学等领域，用于研 究空间自相关性和非线性关系。
02
当前研究的主要贡献
目前，已有大量文献对空间滞后门限 模型的理论基础、模型估计和检验方 法进行了深入研究，为该领域的发展 做出了重要贡献。
可解释性强
03
空间滞后模型的参数具有明确的经济学含义，便于解释和解读
。
空间滞后模型的重要性
处理空间自相关问题
在许多实际问题中，观测值之间可能存在空间自相关问题， 如相邻地区的经济指标可能相互影响。空间滞后模型为这类 问题提供了有效的解决方法。
提供政策启示
通过对空间滞后模型的分析，可以为政策制定提供有益的启 示，例如在制定区域经济发展政策时，需要考虑地区间的相 互影响。
拓展模型应用领域
空间滞后门限模型在经济学、 地理学等领域具有广泛的应用 前景，未来可以进一步拓展其
应用范围。
改进模型效率
目前空间滞后门限模型的估计 方法尚不够完善，未来可以进 一步改进模型的估计效率，提

s 曲线模型的饱和值是指S曲线模型在发展过程中达到的最大值或极限值。

S曲线模型是一个创新的元模型，此模型由一线、两点、三阶段组成，如同生命从诞生、成长、到衰败的过程。

其中一线指一条象征着连续性的“S形曲线”，曲线在开始的时候是呈下降趋势，因为此时的投入一般要高于产出，由下而上的翻转点被称为“破局点”，突破了“破局点”之后会产生自增长，从而实现连续性的上升，曲线一路向上发展，靠近上方时，增长速度开始放缓，由上向下的翻转点被称为“极限点”，也叫“失速点”，一旦过了“极限点”，便会快速向下坠落。

s曲线参数求解方法一、引言S曲线是一种在工程、科研等领域广泛应用的曲线类型，用以描述某一过程的发展变化。

准确地求解S曲线参数，对于过程的监控、预测和控制具有重要意义。

本文将介绍S曲线参数的定义及意义，并提出两种求解方法：数值积分法和解析法。

二、S曲线参数定义及意义1.拐点坐标S曲线的拐点坐标是指曲线在拐点处的横坐标和纵坐标。

拐点是曲线由上升转为下降或由下降转为上升的转折点，对于过程的监控具有实际意义。

2.曲线斜率S曲线的斜率表示曲线在某一段区间内的变化速率。

曲线斜率可以反映过程的加速或减速情况，对于过程的分析和控制具有重要参考价值。

3.曲线面积S曲线的面积表示曲线所围成的图形面积。

曲线面积在过程的量化和评估中具有实用价值，可以用于计算过程中的累积量、平均速率等。

三、S曲线参数求解方法1.数值积分法数值积分法是一种通过离散化求解曲线参数的方法。

基本原理是将S曲线划分为若干小段，计算每段弧长与对应横坐标的乘积，然后对所有乘积求和。

应用实例方面，如求解道路交通事故中车辆行驶轨迹的拐点坐标和曲线斜率等。

2.解析法解析法是通过建立数学模型，直接求解曲线参数的方法。

基本原理是根据S曲线的形状特征，设定相应的数学方程，然后求解方程组。

应用实例方面，如求解生长曲线、降解曲线等。

四、S曲线参数求解注意事项1.数据处理与分析在求解S曲线参数前，应对实验数据进行预处理，如去除异常值、平滑曲线等。

同时，应对数据进行详细分析，以确定合适的拟合方法和参数范围。

2.曲线拟合方法选择根据曲线特点和实际需求，选择合适的拟合方法。

如数值积分法适用于求解具有明显拐点和斜率的曲线，而解析法适用于求解形状较为复杂的曲线。

3.参数估计精度与稳定性在求解过程中，应关注参数估计的精度和稳定性。

可以通过调整拟合参数、增加数据点等方式提高估计精度。

同时，应检验曲线拟合的稳定性，避免因数据波动导致曲线形状发生较大变化。

五、结论与展望本文介绍了S曲线参数的定义及意义，并提出了两种求解方法：数值积分法和解析法。

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：/~bhansen/progs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

一、门限面板模型概览如果您不愿意瞧下面一堆堆得文字,更不想瞧计量模型得估计与检验原理,那就去《数量经济技术经济研究》上,找一篇标题带有“双门槛(或者双门限)”得文章,浏览一遍,瞧瞧文章计量部分列示得统计量与检验结果。

这样,在软件操作时,您就知道每一步得到得结果有什么意义,怎么解释了,起码心里会有点印象。

一般情况下,一个研究生花费在研究上得时间越多,她得成果越丰富,也就就是说,研究成果与研究时间存在某种正向关联。

但就是,这种关联就是线性得吗？在最初阶段,她可能瞧了两三年得文献,也没有写出一篇优秀得文章,但就是一旦过了这个基础期,她得能量与成果将如火山爆发一样喷涌出来,此时,她投入少量得时间,就能产出大量优质文章。

再过几年,她可能会进入另外一种境界,虽然比以前有了极大提高,但就是研究进入新得瓶颈期,文章发表得数量减少。

由此可以瞧出,研究成果与研究年限存在一种阶段性得线性关系。

这个基础期得结点、瓶颈期得起点就像“门槛”一样把研究阶段分成三个部分,在不同部分,成果与时间得线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应,就是指当一个经济参数达到特定得数值后,引起另外一个经济参数发生突然转向其它发展形式得现象。

作为原因现象得临界值称为门限值。

在上面得例子中,成果与时间存在非线性关系,但就是在每个阶段就是线性关系。

有些人将这样得模型称为门槛模型,或者门限模型。

如果模型得研究对象包含多个个体多个年度,那么就就是门限面板模型。

汉森(Bruce E、Hansen)在门限回归模型上做出了很多贡献。

了解门限模型最好得办法,首先就要阅读她得文章。

她得文章很有特点:条理很清晰,推导过程详细,语言简练,语法不复杂。

有关她得论文、程序、数据可以参考Hansen得个人网站:。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》,提出了时间序列门限自回归模型(TAR)得估计与检验。

shamir门限例题Shamir门限是一种密码学算法，用于将秘密信息分割成多个部分，并要求达到一定的门限值才能将信息恢复出来。

这种算法常用于保护敏感信息，确保即使部分秘密泄露，也无法完全获取原始信息。

为了更好地回答你的问题，我将给出一个Shamir门限的例题，并从多个角度进行详细解答。

假设有一个秘密信息，需要将它分割成5个部分，并设置门限值为3。

也就是说，只有当至少有3个部分合并才能恢复出原始信息。

现在，让我们来解答以下问题：1. 如何使用Shamir门限算法将秘密信息分割成5个部分？2. 如果只有2个部分被泄露，是否能够恢复出原始信息？3. 如果有3个部分被泄露，是否能够恢复出原始信息？4. 如果有4个部分被泄露，是否能够恢复出原始信息？5. 如果只有1个部分被泄露，是否能够恢复出原始信息？现在，让我从多个角度回答这些问题。

首先，使用Shamir门限算法将秘密信息分割成5个部分的步骤如下：1. 选择一个大于秘密信息的素数p作为有限域的模数。

2. 随机选择一个非零常数a作为多项式的常数项。

3. 构建一个次数为门限值减1的多项式f(x)，其中f(0)为秘密信息。

4. 选择4个非零随机数作为多项式f(x)的系数，并计算出多项式的其他点值。

5. 将多项式的点值分别作为分割后的部分。

对于第二个问题，如果只有2个部分被泄露，无法恢复出原始信息。

因为门限值为3，至少需要3个部分才能进行恢复。

对于第三个问题，如果有3个部分被泄露，可以恢复出原始信息。

因为门限值为3，当有3个部分时，可以通过插值多项式的方式计算出原始信息。

对于第四个问题，如果有4个部分被泄露，同样可以恢复出原始信息。

因为门限值为3，只要还有一个未泄露的部分，就可以通过插值多项式的方式计算出原始信息。

对于最后一个问题，如果只有1个部分被泄露，同样无法恢复出原始信息。

因为门限值为3，至少需要3个部分才能进行恢复。

综上所述，Shamir门限算法可以将秘密信息分割成多个部分，并通过门限值的设定来保护信息的安全。

s形试件编程方法-概述说明以及解释1.引言1.1 概述概述部分的内容可以包括对于S形试件编程方法的简要介绍和背景说明。

可以按照以下方向展开：S形试件编程方法是一种在程序设计领域中常用的技术，它主要用于解决某些特定问题的编程需求。

S形试件编程方法的核心思想是将问题拆解为多个子问题，并通过特定的算法和逻辑关系进行处理和组合，以实现所需的功能。

在实际应用中，S形试件编程方法经常用于解决诸如数据处理、模型构建和算法优化等复杂任务。

通过将问题分解为多个小问题并以特定的结构组织起来，S形试件编程方法可以提高编程效率、简化程序结构，并且使得程序的可维护性和可扩展性得以提升。

本文将会介绍S形试件编程方法的基本原理和步骤，以及在实际应用中的一些典型案例。

通过深入了解和学习S形试件编程方法，读者将能够更好地理解和运用该方法来解决自己在编程过程中遇到的难题，并提升自己的编程能力。

同时，本文将探讨S形试件编程方法的优势和局限性，帮助读者全面认识该方法的适用范围和限制条件。

并在结论部分对S形试件编程方法的未来发展进行展望，指出该方法可能的拓展方向和应用领域。

通过本文的阐述，相信读者能够对S形试件编程方法有一个较为全面的了解，为今后的编程工作提供一种新的思路和方法。

1.2 文章结构文章结构是指文章的整体组织框架和内容安排。

一个好的文章结构能够使读者更好地理解文章内容，逻辑清晰，条理性强。

本文的结构分为引言、正文和结论三个部分。

引言部分主要是对本文的背景、目的和意义进行介绍。

首先，介绍S 形试件的概念和应用背景，解释为什么研究S形试件编程方法具有重要意义。

同时，对文章结构进行简要说明，明确介绍接下来正文的要点和结论部分的内容。

正文部分是文章的核心，包括多个要点的讨论。

在本文中，我们将重点介绍两个要点。

第一个要点是关于S形试件编程方法的原理和步骤，包括如何确定编程路径、设置刀具参数等。

通过详细讲解这些方法，读者能够深入了解S形试件编程的过程和技巧。

一、门限面板模型概览如果你不愿意看下面一堆堆的文字，更不想看计量模型的估计和检验原理，那就去《数量经济技术经济研究》上，找一篇标题带有“双门槛（或者双门限）”的文章，浏览一遍，看看文章计量部分列示的统计量和检验结果。

这样，在软件操作时，你就知道每一步得到的结果有什么意义，怎么解释了，起码心里会有点印象。

一般情况下，一个研究生花费在研究上的时间越多，他的成果越丰富，也就是说，研究成果和研究时间存在某种正向关联。

但是，这种关联是线性的吗？在最初阶段，他可能看了两三年的文献，也没有写出一篇优秀的文章，但是一旦过了这个基础期，他的能量和成果将如火山爆发一样喷涌出来，此时，他投入少量的时间，就能产出大量优质文章。

再过几年，他可能会进入另外一种境界，虽然比以前有了极大提高，但是研究进入新的瓶颈期，文章发表的数量减少。

由此可以看出，研究成果与研究年限存在一种阶段性的线性关系。

这个基础期的结点、瓶颈期的起点就像“门槛”一样把研究阶段分成三个部分，在不同部分，成果和时间的线性关系都不同。

这个效应被称为门槛效应或门限效应。

门限效应，是指当一个经济参数达到特定的数值后，引起另外一个经济参数发生突然转向其它发展形式的现象。

作为原因现象的临界值称为门限值。

在上面的例子中，成果和时间存在非线性关系，但是在每个阶段是线性关系。

有些人将这样的模型称为门槛模型，或者门限模型。

如果模型的研究对象包含多个个体多个年度，那么就是门限面板模型。

汉森（Bruce E. Hansen）在门限回归模型上做出了很多贡献。

了解门限模型最好的办法，首先就要阅读他的文章。

他的文章很有特点：条理很清晰，推导过程详细，语言简练，语法不复杂。

有关他的论文、程序、数据可以参考Hansen的个人网站：/~bhansen/progs/progs_subject.htm。

Hansen于1996年在《Econometrica》上发表文章《Inference when a nuisance parameter is not identified under the null hypothesis》，提出了时间序列门限自回归模型（TAR）的估计和检验。

STATA面板数据模型操作命令要点D可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

此时，需要采用工具变量法和是使用固定效应模型。

（三）静态面板数据模型估计●1、固定效应模型估计●xtreg sq cpi unem g se5 ln,fe (如下图所示)其中选项fe表明我们采用的是固定效应模型，表头部分的前两行呈现了模型的估计方法、界面变量的名称（id）、以及估计中使用的样本数目和个体的数目。

第3行到第5行列示了模型的拟合优度、分为组内、组间和样本总体三个层面，通常情况下，关注的是组内（within），第6行和第7行分别列示了针对模型中所有非常数变量执行联合检验得到的F统计量和相应的P值，可以看出，参数整体上相当显著。

需要注意的是，表中最后一行列示了检验固定效应是否显著的F统计量和相应的P值。

显然，本例中固定效应非常显著。

●2、随机效应模型估计若假设本例的样本是从一个很大的母体中随机抽取的，且αi与解释变量均不相关，则我们可以将αi视为随机干扰项的一部分。

门限模型中的模型平均估计方法门限模型是广泛使用的技术，它可以用于处理两个群体之间的离散型数据。

门限模型不仅可以处理数据，还可以进行预测，分析和找出其中的规律。

为了更准确地预测结果，需要进行模型平均估计。

下面是10条关于门限模型中模型平均估计方法的详细描述：1. 了解模型平均估计的重要性门限模型中的模型平均估计是指使用多个模型来进行预测，并对这些模型的结果进行平均处理。

这个过程可以提高预测的准确性和稳定性。

2. 理解模型的不确定性在使用门限模型时，需要注意到模型的不确定性，这包括模型参数、数据和模型本身的不确定性。

处理这些不确定性的方法之一是模型平均估计。

3. 选择适合的模型集合模型平均估计需要选择合适的模型集合，这些模型应具有不同的参数和特征，以便在不同情况下提供更准确的预测。

4. 使用信息标准选择模型可以使用信息标准，如AIC和BIC，来选择候选模型，这些标准可以帮助确定哪些模型是最优的。

5. 对模型进行权值分配对于多个模型的情况，需要对这些模型进行权值分配，以反映每个模型在总体预测中的贡献。

这些权值可以基于似然函数或信息标准来计算。

6. 实施模型的组合方法模型平均估计需要实施模型的组合方法。

诸如简单平均、加权平均、贝叶斯模型平均等方法都可用于此目的。

7. 选择可行性的方法根据数据和模型的特征，可以选择不同的组合方法。

使用贝叶斯模型平均方法时需要先使用马尔科夫链蒙特卡罗（MCMC）技术进行后验分布估计。

8. 对预测进行评估完成模型平均估计后，需要对预测进行评估。

这可以通过预测准确性和稳定性的度量来完成。

9. 确认最终的预测结果通过选择可靠的模型集合、确保适当的权值分配和组合方法，以及评估预测的准确性和稳定性，可以提高最终的预测结果的可靠性。

10. 维护模型平均估计的透明度和可重复性为了确保模型平均估计的透明度和可重复性，在选择模型集合、权值分配和组合方法时应记录并报告相关的信息。

这将有助于其他人理解你的分析过程，并尝试复制你的结果。