CityEngine规则语法
- 格式:docx
- 大小:222.35 KB
- 文档页数:8
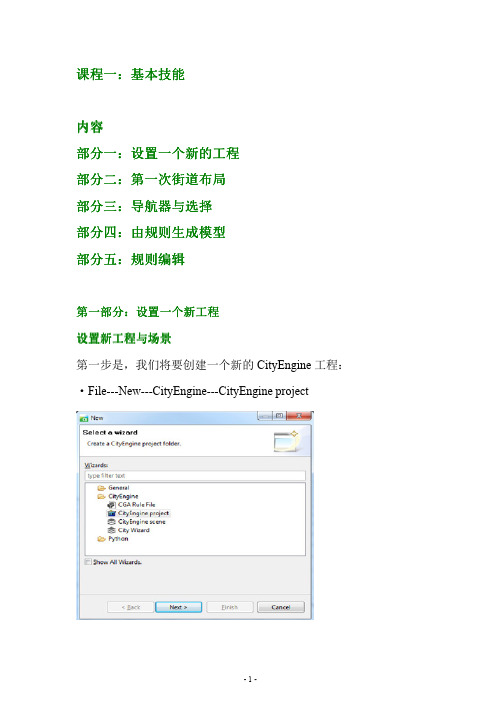

1、单击a键,可以在Viewport视窗中全图显示新建的道路网。
工程:可以理解为一个项目当中所有与CityEngine相关的资源,包括规则、场景、纹理、模型、数据、及其他相关设置。
场景:一个工程中可以有多个场景。
场景中有多个图层。
规则:CityEngine的核心部分,存储在规则文件.Cga中。
通过对 Lot 或 street进行赋予规则可以生成3D模型。
CGA文件:CityEngine中建筑使用CGA文件进行描述的。
一个 CGA 文件可以有多条规则组成,这些规则定义了真实的建筑几何如何生成。
在一个CGA 文件被赋予一个shape之后,建筑模型开始生成。
为了使用方便,默认的项目工程包含的文件夹如下:Assets 文件夹:存放模型零件与纹理图片。
Data 文件夹:存放道路或地块数据,例如:.shp,.dxf,.osm。
Images文件夹:存放场景快照。
Maps文件夹:存放地图图层来源的影像、图片数据。
例如:".jpg", ".png", ".tif"。
Models:导出的3D 模型默认存放位置。
试用版只支持模型导出。
Rules:存放规则文件.cga。
Scenes:存放场景文件.cej。
Scripts:存放脚本文件。
2、CGA计算机生成建筑(Computer Generated Architecture)的缩写。
3、数据导入将(命名一定腰英文,才可以导入)直接复制粘贴到data文件下,然后见.shp格式的数据直接拖到Viewport窗口中即可。
贴材质道路贴图设置:纹理教程TileUV 对贴图进行放大缩小。
可以点击此按钮进行贴图设置setupProjection(0, scope.xz, '1, '1, -18, 36)贴图向左移动贴图向左移动rotateUV(0, -73)旋转的角度。

CityEngine建模⽰例教程6:BasicShapeGrammar之Part1:简单建筑物本着从⽰例中学习使⽤规则建模的⽬的,学习⼀下CityEngine中的教程。
前⼏个教程是熟悉软件以及如何使⽤规则的,第六个教程是开始使⽤规则建模,并给建筑物贴纹理的。
因此⼀边学习教程6中的步骤,⼀边查看其中创建规则的CGA具体语法,希望我们都能从教程中有很多收获。
前提要了解如何创建规则和应⽤规则。
本次学习的教程为Tutorial_06_Basic_Shape_Grammar__2011_1,其中包含四部分,分别为:1.构建简单建筑物;2.为简单建筑物贴纹理;3.添加LOD;4.建筑物属性随机变化。
本节学习该教程中的第⼀部分。
本节学习最终要构建⼀个如下图的建筑物,该建筑物有地⾯⼀楼和其他楼层,⼀楼的正⾯有⼀个⼊⼝的门,其他窗⼝都使⽤的是⼀个提前做好的OBJ模型。
下⾯开始创建规则进⾏建模:为了更好的理解规则,我们⾃⼰创建⼀个新的规则,按照教程中的语句进⾏规则的书写。
1. 在规则⽂件的最开始处定义建筑的属性(也可以放在规则⽂件的其他位置)。
在CGA⽂件中,这些属性将对整个规则⽂件产⽣作⽤。
这些属性将显⽰在属性查看器(Inspector)中,可通过属性查看器修改这些属性。
attr groundfloor_height = 4 //地⾯⼀楼的⾼度attr floor_height = 3.5 //其他楼层的⾼度attr tile_width = 3 //将楼⾯按块划分的宽度attr height = 11 //楼⾼attr wallColor = "#fefefe" //墙⾯颜⾊2. 教程中构建的窗户是使⽤的⼀个已经建好的窗户模型window.obj,这个⽂件存放在assets⽂件夹中,使⽤之前也要先定义出来。
window_asset = "facades/window.obj" //指定obj⽂件3. 下⾯我们定义第⼀条规则为Lot. 在属性检查器中,该规则被指定为开始规则。

Tutorial_06_Basic_Shape_Grammar__2011_11.构建简单建筑物;2.为简单建筑物贴纹理;3.添加LOD;4.建筑物属性随机变化。
一、构建简单建筑物本节学习最终要构建一个如下图的建筑物,该建筑物有地面一楼和其他楼层,一楼的正面有一个入口的门,其他窗口都使用的是一个提前做好的OBJ模型。
下面开始创建规则进行建模:为了更好的理解规则,我们自己创建一个新的规则,按照教程中的语句进行规则的书写。
1. 在规则文件的最开始处定义建筑的属性(也可以放在规则文件的其他位置)。
在CGA文件中,这些属性将对整个规则文件产生作用。
这些属性将显示在属性查看器(Inspector)中,可通过属性查看器修改这些属性。
attr groundfloor_height = 4 //地面一楼的高度attr floor_height = 3.5 //其他楼层的高度attr tile_width = 3 //将楼面按块划分的宽度attr height = 11 //楼高attr wallColor = "#fefefe" //墙面颜色2. 教程中构建的窗户是使用的一个已经建好的窗户模型window.obj,这个文件存放在assets文件夹中,使用之前也要先定义出来。
window_asset = "facades/window.obj" //指定obj文件3. 下面我们定义第一条规则为Lot. 在属性检查器中,该规则被指定为开始规则。
大量的模型是使用拉伸操作创建而来的://对shape使用height中定义的高度进行拉伸,并命名为BuildingLot -->extrude(height) Building拉伸之后如下图:4. 可以通过应用comp()将Building分解为多个面, 生成了正面(FrontFacade)、多个侧面(SideFacade)和一个顶面(Roof)Building-->comp(f){ front : FrontFacade | side : SideFacade | top: Roof}5. 分解完成之后,就开始开始对这些面进行外观造型。

city engine 规则CityEngine是一款用于创建虚拟城市和规划场景的三维建模软件。
它通过编写规则脚本来生成建筑、道路、植被等元素,使用户能够快速创建高度可自定义的城市模型。
以下是一些CityEngine中使用的规则的概述:1. CGA规则语法:CityEngine使用一种称为CGA(Computer Generated Architecture)的规则语言来描述建筑和城市场景。
CGA规则是一种基于规则和参数的语法,允许用户通过定义规则和应用参数来生成建筑物的形状、纹理、风格和细节。
2. 规则库(Rule Library):CityEngine提供了一系列内置的规则库,用户可以使用这些规则库来创建建筑物、道路、街区等元素。
规则库包含了各种建筑风格、道路布局等模板,用户可以选择并进行自定义修改。
3. 层级规则(Hierarchical Rules):CityEngine中的规则可以分为层级结构,这意味着可以使用嵌套规则,从而实现对建筑物和场景的更复杂和详细的描述。
4. 条件语句和迭代语句:CityEngine的规则中可以使用条件语句(如if-else语句)和迭代语句(如for循环),以便根据特定的条件或需要对生成的元素进行逻辑控制和重复操作。
5. 参数化:CityEngine的规则支持参数化,可以在规则中定义参数并通过调整参数的值来改变生成的场景。
这使得用户能够快速进行设计迭代和变化分析。
通过编写和定义规则,用户可以创建高度可定制的城市场景和建筑模型。
CityEngine还提供了可视化和交互式的编辑器,方便用户进行规则的创建、编辑和实时预览。
用户可以根据自己的需求和创意,通过编写规则来生成独特而逼真的虚拟城市模型。

02街道教程本文档为Esri CityEngine学习文档,是CityEngine_2011_Tutorials官方示例教程2——“Tutorial_02_Street_Generation__2011_2”的中文翻译稿,由网友冬冬翻译整理。
教程简介本教程将对CityEngine中建立街道网和建立精细街道模型的方法进行讲解。
自动生成的街道图能够反应出受到各种障碍的影响,如湖泊和地形等。
在本教程的第二部分,将讲解如何根据街道图创建街道图层。
应用道路规则到道路数据上,能够生成精细的街道模型。
在本文的最后部分,展示了一些特定属性信息下生成不同样式的道路网络。
第一部分:创建街道网教程设置将工程“Tutorial_02_Streets”导入到你的CityEngine工作空间中;通过【File】→【New】.. →【CityEngine scene】新建向导在街道教程工程的场景(scenes)文件夹中创建一个新的场景文件,将其命名为“MyStreets.cej”。
创建障碍图层在城市环境中,道路的放置受到很多的限制。
如湖泊、河流或公园,这些地方很可能不会有道路网络分布。
在CityEngine中,你可以创建一个障碍图层(obstacle layer)来控制这种表现方式。
创建一个新的地图图层【Layer】→ 【New Map Layer...】;选择Obstacle(障碍),并单击下一步;从地图文件夹(maps)中选择文件“obstacles.png”作为障碍文件;将对齐位置设置为中心点,并保持比例按键按下;将X size(X的大小)设置为3000;单击Finish结束设置。
提示:如果在viewport视窗中没有显示障碍图层,则通过视图设置菜单切换到纹理阴影模式。
创建地形图层我们创建的街道需要遵循高程地形。
这将通过创建一个由灰度高程图生成的地形图层来获得。
在文件导航(Navigator)窗口的地图文件夹中,选择图像文件“elevation.jpg”;将图像拖拽到你的3D视窗中;从地图文件夹中选择“topo.png”作为纹理贴图文件;将max. elevation(最高海拔)设置为250;与前面一样,将对齐位置设置为中心点,并将保持比例按钮按下;将X size设置为3000;单击“Finish”结束;在场景视窗中选择障碍(Obstacle)图层,在Inspector视窗(可以通过【Window】→【Inspector】方式打开)中,将其Elevation Offset 修改为-15 。
规则创建与分享CityEngine规则创建与分享CityEngine程序化的自动建模3D 城市内容创建属性几何规则3D 城市内容创建程序化、参数化、动态设计3D城市设计添加楼层添加屋顶参数化编辑动态编辑报表•CGA 基础•实用3D建模示例•分享Rule Package内容CGA 基础CGA = Computer Generated Architecture;CityEngine的独特语言;越来越详细地迭代“进化”模型。
CGA:基础规则–基于shape的操作。
CGA:基础Init -->extrude (10)comp (f) {side : Facade. |top :Roof }Roof -->roofHip (30)规则–基于shape的操作。
Init -->extrude (10)ude(10)comp (f) {side : Facade. |top : Roof}Roof -->roofHip (30)CGA:基础规则–基于shape的操作。
CGA:基础Init-->extrude(10)comp(f) {side : Facade. |top : Roof}Roof-->roofHip(30)规则–基于shape的操作。
CGA:基础Init-->extrude(10)comp(f) {side : Facade. |top : Roof}Roof-->roofHip(30)规则–基于shape的操作。
CGA:基础Init-->extrude(10)comp(f) {side : Facade. |top : Roof}Roof-->roofHip(30)定义属性CGA:基础height = 15angle = 35Init -->extrude (height )comp (f) {side : Facade.|top : Roof }Roof -->roofHip (angle )attr函数可以将参数显示到外部,如,Inspector界面。
本文档为Esri CityEngine学习文档,是CityEngine_2011_tutorial官方示例教程 3 “Tutorial_03_Map_Control__2011_2”的中文翻译稿,由网友冬冬翻译整理。
0000教程简介0000城市包含非常多的对象。
通过设置每一个建筑物的属性来控制它们会非常麻烦也是不太可能的。
首先,你将在本教程中学习怎样使用CGA规则参数;然后你将学习怎样使用地图来控制你的城市的属性。
000第一部分:理解CGA规则属性000教程设置0000在你的CityEngine工作空间中导入“Tutorial_03_MapControl”工程,打开场景0000“Tutorial_03_MapControl/scenes/mapcontrolTutorial_01.cej ”0 000当前场景中的图层000地图图层:地形0000地图图层:水体0000道路网图层(包含地块形状)0000规则参数从哪里来?000当你选中一个地块形状,在“Inspector”视窗中查看其属性信息,会发现它并没有被分配规则参数(规则参数组里面是空的),当应用一个规则到这个形状上之后这种状况会发生改变。
0000在“Scene”视窗中选择地块图层中的所有要素0000【Shapes】-->【Assign Rule File...】选择规则文件“rules/simpleBuildingShells_01.cga”0000再次选择地块数据的一个要素。
在“Inspector”视窗中就出现了一个名为“height”的属性。
0000这个属性是从哪里来的呢?在你对你的形状应用规则的时候,规则文件的属性信息就以地块数据的属性(规则属性)的形式显示出来。
高度值来自规则文件。
0000单击“Inspector”视窗中的“Rule File”链接,打开规则文件。
在左上角的位置,放置着“height(高度)”的定义。
0000// height value0000attr height =80000此值用来在规则文件中定义建筑物的高度。
规则文件可以自定义变量值,而且还可以定义变量的分组、排序、值域等显示方式。
以下就列举几个常用的关键字:1. 1.@Group("level_1-group", ..., "level_n-group")控制变量的分组,可以将变量在属性窗口中分组显示,并且可以多层分组。
@Group("Main","Node_1")attr height = 20@Group("Main","Node_2")attr name = ""Lot --> extrude(height)根据上面代码,我们把height变量分在Main组下的Node_1分组内,name变量分在Main组下的Node_2分组内。
在属性窗体中效果如下图:2. 2. @Order(order)控制变量在其分组中的排序,其参数值可以为负数,参数值越高,排序越后。
@Group("Main") @Order(0)attr height = 20@Group("Main") @Order(-1)attr name = ""Lot --> extrude(height)上面的代码表示将height变量和name变量放在Main组中,name排在height前面,效果如下图:3. 3. @Description("description")为变量添加MouseTips信息,当鼠标指向变量时即可显示描述信息,效果如下:4. 4. @File将变量值定义成以文件选择器的方式显示,可以利用文件选择窗体来对变量赋值,也可以加入参数:@File("tif")来设置文件选择器的文件类型限制。
效果如下:5. 5. @Color将变量值定义成以颜色选择器的方式显示,可以利用颜色选择窗体来对变量赋值。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。