山东省胶州市2018届高考数学一轮复习 第7讲 抛物线学案(无答案)文
- 格式:doc
- 大小:238.00 KB
- 文档页数:9

第7讲抛物线,)1.抛物线的定义满足以下三个条件的点的轨迹是抛物线:(1)在平面内;(2)动点到定点F的距离与到定直线l的距离相等;(3)定点不在定直线上.2.抛物线的标准方程和几何性质1.辨明两个易误点(1)抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与定直线垂直的直线.(2)对于抛物线标准方程中参数p ,易忽视只有p >0才能证明其几何意义是焦点F 到准线l 的距离,否则无几何意义.2.与焦点弦有关的常用结论(以右图为依据)设A (x 1,y 1),B (x 2,y 2). (1)y 1y 2=-p 2,x 1x 2=p 24.(2)|AB |=x 1+x 2+p =2psin 2θ(θ为AB 的倾斜角).(3)1|AF |+1|BF |为定值2p. (4)以AB 为直径的圆与准线相切. (5)以AF 或BF 为直径的圆与y 轴相切.1.教材习题改编 抛物线8x 2+y =0的焦点坐标为( ) A .(0,-2) B .(0,2) C .⎝⎛⎭⎪⎫0,-132D .⎝ ⎛⎭⎪⎫0,132C 由8x 2+y =0,得x 2=-18y .2p =18,p =116,所以焦点为⎝⎛⎭⎪⎫0,-132,故选C.2.教材习题改编 以x =1为准线的抛物线的标准方程为( ) A .y 2=2x B .y 2=-2x C .y 2=4xD .y 2=-4xD 由准线x =1知,抛物线方程为y 2=-2px (p >0)且p2=1,p =2,所以方程为y 2=-4x ,故选D.3.M 是抛物线y 2=2px (p >0)位于第一象限的点,F 是抛物线的焦点,若|MF |=52p ,则直线MF 的斜率为( )A .43B .53C .54D .52A 设M (x 0,y 0),由|MF |=52p ,得x 0+p 2=5p2,所以x 0=2p .所以y 20=2px 0=4p 2,取正根得y 0=2p . 即M 的坐标为(2p ,2p ), 又F 的坐标为(p2,0),所以k MF =2p -02p -p 2=43,故选A.4.动圆过点(1,0),且与直线x =-1相切,则动圆的圆心的轨迹方程为________. 设动圆的圆心坐标为(x ,y ),则圆心到点(1,0)的距离与到直线x =-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y 2=4x .y 2=4x5.教材习题改编 抛物线x 2=2py (p >0)上的点P (m ,2)到焦点F 的距离为3,则该抛物线的方程为________.根据抛物线定义可知2+p2=3,所以p =2,所以抛物线的方程为x 2=4y .x 2=4y抛物线的定义及其应用(1)若抛物线y 2=2x 上一点M 到它的焦点F 的距离为32,O 为坐标原点,则△MFO的面积为( )A .22B .24C .12D .14(2)已知抛物线y 2=4x 的焦点是F ,点P 是抛物线上的动点,又有点B (3,2),则|PB |+|PF |的最小值为________.【解析】 (1)由题意知,抛物线准线方程为x =-12.设M (a ,b ),由抛物线的定义可知, 点M 到准线的距离为32,所以a =1,代入抛物线方程y 2=2x , 解得b =±2,所以S △MFO =12×12×2=24.(2)如图,过点B 作BQ 垂直准线于Q ,交抛物线于点P 1,则|P 1Q |=|P 1F |,则有|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=4.即|PB |+|PF |的最小值为4. 【答案】 (1)B (2)4若本例(2)中的B 点坐标改为(3,4),试求|PB |+|PF |的最小值.由题意可知点(3,4)在抛物线的外部.因为|PB |+|PF |的最小值即为B ,F 两点间的距离,所以|PB |+|PF |≥|BF |=42+22=16+4=2 5.即|PB |+|PF |的最小值为2 5.抛物线定义的应用(1)利用抛物线的定义解决此类问题,应灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化.即“看到准线想到焦点,看到焦点想到准线”.(2)注意灵活运用抛物线上一点P (x ,y )到焦点F 的距离|PF |=|x |+p 2或|PF |=|y |+p2.1.(2017·云南省统一检测)设经过抛物线C 的焦点F 的直线l 与抛物线C 交于A 、B 两点,那么抛物线C 的准线与以AB 为直径的圆的位置关系为( )A .相离B .相切C .相交但不经过圆心D .相交且经过圆心B 设圆心为M ,过点A 、B 、M 作准线l 的垂线,垂足分别为A 1、B 1、M 1, 则|MM 1|=12(|AA 1|+|BB 1|).由抛物线定义可知|BF |=|BB 1|,|AF |=|AA 1|, 所以|AB |=|BB 1|+|AA 1|,|MM 1|=12|AB |,即圆心M 到准线的距离等于圆的半径, 故以AB 为直径的圆与抛物线的准线相切.2.(2017·长春调研)已知直线l 1:4x -3y +6=0和直线l 2:x =-1,则抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是( )A .355B .2C .115D .3B 由题可知l 2:x =-1是抛物线y 2=4x 的准线,设抛物线的焦点F 为(1,0),则动点P 到l 2的距离等于|PF |,则动点P 到直线l 1和直线l 2的距离之和的最小值即为焦点F 到直线l 1:4x -3y +6=0的距离,所以最小值是|4-0+6|5=2.抛物线的标准方程及性质(高频考点)抛物线的标准方程及性质是高考的热点,考查时多以选择题、填空题形式出现,个别高考题有一定难度.高考对抛物线的考查主要有以下三个命题角度: (1)求抛物线方程;(2)由已知求参数p ; (3)抛物线方程的实际应用.(1)(2016·高考全国卷乙)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E 两点.已知|AB |=42,|DE |=25,则C 的焦点到准线的距离为( )A .2B .4C .6D .8(2)若抛物线的焦点为直线3x -4y -12=0与坐标轴的交点,则抛物线的标准方程为________.【解析】 (1)由题意,不妨设抛物线方程为y 2=2px (p >0),由|AB |=42,|DE |=25,可取A ⎝ ⎛⎭⎪⎫4p ,22,D ⎝ ⎛⎭⎪⎫-p 2,5,设O 为坐标原点,由|OA |=|OD |,得16p 2+8=p 24+5,得p =4,所以选B.(2)对于直线方程3x -4y -12=0,令x =0,得y =-3,令y =0,得x =4,所以抛物线的焦点坐标可能为(0,-3)或(4,0).当焦点坐标为(0,-3)时,设方程为x 2=-2py (p >0),则p2=3,所以p =6,此时抛物线的标准方程为x 2=-12y ;当焦点坐标为(4,0)时,设方程为y 2=2px (p >0),则p2=4,所以p =8,此时抛物线的标准方程为y 2=16x . 所以所求抛物线的标准方程为x 2=-12y 或y 2=16x . 【答案】 (1)B (2)x 2=-12y 或y 2=16x(1)求抛物线的标准方程的方法①求抛物线的标准方程常用待定系数法,因为未知数只有p ,所以只需一个条件确定p 值即可.②因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量. (2)确定及应用抛物线性质的技巧①利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.②要结合图形分析,灵活运用平面几何的性质以图助解.角度一 求抛物线方程1.以x 轴为对称轴,原点为顶点的抛物线上的一点P (1,m )到焦点的距离为3,则抛物线的方程是( )A .y =4x 2B .y =8x 2C .y 2=4xD .y 2=8xD 设抛物线的方程为y 2=2px (p >0),则由抛物线的定义知1+p2=3,即p =4,所以抛物线方程为y 2=8x .角度二 由已知求参数p2.(2017·襄阳调研测试)抛物线y 2=2px 的焦点为F ,M 为抛物线上一点,若△OFM 的外接圆与抛物线的准线相切(O 为坐标原点),且外接圆的面积为9π,则p =( )A .2B .4C .6D .8B 因为△OFM 的外接圆与抛物线的准线相切,所以△OFM 的外接圆的圆心到准线的距离等于圆的半径,因为圆面积为9π,所以圆的半径为3,又因为圆心在OF 的垂直平分线上,|OF |=p2,所以p 2+p4=3,所以p =4.角度三 抛物线方程的实际应用3.如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽为________米.建立坐标系如图所示.则可设抛物线方程为x 2=-2py (p >0).因为点(2,-2)在抛物线上,所以p =1,即抛物线方程为x 2=-2y . 当y =-3时,x =± 6.所以水位下降1米后,水面宽为26米. 2 6直线与抛物线的位置关系(2016·高考全国卷乙)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :y 2=2px (p >0)于点P ,M 关于点P 的对称点为N ,连接ON 并延长交C 于点H .(1)求|OH ||ON |;(2)除H 以外,直线MH 与C 是否有其他公共点?说明理由.【解】 (1)由已知得M (0,t ),P ⎝ ⎛⎭⎪⎫t 22p ,t . 又N 为M 关于点P 的对称点,故N ⎝ ⎛⎭⎪⎫t 2p ,t , ON 的方程为y =ptx ,代入y 2=2px ,整理得px 2-2t 2x =0, 解得x 1=0,x 2=2t2p.因此H ⎝ ⎛⎭⎪⎫2t 2p ,2t . 所以N 为OH 的中点,即|OH ||ON |=2.(2)直线MH 与C 除H 以外没有其他公共点.理由如下: 直线MH 的方程为y -t =p2t x ,即x =2tp(y -t ).代入y 2=2px 得y 2-4ty +4t 2=0, 解得y 1=y 2=2t ,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其他公共点.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=|x 1|+|x 2|+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.涉及弦的中点、斜率时,一般用“点差法”求解.已知过抛物线y 2=2px (p >0)的焦点,斜率为22的直线交抛物线于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点,且|AB |=9.(1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC →=OA →+λOB →,求λ的值.(1)由题意得直线AB 的方程为y =22·⎝ ⎛⎭⎪⎫x -p 2,与y 2=2px 联立,消去y 有4x 2-5px+p 2=0,所以x 1+x 2=5p4.由抛物线定义得|AB |=x 1+x 2+p =5p4+p =9,所以p =4,从而该抛物线的方程为y 2=8x . (2)由(1)得4x 2-5px +p 2=0, 即x 2-5x +4=0, 则x 1=1,x 2=4,于是y 1=-22,y 2=42,从而A (1,-22),B (4,42),设C (x 3,y 3), 则OC →=(x 3,y 3)=(1,-22)+λ(4,42) =(4λ+1,42λ-22). 又y 23=8x 3,所以2=8(4λ+1), 整理得(2λ-1)2=4λ+1, 解得λ=0或λ=2., )——忽视焦点位置而致误已知抛物线的顶点在原点,对称轴为y 轴,它与圆x 2+y 2=9相交,公共弦MN的长为25,求该抛物线的方程,并写出它的焦点坐标与准线方程.【解】 由题意,设抛物线方程为x 2=2ay (a ≠0). 设公共弦MN 交y 轴于A , 则|MA |=|AN |,且|AN |= 5. 因为|ON |=3,所以|OA |=32-(5)2=2,所以N (5,±2). 因为N 点在抛物线上,所以5=2a ·(±2),即2a =±52,故抛物线的方程为x 2=52y 或x 2=-52y .抛物线x 2=52y 的焦点坐标为⎝ ⎛⎭⎪⎫0,58,准线方程为y =-58.抛物线x 2=-52y 的焦点坐标为⎝⎛⎭⎪⎫0,-58,准线方程为y =58.(1)解决本题易忽视焦点位置可在y 轴的正半轴也可在负半轴上两种情况,误认为a >0,从而导致漏解.(2)对称轴确定,而开口方向不确定的抛物线方程有如下特点: ①当焦点在x 轴上时,可将抛物线方程设为y 2=ax (a ≠0); ②当焦点在y 轴上时,可将抛物线方程设为x 2=ay (a ≠0).若抛物线y 2=2px 的焦点与椭圆x 29+y 25=1的焦点重合,则抛物线的准线方程为________.由椭圆x 29+y 25=1,得c 2=9-5=4,即c =2,故椭圆的焦点坐标为(±2,0). 即抛物线的焦点坐标为(±2,0).所以当p >0时,抛物线的准线方程为x =-2; 当p <0时,抛物线的准线方程为x =2. x =2或x =-2, )1.若抛物线y =4x 2上的一点M 到焦点的距离为1,则点M 的纵坐标是( ) A .1716 B .1516 C .78D .0B M 到准线的距离等于M 到焦点的距离, 又准线方程为y =-116,设M (x ,y ),则y +116=1,所以y =1516.2.若抛物线y 2=2x 上一点P 到准线的距离等于它到顶点的距离,则点P 的坐标为( ) A .⎝ ⎛⎭⎪⎫14,±22B .⎝ ⎛⎭⎪⎫14,±1C .⎝ ⎛⎭⎪⎫12,±22D .⎝ ⎛⎭⎪⎫12,±1 A 设抛物线的顶点为O ,焦点为F ,P (x P ,y P ),由抛物线的定义知,点P 到准线的距离即为点P 到焦点的距离,所以|PO |=|PF |,过点P 作PM ⊥OF 于点M (图略),则M 为OF 的中点,所以x P =14,代入y 2=2x ,得y P =±22,所以P ⎝ ⎛⎭⎪⎫14,±22.3.(2016·高考全国卷甲)设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )A .12B .1C .32D .2D 易知抛物线的焦点为F (1,0),设P (x P ,y P ),由PF ⊥x 轴可得x P =1,代入抛物线方程得y P =2(-2舍去),把P (1,2)代入曲线y =k x(k >0)得k =2.4.设F 为抛物线y 2=2x 的焦点,A 、B 、C 为抛物线上三点,若F 为△ABC 的重心,则|FA →|+|FB →|+|FC →|的值为( )A .1B .2C .3D .4C 依题意,设点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),又焦点F ⎝ ⎛⎭⎪⎫12,0,x 1+x 2+x 3=3×12=32, 则|FA →|+|FB →|+|FC →|=⎝ ⎛⎭⎪⎫x 1+12+⎝ ⎛⎭⎪⎫x 2+12+⎝ ⎛⎭⎪⎫x 3+12=(x 1+x 2+x 3)+32=32+32=3. 5.直线l 过抛物线y 2=-2px (p >0)的焦点,且与抛物线交于A 、B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线的方程是( )A .y 2=12x B .y 2=-8x C .y 2=6xD .y 2=-4xB 设A (x 1,y 1)、B (x 2,y 2),由抛物线定义可得|x 1|+|x 2|+p =8,又AB 的中点到y 轴的距离为2,即|x 1|+|x 2|=4,所以p =4,所以y 2=-8x .故选B.6.已知抛物线y 2=4x ,圆F :(x -1)2+y 2=1,过点F 作直线l ,自上而下顺次与上述两曲线交于点A ,B ,C ,D (如图所示),则下列关于|AB |·|CD |的值的说法中,正确的是( )A .等于1B .等于4C .最小值是1D .最大值是4A 设直线l :x =ty +1,代入抛物线方程,得y 2-4ty -4=0.设A (x 1,y 1),D (x 2,y 2),根据抛物线的定义知,|AF |=x 1+1,|DF |=x 2+1,故|AB |=x 1,|CD |=x 2,所以|AB |·|CD |=x 1x 2=y 214·y 224=(y 1y 2)216.而y 1y 2=-4,故|AB |·|CD |=1.7.(2017·资阳模拟)顶点在原点,对称轴是y 轴,并且经过点P (-4,-2)的抛物线方程是________.设抛物线方程为x 2=my ,将点P (-4,-2)代入x 2=my ,得m =-8. 所以抛物线方程是x 2=-8y . x 2=-8y8.(2017·云南省第一次统一检测)已知抛物线C 的方程为y 2=2px (p >0),○· M 的方程为x 2+y 2+8x +12=0,如果抛物线C 的准线与○·M 相切,那么p 的值为________.将○·M 的方程化为标准方程:(x +4)2+y 2=4,圆心坐标为(-4,0),半径r =2,又因为抛物线的准线方程为x =-p2,所以⎪⎪⎪⎪⎪⎪4-p 2=2,p =12或4.12或49.经过抛物线C 的焦点F 作直线l 与抛物线C 交于A ,B 两点,如果A ,B 在抛物线C 的准线上的射影分别为A 1,B 1,那么∠A 1FB 1=________.由抛物线定义可知|BF |=|BB 1|,|AF |=|AA 1|,故∠BFB 1=∠BB 1F ,∠AFA 1=∠AA 1F . 又∠OFB 1=∠BB 1F ,∠OFA 1=∠AA 1F , 故∠BFB 1=∠OFB 1,∠AFA 1=∠OFA 1, 所以∠OFA 1+∠OFB 1=12×π=π2,即∠A 1FB 1=π2.π210.(2017·豫东、豫北十校联考)已知抛物线的顶点在原点,焦点在x 轴的正半轴上,若抛物线的准线与双曲线5x 2-y 2=20的两条渐近线围成的三角形的面积为45,则抛物线方程为________.由双曲线方程5x 2-y 2=20知其渐近线方程为y =±5x ,由题意可设抛物线方程为y2=2px (p >0),故其准线方程为x =-p2,设准线与双曲线的两条渐近线的交点为A ,B ,则不妨令A ⎝ ⎛⎭⎪⎫-p 2,52p ,B ⎝ ⎛⎭⎪⎫-p 2,-52p ,故S △ABO =12×5p ×p 2=54p 2=45,解得p 2=16,又因为p >0,所以p =4,故抛物线方程为y 2=8x .y 2=8x11.已知抛物线y 2=2px (p >0)的焦点为F ,A 是抛物线上横坐标为4,且位于x 轴上方的点,A 到抛物线准线的距离等于5,过A 作AB 垂直于y 轴,垂足为B ,OB 的中点为M .(1)求抛物线的方程;(2)若过M 作MN ⊥FA ,垂足为N ,求点N 的坐标. (1)抛物线y 2=2px 的准线为x =-p2,于是4+p2=5,所以p =2.所以抛物线方程为y 2=4x .(2)因为点A 的坐标是(4,4), 由题意得B (0,4),M (0,2). 又因为F (1,0),所以k FA =43,因为MN ⊥FA ,所以k MN =-34.所以FA 的方程为y =43(x -1),①MN 的方程为y -2=-34x ,②联立①②,解得x =85,y =45,所以N 的坐标为⎝ ⎛⎭⎪⎫85,45.12.(2017·长春一模)过抛物线y 2=2px (p >0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A ,B 两点,则|AF ||BF |的值等于( )A .13B .23 C.34 D.43A 记抛物线y 2=2px 的准线为l ′,如图,作AA 1⊥l ′,BB 1⊥l ′,AC ⊥BB 1,垂足分别是A 1,B 1,C ,则有cos ∠ABB 1=|BC ||AB |=|BB 1|-|AA 1||AF |+|BF |=|BF |-|AF ||AF |+|BF |,即cos 60°=|BF |-|AF ||AF |+|BF |=12,由此得|AF ||BF |=13.13.已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A 、B 两点. (1)若线段AB 的中点在直线y =2上,求直线l 的方程; (2)若线段|AB |=20,求直线l 的方程.(1)由已知得抛物线的焦点为F (1,0).因为线段AB 的中点在直线y =2上,所以直线l 的斜率存在,设直线l 的斜率为k ,A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),则⎩⎪⎨⎪⎧x 0=x 1+x 22,y 0=y 1+y 22.由⎩⎪⎨⎪⎧y 21=4x 1,y 22=4x2得(y 1+y 2)(y 1-y 2)=4(x 1-x 2),所以2y 0k =4. 又y 0=2,所以k =1,故直线l 的方程是y =x -1. (2)设直线l 的方程为x =my +1,与抛物线方程联立得⎩⎪⎨⎪⎧x =my +1,y 2=4x ,消元得y 2-4my -4=0,所以y 1+y 2=4m ,y 1y 2=-4,Δ=16(m 2+1)>0. |AB |=m 2+1|y 1-y 2|=m 2+1·(y 1+y 2)2-4y 1y 2 =m 2+1·(4m )2-4×(-4) =4(m 2+1).所以4(m 2+1)=20,解得m =±2, 所以直线l 的方程是x =±2y +1, 即x ±2y -1=0.14.已知圆C 过定点F ⎝ ⎛⎭⎪⎫-14,0,且与直线x =14相切,圆心C 的轨迹为E ,曲线E 与直线l :y =k (x +1)(k ∈R )相交于A ,B 两点.(1)求曲线E 的方程;(2)当△OAB 的面积等于10时,求k 的值.(1)由题意,点C 到定点F ⎝ ⎛⎭⎪⎫-14,0和直线x =14的距离相等, 故点C 的轨迹E 的方程为y 2=-x .(2)由方程组⎩⎪⎨⎪⎧y 2=-x ,y =k (x +1),消去x 后,整理得ky 2+y -k =0. 设A (x 1,y 1),B (x 2,y 2),由根与系数的关系有y 1+y 2=-1k,y 1y 2=-1.设直线l 与x 轴交于点N ,则N (-1,0). 所以S △OAB =S △OAN +S △OBN =12|ON ||y 1|+12|ON ||y 2|, =12|ON ||y 1-y 2| =12×1×(y 1+y 2)2-4y 1y 2 =12⎝ ⎛⎭⎪⎫-1k 2+4=10, 解得k =±16.。


第七讲 抛物线知识梳理·双基自测 知识梳理知识点一 抛物线的定义 抛物线需要满足以下三个条件: (1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离__相等__; (3)定点F 与定直线l 的关系为__点F ∉l __. 知识点二 抛物线的标准方程与几何性质 标准 方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F (p2,0)F (-p2,0)F (0,p2)F (0,-p2)离心率 e =__1__准线 方程 x =-p2x =p 2y =-p2y =p 2范围 x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0,x ∈R开口方向 向右 向左 向上 向下 焦半径 (其中P (x 0,y 0))|PF |= x 0+p 2|PF |= -x 0+p2|PF |= y 0+p 2|PF |= -y 0+p2重要结论抛物线焦点弦的处理规律直线AB 过抛物线y 2=2px (p >0)的焦点F ,交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如图.(1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB |=x 1+x 2+p ,x 1+x 2≥2x 1x 2=p ,即当x 1=x 2时,弦长最短为2p . (3)1|AF |+1|BF |=2p. (4)弦长AB =2psin 2α(α为AB 的倾斜角).(5)以AB 为直径的圆与准线相切.(6)焦点F 对A ,B 在准线上射影的张角为90°. (7)A 、O 、D 三点共线;B 、O 、C 三点共线.双基自测题组一 走出误区1.(多选题)下列结论正确的是( CD )A .平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线B .方程y =ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线,且其焦点坐标是(a4,0),准线方程是x =-a4C .AB 为抛物线y 2=2px (p >0)的过焦点F (p 2,0)的弦,若A (x 1,y 1),B (x 2,y 2),则x 1x 2=p 24,y 1y 2=-p 2,弦长|AB |=x 1+x 2+pD .过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫做抛物线的通径,那么抛物线x 2=-2ay (a >0)的通径长为2a题组二 走进教材2.(必修2P 69例4)(2019·甘肃张掖诊断)过抛物线y 2=4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1+x 2=6,则|PQ |等于( B )A .9B .8C .7D .6[解析] 抛物线y 2=4x 的焦点为F (1,0),准线方程为x =-1.根据题意可得,|PQ |=|PF |+|QF |=x 1+1+x 2+1=x 1+x 2+2=8.3.抛物线y =4x 2上的一点M 到焦点F 的距离为1,则点M 的纵坐标是( B )1616C .78D .0[解析] y =4x 2⇒x 2=14y ⇒抛物线准线方程为y =-116.设M 点坐标为(x 0,y 0),则由抛物线定义可知y 0+116=1,∴y 0=1516.故选B .题组三 考题再现4.(2019·课标全国Ⅱ)若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =( D )A .2B .3C .4D .8[解析] ∵抛物线y 2=2px (p >0)的焦点坐标为(p2,0),∴椭圆x 23p +y 2p =1的一个焦点为(p2,0),∴3p -p =p 24,∴p =8.故选D .5.(2019·广东广州天河综合测试)已知抛物线C :y 2=8x 的焦点为F ,直线y =3(x -2)与C 交于A ,B (A 在x 轴上方)两点,若AF →=mFB →,则实数m 的值为( B )A . 3B .3C .2D .32[解析] 由⎩⎨⎧y 2=8x ,y =3(x -2)得3x 2-20x +12=0,∴x A =6,x B =23,又AF →=mFB →且F (2,0),∴2-6=m (23-2),∴m =3,故选B .KAO DIAN TU PO HU DONG TAN JIU考点突破·互动探究考点一 抛物线的定义及应用——多维探究角度1 到焦点与到定点距离之和最小问题例1 (2019·江西赣州模拟)若点A 的坐标为(3,2),F 是抛物线y 2=2x 的焦点,点M在抛物线上移动时,使|MF |+|MA |取得最小值的M 的坐标为( D )2C.(1,2) D.(2,2)[解析]如图,过M点作准线的垂线,垂足是N,则|MF|+|MA|=|MN|+|MA|,所以当A,M,N三点共线时,|MF|+|MA|取得最小值,此时M(2,2).角度2到准线与到定点距离之和最小问题例2已知圆C:x2+y2+6x+8y+21=0,抛物线y2=8x的准线为l,设抛物线上任意一点P到直线l的距离为d,则d+|PC|的最小值为(A)A.41 B.7C.6 D.9[解析]由题意得圆的方程为(x+3)2+(y+4)2=4,圆心C的坐标为(-3,-4).由抛物线定义知,当d+|PC|最小时为圆心与抛物线焦点间的距离,即d+|PC|=(-3-2)2+(-4)2=41.角度3到两定直线的距离之和最小问题例3(2019·湖南省三湘名校联考)已知直线l1:x=-1,l2:x-y+1=0,点P为抛物线y2=4x上的任一点,则P到直线l1,l2的距离之和的最小值为(B) A.2 B. 2C.1 D.2 2[解析]抛物线y2=4x,其焦点坐标F(1,0),准线为x=-1也就是直线l1,故P到直线l1的距离就是P到F的距离,如图所示,P到l1,l2的距离之和的最小值等于焦点F到直线l2的距离.设P到直线l2的距离为d,则d+|PF|≥|1-0+1|2=2,当且仅当P,E,F三点共线时等号成立,故选B.名师点拨 ☞求解与抛物线有关的最值问题的两大转换方法(1)将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”,使问题得解.(2)将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.〔变式训练1〕(1)(角度1)(2020·吉林省吉林市调研)已知抛物线y 2=4x 的焦点F ,点A (4,3),P 为抛物线上一点,且P 不在直线AF 上,则△P AF 周长取最小值时,线段PF 的长为( B )A .1B .134C .5D .214(2)(角度3)(2019·上海虹口区二模)已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和l 2的距离之和的最小值为( D )A .3716B .115C .2D .74[解析] (1)求△P AF 周长的最小值,即求|P A |+|PF |的最小值,设点P 在准线上的射影为D ,根据抛物线的定义,可知|PF |=|PD |,因此,|P A |+|PF |的最小值,即|P A |+|PD |的最小值.根据平面几何知识,可得当D ,P ,A 三点共线时|P A |+|PD |最小,此时P (94,3),且|PF |=94+1=134,故选B .(2)直线l 2:x =-1是抛物线y 2=4x 的准线,抛物线y 2=4x 的焦点为F (1,0),则点P 到直线l 2:x =-1的距离等于PF ,过点F 作直线l 1:4x -3y +6=0的垂线,和抛物线的交点就是点P ,所以点P 到直线l 1:4x -3y +6=0的距离和到直线l 2:x =-1的距离之和的最小值就是点F (1,0)到直线l 1:4x -3y +6=0的距离,所以最小值为|4-0+6|32+42=2,故选C .考点二 抛物线的方程及几何性质——自主练透例4 (1)(2019·安徽蚌埠一中期中)已知抛物线的顶点在原点,焦点在y 轴上,其上的点P (m ,-3)到焦点的距离为5,则抛物线方程为( D )A .x 2=8yB .x 2=4yC .x 2=-4yD .x 2=-8y(2)(2019·江西省九校联考)抛物线y =ax 2的焦点是直线x +y -1=0与坐标轴交点,则抛物线的准线方程为( D )A .x =-14B .x =-1C .y =-14D .y =-1(3)(2019·山东菏泽期末)已知等边△AOB (O 为坐标原点)的三个顶点在抛物线Γ:y 2=2px (p >0)上,且△AOB 的面积为93,则p =( C )A . 3B .3C .32D .2 3(4)已知抛物线y 2=2px (p >0)的焦点F 与双曲线x 212-y 24=1的一个焦点重合,直线y =x -4与抛物线交于A ,B 两点,则|AB |等于( B )A .28B .32C .20D .40(5)如图,过抛物线y 2=2px (p >0)的焦点F 的直线依次交抛物线及准线于点A ,B ,C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程为( B )A .y 2=32xB .y 2=3xC .y 2=92xD .y 2=9x[解析] (1)由题意可知抛物线的焦点在y 轴负半轴上,故设其方程为x 2=-2py (p >0),所以3+p2=5,即p =4,所以所求抛物线方程为x 2=-8y ,故选D .(2)抛物线焦点在y 轴上,即直线x +y -1=0与y 轴的交点F (0,1),∴p2=1,∴抛物线方程为x 2=4y ,准线方程为y =-1,故选D .(3)根据抛物线和等边三角形的对称性,可知A ,B 两点关于x 轴对称,不妨设直线OB :y =33x ,与y 2=2px 联立,解得B (6p ,23p ),故|AB |=43p .因为△AOB 的面积为93,所以34×(43p )2=93,解得p =32.故选C . (4)双曲线x 212-y 24=1的焦点坐标为(±4,0),故抛物线的焦点F 的坐标为(4,0).因此p =8,故抛物线方程为y 2=16x ,易知直线y =x -4过抛物线的焦点.设A 、B 两点坐标分别为(x 1,y 1),(x 2,y 2).由⎩⎪⎨⎪⎧y 2=16x ,y =x -4,可得x 2-24x +16=0,故x 1+x 2=24. 故|AB |=x 1+x 2+p =24+8=32.(5)如图,分别过点A ,B 作准线的垂线,分别交准线于点E ,D ,设|BF |=a ,则由已知得|BC |=2a ,由定义得|BD |=a ,故∠BCD =30°. 在直角三角形ACE 中,∵|AE |=|AF |=3,|AC |=3+3a ,2|AE |=|AC |, ∴3+3a =6,从而得a =1.∵BD ∥FG ,∴|BD ||FG |=|BC ||FC |,即1p =23,求得p =32,因此抛物线的方程为y 2=3x .名师点拨 ☞1.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p ,所以只需一个条件确定p 值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量. 2.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(抛物线焦点在其标准方程中一次项所对应的坐标轴上)(2)要结合图形分析,灵活运用平面几何的性质以图助解. 〔变式训练2〕(1)(2020·福建漳州质检)已知抛物线y 2=2px (p >0)上的点M 到其焦点F 的距离比点M 到y 轴的距离大12,则抛物线的标准方程为( B )A .y 2=xB .y 2=2xC .y 2=4xD .y 2=8x(2)(2019·吉林市五地六校适应性考试)已知抛物线C :x 2=2py (p >0)的准线l 与圆M :(x -1)2+(y -2)2=16相切,则p =( D )A .6B .8C .3D .4[解析] (1)由抛物线的定义可知p 2=12,∴p =1,∴抛物线方程为y 2=2x ,故选B .(2)因为抛物线C :x 2=2py 的准线为y =-p2,又准线l 与圆M :(x -1)2+(y -2)2=16相切,所以p2+2=4,则p =4.故选D .考点三 直线与抛物线的综合问题——师生共研例5 (1)(2019·黑龙江省大庆市模拟)已知F 是抛物线C :y 2=2px (p >0)的焦点,过点R (2,1)的直线l 与抛物线C 交于A ,B 两点,R 为线段AB 的中点,若|F A |+|FB |=5,则直线l 的斜率为( B )A .3B .1C .2D .12(2)(2019·陕西省汉中市模拟)已知抛物线y 2=8x 的焦点为F ,过点F 的直线交抛物线于A 、B 两点,交准线于点C ,若|BC |=2|BF |,则|AB |等于( C )A .12B .14C .16D .28(3)(2019·金华模拟)已知抛物线C :y 2=2px (p >0)在第一象限内的点P (2,t )到焦点F 的距离为52. ①若N (-12,0),过点N ,P 的直线l 1与抛物线相交于另一点Q ,求|QF ||PF |的值;②若直线l 2与抛物线C 相交于A ,B 两点,与圆M :(x -a )2+y 2=1相交于D ,E 两点,O 为坐标原点,OA ⊥OB ,试问:是否存在实数a ,使得|DE |为定值?若存在,求出a 的值;若不存在,请说明由.[解析] (1)由于R (2,1)为AB 中点,根据抛物线的定义|F A |+|FB |=x A +x B +p =2×2+p =5,解得p =1,抛物线方程为y 2=2x .设A (x 1,y 1),B (x 2,y 2),则y 21=2x 1,y 22=2x 2,两式相减并化简得y 2-y 1x 2-x 1=2y 1+y 2=22×1=1,即直线l 的斜率为1,故选B .(2)抛物线y 2=8x ,p =4,分别过A ,B 作准线的垂线,垂足为M ,N ,如下图:则|BN |=|BF |,∵|BC |=2|BF |,∴|BC |=2|BN |, ∴∠NCB =π4,∴k AB =1,∴直线AB 的方程为y =x -2,由⎩⎪⎨⎪⎧y =x -2y 2=8x得x 2-12x +4=0, ∴x A +x B =12,∴|AB |=x A +x B +p =16.故选C . (3)①∵点P (2,t )到焦点F 的距离为52,∴2+p 2=52,解得p =1,故抛物线C 的方程为y 2=2x ,P (2,2), ∴l 1的方程为y =45x +25,联立得⎩⎪⎨⎪⎧y =45x +25,y 2=2x ,可解得x Q =18,又|QF |=x Q +12=58,|PF |=52,∴|QF ||PF |=5852=14. ②设直线l 2的方程为x =ny +m (m ≠0),代入抛物线方程可得y 2-2ny -2m =0, 设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=2n ,y 1y 2=-2m ,① 由OA ⊥OB 得,(ny 1+m )(ny 2+m )+y 1y 2=0, 整理得(n 2+1)y 1y 2+nm (y 1+y 2)+m 2=0,②将①代入②解得m =2或m =0(舍去),满足Δ=4n 2+8m >0, ∴直线l 2:x =ny +2,∵圆心M (a,0)到直线l 2的距离d =|a -2|1+n 2, ∴|DE |=212-(a -2)21+n 2, 显然当a =2时,|DE |=2,∴存在实数a =2,使得|DE |为定值. 名师点拨 ☞(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要将两方程联立,消元,用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点(设焦点在x 轴的正半轴上),可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解. 〔变式训练3〕(1)(2020·甘肃诊断)直线l 过抛物线y 2=2px (p >0)的焦点,且交抛物线于A ,B 两点,交其准线于C 点,已知|AF |=4,CB →=3BF →,则p =( C )A .2B .43C .83D .4(2)(2019·合肥模拟)已知抛物线C 1:y 2=4x 和C 2:x 2=2py (p >0)的焦点分别为F 1,F 2,点P (-1,-1),且F 1F 2⊥OP (O 为坐标原点).①求抛物线C 2的方程;②过点O 的直线交C 1的下半部分于点M ,交C 2的左半部分于点N ,求△PMN 面积的最小值.[解析] (1)过A ,B 分别作准线的垂线交准线于E ,D 两点, 设|BF |=a ,根据抛物线的性质可知,|BD |=a , |AE |=4,根据平行线段比例可知|BD ||AE |=|CB ||AC |,即a 4=3a 3a +a +4,解得a =2, 又|BD ||GF |=|BC ||CF |,即a p =3a4a, 解得p =43a =83,故选C .(2)①F 1(1,0),F 2(0,p 2),∴F 1F 2→=(-1,p 2).F 1F 2→·OP →=(-1,p 2)·(-1,-1)=1-p 2=0, ∴p =2,∴C 2的方程为x 2=4y .②设过点O 的直线为y =kx (k <0),联立⎩⎪⎨⎪⎧ y =kx ,y 2=4x , 得M (4k 2,4k ),联立⎩⎪⎨⎪⎧y =kx ,x 2=4y 得N (4k,4k 2)(k <0), 从而|MN |=1+k 2|4k 2-4k |=1+k 2(4k2-4k ), 点P 到直线MN 的距离d =|k -1|1+k 2, 进而S △PMN =12·|k -1|1+k 2·1+k 2(4k 2-4k ) =2(1-k )(1-k 3)k 2=2(1-k )2(1+k +k 2)k 2=2(k +1k -2)(k +1k+1). 令t =k +1k(t ≤-2),有S △PMN =2(t -2)(t +1), 当t =-2时,S △PMN 有最小值8,此时k =-1.即当过原点的直线为y =-x 时,△PMN 的面积取得最小值8.MING SHI JIANG TAN SU YANG TI SHENG名师讲坛·素养提升巧解抛物线的切线问题例6 抛物线C 1:x 2=2py (p >0)的焦点与双曲线C 2:x 23-y 2=1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线,则p =( D )A .316B .38C .233D .433 [解析] 抛物线C 1:x 2=2py (p >0)的焦点坐标为(0,p 2),双曲线x 23-y 2=1的右焦点坐标为(2,0),两点连线的方程为y =-p 4(x -2),联立⎩⎨⎧ y =-p 4(x -2),y =12p x 2,得2x 2+p 2x -2p 2=0.设点M 的横坐标为m ,易知在M 点处切线的斜率存在,则在点M 处切线的斜率为y ′|x =m =(12p x 2)′|x =m =m p. 又双曲线x 23-y 2=1的渐近线方程为x 3±y =0,其与切线平行,所以m p =33,即m =33p ,代入2x 2+p 2x -2p 2=0,得p =433或p =0(舍去). 名师点拨 ☞利用导数工具解决抛物线的切线问题,使问题变得巧妙而简单,若用判别式解决抛物线的切线问题,计算量大,易出错.〔变式训练4〕已知抛物线x 2=8y ,过点P (b,4)作该抛物线的切线P A ,PB ,切点为A ,B ,若直线AB 恒过定点,则该定点为( C )A .(4,0)B .(3,2)C .(0,-4)D .(4,1)[解析] 设A ,B 的坐标为(x 1,y 1),(x 2,y 2), ∵y =x 28,y ′=x 4, ∴P A ,PB 的方程y -y 1=x 14(x -x 1),y -y 2=x 24(x -x 2), 由y 1=x 218,y 2=x 228,可得y =x 14x -y 1,y =x 24x -y 2, ∵切线P A ,PB 都过点P (b,4), ∴4=x 14×b -y 1,4=x 24×b -y 2, 故可知过A ,B 两点的直线方程为4=b 4x -y , 当x =0时,y =-4,∴直线AB 恒过定点(0,-4).故选C .。
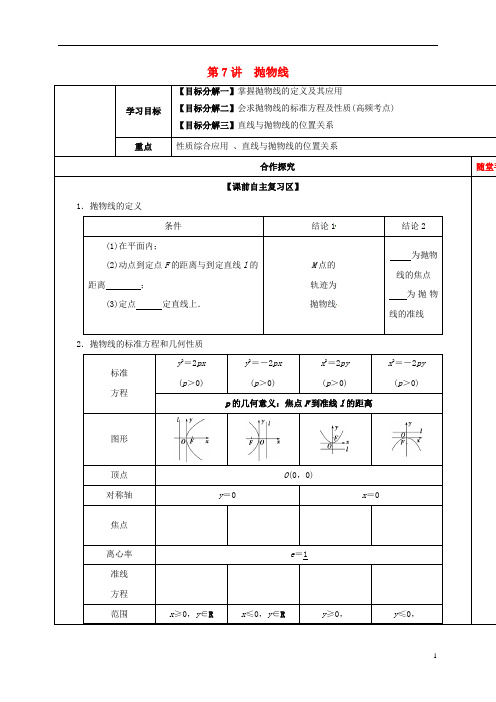
第7讲抛物线学习目标【目标分解一】掌握抛物线的定义及其应用【目标分解二】会求抛物线的标准方程及性质(高频考点)【目标分解三】直线与抛物线的位置关系重点性质综合应用、直线与抛物线的位置关系合作探究随堂手条件结论1结论2(1)在平面内;(2)动点到定点F的距离与到定直线l的距离;(3)定点定直线上.M点的轨迹为抛物线为抛物线的焦点为抛物线的准线标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)p的几何意义:焦点F到准线l的距离x∈R x∈R 开口方向向右向左向上向下焦半径(其中P(x0,y0))|PF|=|PF|=|PF|=|PF|=点且与定直线垂直的直线.+2或+2.→1.(1)已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若FP=4|OF|,△MFO的面积为43,则抛物线的方程为( )=2双曲线a-yA.9 B.4C.3D2.线相切(O为坐标原点),且外接圆的面积为9π,则p=( )【例3】(2016·高考全国卷乙)在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2【规律总结3】(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用的焦点与椭圆9+5=25,求该抛物线的(2017·豫南九校联考)已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A 抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是________.A,B两点,C1的焦点为F,若△FAB的面积等于1,则C1的方程是( )限分别交于A ,B 两点,则|AF ||BF |的值等于( )A .13B .23 C.34 D.43★★9.【2017课标II ,文12】过抛物线2:4C y x =的焦点F ,且斜率为3的直线交C 于点M (M 在x轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为A.5B.22 C . 23 D. 33★10.【2017山东,文15】在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>, 的右支与焦点为F的抛物线22(0)x py p =>交于A ,B 两点,若|AF |+|BF |=4|OF |,则该双曲线的渐近线方程为 .11.(经典考题)如图所示是抛物线形拱桥,当水面在l 时,拱顶离水面2 m ,水面宽4 m . 水位下降1 m 后,水面宽________m.12.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.。

第7讲第八章平面解析几何抛物线(3)定点—不在 定直线卜,1.抛物线的定义满足以下三个条件的点的轨迹是抛物线: (1)在平面内;(2)动点到定点F 的距离与到定直线I 的距离 相等教材回顾▼夯实基础课本温故追根求源知-识“梳理/2・抛物线的标准方程和几何性质要点整食,1.辨明两个易误点(1)抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与定直线垂直的直线.(2)对于抛物线标准方程中参数p,易忽视只有p>0才能证明其几何意义是焦点F到准线Z的距离,否则无几何意义.y 2.与焦点弦有关的常用结论(以下图为依据)设Ji), B(X2, J2).2 _p2(1)J1J2=—P,XiX2—"J.i i 2⑶L4FI + LBFi为定值戸(5)以4F或BF为直径的圆与j轴相切.(4)以AB为直径的圆与准线相切.y(5)以4F 或BF 为直径的圆与j 轴相切.点(―1, 1),则该抛物线焦点坐标为( A. (-1, 0) C. (0, -1)B. (1, 0) D. (0, 1)解析:抛物线y 2=2px(p>0)ff)准线方程为兀= 由题设知—£=—1,艮片=1,所以焦点坐标为(1, 0). 乙Z双基自测,(2015•高考陕西卷)己知抛物线y 2=2px(p>0)^J 准线经过2.已知抛物线C与双曲线兀'一/=1有相同的焦点,且顶点在原点,则抛物线C的方程是(D )A.y2= ±2\[2xB. y2=±2xC. y2=+4x D・y2=±4\/2x 解析:因为双曲线的焦点为(一⑴,0), (\/2, 0).设抛物线方程为y=±2px(p>Q)9贝吃=竝所以卩=2竝所以抛物线方程为犷=±4伍.3.(选修1-1P59练习13⑴改编)抛物线x2=2py(p>0)上的点P(m, 2)到焦点F的距离为3,则该抛物线的方程为_£二^ 解析:根据抛物线定义可知2+|=3,所以p=2,所以抛物线的方程为x=4y.4・动圆过点(1, 0),且与直线兀=一1相切,则动圆的圆心的轨迹方程为一.解析:设动圆的圆心坐标为g j),则圆心到点(1, 0)的距离与到直线兀=一1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y2= 4x.典例剖析▼考点突破*考点一 抛物线的定义及其应用的焦点为F, A(x 0,为)是C 上一点,L4FI=|x 0,则x 0=( c )A. 4B. 2C. 1 (2)已知抛物线y 2=4x 的焦点是F,点P 是抛物线上的动点,又有点B(3, 2),则IPBI+IPF I 的最小值为“名师导悟以例说法(1)(2014-高考课标全国卷I )已知抛物线G j 2=x[解析]⑴如图,F Q, 0),过A 作丄准线 所以 L4FI = IAA r|,所以 *O =X O +$=K +£所以兀0=1.过点B作B0垂直准线于0,交抛物线于点Pi,则IPi0= IPiFI,则有IPBI+ \PF\^IPiBI + \PiQ\= \BQ\= 4.即IPBI+ \PF\的最小值为4.抛物线定义的应用(1)利用抛物线的定义解决此类问题,应灵活地进行抛物线上 的点到焦点的距离与到准线距离的等价转化.即“看到准线 想到焦点,看到焦点想到准线” •(2)注意灵活运用抛物线上一点P(x,丿)到焦点F 的距离IPFI ■■■1.(1)(2016-云南省统一检测)设经过抛物线C的焦点F的直线Z与抛物线C交于A、B两点,那么抛物线C 的准线与以AB为直径的圆的位置关系为(B )A.相离B.相切C.D.相交且经过圆心(2)(2016-长春调研)已知直线人:4x— 3y+ 6= 0和直线心x=一1,则抛物线J2=4r±一动点P到直线人和直线厶的距离之和的最小值是(B )B.2D. 3解析:(1)设4、B、M作准线2的垂线,垂足分别为Bi、Mi,则MM I I=3(IAA I I+IBB I I).由抛物线定义可知= \AF\ = \AAi\9所以L4BI = IBBil + lAAil, IMMil=£lABI,即圆心M到准线的距离等于圆的半径,故以4B为直径的圆与抛物线的准线相切.(2)由题可知佐:兀=一1是抛物线y2=4x的准线,设抛物线的焦点F为(h 0),则动点尸到乙的距离等于则动点P到直线人和直线厶的距离之和的最小值即为焦点F到直=1线4x-3j+ 6= 0的距离,所以最小值是14-0+61考点二抛物线的标准方程及性质(高频考点)抛物线的标准方程及性质是高考的热点,考查时多以选择题、填空题形式出现,个别高考题有一定难度,高考对该内容的考查主要有以下三个命题角度:(1)求抛物线方程;(2)由已知求参数p;(3)与其他知识交汇求解综合问题.4伍的焦点,P 为C 上一点,若IPFI=40,则/XPOF 的面积为(° )A. 2D. 4(2)(2016-岳阳模拟)已知 P(0, 2),抛物线 C : y 2=2px(p>d)的焦点为F,线段PF 与抛物线C 的交点为过M 作抛 物线准线的垂线,垂足为0若ZPQF=9Q° ,则p =⑴(经典考题)0为坐标原点,F 为抛物线C : /=B. 2\[2[解析]⑴设Pdo,旳),则PF\=a+迄=4迄, 所以丸=3迄,所以农=4"\/2xo—4^/2 X 3 寸^—24 ‘所以Ijol—2^/6.因为F(V2, 0),所以8"0尸=才0刊• ly()l =空X寸^X意一点到准线的距离与到焦点的距离的比值为1,即相等) 得I0M1 = IMFI.又因为△P0F 为直角三角形且PF 为斜边(直角三角形斜边上的中线等于斜边的一半),所以IPM1=IMFI, 即点M 为线段PF 的中点.由磴,0), P (0,2)知M 点的£,1),又因为点M 在抛物线上,所以12=2pX? 所以p=\/i 或卩=—心(舍去).(2)由题意得点磴,0) 根据抛物线的定义(抛物线上的任坐标为(1)求抛物线的标准方程的方法①求抛物线的标准方程常用待定系数法,因为未知数只有P,所以只需一个条件确定P值即可.②因为抛物线方程有四种标准形式,因此求抛物线方程时, 需先定位,再定量.(2)确定及应用抛物线性质的技巧①利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.②要结合图形分析,灵活运用平面几何的性质以图助解.2.(1)(2016-襄阳调研测试)抛物线y 2=2px 的焦 点为F, M 为抛物线上一点,若△OFM 的外接圆与抛物线 的准线相切(O 为坐标原点),且外接911,则p=(B )A. 2B. 4C. 6D. 8(2)已知抛物线的顶点在原点,对称轴为y 轴,它与圆<+于=9相交,公共弦MN的长为2质,求该抛物线的方程,并写出它的焦点坐标与准线方程.解:⑴选B・因为△OFM的外接圆与抛物线C的准线相切,所以△OFM的外接径,因为圆面积为9n,所以圆的半径为3,又因为圆心在OF 的垂直平分线上,IOFI=f,所以彳+丫=3,所以p=4.(2)由题意,设抛物线方程为x=2ay(a^Q).设公共弦MN交丿轴于4贝l|IM4l = IA^I,且AN=\/5.因为IOM = 3,所以1041=祚一(质)2 = 2,所以N畑±2).因为N点在抛物线上,所以5=2«•仕2),即加=£,抛物线x2=|y的焦点坐标为@,汀准线方程为尸一|・抛物线x2=—|y的焦点坐标为@,一彳),准线方程为歹=|・故抛物线的方程为X2=|y 或x2=5一*考点三直线与抛物线的位置关系典洌D ⑴(2014•高考辽宁卷)已知点A(~2, 3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点记C的焦点为F,则直线BF的斜率为(D )B-1D.扌A边(2)(2016-九江统考)过抛物线y2=8x的焦点F的直线交抛物线于4 B两点,交抛物线的准线于G若IAF\ = 69BC=2FB9则2的值为(° )D. 3[解析]⑴抛物线y2=2px的准线为直线*=—纟,而点A(-2, 3)在准线上,所以-^=-2, 即p=4,从而C: j2=Sx,点为F(2,0)・设切线方程为y—3=k(x+2),代入y2=8x9得歛―『+2氐+3=0伉HO)①,由于/ = 1—4X点(2疋+3)=0,所以k=—2或反=£.因为切点在第一象限,所以氐=空•将氐=空代入①中,得y=8, 再代入J2=8X中得x=8,所以点B的坐标为(8, 8),所以直线BF的斜率为£=扌.(2)设A(x p ji)(yi>0), B(X29力),C( —2, y3)9则帀+2=6, 解得兀i=4, y\=4远,直线AB的方程为j=2\/2(x-2),令{2 QJ =8^ 厂/ 、解y = 2\l2 (x—2), 得B(l, —2\[Z)9所以IBFI =1+2= 3, IBCI = 9,所以久=3.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式14〃=旳1+込1+0若不过焦点,则必须用一般弦长公式.⑶涉及抛物线的弦长、中点、距离等相关问题时, 般利用根与系数的关系采用“设而不求” “整体代入”等解法.[注意]涉及弦的中点.斜率时,一般用“点差法”求解•跟踪训练 3.(2016*唐山一模)已知抛物线j2=2px(p>0),过点C(-2, 0)的直线I交抛物线于4、B两点,坐标原点为O,OA • OB= 12.(1)求抛物线的方程;⑵当以L4BI为直径的圆与y轴相切时,求直线2的方程.•b==^—H Z X H 昱 0龙 I zz■导 Hzxli ■W /^H M +I i(2)⑴中(*)可化为 /-4my+ 8= 0,yi+y2=伽,丁1^2=8,设AB的中点为M,则\AB\ = 2r/V f—x1H-x2=An(y1+j2)— 4= 4w2—4,①又IABI= ^/1+加»]—旳|= —( 16*n2—32),②由①②得(1+/W2)(16W2-32)=(4W2-4)2,解得加2=3, m =所以直线I的方程为兀+心+2= 0或兀一心+2=0.名师讲坛密素养提升} __________________________ ______________________________________________方法思想——函数思想求圆锥曲线中的最值典例 抛鳄线y=—J 上的点到直线4x+3y —8=0距离的-X 2),则点P 到直线4x+3j-8= 0的距离d 2+|,在抛物线J = -x 2中,x£R,所以当 尸彳时,〃取得最小值?即抛物线 y=—J 上的点到直线拓展升华触类旁通 最小值是亠[解析]设P(x,14兀一3x 2—81 1(=5 3V 1(H)4x+3y—8=0距离的最小值是*讀感悟提高解与抛物线有关的最值问题可通过两点间距离公式或者点到直线的距离公式建立目标函数,再用求函数最值的方法求解•解题的关键是根据所给抛物线方程设出动点坐标.跟踪训练若点p 在抛物线y=x±,点0在圆(x-3)2+旷=1上,则IPQI的最小值为 __________ .解析:由题意得抛物线与圆不相交,且圆的圆心为A(3, 0), 则\PQ\^\PA\~\AQ\=\PA\~l t当且仅当P, Q, A三点共线时取等号,所以当曲1取得最小值时,IPQI*小.设P(x0, Jo),贝U yXo — 6兀o+ 9+ 兀0=IP4I取得最小值半,丿:=兀0,\PA\ — 7 (兀o —3) =2 11 5+牛当且仅当兀。
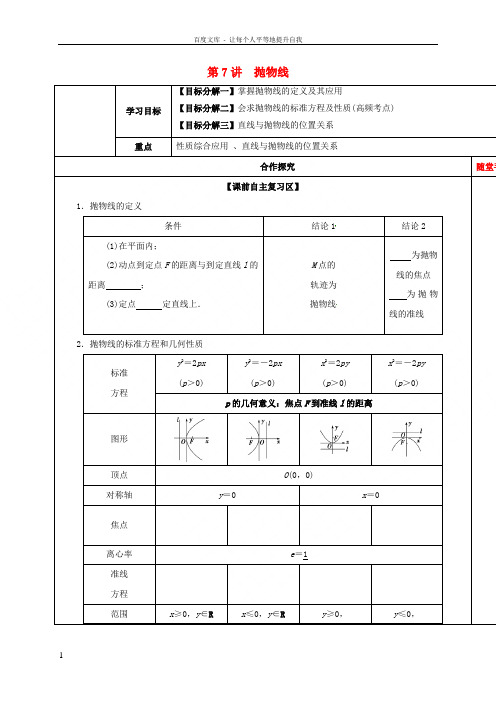
第7讲抛物线学习目标【目标分解一】掌握抛物线的定义及其应用【目标分解二】会求抛物线的标准方程及性质(高频考点) 【目标分解三】直线与抛物线的位置关系重点性质综合应用、直线与抛物线的位置关系合作探究随堂手条件结论1结论2(1)在平面内;(2)动点到定点F的距离与到定直线l的距离;(3)定点定直线上.M点的轨迹为抛物线为抛物线的焦点为抛物线的准线标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0) p的几何意义:焦点F到准线l的距离x∈R x∈R 开口方向向右向左向上向下焦半径(其中P(x0,y0))|PF|=|PF|=|PF|=|PF|=点且与定直线垂直的直线.+2或+2.→1.(1)已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若FP=4|OF|,△MFO的面积为43,则抛物线的方程为( )=2双曲线a-yA.9 B.4C.3D2.线相切(O为坐标原点),且外接圆的面积为9π,则p=( )【例3】(2016·高考全国卷乙)在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2【规律总结3】(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用的焦点与椭圆9+5=25,求该抛物线的(2017·豫南九校联考)已知点P是抛物线x2=4y上的动点,点P在x轴上的射影是点Q,点A 抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是________.A,B两点,C1的焦点为F,若△FAB的面积等于1,则C1的方程是( )限分别交于A ,B 两点,则|AF ||BF |的值等于( )A .13B .23 C.34 D.43★★9.【2017课标II ,文12】过抛物线2:4C y x =的焦点F ,且斜率为3的直线交C 于点M (M 在x轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为A.5B.22 C . 23 D. 33★10.【2017山东,文15】在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>, 的右支与焦点为F的抛物线22(0)x py p =>交于A ,B 两点,若|AF |+|BF |=4|OF |,则该双曲线的渐近线方程为 .11.(经典考题)如图所示是抛物线形拱桥,当水面在l 时,拱顶离水面2 m ,水面宽4 m . 水位下降1 m 后,水面宽________m.12.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.。
(全国通用)2018高考数学一轮复习第8章平面解析几何第7节抛物线课时分层训练文新人教A版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((全国通用)2018高考数学一轮复习第8章平面解析几何第7节抛物线课时分层训练文新人教A版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(全国通用)2018高考数学一轮复习第8章平面解析几何第7节抛物线课时分层训练文新人教A版的全部内容。
课时分层训练(五十一)抛物线A组基础达标(建议用时:30分钟)一、选择题1.(2016·四川高考)抛物线y2=4x的焦点坐标是()A.(0,2) B.(0,1)C.(2,0)D.(1,0)D[由y2=4x知p=2,故抛物线的焦点坐标为(1,0).]2.(2017·云南昆明一中模拟)已知点F是抛物线C:y2=4x的焦点,点A在抛物线C上,若|AF|=4,则线段AF的中点到抛物线C的准线的距离为( )A.4 B.3C.2 D.1B[由题意易知F(1,0),F到准线的距离为2,A到准线的距离为|AF|=4,则线段AF 的中点到抛物线C的准线的距离为错误!=3.]3.抛物线y2=4x的焦点到双曲线x2-错误!=1的渐近线的距离是( )A。
错误! B.错误!C.1 D.3B[由双曲线x2-错误!=1知其渐近线方程为y=±错误!x,即错误!x±y=0,又y2=4x的焦点F(1,0),∴焦点F到直线的距离d=错误!=错误!.]4.已知抛物线C与双曲线x2-y2=1有相同的焦点,且顶点在原点,则抛物线C的方程是( )A.y2=±2错误!x B.y2=±2xC.y2=±4x D.y2=±4错误!xD[因为双曲线的焦点为(-2,0),(2,0).设抛物线方程为y2=±2px(p〉0),则错误!=错误!,p=2错误!.所以抛物线方程为y2=±4错误!x.]5.O为坐标原点,F为抛物线C:y2=42x的焦点,P为C上一点,若|PF|=4错误!,则△POF的面积为( )【导学号:31222325】A.2 B.2错误!C.2 3 D.4C[如图,设点P的坐标为(x0,y0),由|PF|=x0+错误!=4错误!,得x0=3错误!,代入抛物线方程得,y错误!=4错误!×3错误!=24,所以|y0|=26,所以S△POF=错误!|OF||y0|=错误!×错误!×2错误!=2错误!.]二、填空题6.(2017·山西四校三联)过抛物线y2=4x的焦点F作倾斜角为45°的直线交抛物线于A,B 两点,则弦长|AB|为__________. 【导学号:31222326】8 [设A(x1,y1),B(x2,y2).易得抛物线的焦点是F(1,0),所以直线AB的方程是y=x -1。
高考数学一轮复习第九章平面解析几何第7讲抛物线教案理(含解析)新人教A版第7讲抛物线基础知识整合1.抛物线的定义平面内与一个定点F和一条定直线l(l不过F)的距离□01相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的□02准线.其数学表达式:□03|MF|=d(其中d为点M到准线的距离).2.抛物线的标准方程与几何性质抛物线焦点弦的几个常用结论设AB 是过抛物线y 2=2px (p >0)的焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则: (1)x 1x 2=p 24,y 1y 2=-p 2.(2)弦长|AB |=x 1+x 2+p =2psin 2α(α为弦AB 的倾斜角).(3)以弦AB 为直径的圆与准线相切.(4)通径:过焦点垂直于对称轴的弦长等于2p .1.抛物线y =2x 2的准线方程为( ) A .y =-18B .y =-14C .y =-12D .y =-1答案 A解析 由y =2x 2,得x 2=12y ,故抛物线y =2x 2的准线方程为y =-18,故选A.2.(2019·黑龙江联考)若抛物线x 2=4y 上的点P (m ,n )到其焦点的距离为5,则n =( )A.194 B.92C .3D .4 答案 D解析 抛物线x 2=4y 的准线方程为y =-1.根据抛物线的定义可知5=n +1,解得n =4.故选D.3.已知抛物线C :y =x 28的焦点为F ,A (x 0,y 0)是C 上一点,且|AF |=2y 0,则x 0=( )A .2B .±2 C.4 D .±4 答案 D解析 由y =x 28,得x 2=8y ,∴抛物线C 的准线方程为y =-2,焦点为F (0,2).由抛物线的性质及题意,得|AF |=2y 0=y 0+2.解得y 0=2,∴x 0=±4.故选D.4.若抛物线y 2=2px 上一点P (2,y 0)到其准线的距离为4,则抛物线的标准方程为( )A .y 2=4x B .y 2=6x C .y 2=8x D .y 2=10x答案 C解析 ∵抛物线y 2=2px ,∴准线方程为x =-p2.∵点P (2,y 0)到其准线的距离为4.∴⎪⎪⎪⎪⎪⎪-p2-2=4.∴p =4,∴抛物线的标准方程为y 2=8x .5.(2019·广东中山统测)过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点.如果x 1+x 2=6,那么|AB |=( )A .6B .8C .9D .10 答案 B解析 由题意知,抛物线y 2=4x 的准线方程是x =-1.∵过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,∴|AB |=x 1+x 2+2.又∵x 1+x 2=6,∴|AB |=x 1+x 2+2=8.故选B.6.O 为坐标原点,F 为抛物线C :y 2=42x 的焦点,P 为C 上一点,若|PF |=42,则△POF 的面积为( )A .2B .2 2C .2 3D .4 答案 C解析 利用|PF |=x P +2=42,可得x P =32, ∴y P =±2 6.∴S △POF =12|OF |·|y P |=2 3.故选C.核心考向突破考向一 抛物线的定义角度1 到焦点与到定点距离之和最小问题例1 (2019·赣州模拟)若点A 的坐标为(3,2),F 是抛物线y 2=2x 的焦点,点M 在抛物线上移动时,使|MF |+|MA |取得最小值的M 的坐标为( )A .(0,0) B.⎝ ⎛⎭⎪⎫12,1 C .(1,2) D .(2,2)答案 D解析 过M 点作准线的垂线,垂足为N ,则|MF |+|MA |=|MN |+|MA |,当A ,M ,N 三点共线时,|MF |+|MA |取得最小值,此时M (2,2).角度2 到点与准线的距离之和最小问题例2 (2019·邢台模拟)已知M 是抛物线x 2=4y 上一点,F 为其焦点,点A 在圆C :(x +1)2+(y -5)2=1上,则|MA |+|MF |的最小值是________.答案 5解析 依题意,由点M 向抛物线x 2=4y 的准线l :y =-1引垂线,垂足为M 1,则有|MA |+|MF |=|MA |+|MM 1|,结合图形可知|MA |+|MM 1|的最小值等于圆心C (-1,5)到y =-1的距离再减去圆C 的半径,即等于6-1=5,因此|MA |+|MF |的最小值是5.角度3 到定直线的距离最小问题例3 已知直线l 1:4x -3y +6=0和直线l 2:x =-1,抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是( )A.355 B .2 C.115D .3 答案 B解析 由题意可知l 2:x =-1 是抛物线y 2=4x 的准线,设抛物线的焦点为F (1,0),则动点P 到l 2的距离等于|PF |,则动点P 到直线l 1和直线l 2的距离之和的最小值,即焦点F 到直线l 1:4x -3y +6=0的距离,所以最小值是|4-0+6|5=2.触类旁通与抛物线有关的最值问题的两个转化策略(1)将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”,使问题得解.2将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.)即时训练 1.(2019·潍坊质检)在y =2x 2上有一点P ,它到A (1,3)的距离与它到焦点的距离之和最小,则点P 的坐标是( )A .(-2,1)B .(1,2)C .(2,1)D .(-1,2) 答案 B解析 如图所示,直线l 为抛物线y =2x 2的准线,F 为其焦点,PN ⊥l ,AN 1⊥l ,由抛物线的定义,知|PF |=|PN |,∴|AP |+|PF |=|AP |+|PN |≥|AN 1|,即当且仅当A ,P ,N 三点共线时取等号.∴P 点的横坐标与A 点的横坐标相同即为1,则可排除A ,C ,D ,故选B.2.已知P 是抛物线y 2=4x 上一动点,则点P 到直线l :2x -y +3=0和y 轴的距离之和的最小值是( )A. 3B. 5 C .2 D.5-1 答案 D解析 由题意知,抛物线的焦点为F (1,0).设点P 到直线l 的距离为d ,由抛物线的定义可知,点P 到y 轴的距离为|PF |-1,所以点P 到直线l 的距离与到y 轴的距离之和为d +|PF |-1.易知d +|PF |的最小值为点F 到直线l 的距离,故d +|PF |的最小值为|2+3|22+-12=5,所以d +|PF |-1的最小值为5-1.考向二 抛物线的方程例4 (1)(2019·运城模拟)已知抛物线x 2=ay 与直线y =2x -2相交于M ,N 两点,若MN 中点的横坐标为3,则此抛物线的方程为( )A .x 2=32yB .x 2=6y C .x 2=-3y D .x 2=3y答案 D解析 设点M (x 1,y 1),N (x 2,y 2).由⎩⎪⎨⎪⎧x 2=ay ,y =2x -2消去y ,得x 2-2ax +2a =0,所以x 1+x 22=2a 2=3,即a =3,因此所求的抛物线方程是x 2=3y . (2)抛物线x 2=2py (p >0)的焦点为F ,其准线与双曲线x 23-y 23=1相交于A ,B 两点,若△ABF 为等边三角形,则p =________.答案 6解析 抛物线的准线方程为y =-p2,设A ,B 的横坐标分别为x A ,x B ,则|x A |2=|x B |2=3+p 24,所以|AB |=|2x A |.又焦点到准线的距离为p ,由等边三角形的特点,得p =32|AB |,即p 2=34×4×⎝ ⎛⎭⎪⎫3+p 24,所以p =6. 触类旁通求抛物线的标准方程应注意的几点(1)当坐标系已建立时,应根据条件确定抛物线的标准方程属于四种类型中的哪一种. 2要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系. 3要注意参数p 的几何意义是焦点到准线的距离,利用它的几何意义来解决问题. 即时训练 3.(2019·上海模拟)抛物线y 2=2px (p >0)的焦点为F ,O 为坐标原点,M 为抛物线上一点,且|MF |=4|OF |,△MFO 的面积为43,则抛物线的方程为( )A .y 2=6x B .y 2=8x C .y 2=16x D .y 2=152x答案 B解析 设M (x ,y ),∵|OF |=p 2,|MF |=4|OF |,∴|MF |=2p ,由抛物线的定义知x +p2=2p ,∴x =32p ,∴y =±3p ,又△MFO 的面积为43,∴12×p2×3p =43,解得p =4(p =-4舍去).∴抛物线的方程为y 2=8x .4.动直线l 的倾斜角为60°,若直线l 与抛物线x 2=2py (p >0)交于A ,B 两点,若A ,B 两点的横坐标之和为3,则抛物线的方程为________.答案 x 2=3y解析 设直线l 的方程为y =3x +b ,联立⎩⎨⎧y =3x +b ,x 2=2py ,消去y ,得x 2=2p (3x +b ).即x 2-23px -2pb =0,∴x 1+x 2=23p =3.∴p =32,∴抛物线的方程为x 2=3y .考向三 抛物线的性质例5 (1)已知抛物线y 2=2px (p >0),过其焦点且斜率为-1的直线交抛物线于A ,B 两点,若线段AB 的中点的横坐标为3,则该抛物线的准线方程为( )A .x =1B .x =2C .x =-1D .x =-2 答案 C解析 抛物线y 2=2px (p >0)的焦点为⎝ ⎛⎭⎪⎫p2,0,所以过焦点且斜率为-1的直线方程为y=-⎝ ⎛⎭⎪⎫x -p 2,代入抛物线方程,整理得x 2-3px +p 24=0,由AB 中点的横坐标为3,得3p =6,解得p =2,故抛物线y 2=4x 的准线方程为x =-1.(2)(2018·北京高考)已知直线l 过点(1,0)且垂直于x 轴.若l 被抛物线y 2=4ax 截得的线段长为4,则抛物线的焦点坐标为________.答案 (1,0)解析 如图,由题意可得,点P (1,2)在抛物线上,将P (1,2)代入y 2=4ax ,解得a =1,∴y 2=4x ,由抛物线方程可得,2p =4,p =2,p2=1,∴焦点坐标为(1,0).触类旁通1涉及抛物线上的点到焦点的距离或到准线的距离时,常可相互转化. 2应用抛物线的几何性质解题时,常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了数形结合思想解题的直观性.即时训练 5.(2016·全国卷Ⅰ)以抛物线C 的顶点为圆心的圆交C 于A ,B 两点,交C 的准线于D ,E 两点.已知|AB |=42,|DE |=25,则C 的焦点到准线的距离为( )A .2B .4C .6D .8 答案 B解析 不妨设C :y 2=2px (p >0),A (x 1,22),则x 1=2222p=4p,由题意可知|OA |=|OD |,得⎝ ⎛⎭⎪⎫4p 2+8=⎝ ⎛⎭⎪⎫p 22+5,解得p =4.故选B.6.在平面直角坐标系xOy 中有一定点A (4,2),若线段OA 的垂直平分线过抛物线y 2=2px (p >0)的焦点,则该抛物线的准线方程是________.答案 x =-52解析 OA 的中点的坐标为(2,1),斜率k OA =12,OA 的垂直平分线的方程为y -1=-2(x-2),即y =-2x +5.又∵抛物线y 2=2px (p >0)的焦点在x 轴上,即y =0.由⎩⎪⎨⎪⎧y =0,y =-2x +5,得抛物线的焦点F 的坐标为⎝ ⎛⎭⎪⎫52,0,∴52=p 2,∴抛物线的准线方程为x =-52. 考向四 直线与抛物线的位置关系例6 (2018·全国卷Ⅰ)设抛物线C :y 2=2x ,点A (2,0),B (-2,0),过点A 的直线l 与C 交于M ,N 两点.(1)当l 与x 轴垂直时,求直线BM 的方程;。