第七讲 空间计量经济学模型的matlab估计

MATLAB中的统计推断与参数估计方法解析MATLAB（Matrix Laboratory）是一种基于数值计算和编程语言的工具，广泛应用于科学、工程和金融等领域。

在统计学中，MATLAB提供了丰富的函数和工具箱，可以进行统计推断和参数估计等分析。

本文将针对MATLAB中的统计推断和参数估计方法进行解析，包括假设检验、置信区间估计和最大似然估计等。

一、假设检验假设检验是统计学中常用的一种方法，用于验证关于总体参数的假设。

在MATLAB中，可以利用t检验和χ²检验等函数进行假设检验分析。

1. t检验t检验主要用于比较两个样本均值是否存在显著差异。

在MATLAB中，可以使用ttest2函数进行双样本t检验，使用ttest函数进行单样本t检验。

例如，我们有两组数据x和y，想要判断它们的均值是否显著不同。

可以使用以下代码进行双样本t检验：```[h,p,ci,stats] = ttest2(x,y);```其中，h表示假设检验的结果，为0表示接受原假设，为1表示拒绝原假设；p 表示假设检验的p值；ci表示置信区间；stats包含了相关统计信息。

2. χ²检验χ²检验主要用于比较观察频数和期望频数之间是否存在显著差异。

在MATLAB 中，可以使用chi2gof函数进行χ²检验分析。

例如，我们有一组观察频数obs和一组对应的期望频数exp，可以使用以下代码进行χ²检验：```[h,p,stats] = chi2gof(obs,'Expected',exp);```其中，h表示假设检验的结果，为0表示接受原假设，为1表示拒绝原假设；p 表示假设检验的p值；stats包含了相关统计信息。

二、置信区间估计置信区间估计是用于估计总体参数范围的方法，可以帮助我们对总体参数进行合理的推断。

在MATLAB中，可以利用confint函数进行置信区间估计分析。

例如，我们有一组数据x，想要对它的均值进行置信区间估计。

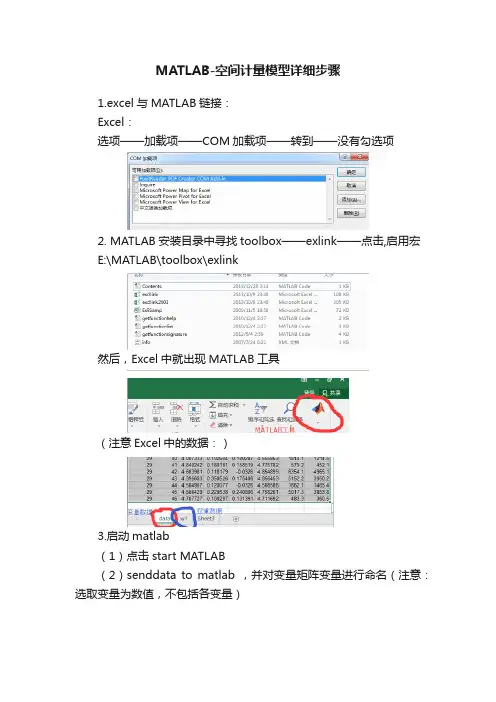
MATLAB-空间计量模型详细步骤1.excel与MATLAB链接：Excel：选项——加载项——COM加载项——转到——没有勾选项2. MATLAB安装目录中寻找toolbox——exlink——点击,启用宏E:\MATLAB\toolbox\exlink然后，Excel中就出现MATLAB工具（注意Excel中的数据：）3.启动matlab（1）点击start MATLAB（2）senddata to matlab ，并对变量矩阵变量进行命名（注意：选取变量为数值，不包括各变量）(data表中数据进行命名)（空间权重进行命名）（3）导入MATLAB中的两个矩阵变量就可以看见4.将elhorst和jplv7两个程序文件夹复制到MATLAB安装目录的toolbox文件夹5.设置路径：6.输入程序，得出结果T=30;N=46;W=norm(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1); [nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests 解释附录：静态面板空间计量经济学一、OLS静态面板编程1、普通面板编程T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);results=ols(y,[xconstant x]);vnames=strvcat('logcit','intercept','logp','logy');prt_reg(results,vnames,1);sige=results.sige*((nobs-K)/nobs);loglikols=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.resid % The (robust)LM tests developed by ElhorstLMsarsem_panel(results,W,y,[xconstant x]); % (Robust) LM tests2、空间固定OLS （spatial-fixed effects）T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=1;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);sfe=meanny-meannx*results.beta; % including the constant term yme = y - mean(y);et=ones(T,1);error=y-kron(et,sfe)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliksfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests3、时期固定OLS（time-period fixed effects）T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=2;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames);tfe=meanty-meantx*results.beta; % including the constant termyme = y - mean(y);en=ones(N,1);error=y-kron(tfe,en)-x*results.beta;rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effectssige=results.sige*((nobs-K)/nobs);logliktfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests4、空间与时间双固定模型T=30;N=46;W=normw(W1);y=A(:,3);x=A(:,[4,6]);xconstant=ones(N*T,1);[nobs K]=size(x);model=3;[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,x, N,T,model );results=ols(ywith,xwith);vnames=strvcat('logcit','logp','logy'); % should be changed if x is changedprt_reg(results,vnames)en=ones(N,1);et=ones(T,1);intercept=mean(y)-mean(x)*results.beta;sfe=meanny-meannx*results.beta-kron(en,intercept);tfe=meanty-meantx*results.beta-kron(et,intercept);yme = y - mean(y);ent=ones(N*T,1);error=y-kron(tfe,en)-kron(et,sfe)-x*results.beta-kron(ent,intercept); rsqr1 = error'*error;rsqr2 = yme'*yme;FE_rsqr2 = 1.0 - rsqr1/rsqr2 % r-squared including fixed effects sige=results.sige*((nobs-K)/nobs);loglikstfe=-nobs/2*log(2*pi*sige)-1/(2*sige)*results.resid'*results.residLMsarsem_panel(results,W,ywith,xwith); % (Robust) LM tests二、静态面板SAR模型1、无固定效应（No fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x],W,T,info); vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应（Spatial fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);3、时点固定效应（Time period fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应（Spatial and time period fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);三、静态面板SDM模型1、无固定效应（No fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sar_panel_FE(y,[xconstant x wx],W,T,info);vnames=strvcat('logcit','intercept','logp','logy','W*logp','W*l ogy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);2、空间固定效应（Spatial fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=1;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W);3、时点固定效应（Time period fixed effects）T=30;N=46;W=norm(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn on% New routines to calculate effects estimatesresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');% Print out coefficient estimatesprt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)4、双固定效应（Spatial and time period fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.bc=0;info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sar_panel_FE(y,[x wx],W,T,info);vnames=strvcat('logcit','logp','logy','W*logp','W*logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lag% Wald test for spatial Durbin model against spatial lagmodelbtemp=results.parm;varcov=results.cov;Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btemp prob_spatial_lag=1-chis_cdf (Wald_spatial_lag, K) wald test spatial error% Wald test spatial Durbin model against spatial error model R=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error=1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_FE(y,x,W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_FE(y,x,W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)5、空间随机效应与时点固定效应模型T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);[ywith,xwith,meanny,meannx,meanty,meantx]=demean(y,[x wx],N,T,2); % 2=time dummiesinfo.model=1;results=sar_panel_RE(ywith,xwith,W,T,info);prt_spnew(results,vnames,1)spat_model=1;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sdm(results,vnames,W)wald test spatial lagbtemp=results.parm(1:2*K+2);varcov=results.cov(1:2*K+2,1:2*K+2);Rafg=zeros(K,2*K+2);for k=1:KRafg(k,K+k)=1; % R(1,3)=0 and R(2,4)=0;endWald_spatial_lag=(Rafg*btemp)'*inv(Rafg*varcov*Rafg')*Raf g*btempprob_spatial_lag= 1-chis_cdf (Wald_spatial_lag, K)wald test spatial errorR=zeros(K,1);for k=1:KR(k)=btemp(2*K+1)*btemp(k)+btemp(K+k); % k changed in 1,7/12/2010% R(1)=btemp(5)*btemp(1)+btemp(3);% R(2)=btemp(5)*btemp(2)+btemp(4);endRafg=zeros(K,2*K+2);for k=1:KRafg(k,k) =btemp(2*K+1); % k changed in 1, 7/12/2010 Rafg(k,K+k) =1;Rafg(k,2*K+1)=btemp(k);% Rafg(1,1)=btemp(5);Rafg(1,3)=1;Rafg(1,5)=btemp(1);% Rafg(2,2)=btemp(5);Rafg(2,4)=1;Rafg(2,5)=btemp(2);endWald_spatial_error=R'*inv(Rafg*varcov*Rafg')*Rprob_spatial_error= 1-chis_cdf (Wald_spatial_error,K)LR test spatial lagresultssar=sar_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_lag=-2*(resultssar.lik-results.lik)prob_spatial_lag=1-chis_cdf (LR_spatial_lag,K)LR test spatial errorresultssem=sem_panel_RE(ywith,xwith(:,1:K),W,T,info);LR_spatial_error=-2*(resultssem.lik-results.lik)prob_spatial_error=1-chis_cdf (LR_spatial_error,K)四、静态面板SEM模型1、无固定效应（No fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=0;info.fe=0;results=sem_panel_FE(y,[xconstant x],W,T,info);vnames=strvcat('logcit','intercept','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);2、空间固定效应（Spatial fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0;info.model=1;info.fe=0;results=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);3、时点固定效应（Time period fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=2;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model);panel_effects_sar(results,vnames,W);4、双固定效应（Spatial and time period fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);for t=1:Tt1=(t-1)*N+1;t2=t*N;wx(t1:t2,:)=W*x(t1:t2,:);endxconstant=ones(N*T,1);[nobs K]=size(x);info.lflag=0; % required for exact resultsinfo.model=3;info.fe=0; % Do not print intercept and fixed effects; use info.fe=1 to turn onresults=sem_panel_FE(y,x,W,T,info);vnames=strvcat('logcit','logp','logy');prt_spnew(results,vnames,1)% Print out effects estimatesspat_model=0;direct_indirect_effects_estimates(results,W,spat_model); panel_effects_sar(results,vnames,W);五、静态面板SDEM模型1、无固定效应（No fixed effects）T=30;N=46;W=normw(W1);y=A(:,[3]);x=A(:,[4,6]);。

Matlab技术经济学应用引言：技术经济学是一门研究科技创新与经济发展之间相互关系的学科，而Matlab作为一种强大的数值计算和科学编程语言，被广泛应用于技术经济学领域。

本文将重点探讨Matlab在技术经济学中的应用，着重介绍其在经济评估、金融模型、企业决策等方面的应用。

一、经济评估1.1 投资成本分析在进行经济评估时，投资成本分析是一个重要的步骤。

Matlab可以帮助分析人员通过数学模型计算出投资成本，并进行灵活的调整和优化。

例如，可以使用Matlab编写一个程序，基于现金流量贴现法（NPV）来计算投资项目的净现值。

通过调整输入参数，可以模拟不同情况下的投资成本，并找到最优方案。

1.2 效益评估Matlab也可以用于效益评估，即对投资项目的经济效益进行分析。

例如，可以使用Matlab编写一个程序来计算投资项目的内部收益率（IRR），并评估其可行性和盈利能力。

通过在程序中引入不同的输入变量，可以进行灵活的模拟和分析，帮助决策者做出科学的投资决策。

二、金融模型2.1 期权定价模型期权定价是金融领域中的一个重要问题，Matlab提供了强大的数学计算功能，可以用于构建和求解各种期权定价模型。

例如，可以使用Matlab编写程序，基于布莱克-斯科尔斯（Black-Scholes）模型来估计欧式期权的价格。

通过调整输入参数，可以对不同情况下的期权价格进行计算和分析。

2.2 风险管理模型金融市场中存在着各种风险，如市场风险、信用风险等。

Matlab可以用于构建和求解各种风险管理模型，以帮助投资者进行风险评估和管理。

例如，可以使用Matlab编写程序，基于Value at Risk（VaR）模型来评估投资组合的风险水平，并制定相应的风险管理策略。

三、企业决策3.1 供应链优化供应链管理是现代企业中的一个重要问题，而Matlab可以帮助企业进行供应链优化。

例如，可以使用Matlab编写程序，基于线性规划模型来优化供应链网络的布局和物流运输方案。

这个notes纯粹是扫盲用的。

我用了一个最简单的线性DSGE，只有两个方程。

先是我用手算的方法找到saddle-path 的policy function，然后手算出impulse response function。

这些我都用Dynare做了计算，程序和结果都写在note里面。

上面是我note的截图，这个DSGE模型实际上就是一个linear rational expecation model (LREM)，但DSGE的线性化后的本质也就是个LRE。

虽然这个note提供的模型非常简单，但是思路在于如何用Dynare来深入学习这个动态系统。

有几个事情需要大家自己来做：1. beta和rho的大小，大家从换很多次calibration，看能对IRF带来什么影响?2. beta和rho都大于1的时候，你应该怎么修改模型，为了维持模型的稳定性？3. 看修改shock的stardard deviation能对模型带了什么影响？4. 如果你再加一个方程进去呢？什么样子的方程？以上内容我都试验过了。

这个东西没法帮大家试验，所以大家必须自己试着做。

这样你可以学到很多关于动态系统的感性认识。

之后，我用最大似然估计对参数估计，然后我故意制造under-identification的问题，让大家看一下结果是什么样子。

最后就是Bayesian estimation，我只估计了1个参数，用了2条平行马尔科夫链，做了超超短程模拟（只有500次，正常情况都是100000），为了省时间(我电脑只用50秒左右)，所以我并没有让电脑跑很长的马尔科夫链和多个平行链条。

所以结果非常差，但是这不是的目的。

目的还是在于让从来没见过整个估计过程的同学看到一个全貌。

所以我没有提及理论内容，或者是一带而过。

对于Bayesian estimation，有个地方要注意的就是shock的个数必须大于等observable的个数，这是启动Kalman filter模拟likelihood function的充分条件。

Matlab技术状态估计方法引言在科学研究和工程领域中，准确地估计某个系统的状态是十分重要的。

通过对系统状态的准确估计，我们可以预测未来的行为、诊断问题、优化控制方案等。

这种状态估计可以应用于各种领域，如机器人导航、信号处理、图像识别等。

在本文中，我们将介绍一些在Matlab中常用的技术状态估计方法。

一、卡尔曼滤波卡尔曼滤波是一种常用的状态估计方法，利用系统模型和观测数据来估计系统的状态。

其基本思想是用一个线性状态空间模型来描述系统，然后利用系统的动态方程和观测方程来进行状态估计。

Matlab提供了一些函数，如`kalman`和`kalmanf`，可以方便地实现卡尔曼滤波。

二、粒子滤波粒子滤波是一种递归贝叶斯估计方法，它通过一组随机样本（粒子）来近似表示概率密度函数。

粒子滤波适用于非线性、非高斯和非线性高斯混合系统的状态估计。

Matlab提供了`pfilter`和`pfilt`等函数来实现粒子滤波。

三、扩展卡尔曼滤波扩展卡尔曼滤波（EKF）是一种对非线性系统进行状态估计的方法。

它通过在每个时间步骤上线性化非线性系统方程，并使用卡尔曼滤波的方法来估计线性化系统的状态。

Matlab提供了`ekf`和`ekfukf`等函数来实现扩展卡尔曼滤波。

四、无迹卡尔曼滤波无迹卡尔曼滤波（UKF）是一种对非线性系统进行状态估计的方法，它通过利用无迹变换将非线性系统映射到高斯分布上来近似非线性系统的概率分布。

UKF在Matlab中的实现可以使用`ukf`和`ukfukf`等函数。

五、粒子群优化算法粒子群优化算法（PSO）是一种用于全局优化问题的群体智能算法。

它通过模拟鸟群中鸟类的行为来寻找最优解。

PSO算法在状态估计中可以用于参数优化、机器学习等问题。

Matlab提供了`pso`和`psooptimset`等函数来实现粒子群优化算法。

六、神经网络神经网络是一种模拟人脑神经元工作原理的计算模型。

它可以用于解决复杂的非线性问题，并在状态估计中可以用于模式识别、预测等任务。

社会科学动态范巧新书评介明于道，精于术，方能经纬天下2018年秋，由武汉大学肖光恩教授编著、北京大学出版社出版的《空间计量经济学———基于MATLAB 的应用分析》面世。

该书是国内第一本基于MATLAB 软件的空间计量经济学应用书籍。

一、明道是空间计量研究的关键逻辑空间计量经济学，源于对经典计量经济学中忽视空间溢出效应的重点考察而形成的一个计量经济学分支学科。

从本质上来看，空间计量经济学仍属于计量经济学范畴，其核心逻辑在于将被解释变量、解释变量和随机扰动项的空间溢出效应纳入经典计量经济学的分析框架之中，从而衍生各种各样的空间计量模型。

空间计量经济学与经典计量经济学一脉相承，又各有特色。

首先，从模型特征上看，空间计量模型源自经典计量模型，既有处理单个被解释变量与多个解释变量关系的空间单方程模型，也有处理多个被解释变量及其解释变量关系的空间联立方程；既有解释变量参数不变的全局空间计量模型，也有解释变量参数可变的局部空间计量模型———地理加权回归模型。

然而，由于空间计量模型在经典计量模型中加入了空间溢出效应项，使得空间计量模型相比较经典计量模型而言又具有相异的模型特征，由此衍生从空间自回归模型、空间误差模型到通用嵌套空间模型等多元化的空间计量模型形式。

其次，从所采用的数据特性来看，经典计量经济学中所采用的数据主要包括截面数据、时间序列数据和面板数据。

空间计量经济学中采用的数据则通常会包含空间位置信息，或者数据必须具备一定的空间载体，所以空间计量经济学中往往会重点处理截面数据或面板数据，不会单独处理时间序列数据。

当然，包含空间位置信息或空间载体信息的数据可以有连续型或离散型数据特征，则与经典计量经济学类似，空间计量经济学模型也同样会对连续型数据和离散型数据做出阐释，由此产生空间Probit 、Logit 和Tobit 等模型。

再次，从模型的参数估计方法上看，经典计量经济学主要采用的方法包括LS 类、LM 类、MM 类和贝叶斯类，其中LS 类主要依据估计值与真值之间的残差平方和最小而确定参数估计方法，LM 类主要依据预设随机扰动项分布条件下似然性质最优而确定参数估计方法，MM 类主要依据预设随机扰动项分布条件下的矩条件而确定参数估计方法，贝叶斯类主要依据预设随机扰动项、随机扰动项方差及其方差-协方差矩阵、解释变量参数等先验分布而计算相关参数后验分布来确定参数估计方法。