菱形矩形正方形的判定

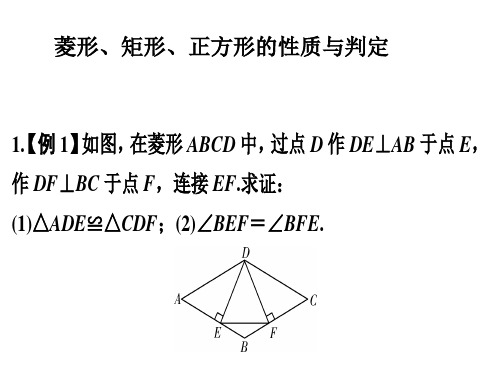
矩形、菱形、正方形的性质及判定一、知识提要1.矩形定义有一个角是直角的平行四边形叫做矩形；性质①矩形的四个角都是直角；②矩形的对角线相等.判定①有一个角是直角的平行四边形叫做矩形；②对角线相等的平行四边形是矩形；③有三个角是直角的四边形是矩形.2.直角三角形斜边的中线等于斜边长的一半.3.菱形定义有一组邻边相等的平行四边形叫做菱形.性质①菱形的四条边都相等；②菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.判定①有一组邻边相等的平行四边形叫做菱形；②对角线互相垂直的平行四边形是菱形；③四边相等的四边形是菱形.4.菱形的面积等于对角线乘积的一半.5.正方形定义四条边都相等、四个角都是直角的四边形是正方形.性质正方形拥有平行四边形、矩形、菱形的所有性质；判定①由一个角是直角的菱形是正方形；②有一组邻边相等的矩形是正方形.二、精讲精练1.矩形ABCD的对角线AC，BD相交于点O，则边与对角线组成的直角三角形的个数是________.2.（2011浙江）如图，在矩形ABCD中，对角线AC，BD交于点O．已知∠AOB= 60°，AC=16，则图中长度为8的线段有( ) A．2条B．4条ODC BA60°C ．5条D ．6条3. 矩形ABCD 中，AB =2BC ，E 为CD 上一点，且AE =AB ，则∠BEC = ___.4. 已知矩形ABCD ，若它的宽扩大2倍，且它的长缩小四分之一，那么新矩形的面积等于原矩形ABCD 面积的__________．5. （2011四川）下列关于矩形的说法中正确的是（ ）A ．对角线相等的四边形是矩形B ．对角线互相平分的四边形是矩形C ．矩形的对角线互相垂直且平分D ．矩形的对角线相等且互相平分6. （2011江苏）在四边形ABCD 中，AB=DC ，AD=BC .请再添加一个条件，使四边形ABCD 是矩形.你添加的条件是_______________(写出一种即可) 7. （2011山东）如图，△ABC 中，AC 的垂直平分线分别交AC 、AB 于点D 、F ，BE ⊥DF 交DF 的延长线于点E ，已知∠A =30°，BC =2，AF =BF ，则四边形BCDE 的面积是（ ）A ．23B ．33C ．4D ．438. 如图，将□ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC 于点F ．（1）求证：△ABF ≌△ECF（2）若∠AFC =2∠D ，连接AC 、BE ．求证：四边形ABEC 是矩形．9. （2011江苏）在菱形ABCD 中，AB=5cm ，则此菱形的周长为（ ）A. 5cmB. 15cmC. 20cmD. 25cm10. （2011河北）如图，已知菱形ABCD ，其顶点A ，B 在数轴对应的数分别为-4和1，则BC =_______．EFDCBAD CBAHFGE ADBC11. 菱形的一边与两条对角线夹角的差是20°，则菱形的各角的度数为___________．12. (2011重庆)如图,菱形ABCD 的对角线AC 、BD 相交于点O ，且AC =8，BD =6，过点O 作OH ⊥AB ，垂足为H ，则点O 到边AB 的距离OH =_________．13. 已知菱形周长是24cm ，一个内角为60°，则菱形的面积为＿_____.14. 菱形ABCD 中，AE ⊥BC 于E ，若S 菱形ABCD =24cm 2，则AE =6cm ，则菱形ABCD的边长为_______.15. （2011山东）已知一个菱形的周长是20cm ，两条对角线的比是4:3，则这个菱形的面积是（ ）A ．12cm 2B ． 24cm 2C ． 48cm 2D ． 96cm 2 16. 菱形有____条对称轴，对称轴之间具有________的位置关系． 17. 菱形具有而一般平行四边形不具有的性质是( )A ．两组对边分别平行B ．两组对边分别相等C ．一组邻边相等D ．对角线相互平分18. （2011四川）如图，点E 、F 、G 、H 分别是任意四边形ABCD 中AD 、BD 、BC 、CA 的中点，当四边形ABCD 的边至少满足__________条件时，四边形EFGH 是菱形.19. （2011浙江）如图，在□ABCD 中，E 、F 分别为边AB 、CD 的中点，BD 是对角线，过点A 作AG ∥DB 交CB 的延长线于点G ． （1）求证：DE ∥BF ；（2）若∠G =90°，求证：四边形DEBF 是菱形．F E B C A D 20. （2011湖州）如图，已知E 、F 分别是□ABCD 的边BC 、AD 上的点，且BE =DF . （1）求证：四边形AECF 是平行四边形；（2）若BC =10， BAC =90，且四边形AECF 是菱形，求BE 的长.21. （2011湖南）下列四边形中，对角线相等且互相垂直平分的是（ ） A.平行四边形 B.正方形 C.等腰梯形 D.矩形22. 有一组邻边_______并且有一个角是________的平行四边形，叫做正方形． 23. （2010湖北）已知正方形ABCD ，以CD 为边作等边△CDE ，则∠AED 的度数是 .24. 已知正方形ABCD 中，AC ，BD 交于点O ，OE ⊥BC 于E ，若OE =2，则正方形的面积为____．25. 如图，已知，正方形ABCD 的对角线交于O ，过O 点作OE ⊥OF ，分别交AB 、BC 于E 、F ，若AE =4，CF =3，则EF 等于（ ）A ．7B ．5C ．4D ．326. （2011贵州）如图，点E 是正方形ABCD 内一点，△CDE 是等边三角形，连接EB 、EA ，延长BE 交边AD 于点F . （1）求证: △ADE ≌△BCE ； （2）求∠AFB 的度数.FED CBA FE ODCBA三、测试提高【板块一】菱形的性质1. 若菱形两邻角的比为1:2，周长为24 cm ，则较短对角线的长为_____． 【板块二】菱形的判定2. （2011湖南）如图，小聪在作线段AB 的垂直平分线时，他是这样操作的：分别以A 和B 为圆心，大于12AB 的长为半径画弧，两弧相交于C 、D ，则直线CD 即为所求．根据他的作图方法可知四边形ADBC 一定是（ ） A ．矩形B ．菱形C ．正方形D ．等腰梯形 3. （2011湖北）顺次连接四边形ABCD 各边的中点所得四边形是菱形，则四边形ABCD 一定是（ ） A.菱形 B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形【板块三】菱形余矩形的性质4. （2011江苏）菱形具有而矩形不一定具有的性质是（ ）A ．对角线互相垂直B ．对角线相等C ．对角线互相平分D ．对角互补 【板块四】特殊四边形的判定5. 下列命题中，正确命题是( )A ．两条对角线相等的四边形是平行四边形；B ．两条对角线相等且互相垂直的四边形是矩形；C ．两条对角线互相垂直平分的四边形是菱形；D ．两条对角线平分且相等的四边形是正方形；四、课后作业1. 矩形ABCD 中，对角线AC ，BD 相交于点O ，∠AOB =60°，若BD =10 cm ，则AD =_____．2. 矩形周长为72cm ，一边中点与对边两个端点连线的夹角为直角，此矩形的长边为_______.3. 矩形的边长为10和15，其中一个内角平分线分长边为两部分，这两部分的长度分别为_________.4. 过矩形ABCD 的顶点D ，作对角线AC 的平行线交BA 的延长线于E ，则△DEB 是( ).A ． 不等边三角形B ． 等腰三角形C ． 等边三角形D ． 等腰直角三角形BACD5. 矩形ABCD 的对角线AC 的垂直平分线与边AD ，BC 分别交于E ，F ，则四边形AFCE 是___________．6. 菱形一个内角为120°，平分这个内角的一条对角线长12 cm ，则菱形的周长为_____．7. 若菱形两条对角线长分别为6 cm 和8 cm ，则它的周长是________，面积是_______．8. 菱形的一个角是60°，边长是8 cm ，那么菱形的两条对角线的长分别是_________．9. 已知菱形的一条对角线与边长相等，则菱形的邻角度数分别为_____. 10. 在菱形ABCD 中，AE ⊥BC ， AF ⊥CD ，且BE =EC ， CF =FD ，则∠AEF 等于_______.11. 如图，小华剪了两条宽为2的纸条，交叉叠放在一起，且它们交角为45°，则它们重叠部分的面积为（ ）. A.22 B.1 C.332 D.2 12. （2011广东）如图，两条笔直的公路1l 、2l 相交于点O ，村庄C 的村民在公路的旁边建三个加工厂A 、B 、D ，已知AB =BC =CD =DA =5公里，村庄C 到公路1l 的距离为4公里，则村庄C 到公路2l 的距离是（ ）. A ．3公里 B ．4公里C ．5公里D ．6公里13. 正方形的对角线__________且_________，每条对角线平分_____． 14. 如图，AC 是菱形ABCD 的对角线，点E 、F 分别在边AB 、AD 上，且AE =AF ． 求证：△ACE ≌△ACF ．FE BCDA15. （2011山东）如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，过点O 作直线EF ⊥BD ，分别交AD 、BC 于点E 和点F ，求证：四边形BEDF 是菱形．OFEDCBA。

初中数学几何的5大考点矩形、菱形、正方形的判定题型
1.矩形的判定
①有一个内角是直角的平行四边形是矩形；
②对角线相等的平行四边形是矩形；
③有三个角是直角的四边形是矩形；
④还有对角线相等且互相平分的四边形是矩形。

2.菱形的判定方法
①有一组邻边相等的平行四边形是菱形；
②对角线互相垂直的平行四边形是菱形；
③四条边都相等四边形是菱形；
④对角线垂直平分的四边形是菱形。

3.正方形的判定
①菱形+矩形的一条特征；
②菱形+矩形的一条特征；
③平行四边形+一个直角+一组邻边相等。

说明一个四边形是正方形的一般思路是：先判断它是矩形，在判断这个矩形也是菱形；或先判断它是菱形，再判断这个菱形也是矩形。

例1. 如图，在△ABC中，AB＝AC，点D是边BC的中点，过点A、D分别作BC与AB的平行线，并交于点E，连续EC、AD。

求证：四边形ADCE是矩形。

例2.如图，△ABC中，∠C=90°，AD平分∠BAC，ED⊥BC，DF//AB.
求证：AD与EF互相垂直平分。

例3.已知如图，在△ABC,∠ACB=900，AD是角平分线，点E、F分别在AB、AD上，且AE=AC，EF∥BC。

求证：四边形CDEF是菱形。

FC D 一、考点分析：矩形、正方形和菱形是特殊的平行四边形，是考试中重要的考点。

二、教学目标：1． 掌握矩形、正方形和菱形的判定方法三、教学内容正方形巩固练习例题1 如图,正方形ABCD 的边长为12,点E 是BC 上的一点,BE=5,点F 是BD 上一动点.（1）AF 与FC 相等吗?试说明理由.（2）设折线EFC 的长为y ，试求y 的最小值,并说明点F 此时的位置.【解】（1）AF 与FC 相等,其理由如下：可证：△ABF ≌△CBF ，∴AF=CF（2）连接AE,则AE 与BD 的交点就是此时F 点的位置 此时y 有最小值,13=.例题2 如图，正方形ABCD 中，P 是对角线AC 上一动点，PE ⊥AB ，PF ⊥BC ，垂足分别为E 、F 小红同学发现：PD ⊥EF ，且PD=EF ，且矩形PEBF 的周长不变．不知小红的发现是否正确，请说说你的看法．【解】小红的发现是正确，其理由如下：连接BP,延长DP 交EF 于Q.（1）∵四边形ABCD 是正方形∴CB=CD,∠BCP=∠DCP=45°∴△BCP ≌△DCP ，∴PD=PB又∵PE ⊥AB ，PF ⊥BC ， ∴∠BEP=∠BFP=∠EBF=90°，∴四边形BEPF 是矩形∴PB=EF,∴PD=EF（2）∵PE ⊥AB ，PF ⊥BC ，∴△AEP 和△CFP 均为等腰直角三角形∴AE=PE,CF=PF∴矩形PEBF 的周长=AB+BC=2AB （为定值）（3）∵PF ∥CD ，∴∠FPQ=∠PDC∵△BCP ≌△DCP ，∴∠PDC=∠PBF A B C D 第28题图 FE∵四边形PEBF 是矩形,∴∠PBF=∠PEF∴∠PEF=∠FPQ又∵∠PEF+∠PFE=90°，∴∠FPQ+∠PFE=90°∴∠PQF=90°，∴PD ⊥EF.【另证】延长EP 交CD 于点R,则CFPR 为正方形∴可证△PEF ≌△RDF∴∠PEF=∠PDR又∵∠DPR=∠EPQ而∠PDR+∠DPR=90°，∴∠PEF+∠EPQ=90°∴∠EQP=90°，∴PD ⊥EF.课堂练习1 如图1，在边长为5的正方形ABCD 中，点E 、F 分别是BC 、DC 边上的点，且AE EF ⊥，2BE =（1）如图2，延长EF 交正方形外角平分线CP P 于点，试判断AE EP 与的大小关系，并说明理由；（2）在图2的AB 边上是否存在一点M ，使得四边形DMEP 是平行四边形？若存在，请给予证明；若不存在，请说明理由．梯形回顾梯形性质及判断定理 梯形 一组对边平行而另一组对边不平行的四边形叫做梯形． （1）一些基本概念（如图）：底、腰、高．底：平行的一组对边叫做梯形的底.（较短的底叫做上底，较长的底叫做下 底）腰：不平行的一组对边叫做梯形的腰.高：两底间的距离叫做梯形的高.直角梯形：一腰垂直于底的梯形叫做直角梯形.等腰梯形：两腰相等的梯形叫做等腰梯形.（2）等腰梯形：两腰相等的梯形叫做等腰梯形． （3）直角梯形：有一个角是直角的梯形叫做直角梯形．结论：①等腰梯形是轴对称图形，上下底的中点连线是对称轴．②等腰梯形同一底上的两个角相等．③等腰梯形的两条对角线相等．解决梯形问题常用的方法：图1A D CB E 图2 BC ED A F P F（1）“平移腰”：把梯形分成一个平行四边形和一个三角形；（2）“作高”：使两腰在两个直角三角形中（3）“平移对角线”：使两条对角线在同一个三角形中（4）“延腰”：构造具有公共角的两个等腰三角形（5）“等积变形”，连结梯形上底一端点和另一腰中点，并延长与下底延长线交于一点，构成三角形（图5）．图1 图2 图3 图4 图5 综上所述：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．例1．如图，梯形ABC D中，AD∥BC，∠B=70°，∠C=40°，AD=6cm，BC=15cm．求CD的长．分析：设法把已知中所给的条件都移到一个三角形中，便可以解决问题．其方法是：平移一腰，过点A作AE∥DC交BC于E，因此四边形AECD是平行四边形，由已知又可以得到△ABE是等腰三角形（EA=EB），因此CD=EA=EB=BC—EC=BC—AD=9cm．解（略）．例2 （补充）已知：如图，在梯形ABCD中，AD∥BC，∠D＝90°，∠CAB ＝∠ABC， BE⊥AC于E．求证：BE＝C D．分析：要证BE=CD，需添加适当的辅助线，构造全等三角形，其方法是：平移一腰，过点D作DF∥AB交BC于F，因此四边形ABFD是平行四边形，则DF=AB，由已知可导出∠DFC=∠BAE，因此Rt△ABE≌Rt△FDC（AAS），故可得出BE=CD．证明（略）另证：如图，根据题意可构造等腰梯形ABFD，证明△ABE≌△FDC即可．例3：如图 4.9-4，梯形ABCD中，AD∥BC，∠B=70°，∠C=40°，AD=6cm，BC=15cm,求CD的长.练习1已知等腰梯形的锐角等于60°它的两底分别为15cm和49cm，求它的腰长.练习2 已知：如图4.9-5，梯形ABCD中，AD∥BC，E是AB的中点，DE⊥CE，求证：AD+BC=DC.练习3：1、填空（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= .（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和 .（3）等腰梯形 ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= .4，（1）求梯形2、如图4.9-6，等腰梯形ABCD中，AB=2CD，AC平分∠DAB，A B＝3的各角.（2）求梯形的面积.3、（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= ．（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和．（3）等腰梯形ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= ．4．已知：如图，在等腰梯形ABCD中，A B∥CD，AB＞CD，AD=BC，BD平分∠ABC，∠A=60°，梯形周长是20cm，求梯形的各边的长．（AD=DC=BC=4，AB=8）课堂小结1、梯形的定义及分类2、等腰梯形的性质：（1）具有一般梯形的性质：AD∥BC.（2）两腰相等：AB=CD.（3）两底角相等：∠B=∠C，∠A=∠D.（4）是轴对称图形，对称轴是通过上、下底中点的直线.（5）两条对角线相等：AC=BD.两条对角线的交点在对称轴上.两腰延长线的交点在对称轴上.等腰梯形的判断例2（补充）证明：对角线相等的梯形是等腰梯形．已知：如图，梯形ABCD中，对角线AC=BD．求证：梯形ABCD是等腰梯形．分析：证明本题的关键是如何利用对角线相等的条件来构造等腰三角形．在ΔABC和ΔDCB中，已有两边对应相等，要能证∠1=∠2，就可通过证ΔABC ≌ΔDCB得到AB=DC．证明：过点D作DE∥AC，交BC的延长线于点E，又AD∥BC，∴四边形ACED为平行四边形，∴DE=AC ．∵ AC=BD ，∴ DE=BD ∴∠1=∠E∵∠2=∠E ，∴∠1=∠2又 AC=DB，BC=CE，∴ΔABC≌ΔDCB．∴ AB=CD．∴梯形ABCD是等腰梯形．说明：如果AC、BD交于点O，那么由∠1=∠2可得OB=OC，OA=OD ，即等腰梯形对角线相交，可以得到以交点为顶点的两个等腰三角形，这个结论虽不能直接引用，但可以为以后解题提供思路．问：能否有其他证法，引导学生作出常见辅助线，如图，作AE⊥BC，DF⊥BC，可证RtΔABC≌RtΔCAE，得∠1=∠2．例3（补充）已知：如图，点E在正方形ABCD的对角线AC上，CF⊥BE交BD 于G，F是垂足．求证：四边形ABGE是等腰梯形．分析：先证明OE＝OG，从而说明∠OEG＝45°，得出EG∥AB，由AE，BG延长交于O，显然EG≠AB．得出四边形ABGE是梯形，再利用同底上的两角相等得出它为等腰梯形．例4 （补充）画一等腰梯形，使它上、下底长分别4cm、12cm，高为3cm，并计算这个等腰梯形的周长和面积．分析：梯形的画图题常常通过分析，找出需添加的辅助线，归结为三角形或平行四边形的作图，然后，再根据它们之间的联系，画出所要求的梯形．如图，先算出AB长，可画等腰三角形ABE，然后完成AECD的画图．画法：①画ΔABE，使BE=12—4=8cm．.②延长BE到C使EC=4cm.③分别过A、C作AD∥BC ，CD∥AE，AD、CD交于点D．四边形ABCD就是所求的等腰梯形．解：梯形ABCD周长＝4＋12＋5×2＝26cm ．cm．答：梯形周长为26cm，面积为242例5：.如图4.9-4，已知等腰梯形ABCD的腰长为5cm，上、下底长分别是6cm和12cm，求梯形的面积. （方法一，过点C作CE∥AD，再作等腰三角形BCE的高CF，可知CF=4cm.然后用梯形面积公式求解；方法二，过点C和D分别作高CF、DG，可知，从而在Rt△AGD中求出高DG=4cm. ）课后练习1、填空（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= .（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和 .（3）等腰梯形 ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= .4，（1）求梯形2、如图4.9-6，等腰梯形ABCD中，AB=2CD，AC平分∠DAB，A B＝3的各角.（2）求梯形的面积.3、（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= ．（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和．（3）等腰梯形ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= ．4．已知：如图，在等腰梯形ABCD中，A B∥CD，AB＞CD，AD=BC，BD平分∠ABC，∠A=60°，梯形周长是20cm，求梯形的各边的长．（AD=DC=BC=4，AB=8）。

判定“矩形、菱形与正方形”的误区矩形、菱形、正方形是三类特殊的平行四边形，有关判定是其重要内容，初学时，不少同学们会出现各种错误．本文将分类对有关常见判定误区进行剖析，供参考．一、有关矩形判定的误区例1判断下列说法是否正确（1）有三个角相等的四边形是矩形．（2）对角线相等的四边形是矩形．错解：（1）正确；（2）正确．剖析：（1）是把矩形的识别方法记错了，应是“有三个角是直角的四边形是矩形”，其中的条件是“三个角是直角”而不是“三个角相等”；（2）中错误地认为“对角线相等的四边形是矩形”，对矩形的识别方法理解不透彻．我们知道只有在平行四边形中加上“对角线相等”的条件，得到的才是矩形．正解：（1）错误；（2）错误．二、有关菱形判定的误区例2如图，已知在平行四边形ABCD 中，∠A 的平分线与BC 交于点E ，∠B 的平分线与AD 交于点F ，AE 与BF 交于点O ，试说明：四边形ABEF 是菱形．错解：因为四边形ABCD 是平行四边形，所以4321F E O DC B AAD∥BC，所以∠ABE∠BAF=180º．因为AE 、BF分别是∠BAF、∠ABE 的平分线，所以∠1=∠2=21 ∠BAF，∠3=∠4=21∠ABE．所以∠1∠3=21（∠BAF∠ABE）=21×180º=90º，即∠AOB=90º，所以AE⊥BF，所以四边形ABEF 是菱形．剖析：本题的说理步骤看似严密，实际上忽略了菱形的判定条件，只有对角线垂直的四边形不是菱形，必须还要说明对角线互相平分，或者再说明四边形是平行四边形才能判定它是菱形．正解：因为四边形ABCD 是平行四边形，所以AD∥BC，所以∠ABE∠BAF=180º．因为AE 、BF 分别是∠BAF、∠ABE 的平分线，所以∠1=∠2=21∠BAF，∠3=∠4=21∠ABE．所以∠1∠3=21（∠BAF∠ABE）=21×180º=90º，即∠AOB=90º，所以AE⊥BF．因为∠4=∠AFB，∠4=∠3．所以∠3=∠AFB．所以AF=AB ．同理BE=AB ．所以AF=BE ．又因为AF∥BE．所以四边形ABEF 是平行四边形．所以ABEF 是菱形．三、有关正方形判定的误区例3判断下列说法是否正确（1）四条边相等的四边形是正方形．（2）两条对角线相等且互相垂直的四边形是正方形．（3）两条对角线分别平分一组对角的四边形是正方形． 错解：（1）正确；（2）正确；（3）正确．剖析：（1）虽有四条边相等，但只能判定它是菱形，要判定它是正方形，还缺少一个条件，这个条件是一角是直角，或其他判定是菱形又是矩形的条件；（2）此题错误是对正方形的识别方法不清楚造成的，对角线相等且互相垂直，但对角线不一定平分，故不能判定它是正方形；（3）片面应用了正方形的性质，虽然正方形的每一条对角线都平分每一组对角，但反过来就不成立了，它只能判定是菱形，还缺少一个再判断它是矩形的条件．正解：（1）错误；（2）错误；（3）错误．。

正方形是菱形吗及其判定
正方形是特殊的菱形。

正方形一定是菱形，而菱形未必是正方形。

不过不管是正方形还是菱形他们的边都是相等的。

正方形与菱形菱形：在同一平面内，有一组邻边相等的平行四边形是菱形，四边都相等的四边形是菱形，菱形的对角线互相垂直平分且平分每一组对角，菱形是轴对称图形，对称轴有2条，即两条对角线所在直线，菱形是中心对称图形。

正方形：有一组邻边相等且一个角是直角的平行四边形叫做正方形。

有一组邻边相等的矩形叫做正方形，有一个角是90°的菱形叫做正方形。

正方形是矩形的特殊形式，也是菱形的特殊形式。

1、正方型是四条边都相等、四个角都是直角、对角线相等。

2、菱型虽四条边都相等、但四个角不一定相等、且对角线都是相互垂直但不一定相等。

菱形的判定1、一组邻边相等的平行四边形是菱形；
2、对角线互相垂直的平行四边形是菱形；
3、四条边均相等的四边形是菱形；
4、对角线互相垂直平分的四边形；
5、两条对角线分别平分每组对角的四边形；
6、有一对角线平分一个内角的平行四边形。

平行四边形、菱形、矩形、正方形性质和判定归纳如表
-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
一、两条平行线的距离：
定义：两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条平行线的距离。

注意：平行线间的距离处处相等。

二、矩形的一条对角线把矩形分成两个直角三角形，与之相联系的还有以下性质：
（1）直角三角形的两个锐角互余。

（2）直角三角形两直角边的平方和等于斜边的平方。

（即勾股定理）
（3）直角三角形斜边上的中线等于斜边的一半。

（4）直角三角形中30 角所对的直角边等于斜边的一半。

四种特殊四边形的性质
3
四种特殊四边形常用的判定方法：
4
一组邻
对角线
对角线对角线垂
5。

§20.3.矩形、菱形、正方形----菱形的判定复习巩固1、矩形的判定定理： 从角考虑：___________________________的平行四边形是矩形。

从对角线考虑：____________________________的平行四边形是矩形。

从角考虑：____________________________的四边形是矩形。

2.矩形的性质：3.菱形的性质：4、菱形的判定方法1: 定义：有一组邻边__________的平行四边形是菱形. 几何表示：∵四边形ABCD 是平行四边形，AB=CD∴四边形ABCD 是菱形。

5、菱形的判定方法2: ________________平行四边形是菱形． 应用判定方法2时，要注意其性质包括两个条件：（1）是平行四边形；（2）两条对角线互相垂直．已知：平行四边形ABCD ，对角线AC⊥BD ，求证：四边形ABCD 是菱形证明：在ABCD 中，OB=OD∵AC ⊥BD∴∠AOB____∠AOD在△AOB 与△AOD 中,∴四边形ABCD 是菱形思考：对角线互相垂直的四边形是菱形吗？为什么？____________________________________ 画一个菱形，使它的边长为6cm 。

（草稿）通过菱形的作图，可以得到从一般四边形直接判定菱形的方法：6.菱形的判定方法3：___________的四边形是菱形．已知:四边形ABCD 中,AB=BC=CD=DA 求证：四边形ABCD 是菱形。

证明：已知：如图ABCD 的垂直平分线与边AD 、BC 分别交12（2011云南保山）如图，在平行四边形ABCD 中，点P 是对角线AC 上一点，PE ⊥AB ，PF ⊥AD ，垂足分别为E 、F ，且PE=PF ，平行四边形ABCD 是菱形吗？为什么？13.如图所示，在梯形ABCD 中，AD ∥BC ，AB=AD ，∠BAD 的平分线AE 交BC 于点E ，连接DE ． （1）求证：四边形ABED 是菱形；（2）若∠ABC=60°，CE=2BE ，试判断△CDE 的形状，并说明理由．15.已知：如图，在梯形ABCD 中，AB ∥CD ，BC =CD ，AD ⊥BD ，E 为AB 中点，求证：四边形BCDE 是菱形．16. 如图，在□ABCD 中，E ，F 分别为边AB ，CD 的中点，连结DE ，BF ，BD ． (1)求证：△ADE ≌△CBF ．(2)若AD ⊥BD ，则四边形BFDE 是什么特殊四边形?请证明你的结论．17.（2011新疆乌鲁木齐）如图，在平行四边形ABCD 中，∠DAB ＝60°，AB ＝2AD ，点 E 、F 分别是CD 的中点，过点A 作AG ∥BD ，交CB 的延长线于点G ．（1）求证：四边形DEBF 是菱形；（2）请判断四边形AGBD 是什么特殊四边形？并加以证明．18.如图，四边形ABCD 中，AB ∥CD ，AC 平分∠BAD ，CE ∥AD 交AB 于E ．(1)求证：四边形AECD 是菱形；(2)若点E 是AB 的中点，试判断△ABC 的形状，并说明理由．19.如图，在四边形ABCD 中，AB ＝CD ，M ，N ，P ，Q 分别是AD ，BC ，BD ，AC 的中点．求证：MN 与PQ 互相垂直平分。

【关键字】分析一、考点分析：矩形、正方形和菱形是特殊的平行四边形，是考试中重要的考点。

二、教学目标：1．掌握矩形、正方形和菱形的判定方法三、教学内容正方形巩固练习例题1 如图,正方形ABCD的边长为12,点E是BC上的一点,BE=5,点F是BD上一动点.（1）AF与FC相等吗?试说明理由.（2）设折线EFC的长为y，试求y的最小值,并说明点F此时的位置.【解】（1）AF与FC相等,其理由如下：可证：△ABF≌△CBF，∴AF=CF（2）连接AE,则AE与BD的交点就是此时F点的位置此时有最小值,最小值为.例题2 如图，正方形ABCD中，P是对角线AC上一动点，PE⊥AB，PF⊥BC，垂足分别为E、F小红同学发现：PD⊥EF，且PD=EF，且矩形PEBF的周长不变．不知小红的发现是否正确，请说说你的看法．【解】小红的发现是正确，其理由如下：连接BP,延长DP交EF于Q.（1）∵四边形ABCD是正方形∴CB=CD,∠BCP=∠DCP=45°∴△BCP≌△DCP，∴PD=PB又∵PE⊥AB，PF⊥BC，∴∠BEP=∠BFP=∠EBF=90°，∴四边形BEPF是矩形∴PB=EF,∴PD=EF（2）∵PE⊥AB，PF⊥BC，∴△AEP和△CFP均为等腰直角三角形∴AE=PE,CF=PF∴矩形PEBF的周长=AB+BC=2AB（为定值）（3）∵PF∥CD，∴∠FPQ=∠PDC∵△BCP≌△DCP，∴∠PDC=∠PBF∵四边形PEBF是矩形,∴∠PBF=∠PEF∴∠PEF=∠FPQ又∵∠PEF+∠PFE=90°，∴∠FPQ+∠PFE=90°∴∠PQF=90°，∴PD⊥EF.【另证】延长EP交CD于点R,则CFPR为正方形∴可证△PEF≌△RDF∴∠PEF=∠PDR又∵∠DPR=∠EPQ而∠PDR+∠DPR=90°，∴∠PEF+∠EPQ=90°∴∠EQP=90°，∴PD⊥EF.课堂练习1 如图1，在边长为5的正方形中，点、分别是、边上的点，且，（1）如图2，延长交正方形外角平分线，试判断的大小关系，并说明理由；（2）在图2的边上是否存在一点，使得四边形是平行四边形？若存在，请给予证明；若不存在，请说明理由．梯形回顾梯形性质及判断定理梯形一组对边平行而另一组对边不平行的四边形叫做梯形．（1）一些基本概念（如图）：底、腰、高．底：平行的一组对边叫做梯形的底.（较短的底叫做上底，较长的底叫做下底）腰：不平行的一组对边叫做梯形的腰.高：两底间的距离叫做梯形的高.直角梯形：一腰垂直于底的梯形叫做直角梯形.等腰梯形：两腰相等的梯形叫做等腰梯形.（2）等腰梯形：两腰相等的梯形叫做等腰梯形．（3）直角梯形：有一个角是直角的梯形叫做直角梯形．结论：①等腰梯形是轴对称图形，上下底的中点连线是对称轴．②等腰梯形同一底上的两个角相等．③等腰梯形的两条对角线相等．解决梯形问题常用的方法：（1）“平移腰”：把梯形分成一个平行四边形和一个三角形；（2）“作高”：使两腰在两个直角三角形中（3）“平移对角线”：使两条对角线在同一个三角形中（4）“延腰”：构造具有公共角的两个等腰三角形（5）“等积变形”，连结梯形上底一端点和另一腰中点，并延长与下底延长线交于一点，构成三角形（图5）．图1 图2 图3 图4 图5 综上所述：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．例1．如图，梯形ABC D中，AD∥BC，∠B=70°，∠C=40°，AD=6cm，BC=15cm．求CD的长．分析：设法把已知中所给的条件都移到一个三角形中，便可以解决问题．其方法是：平移一腰，过点A作AE∥DC交BC于E，因此四边形AECD是平行四边形，由已知又可以得到△ABE是等腰三角形（EA=EB），因此CD=EA=EB=BC—EC=BC—AD=9cm．解（略）．例2 （补充）已知：如图，在梯形ABCD中，AD∥BC，∠D＝90°，∠CAB ＝∠ABC， BE⊥AC于E．求证：BE＝C D．分析：要证BE=CD，需添加适当的辅助线，构造全等三角形，其方法是：平移一腰，过点D作DF∥AB交BC于F，因此四边形ABFD是平行四边形，则DF=AB，由已知可导出∠DFC=∠BAE，因此Rt△ABE≌Rt△FDC（AAS），故可得出BE=CD．证明（略）另证：如图，根据题意可构造等腰梯形ABFD，证明△ABE≌△FDC即可．例3：如图 4.9-4，梯形ABCD中，AD∥BC，∠B=70°，∠C=40°，AD=6cm，BC=15cm,求CD的长.练习1已知等腰梯形的锐角等于60°它的两底分别为15cm和49cm，求它的腰长.练习2 已知：如图4.9-5，梯形ABCD中，AD∥BC，E是AB的中点，DE⊥CE，求证：AD+BC=DC.练习3：1、填空（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= .（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和 .（3）等腰梯形 ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= .4，（1）求梯形2、如图4.9-6，等腰梯形ABCD中，AB=2CD，AC平分∠DAB，A B＝3的各角.（2）求梯形的面积.3、（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= ．（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和．（3）等腰梯形ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= ．4．已知：如图，在等腰梯形ABCD中，A B∥CD，AB＞CD，AD=BC，BD平分∠ABC，∠A=60°，梯形周长是20cm，求梯形的各边的长．（AD=DC=BC=4，AB=8）课堂小结1、梯形的定义及分类2、等腰梯形的性质：（1）具有一般梯形的性质：AD∥BC.（2）两腰相等：AB=CD.（3）两底角相等：∠B=∠C，∠A=∠D.（4）是轴对称图形，对称轴是通过上、下底中点的直线.（5）两条对角线相等：AC=BD.两条对角线的交点在对称轴上.两腰延长线的交点在对称轴上.等腰梯形的判断例2（补充）证明：对角线相等的梯形是等腰梯形．已知：如图，梯形ABCD中，对角线AC=BD．求证：梯形ABCD是等腰梯形．分析：证明本题的关键是如何利用对角线相等的条件来构造等腰三角形．在ΔABC和ΔDCB中，已有两边对应相等，要能证∠1=∠2，就可通过证ΔABC ≌ΔDCB得到AB=DC．证明：过点D作DE∥AC，交BC的延长线于点E，又AD∥BC，∴四边形ACED为平行四边形，∴DE=AC ．∵ AC=BD ，∴ DE=BD ∴∠1=∠E∵∠2=∠E ，∴∠1=∠2又 AC=DB，BC=CE，∴ΔABC≌ΔDCB．∴ AB=CD．∴梯形ABCD是等腰梯形．说明：如果AC、BD交于点O，那么由∠1=∠2可得OB=OC，OA=OD ，即等腰梯形对角线相交，可以得到以交点为顶点的两个等腰三角形，这个结论虽不能直接引用，但可以为以后解题提供思路．问：能否有其他证法，引导学生作出常见辅助线，如图，作AE⊥BC，DF⊥BC，可证RtΔABC≌RtΔCAE，得∠1=∠2．例3（补充）已知：如图，点E在正方形ABCD的对角线AC上，CF⊥BE交BD 于G，F是垂足．求证：四边形ABGE是等腰梯形．分析：先证明OE＝OG，从而说明∠OEG＝45°，得出EG∥AB，由AE，BG延长交于O，显然EG≠AB．得出四边形ABGE是梯形，再利用同底上的两角相等得出它为等腰梯形．例4 （补充）画一等腰梯形，使它上、下底长分别4cm、12cm，高为3cm，并计算这个等腰梯形的周长和面积．分析：梯形的画图题常常通过分析，找出需添加的辅助线，归结为三角形或平行四边形的作图，然后，再根据它们之间的联系，画出所要求的梯形．如图，先算出AB长，可画等腰三角形ABE，然后完成AECD的画图．画法：①画ΔABE，使BE=12—4=8cm．.②延长BE到C使EC=4cm.③分别过A、C作AD∥BC ，CD∥AE，AD、CD交于点D．四边形ABCD就是所求的等腰梯形．解：梯形ABCD周长＝4＋12＋5×2＝26cm ．cm．答：梯形周长为26cm，面积为242例5：.如图4.9-4，已知等腰梯形ABCD的腰长为5cm，上、下底长分别是6cm和12cm，求梯形的面积. （方法一，过点C作CE∥AD，再作等腰三角形BCE的高CF，可知CF=4cm.然后用梯形面积公式求解；方法二，过点C和D分别作高CF、DG，可知，从而在Rt△AGD中求出高DG=4cm. ）课后练习1、填空（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= .（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和 .（3）等腰梯形 ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= .4，（1）求梯形2、如图4.9-6，等腰梯形ABCD中，AB=2CD，AC平分∠DAB，A B＝3的各角.（2）求梯形的面积.3、（1）在梯形ABCD中，已知AD∥BC，∠B=50°，∠C=80°，AD=a，BC=b，,则DC= ．（2）直角梯形的高为6cm，有一个角是30°，则这个梯形的两腰分别是和．（3）等腰梯形ABCD中，AB∥DC，A C平分∠DAB，∠DAB=60°，若梯形周长为8cm，则AD= ．4．已知：如图，在等腰梯形ABCD中，A B∥CD，AB＞CD，AD=BC，BD平分∠ABC，∠A=60°，梯形周长是20cm，求梯形的各边的长．（AD=DC=BC=4，AB=8）此文档是由网络收集并进行重新排版整理.word可编辑版本！。