变形协调条件-选择

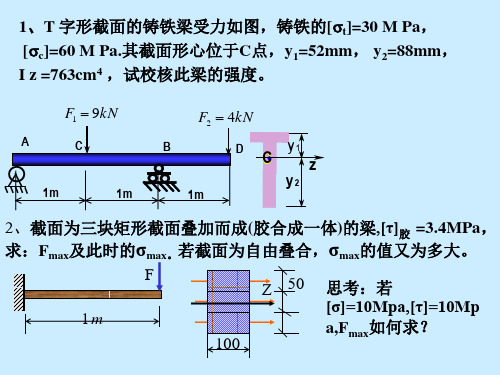
材料力学试题及答案一、单项选择题1. 截面上的全应力的方向（ ）A 、平行于截面B 、垂直于截面C 、可以与截面任意夹角D 、与截面无关 2. 脆性材料的延伸率（ ）A 、小于5%B 、小于等于5%C 、大于5%D 、大于等于5%3. 如图所示简支梁，已知C 点转角为θ。

在其它条件不变的情况下，若将荷载F 减小一半，则C 点的转角为（ ） A 、0.125θ B 、0.5θ C 、θ D 、2θ4.危险截面是（）所在的截面。

A 、最大面积B 、最小面积C 、最大应力D 、最大内力 5. 图示单元体应力状态，沿x 方向的线应变εx 可表示为（ ） A 、E yσ B 、)(1y x Eμσσ- C 、)(1x y E μσσ- D 、Gτ 6. 描述构件上一截面变形前后的夹角叫（A 、线位移B 、转角C 、线应变D 、角应变7. 塑性材料的名义屈服应力使用（ ）A 、σS 表示B 、σb 表示C 、σp 表示 D 、σ0.2表示 8.拉（压）杆应力公式A F N=σ的应用条件是（）A 、应力在比例极限内B 、应力在屈服极限内C 、外力合力作用线必须沿着杆的轴线D 、杆件必须为矩形截面杆9.下列截面中，弯曲中心与其形心重合者是（）A 、Z 字形型钢B 、槽钢C 、T 字形型钢D 、等边角钢10. 如图所示简支梁，已知C 点转角为θ。

在其它条件不变的情况下，若将杆长增加一倍，则C 点的转角为（ ）A 、2θB 、4θC 、8θD 、16θ二、填空题1. 用主应力表示的第四强度理论的相当应力是 。

2. 已知自由落体冲击问题的动荷系数K d ，对应静载荷问题的最大位移为Δjmax ，则冲击问题的最大位移可以表示为 。

3. 图示木榫联接。

横截面为正方形，边长为a ，联接处长度为2t 。

则木榫联接处受剪切面的名义切应力等于 。

4. 主平面上的切应力等于 。

5. 功的互等定理的表达式为 。

6.自由落体冲击问题的动荷系数为jd hK ∆++=211，其中h 表示 。

⼯程⼒学-选择题刚体受三⼒作⽤⽽处于平衡状态，则此三⼒的作⽤线（）。

A.必汇交于⼀点 B.必互相平⾏ C.必都为零 D.必位于同⼀平⾯内答案：A 题型：单选题2.（）的横截⾯是轴向拉压杆件的危险截⾯。

A.轴⼒最⼤ B.正应⼒最⼤ C.⾯积最⼩ D.位移最⼤答案:B 题型:单选题3. 关于平⾯任意⼒系的主⽮和主矩，下述说法正确的是（）。

A.主⽮的⼤⼩.⽅向与简化中⼼⽆关B.主矩的⼤⼩.转向⼀定与简化中⼼的选择有关C.当平⾯任意⼒系对某点的主矩为零时，该⼒系向任何⼀点简化结果为⼀合⼒D.当平⾯⼒系对某点的主矩不为零时，该⼒系向任⼀点简化的结果均不可能为⼀合⼒答案:A 题型:单选题4. 如图所⽰两根梁，l ，b 和P 均相同，若梁的横截⾯⾼度h 减⼩为h/2，则梁中的最⼤正应⼒是原梁的（）。

倍倍倍倍答案:B 题型:单选题5. 梁受⼒如图所⽰，在B 截⾯处：（）。

A.剪⼒图有突变，弯矩图连续光滑B.剪⼒图有折⾓（或尖⾓），弯矩图有突变 C.剪⼒图有突变，弯矩图也有突变 D.剪⼒图没有突变，弯矩图有突变答案:D 题型:单选题6.⼀内外径之⽐为/d D α=的空⼼圆轴，当两端受扭矩时，横截⾯上的最⼤剪应⼒为τ，则内圆周处的剪应⼒为（）。

A.τ B.ατ C.3(1)ατ- D.4(1)ατ-答案:B 题型:单选题7. 如图所⽰的⼒平⾏四边形中，表⽰⼒R F 是1F 和2F 两⼒合⼒的图形是（）。

2 ( d )2( c )2( b )2( a )A.图（a ）B.图（b ）C.图（c ）D.图（d ）答案:A 题型:单选题8. ⼒偶对物体产⽣的运动效应为（）。

A.只能使物体转动 B.只能使物体移动C.既能使物体转动，⼜能使物体移动D.它与⼒对物体产⽣的运动效应有时相同，有时不同答案:A 题型:单选题9.图⽰杆的抗拉（压）刚度为）。

A.PlEA B.Pl EA-C.0D.3PlEA答案:C 题型:单选题10.空⼼圆轴的内外半径分别为d 和D ，其抗扭截⾯系数为（）。

一、填空题:请将正确答案写在划线内（每空1分，计16分）⒈工程构件正常工作的条件是――――――――――――、、――――――――――――、―――――――――――――。

⒉工程上将延伸律的材料称为脆性材料。

⒊矩形截面梁横截面上最大剪应力出现在―――――――――――各点，其值——-——-———-—-—。

4．平面弯曲梁的q、F s、M微分关系的表达式分别为-—---———----—-、、--—-——---—-—-、、。

----——-——--—---—5．四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、――――――――――――――、―――――――――――――――――――――――――――――――――。

6．用主应力表示的广义虎克定律为―――――――――――――――――――――；――――――――――――――――――――――；－―――――――――――――――――――――――。

二、单项选择题⒈没有明显屈服平台的塑性材料，其破坏应力取材料的――――――――――――。

⑴比例极限；⑵名义屈服极限;⑶强度极限; ⑷根据需要确定。

２．矩形截面的核心形状为—--—-—--—-—--—--—-—--————————-——---———-—-——-—-。

⑴矩形；⑵菱形; ⑶正方形；⑷三角形。

3．杆件的刚度是指――――――――――――――－。

⑴杆件的软硬程度；⑵杆件的承载能力；⑶杆件对弯曲变形的抵抗能力；⑷杆件对弹性变形的抵抗能力；4。

图示二向应力单元体,如剪应力改变方向，则―――――――――――――。

⑴主应力的大小和主平面的方位都将改变；⑵主应力的大小和主平面的方位都不会改变;⑶主应力的大小不变,主平面的方位改变；⑷主应力的大小改变,主平面的方位不变。

5、图示拉杆头和拉杆的横截面均为圆形，拉杆头的剪切面积A＝――――――――――――。

A。

B。

C. D.6、当系统的温度升高时，下列结构中的――――――――――不会产生温度应力.A BC D三、简答题（每小题6分，计12分）１．支承情况不同的圆截面压杆如图所示，已知各杆的直径和材料均相同且都为大柔度杆.①若只考虑纸平面内的稳定，问：那个杆的临界力最大?②若在保持截面的面积不变的条件下将各压杆的截面改成正方形，试问各压杆的稳定性是提高了还是降了？２．分别按第三和第四强度理论设计弯扭组合变形杆件的截面，按第三强度论设计的杆件截面比按第四强度理论设计的截面那个大？为什麽?四、（１2分)某形截面的外伸梁如图所示，已知：,截面对中性轴的惯性矩,,.梁上的荷载。

第五章 梁的变形测试练习1. 判断改错题5-1-1 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零. （ ）5-1-2 两根几何尺寸、支承条件完全相同的静定梁，只要所受荷栽相同，则两梁所对应的截面的挠度及转角相同，而与梁的材料是否相同无关。

（ ） 5-1-3 悬臂梁受力如图所示，若A 点上作用的集中力P 在A B 段上作等效平移，则A 截面的转角及挠度都不变。

（ ） 5-1-4 图示均质等直杆（总重量为W ），放置在水平刚性平面上，若A 端有一集中力P 作用，使A C 部分被提起，C B 部分仍与刚性平面贴合矩均为零。

（ ）5-1-5挠曲线近似微分方程不能用于求截面直梁的位移。

（ ） 5-1-6 等截面直梁在弯曲变形时，挠度曲线的曲率最大值发生在转角等于零的截面处。

（ ） 5-1-7两简支梁的抗刚度E I 及跨长2a 均相同，受力如图所示，则两梁跨中截面的挠度不等而转角是相等的。

（ ） 5-1-8 简支梁在图示任意荷载作用下，截面C 产生挠度和转角，若在跨中截面C 又加上一个集中力偶M 0作用，则梁的截面C 的挠度要改变，而转角不变。

( )题5-1-3图 B 题5-1-4图 C 2 2 题5-1-8图题5-1-7图5-1-9 一铸铁简支梁，在均布载荷作用下，当其横截面相同且分别按图示两种情况放置时，梁同一截面的应力及变形均相同。

（ ） 5-1-10 图示变截面梁，当用积分法求挠曲线方程时，因弯矩方程有三个，则通常有6个积分常量。

（ ）2．填空题5-2-1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在 和 。

5-2-2 已知图示二梁的抗弯度E I 相同，若使二者自由端的挠度相等，则=21P P 。

5-2-3 应用叠加原理求梁的变形时应满足的条件是： 。

5-2-4 在梁的变形中挠度和转角之间的关系是 。

5-2-5 用积分法求图示的外伸梁（B D 为拉杆）的挠曲线方程时，求解积分常量所用到的边界条件是 ，连续条件是 。

第一章绪论1. 判断改错题1-1-1 铸铁结构由于没有屈服阶段，所以在静载作用时可以不考虑其应力集中的影响。

( × )应考虑其应力集中的影响。

因铸铁属脆性材料，因此构件在静载作用时，在尺寸突变处，没有明显的塑性变形来缓和应力的增加，应力集中使该处的应力远大于其它各处的应力，构件首先从该处破坏，所以静载作用时应该考虑应力集中的影响。

1-1-2 构件内力的大小不但与外力大小有关，还与材料的截面形状有关。

（ × ）。

静定构件内力的大小只与外力大小有关，与材料的截面无关。

1-1-3 钢筋混凝土柱中，钢筋与混凝土柱高度相同，受压后，钢筋与混凝土柱的压缩量相同，所以二者所受的内力也相同。

（ × ） 它们的内力大小不一定相同。

钢筋混凝土柱受压后，由于钢筋的弹性模量E 1不等于混凝土的弹性模量E 2，钢筋横截面积A 1 也不等于混凝土的横截面积A 2，所以有 ,221121221112122221111,,,2A E AE N N A E N A E N l l A E l N l A E l N l ==∆=∆=∆=∆故在E 1 A 1=E 2 A 2 时，才有N 1=N 2 。

否则21N N ≠。

1-1-4 杆件的某横截面上，若各点的正应力均为零，则该截面上的轴力为零。

（ √）1-1-5 只要构件的强度得到保证，则该构件就能正常的工作。

（ × ）。

只有构件的强度、刚度、稳定性都得到满足，构件才能正常工作。

1-1-6 两根材料、长度l 都相同的等直柱子，一根的横截面面积为A 1，另一根为A 2，且A 2>A 1.如图所示。

两杆都受自重作用。

则两杆的最大压应力相等，最大压缩量也相等。

（ √ ）。

自重作用时，最大压应力在两杆底端，即l AAlA N ννσ===max max也就是说，最大应力与面积无关，只与杆长有关。

所以两者的最大压应力相等。

最大压缩量为El EA lAl l 222max νν=⋅=∆ 即最大压缩量与面积无关，只与杆长有关。

二、轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d) 解：。

2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6) 图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9) 一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11) 受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

试求C点的水平位移和铅垂位移。

解：（1）受力图（a），。

（2）变形协调图（b）因，故=（向下）（向下）为保证，点A移至，由图中几何关系知；返回第三章扭转3-13-23-33-43-53-63-73-83-93-103-113-123-1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮，Ⅰ，Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。

江 苏 科 技 大 学学年第二学期材料力学试题（A 卷）一、 选择题（20分)1、图示刚性梁AB 由杆1和杆2支承，已知两杆的材料相同，长度不等，横截面积分别为A 1和A 2，若载荷P 使刚梁平行下移,则其横截面面积（ ）。

A 、A 1〈A 2B 、A 1 >A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆周的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个？答:（ ）（1）扭矩M T 与剪应力τρ的关系M T =∫A τρρdA （2）变形的几何关系(即变形协调条件) （3）剪切虎克定律（4）极惯性矩的关系式I T =∫A ρ2dAA 、（1）B 、(1）（2)C 、（1）（2）(3）D 、全部 3、二向应力状态如图所示，其最大主应力σ1=( ) A 、σ B 、2σ C 、3σ D 、4σ题一、3图工程技术学院 _______________专业 班级 姓名____________ 学号---------------------------------------------------密 封 线 内 不 准 答 题-------------------------------------------------------------题一、1图4、高度等于宽度两倍(h=2b)的矩形截面梁,承受垂直方向的载荷，若仅将竖放截面改为平放截面，其它条件都不变,则梁的强度（ ) A 、提高到原来的2倍 B 、提高到原来的4倍 C 、降低到原来的1/2倍 D 、降低到原来的1/4倍5。

已知图示二梁的抗弯截面刚度EI 相同，若二者自由端的挠度相等,则P 1/P 2=（ ) A 、2 B 、4C 、8D 、16二、作图示梁的剪力图、弯矩图。

（１５分）三、如图所示直径为d 的圆截面轴，其两端承受扭转力偶矩m 的作用。

设由实验测的轴表面上与轴线成450方向的正应变，试求力偶矩m 之值、材料的弹性常数E 、μ均为已知。