九宫图分析法

四分法、九宫格：⾼效分析和解决问题的法宝
四分法是找到影响⼀个问题的最重要的两个维度（通俗地说是两个⽅⾯），把每个维度划分为
⾼、低两个等级，两两组合得出四种情况。

如果把两个维度的每个维度划分为⾼、中、低三个等级，两个维度组合得出九种情况，就称为
九宫格。

四分法、九宫格可⽤于很多问题的分析和解决。

例如：
关于创业投资机构对被投资企业的考察要点，普遍的说法是，投资就是投“⼈”（即创业者），但
是如何评价创业者是否值得投资呢？
分析这⼀问题的关键，得出最重要的两个⽅⾯（维度）⼀是创业者的领导⼒，⼆是规范和诚
信。

领导⼒可以分解为战略规划、经营管理、凝聚团队三项⼆级指标；
规范和诚信可以分解为决策规范性、资⾦使⽤规范性、预期的夸⼤程度、对问题的掩饰程度四
项⼆级指标。

通过对⼆级指标的评估，综合打分后，如果把两个维度各分为两个等级，就是“四分法”；如果把
两个维度各分为三个等级就是“九宫格”。

四分法和九宫格都是简单⽽有效的分析问题、提炼规律、解决问题的⼯具。

以“九宫格”为例，如果创业者处于两个维度“双⾼”的右上⽅A格中，投资机构都是欢迎的；B格中
也会优先考虑；如果处于“双低”的左下⽅E格中，投资机构是不会投投资的；D中⼀般也不会投
资；C格中要结合项⽬的其它因素来决定。

（来源：⽹络，版权归原作者所有。

）
⼩S：世界很⼤、我们很⼩，但能做⼀点是⼀点。

九宫图法一、九宫图法概述九宫图法是一种有助扩散性思维的思考策略，利用一幅九宫格图，如下图所示，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发，向八个方向去思考，发挥八种不同的创见。

依循此思维方式加以发挥并扩散其思考范围。

图1九宫图二、几种运用九宫图的分析法（一）曼陀罗法曼陀罗法是一种有助扩散性思维的思考策略，利用一幅像九宫图，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余的八个圈内，此法也可配合六何法从多方面进行思考。

[备注]：此九宫格法可作为扩散性思维的基本单位，由此演变出其它九宫图法（如莲花法中央的单位，正是曼陀罗法的基本单位）。

此法之优点乃由事物之核心出发，向八个方向去思巧，发挥八种不同的创见。

而莲花法也是依循此思维方式加以发挥并扩散其思考范围。

（二）莲花法这是从曼陀罗法的基本单位发展扩展而来（图2）。

图2莲花法图(1) 每位讨论者手持一莲花图，并将讨论之主题或问题写于图中央位置。

(2) 把相关的意念写于围着主题四周的八个圈中（每个圈的左上角分别写上英文字母A至H），成为八个子题，并于图中央部分构成了一幅曼陀罗法九宫图。

随后，讨论者可就各个子题再想出另外八个意念，将之写于围着“子题”四周及标着1-8号码的方格内，讨论者可沿以上步骤再延伸构思新的意念。

(3) 讨论直至整个莲花图写满为止。

三、关于九宫数图的概说（1）九宫数图起源目前普遍认为，九宫数图即为“洛书”的主要内容，是最早关于数的起源之说（见图3）。

《周易•系辞上》说：“河出图，洛出书，圣人则之。

”[1]但其中并没有明确记载“洛书”的主要内容。

直至西汉经学家孔安国的《尚书•洪范传》才提到：“天与禹，洛出书。

神龟负文而出列于背，皆有数至于九。

禹遂因而第之，以成九类，常道所以次序。

” 刘歆注1云：“伏羲氏继天而王，受河图而画之，八卦是也。

禹治洪水，赐洛书，法而陈之，九畴是也。

” 其九畴，即“戴九履一，左三右七，二四为肩，六八为足，五居中央，正龟背之象也”。

九宫图分析法什么是九宫图分析法九宫图法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，如下图所示，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发，向八个方向去思考，发挥八种不同的创见。

依循此思维方式加以发挥并扩散其思考围。

九宫图几种运用九宫图的分析法（一）曼陀罗法曼陀罗法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余的八个圈，此法也可配合六何法从多方面进行思考。

[备注]：此九宫格法可作为扩散性思维的基本单位，由此演变出其它九宫格法（如莲花法中央的单位，正是曼陀罗法的基本单位）。

此法之优点乃由事物之核心出发，向八个方向去思巧，发挥八种不同的创见。

而莲花法也是依循此思维方式加以发挥并扩散其思考围。

（二）莲花法这是从曼陀罗法的基本单位发展扩展而来（下图）。

莲花法图(1) 每位讨论者手持一莲花图，并将讨论之主题或问题写于图中央位置。

(2) 把相关的意念写于围着主题四周的八个圈中（每个圈的左上角分别写上英文字母A至H），成为八个子题，并于图中央部分构成了一幅曼陀罗法九宫图。

随后，讨论者可就各个子题再想出另外八个意念，将之写于围着「子题」四周及标着1-8的方格，讨论者可沿以上步骤再延伸构思新的意念。

(3) 讨论直至整个莲花图写满为止。

关于九宫数图的概说（1）九宫数图起源目前普遍认为，九宫数图即为“洛书”的主要容，是最早关于数的起源之说（见图3）。

《周易•系辞上》说：“河出图，洛出书，圣人则之。

”[1]但其中并没有明确记载“洛书”的主要容。

直至西汉经学家孔安国的《尚书•洪传》才提到：“天与禹，洛出书。

神龟负文而出列于背，皆有数至于九。

禹遂因而第之，以成九类，常道所以次序。

” 歆注1云：“伏羲氏继天而王，受河图而画之，八卦是也。

禹治洪水，赐洛书，法而之，九畴是也。

” 其九畴，即“戴九履一，左三右七，二四为肩，六八为足，五居中央，正龟背之象也”。

万茜
图1
图2
二、九宫数图内在的排列规律
九宫数图既是一种组合计算，又是一种益智游戏
后来形成的“九宫算”及“排九宫”等都是以九宫数图
图3）.
图3
九宫数图最基本的规律是，其纵横及对角线上三
15且九个数相加之和为
深入研究其数字的排列组合，可以发现以下规律：
数学拾零
为公差的等差数列（如图4示）.
图5
另四组数列也有一定的规律，从图
这四个数列相邻两数的差颠倒对称，
的相邻两数之差为5，且各个数字均不重复
奇数和偶数相互交错排列，四角上的数为偶数，
图6
三、分形艺术
1973年美籍数学家曼德勃罗特（Mandelbrot
图7
分形艺术是一种计算机图形艺术，通过计算机程序计算，生成某种具有审美情趣和科学内涵的图形、
图8
图9
图9是著名的分形图形谢尔宾斯基（Sierpinski）框地毯.从图中可以直观地看出，所用到基本单元图形正是九宫格.这虽然只是图形运用上的巧合，但正是这种巧合说明了将九宫格作为分形图形的一种生成方式，早已有过经典的例证.。

九宫图分析法案例九宫图分析法是一种在数据分析中运用视觉化技术获取有价值的见解的方法。

它通过将原始数据进行编排，将数据信息用图形显示出来，从而有效解决繁琐复杂的分析问题。

本文将结合“非洲洋口水事件”为案例，来介绍九宫图分析法的用法。

2005年，非洲地区的一家水质检测机构检测出，某洋口的水中污染物超标的情况，比较严重，此消息也被传到了洋口水生产商公司。

公司高层面前，对检测结果有深刻的认识。

为了更好地理清非洲洋口水事件，该公司决定运用九宫图分析法。

下面，将详细介绍九宫图分析法的用法。

首先，为了开展九宫图分析法，该公司先把洋口水的污染源分成九个方面，并为每个方面定义一个参数，这九个参数依次是：水源来源、药物污染物、物理和化学物质、有机污染物、气体排放、污染物泄露、污染物排放量、水源和水质状况以及污染物的运输。

这九个参数分别用九宫图表示出来，比如，水源来源可用红色表示，药物污染物可用橙色表示，物理和化学物质可用黄色表示，依次类推。

接着，公司将每个参数对应的污染物详细测量结果，以及每个参数的水质检测结果，都填入九宫图中，并用不同的颜色大小表示污染物的检测结果的严重程度。

通过这种形式，可以更直观更清晰地看到，什么样的污染物是比较严重，什么样的污染物是比较轻微。

在九宫图的基础上，公司又进行了聚类分析，将某洋口水的污染物分成三类：一类是比较严重的“重度污染物”；一类是“中度污染物”；一类是“轻度污染物”。

有了这样的分类，公司就可以把重点放在最严重的重度污染物上，采取更有效的污染治理措施，从而让洋口水的水质变得更好。

以上是九宫图分析法在非洲洋口水事件上的应用，有效地把洋口水的污染源进行分类，有效地阐明了污染问题的严重程度，从而使治理污染更加有效。

九宫图分析法是一种十分有效的数据分析方法，除了在处理环保问题中能发挥效用，对于其他各类复杂分析问题也都有十分广泛的应用。

例如，在人力资源行业，九宫图分析法可以用来分析员工的人格特点，用以判断员工的胜任能力；在战略管理领域，九宫图分析法可以把市场风险和投资收益分析出来，以决定公司的战略调整等。

什么是九宫图分析法九宫图法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，如下图所示，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发，向八个方向去思考，发挥八种不同的创见。

依循此思维方式加以发挥并扩散其思考范围。

九宫图[编辑]几种运用九宫图的分析法（一）曼陀罗法曼陀罗法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余的八个圈内，此法也可配合六何法从多方面进行思考。

[备注]：此九宫格法可作为扩散性思维的基本单位，由此演变出其它九宫格法（如莲花法中央的单位，正是曼陀罗法的基本单位）。

此法之优点乃由事物之核心出发，向八个方向去思巧，发挥八种不同的创见。

而莲花法也是依循此思维方式加以发挥并扩散其思考范围。

（二）莲花法这是从曼陀罗法的基本单位发展扩展而来（下图）。

莲花法图(1) 每位讨论者手持一莲花图，并将讨论之主题或问题写于图中央位置。

(2) 把相关的意念写于围着主题四周的八个圈中（每个圈的左上角分别写上英文字母A至H），成为八个子题，并于图中央部分构成了一幅曼陀罗法九宫图。

随后，讨论者可就各个子题再想出另外八个意念，将之写于围着「子题」四周及标着1-8号码的方格内，讨论者可沿以上步骤再延伸构思新的意念。

(3) 讨论直至整个莲花图写满为止。

[编辑]关于九宫数图的概说（1）九宫数图起源目前普遍认为，九宫数图即为“洛书”的主要内容，是最早关于数的起源之说（见图3）。

《周易•系辞上》说：“河出图，洛出书，圣人则之。

”[1]但其中并没有明确记载“洛书”的主要内容。

直至西汉经学家孔安国的《尚书•洪范传》才提到：“天与禹，洛出书。

神龟负文而出列于背，皆有数至于九。

禹遂因而第之，以成九类，常道所以次序。

” 刘歆注1云：“伏羲氏继天而王，受河图而画之，八卦是也。

禹治洪水，赐洛书，法而陈之，九畴是也。

” 其九畴，即“戴九履一，左三右七，二四为肩，六八为足，五居中央，正龟背之象也”。

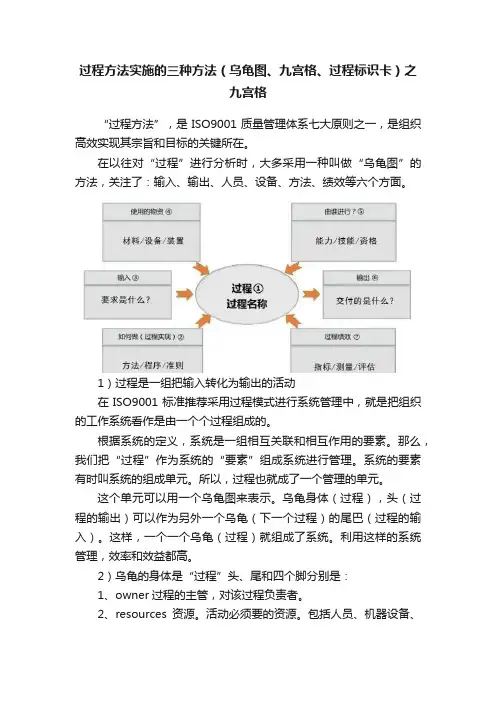
过程方法实施的三种方法（乌龟图、九宫格、过程标识卡）之九宫格“过程方法”，是ISO9001质量管理体系七大原则之一，是组织高效实现其宗旨和目标的关键所在。

在以往对“过程”进行分析时，大多采用一种叫做“乌龟图”的方法，关注了：输入、输出、人员、设备、方法、绩效等六个方面。

1）过程是一组把输入转化为输出的活动在ISO9001标准推荐采用过程模式进行系统管理中，就是把组织的工作系统看作是由一个个过程组成的。

根据系统的定义，系统是一组相互关联和相互作用的要素。

那么，我们把“过程”作为系统的“要素”组成系统进行管理。

系统的要素有时叫系统的组成单元。

所以，过程也就成了一个管理的单元。

这个单元可以用一个乌龟图来表示。

乌龟身体（过程），头（过程的输出）可以作为另外一个乌龟（下一个过程）的尾巴（过程的输入）。

这样，一个一个乌龟（过程）就组成了系统。

利用这样的系统管理，效率和效益都高。

2）乌龟的身体是“过程”头、尾和四个脚分别是：1、owner过程的主管，对该过程负责者。

2、resources资源。

活动必须要的资源。

包括人员、机器设备、工艺用材料3、procedure程序。

也就是操作方法、控制方法等。

4、KPI/PI关键指标/指标。

用来衡量过程的有效性和效率。

5、input 尾。

被加工的材料，或者接到加工的指令、要求等6、output 头。

过程的结果，产品（可能是半成品、零件、部件等）。

3）乌龟尾和四脚本身的质量，以及在过程中相互作用的质量，决定了乌龟头（过程输出）的质量。

最好针对以上五个因素，确定这些因素的PI，KPI，通过对它们的控制来确保乌龟头的质量。

而不是通过检验乌龟头（产品）中KPI来控制过程。

后者发现问题已经晚了。

有的地方乌龟的尾和四脚就用料、人、机、法、测量来表示。

有的把这个过程叫作业。

于是，就得到了一个作业成本管理的方法，利用作业成本管理有关的信息对作业进行管理。

作业组成的更大一级系统，对这个系统的管理就叫作业管理。

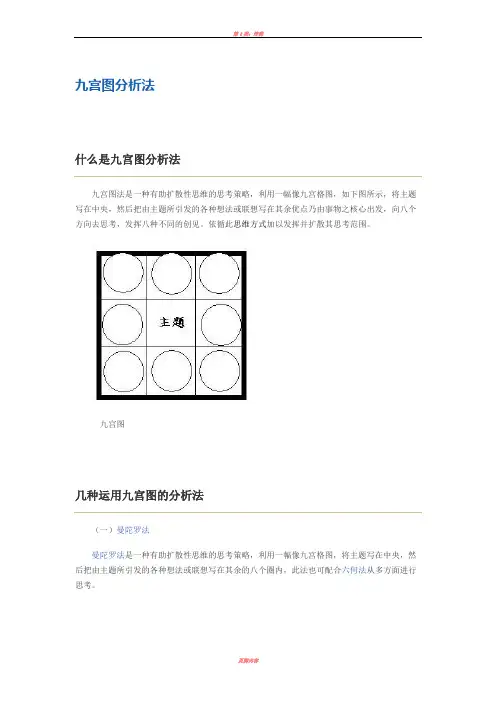
九宫图分析法什么是九宫图分析法九宫图法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，如下图所示，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发，向八个方向去思考，发挥八种不同的创见。

依循此思维方式加以发挥并扩散其思考范围。

九宫图几种运用九宫图的分析法（一）曼陀罗法曼陀罗法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，将主题写在中央，然后把由主题所引发的各种想法或联想写在其余的八个圈内，此法也可配合六何法从多方面进行思考。

[备注]：此九宫格法可作为扩散性思维的基本单位，由此演变出其它九宫格法（如莲花法中央的单位，正是曼陀罗法的基本单位）。

此法之优点乃由事物之核心出发，向八个方向去思巧，发挥八种不同的创见。

而莲花法也是依循此思维方式加以发挥并扩散其思考范围。

（二）莲花法这是从曼陀罗法的基本单位发展扩展而来（下图）。

莲花法图(1) 每位讨论者手持一莲花图，并将讨论之主题或问题写于图中央位置。

(2) 把相关的意念写于围着主题四周的八个圈中（每个圈的左上角分别写上英文字母A至H），成为八个子题，并于图中央部分构成了一幅曼陀罗法九宫图。

随后，讨论者可就各个子题再想出另外八个意念，将之写于围着「子题」四周及标着1-8号码的方格内，讨论者可沿以上步骤再延伸构思新的意念。

(3) 讨论直至整个莲花图写满为止。

关于九宫数图的概说（1）九宫数图起源目前普遍认为，九宫数图即为“洛书”的主要内容，是最早关于数的起源之说（见图3）。

《周易•系辞上》说：“河出图，洛出书，圣人则之。

”[1]但其中并没有明确记载“洛书”的主要内容。

直至西汉经学家孔安国的《尚书•洪范传》才提到：“天与禹，洛出书。

神龟负文而出列于背，皆有数至于九。

禹遂因而第之，以成九类，常道所以次序。

” 刘歆注1云：“伏羲氏继天而王，受河图而画之，八卦是也。

禹治洪水，赐洛书，法而陈之，九畴是也。

” 其九畴，即“戴九履一，左三右七，二四为肩，六八为足，五居中央，正龟背之象也”。

九宫图分析法什么是九宫图分析法九宫图法是一种有助扩散性思维的思考策略，利用一幅像九宫格图,如下图所示,将主题写在中央，然后把由主题所引发的各种想法或联想写在其余优点乃由事物之核心出发，向八个方向去思考，发挥八种不同的创见.依循此思维方式加以发挥并扩散其思考范围。

九宫图几种运用九宫图的分析法（一)曼陀罗法曼陀罗法是一种有助扩散性思维的思考策略，利用一幅像九宫格图，将主题写在中央,然后把由主题所引发的各种想法或联想写在其余的八个圈内，此法也可配合六何法从多方面进行思考。

[备注]:此九宫格法可作为扩散性思维的基本单位,由此演变出其它九宫格法(如莲花法中央的单位,正是曼陀罗法的基本单位)。

此法之优点乃由事物之核心出发，向八个方向去思巧，发挥八种不同的创见。

而莲花法也是依循此思维方式加以发挥并扩散其思考范围.(二）莲花法这是从曼陀罗法的基本单位发展扩展而来(下图）.莲花法图(1) 每位讨论者手持一莲花图，并将讨论之主题或问题写于图中央位置.（2) 把相关的意念写于围着主题四周的八个圈中(每个圈的左上角分别写上英文字母Ａ至Ｈ),成为八个子题,并于图中央部分构成了一幅曼陀罗法九宫图.随后,讨论者可就各个子题再想出另外八个意念,将之写于围着「子题」四周及标着1-８号码的方格内,讨论者可沿以上步骤再延伸构思新的意念。

(３）讨论直至整个莲花图写满为止.关于九宫数图的概说（1）九宫数图起源目前普遍认为,九宫数图即为“洛书”的主要内容,是最早关于数的起源之说（见图3）。

《周易•系辞上》说:“河出图,洛出书，圣人则之.”［1］但其中并没有明确记载“洛书”的主要内容。

直至西汉经学家孔安国的《尚书•洪范传》才提到:“天与禹，洛出书。

神龟负文而出列于背,皆有数至于九。

禹遂因而第之，以成九类，常道所以次序。

” 刘歆注1云:“伏羲氏继天而王,受河图而画之，八卦是也。

禹治洪水,赐洛书,法而陈之,九畴是也．" 其九畴，即“戴九履一,左三右七,二四为肩,六八为足,五居中央，正龟背之象也”。

什么是九宫‎图分析法九宫图法是‎一种有助扩‎散性思维的‎思考策略，利用一幅像‎九宫格图，如下图所示‎，将主题写在‎中央，然后把由主‎题所引发的‎各种想法或‎联想写在其‎余优点乃由‎事物之核心‎出发，向八个方向‎去思考，发挥八种不‎同的创见。

依循此思维方式加以发挥并‎扩散其思考‎范围。

九宫图[编辑]几种运用九‎宫图的分析‎法（一）曼陀罗法曼陀罗法是一种有助‎扩散性思维‎的思考策略‎，利用一幅像‎九宫格图，将主题写在‎中央，然后把由主‎题所引发的‎各种想法或‎联想写在其‎余的八个圈‎内，此法也可配‎合六何法从多方面进‎行思考。

[备注]：此九宫格法‎可作为扩散‎性思维的基‎本单位，由此演变出‎其它九宫格‎法（如莲花法中‎央的单位，正是曼陀罗‎法的基本单‎位）。

此法之优点‎乃由事物之‎核心出发，向八个方向‎去思巧，发挥八种不‎同的创见。

而莲花法也‎是依循此思维方式加以发挥并‎扩散其思考‎范围。

（二）莲花法这是从曼陀罗法的基本单位‎发展扩展而‎来（下图）。

莲花法图(1) 每位讨论者‎手持一莲花‎图，并将讨论之‎主题或问题‎写于图中央‎位置。

(2) 把相关的意‎念写于围着‎主题四周的‎八个圈中（每个圈的左‎上角分别写‎上英文字母‎A至H），成为八个子‎题，并于图中央‎部分构成了‎一幅曼陀罗‎法九宫图。

随后，讨论者可就‎各个子题再‎想出另外八‎个意念，将之写于围‎着「子题」四周及标着‎1-8号码的方‎格内，讨论者可沿‎以上步骤再‎延伸构思新‎的意念。

(3) 讨论直至整‎个莲花图写‎满为止。

[编辑]关于九宫数‎图的概说（1）九宫数图起‎源目前普遍认‎为，九宫数图即‎为“洛书”的主要内容‎，是最早关于‎数的起源之‎说（见图3）。

《周易•系辞上》说：“河出图，洛出书，圣人则之。

”[1]但其中并没‎有明确记载‎“洛书”的主要内容‎。

直至西汉经‎学家孔安国‎的《尚书•洪范传》才提到：“天与禹，洛出书。

神龟负文而‎出列于背，皆有数至于‎九。

九宫格思考法的原则
九宫格思考法的主要原则是将主题或问题作为中心，然后向外扩展思维，从不同角度和方向去考虑问题的解决方法。

这个方法可以用九个格子来表示，其中中心格为问题或主题，周围的八个格子则是与问题或主题相关的各个方面或角度。

具体来说，九宫格思考法可以分为两种类型：向“四面扩散”的辐射线式和“逐步思考”的顺时钟式。

1. 向四面扩散的辐射线式：以九宫格的中央方格为核心主题，向外联想出相关概念，其余八格的概念都与核心有关连，但彼此不必然有相关性。

这种思考方式可以帮助人们从多个方向和角度来思考问题或主题，从而找到更多的解决方法。

2. 逐步思考的顺时钟式：按照顺时针方向，从左上角开始，逐格考虑问题的各个方面或角度。

第一格是问题的定义或背景介绍，第二格是对问题的初步分析或评估，第三格是可能的解决方案或策略，以此类推。

这种思考方式可以帮助人们系统地思考问题的各个方面，从而更全面地解决问题。

在使用九宫格思考法时，需要注意以下几点：
1. 要明确问题的核心或主题，并将其放在九宫格的中央方格中。

2. 要尽可能地联想出与问题相关的各个方面或角度，并将其填入周围的八个格子中。

3. 要注意各个方面的逻辑关系和关联性，避免出现相互矛盾或重复的内容。

4. 要灵活运用九宫格思考法，不要过于拘泥于固定的格式和步骤，要根据具体情况进行调整和改进。

总之，九宫格思考法是一种非常有用的思维方法，可以帮助人们系统地思考问题的各个方面，从而更全面地解决问题。

在使用时要注意灵活运用，并结合实际情况进行调整和改进。

图形推理解题技巧系列之⼀九宫图类图形推理解题技巧系列之⼀九宫图类九宫图类试题寻找规律的顺序解决图形推理试题，其根本在于找到规律，⽽根据各种图形的不同排列形式，我们讲图形推理试题分为“三三”型、“四四”型、“六四”型、“⼀四”型、“五五”型以及九宫图型。

在这些类型中，九宫图形寻找规律的顺序是最多变，也是最复杂的。

九宫图型试题是公务员考试图形推理常考题型之⼀，也是难度相对较⼤的⼀类试题。

九宫图型试题的基本内容是在⼀个有9个（3×3）空格的正⽅形图（九宫图）中，有8个⽅格内各有⼀幅图形，这8个图形呈现⼀定的规律，需要考⽣从4个备选答案中，选出⼀个能够保持这种规律的图形填到九宫图的问号处。

下⾯，就九宫图型试题的找寻规律顺序，笔者将详细论述。

⼀．以⾏为单位九宫图型试题最常见的找寻规律的顺序是以⾏为单位，这种以⾏为单位的试题在考试中也是最常见的。

例如：（2007·国考）[答案]A[解析]九宫图中，每⾏图形含有的封闭区域总数均为8，故正确答案为A。

此题是典型的以⾏为单位找寻规律的九宫图型试题。

此题考查封闭区域数量，涉及数量关系。

遇到涉及数量关系的九宫图类试题时，可先将各图代表的数量关系标出，然后按照数字来找寻规律，判断到底以什么为单位找寻规律。

⼆．以列为单位以列为单位的九宫图试题也较为常见，涉及列的试题，以数量关系为基础的居多，例如：（2007·国考）[答案]D[解析]以列为单位，图⼀含有的直线边的数量等于图⼆、图三含有的直线边的数量之和，故正确答案为D。

以列为单位的试题，有时是⼀列中图⼀、图⼆之和等于图三，或者图⼆、图三之和等于图⼀，亦或图⼀、图三之和等于图⼆。

想要迅速找到规律，也可按写下数字找到数量关系的⽅法。

三．⾏或列均可有些题⽬，不论是以⾏或列为单位，均可找到同⼀规律并得出唯⼀的答案。

（2006·国考）[答案]C[解析]九宫图中，每⾏构成⼩⼈头像的组成元素数量与种类保持⼀致，即⽿朵、眼睛、嘴巴各⾃均有三种，第三⾏缺失的部分重新组合⽽成的图形即为正确答案，故选C。

九宫格思考法
九宫格思考法，是一种帮助我们审视问题、分析问题、找到解决
问题的方法。

它来源于中国传统文化中的“九宫”，将一个大问题分
解成九个小问题，分别从不同角度来思考，最终集成整体，得出全面、准确的结论。

九宫格思考法可以应用在各种领域中，比如说在工作上，我们可
以将一个大的工作项目分成不同的部分，每个部分分别考虑其优点和
问题，再将所有的分析归纳出来，制定全面的解决方案。

同样的，在生活中，九宫格思考法也很有用。

比如说，当我们发
现家庭关系出现问题时，可以将问题分解为九个小问题，如亲情、夫
妻关系、父母子女关系等，然后从每个问题中找到其根源，并集成整
体分析，这样我们就可以制定出有效的改进方案。

此外，在学习中，九宫格思考法也能够发挥一定的作用。

我们可
以将学习过程中遇到的难题分成九个小问题，然后针对每个小问题找
到答案，并将答案归纳出来，以此加深我们的记忆，提高我们的学习
成绩。

总之，九宫格思考法是一种很有用的思考方法，它可以让我们从
不同的角度审视问题，提高我们的思维能力和解决问题的效率。

无论
是在工作、生活还是学习中，我们都可以用它来解决各种难题。

九宫图大家都知道，包括一些固定的口诀网上也可以轻易查到，不过一般也没人去特意记住，也不容易记得住，还是有迹可循的推算更能让大家记住，下面提供两种方法供大家参考。

九宫图：采用1-9个不重复数字，填充在3行3列的方格中，使得每一行、每一列以及对角线上的三个数之和都为15。

第一种方法：最大数尝试法1-9中9最大，与其他两数组成15的排列组合只有9/1/5与9/2/4这两种组合方式，那么，在真正的九宫图中必然也存在该两种排列存在，将这两种排列在图中填好，形成图1样式：此时可发现当9处于四个角位置时，对角线剩余两个数，如图1中（a+d）数值必然大于6（因为剩余数字只有3/6/7/8四个），超出和值15要求。

由此可见，9这个数值不能放在对角线上，那么将9/1/5这个组合整体下移，得到图2；此时又发现问题，这种组合时，当1处于中心位置时，未知数b和d要满足和为15要求时都超出最大数字9了,所以可确定1不能放在中心位置上。

同样9也不能放在中心位置，因为与9相关的组合只有两个，满足不了行/列/对角线四种排列组合的和值都为15要求。

次时将5与1对调，形成图3，再次检查一下，似乎没什么明显问题了，那么按照和为15填空吧，将数字填入后发现恰好满足行/列/对角线和都为15要求，任务完成了，这个办法简单，就是经过三次筛选就完成了。

第二种方法：利用率统计法，设a/b/c/d/e/f/g/h/i对应1-9个数字，要满足九宫图要求，如下图5所示，那么每个数字都得到充分利用，根据九宫图要求，不难算出九个字母利用率：a/c/g/i：利用3次b/d/f/h：利用2次e：利用4次图5将1-9三个不同数和为15的组合列出：数字9: 9+1+5成立，9+2+4成立；9的利用率：2次数字8: 8+1+6成立，8+2+5成立，8+3+4成立；8的利用率：3次数字7: 7+2+6成立，7+3+5成立；7的利用率：2次数字6: 6+1+8成立，6+2+7成立，6+4+5成立；6的利用率：3次数字5: 5+1+9成立，5+2+8成立，5+3+7成立，5+4+6成立；5的利用率：4次数字4: 4+2+9成立，4+3+8成立，4+5+6成立；4的利用率：3次数字3: 3+4+8成立，3+5+7成立；3的利用率：2次数字2: 2+4+9成立，2+5+8成立，2+7+6成立；2的利用率：3次数字1: 1+5+9成立，1+6+8成立；1的利用率：2次统计结果：9/7/3/1：利用2次8/6/4/2：利用3次5：利用4次对比前面字母利用率，可知e=5，a/c/g/i=8/6/4/2，b/d/f/h=9/7/3/1；将a/c/g/i=8/6/4/2结合e=5凑成和为15填入表中（只要满足何为15，8/6/4/2位置可在a/c/g/i位置随意调整），如下图6结合行/列之和为15，求出剩余的四个数字，如图7，验证后发现这就是所需的！！。