三角函数公式合集
- 格式:doc
- 大小:18.00 KB
- 文档页数:1

三角函数公式大全三角函数是数学中非常重要的概念,它们在几何、三角学、物理学等领域都有着广泛的应用。
在学习三角函数的过程中,掌握三角函数的基本公式是非常重要的。
本文将为大家详细介绍三角函数的公式大全,帮助大家更好地理解和掌握三角函数的知识。
1. 正弦函数的公式。
正弦函数是最基本的三角函数之一,其公式为,sinθ = 对边/斜边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
正弦函数的图像是一条连续的曲线,其周期为2π,在0到2π之间有一个完整的周期。
2. 余弦函数的公式。
余弦函数也是常见的三角函数,其公式为,cosθ = 邻边/斜边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
余弦函数的图像也是一条连续的曲线,其周期也为2π,与正弦函数的图像相似。
3. 正切函数的公式。
正切函数是另外一个常见的三角函数,其公式为,tanθ = 对边/邻边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,邻边为与角度θ相邻的直角三角形的斜边。
正切函数的图像在一些特定的角度上会出现无穷大的情况,因此在使用时需要注意。
4. 余切函数的公式。
余切函数是正切函数的倒数,其公式为,cotθ= 邻边/对边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,对边为与角度θ相对的直角三角形的斜边。
余切函数的图像也会在一些特定的角度上出现无穷大的情况。
5. 正割函数的公式。
正割函数是余弦函数的倒数,其公式为,secθ= 斜边/邻边。
其中,θ为角度,邻边为与角度θ相邻的直角三角形的斜边,斜边为直角三角形的斜边。
正割函数的图像是一条连续的曲线,其周期也为2π。
6. 余割函数的公式。
余割函数是正弦函数的倒数,其公式为,cscθ= 斜边/对边。
其中,θ为角度,对边为与角度θ相对的直角三角形的斜边,斜边为直角三角形的斜边。
余割函数的图像也是一条连续的曲线,其周期也为2π。

三角函数转换公式大全总结三角函数是数学中常见的一类函数,由于其定义在一个单位圆上,可以用来描述很多自然现象和物理现象。
在数学中,经常会使用一些三角函数的转换公式来简化计算和推导。
下面是常见的一些三角函数转换公式总结。
1.正、余函数的关系:sin(x) = cos(x - π/2)cos(x) = sin(x + π/2)这两个公式很容易理解,就是将正弦函数和余弦函数互换角度就可以得到。
2.平方和差公式:sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)这两个公式可以用来计算两个三角函数之间的和差关系。
通过平方和差公式,可以将两个三角函数之和或之差转化为两个三角函数之积。
3.和差化积公式:sin(x) + sin(y) = 2sin((x + y)/2)cos((x - y)/2)sin(x) - sin(y) = 2cos((x + y)/2)sin((x - y)/2)cos(x) + cos(y) = 2cos((x + y)/2)cos((x - y)/2)cos(x) - cos(y) = -2sin((x + y)/2)sin((x - y)/2)这四个公式可以用来将两个三角函数的和或差表示为两个三角函数的积。
4.倍角公式:sin(2x) = 2sin(x)cos(x)cos(2x) = cos^2(x) - sin^2(x) = 2cos^2(x) - 1 = 1 - 2sin^2(x) tan(2x) = 2tan(x)/(1 - tan^2(x))这些公式可以用来计算两倍角度的三角函数值,可以用于简化计算和推导。
5.半角公式:sin(x/2) = ±√((1 - cos(x))/2)cos(x/2) = ±√((1 + cos(x))/2)tan(x/2) = ±√((1 - cos(x))/(1 + cos(x)))这些公式可以用来计算半角的三角函数值,同样可以用于简化计算和推导。

三角函数公式大全及记忆口诀
在数学中,三角函数是一类重要的函数,它们在几何、物理、
工程等领域中都有着广泛的应用。
为了更好地掌握三角函数,我们
需要熟练掌握它们的公式,同时也需要一些记忆口诀来帮助我们记忆。
首先,我们来看一下三角函数的公式大全:
1. 正弦函数(sine function),sin(θ) = 对边/斜边。
2. 余弦函数(cosine function),cos(θ) = 邻边/斜边。
3. 正切函数(tangent function),tan(θ) = 对边/邻边。
4. 余切函数(cotangent function),cot(θ) = 邻边/对边。
5. 正割函数(secant function),sec(θ) = 斜边/邻边。
6. 余割函数(cosecant function),csc(θ) = 斜边/对边。
这些公式是我们在解决三角函数相关问题时经常会用到的,熟练掌握它们对我们的学习至关重要。
除了公式外,记忆口诀也是我们学习三角函数的好帮手。
下面是一个简单的记忆口诀:
正弦对,余弦邻,正切比,余切颠,正割斜,余割对。
这个口诀可以帮助我们记忆三角函数的定义和关系,使我们更容易在解题时迅速找到正确的公式和方法。
总之,三角函数是数学中的重要内容,掌握好三角函数的公式和记忆口诀,对我们的学习和工作都有着重要的帮助。
希望大家能够通过不断的练习和记忆,熟练掌握三角函数,为自己的数学学习打下坚实的基础。

所有三角函数公式整理三角函数的出现,使人们可以更好地探究几何学中曲线的形态,并且能够解决许多现实生活中的数学问题。
三角函数是一类特殊的函数,它们使用了角度而不是极坐标来定义它们的起点,因此它们在计算机图形学等方面得到了广泛的应用。
本文将重点介绍三角函数的公式,以及它们的应用方法。
一、三角函数公式1、正弦函数公式:sin x= y/r,其中 x 为角度,r 为该角度的弧长,y 为该角度的纵坐标。
2、余弦函数公式:cos x= x/r,其中 x 为角度,r 为该角度的弧长,x 为该角度的横坐标。
3、正切函数公式:tan x = y/x,其中 x 为角度,y 为该角度的纵坐标,x 为该角度的横坐标。
4、反正弦函数公式:arcsin x= r/y,其中 x 为角度,r 为该角度的弧长,y 为该角度的纵坐标。
5、反余弦函数公式:arccos x= r/x,其中 x 为角度,r 为该角度的弧长,x 为该角度的横坐标。
6、反正切函数公式:arctan x= y/x,其中 x 为角度,y 为该角度的纵坐标,x 为该角度的横坐标。
二、三角函数的应用1、在计算机图形学中,三角函数可以用来描述一个图形的运动。
例如,当我们想让一个图形以椭圆轨迹运动时,就可以使用三角函数来表示这种运动。
2、三角函数在游戏开发中也有着重要作用。
它们可以用来定义游戏中物体以及物体之间的各种关系,从而使游戏更具有立体感。
3、三角函数还可以用来计算直线的斜率,从而实现几何学中的坐标变换。
4、三角函数也可以用来解决物理学中物体的运动问题,例如抛物线的运动路径。
三、总结以上就是有关三角函数的公式整理以及它们的应用方法。
三角函数是一类特殊的函数,通过它们可以更好地探究几何图形形状,并利用它们解决实际生活中的各种数学问题。
无论是在计算机图形学,游戏开发,几何学还是物理学等方面,三角函数都具有重要作用,并衍生出许多应用。

最全三角函数公式汇总三角函数是数学中非常重要的一种函数类型,它由正弦、余弦和正切这三个基本函数构成。
在解决三角关系和计算与角度相关的问题时,三角函数的公式起到了至关重要的作用。
接下来,将详细总结并汇总涉及正弦、余弦和正切的公式,以便读者深入了解和学习。
正弦函数(Sine Function):正弦函数的记号为sin(x),其中x为弧度(radian)。
它的值在-1到1之间变动,对应于实数轴上的一个点的纵坐标。
以下是与正弦函数相关的常用公式:1. 正弦函数的定义:sin(x) = (opposite side of triangle) / (hypotenuse of triangle)2. 正弦函数的周期性:sin(x) = sin(x + 2πn),其中n为整数3. 正弦函数的对称性:sin(-x) = -sin(x)4.正弦函数的和差公式:(a) sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)(b) sin(x + y) = sin(x)cos(y) + cos(x)sin(y)(c) sin(x - y) = sin(x)cos(y) - cos(x)sin(y)5.正弦函数的积和公式:(a) 2sin(x)cos(y) = sin(x + y) + sin(x - y)(b) 2cos(x)sin(y) = sin(x + y) - sin(x - y)(a) sin(2x) = 2sin(x)cos(x)(b) sin(x) = 2sin(x/2)cos(x/2)7.正弦函数的半角公式:(a) sin(x/2) = ±√[(1 - cos(x))/2]余弦函数(Cosine Function):余弦函数的记号为cos(x),其中x为弧度。
它的值在-1到1之间变动,对应于实数轴上的一个点的横坐标。
以下是与余弦函数相关的常用公式:1. 余弦函数的定义:cos(x) = (adjacent side of triangle) / (hypotenuse of triangle)2. 余弦函数的周期性:cos(x) = cos(x + 2πn),其中n为整数3. 余弦函数的对称性:cos(-x) = cos(x)4.余弦函数的和差公式:(a) cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)(b) cos(x + y) = cos(x)cos(y) - sin(x)sin(y)(c) cos(x - y) = cos(x)cos(y) + sin(x)sin(y)5.余弦函数的积和公式:(a) 2cos(x)cos(y) = cos(x + y) + cos(x - y)(b) 2sin(x)sin(y) = cos(x - y) - cos(x + y)(a) cos(2x) = cos^2(x) - sin^2(x)(b) cos(x) = cos^2(x/2) - sin^2(x/2)7.余弦函数的半角公式:(a) cos(x/2) = ±√[(1 + cos(x))/2]正切函数(Tangent Function):正切函数的记号为tan(x),其中x为弧度。
三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦函数:ry=αsin 余弦函数:r x =αcos 正切函数:x y =αtan余切函数:y x =αcot 正割函数:xr=αsec 余割函数:yr=αcsc 二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)=sinα cos(2kπ+α)=cosαtan (2kπ+α)=tanα cot(2kπ+α)=cotα (其中k ∈Z) 公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin (π+α)=-sinα cos(π+α)=-cosα tan (π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系: sin (-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)=sinα cos(π-α)=-cosα tan (π-α)=-tanα cot(π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin (απ-2)=cosα cos(απ-2)=sinα tan (απ-2)=cotα cot(απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin (απ+2)=cosα cos(απ+2)=-sinαtan(απ+2)=-cotα cot(απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系: sin(απ-23)=-cosα cos(απ-23)=-sinαtan (απ-23)=cotα cot(απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin(απ+23)=-cosα cos(απ+23)=sinαtan (απ+23)=-cotα cot(απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)=-sinα cos(2π-α)=cosα tan (2π-α)=-tanα cot(2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
高数三角函数公式大全高等数学中涉及到三角函数的公式实在是非常多,无法在一篇回答中全部列举。
不过,我可以为你列举一些常见的三角函数公式,包括基本的三角函数关系、和差化积公式、倍角公式、半角公式等等。
首先是基本的三角函数关系:1. 正弦函数,sin(x) = 对边/斜边。
2. 余弦函数,cos(x) = 邻边/斜边。
3. 正切函数,tan(x) = 对边/邻边。
这些关系可以通过直角三角形中的对应边长之比来定义。
接下来是和差化积公式:1. sin(A ± B) = sinAcosB ± cosAsinB.2. cos(A ± B) = cosAcosB ∓ sinAsinB.3. tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)。
然后是倍角公式:1. sin(2x) = 2sinxcosx.2. cos(2x) = cos^2(x) sin^2(x) = 2cos^2(x) 1 = 12sin^2(x)。
3. tan(2x) = (2tanx) / (1 tan^2(x))。
再来是半角公式:1. sin(x/2) = ±√((1 cosx)/2)。
2. cos(x/2) = ±√((1 + cosx)/2)。
3. tan(x/2) = ±√((1 cosx)/(1 + cosx))。
除此之外,还有诸如和差化积公式的推广、三角函数的周期性、反三角函数等更加复杂的公式和性质。
总的来说,三角函数的公式非常丰富多样,需要通过不断的练习和理解来掌握它们的用法和特性。
希望这些基本的公式对你有所帮助。
三角函数计算公式大全三角函数的公式有很多,掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
接下来给大家分享三角函数计算公式,供参考!三角函数两角和与差计算公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cossinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)三角函数积化和差计算公式sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数和差化积计算公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)三角函数万能公式sin(a)=[2tan(a/2)]/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=[2tan(a/2)]/[1-tan2(a/2)]三角函数记忆口诀三角函数是函数,象限符号坐标注。
函数图像单位圆,周期奇偶增减现。
同角关系很重要,化简证明都需要。
正六边形顶点处,从上到下弦切割;中心记上数字一,连结顶点三角形。
三角函数公式汇总1. 扇形弧长和面积公式 180rr l απα=⋅'=弧360212r lr s απ==2. 角度与弧度的转换παααπαααππ180)(180)(180180⨯'=−−→−'⨯='−−→−⨯⨯(角度)弧度(弧度)角度3. 终边相同的角(1)βπαβαβα+=+=k k 2360,或是终边相同的角,则 . (2)第一限象角: 第二限象角: 第三限象角: 第四限象角: (3) 坐标轴上的角i) 终边在x 轴上的角:x 正半轴{}{}Z k k x x Z k k x x ∈=∈=,2,360π或x 负半轴{}{}Z k k x x Z k k x x ∈+=∈+=,2,180360ππ或x 轴{}{}Z k k x x Z k k x x ∈=∈=,,180π或ii) 终边在y 轴上的角y 正半轴{}⎭⎬⎫⎩⎨⎧∈+=∈+=Z k k x x Z k k x x ,22,90360ππ或y 负半轴{}⎭⎬⎫⎩⎨⎧∈+=∈+=Z k k x x Z k k x x ,232,270360ππ或y 轴{}⎭⎬⎫⎩⎨⎧∈+=∈+=Z k k x x Z k k x x ,2,90180ππ或4. 三角函数的定义设角 终边上异于原点的任意一点 , 记 , 如图, 则三角函数定义如下:显然, 由三角函数的定义知, 各种三角函数值在平面直角坐标系中符号如下:特殊角的三角函数值表(2) 平方关系 1cos sin 22=+αα(3) αααcos sin tan =两角和差公式:βαβαβαsin cos cos sin )sin(±=± βαβαβαsin sin cos cos )cos( =±βαβαβαtan tan 1tan tan )tan(⋅±=±5. 诱导公式(奇变偶不变符号看限象)6. 设 是任意弧度制的角, 则必存在 满足: , 即任何角都具有可转换为该形式。
三角函数常用公式:(^表示乘方,例如^2表示平方)
正弦函数sinθ=y/r
余弦函数cosθ=x/r
正切函数tanθ=y/x
余切函数cotθ=x/y
正割函数secθ=r/x
余割函数cscθ=r/y
以及两个不常用,
已趋于被淘汰的函数:
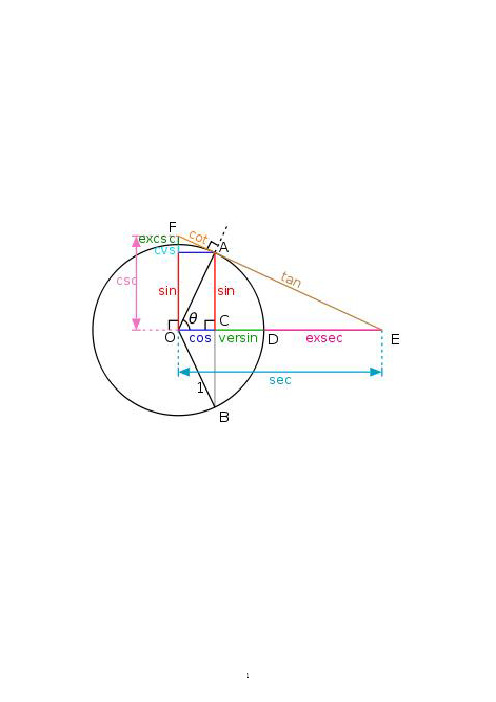
正矢函数versinθ=1-cosθ
余矢函数vercosθ=1-sinθ
同角三角函数间的基本关系式: ·
平方关系: sin^2(α)+cos^2(α)=1 tan^2(α)+1=sec^2(α) cot^2(α)+1=csc^2(α)
·积的关系: sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*csc αsecα=tanα*cscαcscα=secα*cotα·
倒数关系: tanα·cotα=1 sinα·cscα=1 cosα·secα=1
直角三角形ABC中, 角A的正弦值就等于角A的对边比斜边, 余弦等于角A的邻边比斜边正切等于对边比邻边,
三角函数恒等变形公式·两角和与差的三角函数: cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ·
辅助角公式: Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),
其中sint=B/(A^2+B^2)^(1/2) cost=A/(A^2+B^2)^(1/2) ·倍角公式: sin(2α)=2sinα·cos α=2/(tanα+cotα) cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) tan(2α)=2tanα/[1-tan^2(α)] ·
三倍角公式: sin(3α)=3sinα-4sin^3(α) cos(3α)=4cos^3(α)-3cosα·
半角公式: sin(α/2)=±√((1-cosα)/2) cos(α/2)=±√((1+cosα)/2) tan(α/2)=±√((1-cos α)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·
降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2 cos^2(α)=(1+cos(2α))/2=vercos(2α)/2 tan^2(α)=(1-cos(2α))/(1+cos(2α)) ·
万能公式: sinα=2tan(α/2)/[1+tan^2(α/2)] cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] tanα=2tan(α/2)/[1-tan^2(α/2)] ·
积化和差公式: sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)] cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)] cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)] sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)] ·
和差化积公式: sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]。