高中数学三角函数公式大全全解(精选课件)

x
y
在题中横线上。
y
-x
sin(π-α)=
cos(π-α)=
tan(π-α)= －

x
3

tan

( 2)tan
4
4
y
公式四：
sin( ) sin
cos( ) cos
tan( ) tan -1
P′(-x,y)
π-a
α 与π-α关于y轴对称
+(°-°)(°+°)
(2)证明:左边=


(1)解:原式=
( +)( +)


(°+°)+(°+°)

=
=
=
-°°
|°-°|
-
=
=-tan °-°
如：sin(π+a)，假设 a 是锐角，则π+a 是第三象
限角，所以sin(π+a)=-sina
思考2：如果α为锐角，你能得到什么结论？
a

-
2

cos( -)=sin
2
c
α
b

sin ( ) cos
2
思考3：若α为一个任意给定的角，那么 的终边与
角

2
的终边有什么关系？
2k ( k Z ), - , 的三角函数值，等于角
的同名函数值，前面加上一个把 看成锐角时
原函数值的符号。
即：
函数名不变，符号看象限！
“函数名不变”是指等号两边的三角函数同名；
“符号看象限”是指等号右边是正号还是负号，可
以通过先假设a是锐角，然后由等号左边的式子中的

谢谢聆听
02
弧度制
以弧长与半径之比作为角的度量单位，一周角等于2π弧 度。
03
角度与弧度的转换公式
1度=π/180弧度，1弧度=180/π度。
三角函数定义域与值域
正弦函数（sin）
定义域为全体实数，值域为[-1,1]。
余弦函数（cos）
定义域为全体实数，值域为[-1,1]。
正切函数（tan）
定义域为{x|x≠kπ+π/2,k∈Z}，值域为全体实数。
电磁波
三角函数在电磁学中描述电场和磁场的振动，以 及电磁波（如光波、无线电波）的传播。
工程技术中的测量和计算问题
1 2 3
角度测量
三角函数在测量学中用于计算角度、距离和高程 等问题，如使用全站仪进行地形测量。
建筑设计
在建筑设计中，三角函数用于计算建筑物的角度 、高度和间距等参数，确保建筑结构的稳定性和 安全性。
错误产生原因分析
基础知识不扎实
学生对三角函数的基本概念和性 质理解不深入，导致在记忆和使
用诱导公式时出错。
思维方式僵化
学生可能过于依赖记忆而非理解， 导致在面对灵活多变的题目时无法 灵活运用诱导公式。
训练不足
学生可能缺乏足够的练习，无法熟 练掌握诱导公式的使用方法和技巧 。
针对性纠正措施建议
A
强化基础知识
04 学生易错点剖析及纠正措施
常见错误类型总结
公式记忆错误
学生常常将三角函数的诱 导公式混淆，例如将正弦 、余弦、正切的诱导公式 记混。
角度转换错误
在解题过程中，学生可能 会将角度制与弧度制混淆 ，或者在角度加减时出错 。
符号判断错误
在使用诱导公式时，学生 可能会忽略符号的判断， 导致最终结果错误。

例2
(2020届河北衡水金卷周考卷(四),14)若tan
θ-
1-sin6θ 1-sin4θ
-cos6θ -cos4θ
=0,则cos2θ+
1 sin 2θ的值为
.
2
解析
由已知得tan
θ=
1-sin6θ 1-sin4θ
-cos6θ -cos4θ
=
sin2θ sin2θ
cos2θ-sin6θ-cos6θ cos2θ-sin4θ-cos4θ
例1 (2019福建三校联考,3)已知角θ的顶点与坐标原点重合,始边与x轴的
非负半轴重合,终边在直线y=2x上,则cos 2θ = ( )
A.- 4 B.- 3 C. 2 D. 3
5
5
3
4
解析 解法一:设角θ的终边上任一点为P(k,2k)(k≠0),则r= k 2 (2k)2 = 5 |k|.
α
π
2kπ,k
Z
α
|
π
2kπ
α
3π 2
2kπ,k
Z
α
|
3π 2
2kπ
α
2π
2kπ,k
Z
2.终边相同的角
终边落在x轴上的角的集合 终边落在y轴上的角的集合 终边落在坐标轴上的角的集合 终边与角α终边相同的角的集合
{α|α=kπ,k∈Z}
α|α
π 2
kπ,k
Z}
α|α
kπ 2
,k
Z}
{β|β=α+2kπ,k∈Z}
.
解析
∵sin
α-
π 4
=
72 10
,∴
2 (sin α-cos α)= 7 2 ,即sin α-cos α= 7 ①,两边平

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγsinα·cosβ·sinγ-sinα·sinβ·cosγ
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1tanα·tanβ-tanβ·tanγ-tanγ·tanα)
5、幂级数
c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞) c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)
cosh x = 1+x2/2!+x^4/4!+…+x2k/(2k)!+…, x∈R
arcsinh x =x - x3/(2*3) + (1*3)x5/(2*4*5) -(1*3*5)x7/(2*4* 6*7)…, x∈(-1,1)
arctanh x = x + x3/3 + x5/5 + …, x∈(-1,1)
上述两式相比可得： tan3a=tana·tan(60°-a) ·tan(60°+a)
6、四倍角公式
sin4a=-4*[cosa*sina*(2*sina^2-1)] cos4a=1+(-8*cosa^2+8*cosa^4) tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)
7、五倍角公式
5
应用欧拉公式
8、n倍角公式
上式用于求n倍角的三角函数时，可变形为： 所以
其中，Re表示取实数部分，Im表示取虚数部分．而

课堂小结
本节我们学习了二倍角的正弦、 余弦和正切公式，我们要熟记公式， 在解题过程中要善于发现规律，学 会灵活运用.
课后作业
1. 阅读教材P.132到P.134; 2. 《习案》作业三十二.
讲授范例：
例2. 在△ABC中, cos A 4 , tan B 2, 5
求 tan(2A 2B)的值.
讲授范例：
例3. 已知tan 2 1 ,求 tan的值.
3
例4.
已知等腰三角形的一个底角的正弦值为 5 ，
13
求这个三角形的顶角的正弦、余弦及正切值.
练习. 教材P.135练习第1、2、3、4、5题.
cos 2 cos( ) cos cos sin sin cos2 sin2
思考：
cos 2 cos2 sin2
把上述关于cos2的式子能否变成 只含有sin或cos情势的式子呢？
思考：
cos 2 cos2 sin2
把上述关于cos2的式子能否变成 只含有sin或cos情势的式子呢？
复习引入 基本公式：
tan( ) tan tan 1 tan tan
复习引入 基本公式：
tan( ) tan tan 1 tan tan
tan( ) tan tan 1 tan tan
讲授新课
思考：
讲授新课
思考：
由此我们能否得到sin2，cos2， tan2的公式呢？
3.1.3 两倍角的正弦、 余弦、正切公式
复习引入 基本公式：
复习引入 基本公式：
复习引入 基本公式：
复习引入 基本公式：
cos( ) cos cos sin sin
复习引入 基本公式：
cos( ) cos cos sin sin cos( ) cos cos sin sin

其他非重点三角函数
csc(a)=1/sin(a) sec(a)=1/cos(a)
双曲函数
sinh(a)=(e^a-e^(-a))/2 cosh(a)=(e^a+e^(-a))/2 tgh(a)=sinh(a)/cosh(a)
常用公式表（一）
1。乘法公式
（1）（a+b）²=a2+2ab+b2
三角函数和差化积公式
sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2) sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2) cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2) cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)
常用公式表（二）
///
///
1、求导法则：（1）（u+v） =u +v （2）（u-v） =u -v
/
/
（3）（cu） =cu
/
（1）（c） =0
/
//
（4）（uv） =uv +u v
2、基本求导公式：
a/
a 1
（2）（x ） =ax
（5）
u v
uv uv v2
x/x
（3）（a ） =a lna
（1） 直线形式：点斜式： y y0 kx x0
斜截式：y=kx+b
y y1
x
x1
两点式： y2 y1 x2 x1
（2）直线关系： l1 : y k1 x b1
l2 : y k2 x b2
平行：若 l1 // l2 ，则 k1 k2

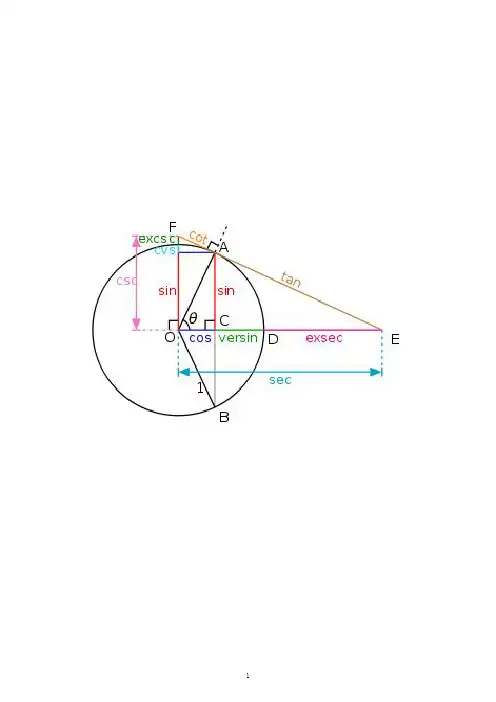
三角公式汇总一、任意角的三角函数在角 的终边上任取 一点 P( x, y) ，记：22rxy ，．．正弦： sinyx余弦： cosrry 正切： tanx注：我们还可以用单位圆中的有向线段表示任意角的三角函数： 如图，与单位圆有关的有向 线段 MP 、 OM 、 AT 分别叫做角 的正弦线、余弦线、正．． 切线。

二、同角三角函数的基本关系式商数关系： tansin ，cos平方关系： sin 2cos 21，三、诱导公式⑴2k ( kZ ) 、 、 、 、2 的三角函数值， 等于 的同名函数值，前面加上一个把看成锐角时原函数值的符号。

（口诀：函数名．．不变，符号看象限）⑵、、3、3的三角函数值， 等于 的异名函数值，2 222前面加上一个把 看成锐角时原函数值的符号。

（口诀：函数名改变，符号看．．象限）四、和角公式和差角公式sin( ) sin cos cos sin sin( ) sin cos cos sin cos() coscossinsincos( ) cos cos sin sintan()tantantan tan1 tan()tan tantantan1五、二倍角公式sin 22sin coscos2cos 2sin 22 cos 21 1 2sin 2( )2 tantan21 tan 2二倍角的余弦公式( ) 有以下常用变形：（规律：降幂扩角，升幂缩角）1 cos2 2cos 2 1 cos22sin 21 sin2 (sincos )21 sin2 (sincos)2cos 21 cos2 ， sin 21 sin2 ， tan1 cos2 sin 2。

22sin 21 cos2六、万能公式（可以理解为二倍角公式的另一种形式）2 tan 1 tan 2 ， tan 22 tan 。

sin 22， cos2tan 2 1 tan 21 tan1万能公式告诉我们，单角的三角函数都可以用半角的正切．．来表示。

三角函数公式大全图解三角函数公式：两角和公式我们常常需要计算两个角度的正弦、余弦和正切值的和或差。

这时候，就需要用到两角和公式。

两角和公式的形式如下：sin(A+B) = sinAcosB + cosAsinBsin(A-B) = sinAcosB - cosAsinBcos(A+B) = cosAcosB - sinAsinBcos(A-B) = cosAcosB + sinAsinBtan(A+B) = (tanA+tanB)/(1-XXX)tan(A-B) = (tanA-tanB)/(1+XXX)其中，A和B为两个角度。

倍角公式倍角公式用于计算一个角度的两倍的正弦、余弦和正切值。

倍角公式的形式如下：sin2A = 2sinAcosAcos2A = cos2A - sin2A = 2cos2A - 1 = 1 - 2sin2Atan2A = 2tanA/(1-tan2A)其中，A为一个角度。

三倍角公式三倍角公式用于计算一个角度的三倍的正弦、余弦和正切值。

三倍角公式的形式如下：sin3A = 3sinA - 4(sinA)3cos3A = 4(cosA)3 - 3cosAtan3A = tanA·tan(A+π/3)·tan(A-π/3)其中，A为一个角度。

半角公式半角公式用于计算一个角度的一半的正弦、余弦和正切值。

半角公式的形式如下：sin(A/2) = ±√[(1-cosA)/2]cos(A/2) = ±√[(1+cosA)/2]tan(A/2) = ±√[(1-cosA)/(1+cosA)]其中，A为一个角度。

和差化积和差化积公式用于将两个三角函数的和或差转化为一个三角函数的积。

和差化积公式的形式如下：sin(A±B) = sinAcosB ± cosAsinBcos(A±B) = cosAcosB ∓ sinAsinBtan(A±B) = (tanA±tanB)/(1∓tanAtanB)cot(A±B) = (cotAcotB ∓ 1)/(cotB±cotA)其中，A和B为两个角度。

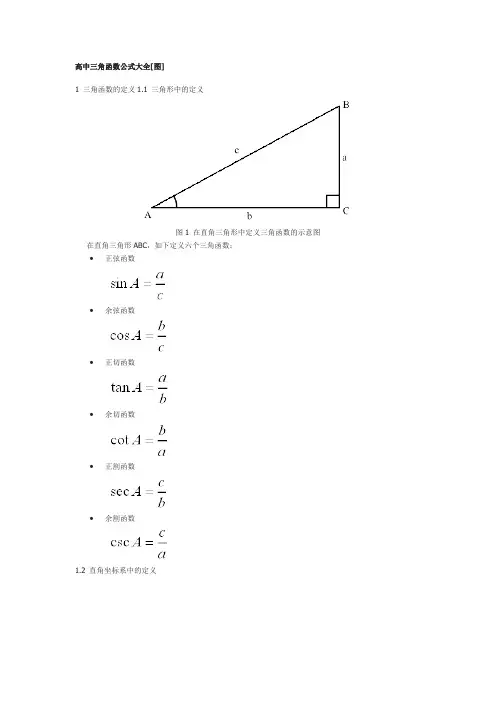
高中三角函数公式大全[图]1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC，如下定义六个三角函数：•正弦函数•余弦函数•正切函数•余切函数•正割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中，如下定义六个三角函数：•正弦函数r•余弦函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式证明过程首先，sin(α+β)=sinαcosβ+sinβcosα（已证。

证明过程见《和角公式与差角公式的证明》）因为sin(α+β)=sinαcosβ+sinβcosα（正弦和角公式）则=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于是sin(α-β)=sinαcosβ-sinβcosα（正弦差角公式）将正弦的和角、差角公式相加，得到sin(α+β)+sin(α-β)=2sinαcosβ则sinαcosβ=sin(α+β)/2+sin(α-β)/2（“积化和差公式”之一）同样地，运用诱导公式cosα=sin(π/2-α)，有cos(α+β)=sin[π/2-(α+β)]=sin(π/2-α-β)=sin[(π/2-α)+(-β)]=sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α)=cosαcosβ-sinαsinβ于是cos(α+β)=cosαcosβ-sinαsinβ（余弦和角公式）那么=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβcos(α-β)=cosαcosβ+sinαsinβ（余弦差角公式）将余弦的和角、差角公式相减，得到cos(α+β)-cos(α-β)=-2sinαsinβ则sinαsinβ=cos(α-β)/2-cos(α+β)/2（“积化和差公式”之二）将余弦的和角、差角公式相加，得到cos(α+β)+cos(α-β)=2cosαcosβ则cosαcosβ=cos(α+β)/2+cos(α-β)/2（“积化和差公式”之三）这就是积化和差公式：sinαcosβ=sin(α+β)/2+sin(α-β)/2sinαsinβ=cos(α-β)/2-cos(α+β)/2cosαcosβ=cos(α+β)/2+cos(α-β)/24.2 和差化积公式部分证明过程：sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαc osβ-sinβcosαcos(α+β)=sin[90-(α+β)]=sin[(90-α)-β]=sin(90-α)cosβ-sinβcos(90-α)=cosαcosβ-sinαsinβcos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαc osβ+sinαsinβtan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+sinβcosα)/(c osαcosβ-sinαsinβ)=(cosαtanαcosβ+cosβtanβcosα)/(co sαcosβ-cosαtanαcosβtanβ)=(tanα+tanβ)/(1-tanαtanβ) tan(α-β)=tan[α+(-β)]=[tanα+tan(-β)]/[1-tanαtan(-β)] =(tanα-tanβ)/(1+tanαtanβ)诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b]•1+sin(a)=(sin(a/2)+cos(a/2))^2•1-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数•csc(a)=1/sin(a)•sec(a)=1/cos(a)双曲函数•sinh(a)=(e^a-e^(-a))/2•cosh(a)=(e^a+e^(-a))/2•tgh(a)=sinh(a)/cosh(a)常用公式表（一）1。

2024/1/26
单调性
在各象限内，正弦、余弦 函数的单调性及其变化规 律。
最值问题
利用三角函数的性质求最 值，如振幅、周期等参导公式与恒等 式
REPORTING
2024/1/26
7
诱导公式及其应用
01
诱导公式的基本形式
通过角度的加减、倍角、半角等关系，将任意角的三角函数值转化为基
8
恒等式及其证明方法
2024/1/26
恒等式的基本形式
两个解析式之间的一种等价关系，即对于某个变量或一组变量的取值范围内，无论这些变 量取何值，等式都成立。
恒等式的证明方法
通常采用代数法、几何法或三角法等方法进行证明。其中，代数法是通过代数运算和变换 来证明恒等式；几何法是通过几何图形的性质和关系来证明恒等式；三角法是通过三角函 数的性质和关系来证明恒等式。
化简为简单的形式。
12
三角函数的乘除运算规则
乘积化和差公式
通过乘积化和差公式，可以将两 个三角函数的乘积转化为和差的
形式，从而简化运算。
商的化简
利用同角三角函数的基本关系， 可以将三角函数的商转化为简单
的三角函数运算。
倍角公式
通过倍角公式，可以将三角函数 的乘方运算转化为简单的三角函
数运算。
2024/1/26
建立三角函数与数列、概率统计相关 的数学模型
结合计算机编程和数学软件，实现模 型的数值模拟和可视化
2024/1/26
利用数学分析、高等代数等方法求解 模型
22
PART 06
总结回顾与拓展延伸
REPORTING
2024/1/26
23
本章节知识点总结回顾
三角函数图像
正弦、余弦、正切函数的图像 及其周期性、奇偶性等性质。

高中三角函数公式大全[图]1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC，如下定义六个三角函数：•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中，如下定义六个三角函数：•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a) 半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b]• 1+sin(a)=(sin(a/2)+cos(a/2))^2 • 1-sin(a)=(sin(a/2)-cos(a/2))^2 其他非重点三角函数• csc(a)=1/sin(a) •sec(a)=1/cos(a)双曲函数• sinh(a)=(e^a-e^(-a))/2 • cosh(a)=(e^a+e^(-a))/2 •tgh(a)=sinh(a)/cosh(a)常用公式表（一）1。

波动问题
波动是物理学中另一个重要的研究领域。在波动问题中，三角函数同样扮演着重 要的角色。利用三角函数诱导公式，可以求解波动方程，得到波的传播速度、波 长、频率等关键参数。
21
拓展延伸：复数域内三角函数性质探讨
复数域内三角函数的定义
在复数域内，三角函数可以通过欧拉公式进行定义。这使得三角函数在复数域内具有了许多独特的性质。
α)等。
12
利用同角关系求值或化简表达式
已知一个角的三角函 数值，求其他角的三 角函数值。
通过同角关系式证明 三角恒等式。
2024/3/26
利用同角关系式化简 复杂的三角函数表达 式。
13
典型例题解析
例题1
已知sinα = 3/5，求cosα ，tanα的值。
2024/3/26
例题2
化简表达式(sinα
5
三角函数值域和极值点
值域
正弦函数和余弦函数的值域均为$[-1, 1]$；正切函数的值域 为$R$。
2024/3/26
极值点
正弦函数在$frac{pi}{2} + kpi(k in Z)$处取得最大值1，在 $frac{3pi}{2} + kpi(k in Z)$处取得最小值-1；余弦函数在 $2kpi(k in Z)$处取得最大值1，在$pi + kpi(k in Z)$处取得 最小值-1。
关注三角函数与其他知识点的 联系，如向量、数列、不等式
等。
2024/3/26
26
THANKS
感谢观看
2024/3/26
27
18
05
实际应用举例与拓展延伸
2024/3/26
19
在几何图形中求解角度问题

的两个顶点上函数值的乘积。（主要是两条虚线两端的 三角函数值的乘积）。由此，可得商数关系式。 （3）平方关系：在带有阴影线的三角形中，上面两个顶点上 的三角函数值的平方和等于下面顶点上的三角函数值的 平方。
3---两角和差公式
两角和与差的三角函数公式 sin（α＋β）＝sinαcosβ＋cosαsinβ sin（α－β）＝sinαcosβ－cosαsinβ cos（α＋β）＝cosαcosβ－sinαsinβ cos（α－β）＝c：
公式五： 利用公式一和公式三可以得到2πα与α的三角函数值之间的关系： sin（2π－α）＝－sinα cos（2π－α）＝cosα tan（2π－α）＝－tanα cot（2π－α）＝－cotα
公式六之二 sin（3π/2＋α）＝－cosα cos（3π/2＋α）＝sinα tan（3π/2＋α）＝－cotα cot（3π/2＋α）＝－tanα
r2 sin2 sin2 2sin sin cos2 cos2 2 cos cos r2 sin2 cos2 sin2 cos2 2sin sin 2 cos cos
r2 11 2sin sin cos cos r2 2 2sin sin cos cos 2r2 1 sin sin cos cos
公式二： 设α为任意角，π+α的三角函数值 与α的三角函数值之间的关系： sin（π＋α）＝－sinα cos（π＋α）＝－cosα tan（π＋α）＝tanα cot（π＋α）＝cotα
公式四： 利用公式二和公式三可以得到π-α 与α的三角函数值之间的关系： sin（π－α）＝sinα cos（π－α）＝－cosα tan（π－α）＝－tanα cot（π－α）＝－cotα
三角函数公式及推导（祥尽解释）

一.复习回顾
任意角三角函数的定义 设α是一个任意角，它的终边与单位圆交于点P(x， y)，那么：
（1）正弦sinα＝ （2）余弦cosα＝
y
P(x,y)
y
x
O
（3）正切tanα＝
y x
x
问题探究
1.终边相同的角的同一三角函数值有什么关系 ? 相等
2.角 -α与α的终边 有何位置关系?
终边关于x轴对称 3.角 -α与α的终边 有何位置关系?
3 当n为奇数时， 4
练习1 求sin(2n+2/3)· cos(n+4/3)的值(nZ)
3 当n为偶数时， 4
2 化简 cos[(4n+1)/4+x]+ cos[(4n-1)/4-x]
当n为奇数时，原式=-2cos(/4+x) 当n为偶数时，原式=2cos(/4+x)
小结
①三角函数的简化过程图：
终边关于y轴对称
4.角 +α与α的终边 有何位置关系? 终边关于原点对称
终边相同的角的同一三角函数值相等
（公式一）
sin( 2k ) sin ( k Z )
cos( 2k ) cos (k Z )
tan( 2k ) tan ( k Z )
三角函数
负化正，大化小，化到锐角为终了。
上述过程体现了由未知到已知的化归思想。
2 (1) cos225 cos(180 45) cos 45 2 11 sin 3 (2) sin sin( 4 ) 3 3 2 3
3 16 n ) (3) sin( ) sin 3 3 2 3 3
-1 0 -1

5．三角函数的和差化积公式 sinα＋sinβ＝2sinα＋2 βcosα－2 β； sinα－sinβ＝2cosα＋2 βsinα－2 β； cosα＋cosβ＝2cosα＋2 βcosα－2 β； cosα－cosβ＝－2sinα＋2 β＋sinα－2 β.
误区警示 (1)注意和角公式中的符号，这是最易出错的地方． (2)半角公式根号前的符号由α2所在象限确定，升降 幂公式中角与指数的关系．
∴tanα＝－34，∴tanα＋π3＝1t－antαa＋nαt·atann3ππ3
＝1－－－34＋34×3
＝19(48－25 3
3)．
• 二、学习本章要在“变”字上下功夫，在 变角变名变结构中实现对问题的突破，它 体现的就是转化与化归的思想方法．
• 1．变角：①设法产生特殊角；②将待求 角向已知角转化求值，或将已知角向待证 式中的角靠拢证明；
方法二：仍然要想着非特殊角跟特殊角的联系，并
且注意到 3＝2cos30°，于是
原式＝
3sin10°＋4sin10°cos10° cos10°
＝
3sin10°＋2sin20° cos10°
＝2cos30°scino1s01°0＋° 2sin20°(积化和差)
＝sin40°－scions2100°°＋2sin20°
＝sin40co°＋s10si°n20°(和差化积)＝2sinc3o0s°1c0o°s10°＝1.
• [点评] 从解题过程来看，本题包含了常 见的各种三角变换的技巧．函数名不同时， 化为同名，角向特殊角进行转换，特殊值 与特殊角的转换以及积化和差、和差化积 等技巧．希望能仔细琢磨．
• 三、给角求值、给值求值(或角)的化简、 计算题是最基本的考查方式．
一、熟练掌握和、差、倍角的三角公式是直接应用 公式进行三角恒等变形的先决条件、半角公式、和积互 化公式虽不要求记忆，能记住应用起来更方便些．

1 2、已知 sin(π +α )=- ,求 cosα 的值 2 1 3、已知 cosα = ，且- ＜α ＜0， 3 2
cot( ) sin(2 ) 求 的值. cos( ) tan
m3 4 2m , cos ( )， 4、若 sin m5 m5 2
公式逆用
两角和与差的三角函数公式
sin(α β) sinαcosβ cosαsinβ asinx bcosx cos(α β) cosαcosβ sinαsinβ a2 b2 sin(xθ) tanα tanβ tan(α β) 1 tanαtanβ
二倍角公式
任意角的三角函数
（1）任意角三角函数的定义
y
P( x, y)
O

y x sin cos r r x y 2 2 tan (r x y ) x
-5/13 ， 已知角α的终边过点P(-5，-12)，则cosα= _______ 12/5 tan α =_______.
(2)三角函数的定义域：
例2、求值问题 （1） 已知α 为第二象限的角，sinα
cosβ
3 = ， β 为第一象限的角， 5
5 = .求 sin (α 13
-β )的值.
1 11 （2） ．已知 cos ， cos( ) ， (0, ) ， 7 14 2
( , ) 求 cos 的值
三角函数 y=sinx y=cosx y=tanx
定义域
R
R
{x|xk+ ,kZ}
2
(3)三角函数值的符号: sin+
tan 和 全+
cos +