(完整版)大连理工自动控制原理打印版(精)

大连理工自动控制原理习题答案自动控制原理课后习题答案编辑者：潘学俊第二章2.1 试分别写出图2.68中各无源电路的输入u r (t )与输出u c (t )之间的微分方程。

图2.68 习题2.1图解：(a)11r c u u i R -=，2()r c C u u i -= ，122c u i i R +=，12122 121212c c r r R R R R R Cu u Cu u R R R R R R +=++++(b)11()r c C uu i -= ，121r u u i R -=，1221i i C u+= ，121c u i R u =+， 121211122112121121()()c c c r r r R R C C uR C R C R C u u R R C C u R C R C u u ++++=+++ (c)11r cu u i R -=，112()r C u u i -=，1122u i i R +=，1121c u i dt u C =+?， 121212222112122221()()c c c r r r R R C C u RC R C R C u u R R C C u R C R C u u ++++=+++2.2 试证明图 2.69(a)所示电路与图 2.69(b)所示的机械系统具有相同的微分方程。

图2.69(b)中X r (t )为输入，X c (t )为输出，均是位移量。

(a) (b)图2.69 习题2.2图解：(a)11r cu u i R -=，12()r c C u u i -= ，12i i i +=，221c u idt iR C =+?，121211122212121122()()c c c r r r R R C C uR C R C R C u u R R C C u R C R C u u ++++=+++ (b)2121()c B xx K x -= ，1121()()()r c r c c B x x K x x B x x -+-=- ，121221212121211212()()c c c r r r B B B B B B B B Bx x x x x x K K K K K K K K K ++++=+++ 2.3 试分别求出图2.70中各有源电路的输入u r (t )与输出u c (t )之间的微分方程。

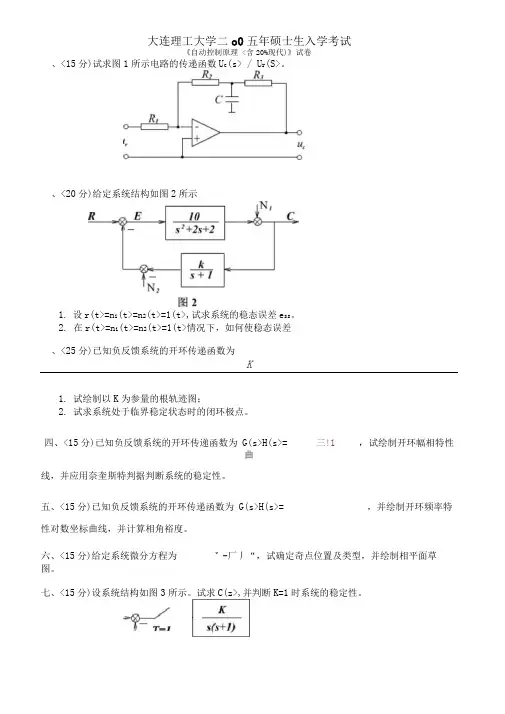
大连理工大学二o0五年硕士生入学考试《自动控制原理 <含20%现代)》试卷、<15分)试求图1所示电路的传递函数U c (s> / U r (S>。

、<25分)已知负反馈系统的开环传递函数为K1.试绘制以K 为参量的根轨迹图；2. 试求系统处于临界稳定状态时的闭环极点。

四、<15分)已知负反馈系统的开环传递函数为 G(s>H(s>=三!1 ，试绘制开环幅相特性曲 线，并应用奈奎斯特判据判断系统的稳定性。

五、<15分)已知负反馈系统的开环传递函数为 G(s>H(s>= ，并绘制开环频率特性对数坐标曲线，并计算相角裕度。

六、<15分)给定系统微分方程为 v-厂丿“，试确定奇点位置及类型，并绘制相平面草图。

七、<15分)设系统结构如图3所示。

试求C(z>,并判断K=1时系统的稳定性。

、<20分)给定系统结构如图2所示1. 设r(t>=n i (t>=n 2(t>=1(t>,试求系统的稳态误差e ss 。

2. 在r(t>=n i (t>=n 2(t>=1(t>情况下，如何使稳态误差八、<10分)已知离散系统的状态方程为0 IX（k+1）= °00 2aa＞0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的01X(k)a 取值范1"s+F1.试建立系统的状态空间描述；2 •试设计状态反馈阵，使系统闭环极点位于-2, -2处;3.K是否可以取为0.5，为什么？大连理工大学二OO四年硕士生入学考试《自动控制原理＜含30%现代）》试卷、＜15分）试求图1所示电路的结构图和传递函数。

/?/ 出、＜10分）已知系统的特征方程为:4 3 2s4+2.5s3+2.5s2+10s -6 = 试求特征根在S平面上的分布。

的=3三、＜10分）试求系统"小八—的单位脉冲响应。

15春⼤连理⼯⼤学《⾃动控制原理》在线作业1满分答案15春⼤连理⼯⼤学《⾃动控制原理》在线作业1满分答案⼀、单选题（共10道试题，共50分。

）1.判定⼀个系统是否稳定有多种⽅法，其中不包括(D)。

A.劳斯判据法B.奈奎斯特判据法C.李雅普诺夫第⼆⽅法D.信号流图法满分：5分得分：52.⾼阶系统找到⼀对(C)就可近似地当作⼆阶系统来分析。

A.主导零点B.主导极点C.共轭复数主导极点D.共轭实数主导极点满分：5分得分：53.测速发电机属于(A)。

A.⽐例环节B.惯性环节C.积分环节D.振荡环节满分：5分得分：54.(A)是经典控制理论中最基本也是最重要的概念。

A.传递函数B.频率法C.根轨迹法D.微分⽅程满分：5分得分：55.(A)⼜称为参考输⼊。

A.给定值B.被控量C.反馈通道D.前向通道满分：5分得分：56.当⼆阶系统为(C)响应时，系统的特征根为共轭虚根。

A.⽋阻尼B.过阻尼C.⽆阻尼D.临界阻尼满分：5分得分：57.⽤(C)建⽴模型时，是通过系统本⾝机理的分析确定模型的结构和参数，从理论上推导出系统的数学模型。

A.数学法B.差分法C.演绎法D.归纳法满分：5分得分：58.若系统劳斯阵列表的第k⾏所有系数(A)，则系统要么不稳定，要么处于临界稳定状态。

A.均为零B.均为1C.不为零D.恒定满分：5分得分：59.下列哪种输⼊信号属于斜坡函数(D)。

A.突然转换B.突然合闸C.负荷突变D.数控机床加⼯斜⾯的进给指令满分：5分得分：510.电枢控制的直流电动机属于(C)。

2014年大连理工大学854自动控制原理考研真题（回忆版）2013年大连理工大学854自动控制原理考研真题（回忆版）大连理工大学2013年硕士生入学考试《自动控制原理（含20%现代）》试题一、简答1．分析单位闭环反馈系统常用什么分析系统的性能？2．超前反馈校正环节与滞后反馈校正环节的优缺点？3．对于受控系统采用状态反馈能镇定的充要条件是什么？4．采取哪种措施可以减少系统稳态误差？5．在系统设计时是否要使系统闭环稳定增益为1或者接近于1？二、系统框图如右所示，其中，1．求PI调节器的传递函数。

2．G（s）=略，求当w=略，=略时的，并说出这样的对系统性能有何影响。

（值过大，过小）。

3．当G（s）=略时，求系统稳定时满足的范围（劳斯判据）。

三、系统框图如图所示,Ur输入，Uc输出。

1．写出系统的微分方程，画出结构图。

2．写出系统的闭环传递函数。

四、根轨迹方程为，求出根轨迹，求出系统衰减震荡时的K值范围。

五、（a,b值略）1．画出极坐标图，并写出系统稳定的K值范围。

2．当K=1时，画出系统的Bode图，并在图中标出相角裕量和幅值裕量。

六、非线性系统方程，求出系统的奇点，并画出相平面草图。

七、闭环离散系统如图所示，其中u（k）=u（k-1）+e（k）,G（s）=，T=11．求闭环脉冲传递函数C（z）/R（z）。

2．求闭环系统稳定时的K值范围。

八、如图所示，状态空间描述1．判断系统的能控性，能观性。

2．采用状态反馈使得配置极点为a,b（a,b值略），求出反馈阵k。

3．已知,求出闭环传递函数Y（S）/V（s），求出稳态输出及闭环稳态增益。

4．如何使系统的闭环稳态增益为1？注：标注略，参数不清楚。

2012年大连理工大学854自动控制原理考研真题大连理工大学2012年硕士生入学考试《自动控制原理（含20%现代）》试题一、求以为输入，的微分方程，B为阻尼器，K为弹簧弹性系数。

二、1．求C（s），当，求。

2．R（t）=1（t），n（t）=0，=G（s）=，求输出响应c（t）。

大连理工大学22春“电气工程及其自动化”《自动控制原理》作业考核题库高频考点版（参考答案）一.综合考核(共50题)1.极限环可以使系统性能变好。

()A.正确B.错误参考答案：B2.每个闭环特征根的变化轨迹都是整个根轨迹的一个分支。

()A.正确B.错误参考答案：A3.零阶保持器相对于其他类型的保持器，具有最小相位滞后，容易实现的特点，在离散控制系统中应用最为广泛。

()A.正确B.错误参考答案：A4.同一个物理系统，可以用不同的数学模型来表达。

()A.正确B.错误参考答案：A5.以开环根轨迹增益为可变参数绘制的根轨迹称做参变量根轨迹。

()A.正确参考答案：B6.一个传递函数只能表示()的函数关系。

A.一个输入对一个输出B.一个输入对多个输出C.多个输入对一个输出D.多个输入对多个输出参考答案：A7.模数转换器与数模转换器为数字计算机的接口。

()A.正确B.错误参考答案：A8.离散时间控制系统的分析包括()。

A.系统的稳定性B.瞬态性能C.稳态性能D.最少拍设计参考答案：ABCD9.频率特性可以用来表示线性系统或环节的动态特性。

()A.正确B.错误参考答案：A10.A.正确B.错误参考答案：B11.典型环节的阶数最高不超过()。

A.4B.3C.2D.1参考答案：C12.垂直于()上的特征根，它们对应有基本相同的调节时间。

A.原点射线B.虚轴直线C.实轴直线D.实轴或虚轴直线参考答案：C13.比例环节的相频特性为()。

A.0°B.60°C.90°D.180°参考答案：A14.系统中如果有()，对系统的稳定性不利。

A.惯性环节B.积分环节C.振荡环节D.延滞环节参考答案：D15.利用超前网络进行串联校正的基本原理是利用其相角的超前特性。

()A.正确B.错误参考答案：A16.实轴上属于根轨迹的部分，其右边开环零、极点的个数之和为()。

A.奇数B.偶数C.零D.正数参考答案：A17.如果遇到Z变换函数是超越函数，则只能用()来求取Z反变换。

3-1 (1) 两边取拉氏变换，()2100.2()2()()()0.2C s C s R s G s R s s s=⇒===, 单位冲激响应：()()r t t δ=, ()1R s =,10()()()()10,(0)C s G s R s c t t s==⇒=≥ 单位阶跃响应：()()1()r t u t t ==, 1()R s s =,210()()()()10,(0)C s G s R s c t t t s==⇒=≥(2) 时间常数T=5，5%,315,3%,420s s t T t T ∆===∆===3-3 (1) 10.2 1.2()6010C s s s s =+-++, 1()R s s=,那么, 2()600()()70600C s G s R s s s ==++(2) 2600n n ωω=⇒=,2270n ζωζ=⇒=3-4 (1) 2n ()50(),21()1050G s s G s s s ζω⎧=⎪Φ==⇒⎨+++⎪⎩欠阻尼单位冲激响应：()()r t t δ=, ()1R s =,5250()()()()sin 10sin5,(0)1050n n t t C s s R s c t e t t s s ζωω--=Φ=⇒==≥++3-14(1) 4322210s s s s ++++=满足必要条件4321011122001221s s s s sεεε→-→-∞第一列变号2次，不稳定，有两个正实部根。

(2) 6543228122016160s s s s s s ++++++=满足必要条件65442321018201621216021216auxiliary equation 21216082406168316s s s s s s s s s ++=：辅助方程的根包含四个纯虚根，临界稳定。

3-15 (1) 32()10(1)()1()4510G s s s G s s s s +Φ==++++, 满足必要条件， 3210154102.510s s s s满足劳斯判据，系统稳定。

2014年大连理工大学854自动控制原理考研真题（回忆版）2013年大连理工大学854自动控制原理考研真题（回忆版）大连理工大学2013年硕士生入学考试《自动控制原理（含20%现代）》试题一、简答1．分析单位闭环反馈系统常用什么分析系统的性能？2．超前反馈校正环节与滞后反馈校正环节的优缺点？3．对于受控系统采用状态反馈能镇定的充要条件是什么？4．采取哪种措施可以减少系统稳态误差？5．在系统设计时是否要使系统闭环稳定增益为1或者接近于1？二、系统框图如右所示，其中，1．求PI调节器的传递函数。

2．G（s）=略，求当w=略，=略时的，并说出这样的对系统性能有何影响。

（值过大，过小）。

3．当G（s）=略时，求系统稳定时满足的范围（劳斯判据）。

三、系统框图如图所示,Ur输入，Uc输出。

1．写出系统的微分方程，画出结构图。

2．写出系统的闭环传递函数。

四、根轨迹方程为，求出根轨迹，求出系统衰减震荡时的K值范围。

五、（a,b值略）1．画出极坐标图，并写出系统稳定的K值范围。

2．当K=1时，画出系统的Bode图，并在图中标出相角裕量和幅值裕量。

六、非线性系统方程，求出系统的奇点，并画出相平面草图。

七、闭环离散系统如图所示，其中u（k）=u（k-1）+e（k）,G（s）=，T=11．求闭环脉冲传递函数C（z）/R（z）。

2．求闭环系统稳定时的K值范围。

八、如图所示，状态空间描述1．判断系统的能控性，能观性。

2．采用状态反馈使得配置极点为a,b（a,b值略），求出反馈阵k。

3．已知,求出闭环传递函数Y（S）/V（s），求出稳态输出及闭环稳态增益。

4．如何使系统的闭环稳态增益为1？注：标注略，参数不清楚。

2012年大连理工大学854自动控制原理考研真题大连理工大学2012年硕士生入学考试《自动控制原理（含20%现代）》试题一、求以为输入，的微分方程，B为阻尼器，K为弹簧弹性系数。

二、1．求C（s），当，求。

2．R（t）=1（t），n（t）=0，=G（s）=，求输出响应c（t）。

《自动控制原理》教学大纲（学分 4 ，学时64 ）一、课程的性质与任务本课程是自动化类专业的理论基础课之一。

本课程的任务是使学生掌握反馈控制系统的构成、控制系统数学模型的建立方法及系统时域、频域分析和校正方法；学习掌握非线性系统和离散控制系统的分析方法。

二、课程内容、基本要求与学时分配（一）自动控制的基本概念 2学时1．了解反馈控制系统的基本工作原理。

2．了解系统的基本控制方式及控制系统的分类方法。

3．了解对控制系统的基本要求。

（二）系统的数学模型 8学时1．掌握数学模型的建立方法。

2．会进行非线性微分方程的线性化。

3．掌握传递函数的基本概念，会求典型环节及自动控制系统的传递函数。

4．熟练掌握动态结构图及其等效变换。

（三）系统分析 10学时1．熟练掌握一阶、二阶系统的单位阶跃响应。

2．了解高阶系统的瞬态响应。

3．熟练掌握劳斯——赫尔维茨判据。

4．掌握稳态误差分析方法。

（四）根轨迹法 6学时1．掌握根轨迹的基本概念。

2．熟练掌握根轨迹的绘制方法。

3．掌握参变量根轨迹的绘制方法。

4．掌握开环零、极点对根轨迹的影响。

5．了解闭环零、极点分布对系统性能指标的影响。

（五）频率响应法 12学时1．掌握频率特性的基本概念。

2．熟练掌握系统开环频率特性的绘制方法。

3．熟练掌握奈魁斯特稳定判据。

4．了解控制系统的相对稳定性。

5．了解系统的闭环频率特性。

6．了解频率特性与瞬态响应。

（六）控制系统的校正 6学时1．了解校正装置及其特性。

2．掌握串联校正装置的设计方法及其参数的确定。

3．了解反馈校正的原理及其特点。

（七）离散控制系统 12学时1．了解采样过程和采样定理。

2．掌握Z变换与Z反变换。

3．掌握离散控制系统的数学描述方法。

4．掌握离散控制系统的分析方法。

（八）非线性控制系统 8学时1．掌握线性与非线性控制系统相平面图的绘制方法。

2．掌握非线性系统的相平面图的分析方法。

3．会求非线性系统的描述函数。

4．会用描述函数分析非线性系统。

自动控制原理孟华第二版课后答案【篇一：自动控制原理_孟华_习题答案大连理工】t>第一章（略）第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。

图2.68 习题2.1图解：(a)ur?ucurrrrr2?c?uc?12cu?r??r?u?c)?i2，i1?i2?c，12cu?i1，c(uurr1r2r1?r2r1?r2r1?r2(b)?r?u?c)?i1，c1(uur?u1?1，uc?i1r2?u1， ?i2，i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)u1ur?uc?i1，c1(ur?u1)?i2，i1?i2?1，uc?i1dt?u1， r1r2c2???c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。

图2.69(b)中xr(t)为输入，xc(t)为输出，均是位移量。

(a)(b)图2.69 习题2.2图解：(a)1ur?uc?r?u?c)?i2，i1?i2?i，uc??i1，c1(uidt?ir2，r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1，b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1)， b2(x b1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。

大连理工自控专业课
【实用版】
目录
1.大连理工自控专业介绍
2.自控专业的课程设置
3.自控专业的就业前景
正文
大连理工自控专业，全名为自动化控制专业，是一门集控制理论、电子技术、计算机技术于一体的综合性工程技术专业。

该专业主要研究自动化控制系统的设计、分析、仿真、优化和技术管理等方面的知识，培养具备自动化控制系统设计、运行、维护和管理能力的高级工程技术人才。

自控专业的课程设置涵盖了控制理论、电子技术、计算机技术、工程管理等多个领域。

主要课程包括：自动控制原理、现代控制理论、检测与仪表、电力电子技术、计算机控制技术、过程控制、运动控制、工程管理等。

这些课程旨在培养学生的专业素质和实践能力，使他们在毕业后能够胜任自动化控制系统的设计、运行、维护和管理工作。

自控专业的就业前景非常广泛，毕业生可在石油化工、机械制造、电力系统、交通运输、环保工程等各个行业找到适合自己的工作岗位。

从事的工作主要包括：自动化控制系统设计、运行、维护和管理；自动化设备和仪器的研发、生产和销售；工程项目的技术咨询、评估和管理等。

随着我国经济的持续发展和自动化技术的广泛应用，自控专业的就业前景将更加光明。

总之，大连理工自控专业是一门综合性强、就业前景广阔的工程技术专业。

从课程设置到就业前景，都充分体现了自控专业的优势和特点。

第1页共1页。

大连理工自控专业课摘要：一、引言1.大连理工自控专业背景2.文章目的与结构二、自控专业核心课程1.自动控制原理2.现代控制理论3.传感器与检测技术4.计算机控制系统5.电力电子与电力驱动三、自控专业实践与应用1.实验室研究与实践2.校企合作项目3.自控技术在典型行业的应用四、自控专业发展前景1.行业需求与就业前景2.国内外知名企业与合作3.科技创新与产业发展五、自控专业人才培养与建议1.学术与实践能力并重2.国际化视野与沟通能力3.团队合作与领导力4.终身学习与创新能力六、结论1.自控专业的重要性2.行业发展趋势与挑战3.学生发展的建议正文：一、引言随着科技的飞速发展，自动化控制技术在我国经济建设中发挥着越来越重要的作用。

大连理工自控专业作为国内一流的高校专业，一直以来都在为我国自控领域培养大量优秀人才。

本文将简要介绍大连理工自控专业课程设置、实践应用、发展前景以及人才培养建议，以期为广大学子提供有益的参考。

二、自控专业核心课程大连理工自控专业旨在培养具备扎实的理论基础和实践能力的高级工程技术人才。

专业核心课程包括：自动控制原理、现代控制理论、传感器与检测技术、计算机控制系统、电力电子与电力驱动等。

这些课程为学生提供了全面而深入的自控知识体系，为将来的工程师职业生涯奠定基础。

三、自控专业实践与应用大连理工自控专业高度重视实践教学，设有丰富的实验课程和校企合作项目。

学生可在实验室开展创新性研究，将所学理论知识应用于实际工程项目中。

此外，自控技术在能源、交通、制造业等领域具有广泛应用，为学生提供了广阔的实践平台。

四、自控专业发展前景随着国家对科技创新的重视，自动化控制行业发展迅速，对人才需求旺盛。

大连理工自控专业毕业生在国内外知名企业、研究机构等领域具有较高的竞争力和就业率。

此外，国际化合作与交流的不断加强，也为学生提供了更多的发展机遇。

五、自控专业人才培养与建议为确保自控专业人才培养质量，大连理工在培养方案中强调学术与实践能力并重。

大连理工大学2017年硕士研究生入学考试大纲科目代码：854科目名称：自动控制原理试题为主观题型（计算题、简答题、简单的推导与证明题），经典控制理论占80%，现代控制理论占20%，具体复习大纲如下：一、自动控制的基本概念1、反馈控制系统的基本工作原理.2、系统的基本控制方式及控制系统的分类方法.3、对控制系统的基本要求.二、控制系统的数学模型1、数学模型及系统微分方程的建立、非线性方程的线性化.2、控制系统传递函数的概念及性质、求解典型环节及自动控制系统的传递函数.3、结构图及等效变换、信号流图及梅逊公式.三、时域分析法1、瞬态响应分析.2、二阶系统性能指标计算.3、稳定性分析、劳斯判据.4、稳态误差分析四、根轨迹分析法1、根轨迹的基本概念.2、根轨迹的绘制方法.3、广义根轨迹的绘制方法.4、控制系统根轨迹分析、开环零极点对根轨迹的影响、闭环零极点分布对系统性能指标的影响.五、频域分析法1、频率特性的基本概念.2、频率特性的图示方法.3、频域稳定性判据.4、控制系统的稳定裕量.5、控制系统的闭环频率特性.六、线性控制系统的校正1、校正装置及其特性.2、串联校正装置的设计方法及其参数的确定.3、反馈校正的原理及其特点.4、复合校正的原理及其参数确定方法.七、非线性系统分析1、非线性系统的特点.2、描述函数的概念.3、用描述函数法分析非线性系统.4、相平面的概念.5、用相平面法分析非线性系统.八、离散控制系统1、采样过程和采样定理.2、Z变换与Z反变换.3、离散控制系统的数学描述.4、离散控制系统的稳定性、瞬态响应和稳态误差分析.5、离散系统数字控制器设计.九、控制系统的状态空间描述1、状态空间的基本概念.2、状态空间描述的建立.3、状态变量图的建立.4、线性变换.5、状态空间表达式求传递函数矩阵.十、线性系统的状态空间运动分析1、状态转移矩阵的概念、性质和方法.2、线性定常系统的齐次方程和非齐次方程的求解.3、连续系统的离散化.4、线性离散系统的运动分析.十一、线性控制系统的能控性和能观测性1、能控性和能观测性的基本概念.2、能控性和能观测性判据.3、能控标准形和能观标准形.4、传递函数中的零、极点对消与状态能控性、能观性之间的关系.十二、控制系统的稳定性——Lyapunov第二方法1、稳定性的定义.2、李亚普诺夫理论的基本方法.3、非线性系统和线性系统的李亚普诺夫稳定性分析.十三、线性定常系统的综合1、状态反馈与输出反馈.2、极点配置.3、状态观测器的设计.。