第六章 异步时序逻辑电路
- 格式:ppt
- 大小:909.54 KB
- 文档页数:75

异步时序逻辑电路的分析与设计异步时序逻辑电路是一种基于信号的到达时间和时序性的电路设计方法。
与同步时序逻辑电路不同,异步时序逻辑电路中的数据传输和处理不依赖于时钟信号,而是根据输入信号的到达顺序和时序关系来进行操作。
本文将详细介绍异步时序逻辑电路的分析与设计。
异步时序逻辑电路的分析主要包括信号流图的建立和状态表的推导。
首先,通过对输入信号的时序关系进行分析和理解,可以根据具体应用需求建立信号流图。
信号流图是一种图形化表示方式,其中包含了电路中信号的流动方式以及各个元件的逻辑功能。
在建立信号流图时,需要注意信号的输入和输出时间以及逻辑功能的实现方式,这是实现异步时序逻辑电路的关键。
在信号流图的基础上,可以根据信号的到达先后顺序推导状态表。
状态表是对电路中每个元件当前状态和下一状态的描述。
通过观察信号流图,可以确定每个元件在不同状态下的输出值,并利用这些信息进行状态表的推导。
在状态表中,可以列出元件的当前状态和下一状态的取值,并根据逻辑功能的要求来确定元件的控制信号。
异步时序逻辑电路的设计主要涉及到逻辑电路元件的选择和电路的优化。
在异步时序逻辑电路中,常用的逻辑电路元件包括触发器、门电路和编码器等。
根据实际需求,可以选择不同类型的逻辑电路元件来实现电路的逻辑功能。
在设计时,需要注意减少电路的延迟和功耗,提高电路的性能和可靠性。
可以通过选择低延迟的元件、合理布局电路和优化信号传输路径等方式来减小电路的延迟。
另外,可以采用时序检测和冗余检测等方法来增加电路的可靠性。
除了分析和设计,测试和验证是异步时序逻辑电路设计中的重要环节。
可以利用仿真软件对电路进行测试和验证,以确保电路的正确性和性能。
通过仿真可以观察电路的输入输出关系,检测是否存在冲突或错误,并进行合理的调整和优化。
总结起来,异步时序逻辑电路的分析与设计涉及到信号流图的建立、状态表的推导、元件的选择和电路的优化等方面。
通过合理的分析和设计,可以实现复杂的时序逻辑功能,并提高电路的性能和可靠性。

异步时序逻辑电路的分析与设计异步时序逻辑电路是指电路中的各个逻辑门的输出不仅仅取决于当前的输入,还取决于先前的输入和输出状态。
与同步时序逻辑电路相比,异步时序逻辑电路具有更高的灵活性和可扩展性。
在本文中,将详细介绍异步时序逻辑电路的分析与设计方法。
首先,异步时序逻辑电路的分析是指通过对电路中各个逻辑门的输入和输出状态进行推导和分析,以获取电路所实现的具体功能和工作原理。
异步时序逻辑电路通常采用状态图或状态转换表来描述其运行过程。
状态图是一个有向图,其中每个节点表示一个状态,而边表示状态之间的转换。
状态转换表则是一种矩阵形式的表示方法,其中行表示当前状态,列表示输入,表格中的元素表示输出和下一个状态的关系。
在进行异步时序逻辑电路的设计之前,通常需要明确电路所要实现的功能和要求。
在设计过程中,需要通过一系列的步骤来完成。
第一步是确定输入和输出信号的数量和类型。
输入信号是电路用来接收外部输入的信号,而输出信号是电路的输出结果。
在这一步骤中,需要明确输入和输出信号所能取的值范围以及其对应的功能。
第二步是确定状态的数量和类型。
在异步时序逻辑电路中,状态是指电路在不同时间点的输出和输入的组合。
状态的数量和类型决定了电路的复杂程度和所能实现的功能。
第三步是绘制状态图或状态转换表。
通过绘制状态图或状态转换表,可以清晰地描述电路的工作原理和功能。
其中,状态图可以直观地表示状态之间的转换关系,而状态转换表则更加直观地表示输入输出和状态的关系。
第四步是推导逻辑表达式。
通过推导逻辑表达式,可以将电路的功能转化为逻辑门的连接方式。
在这一步骤中,可以通过布尔代数和卡诺图等方法来简化逻辑表达式,以减少电路的复杂性和成本。
第五步是选取逻辑门类型。
逻辑门是构成异步时序逻辑电路的基本元件,它决定了电路的工作速度和功耗。
在选择逻辑门类型时,需要考虑到电路的功能和性能要求,以及逻辑门的延迟时间和功耗等特性。
第六步是进行逻辑门的连接和布线。



异步时序逻辑电路的分析异步时序逻辑电路由状态元件和组合逻辑电路构成。
状态元件可以是触发器、锁存器或计数器等,用于存储和更新系统的状态信息。
组合逻辑电路用于根据输入信号和状态元件的当前状态生成输出信号。
异步时序逻辑电路使用特殊的电路元件来处理时序问题,如时序器、分频器、状态机等。
分析是指确定异步时序逻辑电路所需的状态元件和组合逻辑电路,以及它们之间的关系。
在分析过程中,需要识别系统的输入和输出信号,并建立它们之间的关联关系。
通过对系统的输入进行序列和输入/输出的波形分析,可以确定输入和输出之间的时序关系。
合成是指根据分析结果生成实际的电路布局和连接。
在合成过程中,需要选择合适的电路元件,并确定它们之间的连接方式和时序关系。
合成过程可以使用电路设计软件来自动生成电路图和布局。
1.确定系统的输入和输出信号。
根据实际需求和系统功能,确定输入和输出信号的类型和名称。
输入信号通常是一些外部事件或控制信号,输出信号则是系统的响应。
2.建立输入和输出信号之间的关联关系。
根据系统的逻辑功能和时序要求,确定输入和输出信号之间的时序关系。
可以使用状态转换图、状态转移表或状态图等形式来描述这种关系。
3.确定状态元件的类型和数量。
根据系统的状态信息和时序性能要求,选择合适的状态元件。
触发器是最常用的状态元件,可用于存储系统的状态信息。
根据状态元件的类型和数量,可以确定系统的状态变量。
4.建立状态元件和组合逻辑电路之间的关系。
根据系统的逻辑功能和时序要求,确定状态元件和组合逻辑电路之间的逻辑关系。
组合逻辑电路用于根据输入信号和当前状态元件的状态生成输出信号。
5.分析输入/输出时序波形。
通过仿真或实验,分析输入/输出时序波形以验证系统的正确性。
根据时序波形图,可以确定信号的传输延迟和时序约束等重要参数。
6.优化电路设计。
根据分析结果,对电路进行优化。
常见的优化技术包括布局优化、电路复用和逻辑优化等。
优化的目标是减少电路的延迟、功耗和面积,提高系统的性能和可靠性。



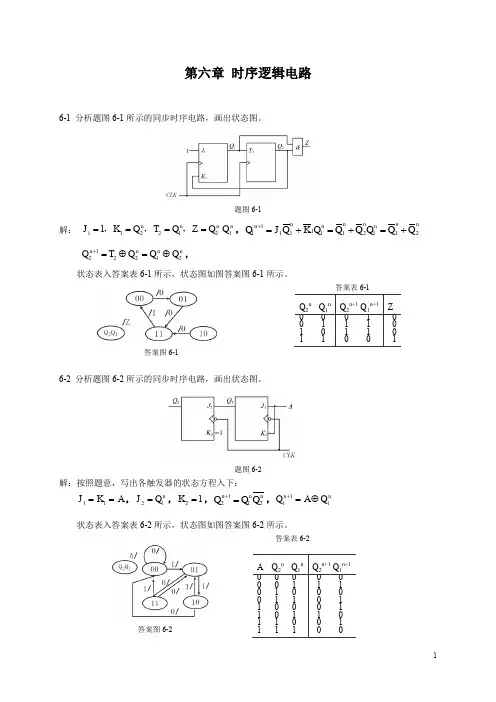
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路,画出状态图。
题图6-1解: 11221211n n n n J K Q T Q Z Q Q ====,,,,11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕,状态表入答案表6-1所示,状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路,画出状态图。
题图6-2 解:按照题意,写出各触发器的状态方程入下:11J K A ==,21n J Q =,21K =,1212n n nQ Q Q +=,111n n Q A Q +=⊕状态表入答案表6-2所示,状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路,画出状态图。
题图6-3解:按照题意,写出各触发器的状态方程入下:1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1,,, 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中,已知寄存器的初始状态Q 1Q 2Q 3=111。

习 题 六1 分析图1所示脉冲异步时序逻辑电路。
(1) 作出状态表和状态图; (2) 说明电路功能。
图1解答(1)该电路是一个Mealy 型脉冲异步时序逻辑电路。
其输出函数和激励函数表达式为211221212Q D x C Q D x Q CQ x Q Z =====(2)电路的状态表如表1所示,状态图如图2所示。
现 态 Q 2 Q 1次态/输出ZX=10 0 0 1 1 0 1 1 01/0 11/0 10/0 00/1图2(3) 由状态图可知,该电路是一个三进制计数器。
电路中有一个多余状态10,且存在“挂起”现象。
2 分析图3所示脉冲异步时序逻辑电路。
(1) 作出状态表和时间图; (2) 说明电路逻辑功能。
图3解答○1 该电路是一个Moore 型脉冲异步时序逻辑电路,其输出即电路状 态。
激励函数表达式为 1321123132233Q C C CP;C 1;K K K 1J ; Q J ; Q Q J =========○2 电路状态表如表2所示,时间图如图4所示。
表2图4○3 由状态表和时间图可知,该电路是一个模6计数器。
3 分析图5所示脉冲异步时序逻辑电路。
(1) 作出状态表和状态图; (2) 说明电路逻辑功能。
图5时 钟CP 现 态 Q 3 Q 2 Q 1 次 态 Q 3(n+1)Q 2(n+1)Q 1(n+1)11111111000 001 010 011 100 101 110 111 001 010 011 100 101 000 111 000解答○1 该电路是一个Moore 型脉冲异步时序逻辑电路,其输出函数和激励函数表达式为322111132212122212x y x R ; x S y x y x x R ; y y x S y y Z +==++===○2该电路的状态表如表3所示,状态图如图6所示。
表3现态 y 2y 1次态y 2(n+1)y 1(n+1)输出 Zx 1 x 2 x 3 0001 11 1001 01 01 0100 11 00 0000 00 10 000 0 0 1图6○3 该电路是一个“x 1—x 2—x 3”序列检测器。