基于模糊控制和PID控制的自主车辆速度跟踪控制(含MATLAB仿真程序)
- 格式:doc
- 大小:203.50 KB
- 文档页数:19


题目:基于模糊PID的汽车巡航控制系统设计基于模糊PID的汽车巡航控制系统设计摘要汽车巡航控制系统是一种辅助驾驶系统,它不但可以减轻驾驶员的负担,还可以提高驾车的舒适性.汽车巡航控制系统具有非线性、时变不确定性,并受到外界扰动、复杂的运行工况等影响。
本文介绍了一种基于模糊PID控制算法的汽车巡航控制系统。
本文对汽巡航控制系统进行了简要的分析,将模糊PID控制方法作为其控制方案,对现有的PID控制进行完善和优化,并设计出系统的模糊控制器。
以轿车为对象,分析了汽车在行驶过程中的驱动力及受到的各种阻力和干扰力,并建立起汽车纵向动力学模型。
利用MATLAB建立了系统的仿真模型,利用MATLAB软件中的模糊逻辑工具箱对系统的设计进行仿真,验证系统设计的可行性,并对汽车巡航控制系统进行了仿真和分析.由仿真结果可知,模糊PID控制方法能使系统的超调减小、反应速度加快、控制效果良好,是一种适用于汽车巡航控制系统的控制方法.关键词:定速巡航控制系统;MATLAB;模糊PID;仿真The Design of Controller of Automobile Cruise Control SystemBased On Fuzzy-PIDABSTRACTAutomobile cruise control system,which could not only relieve the drivers burden,but also could make the driving comfortable.it is a kind of accessorial driving system,Cruise control system has high nonlinearity and non-determinacy with time changing.And CCS,which is effected by some factors such as external load disturbers and complicated running modes,A kind of CCS which is based on Fuzzy PID control,it is introduced in the thesis.Analyzing the cruise control system briefly, Fuzzy—PID is confirmed as the control method of the system,improved and optimized the PID control. Then the Fuzzy PID controller is designed,As the object is a car,the thesis analyzes the resistances and disturbs while the car's running,And the automobile dynamics model is given,After setting up the model by means of MATLAB,use the Fuzzy Logic Toolbox in MATLAB software to simulate the design of the system,to verify the feasibility of the system design, the result is analyzed,From the result,we may know that Fuzzy PID control could make the overshoot smaller and the response time shorter,The effect of Fuzzy PID method is given.SO it is a suitable method for CCS.Keywords:cruise control system;MATLAB;Fuzzy PID;simulation目录1 绪论 (1)1.1 课题的意义 (1)1。




基于模糊控制的自动驾驶系统设计与实现自动驾驶技术是当前科技领域的热门研究领域之一。
基于模糊控制的自动驾驶系统设计与实现是实现自动驾驶的一种常用方法。
本文将详细介绍基于模糊控制的自动驾驶系统的设计与实现过程。
首先,基于模糊控制的自动驾驶系统设计需要考虑系统的架构和功能。
系统的架构通常包括传感器部分、感知与决策部分和执行部分。
传感器部分负责获取车辆周围环境的信息,包括摄像头、雷达、激光雷达等传感器。
感知与决策部分负责对传感器数据进行处理与分析,包括对障碍物的识别与跟踪、路径规划与决策等功能。
执行部分负责控制车辆的行驶,包括油门、刹车、转向等控制。
其次,基于模糊控制的自动驾驶系统的关键技术在于模糊控制器的设计。
模糊控制器根据输入和输出的模糊规则来控制车辆的行驶。
模糊规则的制定是整个系统设计中的关键之一。
模糊规则是通过将输入与输出之间的关系进行模糊化来定义的。
例如,如果车辆与前方的障碍物的距离较近,则需要减小车辆的速度;如果车辆处于弯道,则需要调整车辆的转向角度。
通过制定一系列模糊规则,可以根据不同的情况来调整车辆的行驶。
在模糊控制器设计中,模糊化和解模糊化是非常重要的步骤。
模糊化将输入量和输出量从连续的实数空间映射到隶属函数上。
隶属函数描述了输入量或输出量的模糊程度,常用的隶属函数包括三角函数、梯形函数等。
解模糊化则将经过模糊化的输出量映射回实数空间。
常用的解模糊化方法包括最大值法、面积法等。
通过模糊化和解模糊化的处理,可以将模糊规则转化为实际的车辆控制命令。
此外,在基于模糊控制的自动驾驶系统中,还需要考虑系统的可靠性和安全性。
自动驾驶系统需要能够在各种复杂的场景中进行准确的决策和控制,才能保证车辆的行驶安全。
同时,系统还需要具备故障容忍性,可以在传感器故障或其他系统故障的情况下继续工作。
最后,基于模糊控制的自动驾驶系统的实现需要借助于计算机技术和人工智能算法。
计算机技术提供了高性能的计算能力和大容量的存储空间,可以方便地对传感器数据进行处理和分析。


《基于模糊控制的高精度伺服速度控制器的设计与实现》基于模糊控制的高精度伺服速度控制器设计与实现一、引言随着工业自动化和智能制造的不断发展,对高精度伺服系统的速度控制提出了更高要求。
伺服速度控制器的性能直接影响着工业产品的制造质量和效率。
传统速度控制方法往往存在响应速度慢、精度低等问题。
为了解决这些问题,本文提出了一种基于模糊控制的高精度伺服速度控制器设计与实现方案。
二、系统概述本系统主要由伺服电机、编码器、模糊控制器和上位机组成。
其中,伺服电机负责执行速度控制任务,编码器实时反馈电机速度信息,模糊控制器负责处理反馈信息和进行控制决策,上位机负责与模糊控制器进行通信,并监控整个系统的运行状态。
三、模糊控制器的设计1. 模糊化处理模糊化处理是将电机速度的实时反馈值和目标值进行模糊化处理,将精确的数值转化为模糊语言变量。
这一过程包括确定模糊子集、论域和隶属度函数等。
2. 模糊规则库的设计根据系统特性和经验知识,设计合理的模糊规则库。
这些规则根据电机速度的实时反馈和目标值,决定下一时刻的控制策略。
3. 模糊推理机的实现模糊推理机是模糊控制器的核心部分,根据模糊规则库和实时反馈信息,进行模糊推理,得出下一时刻的控制决策。
4. 解模糊化处理解模糊化处理是将模糊推理结果转化为精确的控制量,以驱动伺服电机执行相应的动作。
四、伺服速度控制器的实现1. 硬件实现伺服速度控制器的硬件部分主要包括微处理器、编码器接口、电机驱动器等。
微处理器负责运行模糊控制器程序,编码器接口负责实时获取电机速度信息,电机驱动器根据控制决策驱动伺服电机执行相应的动作。
2. 软件实现软件部分主要包括模糊控制算法的实现、与上位机的通信等。
在微处理器上运行模糊控制算法,实时处理编码器反馈的电机速度信息,并根据模糊推理结果输出相应的控制量。
同时,与上位机进行通信,接收上位机的指令和监控系统的运行状态。
五、实验结果与分析通过实验验证了基于模糊控制的高精度伺服速度控制器的性能。
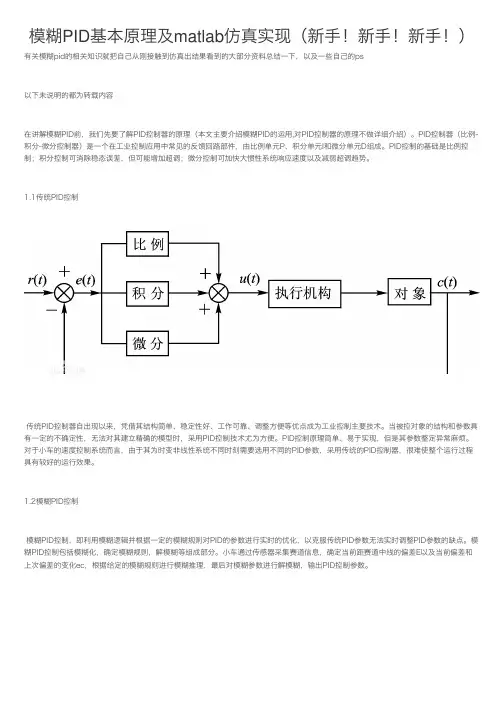
模糊PID基本原理及matlab仿真实现(新⼿!新⼿!新⼿!)有关模糊pid的相关知识就把⾃⼰从刚接触到仿真出结果看到的⼤部分资料总结⼀下,以及⼀些⾃⼰的ps以下未说明的都为转载内容在讲解模糊PID前,我们先要了解PID控制器的原理(本⽂主要介绍模糊PID的运⽤,对PID控制器的原理不做详细介绍)。
PID控制器(⽐例-积分-微分控制器)是⼀个在⼯业控制应⽤中常见的反馈回路部件,由⽐例单元P、积分单元I和微分单元D组成。
PID控制的基础是⽐例控制;积分控制可消除稳态误差,但可能增加超调;微分控制可加快⼤惯性系统响应速度以及减弱超调趋势。
1.1传统PID控制传统PID控制器⾃出现以来,凭借其结构简单、稳定性好、⼯作可靠、调整⽅便等优点成为⼯业控制主要技术。
当被控对象的结构和参数具有⼀定的不确定性,⽆法对其建⽴精确的模型时,采⽤PID控制技术尤为⽅便。
PID控制原理简单、易于实现,但是其参数整定异常⿇烦。
对于⼩车的速度控制系统⽽⾔,由于其为时变⾮线性系统不同时刻需要选⽤不同的PID参数,采⽤传统的PID控制器,很难使整个运⾏过程具有较好的运⾏效果。
1.2模糊PID控制模糊PID控制,即利⽤模糊逻辑并根据⼀定的模糊规则对PID的参数进⾏实时的优化,以克服传统PID参数⽆法实时调整PID参数的缺点。
模糊PID控制包括模糊化,确定模糊规则,解模糊等组成部分。
⼩车通过传感器采集赛道信息,确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec,根据给定的模糊规则进⾏模糊推理,最后对模糊参数进⾏解模糊,输出PID控制参数。
2.1模糊化模糊控制器主要由三个模块组成:模糊化,模糊推理,清晰化。
具体如下图所⽰。
⽽我们将⼀步步讲解如何将模糊PID算法运⽤到智能车上。
(最好⽤笔⼀步步⾃⼰写⼀遍)⾸先我们的智能车会采集到赛道的相关数据,例如摄像头车,其采集到的数据经过算法处理之后会得到与中线的偏差E,以及当前偏差和上次偏差的变化(差值)EC两个值(即此算法为2维输⼊,同理也可以是1维和3维,但2维更适合智能车)。

基于MATLAB的模糊PID控制系统的设计与仿真作者:王超蒋平来源:《电子世界》2013年第04期【摘要】在传统的PID控制基础上,本文介绍了一种基于PID模糊控制的混合型控制,通过MATLAB&Simulink软件和模糊逻辑工具箱设计控制系统结构模型.仿真结果证明,该控制方法具有更优的性能。
【关键词】模糊PID控制;MATLAB仿真1.引言在传统的控制方法中,PID控制凭借其算法简单、精度高、可靠性强、技术成熟、应用广泛的优点脱颖而出,占据了工业控制系统80%以上的份额;然而随着现代控制系统越来越复杂,精度要求也越来越高,传统、单一的控制策略已经无法满足设计性能的要求,同时,随着电子技术和计算机的发展,各种新兴的智能算法也不断涌现,将传统算法和智能算法相结合,成为现代控制系统策略选择的趋势。
作为智能控制中最重要且最有效的手段之一的模糊控制,在应对复杂系统的非线性和时变特征时有着较好的表现,因此越来越多的被应用到工程实践中,并已取得了不俗的成绩。
本文介绍的是基于传统的PID控制和现代控制理论中的智能模糊控制相结合的一种控制方法,用MATLAB&Simulink软件和模糊逻辑工具箱设计控制系统结构模型,并通过仿真结果证明该控制方法具有更优的性能。
2.PID模糊控制系统的结构3.利用MATLAB&Simulink软件进行控制仿真基于现代控制理论的模糊控制,内容比较抽象,理论性较强,比较枯燥。
另外,模糊控制是模糊集合理论、模糊语言变量以及模糊逻辑推理为基础的一种计算机控制,它处理的问题可能难以靠解析求解,需要采用复杂的数值计算方法,采用软件编程,不仅工作量大,而且过程繁杂,大大制约了控制方法的性能验证和工程实现。
MATLAB&simulink是MathWorks公司推出的当今国际控制界最为流行的面向工程和科学计算的高级语言,是公认的最为灵活和有效的仿真软件。
而且随着智能控制的迅速推广应用,MathWorks公司已经添加了智能逻辑控制工具箱,其中包括模糊控制工具箱、神经网络控制箱等热门工具。

基于PID算法的列车自动驾驶控制方法研究发布时间:2021-06-10T10:15:45.890Z 来源:《基层建设》2021年第5期作者:李文龙吴祥民董彦妮张忠杰[导读] 摘要:在现有列车数学模型的基础上,采用PID算法设计了列车速度闭环控制器,当自动控制系统生成期望速度曲线时,适当配置PID控制器的参数,列车可以达到满意的速度跟踪效果。
中车青岛四方机车车辆股份有限公司青岛 266111 摘要:在现有列车数学模型的基础上,采用PID算法设计了列车速度闭环控制器,当自动控制系统生成期望速度曲线时,适当配置PID 控制器的参数,列车可以达到满意的速度跟踪效果。
此外,本文通过极点配置,得到比例系数、积分系数以及微分系数的最佳组合,提高列车自动驾驶系统的精度。
关键词:列车;PID算法;速度控制;仿真 1 前言在列车人工驾驶模式下,司机将根据经验、列车运行情况以及当前路况驾驶列车。
然而,在情绪波动和疲劳的影响下,司机会误操作,导致事故的发生。
列车自动驾驶系统可以根据实际路况信息,获取各设备的工作状态和列车运行情况,并得到智能化的运行计划,从而保证列车运行的独立控制。
与人工驾驶相比,列车自动驾驶在能源节约、时间准确性、乘客舒适度以及安全性等方面具有更大的优势和更好的应用前景。
列车自动驾驶系统(ATO)是列车自动控制系统(ATC)的一个子系统。
与列车自动监督(ATS)子系统、列车自动防护(ATP)子系统协调配合,共同完成列车的自动控制,具体流程为:ATO接收来自ATS发送的目的地编码、运行时分等信息,并且接收来自ATP发送的当前列车速度、加速度、目标速度、当前位置等信息,跟随ATP生成的速度-时间曲线,在ATP的防护下安全运行,实现列车的自动驾驶。
2 PID算法的研究PID算法是基于偏差在过去、现在和将来做出调节量估计的一种简单有效的控制算法,在许多工业控制中得到了广泛的应用,因此采用PID逻辑来实现高速列车的速度控制也应运而生。
模糊PID控制算法在智能小车中的研究与应用智能小车是近年来智能化技术的一项重要应用,模糊PID控制算法作为一种自适应控制算法,被广泛应用于智能小车领域。
本文将从智能小车的研究背景入手,介绍模糊PID控制算法的原理和特点,以及在智能小车中的研究和应用,最后总结并展望未来研究的方向。
一、研究背景智能小车是一种能够自主运动、感知环境并做出决策的机器人,其运动控制是实现智能小车基本功能的核心。
传统的PID控制算法在许多自动控制系统中得到广泛应用,它通过不断地调整比例、积分和微分三个参数来实现系统的稳定控制。
然而,传统PID控制算法的主要问题是在非线性、时变或不确定性的系统中效果不佳。
为了解决这一问题,模糊PID控制算法被引入到智能小车的控制中。
模糊PID控制算法是基于模糊逻辑理论和PID控制理论的结合,通过对系统内外环境进行模糊化表示,将模糊规则集与PID控制算法相结合,从而提高了系统的稳定性和鲁棒性。
二、模糊PID控制算法原理和特点1.模糊化:将系统的输入和输出进行模糊化处理,将连续值转化为模糊变量。
2.模糊规则库构建:根据系统的特性和经验知识,构建一组模糊规则。
3.模糊推理:根据当前的系统输入和模糊规则库,进行模糊推理,得到模糊输出。
4.解模糊化:将模糊输出转化为真实的控制量。
5.输出:将解模糊化得到的控制量输出给被控对象,实现控制。
1.对系统非线性和时变性具有较好的适应性,能够应对实际环境中的各种变化和干扰。
2.理论基础扎实,可以通过专家知识和经验知识来构建模糊规则库,适用于复杂系统。
3.可以处理模糊和不确定性信息,提高了控制系统的稳定性和鲁棒性。
智能小车作为一种自主决策和行动能力的机器人,其控制系统对稳定性要求较高。
模糊PID控制算法在智能小车中得到了广泛的研究和应用。
首先,模糊PID控制算法可以用于智能小车的路径规划和避障。
通过感知环境中的障碍物和目标点,将其模糊化处理,构建模糊规则库,实现智能小车的自主导航和避障功能。
《基于模糊控制的高精度伺服速度控制器的设计与实现》基于模糊控制的高精度伺服速度控制器设计与实现一、引言随着工业自动化和智能制造的快速发展,高精度伺服速度控制器在生产制造和工艺控制领域中的重要性愈发突出。
伺服系统的高效性、准确性和响应速度对于设备的工作效率和产品质量的保证起到了决定性的作用。
为了更好地应对高精度速度控制的要求,本文设计并实现了一种基于模糊控制的高精度伺服速度控制器,以期为现代工业自动化提供更优的解决方案。
二、模糊控制理论概述模糊控制是一种基于模糊集合理论的控制方法,其通过模仿人的决策过程,将精确的数学模型转化为模糊的逻辑规则,从而实现对复杂系统的有效控制。
模糊控制具有对系统参数变化和外部干扰的强鲁棒性,特别适用于非线性、时变或不确定性的系统。
三、高精度伺服速度控制器的设计1. 硬件设计硬件设计是构建高精度伺服速度控制器的基石。
设计过程中,我们主要考虑了电机驱动器、传感器、微处理器等关键部件的选型和配置。
电机驱动器应具备高响应速度和低噪声的特点,传感器应具有高精度和高稳定性的性能,微处理器则应具备强大的数据处理能力和实时性。
2. 软件设计软件设计是实现高精度伺服速度控制器的核心。
在软件设计中,我们采用了模糊控制算法作为主要控制策略。
首先,我们根据系统的特性和需求,定义了输入和输出的模糊变量,并确定了模糊变量的论域和隶属度函数。
然后,我们根据专家的经验和知识,建立了模糊规则库。
最后,通过模糊推理机实现模糊规则的推理和决策,输出控制信号驱动电机执行相应的动作。
四、实现过程1. 搭建实验平台我们搭建了一个包含电机、传感器、微处理器等关键部件的实验平台,用于验证基于模糊控制的高精度伺服速度控制器的性能。
2. 编程实现在编程实现过程中,我们采用了模块化的设计思想,将整个系统划分为模糊控制器、电机驱动器、传感器数据处理等模块。
每个模块都有明确的输入和输出接口,方便后期维护和升级。
在编程过程中,我们特别注意了代码的实时性和稳定性,以保证系统的性能和可靠性。
基于Matlab的模糊PID控制系统设计及仿真窦艳艳;钱蕾;冯金龙【摘要】模糊PID控制是利用PID参数整定经验来使模糊控制器自动整定其参数,从而使PID控制器以变应变.文中采用Matlab软件设计模糊PID控制器,并应用于控制锅炉液位.通过实验仿真比较研究PID控制、模糊控制及模糊PID控制的控制效果.实验结果显示,模糊PID控制效果理想,具有较好的应用前景.【期刊名称】《电子科技》【年(卷),期】2015(028)002【总页数】4页(P119-122)【关键词】模糊控制;PID控制;Matlab仿真;锅炉液位【作者】窦艳艳;钱蕾;冯金龙【作者单位】南京高等职业技术学校电气工程系,江苏南京210019;南京高等职业技术学校电气工程系,江苏南京210019;南京高等职业技术学校电气工程系,江苏南京210019【正文语种】中文【中图分类】TP273+.4PID控制作为经典控制至今仍被广泛应用,面对精确数学模型时,PID控制能取得令人满意的效果。
但在实际应用中,当被控对象数学模型变化时,难以实时调整PID参数,且大量被控过程机理复杂,被控对象数学模型建立复杂,其控制效果并不理想[1]。
模糊控制拥有智能化的特点,它不依赖对象的数学模型,对受控对象的时滞、非线性和时变性具有一定的适应能力。
然而模糊控制的精度受到控制规则的限制还始终存在静差[2]。
模糊PID控制利用整定PID参数的经验来设计模糊控制器自动整定PID控制器的参数,从而使PID控制器以变应变[3]。
本文采用基于Matlab的模糊PID控制器控制锅炉液位,通过实验仿真比较传统PID控制、模糊控制以及模糊PID控制的效果。
1 被控对象选择被控对象选择经典的锅炉液位控制,国内外的电热锅炉液位控制主要采用传统PID 控制[4]。
维持锅炉液位在预期正常范围内是锅炉系统安全运行的必要条件,也是衡量锅炉汽水系统物质是否平衡的标志。
由文献[5]得到某汽包水位在给水流量下的动态特性传递函数为2 模糊PID控制器设计自适应模糊PID控制器结构如图1所示,其以常规PID控制为基础,采用模糊推理的思想,将被控量的偏差e和偏差变化率ec作为二维模糊控制器的输入变量,PID中 Kp,Ki,Kd的变化值作为输出,利用模糊控制规律在线整定PID各个参数,其中模糊控制部分包括模糊化、模糊推理计算和解模糊化[6]。
1910.16638/ki.1671-7988.2020.24.007基于模糊PID 的汽车巡航控制系统研究*张宝玉(江苏食品药品职业技术学院,江苏 淮安 223001)摘 要:汽车巡航控制系统(以下简称“CCS ”)可以降低汽车排气污染,文章为提高汽车巡航的精度和稳定性,在研究模糊PID 控制方法基础上,结合Matlab/Simulink 对汽车巡航模糊控制进行了建模,为后续仿真工作以及结构优化提供了可靠保障。
关键词:模糊巡航;车辆动力学系统;建模;响应速度中图分类号:U495 文献标识码:A 文章编号:1671-7988(2020)24-19-03Research on Automobile Cruise Control System Based on Fuzzy PID *Zhang Baoyu(Jiangsu Food & Pharmaceutical Science College, Jiangsu Huai ’an 223001)Abstract: Automobile cruise control system (Shorthand "CCS") can reduce automobile exhaust pollution. In this paper, in order to improve the accuracy and stability of automobile cruise, based on the study of fuzzy PID control method, com -bined with Matlab/Simulink to model the automobile cruise fuzzy control, Providing a reliable guarantee for subsequent simulation work and structural optimization.Keywords: Fuzzy cruise; Vehicle dynamics system; Modeling; Response speed CLC NO.: U495 Document Code: A Article ID: 1671-7988(2020)24-19-031 汽车巡航控制原理汽车巡航系统是一个典型的闭环反馈控制系统,其原理如下图1所示。
一、设计原理设计思想:油门控制采用增量式PID 控制算法,刹车控制采用模糊控制算法,最后通过选择规则进行选择控制量输入。
选择规则:首先定义速度偏差-50 km/h ≤e (k )≤50km/h ,-20≤ec= e (k )- e (k-1)≤20,阀值e swith =10km/h 。
若:e (k )<0① e (k )>- e swith and throttlr_1≠0 选择油门控制② 否则:先将油门控制量置0,再选择刹车控制 若:0<e (k ) 先选择刹车控制,再选择油门控制 若:e (k )=0 直接跳出选择 刹车控制:刹车采用模糊控制算法1.确定模糊语言变量e 基本论域取[-50,50],ec 基本论域取[-20,20],刹车控制量输出u 基本论域取[-30,30],这里我将这三个变量按照下面的公式进行压缩离散化:)]2(2[ba x ab n y +--= 其中,],[b a x ∈,n 为离散度。
e 、ec 和u 均取离散度n=3,离散化后得到三个量的语言值论域分别为:E=EC=U={-3,-2,-1,0,1,2,3}其对应语言值为{ NB,NM,NS,ZO, PS,PM,PB } 2.确定隶属度函数E/EC 和U 取相同的隶属度函数,边界选取钟形隶属度函数,中间取三角形隶属度函数,即:E EC U(,5,1)(,3,2,0)(,3,1,1)u (,2,0,2)(,1,1,3)(,0,2,3)(,1,5)g x trig x trig x trig x trig x trig x g x ∧∧--⎧⎪--⎪⎪--⎪=-⎨⎪-⎪⎪⎪⎩说明:边界选择钟形隶属度函数,中间选用三角形隶属度函数,图像略。
实际EC 和E 输入值若超出论域范围,则取相应的端点值。
3.模糊控制规则由隶属度函数可以得到语言值隶属度(通过图像直接可以看出)如下表:表1:E/EC 和U 语言值隶属度向量表设置模糊规则库如下表:表2:模糊规则表3.模糊推理由模糊规则表3可以知道输入E 与EC 和输出U 的模糊关系,这里我取两个例子做模糊推理如下:if (E is NB) and (EC is NM) then (U is PB)那么他的模糊关系子矩阵为:1211U EC E R R R R ⨯⨯=其中,711)0,,0,5.0,1(0⨯== P R E ,即表1中NB 对应行向量,同理可以得到,712)0,,0,5.0,1,0(1⨯== P R EC , 711)0,,0,5.0,1(0⨯== P R U77210000000000005.05.00005.010)0,,0,5.0,1,0()0,,0,5.0,1(⨯⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⨯=⨯TEC E R R 49121)0,,0,5.0,5.0,0,0,0,0,0,5.0,1,0(⨯= EC E R7491211000000005.05.00005.0100000)0,,0,5.0,1()0,,5.0,1,0(⨯⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⨯=⨯= TU EC E R R Rif (E is NB or NM) and (EC is NB) then (U is PB)21211()E E EC U R R R R R =⨯⨯,结果略。
按此法可得到27个关系子矩阵,对所有子矩阵取并集得到模糊关系矩阵如下:)27,,2,1(21 ==i R R R R i由R 可以得到模拟量输出为:()U E EC R =⨯4.去模糊化由上面得到的模拟量输出为1×7的模糊向量,每一行的行元素(u (z ij ))对应相应的离散变量z j ,则可通过加权平均法公式解模糊:21210()(1,2,,21)()ijji iji u zz u i j u z=====∑∑从而得到实际刹车控制量的精确值u 。
油门控制:油门控制采用增量式PID 控制,即:)2()1()2()()()1()(-+---++++-=k e k k e k k k e k k k k u k u d d p d i p其中k i =kp ×ts/Ti ,d k =kp ×Td/ts 只需要设置p k 、Ti 、Td 三个参数即可输出油门控制量。
二、调整参数按照上述算法流程,应用MATLAB 进行仿真实现,在参数调试过程中采用如下方法:首先将油门和刹车分开进行调整参数,最后再将调整好的参数写入总程序中调整。
1.油门PID 参数调节油门只需要调整kp 、Ti 、Td 三个参数,根据经验,首先令Ti 、Td 为0,kp 由0逐渐增大,在增大kp 的过程可知,kp 越大系统调节时间越短并趋于稳定,在达到一定程度后,继续增大系统将出现波动。
time(s)v d ,ytime(s)v d ,ykp=0.1kp=0.4time(s)v d ,ykp=0.9调节Ti 的过程发现,Ti 对系统稳定性影响并不大,将Ti 由10增大到30的过程中系统输出没有变化。
time(s)v d ,ytime(s)v d ,yTi=10 Ti=30在给Td 赋值时,最开始从1增大,发现系统越来越不稳定,于是逐渐减小,到0.003时趋于稳定,它的可调节范围很小,随其值的减小最大误差值逐渐减小,增大则系统趋于不稳定。
time(s)v d ,ytime(s)v d ,ykp=0.001 kp=0.002time(s)v d ,ykp=0.0032.刹车调节首先,为了适应该系统,将刹车输出量限制在[-150,150]之内(最初设计其范围为[-30,30]),对于该控制,可调节参数较多,包括隶属度函数、模糊规则表、输入输出变量区间、语言值论域、模糊推理及解模糊方法等等,这里由于模糊规则需要经验设定,本算法没有实际参考,所以这里只调整规则表,其他参数固定不变。
由于实际刹车控制中对于加速采取比较单一的置零(在选择规则中设定)输出,所以在规则表中e<0部分没有规则,然而为了仿真方与此同时,将刹车的输出变量取反,以此来实现减速的效果!在调整模糊规则表的时候,必须依据输入变量e 和ec 的范围逐个检验,按照他们各自的语言值以及相应的输出语言值进行调整。
例如,初始速度为50,期望速度为0,即e=-50,ec=-50,则此时输出对应模糊规则表中第一行第一列PB ,而下一时刻ec 几乎为0,所以在调节过程中,主要进行对EC 变量的ZO 行进行调节,若响应时间短,则增大相应输出语言值,反之亦然。
仿真时,分两段,首先加速,之后减速,采用上面的模糊规则表,得到如下图像:time(s)v d ,y从图像的上升阶段分析可以看出,其加速阶段并不能达到稳态值,但对于刹车控制可以忽略其影响,而减速阶段实际上已经比较理想,我取稳态误差达到5%稳定,则此规则达到稳态的时间为7.4s ,这里尝试进行如下修改,将规则表中带下划线的部分以此改为:PM,PS,PS,ZO,即,增大了输出语言值。
则得到如下图像:time(s)v d ,y此规则达到稳定的时间为6.9s ,由此分析模糊规则的调整规则如下:若想加快响应时间,增大误差和误差变化率负大区域附近的输出语言值,并增大误差变化率零区域附近的输出语言值,可能还会引起超调量的增大,所以只需做临近语言值之间的变化。
3.整体调节此时将刹车与油门同时加到仿真模型中,分别做加速和减速仿真,依据分别调节时的规律做微量调节就可以基本达到要求。
time(s)v d ,y4.待解决问题在调试过程中发现,油门控制(PID )过程在达到稳态时出现抖动,并且三个参数对他的影响很小,具体原因待考证;油门控制给系统的输入值出现大波动,每一次达到峰值持续相同时间后变为0再持续一段时间又变为峰值;模糊控制的语言值论域较小,对于扩大语言值论域对系统的影响还有待验证;模糊控制的输入变量压缩方式有待验证其合理性;模糊控制与PID控制的相互配合,在该程序中,由于两种控制的输出控制量不同,在给到仿真系统时很难统一;油门与上车的选择规则与实际系统还存在很大的改进。
附录MATLAB仿真程序function kk=bingji(A)for i=1:49for k=1:7for j=1:26n=7*j+k;if(A(i,k)>=A(i,n))kk(i,k)=A(i,k);elseA(i,k)=A(i,n);kk(i,k)=A(i,k);endendendendfunction o=dikaer(A,n,B,N)for i=1:nfor j=1:Nif(A(i)<=B(j))C(i,j)=A(i);elseC(i,j)=B(j);endo=C;endendreturn;function T=flisan(a,b,n,x)y=(a+b)/2+(b-a)*x/(2*n);T=round(y);return;function mm=bell(x,a,b,c)z=abs((x-c)/a)^(2b);y=1/(1+z);mm=y;return;function ooo=jbing(A,B)for i=1:49for j=1:7if(A(i,j)<B(i,j))A(i,j)=B(i,j);endendooo=A;endreturn;function MM=jdikaer(A,n,B,m) for i=1:mfor j=1:nif(A(j)<B(j,i))B(j,i)=A(j);endendMM=B;endreturn;function oo=jiao(A,B)for i=1:7for j=1:7if(A(i,j)>B(i,j))A(i,j)=B(i,j);endendoo=A;endreturn;function mm=lbell(x,a,b,c)if(x<c)mm=1;elsez=(x-c)/a;v=abs(z);n=v^(2*b);y=1/(1+n);mm=y;endreturn;function L=lisan(a,b,n,x)y=2*n*x/(b-a)-n*(a+b)/(b-a); L=y;return;function UU=max(A)for i=1:7for j=1:49if(A(j,i)>=Q(i))Q(i)=A(i,j);endendUU=Q;endreturn;function sum1=mean(U)a=[-3 -2 -1 0 1 2 3];sum2=0;sum3=0;for i=1:7sum2=sum2+U(i);sum3=sum3+U(i)*a(i);endsum1=sum3/sum2;return;function mm=rbell(x,a,b,c) if(x>c)mm=1;elsez=(x-c)/a;v=abs(z);n=v^(2*b);y=1/(1+n);mm=y;endreturn;function mww=trig(x,a,b,c) if(x<=a)mww=0;elseif(x>a&&x<=b)mww=(x-a)/(b-a);elseif(x>b&&x<=c)mww=(c-x)/(c-b);elseif(x>c)mww=0;endendendendreturn;function ooo=xbing(A,B)for i=1:7if(A(i)<B(i))A(i)=B(i);endooo=A;endreturn;clear all%************************Ä£ºýËã·¨%/*********Á¥Êô¶ÈÏòÁ¿*****%P0=[1,0.5,0,0,0,0,0];%*********NBP1=[0,1,0.5,0,0,0,0];%*********NMP2=[0,0.5,1,0.5,0,0,0];%*********NSP3=[0,0,0.5,1,0.5,0,0];%*********ZOP4=[0,0,0,0.5,1,0.5,0];%*********PSP5=[0,0,0,0,0.5,1,0];%*********PMP6=[0,0,0,0,0,0.5,1];%*********PB%***********ÓïÑÔÖµ*****%NB=-3;NM=-2;NS=-1;ZO=0;PS=1;PM=2;PB=3;%/*********Ä£ºý¹æÔò±í*****%Pg=[PB PB PM PM PS ZO ZO;PB PM PM PS ZO ZO NS;PM PM PS PS ZO NS NS;PM PS PS ZO ZO NS NM;PS PS ZO ZO ZO NS NM;PS ZO ZO ZO NS NM NB;ZO ZO ZO NS NM NM NB];%/*********¸ù¾ÝÄ£ºý¹æÔò±í¼ÆËãÄ£ºý¹Øϵ¾ØÕóR*****% R1_=dikaer(xbing(P0,P1),7,P0,7);R1_=reshape(R1_,1,49);R1=dikaer(R1_,49,P6,7);R2_=dikaer(xbing(P2,P3),7,P0,7);R2_=reshape(R2_,1,49);R2=dikaer(R2_,49,P5,7);R3_=dikaer(P0,7,P1,7);R3_=reshape(R3_,1,49);R3=dikaer(R2_,49,P6,7);R4_=dikaer(xbing(P1,P2),7,P1,7);R4_=reshape(R4_,1,49);R4=dikaer(R4_,49,P5,7);R5_=dikaer(P3,7,P1,7);R5_=reshape(R5_,1,49);R5=dikaer(R5_,49,P4,7);R6_=dikaer(xbing(P0,P1),7,P2,7);R6_=reshape(R6_,1,49);R6=dikaer(R6_,49,P5,7);R7_=dikaer(xbing(P2,P3),7,P2,7);R7_=reshape(R7_,1,49);R7=dikaer(R7_,49,P4,7);R8_=dikaer(P0,7,P3,7);R8_=reshape(R8_,1,49);R8=dikaer(R8_,49,P5,7);R9_=dikaer(xbing(P1,P2),7,P3,7);R9_=reshape(R9_,1,49);R9=dikaer(R9_,49,P4,7);R10_=dikaer(P3,7,P3,7);R10_=reshape(R10_,1,49);R10=dikaer(R10_,49,P3,7);R11_=dikaer(xbing(P0,P1),7,P4,7); R11_=reshape(R11_,1,49);R11=dikaer(R11_,49,P4,7);P45=xbing(P4,P5);R12_=dikaer(xbing(P2,P3),7,P45,7); R12_=reshape(R12_,1,49);R12=dikaer(R12_,49,P3,7);R13_=dikaer(P0,7,P5,7);R13_=reshape(R13_,1,49);R13=dikaer(R13_,49,P4,7);R14_=dikaer(P1,7,P5,7);R14_=reshape(R14_,1,49);R14=dikaer(R14_,49,P3,7);P01=xbing(P0,P1);R15_=dikaer(xbing(P01,P2),7,P6,7); R15_=reshape(R15_,1,49);R15=dikaer(R15_,49,P3,7);R16_=dikaer(P3,7,P6,7);R16_=reshape(R16_,1,49);R16=dikaer(R16_,49,P2,7);R17_=dikaer(P4,7,P0,7);R17_=reshape(R17_,1,49);R17=dikaer(R17_,49,P4,7);R18_=dikaer(xbing(P5,P6),7,P0,7); R18_=reshape(R18_,1,49);R18=dikaer(R18_,49,P3,7);R19_=dikaer(xbing(P4,P5),7,P1,7); R19_=reshape(R19_,1,49);R19=dikaer(R19_,49,P3,7);R20_=dikaer(P6,7,xbing(P1,P2),7); R20_=reshape(R20_,1,49);R20=dikaer(R20_,49,P2,7);P23=xbing(P2,P3);R21_=dikaer(P4,7,xbing(P23,P4),7); R21_=reshape(R21_,1,49);R21=dikaer(R21_,49,P3,7);R22_=dikaer(P5,7,xbing(P23,P4),7);R22_=reshape(R22_,1,49);R22=dikaer(R22_,49,P2,7);R23_=dikaer(P6,7,xbing(P3,P4),7);R23_=reshape(R23_,1,49);R23=dikaer(R23_,49,P1,7);R24_=dikaer(P4,7,P5,7);R24_=reshape(R24_,1,49);R24=dikaer(R24_,49,P2,7);R25_=dikaer(P5,7,P5,7);R25_=reshape(R25_,1,49);R25=dikaer(R25_,49,P1,7);R26_=dikaer(P6,7,xbing(P6,P5),7);R26_=reshape(R26_,1,49);R26=dikaer(R26_,49,P0,7);R27_=dikaer(xbing(P4,P5),7,P6,7);R27_=reshape(R27_,1,49);R27=dikaer(R27_,49,P1,7);m=[R1,R2,R3,R4,R5,R6,R7,R8,R9,R10,R11,R12,R13,R14,R15 ,R16,R17,R18,R19,R20,R21,R22,R23,R24,R25,R26,R27];R=bingji(m);%*************³õʼ»¯±äÁ¿e=0;ec=0;y_1=0;y_2=0;u=0;u_1=0;u_2=0;u_3=0;e_1=0;e_2= 0;Eswith=10;throttle_1=0;brake_1=0;x=[0 0 0];ts=0.001;sys=tf(1,[1,2,1],'inputdelay',0.5);dsys=c2d(sys,ts,'zoh');[num,den]=tfdata(dsys,'v');for k=1:1:40000%****************¿ØÖÆϵͳtime(k)=k*ts;if(k<20000)vd(k)=50;elsevd(k)=0;endy(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;e=vd(k)-y(k);ec=e-e_1;u_3=u_2;u_2=u_1;u_1=u;y_2=y_1;y_1=y(k);x(1)=e;x(2)=(e-e_1)/ts;x(3)=x(3)+e*ts;%*******************************ÓÍÃÅ¿ØÖÆkp=0.42;Ti=30;Td=0.0018;%*** vd(k)=1% kp=0.42;Ti=30;Td=0.0018;%*** vd(k)=1% kp=0.0015;Ti=0.01;Td=0.002;%***vd(k)=1*time(k)+10 % kp=0.0015;Ti=0.001;Td=0.002;%***vd(k)=1*time(k)^2+time(k)+2;ki=kp*ts/Ti;kd=kp*Td/ts;dthrottle=kp*x(1)+kd*x(2)+ki*x(3);throttle=u_1+dthrottle;if(throttle>2000)throttle=2000;endif(throttle<-2000)throttle=-2000;end%****************************ɲ³µ¿ØÖÆ%/*********ѹËõÊäÈë±äÁ¿*****%E=lisan(-50,50,3,e);EC=lisan(-20,20,3,ec);%/*********¼ÆËãʵ¼ÊÎó²î¡¢Îó²î±ä»¯ÂʵÄÁ¥Êô¶ÈÏòÁ¿*****% E_R(1)=lbell(E,1,4,-3);E_R(2)=trig(E,-3,-2,0);E_R(3)=trig(E,-3,-1,1);E_R(4)=trig(E,-2,0,2);E_R(5)=trig(E,-1,1,3);E_R(6)=trig(E,0,2,3);E_R(7)=rbell(E,1,4,3);EC_R(1)=lbell(EC,1,4,-3);EC_R(2)=trig(EC,-3,-2,0);EC_R(3)=trig(EC,-3,-1,1);EC_R(4)=trig(EC,-2,0,2);EC_R(5)=trig(EC,-1,1,3);EC_R(6)=trig(EC,0,2,3);EC_R(7)=rbell(EC,1,4,3);%/*********¼ÆËãÄ£ºýÁ¿Êä³ö*****%U_R1=dikaer(E_R,7,EC_R,7);U_R1=reshape(U_R1,1,49);U_R2=jdikaer(U_R1,49,R,7);U_R=max(U_R2);u_L=mean(U_R);%ÐèÒª¸Ä½ø%/*********¼ÆË㾫ȷÁ¿Êä³ö*****%brake=-flisan(-2000,2000,3,u_L);e_2=e_1;e_1=e;%/************************Ñ¡Ôñ¹æÔòif (e<0)if ((e>-Eswith)||(throttle_1~=0))if(throttle<=throttle_1)throttle_1=throttle;% throttle_1=throttle_1-throttle; u=throttle;Q(k)=u;W(k)=0;elsethrottle=0;throttle_1=throttle;u=throttle;Q(k)=u;W(k)=0;endelseif(throttle_1==0)brake_1=brake;u=brake;W(k)=u;Q(k)=0;elsethrottle=0;throttle_1=throttle;u=throttle;Q(k)=u;W(k)=0;endendelseif(e~=0)if(brake_1==0)throttle_1=throttle;u=throttle;Q(k)=u;W(k)=0;elsebrake=0;brake_1=brake;u=brake;endelseu=0;W(k)=0;Q(k)=0;endend%********************»-ͼÊä³öÁ¿¶¨ÒåM(k)=u;N(k)=e;%******************************³ÙÖÍ»·½Úif (time(k)<=0.5)u=0;elseu=M(k-0.5/ts);endend% »-ͼfigure(1);plot(time,vd,'r',time,y,'k','linewidth',2); xlabel('time(s)');ylabel('vd,y');legend('ÆÚÍû','ʵ¼Ê');figure(2);plot(time,Q,'r',time,W,'k','linewidth',2); xlabel('time(s)');ylabel('u');figure(2);plot(time,Q,'r','linewidth',2);xlabel('time(s)');ylabel('u');figure(3);plot(time,W,'r','linewidth',2);xlabel('time(s)');ylabel('u');figure(4);plot(time,N,'b'); xlabel('time£¨s£©'); ylabel('e');。