山东省郯城县红花镇2018届中考数学专题复习专题五(19_2)特殊的平行四边形当堂达标题
- 格式:doc
- 大小:183.50 KB
- 文档页数:3


相似的性质【学习目标】1、进一步理解相似图形的性质及其相互联系.2、掌握相似图形的性质解决相关问题的规律.3、能利用位似解决实际问题. 【重点难点】重点:相似的性质,进行相似问题的求解和证明.难点:用相似三角形的性质与判定探索相似三角形中对应边,周长面积之间的关系. 【知识回顾】1.如图,已知AB CD EF ∥∥,那么下列结论正确的是( )A .AD BC DF CE =B .BC DF CE AD =C .CD BC EF BE=D .CD AD EF AF=2.如图所示,给出下列条件:①B ACD ∠=∠; ②ADC ACB ∠=∠;③AC AB CD BC=; ④2AC AD AB =. 其中单独能够判定ABC ACD △∽△的个数为( )A .1B .2C .3D .43.已知△ABC ∽△DEF ,且AB :DE =1:2,则△ABC 的面积与△DEF 的面积之比为( )A .1:2B .1:4C .2:1D .4:14.如图,已知等边三角形ABC 的边长为2,DE 是它的中位线,则下面四个结论:(1)DE =1,(2)△CDE ∽△CAB ,(3)△CDE 的面积与△CAB 的面积之比为1:4.其中正确的有:( )A .0个B .1个C .2个D .3个 【综合运用】1.甲,乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为 米.2.如图,在已建立直角坐标系的4×4正方形方格纸中,△划格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P ,A ,B 为顶点的三角形与△ABC 相似(全等除外),则格点P的坐标是_______.ABD C EF 1题 A CD B(第2题图)小华乙DEF△ 3.如图,在△ABC 中,已知DE ∥BC ,AD =4,DB =8,DE =3,(1)求ADAB的值,(2)求BC 的长【直击中考】 1.在ABC △和 中,22AB DE AC DF A D ==∠=∠,,,如果ABC △的周长是16,面积是12,那么DEF △的周长、面积依次为( ) A .8,3 B .8,6 C .4,3 D .4,62.(湖北孝感)如图,点M 是△ABC 内一点,过点M 分别作直线平行于△ABC 的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC 的面积是 .3.(吉林省)如图,⊙o 中,弦AB 、CD 相交于AB 的中点E 连接AD 并延长至点F ,使DF=AD ,连接BC 、BF .(1)求证:CBE AFB △∽△;(2)当58BE FB =时,求CBAD 的值【总结提升】1.本节课的知识结构。


(第4题图) (第5题图)九年级数学复习单元检测题(九)内容:相似一、选择题(每小题4分,共40分)在每小题给出的四个选项中, 只有一项是符合题目要求的. 1. 若两个相似多边形的面积之比为1∶4,则它们的周长之比为( ).A. 1∶4B. 1∶2C. 2∶1D. 1∶162.太阳光下,某建筑物在地面上的影长为36m ,同时量得高为1.2m 的测杆影长为2m ,那么该建筑物的高为( ). A .21.6 B. 12 C.24 D.103.如图,下列条件不能..判定△A DB ∽△ABC 的是( ). A .∠ABD =∠ACBB . ∠ADB =∠ABCC .2AB AD AC =D .AD ABAB BC=4.在平面直角坐标系中,已知点A (-4,2),B (-6,-4),以原点O 为位似中心,相似比为12,把△ABO 缩小,则点A 的对应点A ¢的坐标是( ). A .(-2,1) B .(-8,4)C .(-8,4)或(8,-4)D .(-2,1)或(2,-1) 5.如图,在方格纸中,△ABC 和△EPD 的顶点均在格点上,要使△ABC ∽△EPD ,则点P 所在的格点为( ) .A .P 1B .P 2C .P 3D .P 46.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x ,那么x 的值( ). A .只有1个B .可以有2个C .可以有3个D .有无数个7.如图,在平行四边形ABCD 中,点 E 是边AD 的中点,EC(第11题图)(第8题图)(第12题图)对角线BD 于点F ,则EF ︰CF 等于( ). A .3∶2 B .3∶1C .1∶1D .1∶28.如图,矩形纸片ABCD 中,点E 是AD 的中点,且AE =1,BE 的垂直平分线MN 恰好过点C ,则矩形的一边AB 的长度为( ).A .1B .2C .3D .2 9.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形; ②位似图形一定有位似中心; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形; ④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是是( ).A .②③B .①②C .③④D .②③④ 10. 如图,AB =4,射线BM 和AB 互相垂直,点D 是AB 上的一个动点,点E 在射线BM 上,12BE DB =,作EF ⊥DE 并截取EF =DE ,连结AF 并延长交射线BM 于点C .设BE=x ,BC=y ,则y 与x 的函数解析式是( ).A .124x y x =-- B .21x y x =-- C .31x y x =-- D .84xy x =-- 二、填空题(每小题4分,共24分)请把答案填写在题中横线上. 11. 如图,在△ABC 中,点D 、E 分别在AB 、AC 上,DE ∥BC ,若AD =4,DB =2,则BCDE的值为__________. 12.如图是一位学生设计的用手电筒来测量某古城墙高度的示意图.点P 处放一水平的平面镜,光线从点A 发出经平面镜反射后刚好到古城墙CD 的顶端C 处,已知AB ⊥BD ,测得AB =2米,BP =3米,PD =12米,那么该古城墙的高度CD 是____米.13.若P 是Rt△ABC 的斜边BC 上异于B ,C 的一点,过点P 作直线截△ABC ,截得的三角形与原△ABC 相似,满足这样条件的直线共有 条.(第10题图)A DM(第16题图)14.如图,正方形OABC 与正方形ODEF 是位似图形,点O 为位似中心,相似比为1,点A 的坐标为(0,1),则点E 的坐标是 . 15.矩形ABCD 中,AB =2,BC =1,点P 是直线BD 上一点,且DP =DA ,直线AP 与直线BC 交于点E ,则CE = .16. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD ,东边城墙AB 长9里,南边城墙AD 长7里,东门点E 、南门点F 分别是AB 、AD 中点,EG ⊥AB ,FH ⊥AD ,EG =15里,HG 经过A 点,则FH= 里. 三、 解答题(本题共3小题,共36分)17.(10分)一天晚上,李明和张龙利用灯光下的影子来测量一路灯D 的高度,如图,当李明走到点A 处时,张龙测得李明直立身高AM 与其影子长AE 正好相等,接着李明沿AC 方向继续向前走,走到点B 处时,李明直立时身高BN 的影子恰好是线段AB ,并测得AB =1.25m 。

山东省郯城县红花镇2018届中考数学专题复习专题五(19-1)平行四边形性质及判定教案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山东省郯城县红花镇2018届中考数学专题复习专题五(19-1)平行四边形性质及判定教案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山东省郯城县红花镇2018届中考数学专题复习专题五(19-1)平行四边形性质及判定教案的全部内容。
平行四边形性质及判定一、【教材分析】二、【教学流程】知识回顾则AD=___㎝.周长= ____ cm.2、已知ABCD, ∠A=50度,则∠C=___度。
∠B=____度.3、ABCD的对角线AC、BD长度之和为20cm,若△OAD的周长为17cm,则AD=____cm4、在四边形ABCD中,若分别给出六个条件:①AB∥CD ②AD=BC③OA=OC④AD∥BC⑤AB=CD ⑥OB=OD. 现在,以其中的两个为一组,能直接确定四边形ABCD为平行四边形的条件是 _________ (只填序号)通过课前热身练习,让学生对知识进行回忆,进一步体会平行四边形的性质、判定.概念再现,知识梳理。
综合运【自主探究】1。
□ABCD的周长为40,△ABC的周长为25,则对角线AC的长( )A、5B、15C、6D、82.在□ABCD中,∠A:∠B:∠ C:∠D的值可以是( )A、1:2:3:4B、3:4:4:3C、3:3:4:4D、3:4:3:43。
已知如图,AB//FE//DC,AD//GH//BC,图中有几个平行四边形?4.如图,在□ABCD中,∠BAD和∠BCD的教师展现问题,学生独立思考完成,要求学生做题时注意知识点和方法的运用,做每一道题进行反思总结。
相似的判定一、选择题1、如图1, 在矩形ABCD 中,E 、F 分别是CD 、BC 上的点,若∠AEF =900,则一定有( )A 、△ADE ∽△AEFB 、△ECF ∽△AEFC 、△ADE ∽△ECFD 、△AEF ∽△ABF2、如图2,AD ⊥BC,CE ⊥AB ,垂足分别为D 、E ,AD 与CE 交于点F ,∠A =∠C ,则图中相似三角形共有( )对A 、5B 、6C 、7D 、93、△ABC 和△DEF 满足下列条件,其中使△AB C)A 、∠A =∠D =500 , ∠B=600 , ∠E =700 B 、AB =1.5, BC =2, AC=3, DE =2, EF =3, FD =4C 、AB =3DE , AC =3DF ,∠A =∠DD 、∠C=∠E =900, ∠A =320, ∠F =580二、填空题4、如图3,在∠C =∠B ,则_________ ∽_________,________ ∽_________5、如图4,∠1=∠2,请补充一个条件 ,使△ABC ∽△ADE6、如图5,BD 平分∠ABC ,且AB =4,BC =9,当BD = 时,△ABD ∽△DB C7、如图6,在平行四边形ABCD 中,E 是BC 上一点,BE :EC =2:3,AE 交BD 于点F ,则BF :FD = 。
三、解答题图3 图4 图5 图68、如图;正方形ABCD中,P是BC上的点,BP=3PC,Q是CD中点,则△ADQ ∽△QCP成立吗?为什么?9、如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上的某一点D处,折痕为EF(点E,F分别在边AC,BC上).(1)若△CEF与△ABC相似.①当AC=BC=2时,AD的长为________;②当AC=3,BC=4时,AD的长为________;(2)当点D是AB的中点时,△CEF与△ABC相似吗?说明理由.答案选择题1. C2. B3. B填空题4. △ABE ∽△ACD ,△BOD ∽△COE5. ∠B =∠D ,6. 6;7.2:5解答题8. 相似,理由略9.解:(1)① 2 ②1.8或2.5(2)相似.理由如下:连接CD ,与EF 交于点O.∵CD 是Rt △ABC 的中线,∴CD =DB =12AB ,∴∠DCB =∠B .由折叠的性质知∠COF =∠DOF =90°,∴∠DCB +∠CFE =90°. ∵∠B +∠A =90°,∴∠C FE =∠A .又∵∠C =∠C ,∴△CEF ∽△CBA .。
中考数学专题复习——特殊平行四边形一、选择题1.(08山东省日照市)只用下列图形不能镶嵌的是 ( )A .三角形B .四边形C .正五边形D .正六边形2、(2018浙江义乌)下列命题中,真命题是 ( )A .两条对角线垂直的四边形是菱形B .对角线垂直且相等的四边形是正方形C .两条对角线相等的四边形是矩形D .两条对角线相等的平行四边形是矩形3、(2018山东威海)将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为 ( )A .1B .2C .2D .34.(2018年山东省临沂市)如图,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD的中点,连接AE 、EF 、AF ,则△AEF 的周长为( ) A . 32 B . 33 C . 34 D . 35. (2018年山东省潍坊市)如图,梯形ABCD 中,AD ∥BC,AD=AB,BC=BD,∠A=100°,则∠C=( )A.80°B.70°C.75°D.60°ACD6.(2018年辽宁省十二市)下列命题中正确的是( ) A .两条对角线互相平分的四边形是平行四边形 B .两条对角线相等的四边形是矩形 C .两条对角线互相垂直的四边形是菱形D .两条对角线互相垂直且平分的四边形是正方形7.(2018年浙江省绍兴市)如图,沿虚线EF 将ABCD 剪开,则得到的四边形ABFE 是( )A .梯形B .平行四边形C .矩形D .菱形ABEABFADEBC8.(2018年天津市)在平面直角坐标系中,已知点A (0,2),B (32-,0),C (0,2-),D (32,0),则以这四个点为顶点的四边形ABCD 是( ) A .矩形B .菱形C .正方形D .梯形9(2018年沈阳市)如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE ,交对角线BD 于点F ,连接CF ,则图中全等三角形共有( ) A .1对 B .2对 C .3对 D .4对10.(2018年四川巴中市如图2.在ABCD 中,对角线AC 和BD 相交于点O ,则下面条件能判定ABCD 是矩形的是( )A .AC BD =B .AC BD ⊥ C .AC BD =且AC BD ⊥ D .AB AD =11.(2018年江苏省南通市)下列命题正确的是( ) A .对角线相等且互相平分的四边形是菱形 B .对角线相等且互相垂直的四边形是菱形 C .对角线相等且互相平分的四边形是矩形 D .对角线相等的四边形是等腰梯形12.(2018年江苏省无锡市)如图,E F G H ,,,分别为正方形ABCD 的边AB ,BC ,CD ,DA 上的点,且13AE BF CG DH AB ====,则图中阴影部分的面积与正方形ABCD 的面积之比为( )A.25 B.49 C.12D.35D CF BAEADCE FB13.(2018广州市)如图2,每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )14.(2018云南省)菱形的两条对角线的长分别是6和8 ,则这个菱形的周长是( ) A .24 B .20C .10D .515.(2018宁夏)平行四边形ABCD 中,AC ,BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( ) A . AB=BC B .AC=BD C . AC ⊥BD D .AB ⊥BD16.(2018年江苏省连云港市)已知AC 为矩形ABCD 的对角线,则图中1∠与2∠一定不相等的是( )A .B .C .D . 17..(2018山东东营)如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC ,CD ,DA 运AB DB AC 1 2 B AD C B A C 1 2 D 1 2 BA D C图2图 1AB 图 2动至点A 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△ABC 的面积是( )A .10B .16C .18D .2018..(2018泰安)如图,下列条件之一能使平行四边形ABCD 是菱形的为( ) ①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD = A .①③B .②③C .③④D .①②③19.(2018年湖南省邵阳市)如图(二),将ABCD 沿AE 翻折,使点B 恰好落在AD 上的点F 处,则下列结论不一定成立.....的是( ) A .AF EF = B .AB EF =C .AE AF =D .AF BE =20.(2018年上海市)如图2,在平行四边形ABCD 中,如果AB a =,AD b =, 那么a b +等于( ) A .BDB .ACC .DBD .CA21.(2018年山东省威海市)将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为A .1B .2C .2D .3ADF C E B图(二)ABCD图222.(2018广东深圳)下列命题中错误..的是 ( ) A.平行四边形的对边相等B.两组对边分别相等的四边形是平行四边形C.矩形的对角线相等 D.对角线相等的四边形是矩形23.(2018湖北襄樊)顺次连接等腰梯形四边中点所得四边形是( )A.菱形B.正方形C.矩形D.等腰梯形24.(2018黑龙江哈尔滨)如图,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是( ). (A )3cm (B )4cm (C )5cm (D )6cm二、填空题1. (08浙江温州) 如图,菱形ABCD 中,60A ∠=,对角线8BD =,则菱形ABCD 的周长等于 .2、(2018浙江义乌)如图,直角梯形纸片ABCD ,AD ⊥AB ,AB=8, AD=CD=4,点E 、F 分别在线段AB 、AD 上,将△AEF 沿EF 翻折, 点A 的落点记为P .(1)当AE=5,P 落在线段CD 上时,PD= ▲ ;(2)当P 落在直角梯形ABCD 内部时,PD 的最小值等于 ▲ .3、(2018山东烟台)红丝带是关注艾滋病防治问题的国际性标志.将宽为1cm 的红丝带交叉成60°角重叠在一起(如图),则重叠四边形的面积为_______2.cm4.(2018年山东省临沂市)如图,矩形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD ,BC 于点E 、F ,连接CE ,则CE 的长________.AB D5、(2018浙江杭州)如图,一个42⨯的矩形可以用3种不同的方式分割成2或5或8个小正方形,那么一个53⨯的矩形用不同的方式分割后,小正方形的个数可以是 .6(2018浙江宁波)如图,菱形OABC 中,120A =∠,1OA =,将菱形OABC 绕点O 按顺时针方向旋转90,则图中由BB ',B A '',A C ',CB 围成的阴影部分的面积是 .7.(2018年天津市)如图,在正方形ABCD 中,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,若1=AG ,2=BF ,︒=∠90GEF ,则GF 的长为 .8 .(2018年沈阳市)如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补充一个条件能使菱形ABCD 成为正方形,则这个条件 是 (只填一个条件即可).9.(2018年四川省南充市)如图,四边形A B C D 中,E FG H ,,,分别是边A B B C C D D A ,,,的中点.请你添加一个条件,使四边形EFGH 为菱形,应添加的条件是 .A D HGF BE或?A DCBO''FADO E BCADC BFG E10.(2018新疆乌鲁木齐市)如图3,在四边形ABCD 中,AD BC ∥,90D ∠=,若再添加一个条件,就能推出四边形ABCD 是矩形,你所添加的条件是 .(写出一种情况即可)11.(2018黑龙江黑河)如图,矩形ABCD 中,3AB =cm ,6AD =cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,且2EF BE=,则AFC S =△2cm .12.(2018桂林市)如图,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=6,BC=8,则梯形的高为 。
B
C D A P
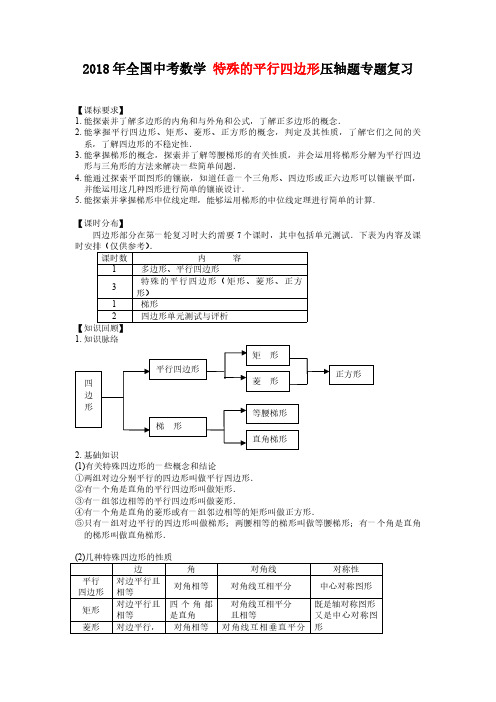
特殊平行四边形
一、选择题
1.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是( ) A .四边形AEDF 是平行四边形
B .如果90BA
C ∠=,那么四边形AEDF 是矩形
C .如果A
D 平分BAC ∠,那么四边形AEDF 是菱形 D .如果AD BC ⊥,那么四边形AEDF 是正方形
第2题图 第3题图
2.如图,把矩形ABCD 沿EF 对折后使两部分重合,若150∠=, 则AEF ∠=( ) A .110° B .115° C .120° D .130°
二、填空题 3. 如图,已知P 是正方形ABCD 对角线BD 上一点,且BP = BC ,则∠ACP 度数是 . 4将两块全等的含30°角的三角尺如图1摆放在一起,设较短直角边为1.
(1)四边形ABCD 是平行四边形吗?说出你的结论和理由:________________________. (2)如图2,将Rt △BCD 沿射线BD 方向平移到Rt △B 1C 1D 1的位置,四边形ABC 1D 1是平行四边形吗?说出你的结论和理由:_________________________________________. (3)在Rt △BCD 沿射线BD 方向平移的过程中,当点B 的移动距离为______时,四边形ABC 1D 1为矩形,其理由是_____________________________________;当点B 的移动距离为______时,四边形ABC 1D 1为菱形,其理由是_______________________________.(图3、图4用于探究)
图1
30︒
30︒B D
A
C
图2
D 1
C 1B 1
C
A
D
B 图3
C
A
D
B 图4
C
A
D
B A
F C D
BE
第1题图
三、解答题
5. 如图,在△ABC 中,O 是AC 边上的一点,过点O 作直线MN∥BC ,直线MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F 。
(1)说明OE=OF ;
(2)当点O 运动到何处时,四边形AECF 是矩形?并说明理由。
6. 如图,△ABC 中,AC 的垂直平分线MN 交AB 于点D ,交AC 于点O ,CE∥AB 交MN 于E ,连结AE 、CD .
则:四边形ADCE 的形状是 .请说明理由
D
B
A E
N
M
O
答案
选择题 1.D , 2. B ,
填空题 3. 22.5o,
4. (1) 是平行性四边形,理由:两组对边分别相等的四边形是平行四边形. (2)是平行性四边形,理由:一组对边平行且相等的四边形是平行四边形. (3)
3
3
,理由:有一个角是直角的平行四边形是矩形;3,四个边都相等的四边形的是菱形. 解答题
5.(1)证明:∵MN∥BC
∴∠OEC =∠BCE ,∠OFC =∠DCF ∵CE 平分∠ACB ,CF 平分∠ACD ∴∠OCE =∠BCE ,∠OCF =∠DCF ∴∠OEC =∠OCE ,∠OFC =∠OCF ∴OE =OC ,OF =OC ∴OE =OF
(2)当点O 运动到AC 中点时,四边形AECF 是矩形,理由略 6.四边形ADCE 的形状是菱形,理由略。