数学学业水平考试模块复习卷4

一、单选题二、多选题三、填空题1. 在中，若，，，则等于（ ）A．B．C．D．2. 已知，，，则a ，b ，c 的大小关系为（ ）A．B．C．D．3. 已知焦点在轴上的椭圆的内接平行四边形的一组对边分别经过其两个焦点（如图所示），当这个平行四边形为矩形时，其面积最大，则的取值范围是（）A．B．C．D．4. 设、是两个不同的平面，m 、n 是两条不同的直线，下列说法正确的是（ ）A ．若，，，则B．若，，则C ．若，，则D ．若，，，则5. 棱长和底面边长均为1的正四棱锥的侧面积为A．B ．2C ．3D．6.将函数的图象向左平移个单位长度后，所得的图象关于原点对称，则的最小值是（ ）A．B．C．D．7. 在棱长为的正方体中，分别是棱的中点，则（ ）A．B．平面C ．到平面的距离为D ．异面直线与所成的角为8. 下列抽样实验中，不适宜用抽签法的是（ ）A ．从某场生产的3000件产品中抽取600件进行质量检验B ．从某厂生产的两箱（每箱15件）产品中抽取6件进行质量检测C ．从甲、乙两厂生产的两箱（每箱15件）产品中抽取6件进行质量检验D ．从某厂生产的3000件产品中抽取10件进行质量检测9.设，函数．若，则实数的取值范围是_________．10. 在中，角A ，，所对的边分别为，，，若，那么______．2023年广东省普通高中学业水平合格性考试模拟(四）数学试题(高频考点版)2023年广东省普通高中学业水平合格性考试模拟(四）数学试题(高频考点版)四、解答题11. 经过的直线与两直线和分别交于两点,且满足则直线的方程为__________.12. 已知为复数，且，写出满足上述条件的一个复数__________；的最大值为__________．13. 在直三棱柱中，，，，与相交于点M．(1)求的长度；(2)求点M到平面的距离．14. 已知函数为奇函数．（1）求常数k 的值；（2）若，试比较与的大小；（3）若函数，且在区间上没有零点，求实数m 的取值范围．15.在等差数列中，，其前项和为，等比数列的各项均为正数，，公比为q ，且.(1)求与；(2)证明：.16. 如图所示,在直三棱柱中,,其中点为棱的中点,为棱上且位于点上方的动点．(1)求证:平面；(2)若平面与平面所成的锐二面角的余弦值为,求直线与平面所成角的正弦值．。

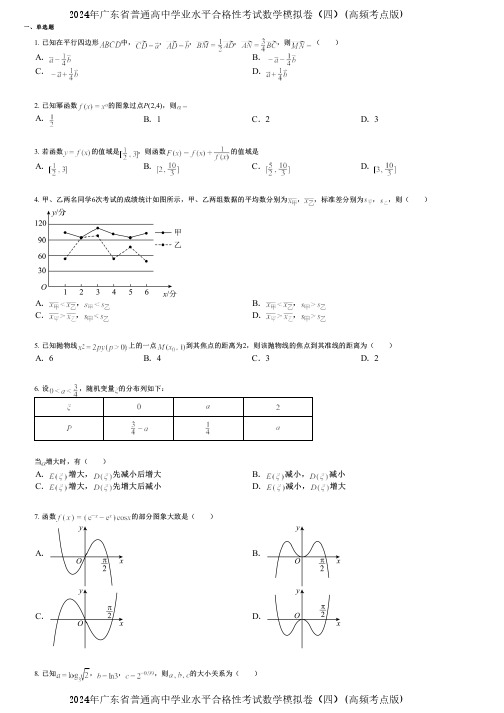
一、单选题1.已知在平行四边形中，，，，，则（ ）A．B．C．D．2. 已知幂函数的图象过点P (2,4)，则A．B ．1C ．2D ．33. 若函数的值域是，则函数的值域是A．B．C．D．4. 甲、乙两名同学6次考试的成绩统计如图所示，甲、乙两组数据的平均数分别为，，标准差分别为，，则（）A ．，B ．，C ．，D ．，5. 已知抛物线上的一点到其焦点的距离为2，则该抛物线的焦点到其准线的距离为（ ）A ．6B ．4C ．3D ．26.设，随机变量的分布列如下：当增大时，有（ ）A ．增大，先减小后增大B ．减小，减小C ．增大，先增大后减小D．减小，增大7. 函数的部分图象大致是（ ）A．B．C．D．8. 已知，，，则的大小关系为（ ）2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(高频考点版)2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(高频考点版)二、多选题三、填空题四、解答题A．B．C．D．9. 已知与线性相关，且求得回归方程为，变量，的部分取值如表所示，则（）A．与负相关B．C ．时，的预测值为D ．处的残差为10. 下列说法正确的是（ ）A．轴截面为等腰直角三角形的圆锥，其侧面展开图的圆心角的弧度数为B．若，则C ．已知为锐角，，角的终边上有一点，则D．在范围内，与角终边相同的角是和11. 已知是定义在上的不恒为零的函数，对于任意都满足，则下列说法正确的是（ ）A．B．是奇函数C ．若，则D ．若当时，，则在单调递减12. 已知函数，则（ ）A．的最大值为2B ．的图象关于点对称C ．在上单调递增D ．直线是图象的一条对称轴13. 已知点M （1，2）在抛物线C ：y 2=2px （p ＞0）上，则点M 到抛物线C 焦点的距离是______．14. 某电池厂有A ，B 两条生产线，现从A 生产线中取出产品8件，测得它们的可充电次数的平均值为210，方差为4；从B 生产线中取出产品12件，测得它们的可充电次数的平均值为200，方差为4．则20件产品组成的总样本的方差为____________．（参考公式：已知总体分为2层，通过分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为：，，；，，．记总的样本平均数为，样本方差为，则；）15. 为了解某小区居民的家庭年收入（万元）与年支出（万元）的关系，随机调查了该小区的10户家庭，根据调查数据的散点图可以看出与之间有线性相关关系，设其回归直线方程为．已知，，．若该小区某家庭的年收入为30万元，则据此估计，该家庭的年支出为____万元．16. 已知圆的圆心在抛物线上，圆过原点且与抛物线的准线相切.（1）求该抛物线的方程；（2）过抛物线焦点的直线交抛物线于，两点，分别在点，处作抛物线的两条切线交于点，求三角形面积的最小值及此时直线的方程.17.已知函数，将的图象向右平移个单位长度，再将所有点的横坐标伸长为原来的2倍，纵坐标不变，得到函数的图象．(1)求的解析式；(2)若函数，求在区间上的所有最大值点．18. 在锐角中，角A，，的对边分别为，，，满足．(1)求角；(2)若，求中边上的高的最大值．19. 某公园有一个湖，如图所示，湖的边界是圆心为O的圆，已知圆O的半径为100米．为更好地服务游客，进一步提升公园亲水景观，公园拟搭建亲水木平台与亲水玻璃桥，设计弓形为亲水木平台区域（四边形是矩形，A，D分别为的中点，米），亲水玻璃桥以点A为一出入口，另两出入口B，C分别在平台区域边界上（不含端点），且设计成，另一段玻璃桥满足．(1)若计划在B，F间修建一休闲长廊该长廊的长度可否设计为70米？请说明理由；（附：）(2)设玻璃桥造价为0.3万元/米，求亲水玻璃桥的造价的最小值．（玻璃桥总长为，宽度、连接处忽略不计）．20. 已知的三个内角A，B，C满足：，，求的值.21. 某中学为研究本校高三学生在县联考中的数学成绩，随机抽取了100位学生的数学成绩（满分150分）作为样本，并整理成五组，制成如图所示的频率分布直方图.(1)若参与测试的学生共12000人，试估计成绩不低于110分的学生有多少人？(2)用分层随机抽样的方法从样本中的和两组抽取8人，再从这8人中随机抽取3人，记这3人得分在范围内的人数为，求的分布列与数学期望.。

一、单选题二、多选题三、填空题1. 复数的实部与虚部相等，则实数( )A．B．C．D．2.若是集合的真子集，则的取值范围是（ ）A．B．C．D．3. 已知i 为虚数单位，若复数（）为纯虚数，则复数在复平面上对应的点（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4. 已知，，，则（ ）A．B．C．D．5. 设和都是等差数列，前项和分别为和，若，，则（ ）A．B．C．D．6. 已知奇函数的定义域为，且当时，，若，则实数的值为（ ）A ．0B ．2C．D ．17. 若复数，则|z |=（ ）A．B ．1C ．2D．8.已知曲线的焦距为4，则其离心率为（ ）A．B．C．D ．29.过双曲线的左焦点的直线交的左､右支分别于两点，交直线于点，若，则（ ）A．B．C．D．10.在中，，，是的中点．将沿着翻折，得到三棱锥，则（ ）A．.B ．当时，三棱锥的体积为4.C．当时，二面角的大小为.D．当时，三棱锥的外接球的表面积为.11. 已知，且，则下列结论中正确的是（ ）A ．有最大值B ．有最小值3C．有最小值D ．有最大值412. 已知，，，若（），则n 的可能值为（ ）A ．6B ．8C ．11D ．1313.设椭圆的左右焦点分别为和，离心率为，过左焦点且倾斜角为的直线与椭圆交于，两点，且线2024年广东省普通高中学业水平合格性考试数学模拟卷（四）2024年广东省普通高中学业水平合格性考试数学模拟卷（四）四、解答题段，则的内切圆半径等于______.14. 已知数列为正项等比数列，，则的最小值为________.15. 用长度为1，4，8，9的4根细木棒围成一个三角形（允许连接，不允许折断），则其中某个三角形外接圆的直径可以是______（写出一个答案即可）．16.设正项等比数列的前项和为，已知，.(1)记，判断数列是否成等差数列，若是，请证明；若不是，请说明理由；(2)记，数列的前项和为，求满足的最小正整数的值.17.设函数，其中 是自然常数．(1)总存在两条直线与曲线和都相切，求的取值范围；(2)当时，证明： ．18. 已知数列中（Ⅰ）求的通项公式；（Ⅱ）若数列中，证明：19.设函数．(1)若时，求的最小值；(2)当时，证明：．20.如图，四棱锥的底面边长为1的正方形，每条侧棱的长均为，为侧棱上的点.(1)求证：；(2)若平面 ，求三棱锥的体积.21. 从某工厂生产的某种产品中抽取1000件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：（1）求这1000件产品质量指标值的样本平均数和样本方差（同一组数据用该区间的中点值作代表）（2）由频率分布直方图可以认为，这种产品的质量指标值服从正态分布，其中以近似为样本平均数，近似为样本方差．（ⅰ）利用该正态分布，求；（ⅱ）某用户从该工厂购买了100件这种产品，记表示这100件产品中质量指标值为于区间的产品件数，利用（ⅰ）的结果，求．附：．若，则，．。

一、单选题二、多选题1. 从甲、乙、丙、丁四名同学中选2人参加普法知识竞赛，则甲被选中的概率为（ ）A．B．C．D．2. 设集合，，则的子集个数为A ．4B ．8C ．16D ．323. 已知函数，若函数在区间上无零点，则正数的取值范围为（ ）A．B．C．D．4. 已知是第一象限的角，且，则A．B．C．D．5. 如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该几何体的表面积为A．B．C．D．6. 已知，则（ ）A．B．C．D．7. 已知各项均为正数的等比数列的前项和为，若，则的值为（ ）A ．4B．C ．2D．8. 已知函数是定义在R 上的周期为2的偶函数，当，则函数的图象与函数的图象交点个数为（ ）A ．6B ．7C ．8D ．99. 已知，，记，则A．的最小值为B ．当最小时，C．的最小值为D ．当最小时，10. 在平面直角坐标系中，将函数的图象绕坐标原点逆时针旋转后，所得曲线仍然是某个函数的图象，则称为“旋转函数”.那么（ ）A ．存在旋转函数B．旋转函数一定是旋转函数C ．若为旋转函数，则D ．若为旋转函数，则2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(3)2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(3)三、填空题四、解答题11. 已知单位向量，的夹角为，则下列结论正确的有（ ）A．B．在方向上的投影向量为C ．若，则D．若，则12. 某商店为了解该店铺商品的销售情况，对某产品近三年的产品月销售数据进行统计分析，绘制了折线统计图，如图．下列结论正确的有（）A ．该产品的年销量逐年增加B ．该产品各年的月销量高峰期大致都在8月C ．该产品2019年1月至12月的月销量逐月增加D ．该产品各年1月至6月的月销量相对于7月至12月波动性更小、变化更平稳13.数列的前项和为．已知,，则________．14.若，则______.15. 若函数在上存在单调递减区间，则m 的取值范围是______．16. 如图所示，在四棱锥P -ABCD 中，PA ⊥平面ABCD ，底面ABCD 是矩形，，，过点B 作BE ⊥AC ，交AD 于点E ，点F ，G 分别为线段PD ，DC的中点．(1)证明：AC ⊥平面BEF ；(2)求三棱锥F -BGE 的体积．17. 已知函数．（1）当时，求函数的单调区间；（2）当时，求证．18.已知函数满足．(1)求的解析式；(2)设，求证：在上存在唯一的极小值点，且．19. 设、，函数.（1）若是偶函数，求的值；（2）若，求时的取值范围（用表示）.20. 在一次数学随堂小测验中，有单项选择题和多项选择题两种.单项选择题，每道题四个选项中仅有一个正确，选择正确得5分，选择错误得0分；多项选择题，每道题四个选项中有两个或三个选项正确，全部选对得5分，部分选对得2分，有选择错误的得0分.(1)小明同学在这次测验中，如果不知道单项选择题的答案就随机猜测.已知小明知道单项选择题的正确答案和随机猜测的概率都是.问小明在做某道单项选择题时，在该道题做对的条件下，求他知道这道单项选择题正确答案的概率；(2)小明同学在做某道多项选择题时，发现该题的四个选项他均无把握判断正误，于是他考虑了以下两种方案：方案①单选：在四个选项中，等可能地随机选择一个；方案②多选：在有可能是正确答案的所有选项组合（如、等）中，等可能地随机选择一种.若该多项选择题有三个选项是正确的，请从数学期望的角度分析，小明应选择何种方案，并说明理由.21. 如图（1）：在直角梯形中，，，，，于点，把沿折到的位置，使，如图（2）.若分别为的中点．(1)求证：平面；(2)求平面与平面的夹角．。

一、单选题二、多选题1.在的展开式中，的系数是（ ）A ．10B．C ．40D．2. 椭圆的两焦点是、，为椭圆上与、不共线的任意一点，为的内心，延长交线段于点，则的值等于（ ）A．B．C．D．3. 已知函数，若函数有两个零点，则实数的取值范围为A．B．C．D．4. “且”是“直线过点”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分又不必要条件5. 设，，，则（ ）A．B．C．D．6. 命题“，”的否定是（ ）A ．，B ．，C ．，D ．，7. 已知，，则a ，b ，c 的大小关系为（ ）A．B．C．D．8. 【2018年天津市南开中学高三模拟】已知，则的大小关系为（ ）A．B．C．D．9. 已知双曲线的左、右焦点分别为，，左、右顶点分别为M ，N ，O 为坐标原点．直线交双曲线C 的右支于P ，Q 两点（不同于右顶点），且与双曲线C 的两条渐近线分别交于A ，B 两点，则（ ）A ．为定值B．C ．点P到两条渐近线的距离之和的最小值为D ．存在直线使10.若数列满足（为正整数），为数列的前项和则（ ）A．B．C．D．11. 已知，，则下列结论正确的是（ ）A ．函数在上存在极大值B．为函数的导函数，若方程有两个不同实根，则实数m的取值范围是C ．若对任意，不等式恒成立，则实数a的最大值为2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(2)2024年广东省普通高中学业水平合格性考试数学模拟卷（四）(2)三、填空题四、解答题D．若，则的最大值为12. 下列结论正确的有（ ）A ．若随机变量，，则B．若随机变量，则C ．样本相关系数越大，两个变量的线性相关性越强；反之，线性相关性越弱D．的第百分位数为13. 若将函数表示为，其中为实数，则___________.14.设集合，，则_________．15. 在平面直角坐标系中，角的顶点与原点重合，始边与轴非负半轴重合，终边经过点，则____________.16. 已知动圆P与直线相切且与圆外切．（1）求圆心P 的轨迹C 的方程；（2）若过定点的两条相互垂直的直线交曲线C 于A ，B ，C ，D 四点，求四边形面积的最小值．17.已知函数（Ⅰ）求的最小正周期，并求的最小值；（Ⅱ）若=2，且，求的值18. 在等比数列{}中，．(1)求{}的通项公式；(2)求数列{}的前n 项和S n ．19.已知，求下列各式的值：(1)；(2).20. 已知.（1）当时，求函数的导函数的最大值；（2）若有两个极值点，求实数a 的取值范围.21. 北京时间2022年11月21日0时，卡塔尔世界杯揭幕战在海湾球场正式打响，某公司专门生产世界杯纪念品，今年的订单数量再创新高，为回馈球迷，该公司推出了盲盒抽奖活动，每位成功下单金额达500元的顾客可抽奖1次．已知每次抽奖抽到一等奖的概率为10%，奖金100元；抽到二等奖的概率为30%，奖金50元；其余视为不中奖．假设每人每次抽奖是否中奖互不影响．(1)任选2名成功下单金额达500元的顾客，求这两名顾客至少一人中奖的概率；(2)任选2名成功下单金额达500元的顾客，记为他们获得的奖金总数，求的分布列和数学期望．。

2024年湖南省初中学业水平考试模拟数学试题（四）一、单选题1．2024的绝对值是（ ）A ．2024-B ．2024C ．12024D ．12024- 2．欣赏图形的对称之美：下列安全标志图片中，是轴对称图形的是（ ）A ．B ．C ．D ．3．脱贫攻坚成果举世瞩目，5575万农村贫困人口实现脱贫，5575万这个数用科学记数法表示为（ ）A ．355.7510⨯B ．20.557510⨯C ．85.57510⨯D ．75.57510⨯ 4．下列计算正确的是（ ）A ．235a a a ⋅=B ．()325a a =C ．325a a a +=D ．()444ab a b -=- 5．在平面直角坐标系xOy 中，点(),A m n ，关于x 轴对称的点B 的坐标是（ ） A ．(),m n - B ．(),m n C ．(),m n - D ．(),m n -- 6．下列说法正确的是（ ）A ．“明天下雨的概率为80%”，意味着明天有80%的时间下雨B ．了解市民知晓“礼让行人”交通新规的情况，适合全面调查C ．一组数据5，5，3，4，1的中位数是3D ．有关部门对某药店在售口罩的合格情况进行抽检，抽检了20包口罩，其中18包合格，该商店共进货100包，估计合格的口罩约有90包7．如图，已知AB CD ∥，点E 在AD 上，若72AEC ∠=︒，30A ∠=︒，则C ∠的度数为（ ）A ．28︒B ．30︒C ．40︒D ．42︒8．如图，在冬奥会滑雪场有一坡度为AC 的长为150m ，则BC 的长为（ ）A ．75mB ．C ．D ．9．已知ABCD Y ，下列条件能使ABCD Y 成为矩形的是（ ）A ．AB BC = B ．AC BD ⊥ C ．AC BD = D ．A C ∠=∠10．如图，二次函数()20y ax bx c a =++≠的图象经过点()1,2，且与x 轴的交点的横坐标分别为1x ，2x ，其中110x -<<，212x <<．下列结论：①0a >；②20a b +<；③<0a b c -+；④对任意0m >，()21a m a bm +<-都成立，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个二、填空题11．写出一个三视图相同的立体图形名称：．12．函数y x 的取值范围是.13．因式分解：24x y y -=．14．在一个不透明袋子中有3个红球和2个黑球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则取出红球的概率是．15．已知点()11,A y ，()23,B y 在反比例函数()0m y m x=>上，则1y 2y （填“>，＜，=”） 16．如图，在ABC V 中，D ，E 分别是边AB ，AC 的中点，ADE V 与ABC V 的面积分别为ADE S V ，ABC S V ，则:ADE ABC S S =V V ．17．《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去本四尺．问折者高几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远，问折断处离地面有多高？设折断处离地而高x 尺，可列方程得．18．如图，在矩形ABCD 中，∠BAC ＝30°，AB =B 为圆心，BC 为半径画弧交矩形的边AB 于点E ，交对角线AC 于点F ，则图中阴影部分的面积为．三、解答题19．计算：()1012cos 4522024π2-⎛⎫︒+--+- ⎪⎝⎭． 20．先化简，再求值：22216911a a a a a a a --+⎛⎫-÷ ⎪---⎝⎭，其中4a =． 21．如图，在ABCD Y 中，BE 平分ABC ∠交CD 延长线于点E ，作CF BE ⊥，垂足为点F ．(1)求证：BF EF =；(2)若6AB =，3DE =，求ABCD Y 的周长．22．“古诗词诵读比赛”结束后，张老师和李老师将所有参赛选手的成绩进行整理(得分均为整数，分段包括起点，不含终点)，并分别绘制扇形图和直方图(未完善)．(1)本次比赛参赛选手共有 人，扇形图中“70～80”这组人数占总参赛人数的百分比为 ．(2)评奖约定：成绩由高到低居前60%获奖，成绩为79分的选手，他 获奖．(3)成绩前三名是1名男生和2名女生，从中任选2人发言，试求男生被选中的概率． 23．如图，已知()1,A m -，()4,1B -是一次函数y kx b =+的图象和反比例函数m y x=的图象的两个交点．(1)求反比例函数与一次函数的表达式，(2)求AOB V 的面积、(3)结合函数图象直接写出不等式m kx b x+>的解集． 24．随着梦天实验舱的顺利发射，我国空间站完成了在轨组装，为了庆祝这令人激动的时刻，某校开展了关于空间站的科学知识问答竞赛．为了奖励在竞赛中表现优异的学生，学校准备一次性购买A ，B 两种航天器模型作为奖品．已知购买1个A 模型和1个B 模型共需159元；购买3个A 模型和2个B 模型共需374元．(1)求A 模型和B 模型的单价．(2)根据学校的实际情况，需一次性购买A 模型和B 模型共20个，但要求购买A 模型的数量多于12个，且不超过B 模型的3倍．请你给出一种费用最少的方案，并求出该方案所需的费用．25．如图，AB 是⊙O 的直径，点C 在⊙O 上，点E 是»BC的中点，延长AC 交BE 的延长线于点D ，点F 在AB 的延长线上，EF ⊥AD ，垂足为G ．（1）求证：GF 是⊙O 的切线；（2）求证：CE ＝DE ；（3）若BF ＝1，EF ⊙O 的半径．26．如图，抛物线2y x bx c =++与x 轴交于()3,0A -，()1,0B 两点，与y 轴交于点C ，连接AC ．(1)求抛物线的表达式．(2)点P 是抛物线上位于线段AC 下方的一个动点，连接AP ，CP ，求APC △面积最大时点P 的坐标；(3)在抛物线上是否存在点Q ，使得以点A ，C ，Q 为顶点的三角形是直角三角形？如果存在，请直接写出所有满足条件的点Q的坐标；如果不存在，请说明理由．。

2024年湖北省初中学业水平考试四月模拟训练数学试题一、单选题1．在- ）A ．−2B ．0C ．2 D2．“守株待兔”这个事件是（ ）A ．随机事件B ．确定性事件C ．必然事件D ．不可能事件 3．下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）A ．B ．C ．D ． 4．下列各式中，计算结果等于2a 的是（ ）A ．23a a ⋅B ．53a a ÷C ．23a a +D ．50a a - 5．如图1是由6个相同的小正方体组成的几何体，移动其中一个小正方体，变成如图2所示的几何体，则移动前后（ ）A ．主视图改变，俯视图改变B ．主视图不变，俯视图改变C ．主视图不变，俯视图不变D ．主视图改变，俯视图不变6．若,a b 是方程2220240x x +-=的两根，则23a a b ++=（ ）A ．2022B ．2023C ．2024D ．20257．一个扇形的弧长是10πcm ，面积是60πcm 2，则此扇形的圆心角的度数是（ ） A ．300° B ．150° C ．120° D ．75°8．如图，在O e 中，直径AB 与弦CD 相交于点P ，连接AC AD BD ，，，若20C ∠=︒，70BPC ∠=︒，则ADC ∠=（ ）A ．70︒B ．60︒C ．50︒D ．40︒9．甲、乙两个工程队同时挖掘某段隧道，两队每天挖掘长度均保持不变，合作一段时间后，乙队因故离开，甲组单独完成了剩下的任务，甲、乙两队挖掘的长度之和()m y 与甲队挖掘时间x （天）之间的关系如右图，则甲队挖掘的总长度比乙队挖掘的总长度多（ ）A ．60mB ．50mC ．40mD ．30m10．已知关于x 的二次函数22436y ax ax a =-+-，当0x <时，y 随x 的增大而减小．且当14x -≤≤时，y 有最大值2．则a 的值为（ ）A ．83B ．1C ．−1D ．83-二、填空题11．计算：(02．12．舌尖上的浪费让人触目惊心，曾统计我国每年浪费的粮食约350亿千克，接近全国粮食总产量的6%，则350亿用科学记数法应表示为．13．一个仅装有球的不透明布袋里只有2个红球和1个白球（仅有颜色不同）．若从中任意摸出1个球，放回后再摸出1个球，两次摸出的球颜色相同的概率是． 14．如图是路灯维护工程车，如图是其工作示意图，工作篮底部与支撑平台平行，4AB BC ==米，当175∠=︒，245∠=︒时，则工作篮底部到支撑平台的距离是米．15．如图，四边形ABCD 是矩形纸片，6AB =，对折矩形纸片ABCD ，使AD 与BC 重合，折痕为EF ．展平后再过点B 折叠矩形纸片，使点A 落在EF 上的点N ，折痕BM 与EF 相交于点Q ，再次展平，连接,BN MN ，延长MN 交BC 于点G ．有如下结论：①60ABN ∠=︒；②3AM =；③BMG △是等边三角形；④P 为线段BM 上一个动点，H 是线段BN 的动点，则PN PH +的最小值是三、解答题16．先化简，再求值：222442342a a a a a a-+-÷+-+，其中3=a ． 17．如图，D 、E 、F 分别在ABC V 的三条边上，且DE AB ∥，12∠=∠．(1)求证：DF AC ∥；(2)若40B ∠=︒，DF 平分BDE ∠，求C ∠的度数．18．某学校开展了社会实践活动，活动地点距离学校12km ，甲、乙两同学骑自行车同时从学校出发，甲的速度是乙的1.2倍，结果甲比乙早到10min ，求乙同学骑自行车的速度． 19．某学校开展“家国情•诵经典”读书活动．为了解学生的参与程度，从全校学生中随机抽取200人进行问卷调查，获取了他们每人平均每天阅读时间的数据（m /分钟）．将收集的数据分为A ，B ，C ，D ，E 五个等级，绘制成如下统计图表（尚不完整）：平均每天阅读时间统计表请根据图表中的信息，解答下列问题：(1)求x 的值；(2)这组数据的中位数所在的等级是 ；(3)学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”予以表扬．若全校学生以1800人计算，估计受表扬的学生人数．20．如图，在ABC V 中，AB AC =，以AB 为直径的O e 交BC 于点D ，DE AC ⊥交BA 的延长线于点E ，交AC 于点F ．（1）求证：DE 是O e 的切线；（2）若tan 36,4AC E ==，求AF 的长．21．如图，在平面直角坐标系xOy 中，O 为坐标原点，直线2y x =+交y 轴于点A ，交x 轴于点B ，与双曲线()0k y k x=≠在一，三象限分别交于C ，D 两点，12AB BC =，连接CO ，DO ．(1)求k 的值；(2)求CDO V 的面积．22．近年来我国无人机设备发展迅猛，新型号无人机不断面世，科研单位为保障无人机设备能安全投产，现针对某种型号的无人机的降落情况进行测试，若该型号无人机在跑道起点处着陆后滑行的距离y （单位：m ）与滑行时间x （单位：s ）之间满足二次函数关系如图所示．(1)求y 关于x 的函数关系式；(2)若跑道长度为700m ，请通过计算说明是否够此无人机着陆；(3)当跑道长度足够时，请求出无人机着陆后最后两秒滑行的距离．23．【探索发现】在矩形ABCD 中，点,E F 分别在边,AD CD 上，E 为AD 的中点，AF BE ⊥于点G ．（1）如图1，若AD AB =，则EG BG 的值为___________； （2）如图2，若FG FC =，求EG BG的值； （3）【迁移拓展】如图3，E 是菱形ABCD 边AD 的中点，点F 在边CD 上，连接,BE AF ，,,2DAF ABE FG FC AB ∠=∠==，分别求AG 和CF 的长．24．如图，抛物线y ＝ax 2+bx +2（a ＜0）与x 轴交于点A （﹣1，0）和点B （2，0），与y 轴交于点C ．（1）求该抛物线的函数解析式；（2）如图1，连接BC ，点D 是直线BC 上方抛物线上的点，连接OD 、CD ，OD 交BC 于点F ，当S △COF ：S △CDF ＝2：1时，求点D 的坐标；（3）如图2，点E 的坐标为（0，﹣1），在抛物线上是否存在点P ，使∠OBP ＝2∠OBE ？若存在，请直接写出符合条件的点P 的坐标；若不存在，请说明理由．。

一、单选题二、多选题1. 函数的导函数，对任意，都有成立，若，则满足不等式的的范围是A．B．C．D．2. 已知边长为2的等边为其中心，对①；②；③；④这四个等式，正确的个数是（ ）A ．1B ．2C ．3D ．43.已知对数函数的图象过点，则（ ）A ．-3B ．1C ．2D ．34. 某学校高一、高二、高三年级的学生人数分别为300，200，400，为了了解学生的课业负担情况，该校采用分层抽样的方法，从这三个年级中抽取18名学生进行座谈，则高一、高二、高三年级抽取人数分别是（ ）A ．6,4,8B ．6，6，6C ．5，6，7D ．4，6，85. 若函数的定义域和值域的交集为空集，则正数的取值范围是（ ）A．B．C．D．6. 已知全集，集合，，则（ ）A．B．C．D．7. 要得到函数的图象，可将的图象向左平移（ ）A ．个单位B ．个单位C ．个单位D ．个单位8. 已知，则（ ）A．B．C．D．9. 已知随机性离散变量的分布列如下，则的值可以是（）12A．B．C．D ．110. 对于，，下列说法正确的有（ ）A ．若，则B ．若，则是纯虚数C．D．11. 已知是定义在上的偶函数，是定义在上的奇函数，且，在单调递减，则（ ）A．B．C．D．12. 已知抛物线的焦点为，点在抛物线上，且，过点作轴于点，则（ ）A．B．抛物线的准线为直线C．D ．的面积为2024年广东省普通高中学业水平合格性考试数学模拟卷（四） (2)2024年广东省普通高中学业水平合格性考试数学模拟卷（四） (2)三、填空题四、解答题13. 已知，又，若满足的有三个，则的取值范围是__________．14. 已知函数，其中，对于任意且，均存在唯一的实数t ，使得，且.①若，则___________；②若关于x 的方程有4个不相等的实数根，则a 的取值范围是___________.15.已知在中，，，若边的中点的坐标为，点的坐标为，则__________．16.已知函数，其图象在点处的切线斜率为.（1）证明：当时，；（2）若函数在定义域上无极值，求正整数的最大值.17. 已知椭圆的离心率为，椭圆经过点.（1）求椭圆的标准方程；（2）设点是椭圆上的任意一点，射线与椭圆交于点，过点的直线与椭圆有且只有一个公共点，直线与椭圆交于两个相异点，证明：面积为定值.18.在如图所示的多面体中，四边形为正方形，底面为直角梯形，为直角，∥，.平面平面.(1)求证：；(2)若，求二面角的余弦值.19.如图，四棱锥中，底面ABCD 是直角梯形，AD ⊥DC，，平面PCD ⊥平面ABCD ，平面PAD 与平面PBC 的交线为l．(1)证明：l ⊥平面PCD ；(2)已知，，平面PAD 与平面PBC 所成的锐二面角为30°，点Q 是l 上一动点，当直线PB 与平面QCD 所成角的正弦值为时，求DQ 的长度．20. 已知函数,且,,其中,若函数相邻两对称轴的距离大于等于．（1）求的取值范围；（2）在锐角三角形中，分别是角的对边，当最大时，，且，求的取值范围．21. 数列是公差为正数的等差数列，和是方程的两实数根，数列满足.(1)求与；(2)设为数列的前项和，求，并求时的最大值.。

高中数学必修4学业水平考试模块卷姓名 学号本试卷包括选择题、填空题和解答题三部分，时量120分钟，满分100分。

一、选择题：本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一个选项是符合题目要求的。

1.已知向量()1,a m =，()3,1b =。

若a b ⊥，则m =( ) A.3- B.1- C.1 D.3 答案：A解：因为a b ⊥，所以1310m ⨯+⋅=，得3m =-，故选A 。

2.在点()1,2A 、()2,3B 、()2,5C -，则AB AC ⋅等于( )A.1-B.0C.1D.2 答案：B解：由已知得()()1,1,3,3AB AC ==-，所以()13130AB AC ⋅=⨯-+⨯=，故选B 。

3.)cos 75sin 752+=( )A.12B.12- C.2 D.2-答案：C解)cos 75sin 75cos 45cos 75sin 45sin 75+=+()3cos 7545cos30=-==。

故选C 。

4.已知向量()1,1a =，()2,0b =，则a b ⋅=( )A.0B.1C.2D.3 答案：C解：a b ⋅=12102⨯+⨯=，故选C 。

5.函数22cos 1y x =+()x R ∈的最小正周期为( ) A.2πB.πC.2πD.4π 答案：B解： 22cos 1cos 22y x x =+=+，它的最小正周期为π。

故选B 。

6.已知()3,4a =，()sin ,cos b αα=，且a b ，则tan α=( )A.34 B.34- C.43 D.43- 答案： 解：由已知得，3cos 4sin 0αα-=，所以tan α=34，故选A 。

7.如果向量()(),1,4,a k b k ==共线且反向，则k =( )A.2±B.2-C.2D.0 答案：B解： a 与b 共线，∴ 140k k ⨯-⨯=，得2k =±，当2k =时，()()2,14,2a b ==与 同向；当2k =-时，()()2,14,2a b =-=-与反向。

一、单选题二、多选题1. 两条平行线与的距离是（ ）A．B．C．D．2. 若函数（且）在区间上的最大值比最小值多2，则（ ）A ．2或B ．3或C ．4或D ．2或3. 已知复数（），则是的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4. 已知集合,则A．B．C．D．5.，使得的否定是（ ）A．，使得B ．，使得C ．，D ．，6. 函数的最小正周期是（ ）A．B ．C．D．7.如图，矩形中，，为边的中点，沿将折起，点折至处（平面），若为线段的中点，则在折起过程中，下列说法错误的是（）A．始终有 //平面B．不存在某个位置，使得平面C ．三棱锥体积的最大值是D ．一定存在某个位置，使得异面直线与所成角为8. 中国古代名词“刍童”原来是草堆的意思，关于“刍童”体积计算的描述，《九章算术》注曰：“倍上袤，下袤从之，亦倍下袤，上袤从之，各以其广乘之，并，以高乘之，皆六而一．”其计算方法是：将上底面的长乘二，与下底面的长相加，再与上底面的宽相乘，将下底面的长乘二，与上底面的长相加，再与下底面的宽相乘；把这两个数值相加，与高相乘，再取其六分之一.已知一个“刍童”的下底面是周长为18的矩形，上底面矩形的长为3，宽为2，“刍童”的高为3，则该“刍童”的体积的最大值为A．B．C ．39D．9.定义在上的函数满足，且.若，则下列说法正确的是（ ）A．为的一个周期B．C ．若，则D ．在上单调递增2024年广东省普通高中学业水平合格性考试数学模拟卷（四）三、填空题四、填空题五、填空题六、解答题七、解答题10. 关于函数，则（ ）A ．是的极大值点B ．函数有且只有1个零点C ．存在正实数，使得恒成立D．对任意两个正实数，，且，若，则11.已知等差数列的前项和为，，，且，则下列说法正确的是（ ）A．B ．使的最大值为8C．的最大值为20D ．的最大值为1812.的展开式中的系数是，则__________．13.已知函数是偶函数，则__________．14. 已知函数，将函数的图象向左平移个单位，得到函数的图象，则在上的单调递减区间为___________；15. 已知函数，则___________，的最大值是___________.16.已知数列的前项和为，且，记，则________；若数列满足，则的最小值是________．17. 直线与轴交于点，交圆于，两点，过点作圆的切线，轴上方的切点为，则__________；的面积为__________．18.如图，在多面体中，四边形为菱形，且∠ABC =60°，AE ⊥平面 ABCD ，AB =AE =2DF ，AE DF.(1)证明：平面AEC ⊥平面 CEF ；(2)求平面ABE 与平面CEF 夹角的余弦值.19. 如图，三棱柱ABC ﹣A 1B 1C 1的底面△ABC 是边长为2的等边三角形，平面AA 1B 1B ⊥平面ABC ，AB 1＝BB 1＝2.（1）过B 1作出三棱柱的一个截面，使AB 与截面垂直，并给出证明；（2）过C 作平面α//平面AB 1C 1，且平面α∩平面ACC 1A 1＝l ，求l 与平面BCC 1B 1所成角的正弦值.八、解答题九、解答题十、解答题20. 如图1，在五边形中，连接对角线，，，，将三角形沿折起，连接，得四棱锥（如图2），且为的中点，为的中点，点在线段上.(1)求证：平面平面；(2)若平面和平面的夹角的余弦值为，求线段的长.21. 某服装公司经过多年的发展，在全国布局了3500余家规模相当的销售门店.该公司每年都会设计生产春季新款服装并投放到各个门店销售.该公司为了了解2022年春季新款服装在某个片区的销售情况，市场部随机调查了该片区6个销售门店当年销售额（单位：万元，不考虑门店之间的其它差异），统计结果如下：门店编号123456年销售额283330404522(1)请用平均数，中位数分别估计2022年该公司的春季新款服装在这个片区的某个销售门店的年销售额；(2)从以上6个门店中随机抽取2个，求恰好有1个门店的该年销售额不低于40万元的概率.22.已知函数(1)求的最小正周期；(2)设为锐角三角形,角A 的对边长角B 的对边长若求的面积.。