19竞赛辅导-立体几何

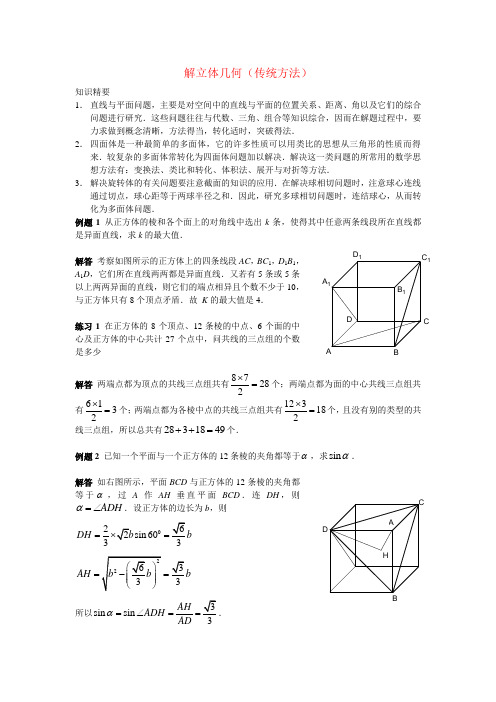
解立体几何（传统方法）知识精要1．直线与平面问题，主要是对空间中的直线与平面的位置关系、距离、角以及它们的综合问题进行研究．这些问题往往与代数、三角、组合等知识综合，因而在解题过程中，要力求做到概念清晰，方法得当，转化适时，突破得法．2．四面体是一种最简单的多面体，它的许多性质可以用类比的思想从三角形的性质而得来．较复杂的多面体常转化为四面体问题加以解决．解决这一类问题的所常用的数学思想方法有：变换法、类比和转化、体积法、展开与对折等方法．3．解决旋转体的有关问题要注意截面的知识的应用．在解决球相切问题时，注意球心连线通过切点，球心距等于两球半径之和．因此，研究多球相切问题时，连结球心，从而转化为多面体问题．例题1 从正方体的棱和各个面上的对角线中选出k条，使得其中任意两条线段所在直线都是异面直线，求k的最大值．解答考察如图所示的正方体上的四条线段AC，BC1，D1B1，A1D，它们所在直线两两都是异面直线．又若有5条或5条以上两两异面的直线，则它们的端点相异且个数不少于10，与正方体只有8个顶点矛盾．故K的最大值是4．练习1 在正方体的8个顶点、12条棱的中点、6个面的中心及正方体的中心共计27个点中，问共线的三点组的个数是多少解答两端点都为顶点的共线三点组共有87282⨯=个；两端点都为面的中心共线三点组共有6132⨯=个；两端点都为各棱中点的共线三点组共有123182⨯=个，且没有别的类型的共线三点组，所以总共有2831849++=个．例题2 已知一个平面与一个正方体的12条棱的夹角都等于α，求sinα．解答如右图所示，平面BCD与正方体的12条棱的夹角都等于α，过A作AH垂直平面BCD．连DH，则ADHα=∠．设正方体的边长为b，则2sin603DH==3AH==所以sin sin3AHADHADα=∠==．练习2 如图所示，正四面体ABCD 中，E 在棱AB 上，F 在棱CD 上，使得(0)AE CFEB FDλλ==<<+∞，记()f λλλαβ=+，其中λα表示E F 与AC 所成的角，λβ表示E F 与BD 所成的角，证明()0f λ'=，即()f λ为常数． 解答 因ABCD 是正四面体，故AC 垂直BD ，作EG 平行AC 交BC 于G ，连G F ，则GEF λα=∠，且CG AE CFGB FD FD==，所以G F 平行BD ．所以G F 垂直EG ，且EFG λβ=∠．所以()f λ为常数．例题3 三棱锥P -ABC 中，若棱P A =x ，其余棱长均为1，探讨x 是否有最值．解答当P -ABC 为三棱锥时，x 的最小极限是P 、A 重合，取值为0，若PBC ∆绕BC 顺时针旋转，P A 变大，最大极限是P 、A 、B 、C 共面时，P A 为菱形ABPC 的对角线，．所以无最值．练习3若正三棱锥底面棱长棱长均为1，探讨其侧棱否有最值．解答 若P 在底面的射影为O ,易知PO 越小，侧棱越小．故P 、O 重合时，侧棱取最小极限值3，PO 无穷大时，侧棱也无穷大．所以无最值． 例题4在单位正方体ABCD -A 1B 1C 1D 1的面对角线A 1B 上存在一点P 使得AP +D 1P 最短，求AP +D 1P 的最小值．解答 将等腰直角三角形AA 1B 沿A 1B 折起至1A A B '，使三角形1A A B '与四边形A 1BCD 1共面，联结1A D '，则1A D '的长即为AP +D 1P 的最小值，所以，1A D '==练习4已知单位正方体ABCD -A 1B 1C 1D 1的对棱BB 1、D 1上有两个动点E 、F ，BE =D 1F=λ（102λ<≤）．设E F 与AB 所成的角为α，与BC 所成的角为β，求αβ+的最小值． 解答 当12λ=时，2παβ+=．不难证明()f αβλ+=是单调减函数．因此αβ+的最小值为2π．例题5 在正n 棱锥中，求相邻两侧面所成的二面角的取值范围．解答 当顶点落在底面的时候，相邻两侧面所成的二面角为π．当顶点在无穷远处的时候，正n 棱锥变为正n 棱柱，这时相邻两侧面所成的二面角为(2)n nπ-．练习5 已知直平行六面体ABCD -A 1B 1C 1D 1的各条棱长均为3，角BAD =600，长为2的线段MN 的一个端点M 在DD 1上运动，另一端点N 在底面ABCD 上运动，求MN 的中点P 的轨迹（曲面）与共一顶点D 的三个面所围成的几何体的体积．解答 联结DP 、DN ，在三角形MDN 为直角三角形，且DP =MN /2=1，又由已知角BAD =600，角ADC =1200，所以点P 的轨迹以点D 为球心，半径为1的1/6球面，所以其与顶点D 以及三个面围成的几何体的体积为31421639ππ⨯⨯=．立体几何（向量方法）知识精要4． 证明两条直线平行，只需证明这两条直线上的向量共线（即成倍数关系）．证明两条直线平行，只需证明这两条直线上的向量的数量积等于零．5． 通过法向量，把线面、面面的角转化为线线的角．从而可以利用公式cos ||||θαβαβ=求解．6． 建立空间直角坐标系．例题1如图，在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝12PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ．(Ⅰ)求证OD ∥平面PAB ；(Ⅱ) 求直线OD 与平面PBC 所成角的大小． 解答OP ABC OA OC AB BC ⊥== 平面，，，.OA OB OA OP OB OP ∴⊥⊥⊥ ，，()O OP z O xyz -以为原点，射线为非负轴，建立空间直角坐标系如图，,0,0,,0,,0,0AB a A B C ⎫⎛⎫⎛⎫=⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭设，则 ()0,0,.OP h P h =设，则 ()D PC 为的中点，Ⅰ212,0,,,0,422OD a h PA a h ⎛⎫⎛⎫∴=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭又，1...2OD PA OD PA OD PAB ∴=-∴∴ 平面∥∥()2,PA a =Ⅱ,h ∴=,OD ⎛⎫∴=- ⎪ ⎪⎝⎭,PBC n ⎛=- ⎝可求得平面的法向量210cos ,OD n OD n OD n ⋅∴〈〉==⋅ OD PBC θ设与平面所成的角为，210sin cos ,OD n θ=〈〉=则 OD PBC ∴ 与平面所成的角为． 练习1如图，已知长方体1111ABCD A B C D -，12,1AB AA ==，直线BD 与平面11AA B B 所成的角为030，AE 垂直BD 于,E F 为11A B 的中点． （Ⅰ）求异面直线AE 与BF 所成的角；（Ⅱ）求平面BDF 与平面1AA B 所成二面角（锐角）的大小； （Ⅲ）求点A 到平面BDF 的距离解答 在长方体1111ABCD A B C D -中，以AB 所在直线为x 轴，AD 所在直线为y 轴，1AA 所在直线为z 轴建立空间直 角坐标系如图．由已知12,1AB AA ==，可得(0,0,0),(2,0,0),(1,0,1)A B F ．又AD ⊥平面11AAB B ，从面BD 与平面11AA B B 所成的角即为030DBA ∠=又2,,1,3ABAE BD AE AD =⊥==从而易得1(2E D （Ⅰ）13(,,0),(1,0,1)2AE BF ==-cos ,AE BF AEBF AE BF∴<>=14-==即异面直线AE 、BF 所成的角为4（Ⅱ）易知平面1AA B 的一个法向量(0,1,0)m =(,,)n x y z =是平面BDF 的一个法向1量．(BD =-由n BF n BD ⎧⊥⎪⎨⊥⎪⎩n BF n BD ⎧=⎪⇒⎨=⎪⎩203x x x y -+=⎧⎪⇒⎨-=⎪⎩x zy=⎧⎪⇒=取(1,3,1)n =∴3cos ,15m n m n m n <>===⨯即平面BDF 与平面1AA B 所成二面角（锐角）大小为（Ⅲ）点A 到平面BDF 的距离，即AB 在平面BDF 的法向量n 上的投影的绝对值所以距离||cos ,d AB AB n =<>||||||AB n AB ABn =||||55AB n n ===所以点A 到平面BDF 5例题2 如图1，已知ABCD 是上．下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴OO 1折成直二面角，如图2（Ⅰ）证明：AC ⊥BO 1；（Ⅱ）求二面角O －AC －O 1的大小．解答（I ）证明 由题设知OA ⊥OO 1，OB ⊥OO 1．所以∠AOB 是所折成的直二面角的平面角， 即OA ⊥OB ． 故可以O 为原点，OA 、OB 、OO 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，如图3，则相关各点的坐标是A （3，0，0），B （0，3，0），C （0，1，3）O 1（0，0，3）．从而.0333),3,3,0(),3,1,3(11=⋅+-=⋅-=-=BO BO 所以AC ⊥BO 1．（II ）解：因为,03331=⋅+-=⋅OC BO 所以BO 1⊥OC ，由（I ）AC ⊥BO 1，所以BO 1⊥平面OAC ，1BO 是平面OAC 的一个法向量．设),,(z y x =是0平面O 1AC 的一个法向图1量，由,3.0,033001=⎩⎨⎧==++-⇒⎪⎩⎪⎨⎧=⋅=⋅z y z y x C O n 取得)3,0,1(=n ． 设二面角O —AC —O 1的大小为θ，由、1BO 的方向可知=<θ，1BO >，所以COS <=cos θ，1BO .43||||1=⋅BO n 即二面角O —AC —O 1的大小是.43arccos练习2 如图, 在直三棱柱111ABC A B C -中，13,4,5,4AC BC AB AA ==== ，点D 为AB 的中点(Ⅰ)求证1AC BC ⊥； (Ⅱ) 求证11AC CDB 平面；(Ⅲ)求异面直线1AC 与1B C 所成角的余弦值解答∵直三棱锥111ABC A B C -底面三边长3,4,5A C B C A B ===，1,,AC BC CC 两两垂直如图建立坐标系，则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0),B 1(0,4,4),D (32,2,0) (Ⅰ)11(3,0,0),(0,4,4)AC BC =-=,11110,AC BC AC BC ∴⋅=∴⊥(Ⅱ)设1CB 与1C B 的交点为E ，则E (0,2,2)13(,0,2),(3,0,4)2DE AC =-=-111,//2DE AC DE AC ∴=∴111,,DE CDB AC CDB ⊂⊄平面平面1//AC CDB ∴平面(Ⅲ)11(3,0,4),(0,4,4),AC CB =-=1111112cos ,5||||AC CBAC CB AC CB ∴<>==∴异面直线1AC 与1B C 5例题3 在ΔABC 中，已知66cos ,364==B AB ，AC 边上的中线BD =5，求SINA ．1A解答 以B 为坐标原点，为x 轴正向建立直角坐标指法，且不妨设点A 位于第一象限由630sin =B，则44(cos ,sin )()3BA B B ==，设=（x ，0），则43(,6x BD +=，由条件得5)352()634(||22=++=x BD ，从而x=2，314-=x （舍去），故2(,33CA =-．于是 141439809498091698098||||cos =+⋅++-=⋅=CA BA A ∴1470cos 1sin 2=-=A A 练习3 在平面上给定ABC ∆，对于平面上的一点P ，建立如下的变换 :f AP 的中点为Q ，BQ 的中点为R ，CR 的中点为'P ，'()f P P =，求证 f 只有一个不动点（指P 与'P 重合的点）．解答：依提意，有12AQ AP =，且111()224AR AB AQ AB AP =+=+，'1111()2248AP AC AR AC AB AP =+=+++，要使'P 与P 重合，应111248AP AC AB AP =++，得1(42)7AP AC AB =+，对于给定的ABC ∆，满足条件的不动点P 只有一个．例题4 如图，在四棱锥P —ABCD 中，底面ABCD 为矩形，PD ⊥底面ABCD ，E 是AB 上一点，PE ⊥EC ． 已知,21,2,2===AE CD PD 求 （Ⅰ）异面直线PD 与EC 的距离； （Ⅱ）二面角E —PC —D 的大小．解答 （Ⅰ）以D 为原点，DA 、、DP 分别为x 、y 、z 轴建立空间直角坐标系．由已知可得D （0，0，0），P （0，0，)2， C （0，2，0）设),0,2,(),0)(0,0,(x B x x A 则>).0,23,(),2,21,(),0,21,(-=-=x x x E由0=⋅⊥CE PE 得，即.23,0432==-x x 故 由CE DE CE DE ⊥=-⋅=⋅得0)0,23,23()0,21,23(， 又PD ⊥DE ，故DE 是异面直线PD 与CE 的公垂线，易得1||=，故异面直线PD 、CE 的距离为1．（Ⅱ）作DG ⊥PC ，可设G （0，Y ，Z ）．由0=⋅得0)2,2,0(),,0(=-⋅z y ,即),2,1,0(,2==y z 故可取作EF ⊥PC 于F ，设F （0，M ，N ），则 ).,21,23(n m EF --= 由0212,0)2,2,0(),21,23(0=--=-⋅--=⋅n m n m PC EF 即得， 又由F 在PC 上得).22,21,23(,22,1,222-===+-=n m m n 故 因,,PC DG PC EF ⊥⊥故平面E —PC —D 的平面角θ的大小为向量与的夹角． 故,4,22||||cos πθθ===EF DG 即二面角E —PC —D 的大小为.4π练习4如图，在三棱柱ABC —A 1B 1C 1中，AB ⊥侧面BB 1C 1C ，E 为棱CC 1上异于C 、C 1的一点，EA ⊥EB 1，已知AB =2，BB 1=2，BC =1，∠BCC 1=3π，求： （Ⅰ）异面直线AB 与EB 1的距离；（Ⅱ）二面角A —EB 1—A 1的平面角的正切值．解答（I ）以B 为原点，1BB 、BA 分别为Y 、Z 轴建立空间直角坐标系． 由于BC =1，BB 1=2，AB =2，∠BCC 1=3π，在三棱柱ABC —A 1B 1C 1中有B （0，0，0），A （0，0，2），B 1（0，2，0），11)0,23,23(),0,21,23(1C C - 设即得由,0,),0,,23(11=⋅⊥EB EA EB EA a E )0,2,23()2,,23(0a a --⋅--=,432)2(432+-=-+=a a a a .,04343)02323()0,21,23()0,21,23(),(2321,0)23)(21(11EB BE EB BE E a a a a ⊥=+-=⋅⋅-⋅=⋅===--即故舍去或即得又AB ⊥面BCC 1B 1，故AB ⊥BE ． 因此BE 是异面直线AB 、EB 1的公垂线， 则14143||=+=BE ，故异面直线AB 、EB 1的距离为1． （II ）由已知有,,1111EB A B EB ⊥⊥故二面角A —EB 1—A 1的平面角θ的大小为向量A B 与11的夹角．.22tan ,32||||cos ),2,21,23(),2,0,0(111111===--===θθ即故因A B EA A B。

数学竞赛教案讲义-立体几何第一章：立体几何基础1.1 空间点、线、面的位置关系点、直线、平面的基本性质点与直线、直线与直线、直线与平面、平面与平面的位置关系1.2 立体几何的基本概念棱柱、棱锥、棱台、球的定义与性质底面、侧面、顶点的概念空间角、二面角的概念与计算第二章：空间几何图形2.1 棱柱直棱柱、斜棱柱的性质棱柱的面积、体积计算2.2 棱锥直棱锥、斜棱锥的性质棱锥的面积、体积计算2.3 棱台棱台的性质棱台的面积、体积计算2.4 球球的性质球的面积、体积计算第三章：立体几何中的线面关系3.1 直线与平面的关系直线与平面平行、直线在平面内的判定与性质直线与平面相交的性质3.2 直线与直线的关系平行线、相交线的性质异面直线、共面直线的性质3.3 平面与平面的关系平面与平面平行的判定与性质平面与平面相交的性质第四章：立体几何中的角与距离4.1 空间角线线角、线面角、面面角的定义与计算空间角的性质与计算方法4.2 距离点与点、点与直线、点与平面的距离计算直线与直线、直线与平面的距离计算第五章：立体几何的综合应用5.1 立体几何图形的放缩与旋转放缩与旋转的性质与方法放缩与旋转在立体几何中的应用5.2 立体几何中的定理与性质欧拉公式、施瓦茨公式等定理的应用立体几何中的重要性质与定理5.3 立体几何与解析几何的综合应用利用解析几何的知识解决立体几何问题立体几何与解析几何的相互转化第六章：立体几何中的立体角与对角线6.1 立体角立体角的定义与性质立体角的计算方法6.2 对角线多面体的对角线长度计算对角线与几何体的性质关系第七章：立体几何中的不等式与最值7.1 立体几何中的不等式利用立体几何图形性质证明不等式利用不等式解决立体几何问题7.2 立体几何中的最值问题利用几何方法求解最值问题利用代数方法求解最值问题第八章：立体几何中的视图与投影8.1 视图正视图、侧视图、俯视图的定义与性质利用视图研究几何体的性质8.2 投影平行投影、中心投影的性质利用投影解决立体几何问题第九章：立体几何中的定理与性质（续）9.1 立体几何中的定理与性质布雷特施奈德定理、莫恩定理等定理的应用立体几何中的其他重要性质与定理9.2 立体几何中的特殊几何体圆柱、圆锥、球台的性质与应用利用特殊几何体解决立体几何问题第十章：立体几何与实际应用10.1 立体几何在实际应用中的案例分析利用立体几何解决工程、物理、艺术等领域的问题立体几何在现实生活中的应用举例10.2 立体几何竞赛题解析分析历年数学竞赛中的立体几何题目讲解解题思路与方法，提高解题能力10.3 立体几何练习题与答案解析提供立体几何练习题，巩固所学知识分析练习题答案，讲解解题过程与思路第十一章：立体几何中的坐标计算11.1 空间点的坐标空间直角坐标系的建立点的坐标表示与运算11.2 空间向量向量的定义与运算向量与立体几何的关系11.3 空间几何体的坐标表示棱柱、棱锥、棱台、球的坐标表示利用坐标解决立体几何问题第十二章：立体几何中的向量计算12.1 向量的线性运算向量的加法、减法、数乘运算向量共线与垂直的判定与性质12.2 向量的数量积与向量积向量的数量积定义与性质向量的向量积定义与性质12.3 空间向量在立体几何中的应用利用向量计算空间角与距离利用向量解决立体几何中的线面关系问题第十三章：立体几何中的解析几何方法13.1 解析几何与立体几何的关系利用解析几何方法解决立体几何问题解析几何在立体几何中的应用举例13.2 参数方程与极坐标方程立体几何图形的参数方程表示利用参数方程与极坐标方程解决立体几何问题第十四章：立体几何中的不等式与最值（续）14.1 立体几何中的不等式问题利用不等式性质解决立体几何问题不等式在立体几何中的应用举例14.2 立体几何中的最值问题（续）利用几何方法求解最值问题利用代数方法求解最值问题第十五章：立体几何的综合与应用15.1 立体几何与其他数学学科的综合立体几何与代数、分析、概率等学科的关系立体几何在交叉学科中的应用15.2 立体几何在实际应用中的案例分析（续）立体几何在工程、物理、艺术等领域中的应用案例立体几何在其他领域中的应用举例15.3 立体几何竞赛题解析与练习题答案解析（续）分析历年数学竞赛中的立体几何题目讲解解题思路与方法，提高解题能力提供立体几何练习题，巩固所学知识分析练习题答案，讲解解题过程与思路重点和难点解析重点：理解并掌握立体几何的基本概念、立体几何图形、空间几何图形、立体几何中的线面关系、立体几何中的角与距离、立体几何中的立体角与对角线、立体几何中的不等式与最值、立体几何中的视图与投影、立体几何中的定理与性质、立体几何中的坐标计算、立体几何中的向量计算、立体几何中的解析几何方法、立体几何中的不等式与最值（续）、立体几何的综合与应用。

2021-2022年高中数学竞赛辅导资料《立体图形，空间向量》一. 直线,平面之间的平行与垂直的证明方法1．运用定义证明(有时要用反证法); 2．运用平行关系证明;3．运用垂直关系证明; 4．建立空间直角坐标系,运用空间向量证明.例如,在证明:直线直线时.可以这样考虑(1)运用定义证明直线与所成的角为; (2)运用三垂线定理或其逆定理; (3)运用“若平面,,则”; (4)运用“若且,则”; (5)建立空间直角坐标系,证明. 二. 空间中的角和距离的计算 1．求异面直线所成的角(1)(平移法)过P 作,,则与的夹角就是与的夹角; (2)证明(或),则与的夹角为(或);(3)求与所成的角(),再化为异面直线与所成的角(). 2,求直线与平面所成的角(1) (定义法)若直线在平面内的射影是直线,则与的夹角就是与的夹角; (2) 证明(或),则与的夹角为(或);(3) 求与的法向量所成的角,则与所成的角为或. 3．求二面角(1) (直接计算)在二面角的半平面内任取一点,过P 作AB 的垂线,交AB 于C,再过P 作的垂线,垂足为D,连结CD,则,故为所求的二面角. (2) (面积射影定理)设二面角的大小为(),平面内一个平面图形F 的面积为,F 在内的射影图形的面积为,则.(当为钝角时取“”).(3) (异面直线上两点的距离公式):22222cos EF d m n mn θ=++-,其中是二面角 的平面角,EA 在半平面内且于点A,BF 在半平面内且FB AB 于B,而,,.(4) (三面角的余弦定理),三面角中,,,,又二面角,则cos cos cos cos sin sin αβγθβγ-=.(5)(法向量法)平面的法向量与平面的法向量所成的角为,则所求的二面角为 (同类)或(异类). 4.求两点A,B 间距离(1)构造三角形进行计算; (2),导面直线上两点间的距离公式; (3),求. 5.求点到直线的距离(1)构造三角形进行计算; (2)转化为求两平行红色之间的距离. 6.求点到平面的距离(1)直接计算从点到平面所引垂线段的长度; (2)转化为求平行线面间的距离或平行平面间的距离; (3) (体积法)转化为求一个棱锥的高,其中V 为棱锥体积,S 为底面面积,为底面上的高.(4)在平面上取一点A,求与平面的法向量的夹角的余弦,则点P 到平面 的距离为.7.求异面直线的距离(1)(定义法)求异面直线公垂线段的长; (2)(体积法)转化为求几何体的高; (3)(转化法)转化为求平行线面间的距离或平行平面间的距离;(4)(最值法)构造异面直线上两点间距离的函数,然后求函数的最小值;(5)(射影法)如果两异面直线在同一平面内的射影分别是一个点P 和一条直线, 则与的距离等于P 到的距离; (6)(公式法)22222cos d EF m n mn θ=--±.8.求平行的线线,线面,面面之间的距离的方法,通常是转化为求点与线或点与面之间的距离. 三.多面体与旋转体 1.柱体(棱柱和圆柱)(1)侧面积(为直截面周长,为侧棱或母线长)(2)体积(为底面积,为高) 2.锥体(棱锥与圆锥)(1)正棱锥的侧面积(为底面周长,为斜高)(2)圆锥的侧面积: (为底面周长,为母线长)(3)锥体的体积:(为底面面积,为高). 3.锥体的平行于底面的截面性质:. 4.球的表面积:; 球的体积:. 四.解题思想与方法导引1.空间想象能力;2.数形结合能力;3.平几与立几间的相互转化;4.向量法例题讲解1．正四面体的内切球和外接球的半径之比为( )A,1:2 B,1:3 C,1:4 D,1:92．由曲线,,,围成的图形绕轴旋转一周所得的几何体的体积为;满足,,的点组成的图形绕 轴旋转一周所得的几何体的体积为,则( )A, B, C, D,3．如右图,底面半径,被过A,D 两点的倾斜平面所截,截面是离心 率为的椭圆,若圆柱母线截后最短处,则截面以下部分的 几何体体积是( )AB A BC A 1B 1C 1ABCD M K N S A, B, C, D,4．在四面体ABCD 中,设,,直线AB 与CD 的距离为2,夹角为,则四 面体ABCD 的体积等于( )A, B, C, D,5．三个圆柱侧面两两相切,且它们的轴也两两相互垂直,如果每个圆柱底面半径都是1, 那么,与这三个圆柱侧面都相切的最小球的半径是( ) A, B, C, D,6．四面体ABCD 的顶点为A,B,C,D,其6条棱的中点为,共10个 点,任取4个点,则这4个点不共面的概率是( )A, B, C, D,7．正方体的棱长为,则异面直线C 与BD 间的距离等于 .8．正四棱锥中,,二面角为且,(,为整数),则 .9．在正三棱锥中,,,过A 作平面分别交平面PBC 于DE.当截面的周长最小时, ,P 到截面ADE 的距离为 .10．空间四个球,它们的半径分别是2,2,3,3.每个球都与其他三个球外切.另一个小球与这 四个球都相切,则这个小球的半径等于 .11．三个的正方形都被连接两条邻边的中点的直线分成A,B 两片,如图,把这六片粘在一个正六边形的外面,然后折成多面体,则这个 多面体的体积为 .12．直三棱柱中,平面平面,且=,则AC 与平面所成的角的取值范围是 .13．如图,直三棱柱中,,连接,, ,若,求证:14．如图,设是一个高为3,底面边长为2的正四棱锥,K 是棱SC 的中点,过AK 作平面与线段SB,SD 分别交于M,N (M,N 可以是线段的端点).试求四棱锥的体积V 的最大值与最小值.AB DEF CDF15．有一个的长方体盒子,另有一个的长方体盒子,其中均为正整数(),并且前者的体积是后者一半,求的最大值.课后练习1．甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四 面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一 个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为,则以四个氢原子为顶点 的这个正四面体的体积为( )A, B, C, D,2．夹在两个平行平面之间的球,圆柱,圆锥在这两个平面上的射影都是圆,则它们的体积之 比为( )A,3:2:1 B,2:3:1 C,3:6:2 D,6:8:3 3．设二面角的大小是,P 是二面角内的一点,P 点到的距离分别为1cm, 2cm,则点P 到棱的距离是( )A, B, C, D,4．如图,E,F 分别是正三棱锥ABCD 的棱AB,BC 的中点,且DEEF.若BC=,则此正三棱锥的体积是( ) A, B, C, D,5．棱长为的正八面体的外接球的体积是( )A, B, C, D,6．若线段AB 的两端点到平面的距离都等于2,则线段AB 所在的直线和平面的位置关系是 .7．若异面直线所原角为,AB 是公垂线,E,F 分别是异面直线上到A,B 距离为 2和平共处的两点,当时,线段AB 的长为 . 8．如图(1),在直四棱柱中,当底面四边形满足条件时,有C(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)9．如图(2),是一个正方体的展开图,在原正方体中,有下列命题: ①AB 与EF 所连直线平行; ②AB 与CD 所在直线异面; ③MN 与BF 所在直线成; ④MN 与CD 所在直线互相垂直. 其中正确命题的序号为 .(将所有正确的都写出)A BCDA BC D图(1)A BENM 图(2)AB C D E OA A BCD PQ10．如图,在中,AB=AC=13,BC=10,DE//BC 分别交AB,AC 于D,E.将沿 DE 折起来使得A 到,且为的二面角,求到直线BC 的最小距离.11．如图,已知矩形ABCD 中,AB=1,BC=,PA 平面ABCD,且PA=1. (1)问BC 边上是否存在点Q 使得PQQD?并说明理由;(2)若边上有且只有一个点Q,使得PQQD,求这时二面角Q 的正切.课后习题答案1．过顶点A,V 与高作一截面交BC 于点M,点O 为正四面体的中心,为底面ABC 的中心, 设正四面体VABC 的棱长为,则AM==VM,=,,13VO m ==,得113OO VO VO m a =-=- 在中,,即222()()33a m a m =-+,得. 则,有203111(sin 60)3227V ABC V m VO -=⋅⋅⋅⋅=.选B. 温馨提示:正四面体外接球的半径:内切球的半径=. 2． 32212341::():(2):(2)2:3:133V V V R R R R R πππ=⋅⋅⋅=,选B. 3．设PA 棱于点A,PM 平面于点M,PN 平面于点N,PA=,,则,得,有或(舍去),所以,选B.4．由DEEF,EF//AC,有DEAC,又ACBD,DEBD=D,得AC 平面ABD. 由对称性得090BAC CAD BAD ∠=∠=∠=,于是.311()3222224B ACD V a a a -=⋅⋅⋅⋅=,选B.5．可由两个相同的四棱锥底面重合而成,有,得,外接球的体积,选D.6．当时,AB//;当时,AB//或AB;当时,AB//或与斜交. 7．由,得22222cos EFEA AB BF EA BF θ=+++⋅⋅(1)当时,有219412212AB =+++⋅⋅⋅,得; (2)当时,有219412212AB =++-⋅⋅⋅,得.8． ACBD.(或ABCD 是正方形或菱形等)9．将展开的平面图形还原为正方体,可得只②,④正确. 10．解:设的高AO 交DE 于点,令, 由AO=,有,在中,,有222011111112cos 60A O A O O O A O O O =+-⋅⋅⋅得.当时,到直线BC 的最小距离为6.11．解:(1)(如图)以A 为原点建立空间直角坐标系,设,则 Q,P(0,0,1),D 得,由,有,得 ①若方程①有解,必为正数解,且小于.由,,得. (i)当时,BC 上存在点Q,使PQQD; (ii)当时, BC 上不存在点Q,使PQQD.(2)要使BC 边上有且只有一个点Q,使PQQD,则方程①有两个相等的实根, 这时,,得,有.又平面APD 的法向量,设平面PQD 的法向量为 而,(0,2,0)(0,0,1)(0,2,1)PD =-=-, 由,得,解得有,则121212cos ,n n n n n n ⋅<>===⋅,则所以二面角的正切为.例题答案：1,B 设棱长为,外接球的半径为R,内切球的半径为,则222))33R a a R -=-ACDE A ’ P解得,,有:R=1:3.2,C 设,则过A 的两个截面都是圆环,面积分别是和222222212(){(4)[2(2)]}(44)x x a a a πππ-=----=-,于是.3,B 在椭圆中,又,得,所求的体积22111(12)22V πππ=⋅⋅+⋅⋅= 4,B 过C 作,以为底面,BC 为侧棱作棱柱,则所求四面体的体积等于上述棱柱体积的,而的面积1sin 2S CE CD ECD =⨯⨯∠,AB 与CD 的公垂线MN 就是棱柱的高,于是21sin 2V MN CE CD ECD =⨯⨯⨯∠=,因此.5,A 三个圆柱的轴为三条两两垂直的异面直线,而异面直线的距离都为2,则所求球的半径为 .6,D 441064106631414727070C C C ---==. 7, 设E 是上的点,过E 作EH 于H,所以EH 面ABCD,过H 在面ABCD内作HF,连接EF,所以EFBD,令,,,所以EF=3==≥.8,5 因各侧面为全等的等腰三角形.在内作高AE,则CE 也是的高,故.设则,,=02458sin 4(1cos 45)42=-=-222cos 32AE CE AC AE CEθ+-==-+⋅得.9, ; 将三棱锥的侧棱PA 剪开,当的周长最小时,其展开图如图 的周长即是展开图中线段的长.易证 ∽,又PA=2AB=,故, ,.中,DE上的高8AH a ==.于是21264ADE S AH DE ∆=⨯⨯=; 从P 向底面作高PO.则PO==.于是23133412P ABC V a a -=⋅⋅=. 又,得33991616A PDE A PBC V V --===.设P 到截面的距离BC DE F O ABCA 1B 1C 1 S HH 1 为,则31364A PDE P ADE ADE V V d S --∆==⋅=,于是. 10, 设半径为3的球心为A,B,半径为2的球心为C,D.则易知AB=6,CD=4,AC=AD=BC=BD=5.设小球中心为O,半径为,则O 在四面体ABCD 内且AO=BO=3+,CO=DO=2+.取AB 中点E,连结 CE,DE,则CEAB,DEAB,故平面CDE 为线段AB 的垂直平分面,所以O 在平面CDE 内,又由OC=OD=2+知O 在CD 的垂直平 分面内,故O 在等腰底边CD 上的高EF 上(F 为CD 中点),易算出ED=EC=,得为等边三角形.于是EF=.而==.OE===,代入OE+OF=EF=2=解得.11,864 将几何体补成一个棱长为12的正方体,几何体的体积为正方体体积的一半,为. 12, 作AD 于D,易证AD 平面,所以.设, ,则sin AD θ==⋅,故.易证BC 平面,故,从而,即,于是,, 又,得.13,证明:设D,分别为AB,的中点.连结CD,及,.因为,所以 四边形为平行四边形,得//.因AC=BC,于是.又D, 分别为 AB,的中点,故CDAB,,而在平面ABC(或)内的射影为AB (或),得CD,,又已知,所以平面B,从而 ,又//,所以.又,得平面CD,从而得证.14,解:为了建立V 与原四棱锥的关系.我们先引用 下面的事实:(如图)设分别在三棱锥的侧棱SA,SB,SC 上, 又与的体积分别是和V,则.事实上,设C,在平面SAB 的射影分别是H,.则,又,所以111111111313SA B SAB C H SV SA SB SC V SA SB SC CH S ∆∆⋅⋅⋅⋅==⋅⋅⋅⋅.下面回到原题. 设,,因的体积为.于是由上面的事实有012S AMN S KMN S AMK S ANK S ABD S CBD S ABC S ADC V V V V VV V V V V --------=+=+.得2V SM SN SA SM SN SK SB SD SA SB SD SC ⋅⋅⋅⋅=+⋅⋅⋅⋅= SM SK SA SN SK SASB SC SA SD SC SA⋅⋅⋅⋅+⋅⋅⋅⋅=,于是,而由,,得.则,().又得'2213(32)1(31)(31)x x V x x -=-=--.所以 (1)当时,,V 为减函数,(2)当时,,V 为增函数.所以得,又,得.15,解:由题意,2(2)(2)(2)mnp m n p =+++,得. (1)当时,由,则32222(1)(1)(1)(1)28m n p +++≤+<,矛盾! (2)当时,,矛盾!(3)当时,则,即.所以的最大值为130; (4)当时,则,即.所以的最大值为54; (5)当时,222(1)2222(1)(1)(1)(1)55p m n +=>++++,得. 综上所述:的最大值为130.33529 82F9 苹36655 8F2F 輯28533 6F75 潵32190 7DBE 綾LGi 36570 8EDA 軚P26023 65A7 斧22005 55F5 嗵27640 6BF8 毸241535E59 幙{。

数学竞赛教案讲义-立体几何教案章节：一、立体几何基本概念1.1 空间点、线、面的基本定义及性质1.2 平面、直线、圆锥、球等基本几何体的性质和方程1.3 空间向量与立体几何的关系二、立体几何中的角度和距离2.1 点与点、点与线、点与面之间的距离公式2.2 线与线、线与面之间的角度和距离公式2.3 空间中的平行公理和推论三、立体几何中的体积和表面积3.1 棱柱、棱锥、圆柱、圆锥等几何体的体积计算公式3.2 棱柱、棱锥、圆柱、圆锥等几何体的表面积计算公式3.3 空间几何体的对称性和轴截面四、立体几何中的定理和性质4.1 线面垂直、线面平行、面面垂直、面面平行等定理及其应用4.2 三垂线定理、射影定理等的重要性质和应用4.3 空间几何中的等体积转换和等角转换五、立体几何在数学竞赛中的应用题型及解题策略5.1 立体几何与解析几何的综合题型5.2 立体几何中的构造题型5.3 立体几何中的极限与最值问题5.4 立体几何中的几何计数问题六、立体几何中的坐标系和变换6.1 空间直角坐标系的定义和性质6.2 坐标变换公式及应用6.3 利用坐标系解决立体几何问题七、立体几何中的视图和投影7.1 平行投影和中心投影的定义和性质7.2 三视图的画法和性质7.3 利用视图和投影解决立体几何问题八、立体几何中的定积分和面积计算8.1 立体几何中的定积分定义和性质8.2 利用定积分计算立体几何体的表面积和体积8.3 立体几何中的面积计算方法和技巧九、立体几何中的概率和组合问题9.1 立体几何中的几何概率定义和性质9.2 利用几何概率解决立体几何问题9.3 立体几何中的组合问题和解题策略十、立体几何在数学竞赛中的应用实例解析10.1 立体几何与解析几何的综合实例解析10.2 立体几何中的构造实例解析10.3 立体几何中的极限与最值问题实例解析10.4 立体几何中的几何计数问题实例解析重点和难点解析一、立体几何基本概念重点和难点解析：空间点、线、面的关系及性质是立体几何的基础，理解并熟练运用这些基本概念对于解决复杂立体几何问题至关重要。

专题082立体几何问题第二季1．如图所示，已知面，于，，令，，则（）A．B．C．D．【答案】A【解析】因为PA⊥平面ABC，AD⊥BC于D，BC=CD=AD=1，设PD=x，所以，在△PBC中，根据余弦定理可得所以所以所以选A2．在△ABC中，已知, ,，D是边AC上的一点，将△ABC沿BD折叠，得到三棱锥ABCD，若该三棱锥的顶点A在底面BCD的射影M在线段BC上，设BM=x，则x的取值范围是（）A．B．C．D．【答案】C【解析】∵将沿折起，得到三棱锥，且点在底面的射影在线段上，∴在图2中，平面，、都与垂直因此，折叠前在图1中，，垂足为．在图1中过作于，运动点可得当点与点无限接近时，折痕接近，此时与点无限接近；在图2中，由于是的斜边，是直角边，所以．由此可得：，∵中，, ,，，∴，可得，由此可得中，，∴，由可得的取值范围为，故选C．3．在正方体ABCDA1B1C1D1中，三棱锥A1BC1D内切球的表面积为，则正方体外接球的体积为( ) A．B．36C．D．【答案】B【解析】设正方体的棱长为，则，因为三棱锥内切球的表面积为，所以三棱锥内切球的半径为1，设内切球的球心为，到面的距离为，则，，，又，，又因为正方体外接球直接就是正方体对角线长，正方体外接球的半径为，其体积为，故选B.4．在棱长为1的正方体中，为线段的中点，是棱上的动点，若点为线段上的动点，则的最小值为（）A．B．C．D．【答案】A【解析】图1连接,则，点在平面中，且，如图1所示，在中，以为轴，为轴，建立平面直角坐标系，如图2所示，图2,设点关于直线的对称点为，的方程为，①，直线的方程为，②由①②组成方程组，解得，直线与的交点，对称点，，最小值为到直线的距离为，故选A.5．如图，正方体的对角线上存在一动点，过点作垂直于平面的直线，与正方体表面相交于两点.设，的面积为，则当点由点运动到的中点时，函数的图象大致是（）A．B．C．D．【答案】D6．已知三棱锥，记二面角的平面角是，直线与平面所成的角是，直线与所成的角是，则（）A．B．C．D．【答案】A【解析】不妨设三棱锥是棱长为2的正四面体，取中点中点中点，连结，过作，交于，连结，则，，，，，，因为成立，故选A.7．已知矩形，，，将沿矩形的对角线所在的直线进行翻折，在翻折过程中，则（）．A．当时，存在某个位置，使得B．当时，存在某个位置，使得C．当时，存在某个位置，使得D．时，都不存在某个位置，使得【答案】C【解析】∵，∴若存在某个位置，使得直线，则平面，则，在中，，，则由直角边小于斜边可知，，即，结合选项可知只有选项中时，存在某个位置，使得，故选．8．如图所示，正方体的棱长为，动点在对角线上，过点作垂直于的平面，记这样得到的截面多边形（含三角形）的面积为，设，则当时，函数的值域为（）A．B．C．D．【答案】C当截面为正六边形的边长为，∴y max=6．∴当x∈[1，5]时，函数y=f（x）的值域为．故选：C．9．如图，在正方体中，点，分别为棱，的中点，点为上底面的中心，过，，三点的平面把正方体分为两部分，其中含的部分为，不含的部分为，连结和的任一点，设与平面所成角为，则的最大值为A．B．C．D．【答案】B【解析】连结.因为平面.所以过的平面与平面的交线一定是过点且与平行的直线.过点作交于点，交于点，则，连结，.则平行四边形即为截面.则五棱柱为，三棱柱为，设点为的任一点，过点作底面的垂线，垂足为，连结，则即为与平面所成的角，所以.学科_网因为，要使的正弦值最大，必须最大，最小，当点与点重合时符合题意.故.故选B.10．设点是棱长为2的正方体的棱的中点，点在面所在的平面内，若平面分别与平面和平面所成的锐二面角相等，则点到点的最短距离是（）A．B．C．1 D．【答案】A【解析】设在平面上的射影为在平面上的射影为，平面与平面和平面成的锐二面角分别为，则，，设到距离为，则，即点在与直线平行且与直线距离为的直线上，到的最短距离为，故答案为：A11．如图，在长方体中，，，而对角线上存在一点P，使得取得最小值，则此最小值为（）A．2 B．3 C．D．【答案】D12．在四面体中，，二面角的余弦值是，则该四面体外接球的表面积是（）A．B．C．D．【答案】C【解析】取中点，连接，，平面，为二面角，在中，，，取等边的中心，作平面，过作平面，（交于），因为二面角的余弦值是，，，点为四面体的外接球球心，其半径为，表面积为，故选C.13．已知三棱锥的四个顶点都在半径为3的球面上，，则该三棱锥体积的最大值是（）A．B．C．D．32【答案】B【解析】设，则，外接圆直径为，如图，体积最大值为，设，则，，令，得，在上递增，在上递减，，即该三棱锥体积的最大值是，故选B.14．如图，已知正方体的棱长为1，E为棱的中点，F为棱上的点，且满足，点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体在棱上的交点，则下列说法错误的是A．HF//BE B．C．∠MBN的余弦值为D．△MBN的面积是【答案】C【解析】因为面面，且面与面的交线为,面与面的交线为，所以正确；，且，，，在中，，正确；在中，为棱的中点，为棱上的中点，，在中，，，，在中，，错误；，，正确，故选C. 15．如图，在中，，，，是斜边的中点，将沿直线翻折，若在翻折过程中存在某个位置，使得，则的取值范围是（）A．B．C．D．【答案】D【解析】由题意得，，BC=x，取BC中点E，翻折前，在图1中，连接DE，CD，则，翻折后，在图2中，此时 CB⊥AD．∵BC⊥DE，BC⊥AD，∴BC⊥平面ADE，∴BC⊥AE，DE⊥BC，又BC⊥AE，E为BC中点，∴AB=AC=1，∴，在△ADE中：①，②，③x＞0；由①②③可得．如图3，翻折后，当△B1CD与△ACD在一个平面上，AD与B1C交于M，且AD⊥B1C，AD=B1D=CD=BD，∠CBD=∠BCD=∠B1CD，又∠CBD+∠BCD+∠B1CD=90°，∴∠CBD=∠BCD=∠B1CD=30°，∴∠A=60°，BC=ACtan60°，此时，综上，x的取值范围为.故选：D．16．如图，在三棱柱中，底面为边长为的正三角形，在底面的射影为中点且到底面的距离为，已知分别是线段与上的动点，记线段中点的轨迹为，则等于（）(注：表示的测度，本题中若分别为曲线、平面图形、空间几何体，分别对应为其长度、面积、体积）A．B．C．D．【答案】D【解析】当E位于B1（或A），而F在A1C上移动时，M的轨迹为平行于A1C的一条线段，当F位于A1（或C），而E在AB1上移动时，M的轨迹为平行与AB1的一条线段．其它情况下，M的轨迹构成图中平行四边形内部区域．设异面直线AB1与CA1所成角为θ，∴|L|=2×|AB1|•|CA1|•sinθ=|AB1|•|CA1|•sinθ．以O为原点，OB、OC、O为x轴，y轴，z轴建立空间坐标系，则∴∴,,∴|L|=故选：D17．如图1，直线将矩形纸分为两个直角梯形和，将梯形沿边翻折，如图2，在翻折的过程中（平面和平面不重合），下面说法正确的是图1 图2A．存在某一位置，使得平面B．存在某一位置，使得平面C．在翻折的过程中，平面恒成立D．在翻折的过程中，平面恒成立【答案】C【解析】学_科网由题意知与不平行，且在同一平面内.所以，与相交，所以与平面相交，故A错误.在任何位置都不垂直于，如果“存在某一位置，使得平面”，则存在某一位置，使得，两者矛盾，故B错误.在任何位置都不垂直于，如果“在翻折的过程中，平面恒成立”，那么恒成立，两者矛盾，故D错误.综上，选C.18．已知奇函数图象经过点，若矩形的顶点，在轴上，顶点，在函数的图象上，则矩形绕轴旋转而成的几何体的体积的最大值为（）A．B．C．D．【答案】D19．已知三棱锥的底面是以为斜边的等腰直角三角形，且，则该三棱锥的外接球的体积为( )A．B．C．D．【答案】D【解析】因为三棱锥的底面是以为斜边的等腰直角三角形，，所以S在ABC上的射影为AB中点H，所以平面，所以SH上任意一点到A,B,C的距离相等，因为，在面SHC内作SC的垂直平分线MO与SH交于O，则O为的外接球球心，所以，即，解得，学科_网所以该三棱锥的外接球的体积为，故选D.20．如图，在长方体ABCD﹣A1B1C1D1中，AB=1，BC=，点M在棱CC1上，且MD1⊥MA，则当△MAD1的面积最小时，棱CC1的长为（）A．B．C．2 D．【答案】A【解析】如图所示，建立空间直角坐标系，，设，，，即，，当且仅当时取等号，所以，故选A．学!科网。

专题083立体几何问题第三季1．已知的一边在平面内，，点在平面内的射影为点，则与的大小关系为（）A．B．C．D．以上情况都有可能【答案】D【解析】分情况讨论：（1）为锐角三角形时，当绕顺时针旋转时（起始位置为与重合），从变化到（平面平面时），故旋转过程中会有.（2）为钝角时，当绕顺时针旋转时（起始位置为与重合），从变化到（平面平面时），故旋转过程中会有.综上，应选D.2．在三棱锥ABCD中，AC＝BD＝3，AD＝BC＝4，AB＝CD＝m，则m的取值范围是（）A．(1，5) B．(1，7) C．(，7) D．(，5)【答案】D【解析】将三棱锥放置于长方体中，如图所示：3．如图，已知平面，，、是直线上的两点，、是平面内的两点，且，，，，．是平面上的一动点，且直线，与平面所成角相等，则二面角的余弦值的最小值是（）A．B．C．D．【答案】B【解析】，，，，同理为直线与平面所成的角，为直线与平面所成的角，又，在平面内，以为轴，以的中垂线为轴建立平面直角坐标系则，设，整理可得：在内的轨迹为为圆心，以为半径的上半圆平面平面，，为二面角的平面角，当与圆相切时，最大，取得最小值此时故选4．在正三棱锥(底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥)中，三条侧棱两两垂直，正三菱锥的内切球与三个侧面切点分别为,与底面切于点,则三棱锥与的体积之比为（）A．B．C．D．【答案】B【解析】如图，设正三棱锥的棱长为，内切球半径为，内切球的球心为，则有．又，∴，解得．把面单独拿出来分析，如图．学_科网故选B．5．已知三棱锥的四个顶点都在球的球面上，平面，是边长为2的等边三角形，若球的体积为，则直线与平面所成角的正切值为A．B．C．D．【答案】A【解析】设的中心为为的中点，过作，则为的中点，∴是直线与平面所成角．∵是边长为2的等边三角形，，．．故选：A．6．在三棱锥中，，点为所在平面内的动点，若与所成角为定值，，则动点的轨迹是A．圆B．椭圆C．双曲线D．抛物线【答案】B【解析】由题，三棱锥为正三棱锥，顶点在底面的射影是底面三角形的中心，则以为坐标原点，以为轴，以为轴，建立如图所示的空间直角坐标系，根据题意可得，设为平面内任一点，则，由题与所成角为定值，，则则，化简得，故动点的轨迹是椭圆.选B7．已知边长为的菱形，，沿对角线把折起，二面角的平面角是，则三棱锥的外接球的表面积是（）A．B．C．D．【答案】B【解析】如图所示，设菱形的对角线交于，由菱形的性质可得，二面角的平面角是因为菱形的边长为，，，设，则，由勾股定理可得，，即，解得，，四面体的外接球的表面积为，故选B.8．如图，矩形中，，是线段（不含点）上一动点，把沿折起得到，使得平面平面，分别记，与平面所成角为，平面与平面所成锐角为，则（）A．B．C．D．【答案】A【解析】如图，过作，在中，由，可得．由等积法可得，则∵平面平面，且，可得平面，则．过作，垂足为，连接，则为平面与平面所成的锐角．∵到的距离即．故选：A．9．已知两异面直线，所成的角为80°，过空间一点作直线，使得与，的夹角均为50°，那么这样的直线有（）条A．1 B．2 C．3 D．4【答案】C【解析】过作与平行的直线，如图，，直线过点且，这样的直线有两条.又，直线为的平分线，则，综上，满足条件的直线的条数为3.10．已知在矩形中，，沿直线折成，使得点在平面上的射影在内（不含边界），设二面角的大小为，直线与平面所成的角分别为，则（）A．B．C．D．【答案】D【解析】如图，∵四边形ABCD为矩形，∴BA′⊥A′D，当A′点在底面上的射影O落在BC上时，有平面A′BC⊥底面BCD，又DC⊥BC，可得DC⊥平面A′BC，则DC⊥BA′，∴BA′⊥平面A′DC，在Rt△BA′C中，设BA′=1，则BC=，∴A′C=1，说明O为BC的中点；当A′点在底面上的射影E落在BD上时，可知A′E⊥BD，11．已知正中，点为的中点，把沿折起，点的对应点为点，当三棱锥体积的最大值为时，三棱锥的外接球的体积为（）A．B．C．D．【答案】D【解析】设正三角形边长为，由于，当时，，三棱锥的外接球是以为棱的长方体的外接球，长方体的对角线等于球半径，即，，球体积，故选D.12．在棱长为1的正方体中，点分别是棱的中点，是侧面内一点，若∥平面，则线段长度的取值范围是( )A．B．C．D．【答案】B【解析】分别取棱BB1、B1C1的中点M、N，连接MN，∵M、N、E、F为所在棱的中点，∴MN∥BC1，EF∥BC1，∴MN∥EF.∵MN⊄平面AEF，EF⊂平面AEF，∴MN∥平面AEF.∵AA1∥NE，AA1=NE，∴四边形AENA1为平行四边形，∴A1N∥AE.∵A1N⊄平面AEF，AE⊂平面AEF，∴A1N∥平面AEF.∵A1N∩MN=N，∴平面A1MN∥平面AEF.∵P是侧面BCC1B1内一点，A1P∥平面AEF，∴P必在线段MN上.∵在Rt△A1B1M中，A1B1=1，，∴，同理可得在Rt△A1B1N中，∴△A1MN是等腰三角形.当P在MN中点O时A1P⊥MN，此时A1P最短，P位于M、N处时A1P最长. ∵在Rt△B1MN中，，∴.∵点O是MN中点，∴.∵在Rt△A1MO中，，∴.∵，∴线段A1P长度的取值范围是.本题选择B选项.13．在棱长为1的正方体中，分别是的中点．点在该正方体的表面上运动，则总能使与垂直的点所构成的轨迹的周长等于（）A．B．C．D．【答案】B【解析】如图：取的中点，的中点，连接，，，则平面设在平面中的射影为，过与平面平行的平面为能使与垂直的点所构成的轨迹为矩形，其周长与矩形的周长相等正方体的棱长为矩形的周长为故选14．已知三棱柱ABC﹣A1B1C1的六个顶点都在球O的球面上，且侧棱AA1⊥平面ABC，若AB=AC=3，，则球的表面积为（）A．36π B．64π C．100π D．104π【答案】C【解析】，，∴三角形的外接圆直径，，平面，，∴该三棱柱的外接球的半径，∴该三棱柱的外接球的表面积为，故选C．15．已知四棱锥的底面是正方形，侧棱长均相等，是线段上的点（不含端点）.设与所成的角为，与平面所成的角为，二面角的平面角为，则（）A．B．C．D．【答案】D16．如图，正四面体的顶点，，分别在两两垂直的三角射线，，上，则在下列命题中，错误．．的为（）．A．是正三棱锥B．C．直线与所成的角是D．直线平面【答案】D【解析】四面体为正四面体，且，，分别在两两垂直的射线，，上点均为正方体的顶点，如图所示.选项A，，，是正三棱锥，A正确.选项B，连接OE，易得，四边形为正方形，，则，B正确.选项C，四边形为正方形，，与直线与所成的角相等,易得，故C正确.选项D，延长BO至点，使，连接，，由题意易得，所以点四点共面，即点平面；又点直线，直线平面，D错误.故选D.学_科网17．在长方体中，底面是边长为的正方形，侧棱为矩形内部（含边界）一点，为中点，为空间任一点且，三棱锥的体积的最大值记为，则关于函数，下列结论确的是（）A．为奇函数B．在上不单调；C．D．【答案】D【解析】分析：根据Rt△ADP∽△Rt△PMC，PD=2PC，利用体积公式求解得出PO⊥CD，求解OP最值，根据勾股定理得出：3h2=3x2+48x144，0≤x≤6，利用函数求解即可详解：∵在长方体中，为中点，为矩形内部（含边界）一点，即，则在以为球心的球面上，而到面的距离为，则由此可知A,B,C选项都不正确，而.故选D.18．如图，在正方体中，点在线段上运动，则下列判断中不正确的是( )A．B．C．异面直线与所成角的范围是D．三棱锥的体积不变【答案】C当与线段的两点端点重合时，与所成角取最小值，当与线段的中点重合时，与所成角取最大值，故与所成角的范围是，错误，故选C.19．已知四面体的四个顶点都在半径为的球面上，是球的直径，且，则四面体的体积为（）A．B．C．D．【答案】B取AB中点为O，连接OD、OC，已知四面体的四个顶点都在半径为的球面上，是球的直径，且，OD=OC=OA=OB=BC=3，，，.已知四面体的四个顶点都在半径为的球面上，是球的直径，且，可设，，取BO中点为G，连接DG、OG，则，，则平面DCG，过D作，交CG于H，则平面ABC，，，四面体ABCD的体积.故选：B.20．已知三棱锥的所有顶点都在球的球面上，，，若三棱锥体积的最大值为2，则球的表面积为( )A．B．C．D．【答案】D因为，所以，过的中点作平面的垂下，则球心在上，设，球的半径为，则棱锥的高的最大值为，因为，所以，由勾股定理得，解得，所以球的表面积为，故选D．学!科网。

浙江省第19题立体几何强化训练（一）练习目标：1、掌握直线与平面的位置关系中的各个定理；2、掌握空间角的求法；3、掌握空间向量中的强建系方法。

练习重点：掌握证明题的书写格式。

【典型习题】1、如图，在四棱锥P-ABCD 中，AB//CD, PD ⊥DA, AD=DP=DC=CB=1, AB=2, CM ⊥PB, CM//平面PAD.(1) 求证：PB ⊥平面PAD ；(2) 求直线CM 与平面PDC 所成角的正弦值.2. 如图，四棱台ABCD −A 1B 1C 1D 1中，底面ABCD 是菱形，CC 1⊥底面ABCD ，且∠BAD =60°，CD =CC 1=2C 1D 1=4，E 是棱1BB 的中点.（1）求证：AA 1⊥BD ；（2）求直线AA 1与平面A 1EC 1所成线面角的正弦值.M A B D P C3、四棱锥P-ABCD 中，底面ABCD 是矩形，AD=2, AB=√32, △PAB 中PA=√3, PD=1, M ，N 分别是PA 、BC 的中点。

(1) 证明：MN//平面PCD;(2) 若PC=1, 求AC 与平面PBC 所成角的正弦值。

4、已知四棱锥P-ABCD 的底面为等腰梯形；BC//AD, PA=AD=2AB=2BC=2CD, ∠PAB=∠PAD=60°. (1) 求证：CD ⊥PA;(2) 点E 为PB 的中点，求直线CE 与平面PCD 所成角的余弦值。

AA【巩固练习】1. 如图，在四棱柱ABCD−A1B1C1D1中，AA1⊥平面ABCD，底面ABCD满足AD∥BC，且AB=AD=AA1=2，BD=DC=2√2．（1）求证：AB⊥平面ADD1A1；（2）求直线AB与平面B1CD1所成角的正弦值．2. 在三棱锥S−ABC中，∠BAC=∠SBA=∠SCA=90∘，∠SAB=45∘，∠SAC=60∘，D为棱AB的中点，SA=2．（1）证明：SD⊥BC；（2）求直线SD与平面SBC所成角的正弦值．3. 如图，已知四棱锥P−ABCD，BC∥AD，平面PAD⊥平面PBA，且DP=DB，AB= BP=PA=AD=2BC．（1）证明：AD⊥平面PBA；（2）求直线AB与平面CDP所成角的正弦值．4. 如图，四边形ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE与平面ABCD所成角为60∘．（1）求证：AC⊥平面BDE；（2）求二面角F−BE−D的余弦值；（3）设点M是线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．。

第十二章立体几何一、基础知识公理1 一条直线。

上假如有两个不一样旳点在平面。

内．则这条直线在这个平面内，记作：a a．公理2 两个平面假如有一种公共点，则有且只有一条通过这个点旳公共直线，即若P∈α∩β，则存在唯一旳直线m，使得α∩β=m,且P∈m。

公理3 过不在同一条直线上旳三个点有且只有一种平面。

即不共线旳三点确定一种平面．推论l 直线与直线外一点确定一种平面．推论2 两条相交直线确定一种平面．推论3 两条平行直线确定一种平面．公理4 在空间内，平行于同一直线旳两条直线平行．定义1 异面直线及成角：不一样在任何一种平面内旳两条直线叫做异面直线．过空间任意一点分别作两条异面直线旳平行线，这两条直线所成旳角中，不超过900旳角叫做两条异面直线成角．与两条异面直线都垂直相交旳直线叫做异面直线旳公垂线，公垂线夹在两条异面直线之间旳线段长度叫做两条异面直线之间旳距离．定义2 直线与平面旳位置关系有两种；直线在平面内和直线在平面外．直线与平面相交和直线与平面平行(直线与平面没有公共点叫做直线与平面平行)统称直线在平面外．定义3 直线与平面垂直：假如直线与平面内旳每一条直线都垂直，则直线与这个平面垂直．定理1 假如一条直线与平面内旳两条相交直线都垂直，则直线与平面垂直．定理2 两条直线垂直于同一种平面，则这两条直线平行．定理3 若两条平行线中旳一条与一种平面垂直，则另一条也和这个平面垂直．定理4 平面外一点到平面旳垂线段旳长度叫做点到平面旳距离，若一条直线与平面平行，则直线上每一点到平面旳距离都相等，这个距离叫做直线与平面旳距离．定义 5 一条直线与平面相交但不垂直旳直线叫做平面旳斜线．由斜线上每一点向平面引垂线，垂足叫这个点在平面上旳射影．所有这样旳射影在一条直线上，这条直线叫做斜线在平面内旳射影．斜线与它旳射影所成旳锐角叫做斜线与平面所成旳角．结论1 斜线与平面成角是斜线与平面内所有直线成角中最小旳角．定理4 (三垂线定理)若d为平面。