立体几何大题练习题答案
- 格式:docx
- 大小:126.97 KB
- 文档页数:7

立体几何试题一.选择题(每题4分,共40分)1.已知AB 0300300150空间,下列命题正确的个数为( )(1)有两组对边相等的四边形是平行四边形,(2)四边相等的四边形是菱形(3)平行于同一条直线的两条直线平行 ;(4)有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 4 3.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是( )A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作( ) A 1个 或2个 B 0个或1个 C 1个 D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是( )A 平行B 垂直相交C 异面D 相交但不垂直 7.经过平面α外一点和平面α内一点与平面α垂直的平面有( )A 0个B 1个C 无数个D 1个或无数个 8.下列条件中,能判断两个平面平行的是( ) A 一个平面内的一条直线平行于另一个平面; B 一个平面内的两条直线平行于另一个平面 C 一个平面内有无数条直线平行于另一个平面 D 一个平面内任何一条直线都平行于另一个平面 9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是( ) A //,,m n n m βα⊥⊂ B //,,m n n m βα⊥⊥ C ,,m n m n αβα⊥=⊂ D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有( ) A 1个 B 2个 C 3个 D 4个二.填空题(每题4分,共16分)11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N ,设直线AB 与平面α交于点O ,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题15(10分)如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =。

A BCDEFGH I J立体几何一、选择题1. 给出下列四个命题①垂直于同一直线的两条直线互相平行;②垂直于同一平面的两个平面互相平行;③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行;④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线。
其中假命题的个数是( ) A .1 B .2 C .3 D .4 2. 将正方形ABCD 沿对角线BD 折成一个120°的二面角,点C 到达点C 1,这时异面直线AD 与BC 1所成角的余弦值是( ) A .22B .21C .43D .43 3. 一个长方体一顶点的三个面的面积分别是2、3、6,这个长方体对角线的长为( )A .23B .32C .6D .64. 如图,在正三角形ABC 中,D 、E 、F 分别为各边的中点,G 、H 、I 、J 分别为AF 、AD 、BE 、DE 的中点.将△ABC 沿DE 、EF 、DF 折成三棱锥以后,GH 与IJ 所成角的度数为( ) A .90° B .60° C .45° D .0°5. 两相同的正四棱锥组成如图所示的几何体,可放棱长 为1的正方体内,使正四棱锥的底面ABCD 与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( ) A .1个 B .2个 C .3个 D .无穷多个6. 正方体A ′B ′C ′D ′—ABCD 的棱长为a ,EF 在AB 上滑动,且|EF |=b (b <a =,Q 点在D ′C ′上滑动,则四面体A ′—EFQ 的体积( ) A .与E 、F 位置有关 B .与Q 位置有关 C .与E 、F 、Q 位置都有关 D .与E 、F 、Q 位置均无关,是定值7. 三个两两垂直的平面,它们的三条交线交于一点O ,点P 到三个平面的距离比为1∶2∶3,PO=214,则P 到这三个平面的距离分别是( ) A .1,2,3 B .2,4,6 C .1,4,6 D .3,6,98. 如图,在四面体ABCD 中,截面AEF 经过四面体的内切球(与四个面都相切的球)球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A -BEFD 与三棱锥A -EFC 的表面积分别是S 1, S 2,则必有( ) A .S 1<S 2 B .S 1>S 2C .S 1=S 2D .S 1,S 2的大小关系不能确定 9. 条件甲:四棱锥的所有侧面都是全等三角形,条件乙:这个四棱锥是正四棱锥,则条件甲是条件乙的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件10. 已知棱锥的顶点为P ,P 在底面上的射影为O ,PO=a ,现用平行于底面的平面去截这个棱锥,截面交PO 于点M ,并使截得的两部分侧面积相等,设OM=b ,则a 与b 的关系是( )CC .b =222a- D .b =222a+ 11. 已知向量a =(2,4,x),b =(2,y ,2),若|a |=6,a ⊥b ,则x+y 的值是 ( )12. 一个长方体共一顶点的三个面的面积分别是6,3,2,这个长方体它的八个顶点都在同一个球面上,这个球的表面积是( )A.12πB. 18πC.36πD. 6π13. 已知某个几何体的三视图如下,图中标出的尺寸(单位:cm),则这个几何体的体积是( ) A .34000cm 3 B .38000cmC .32000cm D.34000cm14. 已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为 ( )A.1200B.1500 C.1800 D.240015. 在一个倒置的正三棱锥容器内,放入一个钢球,钢球恰好与棱锥的四个面都接触,经过棱锥的一条侧棱和高作截面,正确的截面图形是( )16. 正四棱柱ABCD –A 1B 1C 1D 1中,AB=3,BB 1=4.长为1的线段PQ 在棱AA 1上移动,长为3的线段MN 在棱CC 1上移动,点R 在棱BB 1上移动,则四棱锥R –PQMN 的体积是( ) A .6 B .10 C .12 D .不确定17. 已知三棱锥O -ABC 中,OA 、OB 、OC 两两互相垂直,OC =1,OA =x ,OB =y ,若x+y=4,则已知三棱锥O -ABC 体积的最大值是 ( )A.1B.13 C.23 D.318. 如图,在正四面体A -BCD 中,E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心,则△EFG 在该正四面体各个面上的射影所有可能的序号是 ( ) A .①③ B .②③④ C .③④ D .②④19. S,那么圆柱的体积等于 ( ) A.S 2S B.πS 2S C.S 4SD.πS 4S 20. 已知直线AB 、CD 是异面直线,AC ⊥AB ,AC ⊥CD ,BD ⊥CD ,且AB=2,CD=1,则异面直线AB 与CD 所成角的大小为 ( )A .300B .450C .600D .750(1,1,0)a = (1,0,2)b =- 正视图 侧视图 B A D C A BC DA 1B 1C 1D 1P Q R NM ① ② ③ ④A B C ∙∙∙EF GA B C DA 1B 1C 1D 1 αA A .1 B .51 C .53 D .57 22. 在四棱锥的四个侧面中,直角三角形最多可有 ( )A.4个B.2个C.3个D.1个23. 三棱锥A-BCD 中,AC ⊥BD ,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,则四边形EFGH 是( )A.菱形B.矩形C.梯形D.正方形24. 在正四面体P —ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不成立的是( )A.BC//平面PDFB.DF ⊥平面PAEC.平面PDF ⊥平面ABCD.平面PAE ⊥平面ABC25. 一棱锥被平行于底面的平面所截,若截面面积与底面面积的比为1:3,则此截面把一条侧棱分成的两线段之比为( )A.1:3B.1:2C.1: 3D.1: 3 —126. 正四面体P —ABC 中,M 为棱AB 的中点,则PA 与CM 所成角的余弦值为( )A. 3 2B. 3 6C. 3 4D. 3 327. 一个三棱锥S —ABC 的三条侧棱SA 、SB 、SC 两两互相垂直,且长度分别为1, 6 ,3已知该三棱锥的四个顶点都在一个球面上,则这个球的表面积为( ) A.16π B.32π C.36π D.64π28. 在棱长为a 的正方体ABCD —A1B1C1D1中,P 、Q 是对角线A 1C 上的点,PQ=a2,则三棱锥P —BDQ的体积为( ) A.318a 3 B.324a 3 C.336a 3 D.不确定 29. 若三棱锥P —ABC 的三条侧棱两两垂直,且满足PA=PB=PC=1,则P 到平面ABC 的距离为( )A. 6 6B. 6 3C. 3 6D. 3 330. 将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为( )A. 3 +2 6 3B.2+2 6 3C.4+ 2 6 3D.4 3 +2 6 331. PA 、PB 、PC 是从P 点出发的三条射线,每两条射线的夹角均为60°,那么直线PC 与平面PAB 所成角的余弦值是( ) A.12 B. 2 2 C. 3 3 D. 6 332. 正方体ABCD —A 1B 1C 1D 1中,任作平面α与对角线AC 1垂直,使得α与正方体的每个面都有公共点,设得到的截面多边形的面积为S ,周长为l ,则( ) A.S 为定值,l 不为定值 B.S 不为定值,l 为定值 C.S 与l 均为定值 D.S 与l 均不为定值二、填空题33. 若一条直线与一个正四棱柱各个面所成的角都为α,则cos α=______.34. 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A 在平面α内,其余顶点在α的同侧,正方体上与顶点A 相邻的三个顶点到α的距离分别为1,2和4,P 是正方体的其余四个顶点中的一个,则P 到平面α的距离可能是:( )①3; ②4; ③5; ④6; ⑤7以上结论正确的为______________.(写出所有正确结论的编号)35. 如图,已知正三棱柱111ABC ABC -的底面边长为1,高为8,一质点自A 点出发,沿着三棱柱的侧面绕行两周到达1A 点的最短路线的长为.36. 如图,表示一个正方体表面的一种展开图,图中的四条线段AB 、CD 、EF 和GH 在原正方体中相互异面的有_____对37. 如图是一个长方体ABCD-A 1B 1C 1D 1截去一个角后的 多面体的三视图,在这个多面体中,AB=4,BC=6, CC 1=3.则这个多面体的体积为 .38. 如图,已知正三棱柱ABC -A 1B 1C 1的所有棱长都相等D 是A 1C 1的 中点,则直线AD 与平面B 1DC 所成角的正弦值为_______ . 39. 如图,在直三棱柱ABC -A 1B 1C 1中,底面为直角三角形,∠ACB =90︒,AC =6,BC =CC 1,P是BC 1上一动点,则CP +PA 1的最小值是_________. 40. 已知平面α和平面β交于直线l ,P 是空间一点,PA ⊥α,垂足为A ,PB ⊥β,垂足为B ,且PA=1,PB=2,若点A 在β内的射影与点B 在α内的射影重合,则点P 到l 的距离为 ___________ .41. 若三角形内切圆半径为r ,三边长为a,b,c ,则三角形的面积S= 12r (a+b+c ) ,根据类比思想,若四面体内切球半径为R ,四个面的面积为S 1,S 2,S 3,S 4,则四面体的体积V=______________.42. 四面体ABCD 中,有如下命题:①若AC ⊥BD ,AB ⊥CD ,则AD ⊥BC ;②若E 、F 、G 分别是BC 、AB 、CD 的中点,则∠FEG 的大小等于异面直线AC 与BD 所成角的大小;③若点O 是四面体ABCD 外接球的球心,则O 在面ABD 上的射影为△ABD 的外心;④若四个面是全等的三角形,则ABCD 为正四面体 _ (填上所有正确命题的序号). 三、解答题43. 在长方体1111D C B A ABCD -中,已知3,41===DD DC DA ,求异面直线B A 1与C B 1所成角的大小(结果用反三角函数值表示).44. 如图,1l 、2l 是互相垂直的异面直线,MN 是它们的公垂线段。

PE BC9分立 体 几 何 大 题 专 练1、如图,已知PA ^矩形ABCD 所在平面,M N 分别为AB PC 的中点;(1) 26证明,1》取FD 的中点匚连AE.NE* 丁 W 是PC 的中点.・;NEX^CP r S' * S -F >又四边形ABCD 为矩带且XI 是tU 中工A 儿寺CD 星MA * (3):* ME 基MA,即四边形MAEN 是平行佃询 ................................ 41 A MN^AE . (5)』由于AEU 平面PAD’MNE 平面PAD, 二 MN"平面 PAD,.6’ (2)V PA 丄平面 ABCD,ZPDA-45%APAD 是尊腰三角常磁AE J PD 8* 由题蠹.CD 丄AD t CD 丄卩A* :.CD 丄平面 PAD. .■….io*从而AE 丄CD, ir :、AE 丄平面PCD,故 丄平面FVD . ...... 1FMN 严*⑴设■【:的方程为(x-aJ'+Cy-bP-?f2a4 b —0t P ABC E,F AC, BC EF // PAB PAC ABC PA PC ABC 90 PEF PBC EF Q E F AC BC EF // AB ............................ 2 分又EF 平面PAB , AB 平面PAB , EF//平面PAB .......................... 5 分(2) Q PA PC , E 为 AC 的中点, PE AC又Q 平面PAC 平面ABCPE 面 ABC又因为F为BC的中点,Q ABC 90°, BC EF ............................................ 10 分BC 面PEF .................................. 11 分又Q BC 面PBC面PBC 面PEF .................................. 12分3.如图,在直三棱柱ABC—ABQ中,AC=BC点D是AB的中点(1) 求证:BGPA 矩形ABCD所在的平面,M、N分别是AB、PCMN //平面PAD MN CD图,正方形ABCD所在的平面与三角形A D E所在平面互相垂直,AAEE是等腰直角三角形,且AE = E D段BC AE的中点分别为F、M,求证:(1) FM //平面ECD ; (2) 求二面角E-BD — A的正切值.(1)证明:取AD的中点N,连结FN,M“贝卩MIN/ ED,FN// CD•••平面FM/平面ECD.••• MF 在平面FMN内,••• FM //平面ECD ……5分(2)连接EN, T AE=ED N为AD的中点,••• EN 丄AD. 设线B F L又•••面 ADEL 面 ABCD 二 EN L 面 ABCD. 作 NP L BD,连接 EP,贝V EP L BD •••/ EPN 即二面角E-BD-A 的平面角,设AD=a,v ABCD 为正方形,/ ADE 为等腰三角形,二EN=1a,NP^2a.24••• tan / EPN=2 ........ 10 分7.如图,一个圆锥的底面半径为 2cm 高为6cm,其中有一个高为X cm 的内接圆23cm 时,它的侧面积最大为 6 cm ……10 分8. (10 分) ABC 中,/ PAB 是等边三角形,/ PAC W PBC=90 0.(1) 证明:AB 丄PC;(2) 若PC 4,且平面PAC 丄平面PBC ,求三棱锥P ABC 体积.解:(1)因为 PAB 是等边三角形, PAC PBC 90(1)试用X 表示圆柱的侧面积;(2)当X 为何值时,圆柱的侧面积最大•19. (1)解:设所求的圆柱的底面半径为 r'柱侧2 rx 2 (2x3 *x)x 4 x 3—x 2 .……5 3(2)由 (1)知当3时,这个二次函数有最大值为-6所以当圆柱的高为 如图,在三棱锥P所以Rt PBC Rt PAC ,可得AC BC。

第7章 立体几何习题练习9.1.11、判断题,下列语句说法正确的打“√”,错误的打“Χ”(1)一个平面长是4cm ,宽是2cm ( );(2)10个平面重叠在一起比5个平面重叠在一起要厚( );(3)一个平面将空间分成两部分( )。
2、选择题(每题只有一个正确答案)(1)以下命题中,正确的个数是( )①平面是没有边界且光滑的图形,②四条线段首首尾连接,所得图形一定是平面图形,③画两个相交平面时,一定要画出交线。
A .0 B .1 C .2 D .3(2)下列说法中,正确的是( )A .教室里的黑板面就是平面 B .过一条直线的平面只有1个C .一条线段在一个平面内,这条线段的延长线可以不在这个平面内D .平面是没有厚薄之分的3、如图,在长方体ABCD —A 1B 1C 1D 1中,请表示出该图形的6个平面(要求用各面的四个顶点来表示)参考答案:1、(1)Χ(2)Χ(3)√2、(1)C (2)D3、平面ABCD ,平面A 1B 1C 1D 1,平面ADD 1 A 1,平面BCC 1 B 1,平面ABB 1 A 1,平面D CC 1D 1练习9.1.21、选择题(每题只有一个正确答案)(1)下列说法中有错误的是( )①三个点可以确定一个平面,②若两个平面有一个公共点,则它们有无数多个公共点,③空间任意两条直线可以确定一个平面,④直线与直线外一点可以确定一个平面。
A .①② B .①③ C .②④ D .③④(2)下列图形中不一定是平面图形的是( )A .三角形 B .平行四边形 C .四条线段首尾连接而成的四边形 D .梯形(3)用符号表示语句“直线a ,b 相交于平面α内一点M”,正确的是( )A . B .,,a b M a b αα=⊆⊆ ,a b M M α=∈re go C . D .,,a b M a b ααα=∈ ØØ,,,M M a b a b ααα∈∈ ØØ2、用符号表示下列语句(1)点A 在直线a 上,直线a 在平面α内(2)平面β过直线b 及b 外一点M ,点N 在平面β外,直线c 过点M ,N 3、如图所示,对于长方体ABCD —A 1B 1C 1D 1,回答下列问题。

立体几何练习题及解答《立体几何练习题及解答》练习一:体积计算题目:一个正方体箱子的边长为3cm,请计算该正方体箱子的体积。
解答:正方体的体积计算公式为边长的立方,即V = a³,其中a为正方体的边长。
代入已知条件,正方体箱子的边长a = 3cm。
则体积V = 3³ = 27cm³。
所以该正方体箱子的体积为27cm³。
练习二:表面积计算题目:一个长方体的长为5cm,宽为3cm,高为4cm,请计算该长方体的表面积。
解答:长方体的表面积计算公式为2ab + 2bc + 2ac,其中a、b、c分别为长方体的三个边长。
代入已知条件,长方体的长a = 5cm,宽b = 3cm,高c = 4cm。
则表面积S = 2(5×3) + 2(3×4) + 2(5×4) = 30 + 24 + 40 = 94cm²。
所以该长方体的表面积为94cm²。
练习三:棱柱的体积计算题目:一个棱柱的底面为边长为5cm的正方形,高为8cm,请计算该棱柱的体积。
解答:棱柱的体积计算公式为底面积乘以高,即V = S × h,其中S为底面积,h为高度。
代入已知条件,棱柱的底面为正方形,边长a = 5cm,高度h = 8cm。
底面积S = a² = 5×5 = 25cm²。
则体积V = S × h = 25 × 8 = 200cm³。
所以该棱柱的体积为200cm³。
练习四:金字塔的体积计算题目:一个金字塔的底边是边长为6cm的正方形,高为10cm,请计算该金字塔的体积。
解答:金字塔的体积计算公式为底面积乘以高再除以3,即V = S ×h ÷ 3,其中S为底面积,h为高度。
代入已知条件,金字塔的底边为正方形,边长a = 6cm,高度h =10cm。
底面积S = a² = 6×6 = 36cm²。

高中数学立体几何高难度练习题及参考答案2023【题目1】已知立方体ABCDEFGH的棱长为a,M为AD的中点,N为BF的中点,P为MN的中点。
求证:四边形MNHP是一个矩形。
【解答1】根据题意,我们可以先求出MN的长度。
由于M为AD的中点,因此DM = a/2。
同理,BN = a/2。
根据勾股定理,可以得到三角形MND的斜边ND的长度:ND = √(MN² + DM²)= √(MN² + (a/2)²)根据三角形BNF的性质,可以得到BNF是一个等腰直角三角形,因此NF = BN = a/2。
同理,我们可以计算出FP的长度:FP = NF = a/2最后,我们可以比较四边形MNHP的对角线长度。
根据反证法,如果MNHP不是一个矩形,那么MN和HP的长度应该不相等,即MN ≠ HP。
假设MN > HP,即MN² > HP²由于HP = FP = a/2,我们可以得到:MN² > (a/2)²将MN²和(a/2)²的值代入,得到:(MN² + (a/2)²) > (a/2)²经过整理化简,可得:MN > a/2这与MN = a/2矛盾,因此假设成立。
同理,可以得出假设MN < HP亦不成立。
由以上推理可知,四边形MNHP是一个矩形。
证毕。
【题目2】在三棱柱ABC-A'B'C'中,已知AB = 3,BC = 4,CA = 5,且AA'垂直于平面ABCD。
求证:A'B'² = 4² + 3² + 5²。
【解答2】根据题意,我们可以利用勾股定理和垂直平面的性质来解答此题。
首先,考虑三角形ABC。
由已知条件可知,它是一个直角三角形,且AB = 3,BC = 4,CA = 5。

CBAC1B1A1高三立体几何习题一、填空题1.已知AB是球O的一条直径,点1O是AB上一点,若14OO=,平面α过点1O且垂直AB,截得圆1O,当圆1O的面积为9π时,则球O的表面积是.【答案】100p2.把一个大金属球表面涂漆,共需油漆2.4公斤.若把这个大金属球熔化制成64个大小都相同的小金属球,不计损耗,将这些小金属球表面都涂漆,需要用漆公斤.【答案】9.63.已知球的表面积为64π2cm,用一个平面截球,使截面圆的半径为2cm,则截面与球心的距离是cm【答案】234.一个圆锥与一个球体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为.【答案】4p5.一个底面置于水平面上的圆锥,若主视图是边长为2的正三角形,则圆锥的侧面积为.【答案】4p6.如图所示:在直三棱柱111ABC A B C-中,AB BC⊥,1AB BC BB==,则平面11A B C与平面ABC所成的二面角的大小为.【答案】4π二、选择题1.如图,已知圆锥的底面半径为10r=,点Q为半圆弧AB的中点,点P为母线SA的中点.若PQ与SO所成角为4π,则此圆锥的全面积与体积分别为()A.100051006,3ππB.10005100(16),3ππ+C.100031003,3ππD.10003100(13),3ππ+【答案】B2.如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么()A.S圆>S圆环 B.S圆<S圆环 C.S圆=S圆环 D.不确定3.如图所示,PAB∆所在平面α和四边形ABCD所在的平面β互相垂直,且ADα⊥,BCα⊥,4AD=,8BC=,6AB=,若tan2tan1ADP BCP∠-∠=,则动点P在平面α内的轨迹是()A.线段B.椭圆的一部分C.抛物线D.双曲线的一部分PSAQOBβαPBADC【答案】D4.在空间中,下列命题正确的是( )A .若两直线,a b 与直线l 所成的角相等,那么//a bB .空间不同的三点A 、B 、C 确定一个平面C. 如果直线//l 平面α且//l 平面β,那么//αβ D .若直线a 与平面M 没有公共点,则直线//a 平面M 【答案】D5.如图,已知直线l ⊥平面α,垂足为O ,在ABC △中,2,2,22BC AC AB ===,点P 是边AC 上的动点.该三角形在空间按以下条件作自由移动:(1)A l ∈,(2)C α∈.则OP PB +的最大值为( ) (A) 2. (B) 22. (C) 15+. (D) 10. 【答案】C6.平面α上存在不同的三点到平面β的距离相等且不为零,则平面α与平面β的位置关系为( ))(A 平行 )(B 相交)(C 平行或重合 )(D 平行或相交 【答案】D7.a b c 、、表示直线,α表示平面,下列命题正确的是( )A .若//,//αa b a ,则//αbB . 若,α⊥⊥a b b ,则α⊥aC .若,⊥⊥a c b c ,则//a bD .若,αα⊥⊥a b ,则//a b 【答案】D8.下列命题中,正确的个数是【 】① 直线上有两个点到平面的距离相等,则这条直线和这个平面平行; ② a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; ③ 直四棱柱是直平行六面体;④ 两相邻侧面所成角相等的棱锥是正棱锥.A 、0B 、1C 、2D 、3 【答案】B9.在四棱锥ABCD V -中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11CD AB 的体积与四棱锥 ABCD V -的体积之比为( )A .6:1B .5:1C .4:1D .3:1【答案】C三、解答题1.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)证明:11D E A D ⊥;(2)AE 等于何值时,二面角1D EC D --的大小为4π. 【答案】解:(1)在如图所示的空间直角坐标系中,11(1,0,1),(0,0,0),(0,0,1)A D D设(1,,0)([0,2])E y y ∈ 则11(1,,1),(1,0,1)D E y DA =-=…所以110D E DA ⋅=……所以11D E A D ⊥……(2)方法一:设(,,)n u v w =为平面1D CE 的一个法向量 D 1 C 1A 1AE D B 1B C Oxy zABl CαNPO由1100n CD n D E ⎧⋅=⎪⎨⋅=⎪⎩,得200v w u yv w -+=⎧⎨+-=⎩,所以(2)2u y vw v =-⎧⎨=⎩…因为二面角1D EC D --的大小为4π,所以2222(0,0,1)(,,)22cos||42(2)5u v w u v w y π⋅===++-+又[0,2]y ∈,所以23y =-,即当23AE =-时二面角1D EC D --的大小为4π2.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)当E 为AB 的中点时,求四面体1E ACD -的体积; (2)证明:11D E A D ⊥. 【答案】解:(1)1122ACE S AE BC ∆=⋅=…因为1D D ACE⊥平面,所以1111136E ACD D ACEACE V V S D D --∆==⋅=… (2)正方形11ADD A 中,11A D AD ⊥……因为11AB ADD A ⊥平面,所以1AB A D ⊥…所以11A D AD E ⊥平面…所以11D E A D ⊥……3.三棱柱111C B A ABC -中,它的体积是315,底面ABC ∆中,090=∠BAC ,3,4==AC AB ,1B 在底面的射影是D ,且D 为BC 的中点.(1)求侧棱1BB 与底面ABC 所成角的大小;(7分) (2)求异面直线D B 1与1CA 所成角的大小.(6分)【答案】解:(1)依题意,⊥D B 1面ABC ,BD B 1∠就是侧棱1BB 与底面ABC 所成的角θ 2分111111431532ABC A B C ABC V S B D B D -∆=⋅=⨯⨯⨯=4分1532B D =5分计算25=BD ,θθtan 25tan 1==BD D B , tan 3,3πθθ=∴= 7分 (2)取11C B 的中点E ,连E A EC 1,,则1ECA ∠(或其补角)为所求的异面直线的角的大小 9分 ⊥D B 1面ABC ,D B 1‖CE ,面ABC ‖面111C B A ⊥∴CE 面111C B A ,E A CE 1⊥∴ 11分33325tan 251===∠EC AE CE A 12分 所求异面直线D B 1与1CA 所成的角6π13分 D 1C 1A 1A EDB 1BC1A(第20题图)D 1C 1B 1BCDA 1A4.在如图所示的几何体中,四边形CDPQ 为矩形,四边形ABCD 为直角梯形,且90BAD ADC ∠=∠=,平面CDPQ ⊥平面ABCD ,112AB AD CD ===,2PD =.(1)若M 为PA 的中点,求证:AC //平面DMQ ;(2)求平面PAD 与平面PBC 所成的锐二面角的大小.【答案】解:(1)如图,设CP 与M 的交点为N ,连接MN .易知点N 是CP 的中点,又M 为PA 的中点,故//AC MN .…4分 于是,由MN ∉平面DMQ ,得//AC 平面DMQ .……………6分(2)如图,以点D 为原点,分别以DA DB DC 、、为x 轴,y 轴,z 轴,建立空间直角坐标系,则(0,0,0),(1,0,0),(1,1,0),(0,2,0),(0,0,2)D A B C P .易知1(0,1,0)n =为平面PAD 的一个法向量,设2(,,)n x y z =为平面PBC 的一个法向量. 则220220n BC x y n PC y z ⎧=-+=⎪⎨=-=⎪⎩2x yz y =⎧⎪⇒⎨=⎪⎩,令1y =,得2(1,1,2)n =.…………………10分 设平面PAD 与平面PBC 所成的锐二面角为θ,则12121cos 2n n n n θ==,…………………12分 故平面PAD 与平面PBC 所成的锐二面角的大小为3π.………………………………………14分5.(本题满分14分) 本题共2个小题,第1小题6分,第2小题8分. 在如图所示的直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为2的 菱形,且60,BAD ∠=︒1 4.AA =(1)求直四棱柱1111ABCD A B C D -的体积; (2)求异面直线11AD BA 与所成角的大小.【答案】解:(1)因菱形ABCD 的面积为2sin6023,AB ⋅︒= ……2分故直四棱柱1111ABCD A B C D -的体积为:12348 3.ABCD S AA ⋅=⨯=底面……6分(2)连接111BC A C 、,易知11//BC AD ,故11A BC ∠等于异面直线11AD BA 与所成角. ……8分由已知,可得111125,23,A B BC AC === ……10分 则在11A BC ∆中,由余弦定理,得222111111117cos .210A B BC AC A BC A B BC +-∠==⋅……12分 故异面直线11AD BA 与所成角的大小为7cos.10arc……14分 6.(本题满分12分)本题共2小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过11,,A C B 三点的平面截去长方体的一个角后,得到如下所示的几何体111ABCD AC D -.(1)若11A C 的中点为1O ,求求异面直线1BO 与11A D 所成角的大小(用反三角函数值表示); (2)求点D 到平面11A BC 的距离d .【答案】解:(1)按如图所示建立空间直角坐标系.由题知,可得点D(0,0,0)、(2,2,0)B 、1(0,0,3)D 、1(2,0,3)A 、1(0,2,3)C .ABCQP D M CD1A 1C 1D由1O 是11A C 中点,可得1(1,1,3)O . 于是,111(1,1,3),(2,0,0)BO A D =--=-. 设异面直线1BO 与11A D 所成的角为θ,则111111211cos 11||||211BO A D BO A D θ⋅===.因此,异面直线1BO 与11A D 所成的角为11arccos 11. (2)设(,,)nx y z =是平面ABD 的法向量. ∴110,0.n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩ 又11(0,2,3),(2,0,3)BA BC =-=-,∴230,230.y z x z -+=⎧⎨-+=⎩ 取2z =, 可得3,3,2.x y z =⎧⎪=⎨⎪=⎩即平面11BA C 的一个法向量是(3,3,2)n =. ∴||n DB d n ⋅=62211=. 7.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过1A 、1C 、B 三点的平面截去长方体的 一个角后,得到如下所示的几何体111ABCD AC D -.(1)求几何体111ABCD AC D -的体积,并画出该几何体的左视图(AB 平行主视图投影所在的平面); (2)求异面直线1BC 与11A D 所成角的大小(结果用反三角函数值表示). 【答案】解:2AB BC ==,13AA =,左视图如右图所示. (2)依据题意,有11,A D AD AD BC ,即11A D BC .∴1C BC ∠就是异面直线1BC 与11A D 所成的角. 又1C C BC ⊥,∴113tan 2C C C BC BC ∠==.∴异面直线1BC 与11A D 所成的角是3tan2arc . 8. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在直三棱柱111C B A ABC -中,已知21===AB BC AA ,AB ⊥BC . (1)求四棱锥111A BCC B -的体积; (2)求二面角111C C A B --的大小.【答案】解:(1)因为AB ⊥BC ,三棱柱111C B A ABC -是直三棱柱,所以11AB BCC B ⊥, 从而11A B 是四棱锥111A BCC B -的高. ……………………………………2分 四棱锥111A BCC B -的体积为1822233V =⨯⨯⨯=…………………………4分 (2)如图(图略),建立空间直角坐标系.则A (2,0,0),C (0,2,0),A 1(2,0,2),B 1(0,0,2),C 1(0,2,2), …………………………………………………6分 设AC 的中点为M ,,,1CC BM AC BM ⊥⊥)0,1,1(11=⊥∴BM C ,C A BM 即平面是平面A 1C 1C 的一个法向量.ABCD1A 1C 1D CBAC 1B 1A 1PSAQOB设平面A 1B 1C 的一个法向量是),,(z y x n =,)0,0,2(),2,2,2(11-=--=B A AC …8分 令z=1,解得x=0,y=1.)1,1,0(=∴n , …………………………………………9分 设法向量n 与BM 的夹角为ϕ,二面角B 1—A 1C —C 1的大小为θ,显然θ为锐角.111.3B AC C π∴--二面角的大小为………………………………………………12分9. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在正三棱柱111C B A ABC -中,已知16AA =, 三棱柱111C B A ABC -的体积为183. (1)求正三棱柱111C B A ABC -的表面积; (2)求异面直线1BC 与1AA 所成角的大小.【答案】解:(1)因为三棱柱的体积为183,16AA =,从而23334ABC S BC ∆==, 因此23BC =. ………………………2分 该三棱柱的表面积为2+=63+363423ABC S S S ∆=⋅=全侧. ………4分(2)由(1)可知23BC =因为1CC //1AA .所以1BC C ∠为异面直线1BC 与1AA 所成的角, ………8分 在Rt 1BC C ∆中,1233tan 63BC C ∠==, 所以1BC C ∠=6π. 异面直线1BC 与1AA 所成的角6π……………………………………………12分 10.如图,已知圆锥的底面半径为10r =,点Q 为半圆弧AB 的中点,点P 为母线SA 的中点.若直线PQ 与SO 所成的角为4π,求此圆锥的表面积.【答案】解:取OA 的中点M ,连接PM ,又点P 为母线SA 的中点 所以//PM OS ,故MPQ ∠为PQ 与SO 所成的角.………………………2分在Rt MPQ △中,4MPQ π∠=,PM QM =,………………………4分由点Q 为半圆弧AB 的中点知 OQ AB ⊥,在Rt MOQ △中,10,555OQ OM MQ ==⇒=故55PM =,所以105OS =,=106SA . ………………………8分 所以2S 100r ππ==底,101061006S r SA πππ=⋅=⨯⨯=侧………………10分1001006100(16)S S S πππ=+=+=+全底侧.…………………………………12分11.(本大题共有2个小题,满分14分)第(1)小题满分7分,第(2)小题满分7分. 如图,在四棱锥P ABCD -中,底面正方形ABCD 为边长为2,PA ⊥底面ABCD , E 为BC 的中点,PC 与平面PAD 所成的角为2arctan 2.(1)求异面直线AE 与PD 所成角的大小(结果用反三角函数表示); (2)求点B 到平面PCD 的距离.【答案】解:方法1,(1)因为底面ABCD 为边长为2的正方形,⊥PA 底面ABCD ,P S AQ O BMPABCD则 ⊥⇒⎪⎭⎪⎬⎫=⊥⊥CD A PA AD PA CD ADCD 平面PAD ,所以CPD ∠就是CP 与平面PAD 所成的角.………………2分在CDP Rt ∆中,由22tan ==∠PD CD CPD ,得22=PD ,…………………………3分 在PAD Rt ∆中,2=PA .分别取AD 、PA 的中点M 、N ,联结MC 、NC 、MN , 则NMC ∠异面直线AE 与PD 所成角或补角.……………4分 在MNC ∆中,2=MN ,5MC =,3NC =,由余弦定理得,()()22225310cos 10225NMC +-∠==-⋅, 所以10arccos10NMC π∠=-,………6分 即异面直线AE 与PD 所成角的大小为1010arccos .……7分(2)设点B 到平面PCD 的距离为h ,因为BCD P PCD B V V --=,…………………………9分 所以,11113232CD PD h BC CD PA ⨯⋅⋅=⨯⋅⋅,得2h =.……………………………14分 方法2,(1) 如图所示,建立空间直角坐标系,同方法1,得2=PA ,……………3分 则有关点的坐标分别为()0,0,0A ,()2,1,0E ,()0,2,0D ,()2,0,0P .………………5分 所以()2,1,0AE =,()2,2,0-=PD .设θ为异面直线AE 与PD 所成角, 则()101085202102cos =⨯-⨯+⨯+⨯=θ,所以,1010arccos =θ,即异面直线AE 与PD 所成角的大小为1010arccos.…………………………………7分 (2)因为()2,2,0-=PD ,()0,0,2=CD ,()0,2,0=BC ,设()w v u n ,,=, 则由⎩⎨⎧==⇒⎪⎩⎪⎨⎧==⋅=-=⋅w v u u CD n w v PD n 002022,………………………………………………11分 可得()1,1,0=n ,所以222n BC d n⋅===.……………………………………14分 12.(本题共有2个小题,满分14分);第(1)小题满分7分,第(2)小题满分7分.如图,在四棱锥ABCD P -中,底面ABCD 为边长为2的正方形,P ABCD EMNPAB CD Exyz PABCD⊥PA 底面ABCD , 2=PA .(1)求异面直线PC 与BD 所成角的大小; (2)求点A 到平面PBD 的距离.【答案】解:(1)联结AC 与BD 交于点M ,取PA 的中点N ,联结MN ,则CP MN //, 所以NMB ∠为异面直线PC 与BD 所成角或补角.……………………2分 在BMN ∆中,由已知条件得,5=BN ,2=BM ,3=MN ,…………5分所以222MN BM BN +=,2π=∠BMN ,所以异面直PC 与BD 所成角为2π.…7分 (或用线面垂直求异面直线PC 与BD 所成角的大小)(2)设点A 到平面PBD 的距离为h ,因为ABD P PBD A V V --=,……………9分所以,11113232BD PM h BC CD PA ⨯⋅⋅=⨯⋅⋅,得332=h .(或在MAN Rt ∆中求解)………14分 13.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点.(1)求直线BE 与平面11ABB A 所成的角的大小(结果用反三角函数值表示); (2)在棱11C D 上是否存在一点F ,使得1//B F 平面1A BE ,若存在,指明点F 的位置;若不存在,说明理由.【答案】解:(1)以A 为坐标原点,以射线1AB AD AA 、、分别为x y z 、、轴,建立空间 直角坐标系,如图所示.不妨设正方体1111ABCD A B C D -的棱长为a (0a >),则(,0,0),(0,,)2aB a E a ,于是(,,)2a BE a a =- 3分 根据正方体的性质,可知11DA ABB A ⊥平面,故11AD ABB A 是平面的一个法向量且AD =(0,,0)a 4分设直线BE 与平面11ABB A 所成的较为θ,则22sin 0332BE AD a BE ADa a θ===>⨯ 5分 所以2arcsin3θ=,故直线BE 与平面11ABB A 所成的角的大小为2arcsin 3. 6分(2)假设在棱11C D 上是存在一点F ,使得11//B F A BE 平面,设(,,)F x a a (其中0x a ≤≤)111(,0,0),(0,0,),(,0,),(,,0)B a A a BA a a B F x a a =-=- 8分根据(1)可知,(,,)2aBE a a =- 9分设(,,)n x y z =平面1A BE 的一个法向量,则100n BA n BE ⎧=⎪⎨=⎪⎩,即002ax az aax ay z -=⎧⎪⎨--=⎪⎩, 10分 取2z =,则(2,1,2)n =,由于直线11//B F A BE 平面,所以10B F n = 11分NPAB CDMBCDAO zxy即(,,0)(2,1,2)0x a a -=,化简得2()0x a a -+=,解得2ax = 12分 故在棱11C D 上是存在一点F ,使得11//B F A BE 平面,且点F 是棱11C D 的中点. 14分14.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点. 求直线BE 与11B A 所成的角的大小(结果用反三角函数值表示); 【答案】解:设正方体的棱长为a ,根据正方体的性质可得: 四棱锥E ABCD -的底面积2ABCD S a =,高2aED =2分21143323ABCD a V S ED a =⨯⨯=⨯=,解得2a = 5分因为11//AB A B ,所以ABE ∠即为异面直线BE 与11B A 所成角 或其补角, 8分在ABE 中,2,5,3AB AE BE ===,由余弦定理可得4952cos 02233ABE +-∠==>⨯⨯,即2arccos 3ABE ∠= 11分所以异面直线BE 与11B A 所成的较的大小为2arccos 3ABE ∠=. 12分15.(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分. 如图,在Rt AOB ∆中,6OAB π∠=,斜边4AB =,D 是AB 的中点.现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥,点C 为圆锥底面圆周上的一点,且2BOC π∠=.(1)求该圆锥的全面积;(2)求异面直线AO 与CD 所成角的大小.(结果用反三角函数值表示)【答案】解:(1)在Rt AOB ∆中,2OB =,即圆锥底面半径为2圆锥的侧面积8S rl ππ==侧………………..4’故圆锥的全面积=+8+412S S S πππ==全侧底……………….6’(2)解法一:如图建立空间直角坐标系.则(0,0,23),(2,0,0),(0,1,3)A C D(0,0,23),(2,1,3)AO CD ∴=-=-………………..8’设AO 与CD 所成角为θ,则66cos 42322AO CD AO CDθ⋅-===-⋅⋅………………..10’∴异面直线AO 与CD 所成角为6arc cos4………………..12’ 解法二:过D 作//DM AO 交BO 于M ,连CM则CDM ∠为异面直线AO 与CD 所成角………………..8’ 在Rt AOB ∆中,23AO = 3DM ∴= D Q 是AB 的中点 M ∴是OB 的中点 1OM ∴=5CM ∴=在Rt CDM ∆中,515tan 33CDM ∠==,………………..10’ ED 1C 1A 1B 1CDBA15arctan3CDM ∴∠=,即异面直线AO 与CD 所成角的大小为15arctan 3……………….12’ 16.在棱长为1的正方体1111ABCD A B C D -中,点E 是棱BC 的中点,点F 是棱CD 上的动点. (1)试确定点F 的位置,使得1D E ⊥平面1AB F ;(2)当1D E ⊥平面1AB F 时,求二面角1C EF A --的大小(结果用反三角函数表示). 【答案】解:(1)如图建系,设 ),10(≤≤=x x DF 1分则)0,1,()0,21,1()1,1,0()1,0,1(),0,1,0(),0,0,1(),0,0,0(11x F E D B D B A 2分)0,1,(),1,0,1(),1,21,1(11x AF AB E D ==--=∴, 3分1111,011AB E D AB E D ⊥∴=-=⋅ 4分 由AF E D F AB E D ⊥∴⊥111,平面 5分21,01=⇒=⋅∴x AF E D 6分)0,1,21(F ∴,即F 为CD 中点时F AB E D 11平面⊥。

立体几何练习题及答案立体几何练习题及答案立体几何是数学中的一个重要分支,它研究的是空间中的几何形体。
在我们的日常生活中,立体几何无处不在,比如建筑物、雕塑、家具等。
掌握立体几何的基本概念和解题方法,不仅可以提高我们的空间想象能力,还能帮助我们解决实际问题。
下面,我将给大家提供一些立体几何的练习题及答案,希望能对大家的学习有所帮助。
1. 题目:一个正方体的体积是64立方单位,求它的边长。
解答:设正方体的边长为a,则根据正方体的性质可知,它的体积等于边长的立方,即a³=64。
两边开立方根,得到a=4。
所以,这个正方体的边长是4个单位。
2. 题目:一个圆柱的底面半径为3cm,高为8cm,求它的体积和表面积。
解答:圆柱的体积公式为V=πr²h,其中r是底面半径,h是高。
代入已知条件,可得V=π×3²×8=72π。
所以,这个圆柱的体积是72π立方厘米。
圆柱的表面积公式为A=2πrh+2πr²。
代入已知条件,可得A=2π×3×8+2π×3²=48π+18π=66π。
所以,这个圆柱的表面积是66π平方厘米。
3. 题目:一个球的半径为5cm,求它的体积和表面积。
解答:球的体积公式为V=4/3πr³,其中r是半径。
代入已知条件,可得V=4/3π×5³=500/3π。
所以,这个球的体积是500/3π立方厘米。
球的表面积公式为A=4πr²。
代入已知条件,可得A=4π×5²=100π。
所以,这个球的表面积是100π平方厘米。
4. 题目:一个圆锥的底面半径为6cm,高为10cm,求它的体积和表面积。
解答:圆锥的体积公式为V=1/3πr²h,其中r是底面半径,h是高。
代入已知条件,可得V=1/3π×6²×10=120π。
所以,这个圆锥的体积是120π立方厘米。
高中立体几何典型500题及解析(一)1、二面角βα--l 是直二面角,βα∈∈B A ,,设直线AB 与βα、所成的角分别为∠1和∠2,则(A )∠1+∠2=900 (B )∠1+∠2≥900 (C )∠1+∠2≤900 (D )∠1+∠2<900 解析:C分别作两条与二面角的交线垂直的线,则∠1和∠2分别为直线AB 与平面,αβ所成的角。
根据最小角定理:斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤2. 下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共..面.的一个图是PPQQRSSPPPQQRR RSSSPP PQQQ R RS SS PP Q QR RRSS(A ) (B ) (C ) (D ) D解析: A 项:PS 底面对应的中线,中线平行QS ,PQRS 是个梯形B 项:如图C 项:是个平行四边形D 项:是异面直线。
3. 有三个平面α,β,γ,下列命题中正确的是(A )若α,β,γ两两相交,则有三条交线 (B )若α⊥β,α⊥γ,则β∥γ(C )若α⊥γ,β∩α=a ,β∩γ=b ,则a ⊥b (D )若α∥β,β∩γ=∅,则α∩γ=∅ D解析:A 项:如正方体的一个角,三个平面相交,只有一条交线。
B 项:如正方体的一个角,三个平面互相垂直,却两两相交。
C 项:如图4. 如图所示,在正方体ABCD -A 1B 1C 1D 1的侧面AB 1内有一动点P到直线AB 与直线B 1C 1的距离相等,则动点P 所在曲线的形状为1111C解析:11B C ⊥平面AB 111,B C PB ∴⊥,如图:点到定点B 的距离与到定直线AB 的距离相等,建立坐标系画图时可以以点B 1B 的中点为原点建立坐标系。
5. 在正方体ABCD -A 1B 1C 1D 1中与AD 1成600角的面对角线的条数是(A )4条 (B )6条 (C )8条 (D )10条C解析:如图这样的直线有4条,另外,这样的直线也有4条,共8条。
1.(本小题总分值14分)如图,在四棱锥 P ABCD 中,底面ABCD 是正方形,侧棱PD 底面ABCD, PD DC 1, E 是PC 的中点,作EF PB 交PB 于点F.(I)证实: PA //平面EDB; (II)证实:PB ,平面EFD; (III)求三棱锥P DEF 的体积.2 .(本小题总分值(m)求三棱锥(I )求证:B 118.(本小题总分值14分)如右图,在直角梯形ABCD中, B=90 °,1DC//AB,BC=CD= -AB=2 , G 为线段AB 的中点,将VADG 沿GD 2折起,使平面ADG 平面BCDG,得到几何体A-BCDG.(1)假设E,F分别为线段AC,AD的中点,求证:EF//平面ABG;(2)求证:AG 平面BCDG;(3)求V C-ABD 的值.4、(本小题总分值14分)如图4, AA是圆柱的母线, AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点, AA AB 2.(1)求证:BC 平面A〔AC ;(2)求三棱锥A ABC的体积的最大值.图4C (n ) 求证:EF 面PAC;〔出〕求三棱锥B-PAC的体积.6 .〔本小题总分值14分〕如图,平行四边形ABCD中,CD 1, BCD 60,且BD CD ,正方形ADEF 和平面ABCD成直二面角,G, H是DF , BE的中点.〔I〕求证:BD 平面CDE ;〔n〕求证:GH 〃平面CDE;〔出〕求三棱锥D CEF的体积.7.〔本小题总分值14分〕右图是一个直三棱柱〔以A i B i C i为底面〕被一平面所截得到的几何体,截面为ABC.A i B i = B i C i = l, ZAi B i C i = 90 ,AA i = 4,BB i=2, CC i=3.(I)设点O是AB的中点,证实:OC//平面A i B i C i;(II)求此几何体的体积.8 .(本小题总分值i4分)如图,在正方体ABCD—A i B i C i D i中,E、F为棱AD、AB的中点.(i )求证:EF//平面CB i D i;(2)求证:平面CAA i C■平面CB i D i.9 .(本小题总分值i4分)如图i ,在直角梯形ABEF中(图中数字表示线段的长度),将直角梯形DCEF沿CD折起,使平面DCEF 平面ABCD,连结局部线段后围成一个空间几何体,如图2.(I)求证:BE〃平面ADF ;(n)求三棱锥F BCE的体积.图图-10 .(本小题总分值14分)在直三棱柱ABC ABG中,AD 平面ABC,其垂足D落在直线A〔B上.(I )求证:BC A1B ;(n)假设AD J3, AB BC 2, P为AC的中点,求三棱锥P ABC的体积.B1…1 .解:(1)证实:连结AC, AC交BD于O,连结EO••・底面ABCD是正方形,,点O是AC的中点在PAC中,EO是中位线,,PA // EO而EO 平面EDB且PA 平面EDB,所以,PA //平面EDB.(2)证实:PD,底面ABCD 且DC 底面ABCD,,PD DCPD=DC,可知PDC是等腰直角三角形,而DE是斜边PC的中线,.DE PC ①同样由PD,底面ABCD,得PDXBC•••底面ABCD是正方形,有DCXBC,,BC,平面PDC 而DE 平面PDC, BC DE ②由①和②推得DE 平面PBC而PB 平面PBC, . DE PB又EF PB 且DE EF E,所以PB ,平面EFD................................ 8分(3) . PD DC 1,由 PD ,平面 ABCD,PDXBC,又.BCXCD, PDACD = D,BC± PC.-CL 2f在Z^BDE 中,DE -------- , BD22221 DE2 BE 2 BD 2 — 2 而由(2), PB,平面EFD,••.BC,平面 PCD,3 c-一 2 0,即 DEL BE.2PBXDE,因而 DEL 平面 BEF,2在 RtABPD 中,BF BP BD , BF1 1 . V DE EF PF 32 2.解:(I)证实:连结 BD ,那么 BD // B 1D 1,ABCD 是正方形,,AC BD. CE 面 ABCD,,CE BD .又 A .CE C, BD 面 ACE. . AE 面 ACE, . . BD AE ,• .B 1D 1 AE .(n)证实:作BB 1的中点F,连结AF 、CF 、EF.• •・E 、F 是 CC 、BB 1 的中点,,CE?B 1F , • •・四边形B 〔FCE 是平行四边形,, CF// B 1E .E,F 是 CC 、BB 1 的中点,,EF//BC ,又 BC//AD , EF //AD ...............14分136;Rt 革EFEF. AF I CF C , B 1EI ED E ,,平面 ACF 〃面 B 1DE .又 AC 平面 ACF , . . AC 〃面 B 1DE .4证实:二.是底面圆周上异于 A, B 的任意 柱底面圆的直径, •••BCXAC,……2 分,.AA1,平面 ABC , BC i 平面 ABC, . AAiXBC,…… 4 分•.AA i AAC=A , AA 1 i 平面 AA i C, AC i 平面 AA1 C, . EC ,平面AA1C.……6分 (2)解法 1 :设 AC=x ,在 RtMBC 中,BC = J AB 2 AC 2 h x 2(o<x<2),……7 分....1 一 … 1 11 -~~2故 V ARABC = —S VABC AA 1— — AC BC AA 1 _x \ 4x (0<x<2),13 3 23即 V A 「ABC =4“ x 2 1 \/x 2 (4 x 2):J (x 2~2)2~4 . ……11 分 23 33,-0<x<2 , 0<x 2<4 ,「.当 x 2=2,即 x = 五时, 三棱锥A 1-ABC 的体积的最大值为 -.……14分35(1)证实:在三角形 PBC 中,E 是PC 中点.F 为PB 中点所以 EF//BC , BC 面ABC, EF 面ABC, 所以 EF 〃面ABC ……4分,四边形ADEF 是平行四边形,AF // ED ,(3)S ABD - AB AD 2 •2VA BDE VE ABD1S ~ SABDCE1S3 SABDCE2 3又AB 是.O 的直径,所以BC AC …… ⑵ ……7分 由(1) (2)得 BC 面PAC 因EF//BC BC 面PAC ,所以EF 面PAC ……9分(出)因PA OO 所在的平面,AC 是PC 在面ABC 内的射影,1V B PACV P ABC S ABC PA37 . (1)证实:作OD //.交片81于口,连C 1D .那么 OD // BB 1 // CC 1 .作BH(n) PA BC面ABC 面ABCBC PA所成角 PCA 450,PA=AC11分在Rt ABC 中,E 是PC 中点,BAC -, AC BC 2412分Q O 是AB 的中点,OD1-(AA 1 BB 1) 3 CC 1 .2那么ODCQ 是平行四边形,OC // C 1D .……4分Q C 1D 平面 C 1B 1A 且 OC 平面C1B1A ,OC // 面 A 1B 1C 1.(2)如图,过B 作截面BA 2c 2CC 1 于 A 2,//面ABG,分别交AA1,Q CC 1 面 BA 2c 2, CC 1BH ,那么BH 平面AC .又Q A 2B AB 1 1 , BC 2B 1c l 1 , BH --, 2V B AA 2C 2C1 S A A 2c 2c3BH 1 1 厂J.21 (1 2) '2 -3 2 22PCA 即为PC 与面ABC'.2----- …14分3所求几何体体积为:V V B AACC . 八八 2 J 2 J8 .〔本小题总分值14分〕折叠之后平行关系不变. BC 平面ADF , AD 平面 • .BC//平面 ADF ,V AB|C 1 A2BC 21八, SA A 1B 1C 1BB 1 - 2 1〔1〕证实:连结 BD .在长方体AC i 中, 对角线BD//B 1D 1. 又Q E 、F 为棱AD 、AB 的中点, ・.EF //BD . . .EF //BD 1. 又 B 1D 1 平面 CBD 1, EF 平面 CB 1D 1,,EF//平面 CB 1D 1. (2) Q 在长方体 AC [中,AA 1,平面 A 1B 1C 1D 1,而 B 1D 1 平面 A 1B 1C 1D 1, . AA iX B i D i . 又Q 在正方形 A 1B 1C 1D 1 中,A 1C 1 XB 1D 1, .. B 1D 1,平面 CAA 1C 1. 又Q B 1D 1 平面 CB 1D 1,,平面 CAA 1C 1,平面 CB 〔D 1. 14分9 .〔本小题总分值14分〕 证实:〔I 〕证法一:取 DF 中点为G,连结AG, EG 中, 八 1一 八 一八.CE — DF ,,EG 〃CD 且 EG CD 2 又•••AB 〃CD 且AB CD,,EG 〃AB 且 EG AB四边形ABEG 为平行四边形,,BE//AG. BE 平面ADF , AG 平面 ADF,. ・BE 〃平面 ADF ,证法二:由图1可知BC // AD , CE//DFV A 1B 1C 1 A 2BC 2同理CE〃平面ADF ................... 4分. BCI CE C , BC , CE 平面BCE ,,平面BCE 〃平面ADF ......... 6分. BE 平面BCE ,,BE 〃平面ADF ......... 7 分(II)解法1:V F BCE V B CEF .................... 8分由图1可知BC CD.平面DCEF 平面ABCD ,平面DCEF I平面ABCD CDBC 平面ABCD,..BC 平面DCEF ,1 1由图 1 可知DC CE 1 S CEF -CE DC .................. ........... 12 分2 2V F BCE V B CEF 3 BC S CEF解法2:由图1可知CD BC , CD CEBCI CE C. .CD 平面BCE ,. DF //DC点F到平面BCE的距离等于点D到平面BCE的距离为1 ,由图1可知BC CE 1 S BCE 1-BC CE 2BCE 1 … c 13 CD S BCE 6解法3:过E作EH FC ,垂足为H , ....................... 8分由图1可知BC CD•••平面DCEF 平面ABCD,平面DCEFI 平面ABCD CD11分A B11分BC 平面 ABCD,. BC 平面 DCEF ,EH 平面 DCEF.BC EH,EH 平面BCF 1 、5S BCF -BC DF —, .......... 12 分 2 2又 BD CD. .BD ¥® CDE(n )证实:连结 EA ,那么G 是AE 的中点••• EAB 中,GH // AB又 AB//CD . GH //CD . .GH 〃平面CDE 11分 由 BC FC , FC .DC 2 DF 2 5, 在 CEF 中,由等面积法可得 EHV F BCE V E BCF EH S BCF13分 14分 6.(本小题总分值14分)(I )证实:平面 ADEF 平面ABCD ,交线为ADED AD• .ED 平面ABCDED BD2〔出〕解:设Rt BCD中BC边上的高为h1 1 -依题意:一2 h 1 32 23• • h —2_ ___ _____ .. 一、. .3即:点C到平面DEF的距离为- ---------------- 10•V D CEF V C DEF .32,33分------- 14 分。

立体几何基础A 组题一、选择题:1.下列命题中正确命题的个数是 ( ) ⑴ 三点确定一个平面⑵ 若点P 不在平面α内,A 、B 、C 三点都在平面α内,则P 、A 、B 、C 四点不在同一平面内 ⑶ 两两相交的三条直线在同一平面内⑷ 两组对边分别相等的四边形是平行四边形A.0B.1C.2D.3答案:A2.已知异面直线a 和b 所成的角为︒50,P 为空间一定点,则过点P 且与a 、b 所成的角都是︒30的直线条数有且仅有 ( ) A.1条 B.2条 C.3条 D.4条答案:B 3.已知直线⊥l 平面α,直线⊂m 平面β,下列四个命题中正确的是 ( ) (1) 若βα//,则m l ⊥ (2) 若βα⊥,则m l // (3) 若m l //,则βα⊥ (4) 若 m l ⊥,则βα//A.(3)与(4)B.(1)与(3)C.(2)与(4)D.(1)与(2)答案:B4.已知m 、n 为异面直线,⊂m 平面α,⊂n 平面β,l =βα ,则l ( ) A.与m 、n 都相交 B.与m 、n 中至少一条相交 C.与m 、n 都不相交 D.至多与m 、n 中的一条相交答案:B5.设集合A={直线},B={平面},B A C =,若A a ∈,B b ∈,C c ∈,则下列命题中的真命题是 ( )A. c a b a b c ⊥⇒⎭⎬⎫⊥// B.c a c b b a //⇒⎭⎬⎫⊥⊥ C.c a b c b a //////⇒⎭⎬⎫ D. c a b c b a ⊥⇒⎭⎬⎫⊥//答案:A6.已知a 、b 为异面直线,点A 、B 在直线a 上,点C 、D 在直线b 上,且AC=AD ,BC=BD ,则直线a 、b 所成的角为 ( ) A. ︒90 B. ︒60 C. ︒45 D. ︒30答案:A7.下列四个命题中正确命题的个数是 ( ) 有四个相邻侧面互相垂直的棱柱是直棱柱 各侧面都是正方形的四棱柱是正方体底面是正三角形,各侧面都是等腰三角形的三棱锥是正三棱锥A.1个B.2个C.3个D.0个答案:D8.设M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},则这些集合之间关系是 ( ) A.Q M N P B.Q M N P C.Q N M P D.Q N M P答案:B9.正四棱锥P —ABCD 中,高PO 的长是底面长的21,且它的体积等于334cm ,则棱AB 与侧面PCD 之间的距离是 ( ) A.cm 2 B. cm 2 C. cm 1 D.cm 22答案:A10.纬度为α的纬圈上有A 、B 两点,弧在纬圈上,弧AB 的长为απcos R (R 为球半径),则A 、B 两点间的球面距离为 ( )A. R πB. R )(απ-C. R )2(απ-D. R )2(απ-答案:D11.长方体三边的和为14,对角线长为8,那么 ( ) A.它的全面积是66 B.它的全面积是132C.它的全面积不能确定D.这样的长方体不存在答案:D12.正四棱锥P —ABCD 的所有棱长都相等,E 为PC 的中点,那么异面直线BE 与PA 所成角的余弦值等于( )A.21B. 22C. 32D. 33答案:D13.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是 ( )A.正方形B.矩形C.菱形D.一般平行四边形答案:B二、填空题:14.正方体1111D C B A ABCD -中,E 、F 、G 分别为AB 、BC 、CC 1的重点,则EF 与BG 所成角的余弦值为________________________答案:510 15.二面角βα--a 内一点P 到两个半平面所在平面的距离分别为22和4,到棱a 的距离为24,则这个二面角的大小为__________________答案:︒︒16575或16.四边形ABCD 是边长为a 的菱形,︒=∠60BAD ,沿对角线BD 折成︒120的二面角A —BD —C 后,AC 与BD 的距离为_________________________答案:a 43 17.P 为︒120的二面角βα--a 内一点,P 到α、β的距离为10,则P 到棱a 的距离是_________________答案:3320 18.如图:正方形ABCD 所在平面与正方形ABEF 所在平面成︒60的二面角,则异面直线AD 与BF 所成角的余弦值是______________________答案:4219.已知三棱锥P —ABC 中,三侧棱PA 、PB 、PC 两两互相垂直,三侧面与底面所成二面角的大小分别为γβα,,,则=++γβα222cos cos cos _______________答案:1 20.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值)。
高考数学立体几何多选题专项练习及答案一、立体几何多选题1.如图,正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2,则下列说法正确的是( )A .异面直线1AB 与1AD 所成的角是3πB .1BD ⊥平面11AC DC .平面1ACB 截正四面体11A BDC -所得截面面积为3D .正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ,利用正方体的结构特征找到异面直线所成的角;选项B ,根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证;选项C ,由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一;选项D ,分别求出正方体的体对角线长和正四面体11A BDC -的高,然后判断数量关系即可得解. 【详解】A :正方体1111ABCD ABCD -中,易知11//AD BC ,异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角,即11A BC ∠,11A BC 为等边三角形,113A BC π∠=,正确;B :连接11B D ,1B B ⊥平面1111DC B A ,11A C ⊂平面1111D C B A ,即111AC B B ⊥,又1111AC B D ⊥,1111B B B D B ⋂=,有11A C ⊥平面11BDD B ,1BD ⊂平面11BDD B ,所以111BD AC ⊥,同理可证:11BD A D ⊥,1111AC A D A ⋂=,所以1BD ⊥平面11AC D ,正确;C :易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=,错误;D :易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -的高为22222262213⎛⎫--⨯= ⎪⎝⎭,故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23,正确. 故选:ABD. 【点睛】关键点点睛:利用正方体的性质,找异面直线所成角的平面角求其大小,根据线面垂直的判定证明1BD ⊥平面11AC D ,由正四面体的性质,结合几何图形确定截面的面积,并求高,即可判断C 、D 的正误.2.如图,在棱长为2的正方体ABCD A B C D ''''-中,M 为BC 边的中点,下列结论正确的有( )A .AM 与DB ''所成角的余弦值为1010B .过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C .四面体A C BD ''的内切球的表面积为3π D .正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动并且使MAC PAC ''∠=∠,那么点P 的轨迹是椭圆 【答案】AB 【分析】构建空间直角坐标系,由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误;同样设(,,0)P x y 结合向量夹角的坐标表示,22221543y x y +=++⨯P 的轨迹知D 的正误;由立方体的截面为梯形,分别求,,,MN AD AM D N '',进而得到梯形的高即可求面积,判断B 的正误;由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ,进而求内切球表面积,判断C 的正误.【详解】A :构建如下图所示的空间直角坐标系:则有:(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D '', ∴(1,2,0),(2,2,0)AM D B ''==-,10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯,故正确.B :若N 为CC '的中点,连接MN ,则有//MN AD ',如下图示,∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面, 而2,2,5MN AD AM D N ''====322, ∴梯形的面积为132932222S =⨯=,故正确. C :如下图知:四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积,∴118848323V =-⨯⨯⨯=,而四面体的棱长都为22,有表面积为142222sin 8323S π=⨯⨯⨯⨯=,∴若其内切圆半径为r ,则有188333r ⨯⋅=,即33r =,所以内切球的表面积为2443r ππ=.故错误. D :正方体ABCD A B C D ''''-中,点P 在底面A B C D ''''(所在的平面)上运动且MAC PAC ''∠=∠,即P 的轨迹为面A B C D ''''截以AM 、AP 为母线,AC’为轴的圆锥体侧面所得曲线,如下图曲线GPK ,构建如下空间直角坐标系,232(0,0,2),(2),(0,22,0)22A M C '-,若(,,0)P x y ,则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-,∴15cos ||||512AM AC MAC AM AC '⋅'∠==='⨯222cos ||||43AP AC PAC AP AC x y '⋅'∠=='++⨯22215543x y =++⨯,整理得22(102)9216(0)y x y +-=>,即轨迹为双曲线的一支,故错误.故选:AB 【点睛】关键点点睛:应用向量的坐标表示求异面直线的夹角,并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹,综合立方体的性质求截面面积,分割几何体应用等体积法求内切球半径,进而求内切球的表面积.3.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥ B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值 D .1MB P 在侧面11D C CD 上射影图形是三角形 【答案】BC 【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误. 【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时, 若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥,由勾股定理可得2211115D N C N C D =+=,同理可得15B N =,1122B D =,2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误;对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=,190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥, 1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBCa a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △,且21224MBGa a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误. 故选:BC. 【点睛】方法点睛:证明面面垂直常用的方法: (1)面面垂直的定义; (2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.4.如图,已知正方体1ABCD ABC D -的棱长为a ,E 是棱CD 上的动点.则下列结论中正确的有( )A .11EB AD ⊥B .二面角11E A B A --的大小为4π C .三棱锥11A B D E -体积的最小值为313a D .1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ,则易证1AD ⊥平面11A DCB ,1EB ⊂平面11A DCB ,则由线面垂直的性质定理可以判断选项A 正确;二面角11E A B A --的平面角为1DA A ∠,易知14DA A π∠=,则可判断选项B 正确;用等体积法,将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积,当点E 与D 重合时,三棱锥11E AB D -的体积最小,此时的值为316a ,则选项C 错误;易知平面11//D DCC 平面11A B BA ,而1D E ⊂平面11D DCC ,则根据面面平行的性质定理可得1//D E 平面11A B BA ,可判断选项D 正确. 【详解】选项A ,连接1A D 、1B C ,则由正方体1ABCD ABC D -可知,11A D AD ⊥,111A B AD ⊥,1111A D A B A =,则1AD ⊥平面11A DCB ,又因为1EB ⊂平面11A DCB , 所以11EB AD ⊥,选项A 正确;选项B ,因为11//DE A B ,则二面角11E A B A --即为二面角11D A B A --, 由正方体1ABCD ABC D -可知,11A B ⊥平面1DA A , 则1DA A ∠为二面角11D A B A --的平面角,且14DA A π∠=,所以选项B 正确;选项C ,设点E 到平面11AB D 的距离为d , 则11111113A B D E E AB D AB D V V S d --==⋅,连接1C D 、1C B ,易证平面1//BDC 平面11AB D ,则在棱CD 上,点D 到平面11AB D 的距离最短, 即点E 与D 重合时,三棱锥11A B D E -的体积最小, 由正方体1ABCD ABC D -知11A B ⊥平面1ADD , 所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=, 则选项C 错误;选项D ,由正方体1ABCD ABC D -知,平面11//CC D D 平面11A B BA ,且1D E ⊂平面11CC D D , 则由面面平行的性质定理可知1//D E 平面11A B BA ,则选项D 正确. 故选:ABD. 【点睛】关键点点睛:本题对于选项C 的判断中,利用等体积法求三棱锥的体积是解题的关键.5.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F∠==22C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62D 错误.故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.6.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且2EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图,研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,11122122BEF S EF BB ∆∴=⋅=⨯⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO =11221334212A BEF BEF V S AO -∆∴=⨯=⨯⨯=A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB , 由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan 2MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯= 12HG FT ∴==选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=22AR = 由余弦定理得13cos 6AD R ∠= 故选:AC 【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.7.M ,N 分别为菱形ABCD 的边BC ,CD 的中点,将菱形沿对角线AC 折起,使点D 不在平面ABC 内,则在翻折过程中,下列结论正确的有( )A .MN ∥平面ABDB .异面直线AC 与MN 所成的角为定值C .在二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径先变小后变大D .若存在某个位置,使得直线AD 与直线BC 垂直,则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ;利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ;借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ,N 分别为菱形ABCD 的边BC ,CD 的中点,所以MN 为BCD ∆的中位线,所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ,所以MN ∥平面ABD ,故选项A 正确;对于选项B :取AC 的中点O ,连接,DO BO ,作图如下:则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知,AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90,故选项B 正确;对于选项C:借助极限状态,当平面DAC 与平面ABC 重合时,三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心,外接圆的半径为球的半径,当二面角D AC B --逐渐变大时,球心离开平面ABC ,但是球心在底面的投影仍然是ABC ∆外接圆圆心,故二面角D AC B --逐渐变小的过程中,三棱锥D ABC -外接球的半径不可能先变小后变大, 故选项C 错误;对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角,H 在线段BC 上;若ABC ∠为直角,H 与B 重合;若ABC ∠为钝角,H 在线段BC 的延长线上;若存在某个位置,使得直线AD 与直线BC 垂直,因为AH BC ⊥,所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角,H 与B 重合,所以CB BD ⊥,在CBD ∆中,因为CB CD =, 所以CB BD ⊥不可能成立,即ABC ∠为直角不可能成立;若ABC ∠为钝角,H 在线段BC 的延长线上,则在原平面图菱形ABCD 中,DCB ∠为锐角,由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小,,所以DCB ∠为锐角,CB HD ⊥,故点H 在线段BC 与H 在线段BC 的延长线上矛盾,因此ABC ∠不可能为钝角;综上可知,ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确;故选:ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题;考查空间想象能力和逻辑推理能力;借助极限状态和反证法思想的运用是求解本题的关键;属于综合型强、难度大型试题.8.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴=== N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1.故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.9.如图,正三棱柱11ABC A B C -中,11BC AB ⊥、点D 为AC 中点,点E 为四边形11BCC B 内(包含边界)的动点则以下结论正确的是( )A .()1112DA A A B A BC =-+ B .若//DE 平面11ABB A ,则动点E 的轨迹的长度等于22AC C .异面直线AD 与1BC 6D .若点E 到平面11ACC A 3EB ,则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案. 【详解】解析:对于选项A ,()1112AD A A B A BC =-+,选项A 错误; 对于选项B ,过点D 作1AA 的平行线交11A C 于点1D .以D 为坐标原点,1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz .设棱柱底面边长为a ,侧棱长为b ,则002a A ⎛⎫⎪⎝⎭,,,3002B a ⎛⎫ ⎪ ⎪⎝⎭,,,130B a b ⎛⎫ ⎪ ⎪⎝⎭,,,102a C b ⎛⎫- ⎪⎝⎭,,,所以1322a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,,1322a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,. ∵11BC AB ⊥,∴110BC AB ⋅=,即222302a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭,解得2b a =. 因为//DE 平面11ABB A ,则动点E 的轨迹的长度等于122BB AC =.选项B 正确. 对于选项C ,在选项A 的基础上,002a A ⎛⎫⎪⎝⎭,,,3002B a ⎛⎫ ⎪ ⎪⎝⎭,,,()0,0,0D ,12022a C a ⎛⎫- ⎪ ⎪⎝⎭,,,所以002a DA ⎛⎫= ⎪⎝⎭,,,13222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭,-,, 因为211162cos ,6||||622a BC DA BC DA BC DA a a ⎛⎫- ⎪⋅⎝⎭<>===-,所以异面直线1,BC DA 所成角的余弦值为6,选项C 正确. 对于选项D ,设点E 在底面ABC 的射影为1E ,作1E F 垂直于AC ,垂足为F ,若点E 到平面11ACC A 的距离等于32EB ,即有31E F EB =,又因为在1CE F ∆中,311E F E C =,得1EB E C =,其中1E C 等于点E 到直线1CC 的距离,故点E 满足抛物线的定义,另外点E 为四边形11BCC B 内(包含边界)的动点,所以动点E 的轨迹为抛物线的一部分,故D 正确.故选:BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题,其中涉及到抛物线定义的应用.10.如图,1111ABCD A B C D -为正方体,下列结论中正确的是( )A .11A C ⊥平面11BB D D B .1BD ⊥平面1ACBC .1BD 与底面11BCC B 2 D .过点1A 与异面直线AD 与1CB 成60角的直线有2条 【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ;求解1BD 与底面11BCC B 所成角的正切值判断C ;利用空间向量法可判断D . 【详解】对于A 选项,如图,在正方体1111ABCD A B C D -中,1BB ⊥平面1111D C B A ,11A C ⊂平面1111D C B A ,则111BB A C ⊥, 由于四边形1111D C B A 为正方形,则1111AC B D ⊥, 1111BB B D B =,因此,11A C ⊥平面11BB D D ,故A 正确;对于B 选项,在正方体1111ABCD A B C D -中,1DD ⊥平面ABCD ,AC ⊂平面ABCD ,1AC DD ∴⊥,因为四边形ABCD 为正方形,所以,AC BD ⊥,1D DD BD =,AC ∴⊥平面11BB D D , 1BD ⊂平面11BB D D ,1AC BD ∴⊥,同理可得11BD B C ⊥,1ACB C C =,1BD ∴⊥平面1ACB ,故B 正确;对于C 选项,由11C D ⊥平面11BCC B ,得11C BD ∠为1BD 与平面11BCC B 所成角, 且111112tan 2C D C BD BC ∠==,故C 错误; 对于D 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设正方体的棱长为1,则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ,()1,0,0DA =,()11,0,1CB =,设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =, 则221cos ,21DA mDA m DA m y z ⋅<>===⋅++, 1122111cos ,221CB m z CB m CB m y z ⋅+<>===⋅⋅++, 整理可得2222341y z y z z ⎧+=⎨=++⎩,消去y 并整理得2210z z +-=,解得12z =-12z =-由已知可得3z ≤,所以,12z =-+22y =±因此,过点1A 与异面直线AD 与1CB 成60角的直线有2条,D 选项正确.故选:ABD.【点睛】方法点睛:证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.。
第九章立体几何与空间向量第1节简单几何体的结构、三视图和直观图一、选择题1.如图是由哪个平面图形旋转得到的( A )解析:根据面动成体的原理即可解,一个直角三角形绕直角边旋转一周可以得到一个圆锥.一个直角梯形绕着直角腰旋转一周得到圆台.该几何体的上部分是圆锥,下部分是圆台,圆锥的轴截面是直角三角形,圆台的轴截面是直角梯形,所以这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到.故选A.2.已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4, AB⊥AC,AA1=12,则球O的半径为( C )(A) (B)2 (C) (D)3解析:构建长方体的棱长分别为3,4,12.体对角线长为=13,外接球的半径为,故选C.3.用长为4,宽为2的矩形做侧面围成一个圆柱,此圆柱轴截面面积为( B )(A)8 (B)(C)(D)解析:若以4作为圆柱的高、2作为底面圆的周长,则圆柱轴截面面积为;若以2作为圆柱的高、4作为底面圆的周长,则圆柱轴截面面积为,所以此圆柱轴截面面积为.故选B.4.正四棱锥S-ABCD的底面边长为4,高SE=8,则过点A,B,C,D,S的球的半径为( C )(A)3 (B)4 (C)5 (D)6解析:由正四棱锥及其外接球的对称性,球心O在正四棱锥的高线SE上,球半径R=OS=OB,EB=BD=4.所以在直角三角形OEB中,由勾股定理得,(8-R)2+42=R2,解得R=5,故选C.5.三棱锥P-ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( B )(A)16 (B)(C)(D)32解析:因为PA,PB,PC两两垂直,又因为三棱锥P-ABC的四个顶点均在半径为1的球面上,所以以PA,PB,PC为棱的长方体的对角线即为球的一条直径.所以16=PA2+PB2+PC2,因为PA=2PB,则这个三棱锥的三个侧棱长的和PA+PB+PC=3PB+PC,因为5PB2+PC2=16,设PB=4cos α,PC=4sin α,则3PB+PC=cos α+4sin α=sin(α+φ)≤=. 可知其最大值为,选B.6.已知一个四面体其中五条棱的长分别为1,1,1,1,,则此四面体体积的最大值是( B )(A) (B) (C) (D)解析:设四面体为P-ABC,则设PC=X,AB=,其余的各边为1,那么取AB 的中点D,那么连接PD,因此可知,AB垂直于平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可.由于PD=CD=,那么可知三角形PDC的面积越大,体积越大,可知S△PDC=××sin θ≤=,也就是当PD垂直于CD时,面积最大,因此可得四面体的体积的最大值为××=,选B.二、填空题7.圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为.解析:因为圆柱的侧面展开图是边长为6π和4π的矩形,①若6π=2πr,r=3,所以圆柱的表面积为4π×6π+2×πr2=24π2+18π;②若4π=2πr,r=2,所以圆柱的表面积为4π×6π+2×πr2=24π2+8π.答案:24π2+8π或24π2+18π8.一个圆柱和一个圆锥的底面直径和它们的高都与某一个球的直径相等,这时圆柱、圆锥、球的体积之比为.解析:设球的半径为r,则V圆柱=πr2×2r=2πr3,V圆锥=πr2×2r=,V球=πr3,所以V圆柱∶V圆锥∶V球=2πr3∶∶πr3=3∶1∶2.答案:3∶1∶29.将4个半径都是R的球体完全装入底面半径是2R的圆柱形桶中,则桶的最小高度是.解析:由题意知,小球要分两层放置且每层两个,令下层两小球的球心分别是A,B,上层两小球的球心分别是C,D.此时,圆柱底面的半径=两小球半径的和,恰好使小球相外切,且与圆柱母线相切.圆柱的高=上层小球的上方半径+AB与CD间的距离+下层小球的下方半径=2R+AB与CD间的距离.令AB,CD的中点分别为E,F.很明显,四面体ABCD每条棱的长都是2R,容易求出:EC=ED,FA=FB,由EC=ED,CF=DF,得EF⊥CD.由FA=FB,AE=BE,得EF⊥AB.所以EF是AB与CD间的距离,所以圆柱的高=2R+EF.由勾股定理,有CE2+AE2=AC2,CE2=EF2+CF2.两式相减,消去CE,得AE2=AC2-EF2-CF2,所以EF2=AC2-AE2-CF2=(2R)2-R2-R2=2R2,所以EF=R.所以圆柱的高=2r+R=(2+)R.答案:(2+)R10.一个圆锥有三条母线两两垂直,则它的侧面展开图的圆心角大小为.解析:设母线长为l,因圆锥有三条母线两两垂直,则这三条母线可以构成以它们为侧棱、以底面边长为l的正三角形的正三棱锥,故由正弦定理得,圆锥的底面直径2R=,解得R=,因此可知侧面展开图的圆心角大小为π.答案:π11.若圆锥的侧面展开图是圆心角为180°,半径为4的扇形,则这个圆锥的表面积是.解析:因为圆锥的侧面展开图是圆心角为180°,母线长等于4,半径为4的扇形,则这个圆锥的表面积是底面积加上侧面积,扇形面积加上底面面积的和为12π.答案:12π12.若长方体的一个顶点上的三条棱的长分别为3,4,5,从长方体的一条对角线的一个端点出发,沿表面运动到另一个端点,其最短路程是.解析:从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有三种方案,如图是它们的三种部分侧面展开图,AB路程可能是:最短路程是.答案:三、解答题13.某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,求a+b的最大值.解:如图,把几何体放到长方体中,使得长方体的体对角线刚好为几何体的已知棱,则长方体的体对角线A 1C=,则它的正视图投影长为A 1B=,侧视图投影长为A1D=a,俯视图投影长为A1C1=b,则a2+b2+()2=2·()2,即a2+b2=8,又≤,当且仅当“a=b=2”时等号成立.所以a+b≤4,即a+b的最大值为4.14.某几何体的三视图如图所示.(1)判断该几何体是什么几何体?(2)画出该几何体的直观图.解:(1)该几何体是一个正方体切掉两个圆柱后得到的几何体.(2)直观图如图所示.15.已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该正三棱锥的侧视图和直观图;(2)求出侧视图的面积.解:(1)如图.(2)侧视图中V A===2,则S △VBC=×2×2=6.第2节简单几何体的表面积与体积一、选择题1.如图所示是一个几何体的三视图,则该几何体的体积为( B )(A)16+2π(B)8+2π(C)16+π (D)8+π解析:由图可知该几何体是由两个相同的半圆柱与一个长方体拼接而成,因此V=1×2×4+π×12×2=8+2π.故选B.2.一个三条侧棱两两互相垂直并且侧棱长都为a的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( B )(A)πa2(B)3πa2(C)6πa2(D)πa2解析:由题可知该三棱锥为一个棱长a的正方体的一角,则该三棱锥与该正方体有相同的外接球,又正方体的对角线长为a,则球半径为a,则S=4πr2=4π(a)2=3πa2.故选B.3.一个棱长都为a的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( A )(A)πa2(B)2πa2(C)πa2(D)πa2解析:如图,设O1,O2为棱柱两底面的中心,球心O为O1O2的中点.又直三棱柱的棱长为a,可知OO1=a,AO1=a,所以R2=OA2=O+A=,因此该直三棱柱外接球的表面积为S=4πR2=4π×=πa2,故选A.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A) (B)2 (C) (D)解析:由三视图可知,该几何体的直观图为一个竖立的圆锥和一个倒立的圆锥组成,其体积为V=2×π×12×1=,选D.5.某四棱锥的三视图如图所示,则该四棱锥的体积是( C )(A)5 (B)2 (C) (D)解析:由三视图知,该四棱锥的底面是直角梯形,上底长为2,下底长为3,高为,四棱锥的高为h=2,故该四棱锥的底面积S=(2+3)×=,所以该四棱锥的体积V=Sh=××2=.6.已知边长为2的菱形ABCD中,∠A=60°,现沿对角线BD折起,使得二面角A BD C为120°,此时点A,B,C,D在同一个球面上,则该球的表面积为( C )(A)20π(B)24π(C)28π(D)32π解析:如图,分别取BD,AC的中点M,N,连接MN,则容易算得AM=CM=3,MN=,MD=,CN=,由图形的对称性可知球心必在MN的延长线上,设球心为O,半径为R,ON=x,则由题设可得解得x=,则R2=+=7,所以球面面积S=4πR2=28π,故选C.二、填空题7.一个圆柱的轴截面为正方形,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.解析:令正方形的边长为a,则圆柱的侧面积S1=2π××a=πa2,与它同底等高的圆锥的侧面积S2=πrl=π××a=,则与它同底等高的圆锥的侧面积与该圆柱的侧面积的比为.答案:8.球O与直三棱柱ABC-A1B1C1的各个面都相切,若三棱柱的表面积为27,△ABC的周长为6,则球的表面积为.解析:设内切球半径为r,那么直三棱柱的底面内切圆半径为r,棱柱的高为2r,由等面积法,则直三棱柱底面面积S 底=r×6=3r,由等体积法,V三棱柱=S底·2r=r·27,所以9r=6r2,解得r=.其表面积为4π×()2=3π.答案:3π9.已知母线长为6,底面半径为3的圆锥内有一球,球与圆锥的底面及圆锥的所有母线都相切,则球的体积是 .解析:取圆锥的轴截面,则截面是边长为6的正三角形,正三角形的内切圆的圆心即为球心,R=6××,所以R=,所以V=πR3=4π.答案:4π10.棱长为a的正方体ABCD A 1B1C1D1的8个顶点都在球O的表面上,E,F 分别是棱AA1,DD1的中点,则过E,F两点的直线被球O截得的线段长为.解析:设过E,F两点的直线与球O交于M,N,所以△OMN,△OEF均为等腰直角三角形,所以OM=ON=R=a,点O到EF的距离为棱长一半,所以|MN|=2= a.答案: a11.四棱锥P-ABCD的各顶点都在同一球面上,且矩形ABCD的各顶点都在同一个大圆上,球半径为R,则此四棱锥的体积的最大值为.解析:点P到平面ABCD的最大距离为R,设矩形ABCD的长宽分别为x,y,则x2+y2=4R2,四棱锥P ABCD的体积V=xyR≤×=R3,当且仅当x=y=R时,V max=R3.答案:R312.设正四面体ABCD的棱长为a,P是棱AB上的任意一点,且P到平面ACD,BCD的距离分别为d1,d2,则d1+d2= .解析:根据题意,由于正四面体ABCD的棱长为a,各个面的面积为a2,高为a,所以V=×a2×a=×a2×(d1+d2),所以d1+d2= a.答案: a三、解答题13.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P,Q在正视图中所示位置,P为所在线段中点,Q为顶点,求在几何体表面上,从P点到Q点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥加一个圆柱组成的,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=(2πa)·(a)=πa2,S圆柱侧=(2πa)·(2a)=4πa2,S圆柱底=πa2,所以S 表=πa2+4πa2+πa2=(+5)πa2.(2)沿P点所在母线剪开圆柱侧面,如图.则PQ===a,所以从P点到Q点在侧面上的最短路径长为a.14.如图,四棱锥P ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求四面体NBCM的体积.(1)证明:由已知得AM=AD=2.如图,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.所以AM=TN,又AD∥BC,故TN AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)解:因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE==.由AM∥BC得M到BC的距离为,故S △BCM=×4×=2.所以四面体NBCM的体积V N-BCM=×S△BCM×=.15.如图所示,在空间几何体ADE BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC,AB=AD=DE=2,EF=4,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;(2)在(1)的条件下,平面MDF将几何体ADE-BCF分成两部分,求空间几何体M-DEF与空间几何体ADM BCF的体积之比.解:(1)当M是线段AE的中点时,AC∥平面MDF.理由如下:连接CE交DF于点N,连接MN.因为M,N分别是AE,CE的中点,所以MN∥AC.又因为MN⊂平面MDF,AC⊄平面MDF,所以AC∥平面MDF.(2)将几何体ADE-BCF补成三棱柱ADE-B′CF,如图所示,三棱柱ADE-B′CF的体积为V=S△ADE·CD=×2×2×4=8,则几何体ADE-BCF的体积=-=8-×(×2×2)×2=.因为三棱锥M-DEF的体积=×(×2×4)×1=,所以=-=,所以两几何体的体积之比为∶=1∶4.第3节空间图形的基本关系与公理一、选择题1.设m,n是两条不同的直线,α,β是两个不同的平面( C )(A)若m∥α,n∥α,则m∥n(B)若m∥α,m∥β,则α∥β(C)若m∥n,m⊥α,则n⊥α(D)若m∥α,α⊥β,则m⊥β解析:设直线a⊂α,b⊂α,a∩b=A,因为m⊥α,所以m⊥a,m⊥b.又n∥m,所以n⊥a,n⊥b,所以n⊥α.故选C.2.下列命题中,错误的是( D )(A)平行于同一平面的两个不同平面平行(B)一条直线与两个平行平面中的一个相交,则必与另一个平面相交(C)如果两个平面不垂直,那么其中一个平面内一定不存在直线与另一个平面垂直(D)若直线不平行于平面,则此直线与这个平面内的直线都不平行解析:当直线l在平面α内,即l⊂α时,直线l不平行于平面α,但平面α内存在直线与直线l平行,可知D选项错误,故选D.3.下列四个命题:①若一个平面内的两条直线都与另一个平面平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( D )(A)①和②(B)②和③(C)③和④(D)②和④解析:①显然错误,因为这两条直线相交才满足条件;②成立;③错误,这两条直线可能平行、相交,也可能异面;④成立,用反证法容易证明.故选D.4.若α,β是两个相交平面,则在下列命题中,真命题的序号为( C )①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线;②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直;③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线;④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.(A)①③(B)②③(C)②④(D)①④解析:若α⊥β且直线m⊥α,则在平面β内,一定存在与直线m平行的直线,所以①错误;若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直,故②正确;若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线,故③错误,④正确,故选C.5.设不在同一条直线上的A,B,C三点到平面α的距离相等,且A∉α,则( B )(A)α∥平面ABC(B)△ABC中至少有一条边平行于α(C)△ABC中至多有两条边平行于α(D)△ABC中只可能有一条边平行于α解析:因为A∉α,所以A,B,C均不在平面α内.当A,B,C三点在平面α的同侧时,α∥平面ABC,此时△ABC的三条边都平行于α,排除C,D;当A,B,C三点不在平面α的同侧时,易知△ABC中只有一条边平行于α,此时平面α和平面ABC相交,故选B.6.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( B )(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件解析:因为l⊥m,m⊥α,所以l∥α或l⊂α.故充分性不成立.若l∥α,m⊥α,一定有l⊥m.故必要性成立.选B.二、填空题7.长方体ABCD-A1B1C1D1的底面是边长为1的正方形,点E在侧棱AA1上(不与A,A1重合),满足∠C1EB=90°,则异面直线BE与C1B1所成的角为,侧棱AA1的长的最小值为.解析:在长方体ABCD-A1B1C1D1中,CB⊥平面ABB1A1,所以∠CBE=90°,又C1B1∥BC,所以异面直线BE与C1B1所成的角为90°.连接BC1,设AA1=x,AE=m(m>0),则有BE2=1+m2,C1E2=(x-m)2+2,C1B2=1+x2,因为∠C1EB=90°,所以C1B2=C1E2+BE2,即1+x2=(x-m)2+2+1+m2,即m2-mx+1=0,所以x=m+≥2,当且仅当m=,即m=1时,“=”成立.答案:90° 28.四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A1-BCD,使平面A1BD⊥平面BCD,给出下列结论:(1)A1C⊥BD;(2)∠BA1C=90°;(3)四面体A1-BCD的体积为.其中正确的命题是.(把所有正确命题的序号都填上) 解析:若A1C⊥BD,因为BD⊥CD,A1C∩CD=C,所以BD⊥平面A1CD,所以BD⊥A1D.而由A 1B=AB=1,A1D=AD=1,BD=,得A1B⊥A1D,与BD⊥A1D矛盾,故(1)错.因为CD⊥BD,平面BCD⊥平面A1BD,所以CD⊥平面A1BD,则CD⊥A1B.又A1B⊥A1D,A1D∩CD=D,所以A1B⊥平面A1CD,则A1B⊥A1C,故(2)正确.由(2)知==×·A1D·DC·A1B=,故(3)错.答案:(2)9.在正方体ABCD A 1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线有条.解析:在A1D1上任取一点P,过点P与直线EF作一个平面α,因为CD 与平面α不平行,所以它们相交,设α∩CD=Q,连接PQ,则PQ与EF必然相交.由点P的任意性,知有无数条直线与A1D1,EF,CD都相交.答案:无数10.如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形.∠ACB =90°,AC=6,BC=CC 1=,P是BC1上一动点,则CP+PA1的最小值为.解析:连接A1B,将△A1BC1与△CBC1同时展开形成一个平面四边形A1BCC1,则此时对角线CP+PA1=A1C达到最小,在等腰直角三角形△BCC1中,BC1=2,∠CC1B=45°,在△A 1BC1中,A1B==2,A1C1=6,BC1=2,所以A1+B=A1B2,即∠A1C1B=90°.对于展开形成的四边形A1BCC1,如图,在△A 1C1C中,C1C=,A1C1=6,∠A1C1C=135°,由余弦定理有,CP+PA 1=A1C===5.答案:511. 如图,三棱锥A BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是.解析:如图所示,连接DN,取线段DN的中点K,连接MK,CK.因为M为AD的中点,所以MK∥AN,所以∠KMC为异面直线AN,CM所成的角.因为AB=AC=BD=CD=3,AD=BC=2,N为BC的中点,由勾股定理求得AN=DN=CM=2,所以MK=.在Rt△CKN中,CK==.在△CKM中,由余弦定理,得cos∠KMC===.答案:12.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE 翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是.①BM是定值;②点M在某个球面上运动;③存在某个位置,使DE⊥A1C;④存在某个位置,使MB∥平面A1DE.解析:取DC中点F,连接MF,BF,MF∥A1D且MF=A1D,FB∥ED且FB=ED,所以∠MFB=∠A1DE.由余弦定理可得MB2=MF2+FB2-2MF·FB·cos∠MFB 是定值,所以M是在以B为圆心,MB为半径的球上,可得①②正确;由MF∥A1D与FB∥ED可得平面MBF∥平面A1DE,可得④正确;A1C在平面ABCD中的投影与AC重合,AC与DE不垂直,可得③不正确.答案:③三、解答题13.如图所示,等腰直角三角形ABC中,∠A=90°,BC=,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.解:如图所示,取AC的中点F,连接EF,BF,在△ACD中,E,F分别是AD,AC的中点,所以EF∥CD.所以∠BEF或其补角即为异面直线BE与CD所成的角.在Rt△EAB中,AB=AC=1,AE=AD=,所以BE=.在Rt△EAF中,AF=AC=,AE=,所以EF=.在Rt△BAF中,AB=1,AF=,所以BF=.在等腰三角形EBF中,cos∠FEB===.所以异面直线BE与CD所成角的余弦值为.14.已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.求证:(1)D,B,F,E四点共面;(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.证明:(1)如图所示,因为EF是△D1B1C1的中位线,所以EF∥B1D1.在正方体ABCD-A1B1C1D1中,B1D1∥BD,所以EF∥BD.所以EF,BD确定一个平面.即D,B,F,E四点共面.(2)在正方体ABCD-A1B1C1D1中,设平面A1ACC1确定的平面为α,又设平面BDEF为β.因为Q∈A1C1,所以Q∈α.又Q∈EF,所以Q∈β.则Q是α与β的公共点,同理,P点也是α与β的公共点.所以α∩β=PQ.又A1C∩β=R,所以R∈A1C,则R∈α且∈β.则R∈PQ,故P,Q,R三点共线.15.在长方体ABCD A 1B1C1D1的A1C1面上有一点P(如图所示,其中P点不在对角线B1D1)上.(1)过P点在空间内作一条直线l,使l∥直线BD,应该如何作图?并说明理由;(2)过P点在平面A1C1内作一条直线m,使m与直线BD成α角,其中α∈(0°,90°],这样的直线有几条,应该如何作图?解:(1)连接B1D1,BD,在平面A1C1内过P点作直线l,使l∥直线B1D1,则l即为所求作的直线.因为直线B1D1∥直线BD,l∥直线B1D1,所以l∥直线BD.如图(1).(2)在平面A1C1内作直线m,使直线m与B1D1相交成α角,因为BD∥B1D1,所以直线m与直线BD也成α角,即直线m为所求作的直线,如图(2).由图(2)知m与BD是异面直线,且m与BD所成的角α∈(0,90°].当α=90°时,这样的直线m有且只有一条,当α≠90°时,这样的直线m 有两条.第4节直线、平面平行的判定与性质一、选择题1.若直线l∥平面α,直线a⊂平面α,则l与a的位置关系是( D )(A)l∥a (B)l与a异面(C)l与a相交 (D)l与a没有公共点解析:因为直线平行于平面,那么l与平面内的任何一条直线都没有公共点,因此l与a的位置关系是没有公共点,选D.2.下列条件能推出平面α∥平面β的是( D )(A)存在一条直线a,a∥α,a∥β(B)存在一条直线a,a⊂α,a∥β(C)存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α(D)存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α解析:因为根据面面平行的判定定理可知,如果存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α,则可以利用线线平行得到面面平行,选D.3.已知直线l,m,平面α,β,则下列命题中:①若α∥β,l⊂α,则l∥β②若α⊥β,l⊥α,则l∥β③若l∥α,m⊂α,则l∥m④若α⊥β,α∩β=l,m⊥l,则m⊥β,其中真命题有( B )(A)0个(B)1个(C)2个(D)3个解析:当两个平面平行时,一个平面上的线与另一个平面平行,故①正确;一条直线垂直于两个垂直平面中的一个平面,那么这条直线平行于或包含于另一个平面,故②不正确;④不正确;③中l,m的关系是不相交,故③不正确,故选B.4.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( B )(A)①③(B)①④(C)②③(D)②④解析:对图①,构造AB所在的平面,即对角面,可以证明这个对角面与平面MNP平行,由线面平行的定义可得AB∥平面MNP;对图④,通过证明AB∥PN得到AB∥平面MNP;对于②,证MP中点为K,延长BA,KN则相交,所以BA与平面MNP相交,②错;对于③平面MNP与直线AB相交于点B,③错.故选B.5.类比平面几何中的定理“设a,b,c是三条直线,若a⊥c,b⊥c,则a∥b”,得出如下结论:①设a,b,c是空间的三条直线,若a⊥c,b⊥c,则a∥b;②设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b;③设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β;④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β.其中正确命题的个数是( B )(A)1 (B)2 (C)3 (D)4解析:①错;②垂直于同一个平面的两条直线平行,正确;③垂直于同一条直线的两个平面平行,正确;④错;两个平面也可能相交.6.在空间中,下列命题正确的是( D )(A)平面α内的一条直线a垂直于平面β内的无数条直线,则α⊥β(B)若直线m与平面α内的一条直线平行,则m∥α(C)若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β(D)若直线a与平面α内的无数条直线都垂直,则不能说一定有a⊥α解析:直线a与平面α内的任意直线都垂直,则有a⊥α,所以D正确.二、填空题7.点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF= .解析:取BC的中点D,连接ED与FD,因为E,F分别是SC和AB的中点,点D为BC的中点所以ED∥SB,FD∥AC,而SB⊥AC,SB=AC=2,则三角形EDF为等腰直角三角形,则ED=FD=1,即EF=.答案:8.正四棱锥S ABCD的底面边长为2,高为2,E是边BC的中点,动点P 在这个棱锥表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为.解析:由题意知,点P的轨迹为如图所示的三角形EFG,其中G,F为其所在棱的中点,所以EF=BD=,GE=GF=SB=,所以轨迹的周长为+.答案:+9.将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E,F分别为AC,BD的中点,则下列命题中正确的是.①EF∥AB;②EF⊥BD;③EF有最大值,无最小值;④当四面体ABCD的体积最大时,AC=;⑤AC垂直于截面BDE.解析:因为将边长为2,一个内角为60°的菱形ABCD沿较短对角线BD 折成四面体ABCD,点E,F分别为AC,BD的中点,则可知EF⊥BD,当四面体ABCD的体积最大时,AC=,AC垂直于截面BDE成立.答案:②④⑤10.已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于A,C,过点P的直线n与α,β分别交于B,D且PA=6,AC=9,PD=8,则BD的长为.解析:因为平面α∥平面β,所以AB∥CD,①当P在两平面外时,==,所以=,所以BD=.②当P在两平面之间时,=,所以=,所以BD=24,所以BD的长为或24.答案:或2411.给出下列四个命题:①过平面外一点,作与该平面成θ角的直线一定有无穷多条;②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等.其中正确的命题序号为.解析:①中,成90度角的时候,就只有一条,因此错误.②中是线面平行的性质定理,显然成立.③不正确.④中,利用等角定理,可知成立. 答案:②④12.侧棱长为2的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过A 作截面AEF,则截面△AEF周长的最小值为.解析:沿着侧棱VA把正三棱锥V ABC展开在一个平面内,则设VA的另一边为VA′,则AA′即为截面△AEF周长的最小值,且∠AVA′=3×40=120°.△VAA′中,由余弦定理可得AA′=6.答案:6三、解答题13.已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AB=4,AA1=2,点E 在棱C1D1上,且D1E=3.(1)试在棱CD上确定一点E1,使得直线EE1∥平面D1DB,并证明;(2)若动点F在底面ABCD内,且AF=2,请说明点F的轨迹,并探求EF 长度的最小值.解:(1)取CD的四等分点E1,使得DE1=3,则有EE1∥平面D1DB.证明如下:因为D1E∥DE1且D1E=DE1,所以四边形D1EE1D为平行四边形,则D1D∥EE1,因为DD1⊂平面D1DB,EE1⊄平面D1DB,所以EE1∥平面D1DB.(2)因为AF=2,所以点F在平面ABCD内的轨迹是以A为圆心,半径等于2的四分之一圆弧.因为EE1∥DD1,D1D⊥平面ABCD,所以E1E⊥平面ABCD,故EF==.所以当E1F的长度取最小值时,EF的长度最小,此时点F为线段AE1和四分之一圆弧的交点,即E1F=E1A-AF=5-2=3,所以EF==.即EF长度的最小值为.14.在正方体ABCD-A1B1C1D1中,棱长为2,E是棱CD的中点,P是棱AA1的中点,(1)求证:PD∥平面AB1E;(2)求三棱锥B-AB1E的体积.(1)证明:取AB1中点Q,连接PQ,则PQ为中位线,PQ A1B1,而正方体ABCD-A1B1C1D1,E是棱CD的中点,故DE A1B1,所以PQ DE,所以四边形PQED为平行四边形.所以PD∥QE,而QE⊂平面AB1E,PD⊄平面AB1E,故PD∥平面AB1E.(2)解:正方体ABCD-A1B1C1D1中,BB1⊥平面ABE,故BB1为高,BB1=2,因为CD∥AB,所以S△ABE=S△ABC=AB·BC=×2×2=2.故==BB1·S△ABC=.15.如图,在四面体PABC中,PA=PB,CA=CB,D,E,F,G分别是PA,AC,CB,BP的中点.(1)求证:D,E,F,G四点共面;(2)求证:PC⊥AB;(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,PC=,求四面体PABC的体积.(1)证明:依题意DG∥AB,EF∥AB,所以DG∥EF,DG,EF共面,从而D,E,F,G四点共面.(2)证明:取AB中点为O,连接PO,CO.因为PA=PB,CA=CB,所以PO⊥AB,CO⊥AB,因为PO∩CO=O,所以AB⊥平面POC,PC⊂平面POC,所以AB⊥PC.(3)解:因为△ABC和△PAB是等腰直角三角形,所以PO=CO=AB=1,因为PC=,OP2+OC2=PC2,所以OP⊥OC,又PO⊥AB,且AB∩OC=O,所以PO⊥平面ABC,=PO·S△ABC=×1×2×1×=.第5节直线、平面垂直的判定与性质一、选择题1.已知直线l,m和平面α, 则下列命题正确的是( C )(A)若l∥m,m⊂α,则l∥α(B)若l∥α,m⊂α,则l∥m(C)若l⊥α,m⊂α,则l⊥m(D)若l⊥m,l⊥α,则m∥α解析:A项中直线l与平面α可能平行,可能直线在平面内;B项中直线l,m平行或异面;C项中当直线垂直于平面时,直线垂直于平面内任意直线;D项中直线m与平面α平行或直线在平面内.2.在Rt△ABC中,∠ABC=90°,P为△ABC所在平面外一点,PA⊥平面ABC,则四面体P ABC中共有直角三角形个数为( A )(A)4 (B) 3 (C) 2 (D) 1解析:因为PA⊥平面ABC,AB⊥BC,所以PA⊥AB,PA⊥AC,PB⊥CB,所以△ABC,△PBC, △ABP, △APC都是直角三角形,故选A.3.已知直线m,n和平面α,β满足m⊥n,m⊥α,α⊥β,则( C )(A)n⊥β (B)n∥β,或n⊂β(C)n∥α或n⊂α(D)n⊥α解析:由题意画出图形,容易判断选项.由于直线m⊥n,m⊥α,α⊥β,选项A,中线面可能相交,也可能垂直,选项B中,n与β还可能相交,错误,选项D中,直线不能垂直于平面,故结合图象不难得到选项为C.4.正方体的棱长为1,C,D,M分别为三条棱的中点,A,B是顶点,那么点M到截面ABCD的距离是( B )(A)(B)(C)(D)解析:过M作AB的垂线MN交AB于N,连接CN.由于CM⊥AB,MN⊥AB,则AB⊥平面CMN,所以,M到面ABCD的距离h是直角三角形CMN的斜边CN上的高.由于BM=,CM=1,MN=,CN=,则结合=求得h=.故选B.。
高中数学立体几何经典题型练习题集学校:______姓名:_____班级:______考号:______题号一二三总分得分评卷人得 分一.单选题1.正三棱锥的底边长和高都是2,则此正三棱锥的斜高长度为( )A.B.C.D.2.在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为( )A.1B.C.D.3.一个棱柱是正四棱柱的条件是( )A.底面是正方形,有两个侧面是矩形B.底面是正方形,有两个侧面垂直于底面C.底面是菱形,且有一个顶点处的三条棱两两垂直D.每个侧面都是全等矩形的四棱柱4、如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )A.B.C.D.5、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O 所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是( )A.1B.2C.3D.46、如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:⊥;①FG BD②B1D⊥面EFG;③面EFG∥面ACC1A1;④EF∥面CDD1C1.正确结论的序号是( )A.①和②B.③和④C.①和③D.②和④⊥,垂足为⊥,CH PB7、三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB BCH,D是PA的中点,则△CDH的面积最大时,CB的长是( )A.B.C.D.8、正方体的直观图如图所示,则其展开图是( )A.B.C.D.评卷人得 分二.填空题(共__小题)9、如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且⊥,AC=m,BD=n,则四 边形EFGH的面积为______.AC BD10、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结⊥;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与论:①PB AE平面PAB所成角的余弦值为.其中正确的有______(把所有正确的序号都填上).11.如图所示,三棱锥M,PA⊥底面ABC,∠ABC=90°,则此三棱锥P-ABC中直角三角形有_ _____个.12、如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且⊥1,有下述结论FD AC⊥;(1)AC1BC(2)=1;(3)二面角F-AC1-C的大小为90°;(4)三棱锥D-ACF的体积为.正确的有______.13.各棱长为a的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为______.14.一四棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:4,则此截面把一条侧棱分成的两段之比为______.15、如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论⊥①AC BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF的体积为定值其中正确的结论有:______(写出所有正确结论的编号)评卷人得 分三.简答题(共__小题)16、如图,立体图形A-BCD的四个面分别为△ABC、△ACD、△ADB和△BCD,E、F、G分别是线段AB、AC、AD上的点,且满足AE:AB=AF:AC=AG:AD,∽△.求证:△EFG BCD17、如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC 的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC的表面积;(2)求证AC⊥平面DEF;(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N 的位置;若不存在,试说明理由.参考答案一.单选题(共__小题)1.正三棱锥的底边长和高都是2,则此正三棱锥的斜高长度为( )A.B.C.D.解析:解:在正三棱锥中,顶点P在底面的射影为底面正三角形的中心O,延长A0到E,则E为BC的中点,连结PE,则PE为正三棱锥的斜高.∵正三棱锥的底边长和高都是2,∴AB=PO=2,即AE=,OE=,∴斜高PE==,故选:D.2、在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为( )A.1B.C.D.答案:B解:过E点做EH垂直CD于H,连接EH,易得H即为E在平面ABCD上的射影,连接AH,BH,如下图所示则AH,BH,AB分别为FE,EG,FB在平面ABCD上的射影,又由G在平面ABCD上的射影为B,故△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影∵S ABH△=S ABCD=故选B3.一个棱柱是正四棱柱的条件是( )A.底面是正方形,有两个侧面是矩形B.底面是正方形,有两个侧面垂直于底面C.底面是菱形,且有一个顶点处的三条棱两两垂直D.每个侧面都是全等矩形的四棱柱答案:C解析:解:上、下底面都是正方形,且侧棱垂直于底面的棱柱叫做正四棱柱.故A和B错在有可能是斜棱柱,D错在上下底面有可能不是正方形,底面是菱形,且有一个顶点处的三条棱两两垂直能保证上、下底面都是正方形,且侧棱垂直于底面.故选C.4、如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )A.B.C.D.答案:A解析:解:设正方体的棱长为1,连接AC交BD于O,连PO,则PO是等腰△PBD的高,故△PBD的面积为f(x)=BD×PO,在三角形PAO中,PO==,∴f(x)=××=,画出其图象,如图所示,对照选项,A正确.故选A.5、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是( )A.1B.2C.3D.4答案:D解析:证明:∵AB是圆O的直径⊥,三角形ABC是直角三角形∴∠ACB=90°即BC AC又∵PA⊥圆O所在平面,∴△PAC,△PAB是直角三角形.且BC在这个平面内⊥因此BC垂直于平面PAC中两条相交直线,∴PA BC∴BC⊥平面PAC,∴△PBC是直角三角形.从而△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是,4.故选D.6、如图,在正方体ABCD-A 1B 1C 1D 1中,E 、F 、G 分别是棱A 1B 1、BB 1、B 1C 1的中点,则下列结论中:①FG BD ⊥;②B 1D ⊥面EFG ;③面EFG ∥面ACC 1A 1;④EF ∥面CDD 1C 1.正确结论的序号是( )A .①和②B .③和④C .①和③D .②和④答案:D 解析:解:如图连接A 1C 1、A 1B 、BC 1、BD 、B 1D ,因为E 、F 、G 分别是棱A 1B 1、BB 1、B 1C 1的中点对于①因为FG BC ∥1,△BDC 1是正三角形,FG BD ⊥,不正确.对于②因为平面A 1C 1B ∥平面EFG ,并且B 1D ⊥平面A 1C 1B ,所以B 1D ⊥面EFG ,正确.③面EFG ∥面ACC 1A 1;显然不正确.④EF ∥平面CDD 1C 1内的D 1C ,所以EF ∥面CDD 1C 1.正确.故选D7、三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,⊥,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是(PA=4,AB BC⊥,CH PB)A.B.C.D.答案:D解析:⊥;解:三棱锥P-ABC中,PC⊥面ABC,AB⊂平面ABC,∴PC AB⊥,BC∩PC=C,又AB BC∴AB⊥平面PBC;又CH⊂平面PBC,⊥,∴AB CH⊥,又CH PBPB∩AB=B,∴CH⊥平面PAB,又DH⊂平面PAB,⊥;∴CH DH又△PAC是等腰直角三角形,且PA=4,D是PA的中点,∴CD=PA=2,设CH=a,DH=b,则a2+b2=CD2=4,∴4=a2+b2≥2ab,即ab≤1,当且仅当a=b=时,“=”成立,此时△CDH的面积最大;△,设BC=x,在Rt PBC则PB===,∴PC•BC=PB•CH,即2•x=•;解得x=,∴CB的长是.故选:D.8、正方体的直观图如图所示,则其展开图是( )A.B.C.D.答案:D解析:解:根据题意,可得对于A,展开图中的上下两边的正方形的对边中点连线应该呈左右方向显现,故A的图形不符合题意;对于B,展开图中最右边的“日”字形正方形的对边中点连线应该是上下方向呈现,且应该在含有圆形的正方形的左边放置,故B的图形不符合题意;对于C,展开图中最右边的正方形应该与含有圆形的正方形相邻,故C的图形不符合题意;对于D,沿如图的红线将正方体的侧面剪裁,展开可得如D项图的形状,故D的图形符合题意故选:D评卷人得 分二.填空题(共__小题)9、如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的中点,⊥,AC=m,BD=n,则四 边形EFGH的面积为______.并且AC BD答案:解析:⊥,可得四边形解:由ABCD是空间四边形,E、F、G、H分别是四边上的中点,并且AC BDEFGH为矩形,且此矩形的长和宽分别为和 ,故四边形EFGH的面积为=,故答案为:.10、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面⊥;②平面ABC⊥平面PBC;③直线BC∥平面PAE;ABC,PA=2AB,给出下列结论:①PB AE④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为.其中正确的有______(把所有正确的序号都填上).答案:①④⑤解析:⊥,解:对于①、由PA⊥平面ABC,AE⊂平面ABC,得PA AE⊥,PA∩AB=A,得AE⊥平面PAB,又PB⊂平面PAB,又由正六边形的性质得AE AB⊥,①正确;∴AE PB对于②、又平面PAB⊥平面ABC,所以平面ABC⊥平面PBC不成立,②错;∥,又AD⊂平面PAD,∴BC∥平面PAD,∴直线BC∥平面对于③、由正六边形的性质得BC ADPAE也不成立,③错;△中,PA=AD=2AB,∴∠PDA=45°,∴④正确;对于④、在Rt PAD∥,∴D到平面PAB的距离即为E到平面PAB的距离,即E到直线PA的对于⑤、由于DE AB距离,即EA,EA=AB,在Rt PAD △中,PA=AD=2AB ,∴PD=2AB ,∴直线PD 与平面PAB 所成角的正弦值为=,∴直线PD 与平面PAB 所成角的余弦值为=,∴⑤正确.故答案为:①④⑤.11.如图所示,三棱锥M ,PA ⊥底面ABC ,∠ABC=90°,则此三棱锥P-ABC 中直角三角形有______个.答案:4解析:解:由已知PA ⊥底面ABC ,∠ABC=90°,所以CB PA ⊥,CB AB ⊥,又PA∩AB=A ,所以CB ⊥平面PAB ,所以CB PB ⊥,所以此三棱锥P-ABC 中直角三角形有△ABC ,△ABP ,△ACP ,△PBC 共有4个.故答案为:4.12、如图,正三棱柱ABC-A1B1C1的各棱长⊥1,有下述结论都等于2,D在AC1上,F为BB1中点,且FD AC⊥;(1)AC1BC(2)=1;(3)二面角F-AC1-C的大小为90°;(4)三棱锥D-ACF的体积为.正确的有______.答案:(2)(3)(4)解析:解:(1)连接AB1,则∠B1C1A即为BC和AC1所成的角,在三角形AB1C1中,B1C1=2,AB1=2,∠1C1A==,AC 1=2,cos B故(1)错;(2)连接AF ,C 1F ,则易得AF=FC 1=,又FD AC ⊥1,则AD=DC 1,故(2)正确;(3)连接CD ,则CD AC ⊥1,且FD AC ⊥1,则∠CDF 为二面角F-AC 1-C 的平面角,CD=,CF=,DF===,即CD 2+DF 2=CF 2,故二面角F-AC 1-C 的大小为90°,故(3)正确;(4)由于CD AC ⊥1,且FD AC ⊥1,则AD ⊥平面CDF ,则VD-ACF =V A-DCF =•AD•S DCF △=×××=.故(4)正确.故答案为:(2)(3)(4)13.各棱长为a 的正三棱柱的六个顶点都在同一个球面上,则此球的表面积为______.答案:解析:解:∵正三棱柱的六个顶点都在同一个球面上,所以球心在上下底面中心的连线的中点上,AB=a ,OA=R ,在△OEA 中,OE=,AE=,∵AO 2=OE 2+AE 2,∴,∴球的表面积为4πR2=,故答案为.14.一四棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:4,则此截面把一条侧棱分成的两段之比为______.答案:1:1解析:解:根据题意,设截得小棱锥的侧棱长为l,原棱锥的侧棱长为L,∵截面与底面相似,且截面面积与底面面积之比为1:4,∴相似比为:==,∴截面把棱锥的一条侧棱分成的两段之比是l:(L-l)=1:1.故答案为:1:1.15、如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=,给出下列五个结论⊥①AC BE②EF∥平面ABCD③异面直线AE,BF所成的角为60°④A1点到面BEF的距离为定值⑤三棱柱A-BEF 的体积为定值其中正确的结论有:______(写出所有正确结论的编号)答案:①②④⑤解析:解:①AC BE ⊥,由题意及图形知,AC ⊥面DD 1B 1B ,故可得出AC BE ⊥,此命题正确;②EF ∥平面ABCD ,由正方体ABCD-A 1B 1C 1D 1的两个底面平行,EF 在其一面上,故EF 与平面ABCD 无公共点,故有EF ∥平面ABCD ,此命题正确;③由图知,当F 与B 1重合时,令上底面顶点为O ,则此时两异面直线所成的角是∠A 1AO ,当E 与D 1重合时,此时点F 与O 重合,则两异面直线所成的角是∠OBC 1,此二角不相等,故异面直线AE 、BF 所成的角不为定值,故不正确.④A 1点到面DD 1B 1B 距离是定值,所以A 1点到面BEF 的距离为定值,正确;⑤三棱锥A-BEF 的体积为定值,由几何体的性质及图形知,三角形BEF 的面积是定值,A 点到面DD 1B 1B 距离是定值,故可得三棱锥A-BEF 的体积为定值,此命题正确.故答案为:①②④⑤.评卷人得 分三.简答题(共__小题)16、如图,立体图形A-BCD 的四个面分别为△ABC 、△ACD 、△ADB 和△BCD ,E 、F 、G 分别是线段AB 、AC 、AD 上的点,且满足AE :AB=AF :AC=AG :AD ,求证:△EFG BCD ∽△.答案:证明:在△ABD 中,∵AE :AB=AG :AD ,∴EG BD ∥.同理,GF DC ∥,EF BC ∥.又∠GEF 与∠DBC 方向相同.∴∠GEF=DBC ∠.同理,∠EGF=BDC ∠.∴△EFG BCD ∽△.17、如图,在三棱锥D-ABC 中,已知△BCD 是正三角形,AB ⊥平面BCD ,AB=BC=a ,E 为BC 的中点,F 在棱AC 上,且AF=3FC .(1)求三棱锥D-ABC 的表面积;(2)求证AC ⊥平面DEF ;(3)若M 为BD 的中点,问AC 上是否存在一点N ,使MN ∥平面DEF ?若存在,说明点N 的位置;若不存在,试说明理由.答案:解:(1)∵AB ⊥平面BCD ,∴AB BC ⊥,AB BD ⊥.∵△BCD 是正三角形,且AB=BC=a ,∴AD=AC=.设G 为CD 的中点,则CG=,AG=.∴,,.三棱锥D-ABC 的表面积为.(2)取AC 的中点H ,∵AB=BC ,∴BH AC ⊥.∵AF=3FC ,∴F 为CH 的中点.∵E 为BC 的中点,∴EF BH ∥.则EF AC ⊥.∵△BCD 是正三角形,∴DE BC ⊥.∵AB ⊥平面BCD ,∴AB DE ⊥.∵AB∩BC=B ,∴DE ⊥平面ABC .∴DE AC ⊥.∵DE∩EF=E ,∴AC ⊥平面DEF .(3)存在这样的点N ,当CN=时,MN ∥平面DEF .连CM ,设CM∩DE=O ,连OF .由条件知,O 为△BCD 的重心,CO=CM .∴当CF=CN 时,MN OF ∥.∴CN=.。
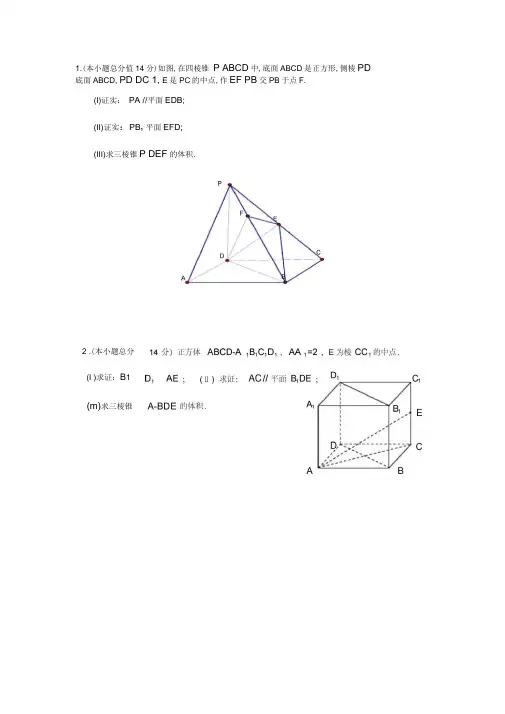
立体几何练习题1.四棱锥ABCD S -中,底面ABCD 为平行四边形,侧面⊥SBC 面ABCD ,已知45=∠ABC ,2=AB ,22=BC ,3==SC SB .(1)设平面SCD 与平面SAB 的交线为l ,求证:AB l //; (2)求证:BC SA ⊥;(3)求直线SD 与面SAB 所成角的正弦值.2.如图,在四棱锥P-ABCD 中,底面ABCD 是平行四边形,,AD=AC=1,O 为AC的中点,PO平面ABCD ,PO=2,M 为PD 的中点。
(1)证明:PB//平面ACM ; (2)证明:AD平面PAC(3)求直线AM 与平面ABCD 所成角的正切值。
如图,四棱锥P ABCD -中,90ABC BAD ∠=∠=︒,2BC AD =,△PAB 与△PAD 都是等边三角形. (1)证明:CD ⊥平面PBD ;(2)求二面角C PB D --的平面角的余弦值.4.如图,四棱锥P ﹣ABCD 中,PA ⊥底面ABCD ,AC ⊥AD .底面ABCD 为梯形,AB ∥DC ,AB ⊥BC ,PA=AB=BC=3,点E 在棱PB 上,且PE=2EB . (Ⅰ)求证:平面PAB ⊥平面PCB ; (Ⅱ)求证:PD ∥平面EAC ;(Ⅲ)求平面AEC 和平面PBC 所成锐二面角的余弦值.5.如图,已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面于直线AB ,平面ABCD 平面ABPE AB =,且2AB BP ==,1AD AE ==,AE AB ⊥,且//AE BP .(1)设点M 为棱PD 中点,在面ABCD 内是否存在点N ,使得MN ⊥平面ABCD ?若存在,请证明;若不存在,请说明理由; (2)求二面角D PE A --的余弦值.如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.(1)求证:AB⊥BC;(2)若直线AC与平面A1BC所成的角为,求锐二面角A﹣A1C﹣B的大小.7.在四棱锥V﹣ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(1)求证AB⊥面VAD;(2)求面VAD与面VDB所成的二面角的大小.8.如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=,对角线AC与BD相交于O,OF⊥平面ABCD,BC=CE=DE=2EF=2.(Ⅰ)求证:EF∥BC;(Ⅱ)求面AOF与平面BCEF所成锐二面角的正弦值.如图,在四棱锥P ﹣ABCD 中,底面为直角梯形,AD ∥BC ,∠BAD=90°,PA ⊥底面ABCD ,且PA=AD=AB=2BC ,M 、N 分别为PC 、PB 的中点. (Ⅰ)求证:PB ⊥DM ;(Ⅱ)求BD 与平面ADMN 所成的角.10.如图,在等腰梯形ABCD 中,//AB CD ,1AD DC CB ===,60ABC ∠=,四边形ACFE为矩形,平面ACFE ⊥平面ABCD ,1CF =. (1)求证:BC ⊥平面ACFE ;(2)点M 在线段EF 上运动,设平面MAB 与平面FCB 二面角的平面角为(90)θθ≤,试求cos θ的取值范围.立体几何试卷答案(2)证明:连接AC ,45222ABC AB BC ∠===,,,由余弦定理得2AC =,AC AB ∴= 6分 取BC 中点G ,连接,SG AG ,则AG BC ⊥.,,,SB SC SG BC SG AG G =∴⊥=BC ∴⊥面,.SAG BC SA ∴⊥ …………………8分(Ⅲ)如图,以射线OA 为x 轴,以射线OB 为y 轴,以射线OS 为z 轴,以O 为原点,建立空间直角坐标系xyz O -,B ySCAD2、试题解析:(1)证明:为AC的中点,即O为BD的中点,且 M为PD的中点,又平面ACM,平面ACM,所以PB//平面ACM。
一、解答题1.(2023高一下·重庆沙坪坝·百强名校期末)如图,有一个正四棱柱,E 、F 高中数学立体几何大题练习与答案分别为底面棱A D 11,D C 11的中点,=AB 4,=AA 61,点G 在AA 1上,且=AA AG 321.(1)判断直线BG 是否在平面BEF 内?说明理由; (2)求二面角A EF G −−1的余弦值.【答案】(1)直线BG 在平面BEF 内,理由见解析【分析】(1)建立空间直角坐标系,求平面BEF 的法向量,根据法向量与BG 的关系可判断;(2)运用几何法,得到二面角的平面角即可求解.【详解】(1)以D 为坐标原点,DA ,DC ,DD 1分别为x ,y ,z 轴建立空间直角坐标系 则E F B G (2,0,6),(0,2,6),(4,4,0),(4,0,4)所以(2,2,0)EF =−,(2,4,6)BE =−−,(0,4,4)BG =−设平面BEF 的法向量为(,,)n x y z =,则(1,1,1)n ⇒=⎩−−+=⎨⎧−++=x y z x y z 24602200所以其0BG n ⋅=且点B 在平面BEF 内,故直线BG 在平面BEF 内.(2)连接B D 11交EF 于O ,连接BO因为平面EFG 与平面BEF 是同一平面,平面A EF 1与平面B EF 1是同一平面, 则BOB 1为二面角−−B EF B 1的平面角,记为又==B O B D 43111,=BB 61所以==BO所以==θBO B O cos 12.(2023·江苏·百强名校期末)如图,在直三棱柱ABC-A 1B 1C 1中,D ,E 分别为AB ,BC 的中点,点F 在侧棱B 1B 上,且⊥B D A F 11 ,⊥AC A B 1111.求证:(1)直线DE 平面A 1C 1F ;(2)平面B 1DE ⊥平面A 1C 1F. 【答案】(1)详见解析(2)详见解析【详解】试题分析:(1)利用线面平行判定定理证明线面平行,而线线平行的寻找往往结合平面几何的知识,如中位线的性质等;(2)利用面面垂直判定定理证明,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直性质定理与判定定理. 试题解析:证明:(1)在直三棱柱111ABC A B C 中,A C 11,AC 在三角形ABC 中,因为D ,E 分别为AB ,BC 的中点, 所以DE AC ,于是11DE AC ,又因为DE ⊄平面⊂AC F AC ,1111平面AC F 11, 所以直线DE//平面AC F 11.(2)在直三棱柱111ABC A B C 中,面平⊥AA A B C 1111 因为⊂AC 11平面A B C 111,所以⊥AA AC 111,又因为面平面平,⊥⊂⊂⋂=AC A B AA ABB A A B ABB A A B AA A ,,111111*********, 所以⊥AC 11平面ABB A 11.因为⊂B D 1平面ABB A 11,所以⊥AC B D 111.又因为面平面平,⊥⊂⊂⋂=B D A F AC AC F A F AC F AC A F A ,,1111111111111, 所以面平⊥B D AC F 111.因为直线面平⊂B D B DE 11,所以面平B DE 1面平⊥AC F .11 【考点】直线与直线、直线与平面、平面与平面的位置关系【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型:(1)证明线面、面面平行,需转化为证明线线平行;(2)证明线面垂直,需转化为证明线线垂直;(3)证明线线垂直,需转化为证明线面垂直;(4)证明面面垂直,需转化为证明线面垂直,进而转化为证明线线垂直.3.(2023高一下·吉林长春·百强名校期末)在四棱锥−P ABCD 中,底面ABCD 是边长为2的菱形,∠=︒BAD 60,若==PA PD ∠=PAB 10cos .(1)证明:平面⊥PAD 平面ABCD ; (2)求二面角−−B PD A 的正切值.【答案】(1)证明见解析;(2 【分析】(1)取AD 中点O ,连结PO ,BO ,BD ,推导出⊥PO AD ,及⊥PO BO ,从而⊥PO 平面ABCD 由此得到平面⊥PAD 平面ABCD .(2)由面面垂直的性质得到⊥BO 平面ABCD ,作⊥OE PD 于E ,由三垂线定理,得⊥BE PD ,从而∠BEO 就是二面角−−B PD A 的平面角,在POD Rt 中,计算各数据,得到所求角的正切值.【详解】(1)证明:取AD 中点O ,连结PO ,BO ,BD ,在PAD 中,=PA PD=AD 2,则⊥PO AD ,===PO 2.在菱形ABCD 中,∠=︒BAD 60,==AB AD 2,∴===AB AD BD 2,∴⊥BO AD ,且===BO PAB 中,∠=PAB cos ,∴=+−⋅⋅∠=+−=PB PA AB PA AB PAB 2cos 54227222. 在POB 中,+=+==OB PO PB 347222,∴⊥PO BO ,且ADBO O =∴⊥PO 平面ABCD .又⊂PO 平面PAD ∴平面⊥PAD 平面ABCD .(2)由(1)知平面⊥PAD 平面ABCD ,且平面⋂PAD 平面=ABCD AD ,且⊥BO AD , ∴⊥BO 平面ABCD ,作⊥OE PD 于E ,由三垂线定理,得⊥BE PD . ∴∠BEO 就是二面角−−B PD A 的平面角,在POD Rt 中,⊥OE PD ,有⋅=⋅PD OE PO OD =⨯OE 21,∴=OE在BOE Rt 中,∠===OE BEO OBtan∴二面角−−B PD A4.(2023高一下·吉林长春·百强名校期末)如图.已知正三棱柱111ABC A B C 的底面边长=AB 6,D ,E 分别是CC 1,BC 的中点,=AE DE .(1)三棱锥−A ECD 的体积; (2)正三棱柱111ABC A B C 的表面积.【答案】(2)【分析】(1)依题意可得⊥AE BC ,在由正三棱柱的性质得到⊥CC BC 1,利用勾股定理求出线段的长度,最后由A ECD D AEC AECV V SCD ==⋅−−31计算可得;(2)求出上下底面积及侧面积,即可求出棱柱的表面积.【详解】(1)因为E 是BC 的中点,ABC 为等边三角形,所以⊥AE BC , 在正三棱柱111ABC A B C 中⊥CC 1平面ABC ,⊂BC 平面ABC ,所以⊥CC BC 1,又=AB 6,所以=EC 3,AE ===AE DE ,所以==CD所以AECS=⨯⨯=231所以33A ECD D AEC AECV V SCD ==⋅=⨯=−−11.(2)由(1)可知==CC CD 211112ABC A B C S S ==⨯⨯=61ABCS CCC =⋅=⨯⨯=侧366210821,所以棱柱的表面积=⨯=S 25.(2023高一下·四川成都·百强名校期末)如图,在四棱锥−P ABCD 中,⊥PC 底面ABCD ,在直角梯形ABCD 中,⊥AB AD ,BC AD //,==AD AB BC 22,E 是PD 中点.求证:(1)CE //平面PAB ; (2)平面⊥PCD 平面ACE . 【答案】(1)证明见解析 (2)证明见解析【分析】(1)取线段AP 的中点F ,可证得四边形BCEF 为平行四边形,从而得到CE BF //,由线面平行的判定可证得结论;(2)由线面垂直性质和勾股定理可分别证得⊥PC AC ,⊥AC CD ,由线面垂直和面面垂直的判定可证得结论.【详解】(1)取线段AP 的中点F ,连接EF BF ,,,E F 分别为PD AP ,中点,∴EF AD //,=EF AD 21, 又BC AD //,=BC AD 21,∴EF BC //,=EF BC , ∴四边形BCEF 为平行四边形,∴CE BF //,BF ⊂平面PAB ,⊄CE 平面PAB ,∴CE //平面PAB . (2)PC ⊥平面ABCD ,⊂AC 平面ABCD ,∴⊥PC AC ; 设=AD 2,则==AB BC 1,//BC AD ,⊥AB AD ,∴⊥AB BC ,∴=AC ==CD∴+=AC CD AD 222,∴⊥AC CD ;PCCD C =,⊂PC CD ,平面PCD ,∴⊥AC 平面PCD ,AC ⊂平面ACE ,∴平面⊥PCD 平面ACE .6.(2023高一下·安徽六安·百强名校期末)在正三角形ABC 中,E ,F ,P 分别是AB 、AC 、BC 边上的点,满足===AE EB CF FA CP PB :::1:2(如图1).将△AEF 沿EF 折起到的1A EF 位置,使平面⊥A EF 1平面BEF ,连结A B 1,P A 1(如图2).(1)求证:FP //平面A EB 1;(2)求直线A E 1与平面A BP 1所成角的大小. 【答案】(1)证明见解析(2)︒60.【分析】(1)依题意可得FP BA //,即FP BE //,从而得证;(2)法一:设E 到面A BP 1距离为h ,根据=−−V V A BPE E A BP 11,即可求得h 的值,进而求解即可.法二:在图1中过点F 作FD BC //交AB 于点D ,即可得到△ADF 为等边三角形,则⊥FE A E 1,再由面面垂直的性质得到⊥A E 1平面BEP ,设A E 1在平面A BP 1内的射影为A Q 1,且A Q 1交BP 于点Q ,则可得⊥BP 平面A EQ 1,则∠E AQ 1就是A E 1与平面A BP 1所成的角,再由锐角三角函数计算可得.【详解】(1)∵=CP PB CF FA ::,∴FP BA //, ∴FP BE //,∵⊂BE 平面A EB 1,⊄FP 平面A EB 1,∴BP //平面A EB 1; (2)法一:在图1中过点F 作FD BC //交AB 于点D ,因为===AE EB CF FA CP PB :::1:2, 所以==BD AD CF AF ::1:2,即D 、E 为AB 的三等分点,所以E 为AD 的中点,又ABC 为等边三角形,所以△ADF 也为等边三角形, 所以⊥FE AD ,则⊥FE A E 1,又平面⊥A EF 1平面BEF ,平面A EF 1平面=BEF FE ,⊂A E 1平面A EF 1,所以在图2中,⊥A E 1平面BEP ,又⊂BP 平面BEP ,∴⊥A E BP 1,设A E 1在平面A BP 1内的射影为A Q 1,且A Q 1交BP 于点Q , 则可得⊥BP 平面A EQ 1,又⊂AQ 1平面A EQ 1,∴⊥BP AQ 1,则∠E AQ 1就是A E 1与平面A BP 1所成的角,设=AB 3,在△EBP 中,∵==BE BP 2,60=︒∠EBP , ∴△EBP 是等边三角形,∴=BE EP ,又⊥A E 1平面BEP ,∴=A B A P 11,∴Q 为BP 的中点,且=EQ又=A E 11,在1A EQ Rt ,∠==A EEA Q EQtan 11601∠=︒EA Q , 所以直线A E 1与平面A BP 1所成的角为︒60.法二:同法一可得⊥A E 1平面BEP ,设E 到面A BP 1距离为h ,设=AB 3,则==A B A P 11,则=−−V V A BPE E A BP 11,∴△△⋅=⋅S A E S h BPE A BP 331111,∴△△⨯===⋅⨯S h S A E A BP BPE 221221111,设A E 1与面A BP 1所成角为θ,则=θA E h sin 1︒≤≤︒θ090,∴=︒θ60. 所以直线A E 1与平面A BP 1所成的角为︒60.7.(2023高一下·重庆沙坪坝·百强名校期末)如图,四边形ABCD 是圆柱下底面的内接四边形,AC 是圆柱底面的直径,PC 是圆柱的一条母线,=AB AD ,∠=BAD 60,点F 在线段AP 上,=PA PF 4.(1)求证:平面⊥PCD 平面PAD ;(2)若==CP CA 4,求直线AC 与平面FCD 所成角的正弦值. 【答案】(1)证明见解析【分析】(1)先证⊥AD 平面PCD ,再根据面面垂直的判定定理可证平面⊥PCD 平面PAD ;(2)以C 为原点,CA 所在直线为x 轴,过C 且垂直于平面APC 的直线为y 轴,CP 所在直线为z 轴,建立空间直角坐标系,利用线面角的向量公式可求出结果. 【详解】(1)因为PC 是圆柱的一条母线,所以⊥PC 底面ABCD , 又⊂AD 底面ABCD ,所以⊥PC AD , 因为AC 是圆柱底面的直径,所以⊥AD CD , 因为⊂PC CD ,平面PCD ,⋂=PC CD C , 所以⊥AD 平面PCD ,又因为⊂AD 平面PAD ,所以平面⊥PCD 平面PAD .(2)以C 为原点,CA 所在直线为x 轴,过C 且垂直于平面APC 的直线为y 轴,CP 所在直线为z 轴,建立空间直角坐标系, 因为=AB AD ,=AC AC ,∠=∠=ADC ABC 2π, 所以R R t ADC t ABC ≅,又∠=BAD 60,所以π6DAC BAC ==, 因为==CP CA 4,=PA PF 4,所以==CD AC221,=AD所以C (0,0,0),A (4,0,0), D ,F (1,0,3), 所以(4,0,0)AC =−,(1,3,0)CD =,(1,0,3)CF =, 设平面FCD 的一个法向量为(,,)n x y z =,则n CD x y n CF x z ⋅=+=⋅=+=⎩⎪⎨⎪⎧3030,取=−x 3,得y =z 1,则(3,3,1)n =−,设直线AC 与平面FCD 所成角为θ,则sin cos ,||||AC n AC n AC n ⋅=<>=θ==.即直线AC 与平面FCD 所成角的正弦值为13.8.(2023高一下·重庆沙坪坝·百强名校期末)如图,在四棱锥−P ABCD 中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD ,=PD DC ,E 、F 分别是PC 、AD 中点.(1)求证:DE //平面PFB ;(2)求PC 与面PFB 所成角的正弦值.【答案】(1)见解析;(2【分析】(1)取PB 的中点为G ,连接EG FG ,,可证四边形DEGF 为平行四边形,从而可证DE //平面PFB ;(2)利用等积法可求C 到平面PFB 的距离,从而可求PC 与面PFB 所成角的正弦值. 【详解】(1)取PB 的中点为G ,连接EG FG ,, 因为E G ,分别为所在棱的中点,故=EG BC EG BC 2//,1, 而=DF AD 21,=AD BC AD BC //,,故=EG DF EG DF //,, 故四边形DEGF 为平行四边形,所以FG DE //, 而⊂FG 平面PBF ,⊄DE 平面PBF ,故DE //平面PFB .(2)设=DC a ,连接CF ,设C 到平面PBF 的距离为h .因为⊥PD 底面ABCD ,⊂CD 平面ABCD ,故⊥PD CD ,同理⊥⊥PD AD PD BC ,, 而=PD DC,故PC .故=PF a 2,同理=BF a 2. 因为⊥BC CD ,而⋂=PD DC D ,故⊥BC 平面PCD , 而⊂PC 平面PCD ,故⊥BC PC,所以==PB ,故△==S a PFB 2412, 又△=⨯⨯=S a a a FCB2212, 因为=−−V V P FCB C PFB,故⨯⨯=⨯a a h 32311122,故=h ,设PC 与面PFB 所成角为θ,则=θsin9.(2023高一·全国·课后作业)如图,在三棱锥P ABC −中,∠=︒ACB 90,⊥PA 底面ABC(1)证明:平面⊥PBC 平面P AC(2)若==AC BC PA ,M 是PB 中点,求AM 与平面PBC 所成角的正切值 【答案】(1)证明见解析【分析】(1)由∠=︒ACB 90,得到⊥AC CB ,再根据⊥PA 底面ABC ,得到⊥PA CB ,然后利用线面垂直和面面垂直的判定定理证明;(2)作⊥AO PC ,连接OM ,由平面⊥PBC 平面P AC ,得到⊥AO 平面PBC , 则∠AMO 即为AM 与平面PBC 所成的角求解. 【详解】(1)证明:因为∠=︒ACB 90, 所以⊥AC CB ,又⊥PA 底面ABC , 所以⊥PA CB ,又⋂=AC PA A , 所以⊥BC 平面P AC , 因为⊂BC 平面PBC , 所以平面⊥PBC 平面P AC ; (2)如图所示:作⊥AO PC ,连接OM ,因为平面⊥PBC 平面P AC ,平面⋂PBC 平面P AC=PC , 所以⊥AO 平面PBC ,则∠AMO 即为AM 与平面PBC 所成的角,设===AC BC PA t ,则==AB PB ,,所以=AM 2,又=AO 2,所以==OM t 21,所以AM 与平面PBC 所成角的正切值为∠==OMAMO AOtan10.(2023高一下·重庆北碚·百强名校期末)如图,四棱锥S —ABCD 中,底面ABCD 为菱形,602ABC SA SD AB ====,∠,侧面SAB ⊥侧面SBC ,M 为AD 的中点.(1)求证:平面SMC ⊥平面SBC ;(2)若AB 与平面SBC 成30角时,求二面角−−A SC D 的大小, 【答案】(1)证明见解析 (2)︒90【分析】(1)由线面垂直与面面垂直的判定定理求解即可;(2)取BS 的中点N ,连接AN ,由题意可得=BS CS 的中点E ,连接AE DE ,,可证明∠AED 是二面角−=A SC D 的平面角,求出角∠AED 的大小即可求解 【详解】(1)因为=SD SA ,又M 为AD 的中点, 所以⊥SM AD , 又BC AD //, 所以⊥SM BC ,又M 为AD 的中点,底面ABCD 为菱形,∠=︒ABC 60, 所以⊥CM AD AD BC ,//, 所以⊥CM BC ,因为⊥CM BC ,⊥SM BC ,⊥=SM CM M ,⊂SM 平面SCM ,⊂CM 平面SCM ,所以⊥BC 平面SCM ,因为⊂BC 平面SBC , 所以平面⊥SBC 平面SCM ,(2)取BS 的中点N ,连接AN ,又=SA AB , 所以⊥AN BS ,又平面⊥SAB 平面SBC ,平面SAB 平面=SBC SB ,⊂AN 平面SAB ,所以⊥AN 平面SBC ,又AB 与平面SBC 所成的角为︒30, 所以∠=︒ABN 30, 又=⊥AB AN BN 2,,所以===AN BN BS 1,由(1)知⊥BC 平面SCM ,又⊂SC 平面SBC , 所以⊥BC SC ,又==BS BC 2,所以==CS 取CS 的中点E ,连接AE DE ,, 因为===SA AC CD SD , 所以⊥⊥AE CS DE CS ,,所以∠AED 是二面角−=A SC D 的平面角,又====AC CD CE CS 22,1所以==AE 又+=+==AE DE AD 224222, 所以⊥AE DE ,即∠=︒AED 90, 所以二面角−=A SC D 的大小为︒90,11.(2023高一下·重庆北碚·百强名校期末)如图,三棱柱ABC —A B C 111的底面是等腰直角三角形,侧面BB 1C 1C 是矩形,∠=CAB 90,==AB AC AA 1 ,点P 是棱A B 11的中点,且P 在平面ABC 内的射影O 在线段BC 上,=BO BC 41,点M ,N 分别是线段CP ,CA 的中点(1)求证: MN //平面AA B B 11 (2)求二面角−−M AC B 的正切值. 【答案】(1)见解析【分析】(1)连接AP ,则由三角形中位线定理可得MN ∥AP ,然后利用线面平行的判定定理可证得结论,(2)连接OB 1,取CO 的中点E ,连接ME ,过点E 作⊥EF AC 于F ,连接MF ,可证得∠MFE 为 二面角−−M AC B 的平面角,然后计算即可 【详解】(1)证明:连接AP ,因为M ,N 分别是线段CP ,CA 的中点, 所以MN ∥AP ,因为⊄MN 平面AA B B 11,⊂AP 平面AA B B 11, 所以MN ∥平面AA B B 11,(2)解:连接OB 1,取CO 的中点E ,连接ME ,过点E 作⊥EF AC 于F ,连接MF , 因为M ,是线段CP 的中点,所以ME ∥OP ,=ME OP 21,因为⊥OP 平面ABC ,所以⊥ME 平面ABC , 因为⊂AC 平面ABC ,所以⊥ME AC , 因为⋂=ME EF E , 所以⊥AC 平面MEF ,因为⊂MF 平面MEF ,所以⊥AC MF , 所以∠MFE 为 二面角−−M AC B 的平面角, 设===AB AC AA 21,因为∠=CAB 90,所以=BC所以==BO BC 41==CO BC 43,所以==CE CO 21,=︒==EF CE 4sin 453, 在1OBB Rt 中,=+=+=OB OB BB 2241911222, 因为⊥OP 平面ABC ,平面ABC ∥平面A B C 111, 所以⊥OP 平面A B C 111, 因为⊂A B 11平面A B C 111, 所以⊥OP A B 11,所以===OP 2,所以==ME OP 21,在MEF Rt 中,∠===EF MEF ME 43tan 4,所以二面角−−M AC B 的正切值为312.(2023高一下·重庆渝中·百强名校期末)如图;正四棱柱−ABCD A B C D 1111中;=AA AB 21;点P 为DD 1的中点.(1)求证:直线∥BD 1平面PAC ;(2)求直线BC 1与平面APC 所成线面角的正弦值. 【答案】(1)证明见解析(2)15【分析】(1)设AC 和BD 交于点O ,则O 为BD 的中点,连接PO ,可得PO BD //1,可得直线BD //1平面PAC ;(2)设==AA AB 241,利用等体积法可求点D 到平面APC 的距离为d ,进而利用直线BC 1与平面APC 所成线面角与直线AD 1与平面APC 所成线面角相等,可求直线BC 1与平面APC 所成线面角的正弦值.【详解】(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点,连接PO ,P 是DD 1的中点,∴PO BD //1,又PO ⊂平面PAC ,⊂BD 1平面PAC ,∴直线BD //1平面PAC ,(2)设==AA AB 241,则三角形APC为正三角形,===AP AC PC ,APCSAP ==42 设点D 到平面APC 的距离为d ,由等体积法:=−−V V P ADC D APC , 所以1133ADC APCPD Sd S ⋅=⋅,则ADC APC PD S S ===⋅d 233423,由点P 为中点,所以点D ,D 1到平面APC 距离相等,由AD BC //11,所以直线BC1与平面APC 所成线面角与直线AD 1与平面APC 所成线面角相等, 设直线AD1与平面APC 所成线面角为θ,所以==θAD d sin 1∴直线BC 1与平面APC 所成线面角的正弦值为15.13.(2023高一下·重庆沙坪坝·百强名校期末)如图,在直三棱柱111ABC A B C 中,∠=︒BAC 90,===AB AC AA 21,M 为AB 的中点,点G 为△A B C 111的重心.(1)证明:BG 平面ACM 1(2)求三棱锥−G A MC 1的体积. 【答案】(1)证明见解析; (2)32.【分析】(1)先证明平面BGN //平面ACM 1,再由面面平行的性质可得线面平行; (2)利用等体积法求解即可.【详解】(1)连接C G 1并延长交A B 11于点N ,连接BN CM BG ,,,如图,在直三棱柱111ABC A B C 中,点G 为△A B C 111的重心, 所以C N CM //1,又⊄C N 1平面ACM 1,⊂CM 平面ACM 1, 所以C N //1平面ACM 1,因为A N BM A N BM //,=11,所以四边形BMA N 1是平行四边形, 所以BN A M //1,又⊄BN 平面ACM 1,⊂A M 1平面ACM 1, 所以BN //平面ACM 1,又1=BN C N N ,所以平面BGN //平面ACM 1, 又⊂BG 平面BGN ,所以BG 平面ACM 1.(2)由(1)知BG平面ACM 1, 所以==−−−V V V G A MC B A MC A BMC 111, 三棱锥−A BMC 1的高=A A 21,△=⋅=⨯⨯=S BM AC BMC 2212111, 所以△==⋅=⨯⨯=−−V V AA S G A MC A BMC BMC 33321112111. 14.(2023高一下·重庆沙坪坝·百强名校期末)在直三棱柱111ABC A B C 中,=AB 3,=BC 4,=AA 21,︒∠=ABC 90,点D 为AC 的中点.(1)求证:AB 1//平面C BD 1; (2)求三棱锥−B BDC 11的体积. 【答案】(1)证明见详解 (2)2【分析】(1)根据线面平行的判定定理分析证明;(2)根据题意可证⊥AB 平面BCC B 11,再利用转换顶点法求体积. 【详解】(1)连接B C 1交BC 1于点O ,连接DO , 因为BCC B 11为平行四边形,则O 为B C 1的中点, 且点D 为AC 的中点,则AB 1//DO ,又因为⊄AB 1平面C BD 1,⊂DO 平面C BD 1, 所以AB 1//平面C BD 1.(2)因为⊥BB 1平面ABC ,⊂AB 平面ABC ,所以⊥BB AB 1, 又因为⊥AB BC , 且BB BC B =1,⊂BB BC ,1平面BCC B 11,所以⊥AB 平面BCC B 11,且点D 为AC 的中点,故三棱锥−D BB C 11的高为=AB 2213,所以三棱锥−B BDC 11的体积==⨯⨯⨯⨯=−−V V B BDC D BB C 3222421311111.15.(2023·江苏苏州·百强名校期末)如图,在三棱锥P ABC −中,ABC 是边长为等边三角形,且===PA PB PC 6,⊥PD 平面ABC ,垂足为⊥D DE ,平面PAB ,垂足为E ,连接PE 并延长交AB 于点G .(1)求二面角P AB C 的余弦值;(2)在平面PAC 内找一点F ,使得⊥EF 平面PAC ,说明作法及理由,并求四面体PDEF 的体积.【答案】(2)答案见解析,34.【分析】(1)根据条件确定∠PGD 就是二面角PAB C 的平面角,构造三角形求解;(2)根据给定的条件知⊥PB 平面PAC ,过点E 作PB 的平行线与P A 交于F ,则⊥EF 平面P AC ,再求出三棱锥−P EFD 的底面积和高即可.【详解】(1)PA PB PC ==,并且ABC 是等边三角形,∴三棱锥P ABC −是正三棱锥,D 是ABC 的中心,点G 是AB 边的中点;由⊥PD 平面ABC , ⊥DE 平面PAB ,⊂AB 平面PAB ,可知⊥⊥⋂=AB PD AB DE PD DE D ,,,⊂PD 平面PDG ,⊂DE 平面PDG ,所以⊥AB 平面PDG ,进而得⊥⊥AB PG AB DG ,, 所以∠PGD 就是二面角PAB C 的平面角,又ABC 是边长为===PA PB PC 6,+=PA PB AB 222,PAB ∴是等腰直角三角形,同理△△PAC PBC ,都是等腰直角三角形;∴==PG AB 21===GD CG 3311∠==PG PGD GD cos P AB C ;(2),,,PB PC PB PA PA PC P PA ⊥⊥=⊂平面PAC ,⊂PC 平面PAC , ∴⊥PB 平面PAC ,同理⊥PC 平面PAB ,又⊥DE 平面PAB ,∴ED PC //,∴E 与点P ,D ,C 共面,即E 点在线段PG 上,又,2EDGPGC ED PC ∴==31,===PG CG PE PE CD 3,2∠=APG 4π,过E 点在平面P AB 内作PB 的平行线,与P A 交于F ,则⊥EF 平面PAC , PEF 也是等腰直角三角形,==EF2, 又⊥DE 平面P AB ,⊂EF 平面P AB ,∴⊥DE EF ,将PEF 作为底面,则ED 是三棱锥−D PEF 的高,11143323P DEF D PEF PEFV V SDE ∴===⨯⨯⨯⨯=−−222,即四面体PDEF 的体积为34.16.(2023·上海嘉定·百强名校期末)在长方体−ABCD A B C D 1111中,==AD DD 11,=AB E 、F 、G 分别为AB 、BC 、C D 11的中点.(1)求三棱锥−A GEF 的体积;(2)点P 在矩形ABCD 内,若直线D P //1平面EFG ,求线段D P 1长度的最小值.【答案】【分析】(1)等体积由=−−V V A GEF G AEF 可得.(2)先证平面EFG //平面ACD 1,则由直线D P //1平面EFG 可得点P 在直线AC 上,进而可得线段D P 1长度的最小值【详解】(1)依题意有AEFSAE BF =⋅⋅=⋅=22228111,所以三棱锥−A GEF 的体积1133A GEF G AEF AEFV V SDD ==⋅⋅==−−11 (2)如图,连结D A D C AC ,,11,∵E F G ,,分别为AB BC C D ,,11的中点,∴⊄AC EF EF //,平面ACD 1,⊂AC 平面ACD 1, ∴EF //平面ACD ,1∵⊄EG AD EG //,1平面ACD 1,⊂AD 1平面ACD 1,∴EG //平面ACD 1, ∵EFEG E =,∴平面EFG //平面ACD 1,∵D P //1平面EFG ,∴点P 在直线AC 上,在△ACD 1中,AD AC CD ===2,211,1AD CS==21∴当⊥D P AC 1时,线段D P 1的长度最小,最小值为△⨯⨯AC S AD C 22211=21=2. 17.(2023高一下·安徽合肥·百强名校期末)在多面体ABCDE 中,=BC BA ,DE BC //,AE ⊥平面BCDE ,=BC DE 2,F 为AB 的中点.(1)求证:EF //平面ACD ;(2)若==EA EBCD ,求二面角−−B AD E 的平面角正弦值的大小. 【答案】(1)证明见解析【分析】(1)取AC 中点G ,连接DG FG ,,由已知得四边形DEFG 是平行四边形,由此能证明EF //平面ACD .(2)过点B 作BM 垂直DE 的延长线于点M ,过M 作⊥MH AD ,垂足为H ,连接BH ,则∠BHM 是二面角−−B AD E 的平面角,由此即可求出二面角−−B AD E 的正弦值的大小.【详解】(1)证明:取AC 中点G ,连接DG ,FG .因为F 是AB 的中点,所以FG 是ABC 的中位线, 则∥FG BC ,=FG BC 21,所以∥FG DE ,=FG DE , 则四边形DEFG 是平行四边形,所以∥EF DG ,又⊄EF 平面ACD ,⊂DG 平面ACD ,故∥EF 平面ACD . (2)过点B 作BM 垂直DE 的延长线于点M ,因为AE ⊥平面BCDE ,⊂BM 平面ADE ,所以⊥AE BM , 且⊥BM DE ,、DE AE平面ADE ,DEAE E =,则⊥BM 平面ADE ,⊂AD 平面ADE ,⊥BM AD , 过M 作⊥MH AD ,垂足为H ,连接BH ,、⊂BM MH 平面BMH ,BM MH M =,则⊥AD 平面BMH ,所以⊥AD BH ,则∠BHM 是二面角−−B AD E 的平面角.设=DE a ,则==BC AB a 2,在△BEM 中,=EM a2,=BE ,所以=BM .又因为△△∽ADE MDH ,所以=HM ,则∠=BHM 6tan∴∠=BHM 13sin . 18.(2023高一下·浙江绍兴·百强名校期末)如图,四棱锥−P ABCD 中,∠=∠=︒ABC BCD 90,∆PAD 是以AD 为底的等腰直角三角形,===AB BC CD 224,E为BC 中点,且=PE(Ⅰ)求证:平面⊥PAD 平面ABCD ; (Ⅱ)求直线PE 与平面PAB 所成角的正弦值.【答案】(Ⅰ)见解析(Ⅱ【分析】(Ⅰ) 过P 作AD 垂线,垂足为F ,由=+PE PF FE 222得,︒∠=PFE 90.又⊥PF AD ,可得⊥PF 平面ABCD ,即可证明.(Ⅱ)易得E 到平面PAB 距离等于F 到平面PAB 距离.过F 作AB 垂线,垂足为G ,在∆PFG 中,过F 作PG 垂线,垂足为Q ,可证得:⊥FQ 平面PAB .求得:FQ ,从而==θPE FQ sin ,即可求解. 【详解】(Ⅰ) 过P 作AD 垂线,垂足为F ,由=+PE PF FE 222得,︒∠=PFE 90. 又⊥PF AD ,∴⊥PF 平面ABCD , ∴平面⊥PAD 平面ABCD ;(Ⅱ)∵EF AB //,∴E 到平面PAB 距离等于F 到平面PAB 距离. 过F 作AB 垂线,垂足为G ,在∆PFG 中,过F 作PG 垂线,垂足为Q , 可证得:⊥FQ 平面PAB .求得:=FQ ,从而=θPE FQ sin即直线PE 与平面PAB【点睛】本题考查面面垂直的证明,考查线面角的求解、是中档题.19.(2023高一下·湖南长沙·百强名校期末)已知正三棱柱111ABC A B C 中,=AB 2,M是B C 11的中点.(1)求证:AC //1平面A MB 1;(2)点P 是直线AC 1上的一点,当AC 1与平面ABC 所成的角的正切值为2时,求三棱锥−P A MB 1的体积. 【答案】(1)证明见解析【分析】(1)连接AB 1交A B 1于点N ,连接MN ,利用中位线的性质可得出MN AC //1,再利用线面平行的判定定理可证得结论成立;(2)利用线面角的定义可求得CC 1的长,分析可知点P 到平面A MB 1的距离等于点C 1到平面A MB 1的距离,可得出==−−−V V V P A MB C A MB B A C M 11111,结合锥体的体积公式可求得结果. 【详解】(1)证明:连接AB 1交A B 1于点N ,连接MN ,因为四边形AA B B 11为平行四边形,⋂=AB A B N 11,则N 为AB 1的中点, 因为M 为B C 11的中点,则MN AC //1,1AC ⊄平面A MB 1,⊂MN 平面A MB 1,故AC //1平面A MB 1.(2)解:因为⊥CC 1平面ABC ,∴AC 1与平面ABC 所成的角为∠CAC 1, 因为ABC 是边长为2的等边三角形,则=AC 2,1CC ⊥平面ABC ,⊂AC 平面ABC ,∴⊥CC AC 1,则∠==ACCAC CC tan 211, 所以,==CC AC 241,1//AC 平面A MB 1,∈P AC 1,所以,点P 到平面A MB 1的距离等于点C 1到平面A MB 1的距离,因为M 为B C 11的中点,则△△===S S A MC A B C 22211211111则△===⋅=⨯−−−V V V BB S P A MB C A MB B A C M A C M 3341111111111. 20.(2023高一下·湖南长沙·百强名校期末)如图,在棱长为3的正方体ABCD −A'B'C'D'中,M 为AD 的中点.(1)求证:'DB //平面'BMA ;(2)在体对角线'DB 上是否存在动点Q ,使得AQ ⊥平面'BMA ?若存在,求出DQ 的长;若不存在,请说明理由. 【答案】(1)证明见解析 (2)【分析】(1)连接'AB 交'BA 于点E ,连接EM ,证得'EM DB //,结合线面平行的判定定理,即可证得'DB //面'BMA .(2)根据题意,证得BA ⊥'平面'ADB ,得到平面⊥'BMA 平面'ADB ,作⊥'AQ DB ,利用面面垂直的性质,证得⊥AQ 平面'BMA ,再由△△∽'ADB QDA Rt Rt ,即可求得DQ 的长. 【详解】(1)证明:连接'AB ,交'BA 于点E ,连接EM . 因为四边形''ABB A 是正方形,所以E 是'AB 的中点, 又M 是AD 的中点,所以'EM DB //,因为⊂EM 面'BMA ,/⊂'DB 面'BMA ,所以'DB //面'BMA .(2)在对角线'DB 上存在点Q ,且=DQ ⊥AQ 平面'BMA , 证明如下:因为四边形''ABB A 是正方形,所以⊥''AB BA , 因为⊥AD 平面''ABB A ,⊂'BA 面''ABB A ,所以⊥'AD BA , 因为AB AD A =',且⊂'AB AD ,平面'ADB ,所以BA ⊥'平面'ADB ,因为⊂'BA 平面'BMA ,所以平面⊥'BMA 平面'ADB , 作⊥'AQ DB 于Q ,因为'EM DB //,所以⊥AQ EM ,因为⊂AQ 平面'ADB ,平面'ADB 平面='BMA EM ,所以⊥AQ 平面'BMA ,由△△∽'ADB QDA Rt Rt ,可得'==DB DQ AD 2所以当=DQ ⊥AQ 平面'BMA .21.(2023高一下·湖南长沙·百强名校期末)如图,在四棱锥P −中,底面ABCD 为正方形,侧面ADP 是正三角形,侧面ADP ⊥底面ABCD ,M 是DP 的中点.(1)求证:AM ⊥平面CDP ;(2)求直线BP 与底面ABCD 所成角的正弦值. 【答案】(1)证明见解析【分析】(1)先证得⊥AM DP ,由⊥CD AD ,结合面面垂直的性质,证得⊥CD 平面ADP ,进而得到⊥CD AM ,利用线面垂直的判定定理,即可证得⊥AM 平面CDP ; (2)取AD 的中点E ,连BE ,EP ,证得⊥PE 平面ABCD ,得到∠EBP 是所求直线与平面所成角,在直角△BEP 中,即可求解.【详解】(1)证明:因为侧面ADP 为正三角形,且M 为DP 中点,所以⊥AM DP , 又因为底面ABCD 为正方形,所以⊥CD AD .因为平面⊥ADP 平面ABCD 且平面⋂ADP 平面=ABCD AD ,⊂CD 平面ABCD , 所以⊥CD 平面ADP ,又因为⊂AM 平面ADP ,所以⊥CD AM , 因为CDDP D =,且⊂CD DP ,平面CDP ,所以⊥AM 平面CDP .(2)解:取AD 的中点E ,连BE ,EP ,因为△ADP 为正三角形,且E 为AD 中点,所以⊥PE AD ,又因为平面⊥ADP 平面ABCD ,平面⋂ADP 平面=ABCD AD ,且⊂PE 平面PAD , 所以⊥PE 平面ABCD ,所以∠EBP 是所求直线与平面所成角,不妨设=AD a 2,则在等边△ADP 中,可得EP =,在直角ABE 中,==BE ;在直角中,=BP ,故∠==BP EBP EP sin所以直线与底面22.(2023高一下·浙江·百强名校期末)如图,正三棱柱的底面边长为2,高,过的截面与上底面交于PQ ,且点是棱A C 11的中点,点在棱上.(1)试在棱上找一点,使得QD //平面,并加以证明;(2)求四棱锥−C ABQP 的体积. 【答案】(1)点为棱的中点,证明见解析;(2)43.【分析】(1)证法1:取的中点,连接DM ,B M 1,可得A B //11平面ABQP ,再由线面平行的性质可得A B PQ //11,则可得是棱的中点,由三角形中位线定理结合已知可得四边形DMB Q 1是平行四边形,可得QD B M //1,然后由线面平行的判定定理可证得结论;证法2:由已知条件可证得PQ //平面,从而得PDAA 1是平行四边形,PD AA //1,由线面平行的判定可得PD //面,从而得面PDQ //面,再由面面平行的性质可得结论; (2)解法一:连接,四棱锥−C ABQP 可视为三棱锥−C BPQ 和−C ABP 组合而成,然后分别求出两个三棱锥的体积即可;解法二:分别取和的中点,,连接,CM ,连接C N 1交PQ 于点,连接MG ,CG ,可证得平面⊥ABQP 平面CMNC 1,则⊥CG 平面ABQP ,然后结合已知条件求出等腰梯形ABQP 的面积,从而可求得四棱锥的体积【详解】(1)证法1:点为棱的中点,证明如下:取的中点,连接DM ,B M 1.∵AB A B //11,平面ABQP ,⊄A B 11平面ABQP ,∴A B //11平面ABQP ,∵平面,平面ABQP 平面=A B C PQ 111,∴A B PQ //11.又是棱A C 11的中点,∴是棱的中点,∴QB 1∥,=QB BC 211 ∵,分别为棱,的中点,∴DM ∥,=DM BC 21∴QB 1∥DM ,=QB DM 1∴四边形DMB Q 1是平行四边形,∴QD B M //1, ∵⊂B M 1平面,⊄OD 平面,∴QD //平面.证法2:为的中点时,QD //平面.证明如下: ∵AB //平面,平面ABQP ,平面ABQP 平面=A B C PQ 111,∴PQ AB //,⊄PQ 平面,平面,所以PQ //平面,又∵为的中点,为A C 11的中点,∴PDAA 1是平行四边形,∴PD AA //1,又∵⊄PD 平面,⊂AA 1平面,∴PD //面,又∵与PQ 在平面PDQ 内相交,∴面PDQ //面,又∵⊂QD 面PDQ ,∴DQ //平面.(2)解法一:连接,四棱锥−C ABQP 可视为三棱锥−C BPQ 和−C ABP 组合而成,三棱锥−C ABP 可视为,底面积ABCS==22,设=−V V C BAP 1,体积为==V 32111.三棱锥−C BPQ 与−C ABP 等高,体积比为底面积之比,设=−V V C BPQ 2,则△△===V V S S PQ AB BPQ BAP :::1:221,故==V V 241121,因此,=+=−V V V C ABPQ 4312,即为所求. 解法二:分别取和的中点,,连接,CM ,连接C N 1交PQ 于点,连接MG ,CG . ∵和是正三角形,且,分别是和的中点, ∴⊥CM AB ,且CM ∥C N 1,=CM C N 1,则,,,四点共面.∵平面,平面,∴⊥CC AB 1,又平面CMNC 1,⊂CC 1平面CMNC 1,⋂=CM CC C 1,∴平面CMNC 1,∵平面ABQP ,∴平面⊥ABQP 平面CMNC 1.在矩形CMNC 1中,==MN CC 1===CN CM AB 1∴===C G NG CC MN 11,∴∠=∠=︒C GC NGM 451,且==CG 1,∴∠=︒CGM 90,即⊥CG MG .又平面⊥ABQP 平面CMNC 1,平面ABQP 平面=CMNC MG 1,⊂CG 平面CMNC 1,∴⊥CG 平面ABQP .在等腰梯形ABQP 中,==PQ A B 21111,,===BQ AP∴等腰梯形ABQP 的高=h , ∴四棱锥−C ABQP 的体积形梯=⋅=⨯+⨯V CG S CG PQ AB hABQP 332111)(=+=32412113)(.23.(2023高一下·广西玉林·百强名校期末)在如图所示的七面体AA B C D C 1111中,四边形A B C D 1111为边长为2的正方形, ⊥AA 1平面A B C D 1111,∥CC AA 11,且==CC AA 211,,,分别是C C 1,,的中点.(1)求点到平面MNP 的距离;(2)若直线A C 11交PN 于点,直线交平面MNP 于点,证明:,,三点共线.【答案】(1)(2)证明见解析【分析】(1)利用三棱锥体积转换思想,先求三棱锥−C MNP 1的体积,再确定底面积△MNP ,最后得点到平面MNP 的距离即可【详解】(1)解:==⨯⨯⨯⨯=−−V V C MNP M C NP 32611111111记到平面MNP 的距离为d ,在△MNP 中,===MN NP MP △==S MNP 2221,∴△==−S d V MNPC 31MNP 1,(2)证明:∵∥AA CC 11, ∴与确定平面AA C C 11,∵,∈E 平面AA C C 11,且,∈E 平面MNP ,∴平面AAC C11平面=PMN ME ,∵⋂AC 1平面=MPN F ,∴∈F 平面PMN ,∈F 平面AA C C 11, ∴点在直线上,则,,三点共线.24.(2023高一下·福建泉州·百强名校期末)如图所示,在四棱锥中,已知P A ⊥底面ABCD ,且底面ABCD 为梯形,,,====PA AD BC AB 33,点E 在线段PD 上,=PD PE 3.(1)求证:CE //平面P AB ; (2)求证:平面P AC ⊥平面PCD . 【答案】(1)证明见解析 (2)证明见解析【分析】(1)由线面平行的判定定理证明即可; (2)由线面垂直与面面垂直的判定定理证明即可【详解】(1)(1)过E 作EF AD //交P A 于点F ,连接BF , 因为,所以EF BC //.又=PD PE 3,所以=AD EF 3. 又=AD BC 3,所以所以四边形BCEF 为平行四边形, 所以CE BF //,又CE ⊄平面P AB ,BF ⊂平面P AB , 所以CE //平面P AB .。
⾼中数学⽴体⼏何专题练习题1(含答案)⾼中数学⽴体⼏何专题练习题姓名班级学号得分说明:1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(⾮选择题)两部分。
满分100分。
考试时间90分钟。
2、考⽣请将第Ⅰ卷选择题的正确选项填在答题框内,第Ⅱ卷直接答在试卷上。
考试结束后,只收第Ⅱ卷第Ⅰ卷(选择题)⼀、选择题(每题2分,共40分)1、⼀个正⽅体的展开图如图所⽰,A、B、C、D为原正⽅体的顶点,则在原来的正⽅体中A.AB∥ CDB. AB与 CD相交C. AB⊥CDD. AB与CD所成的⾓为60°2、(多选)如果⼀个棱锥的底⾯是正⽅形,且顶点在底⾯内的射影是底⾯的中⼼,那么这样的棱锥叫正四棱锥.若⼀正四棱锥的体积为18,则该正四棱锥的侧⾯积最⼩时,以下结论正确的是().A.棱的⾼与底边长的⽐为 22B.侧棱与底⾯所成的⾓为π4C.棱锥的⾼与底⾯边长的⽐为 2 D.侧棱与底⾯所成的⾓为π33、某⼏何体的三视图如图所⽰,则该⼏何体的体积为()A .43B .4C .2D .234、某⼏何体的三视图如图所⽰,则此⼏何体的体积为()A.23 B. 1C.43D.135、已知圆锥的轴截⾯为正三⾓形,且边长为2,则圆锥的表⾯积为() A .3π3B .πC .2πD .3π6、如图,在正⽅体中, E 为线段A 1C 1的中点,则异⾯直线与所成⾓的⼤⼩为()度.A. 60B. 45C. 30D. 157、已知⼀个⽔平放置的平⾯四边形ABCD 的直观图是⾯积为2的正⽅形,则原四边形ABCD 的⾯积为()A .2B .22C .2 2D .4 28、下列说法正确的是()A .通过圆台侧⾯上⼀点可以做出⽆数条母线B .直⾓三⾓形绕其⼀边所在直线旋转⼀周得到的⼏何体是圆锥C .圆柱的上底⾯下底⾯互相平⾏D .五棱锥只有五条棱9、如图,是⼀个⼏何体的三视图,主视图和侧视图是全等的半圆,俯视图是⼀个圆,则该⼏何体的体积是()A 、32π3.B .26π3C .16π3D .64π310、某⼏何体的三视图如图所⽰,则该⼏何体的体积为()A. 56B. 23C. 43D. 4511、⼀个⼏何体的三视图如图,则该⼏何体的体积为()A.263 B .283C. 10D.32312、某⼏何体的三视图如图所⽰,则该⼏何体中的最长棱长为()A .3 2B .2 5C .2 6D .2 713、(多选题)如图,在棱长为1的正⽅体中,下列结论正确的是A .异⾯直线AC 与BC1所成的⾓为60°B .直线AB 1与平⾯ABC 1D 1所成⾓为45° C .⼆⾯⾓A-B 1C-B 的正切值为 2D .四⾯体D 1-AB 1C 的的体积为1214、下列命题错误的是A .不在同⼀直线上的三点确定⼀个平⾯B .两两相交且不共点的三条直线确定⼀个平⾯C .如果两个平⾯垂直,那么其中⼀个平⾯内的直线⼀定垂直于另⼀个平⾯D .如果两个平⾯平⾏,那么其中⼀个平⾯内的直线⼀定平⾏于另⼀个平⾯15、某四棱锥的三视图如图所⽰,俯视图是⼀个等腰直⾓三⾓形,则该四棱锥的体积为()A .2B .C. D .16、如图所⽰,O 是正⽅体ABCD-A 1B 1C 1D 1对⾓线A 1C 与AC 1的交点,E 为棱BB 1的中点,则⼏何体OEC 1D 1 在正⽅体各⾯上的正投影不可能是()A. B. C. D.17、如图,在正⽅体ABCD -A1B l C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG =GC1.则下列直线与平⾯A1BD平⾏的是(A) CE (B) CF (C) CG (D) CC118、⼏何体的三视图如图所⽰,则它的体积是A. B.C. D.19、如图,三棱P-ABC中,PC⊥平⾯ABC,PC=3,∠ACB=90°D、E.分别为线段AB、BC上的点,且CD=DE= 2,CE=2EB=2,则⼆⾯⾓A-PD-C的余弦值是().A、 24B、62C、33D、3620、下图为某⼏何体的三视图,则该⼏何体的表⾯积是()A. 6+4B. 4+4C. 6+2D. 4+2⼆、填空题(15分)21、如图,点P在长⽅体ABCD-A1B1C1D1的⾯对⾓线BC1(线段BC1)上运动,给出下列四个说法:①直线AD与直线B1P为异⾯直线;②恒有A1P∥⾯ACD1;③三棱锥A-D1PC的体积为定值;④当长⽅体各棱长都相等时,⾯PDB1⊥⾯ACD1.其中所有正确说法的序号是.22、已知⼀个⼏何体是由上下两部分构成的组合体,其三视图如下,若图中圆的半径为,等腰三⾓形的腰长为,则该⼏何体的体积是。
立体几何大题专练1、如图,已知PA丄矩形ABCD所在平面,M、N分别为AB、PC的中点;⑴求证:2Q.证明江1〉取FD的中点AE,NE t丁Nft PC 的中点.A NEX^CD .又四边形ABCU为矩形且M星BA中点'MN:* 寺CD垒MA ,£:■ NEXMA.KP四边形MAEN是平行四也形, 昇MN〃AE*由于AEU罕面PAD,MN(Z^ffi PAD・A MN"平廊PAD,(2>V FA 丄平ABCD,ZPDA-45\ 代APAD是等B?三肃形•桩AE」PH 由题意,CD丄AD,CD丄叭:.CD丄平面PAD.从而AE_LCD,代AE丄平面PCD,故VIN丄平而PCH .Ml、If :< 1)「1 {' 的方程为(x —a)* + (y一h J —pf(2a+ b・0*... IQ*V ■ ■ ■ V ■]... 12*……rABC PA PC ABC 90 PEF PBC EF QE F AC BC EF // AB....2 分又EF 平面PAB,AB 平面PAB,EF //平面PAB.• (5)(2)Q PA PC,E为AC的中点,PE AC (6)P ABC E,F AC, BC EF // PAB PAC又Q平面PAC 平面ABCPE 面ABC ................. 8 分PE BC ............... 9 分又因为F为BC的中点,Q ABC 900, BC EF .................... 10 分BC 面PEF ............... 11 分又Q BC 面PBC面PBC 面PEF ............... 12分3.如图,在直三棱柱ABC-ABQ中,AC=BC点D是AB的中点(1)求证:MN //平面PAD MN GD 图,正方形ABGD所在的平面与三角形A D E 所在平面互相垂直,AAEE 是等腰直角三角形,且AE =ED设线段BG AE 的中点分别为F 、M ,求证:(1) FM II 平面EGD ;(2)求二面角E-BD — A 的正切值.(1)证明:取 AD 的中点 N,连结FN,MN,则MN I ED ,FN II GD•••平面 FMN I 平面 EGD.•/ MF 在平面FMN 内,• FM I 平面EGD……5分(2)连接EN, v AE=ED ,N 为AD 的中点, • EN 丄 AD.又•••面 ADE 丄面 ABGD ,• EN 丄面 ABGD.作NP 丄BD,连接EP,贝U EP 丄BD , • / EPN 即二面角 E-BD-A 的平面角,设AD=a, •/ ABGD 为正方形,/ ADE 为等腰三角形,• tan / EPN= . 2 ..... 10 分7.如图,一个圆锥的底面半径为 2cm,高为6cm ,其中有一个高为⑴试用X 表示圆柱的侧面积;BG PA矩形ABGD 所在的平面,M 、N 分别是AB 、PGF N(2)当X为何值时,圆柱的侧面积最大 . r 则有一 2 6 x ,即r 6 2 X 3.…s 圆柱侧 2 rx 2 (2 2X)x 4 x 2 x 2... 3 3 ....5 分19. (1)解:设所求的圆柱的底面半径为 r •- EN= a,NP= 2.2 --a. X cm 的内接圆柱x—纟2— 3时,这个二次函数有最大值为62(厅)23cm 时,它的侧面积最大为6 Cm ……10 分ABC 中,/ PAB 是等边三角形,/ PACK PBC=90 o.由已知,平面PAC 平面PBC ,故AEB 90 . 因为 Rt AEB Rt PEB ,所以AEB, PEB,CEB1PABC 的体积V S PC39.(本题满分12分)如图,在四棱锥 P -ABCD 中,底面ABCD 为平行四边形,/ ADC = 45° AD = AC = 1,O 为 AC 的中点,P0丄平面 ABCD ,P0= 2,M 为PD 的中点.(1) 证明:AB 丄PC; 若PC 4,且平面PAC 丄平面PBC ,求三棱锥P ABC 体积.解: (1) 因为 PAB 是等边三角形, PAC PBC 90 ,所以 Rt PBC Rt PAC ,可得 AC BC 如图,取 AB 中点D ,连结PD , CD , 则PD AB , CD AB , 所以 AB 平面PDC , 所以 AB PC (2) 作BE PC ,垂足为E ,连结AE . 因为 Rt PBC Rt PAC 所以 AE PC ,AE BE .由已知PC 4,得AE BE 2, AEB 的面积S因为PC平面AEB ,(2)由(1)知当 所以当圆柱的高为8.( 10 分)如图,在三棱锥P都是等腰直角三角形。
所以三角锥10(1)证明PB //平面ACM ;⑵证明AD 丄平面PAC ;(3)求直线AM 与平面ABCD 所成角的正切值.解析: (1)证明:如图,连接 BD , MO ,在平行四边形 ABCD 中,因为O 为AC 的中点,所以0为BD 的中点.又M 为PD 的中点,所以 PB // M0.因为PB?平面ACM , MO?平面ACM , 所以PB //平面ACM .(2)证明:因为/ ADC = 45° 且 AD = AC = 1,所以/ DAC = 90° 即 AD 丄 AC.又PO 丄平面 ABCD , AD?平面ABCD ,所以PO 丄AD.而AC APO = O ,所以AD 丄 平面PAC.⑶如图,取DO 中点N ,连接MN , AN.因为M 为PD 的中点,所以 MN // PO ,1且MN = 2卩。
=1,由PO 丄平面 ABCD ,得 MN 丄平面 ABCD ,所以/ MAN 是1直线AM 与平面 ABCD 所成的角.在 Rt △ DAO 中,AD = 1, AO =㊁,即直线AM 与平面ABCD 所成角的正切值为10 (本小题满分12分)如图,在侧棱垂直于底面的三棱柱ABC ^B 1C 1中,AC 3, AB 5, BC 4, AA 4,点 D 是占八、、•(I)求证:AC BC 1 ;(II )求证:AC,/ 平面 CDB 1 ; (III )求三棱锥 A B 1CD 的体积.证明:(I )在厶 ABC 中,••• AC 3, AB 5, BC 4, •••△ABC 为直角三角形,••• AC BC ,DO =扌从而 AN = *DO =于在 Rt △ ANM中, tan / MANMN _ 丄 _4/5AN _ ^5_ 5 ,T••• AC 平面 BCC 1 AC BC 1. (II )设B i C 与BC i 交于点E ,则E 为BC i 的中点,连结 DE 则在△ ABC i 中,DE //AC i ,又 DE 面 CDB i , …AC i // 平面 B i CD . (Ill )在厶ABC 中,过C 作CF AB ,F 为垂足, •••平面ABB iA 平面 ABCAC ••• CF 平面 ABB 1A I ,而 CF BC AB3 4 12VA BiCDV C A |DB 1 , io 分 而 SVDA 1B 1 (V)A BiCD 1 A |B I gAA i2 1 1 10 ,2 ii 分 311.(本小题满分12分) io i2 i2分 如图,在四棱锥 P-ABCD 中, 平面 PADL 平面 ABCD AB=AD,Z BAD=60 ,E 、F 分别是 AP 、AD 的中点 求下:(1)直线 EF12.(本小题满分 如图所示,在四棱锥 P ABCD 中,底面ABCD 是正方形,侧棱 i2 分)ABCD , PD CD, E 是 PC 的中点,作 EF PB 交PB 于点F 。
(I) 求证:PA//平面EDB ; (II) 求证:PB 平面EFD ; (Ill )求二面角P BC D 的大小。
13.(本小题满分 如图,四棱锥 i2分) P ABCD 中,底面ABCD 是边长为2的 正方形, PA PB PC PD ,5 DPD 底面 求二面角P AB C 的度数 若M 是侧棱PC 的中点,求异面直线PA 与BM 所成角的正切值 (1) (2) 14 .(本小题满分 12分) 若图为一简单组合体,其底面 ABCD 为正方形, PD 平面 ABCD EC//PD , 且 PD=2EC (i )求证:BE//平面PDA (2)若N 为线段PB 的中点, 求证:EN 平面 PDB(1) (2)i5. 证明:EC// PDA EC//面证明:取BD 的中点O, (本小题满分 12分)PAD 同理BC//面 连NO CO 易知,PAD •••面 BEC//面 PA COL BD 又 J CO 丄 PD D • BE//面 PAD :• CO L 面 PBD是菱形,0点是BC的中点,EO 平面ABC。
(1)求异直线AC和BE所成角的大小;(2)求平面ABE与平面ADE所成锐二面角的余弦值。