第05动态电路的瞬态分析-时域经典分析法
- 格式:ppt
- 大小:3.65 MB
- 文档页数:115






动态电路瞬态过程的时域分析与复频域分析动态电路瞬态过程的时域分析与复频域分析动态电路是现代电子技术中的重要内容之一,它涉及到大量的瞬态过程。
对于这些瞬态过程的分析,常使用时域分析和复频域分析两种方法。
本文将分别对这两种方法进行介绍和分析。
一、时域分析时域分析是指对电路的时间响应进行分析。
在分析中,假设电路中的各种参数以及输入信号都是时间函数,因此需要将它们表示为某种数学形式,然后通过对这些数学形式的运算进行分析。
其中,最基本的数学工具是微积分,因为微积分可以表示出电路中的各种参数以及输入信号的变化规律。
对于时域分析来说,最常用的工具是拉普拉斯变换和傅里叶变换。
其中,拉普拉斯变换是把时间域函数转变为复频域函数的一种数学方法,它可以方便地求出电路的瞬态响应和稳态响应。
而傅里叶变换是把一个周期信号转化为谱函数的一种数学方法,它可以对电路中的各种波形进行分析和处理。
在进行时域分析时,需要注意以下几点:1.需要对电路进行合理简化:电路越简单,分析就越容易。
2.需要根据电路的性质选择合适的求解方法:对于不同的电路,可以采用不同的求解方法,例如微积分、拉普拉斯变换或傅里叶变换等。
3.需要进行量化分析:对于电路中的各种参数和信号,需要进行量化分析,例如幅度、相位角、频率等。
二、复频域分析复频域分析是指对电路的复频特性进行分析。
在分析中,假设电路中的各种参数都是复数函数,因此需要对这些复数函数进行分析。
其中,最常用的工具是复数函数的运算和分析。
与时域分析相比,复频域分析更注重电路的频率响应特性,例如幅频特性、相频特性、群延迟特性等。
而复频域分析最重要的工具是频谱分析和极坐标分析。
在进行复频域分析时,需要注意以下几点:1.需要正确理解电路的频域特性:对于不同的电路,具有不同的频域特性,例如低通滤波器、高通滤波器、带通滤波器等。
2.需要正确分析电路的复频域函数:对于电路中的各种复数函数,需要进行运算和分析,例如求导、求积、傅里叶变换等。



动态电路的时域分析 第一节 换路及其初始条件一、电路的两种工作状态(稳态、动态) 1、稳态电路: (1)定义当电路在直流电源的作用下,各条支路的响应也是直流;当电路在正弦交流电源的作用下,各条支路的响应也是正弦交流,这种类型的电路称为稳态电路。
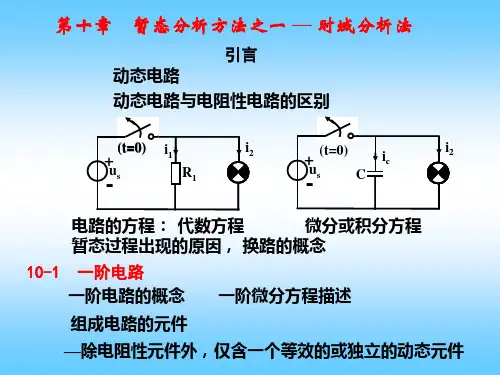
(2)特征:稳态电路中不存在换路现象,描述稳态电路的方程是代数方程。
2、动态电路: (1)定义当电路中含有储能元件或称动态元件(如电容或电感),电路中的开关在打开或闭合的过程中参数发生变化时,可使电路改变原来的工作状态,转变到另一个工作状态。
电路从一种稳态到达另一种稳态的中间过程称为动态过程或过渡过程。
过渡过程中的电路称为动态电路。
(2)待征:动态电路中存在动态元件且有换路现象,描述动态电路的方程是微分方程。
一阶电路:能够用一阶微分方程描述的电路; 二阶电路:能够用二阶微分方程描述的电路; n 阶电路:能够用n 阶微分方程描述的电路。
(3)存在原因:1)含有动态元件电感或电容 ::di L u L dtdu C i Cdt ⎧=⎪⎪⎨⎪=⎪⎩2)存在换路:电路结构或参数发生变化 二、换路 1、定义:电路中含有储能元件,且电路中开关的突然接通或断开、元件参数的变化、激励形式的改变等引起的电路变化统称为“换路”。
(1)换路是在0t =时刻进行的(2)换路前一瞬间定义为:0t -=;换路后一瞬间定义为:0t +=; (3)换路后达到新的稳态表示为:t =∞。
2、换路定律:在换路时电容电流和电感电压为有限值的条件下,换路前后瞬间电容电压和电感电流不能跃变。
即:(0)(0),(0)(0)c c L L u u i i +-+-==。
注意:00()()C C i t i t +-≠,00()()L L u t u t +-≠,00()()R R i t i t +-≠,00()()R R t u t +-≠ 三、独立初始条件 1、定义:一个动态电路的电容电压(0)C u +和电感电流(0)L i +称为独立初始条件,其余的称为非独立初始条件,非独立初始条件需通过已知的独立初始条件来求得。
动态电路的时域分析
动态电路分析的基本方法是建立电路的微分方程,利用电路中的基尔
霍夫定律和伏安定律,推导出描述电路元件电压和电流变化关系的微分方程。
然后,通过求解微分方程,得到电路的时间响应,即电压和电流随时
间的变化规律。
动态电路的分析过程中需要考虑电路元件的动态特性,包括电容元件
和电感元件的存储能量和存储效应。
对于电容元件,其电压和电流之间的
关系可以用电容的充放电方程来描述。
而对于电感元件,其电压和电流之
间的关系可以用电感的变化率来描述。
在时域分析中,最常用的方法是Laplace变换法。
通过将电路中的微
分方程转化为复频域中的代数方程,可以大大简化电路的分析过程。
利用Laplace变换后的电路方程,可以通过进行代数运算和逆变换,得到电路
的时间响应。
动态电路的时域分析还需要考虑电路的初始条件。
对于包含存储元件
的电路,初始条件是指电容电压和电感电流在初始时刻的取值。
有时候,
电路的初始条件会影响电路的稳定性和响应速度,因此在进行时域分析时,需要充分考虑初始条件的影响。
此外,动态电路的时域分析还可以通过脉冲响应法进行。
该方法利用
电路的单位阶跃响应和冲击响应的线性叠加原理,可以将任意输入信号分
解为一系列单位阶跃函数和冲击函数,并通过对各个分量的处理来得到电
路的时间响应。
总之,动态电路的时域分析是电路理论中的重要内容。
通过对电路中各个元件的电压和电流随时间的变化进行分析,可以揭示电路的动态行为和响应过程,为电路设计和故障诊断提供重要的理论依据。