随机型时间序列

时间序列的成分可以分为四种：趋势（T）、季节性或季节变动（S）、周期性或循环波动（C）、随机性或不规则波动（I）。

时间序列可以分为平稳序列和非平稳序列两大类。

平稳序列是基本上不存在趋势的序列。

这类序列中的各观察值基本上在某个固定的水平上波动，虽然在不同的时间段波动的程度不同，但并不存在某种规律，波动可以看成是随机的。

非平稳序列（non-stationary series）是包含趋势、季节性或周期性的序列，它可能只含有其中一种成分，也可能含有几种成分。

因此非平稳序列又可以分为有趋势的序列、有趋势和季节性的序列、几种成分混合而成的复合型序列。

趋势（Trend）：是时间序列在长期内呈现出来的某种持续上升或持续下降的变动，也称长期趋势。

时间序列中的趋势可以是线性的，也可以是非线性的。

季节性（seasonality）也称季节变动（seasonal fluctuation），它是时间序列在一年内重复出现的周期性波动。

例如：在商业活动中，常常听到的“销售旺季”或“销售淡季”这类术语。

其本质上指的是一种周期性的变化。

含有季节成分的序列可能含有趋势，也可能不含有趋势。

周期性（cyclicity）也称循环波动（cyclical fluctuation），是时间序列中呈现出来的围绕长期趋势的一种波浪形或震荡式变动。

周期性通常是由商业和经济活动引起的，它不同于趋势变动，不是朝着单一方向的持续运动，而是涨落相同的交替波动；它也不同于季节变动，季节变动有比较固定的规律，而且变动周期大多为一年，循环波动则无固定规律，变动周期多在一年以上，且周期长短不一。

周期性通常是由经济环境的变化引起的。

除此之外，还有些偶然性因素对时间序列产生影响，致使时间序列呈现出某种随机波动。

时间序列中除去趋势、周期性和季节性之后的偶然性波动称为随机性（randomness），也称不规则波动（irregular variations）。

构成要素：长期趋势，季节变动，循环变动，不规则变动。

第5章 随机型时间序列预测方法随机时间序列分析方法的出现虽然有相当长的历史，但广泛用于经济、商业预测和经济分析还是第二次世界大战之后。

一方面计算机技术的迅速发展，为随机时间序列分析的建模和预测提供了强有力的工具；另一方面，是由于美国著名的统计学家博克斯（Box ）和英国的詹金斯（Jenkins ）于1968年在理论上提出了一整套的随机时间序列的模型识别、参数估计和诊断检验的建模方法，并于1970年出版了专著《时间序列分析——预测与控制》。

该书对随机序列的理论分析和应用作了系统的论述，尤其是1976年出第2版以后，其应用更为广泛。

优点：它能利用一套相当明确规定的准则来处理复杂的模式，预测精度也比较高。

缺点：但同时为了达到高的精确性，其计算过程复杂，计算工作量大，花费也大。

利用随机型时间序列预测方法建立预测模型的过程可以分为4个阶段： （1） 第一阶段：根据建模的目的和理论分析，确定模型的基本形式。

（2） 第二阶段：进行模型识别，即从一大类模型中选择出一类试验模型。

（3） 第三阶段：将所选择的模型应用于所取得的历史数据，求得模型参数。

（4） 第四阶段：检验得到的模型是否合适。

若合适，则可以用于预测和控制；若不合适，则返回到第二阶段重新选择模型。

5.1 随机型时间序列模型 1．时间序列随机时间序列是指{}n X ，对于每个n ，n X 都是一个随机变量。

定义：时间序列{}n X 是平稳的，如果它满足：（1）对于任一n ，()n E X C =，C 是与n 无关的常数；（2）对于任意的n 和k ，[()()]n k n k E X C X C γ+--=，其中k γ与n 无关。

k γ称为时间序列{}n X 的自协方差函数。

0/k k ργγ=称为自相关函数。

平稳性定义中的两条也就是说时间序列的均值和自协方差函数不随时间的变化而变化。

通常我们可以假设一个平稳时间序列{}n X 的均值为0。

如果均值不为零的话，我们可以对原有的时间序列进行一次平移变换，即令nn X X C '=-，则{}n X '是一个零均值的平稳序列。

第5章随机型时间序列预测方法本章将讨论随机型时间序列预测技术。

此方法的优点在于它能利用一套相当明确规定的准则来处理复杂的模式，预测精度也比较高。

但同时为了达到高的精确性，其计算过程复杂，计算工作量大，花费也大。

随机型时间序列预测技术建立预测模型的过程可以分为四个阶段：第一阶段：根据建模的目的和理论分析，确定模型的基本形式。

第二阶段：进行模型识别，即从一大类模型中选择出一类试验模型。

第三阶段：将所选择的模型应用于所取得的历史数据，求得模型的参数。

第四阶段：检验得到的模型是否合适。

若合适，则可以用于预测或控制；若不合适，则返回到第二阶段重新选择模型。

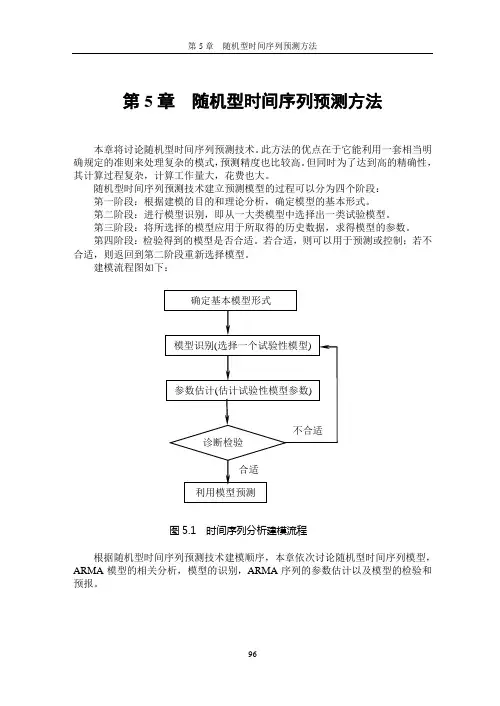
建模流程图如下：图5.1 时间序列分析建模流程根据随机型时间序列预测技术建模顺序，本章依次讨论随机型时间序列模型，ARMA模型的相关分析，模型的识别，ARMA序列的参数估计以及模型的检验和预报。

5.1 随机型时间序列模型本节讨论时间序列的几种常用模型。

从实用观点来看，这些模型能够表征任何模式的时间序列数据。

这几类模型是：1)自回归(AR)模型；2)移动平均(MA )模型；3) 自回归移动平均(ARMA)模型；4)求和自回归移动平均(ARIMA)模型。

5.1.1 时间序列所谓随机时间序列是指{|,1,2,,,}n X n o N =±±± ，这里对每个n ，n X 都是一个随机变量。

以下我们简称为时间序列。

定义5.1 时间序列{|0,1,2,}n X n =±± 称为平稳的，如果它满足： (1)对任一n ，()n E X C =，C 是与n 无关的常数；(2)对任意的n 和k ，()()n k n k E X C X C γ+--=其中k γ与n 无关。

k γ称为时间序列{}n X 的自协方差函数，0/k k ργγ=称为自相关函数。

平稳性定义中的两条也就是说时间序列的均值和自协方差函数不随时间的变化而变化。

随机型时间序列预测法概述随机型时间序列预测法的核心思想是通过对历史观测值的统计分析，来获得对未来观测值的概率分布预测。

常用的方法包括随机游走模型、ARIMA模型和蒙特卡洛模拟等。

随机游走模型是基于随机游走过程的思想，认为未来的观测值仅仅取决于当前的观测值，而不受其他因素的影响。

随机游走模型假设未来观测值是当前观测值的随机扰动，因此只需要根据历史观测值的方差来预测未来的观测值的方差。

ARIMA模型是一种基于自回归移动平均的方法，可以对时间序列数据进行拟合和预测。

ARIMA模型的核心思想是通过对时间序列数据进行平稳化处理，然后利用自回归和移动平均的效应来对未来观测值进行预测。

蒙特卡洛模拟是一种基于随机采样的方法，通过对历史观测值的概率分布进行抽样，得到多个可能的未来观测值序列。

然后，可以通过对这些样本序列的统计分析来获得对未来观测值的概率分布预测。

总之，随机型时间序列预测法通过对时间序列数据的随机性特征进行建模和分析，可以得到对未来观测值的概率分布预测。

这些方法可以帮助我们更好地理解和预测时间序列数据的随机性，提供数据分析和决策支持。

随机型时间序列预测法的应用领域非常广泛。

它可以用于金融市场预测、天气预报、股票市场分析、经济指标预测等许多领域。

在这些领域中，时间序列数据经常呈现出一定的随机性，传统的预测方法往往无法准确捕捉到这种随机性，因此随机型时间序列预测法成为了一种有效的预测方法。

随机游走模型是一种简单而又直观的随机型时间序列预测方法。

它假设未来的观测值仅仅取决于当前的观测值，并且通过随机扰动来进行模拟。

这种方法的一个重要特点是不考虑任何外部因素对未来观测值的影响，因此被广泛应用于金融市场预测中。

例如，在股票市场中，随机游走模型被用来预测股票价格的波动范围，从而帮助投资者制定买卖策略。

ARIMA模型是一种比较常用的随机型时间序列预测方法。

它基于自回归和移动平均的效应，旨在通过对时间序列数据进行平稳化处理，然后根据历史观测值的自相关性和移动平均性来预测未来观测值。

第3章时间序列预测法§3.1 时间序列分析的基本问题3.1.1时间序列时间序列是指同一变量按发生时间的先后排列起来的一组观察值或记录值。

例如：1953～2001年的国民收入；1958～2001年全国汽车的产量；某物资公司1996～2001年逐月的机电产品月销售量；某省1962～2001年工业燃料消费量等等。

所用的时间单位可以根据情况取年、季、月等。

3.1.2时间序列预测经济预测中的预测目标及其影响因素的统计资料，大多是时间序列。

任何预测目标都有各自的时间演变过程，研究它如何由过去演变到现在的演变规律，并分析、研究它今后的变化规律，即可对它们进行预测，时间序列预测技术就是利用预测目标本身的时间序列，分析、研究预测目标未来的变化规律而进行预测的。

时间序列预测法，只要有预测目标的历史统计数据即可进行预测，统计资料易于收集，计算又比较简单，不仅可用来预测目标，还可用于预测回归预测法的影响因素。

因此，广泛地用于各方面的预测。

而当找不到预测目标的主要影响因素或者虽然知道其主要影响因素，但找不到有关的统计数据时，时间序列预测法的优越性更为显著。

时间序列预测技术，可分为确定型和随机型两大类。

本章只介绍确定型时间序列预测，第四章将介绍随机型时间序列预测。

3.1.3四类影响因素世间各种各样的事物，在各时间都可能受很多因素的影响，因此，所形成的时间序列，实际上是各个影响因素同时作用的综合结果。

我们想从给定的时间序列，分析出作用于所观察事物的每一个影响因素，是无法办到的。

因此，我们在分析各种时间序列时，通常把各种可能的影响因素，按其作用的效果分为四大类：1）趋势变动[记为T（t）]：指预测目标在长时间内的变动趋势——持续上升或持续下降。

2）季节变动[记为S（t）]：指每年受季节影响重复出现的周期性变动，一般是以十二个月或四个季度为一个周期。

3）循环变动[记为C（t）]：指以数年为周期（各周期的长短可能不一致）的一种周期性变动，例如经济景气指数，银行储蓄。

简述时间序列的构成要素及其含义
时间序列是指按照时间顺序排列的一系列数据点的集合。

它通常用于分析和预测时间相关的数据，例如股票价格、气温、销售量等。

时间序列的构成要素包括趋势、季节性、周期性和随机性。

首先，趋势是指时间序列数据在长期内呈现出的整体增长或下降的趋势。

它反映了数据的长期变化趋势和潜在的增长或衰退模式。

趋势可以是线性的，即呈现出直线的增长或下降，也可以是非线性的，即呈现出曲线的形状。

其次，季节性是指时间序列数据在特定时间段内周期性地重复出现的变动模式。

季节性通常与自然因素或周期性事件相关，例如每年的季节变化、假期、节日等。

季节性可以是固定的，即在每个季节都有相同的模式，也可以是变动的，即在不同的季节内有不同的模式。

第三，周期性是指时间序列数据在较长时间范围内出现的波动或周期性变动。

周期性往往与经济周期或其他周期性事件相关，例如经济衰退和繁荣、房地产周期等。

周期性通常具有较长的时间跨度，可以是几年或几十年。

最后，随机性是指时间序列数据中无法被趋势、季节性和周期性解释的随机变动。

随机性是由不可预测的外部因素和偶然事件引起的。

它
代表了数据中的噪声或随机波动，通常表现为数据的波动性或波动幅度的变化。

时间序列的构成要素可以帮助我们理解和解释数据的变化规律，并用于预测未来的趋势和趋势变化。

通过分析趋势、季节性、周期性和随机性，我们可以识别数据中的规律性模式，从而制定相应的决策和策略。

例如，对股票价格的时间序列分析可以帮助投资者判断股票的长期趋势和短期波动，从而做出更明智的投资决策。

简述时间数列的概念和种类
时间序列：概念与种类
时间序列（time series）是引用数据统计观察数据变化趋势和特点的方式，
也是一种时间序列分析，又可称为时间系列分析。

它是收集不同时期的数据，以量化的方式去衡量数据的变化趋势，以此做出相应的数据预测。

在数量研究中，时间序列分析一般分为两类：一类是定量时间序列，它是以一
种量度去收集信息，比如数值、百分比等；另一类是定性时间序列，它是以数量模式来收集数据，比如yes/no、有/无、异常/正常等。

时间序列可以分为三大种类：第一是非平稳序列，它是由于环境变化极其复杂
的影响，产生了突变性变化而产生的；其次是单调性，它受外界环境的施加，导致了它的增长或减少的影响；第三种是随机序列，他由于多种因素的共同影响，使得他改变随机，形成了一定的变化规律。

时间序列的分析可以为我们提供很多有用的信息，它可以帮助我们预测数据变
化趋势。

它们被广泛应用于各类工程、经济、金融和流行病学等领域，特别是对于大规模数据分析，时间序列分析技术是解决之道。

最后，时间序列分析是数据可视化的重要组成部分。

它结合时间维度，绘制出
衡量某一段时间里事件发展趋势的良好图形，使我们看到不同时段内数据变化特征，从中捕捉最具价值的信息。

预测值校正和预测精度提高的探讨作者：齐晓丽徐晓明吴遐来源：《中小企业管理与科技·下旬》2010年第02期摘要:预测就是根据事物的运动规律推断它的未来。

在预测问题中存在很多种预测方法,在分析过程中采用的预测方法不同得到的预测精度就不同,组合预测是提高预测准确度的有效途径。

本文利用对各种预测方法的结果的比较说明了组合预测对预测准确度提高的作用。

关键词:单项预测组合预测预测精度0 引言预测就是根据事物的运动规律推断它的未来,是将预测的理论和方法应用于实际问题。

在预测问题中,由于建模机制和出发点不同,通常同一问题有不同的预测方法,但由于各种预测方法都有相应的特点和应用范围,其预测精度不尽相同,所以在分析过程中采用的预测方法不同得到的预测精度就不同。

为了对预测值进行校正,提高预测的准确度,可以将不同的预测方法进行适当组合,重新得到组合预测后的预测值,这将有利于综合利用各种方法的优势而达到提高预测精度的目的。

1 组合预测的构建1.1 组合预测由于各种预测方法均存在着各自的优缺点,将各类不同的单项预测方法适当的加以组合,综合利用各种方法所提供的信息,尽可能提高预测效果是更科学的办法,即得到组合预测方法。

组合预测法是指建立一个模型,把两个或两个以上的不同预测方法得出的不同预测值通过适当的加权平均,最后取其加权平均值作为最终预测结果的一种预测方法。

组合预测的关键是如何恰当地确定各个单项预测方法的加权权重数,而且采用不同的最优准则就会有不同的最优组合预测模型,其权重数的获得也就存在着一定的差异。

通常都是把预测精度作为衡量某一组合预测模型优劣的指标。

1.2 组合预测权重的确定组合预测的关键是如何恰当地确定各个单项预测方法的加权权重数,而且采用不同的最优准则就会有不同的最优组合预测模型,其权重数的获得也就存在着一定的差异。

通常都是把预测精度作为衡量某一组合预测模型优劣的指标。

可采用“估计误差的方差最小”作为组合预测的最优准则,建立组合预测模型。

第5章 随机型时间序列预测方法思考与练习（参考答案）1.写出平稳时间序列的三个基本模型的基本形式及算子表达式。

如何求它们的平稳域或可逆域？解：(1)自回归模型(AR)的基本模型为：1122n n n p n p nX X X X ϕϕϕε---=++++算子表达式为：()p n n B X εΦ=，其中)1()(221p p p B B B B ϕϕϕ----=Φ令多项式方程()0p λΦ=，求出它的p 个特征根p λλλ,,,21 。

若这p 个特征根都在单位圆外，即1,1,2,...,i i p λ>=，则称AR()p 模型是稳定的或平稳的。

(2)移动平均模型(MA)的基本模型为：1122n n n n q n q X εθεθεθε---=---- 算子形式：()n q n X B ε=Θ ，其中q q q B B B B θθθ----=Θ 2211)(令多项式方程()0q λΘ=为MA()q 模型的特征方程，求出它的q 个特征根。

若MA()q 的特征根都在单位圆外，则称此MA()q 模型是可逆的。

(3)自回归移动平均模型(ARMA)的基本模型为:1111...n n p n p n n q n q X X X ϕϕεθεθε-------=---算子形式：()()p n q n B X B εΦ=Θ若特征方程()0λΦ=的所有跟都在单位圆外，那么，()()p n q n B X B εΦ=Θ就定义一个平稳模型。

与此类似，要是过程是可逆的，()0λΘ=的根必须都在单位圆外。

2. 从当前系统的扰动对序列的影响看，AR(p)序列与MA(q)序列有何差异？答：对于任意的平稳AR()p 模型n X 都可由过去各期的误差来线性表示，而对于可逆的MA()q 模型，n ε表示为过去各期数据n k X -的线性组合。

3. 把下面各式写成算子表达式：（1）t t t X X ε+=-15.0，（2）1217.05.03.0---+++=t t t t t X X X εε， （3）1145.0---=-t t t t X X εε。