下载文档原格式
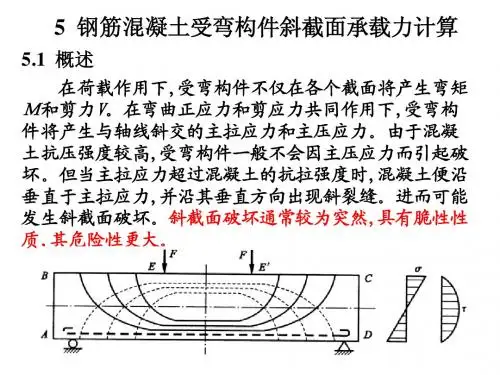
第五章钢筋混凝土受弯构件斜截面承载力计算本章学习要点：1、掌握无腹筋梁和有腹筋梁斜截面受剪承载力的计算公式和适用条件，防止斜压破坏和斜拉破坏的措施；2、掌握纵向受力钢筋伸入支座的锚固要求和箍筋的构造要求；3、了解斜截面破坏的主要形态，影响斜截面抗剪承载力的主要因素；4、了解受弯承载力图的作法，弯起钢筋的弯起位置和纵向受力钢筋的截断位置；§5-1 概述5.1.1受弯构件斜截面受力与破坏分析1、斜截面开裂前的受力分析图5-1所示矩形截面简支梁，在跨中正截面抗弯承载力有保证的情况下，有可能在剪力和弯矩的联合作用下，在支座附近区段发生沿斜截面破坏。
图5-1 对称加载简支梁梁在荷载作用下的主应力迹线图5-2。
图中实线为主拉应力迹线，虚线为主压应力迹线。
图5-2 梁的主应力迹线和单元体应力图位于中和轴处的微元体1，其正应力为零，切应力最大，主拉应力和主压应力与梁轴线成45°角。
位于受压区的微元体2，主拉应力减小，主压应力增大，主拉应力与梁轴线夹角大45°。
位于受拉区的微元体3，主拉应力增大，主压应力减小，主拉应力与梁轴线夹角小于45°。
当主拉应力或主压应力达到材料的抗拉或抗压强度时，将引起构件截面的开裂和破坏。
2、无腹筋梁的受力及破坏分析腹筋是箍筋和弯起钢筋的总称。
无腹筋梁是指不配箍筋和弯起钢筋的梁。
实验表明，当荷载较小，裂缝未出现时，可将钢筋混凝土梁视为均质弹性材料的梁，其受力特点可用材料力学的方法分析。
随着荷载的增加，梁在支座附近出现斜裂缝。
取CB为隔离体。
图5-3 隔离体受力与剪力V平衡的力有：AB面上的混凝土切应力合力Vc；由于开裂面BC两侧凹凸不平产生的骨料咬合力Va的竖向分力；穿过斜裂缝的纵向钢筋在斜裂缝相交处的销栓力Vd。
与弯矩M平衡的力矩主要由纵向钢筋拉力T和AB面上混凝土压应力合力DC组成的内力矩。
由于斜裂缝的出现，梁在剪弯段内的应力状态将发生变化，主要表现在：（1）开裂前的剪力是全截面承担的，开裂后则主要由剪压区承担，混凝土的切应力大大增加，应力的分布规律不同于斜裂缝出现前的情景。
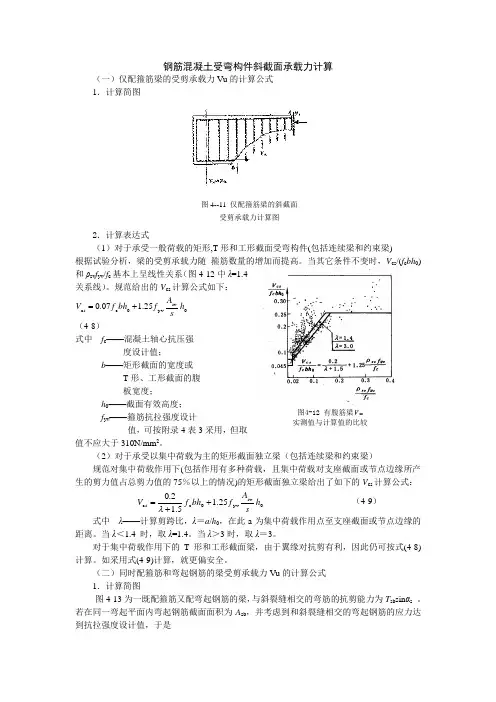
钢筋混凝土受弯构件斜截面承载力计算（一）仅配箍筋梁的受剪承载力Vu 的计算公式 1．计算简图2．计算表达式（1）对于承受一般荷载的矩形,T 形和工形截面受弯构件(包括连续梁和约束梁)根据试验分析，梁的受剪承载力随 箍筋数量的增加而提高。
当其它条件不变时，V cs /(f c bh 0)和ρsv f yv /f c 基本上呈线性关系（图4-12中λ=1.4关系线）。
规范给出的V cs 计算公式如下：sv y v 0c cs 25.107.0h sAf bh f V += （4-8）式中 f c ——混凝土轴心抗压强 度设计值；b ——矩形截面的宽度或T 形、工形截面的腹板宽度；h 0——截面有效高度；f yv ——箍筋抗拉强度设计值，可按附录4表3采用，但取值不应大于310N/mm 2。
（2）对于承受以集中荷载为主的矩形截面独立梁（包括连续梁和约束梁）规范对集中荷载作用下(包括作用有多种荷载，且集中荷载对支座截面或节点边缘所产生的剪力值占总剪力值的75％以上的情况)的矩形截面独立梁给出了如下的V cs 计算公式：0sv y v 0c cs 25.15.12.0h sA f bh f V ++=λ （4-9）式中 λ——计算剪跨比，λ＝a /h 0，在此a 为集中荷载作用点至支座截面或节点边缘的距离。
当λ＜1.4 时，取λ=1.4。
当λ＞3时，取λ＝3。
对于集中荷载作用下的T 形和工形截面梁，由于翼缘对抗剪有利，因此仍可按式(4-8)计算。
如采用式(4-9)计算，就更偏安全。
（二）同时配箍筋和弯起钢筋的梁受剪承载力Vu 的计算公式 1．计算简图图4-13为一既配箍筋又配弯起钢筋的梁，与斜裂缝相交的弯筋的抗剪能力为T sb sin αs 。
若在同一弯起平面内弯起钢筋截面面积为A sb ，并考虑到和斜裂缝相交的弯起钢筋的应力达到抗拉强度设计值，于是图4--11 仅配箍筋梁的斜截面受剪承载力计算图图4-12 有腹筋梁V cs实测值与计算值的比较s s A f T V ααs i n s i n sb y sb sb == （4-10）式中 A sb ——同一弯起平面内弯起钢筋截面面积；αs ——斜截面上弯起钢筋与 构件纵向轴线的夹角2．计算表达式矩形、T 形和工形截面的受弯构件，当同时配有箍筋和弯起钢筋时的斜截面受剪承载力计算公式s sb y cs sb cs u sin αA f V V V V +=+=（三）受剪承载力计算设计表达式在设计中为保证斜截面受剪承载力，应满足 （1）仅配箍筋的梁V ≤V u /γd =V cs /γd （4-12）（2）同时配箍筋和弯起钢筋的梁V ≤V u /γd =（V cs +V sb ）/γd （4-13）式中 γd ——钢筋混凝土结构的结构系数，按附录3表2取用；V ——剪力设计值。
第四章 钢筋混凝土受弯构件斜截面承载力计算一、填空题：1、斜裂缝产生的原因是：由于支座附近的弯矩和剪力共同作用，产生 超过了混凝土的极限抗拉强度而开裂的。
2、斜裂缝破坏的主要形态有：、、，其中属于材料充分利用的是。
3、梁的斜截面承载力随着剪跨比的增大而。
4、梁的斜截面破坏形态主要有三种，其中，以破坏的受力特征为依据建立斜截面承载力的计算公式。
5、随着混凝土强度的提高，其斜截面承载力。
6、随着纵向配筋率的提高，其斜截面承载力。
7、对于情况下作用的简支梁，可以不考虑剪跨比的影响。
对于情况的简支梁，应考虑剪跨比的影响。
8、当梁的配箍率过小或箍筋间距过大并且剪跨比较大时，发生的破坏形式为；当梁的配箍率过大或剪跨比较小时，发生的破坏形式为。
9、对梁的斜截面承载力有有利影响，在斜截面承载力公式中没有考虑。
10、设置弯起筋的目的是、。
11、为了防止发生斜压破坏，梁上作用的剪力应满足 ；为了防止发生斜拉破坏，梁配置的箍筋应满足。
12、梁设置鸭筋的目的是，它不能承担弯矩。
二、判断题：1、某简支梁上作用集中荷载或作用均布荷载时，该梁的抗剪承载力数值是一样的。
（ ）2、剪压破坏时，与斜裂缝相交的腹筋先屈服，随后剪压区的混凝土压碎，材料得到充分利用，属于塑性破坏。
（ ）3、梁设置箍筋的主要作用是保证形成良好的钢筋骨架，保证钢筋的正确位置。
（ ）4、当梁承受的剪力较大时，优先采用仅配置箍筋的方案，主要的原因是设置弯起筋抗剪不经济。
（ ）5、当梁上作用有均布荷载和集中荷载时，应考虑剪跨比λ的影响，取0Vh M=λ（ ）6、当剪跨比大于3时或箍筋间距过大时，会发生剪压破坏，其承载力明显大于斜裂缝出现时的承载力。
（ ）7、当梁支座处允许弯起的受力纵筋不满足斜截面抗剪承载力的要求时，应加大纵筋配筋率。
（ ）8、当梁支座处设置弯起筋充当支座负筋时，当不满足斜截面抗弯承载力要求时，应加密箍筋。
（ ）9、梁设置多排弯起筋抗剪时，应使前排弯起筋在受压区的弯起点距后排弯起筋受压区的弯起点之距满足：max s s ≤（ ）10、由于梁上的最大剪力值发生在支座边缘处，则各排弯起筋的用量应按支座边缘处的剪力值计算。
第五章钢筋混凝土受弯构件斜截面承载力计算本章学习要点：1、掌握无腹筋梁和有腹筋梁斜截面受剪承载力的计算公式和适用条件，防止斜压破坏和斜拉破坏的措施；2、掌握纵向受力钢筋伸入支座的锚固要求和箍筋的构造要求；3、了解斜截面破坏的主要形态，影响斜截面抗剪承载力的主要因素；4、了解受弯承载力图的作法，弯起钢筋的弯起位置和纵向受力钢筋的截断位置；§5-1 概述5.1.1受弯构件斜截面受力与破坏分析1、斜截面开裂前的受力分析图5-1所示矩形截面简支梁，在跨中正截面抗弯承载力有保证的情况下，有可能在剪力和弯矩的联合作用下，在支座附近区段发生沿斜截面破坏。
图5-1 对称加载简支梁梁在荷载作用下的主应力迹线图5-2。
图中实线为主拉应力迹线，虚线为主压应力迹线。
图5-2 梁的主应力迹线和单元体应力图位于中和轴处的微元体1，其正应力为零，切应力最大，主拉应力和主压应力与梁轴线成45°角。
位于受压区的微元体2，主拉应力减小，主压应力增大，主拉应力与梁轴线夹角大45°。
位于受拉区的微元体3，主拉应力增大，主压应力减小，主拉应力与梁轴线夹角小于45°。
当主拉应力或主压应力达到材料的抗拉或抗压强度时，将引起构件截面的开裂和破坏。
2、无腹筋梁的受力及破坏分析腹筋是箍筋和弯起钢筋的总称。
无腹筋梁是指不配箍筋和弯起钢筋的梁。
实验表明，当荷载较小，裂缝未出现时，可将钢筋混凝土梁视为均质弹性材料的梁，其受力特点可用材料力学的方法分析。
随着荷载的增加，梁在支座附近出现斜裂缝。
取CB为隔离体。
图5-3 隔离体受力与剪力V平衡的力有：AB面上的混凝土切应力合力Vc；由于开裂面BC两侧凹凸不平产生的骨料咬合力Va的竖向分力；穿过斜裂缝的纵向钢筋在斜裂缝相交处的销栓力Vd。
与弯矩M平衡的力矩主要由纵向钢筋拉力T和AB面上混凝土压应力合力DC组成的内力矩。
由于斜裂缝的出现，梁在剪弯段内的应力状态将发生变化，主要表现在：（1）开裂前的剪力是全截面承担的，开裂后则主要由剪压区承担，混凝土的切应力大大增加，应力的分布规律不同于斜裂缝出现前的情景。
（2）混凝土剪压区面积因斜裂缝的出现和发展而减小，剪压区内的混凝土压应力将大大增加。
（3）与斜裂缝相交的纵向钢筋应力，由于斜裂缝的出现而突然增大。
（4）纵向钢筋拉应力的增大导致钢筋与混凝土间粘接应力的增大，有可能出现沿纵向钢筋的粘结裂缝或撕裂裂缝。
图5-4 粘接裂缝和撕裂裂缝当荷载继续增加，斜裂缝条数增多，裂缝宽度增大，骨料咬合力下降，沿纵向钢筋的混凝土保护层被撕裂，钢筋的销栓力也逐渐减弱；斜裂缝中的一条发展成为主要斜裂缝，称为临界斜裂缝。
无腹筋梁如同拱结构，纵向钢筋成为拱的拉杆。
破坏情形：混凝土剪压区在切应力和压应力共同作用下被压碎，梁发生破坏。
图5-5 无腹筋梁的拱体受力机制3、有腹筋梁的受力及破坏分析配置箍筋可以有效提高梁的斜截面受剪承载力。
箍筋最有效的布置方式是与梁腹中的主拉应力方向一致，但为了施工方便，一般和梁轴线成90°布置。
在斜裂缝出现后，箍筋应力增大。
有腹筋梁如桁架，箍筋和混凝土斜压杆分别为桁架的受拉腹杆和受压腹杆，纵向受拉钢筋成为桁架的受拉弦杆，剪压区混凝土成为桁架的受压弦杆。
图5-6 有腹筋梁的剪力传递图5-7 抗剪计算模式当将纵向受力钢筋在梁的端部弯起时，弯起钢筋和箍筋有相似的作用，可提高梁斜截面的抗剪承载力。
5.1.2 影响斜截面承载力的主要因素1. 剪跨比和跨高比定义：对于承受集中荷载作用的梁，剪跨比是影响其斜截面受力性能的主要因素之一。
剪跨比用表示，则集中荷载作用下的梁的某一截面的剪跨比等于该截面的弯矩值与截面的剪力值和有效高度乘积之比。
实验表明：*对于承受集中荷载的梁，随着剪跨比的增大，受剪承载力下降。
对于承受均布荷载的梁来说，构件跨度与截面高度之比（跨高比）是影响受剪承载力的主要因素。
*随着跨高比的增大，受剪承载力下降。
2、腹筋（箍筋和弯起钢筋）配筋率配筋率增大，斜截面的承载力增大3、混凝土强度等级4、纵筋配筋率5、其他因素（1）截面形状实验表明，受压区翼缘的存在可提高斜截面承载力。
（2）预应力预应力能阻滞斜裂缝的出现和开展，增加混凝土剪压区的高度，从而提高混凝土所承担的抗剪能力。
（3）梁的连续性实验表明，连续梁的受剪承载力与相同条件下的简支梁相比，仅在受集中荷载时低于简支梁。
而在受均布荷载时是相当的。
5.1.3 斜截面的主要破坏型态1、斜拉破坏产生条件λ>3且腹筋量少。
破坏特点受拉边缘一旦出现斜裂缝便急速发展，构件很快破坏。
图5-8 斜拉破坏2、剪压破坏产生条件：1.5≤λ≤3且腹筋量适中。
破坏特点：受拉区边缘先开裂，然后向受压区延伸。
破坏时，与临界斜裂缝相交的腹筋屈服，受压区混凝土随后被压碎。
图5-9 剪压破坏3、斜压破坏产生条件：λ <1.5或腹筋多、腹板薄。
破坏特点中和轴附近出现斜裂缝，然后向支座和荷载作用点延伸，破坏时在支座与荷载作用点之间形成多条斜裂缝，斜裂缝间混凝土突然压碎，腹筋不屈服。
图5-10 斜压破坏*进行受弯构件设计时，应使斜截面破坏呈剪压破坏，避免斜拉、斜压和其他形式的破坏。
5.1.4 防止斜截面破坏的承载力条件斜截面上有剪力，也有弯矩。
为了防止斜截面破坏，要求：V≤Vu 通过计算满足;M≤Mu 用构造措施保证§5.2 受弯构件斜截面设计方法5.2.1一般受弯构件斜截面设计1、受弯构件斜截面受剪承载力的计算（1）不配置箍筋和弯起钢筋的一般类板类受弯构件板类构件通常承受的荷载不大，剪力较小，因此一般不必进行斜截面承载力的计算，也不配箍筋和弯起钢筋。
当板上承受的荷载较大时，需要对其斜截面承载力进行计算。
不配腹筋的一般板类受弯构件，其斜截面的受剪承载力计算公式：截面高度影响系数，当h0小于800mm时，取h0等于800mm，当h0大于2000mm时，取h0等于2000mm。
（2）矩形、T形和I形截面受弯构件构件截面上的最大剪力设计值V应满足：当仅配置箍筋时当仅配置箍筋和弯起钢筋时式中——混凝土和箍筋共同承受的剪力——弯起钢筋承受的剪力——箍筋抗拉强度设计值——配置在同一截面内箍筋各肢的全部截面面积，此处，n为在同一截面内箍筋的肢数，为单肢箍筋的截面面积；S ——沿构件长度方向的箍筋间距；此公式用于：矩形截面梁承受均布荷载；截面梁承受均布荷载和集中荷载但以均布荷载为主；T形、工字形截面梁受任何荷载。
集中荷载作用下的独立梁：（包括作用有多种荷载，其中集中荷载对支座截面或结点所产生的剪力值占总剪力值的75%以上的情况），考虑剪跨比的影响。
计算公式为：——计算截面的剪跨比。
当取；当取弯起钢筋能承受的剪力——弯起钢筋的截面面积0.8——应力不均匀系数。
用来考虑靠近剪压区的弯起钢筋在斜截面破坏时，可能达不到钢筋抗拉强度设计值。
——弯起钢筋与梁轴线的夹角，一般取45°，当梁高大于800m时，取60。
2、基本公式的适用范围适用于剪压破坏A．上限值——最小截面尺寸当发生斜压破坏时，梁腹的混凝土被压碎、箍筋不屈服，其受剪承载力主要取决于构件的腹板宽度、梁截面高度和混凝土强度。
因此，只要保证构件截面尺寸不要太小，就可防止斜压破坏的发生。
当时当时当时，按线性内插法或按以下公式计算——构件斜截面上的最大剪力设计值；——混凝土强度影响系数。
当混凝土强度等级不超过C50时，取1.0.为C80时取0.8，其间按内插法取用；——矩形截面的宽度，T形截面或工字型截面的腹板宽度；——截面的腹板高度；矩形截面取有效高度，T形截面取有效高度减去翼缘高度，工字型截面取腹板净高。
图5-11 梁的腹板高度B．下限值——最小配筋率和箍筋最大间距实验表明，若箍筋的配筋率过小或箍筋间距过大，在较大时，一旦出现斜裂缝，可能使箍筋迅速屈服甚至拉断，斜裂缝急剧开展，导致发生斜拉破坏。
箍筋直径过小也不能保证钢筋骨架的刚度。
为了防止斜拉破坏，梁中箍筋间距和直径都应符合一定要求。
当时，配箍率应满足最小配箍率的要求：3、斜截面受剪承载力的计算位置图5-12 斜截面受剪承载力计算位置1 支座边缘处截面。
该截面承受的剪力最大。
在计算简图中跨度取至支座中心。
但支座和构件连在一起，可以共同承受剪力，所以受剪控制截面是支座边缘截面。
计算该截面剪力设计值时，跨度取净跨。
用支座边缘的剪力设计值确定第一排弯起钢筋和1-1截面的箍筋。
2 受拉区弯起钢筋弯起点处截面。
（2-2截面和3-3截面）3 箍筋截面面积或间距改变处截面。
（4-4截面）4 腹板宽度改变处的截面4、斜截面受剪承载力计算步骤①确定计算截面及其剪力设计值；②验算截面尺寸是否足够；③验算是否可以按构造配筋；④当不能按构造配箍筋时，计算腹筋用量；⑤验算箍筋间距、直径和最小配箍率是否满足要求。
5、斜截面的构造要求目的：保证梁斜截面受弯承载力正截面受弯承载力图：按实际配置的纵向钢筋绘制的梁上各正截面所能承受的弯矩图。
它反应了沿梁长正截面上材料的抗力，简称为材料图。
图中竖标所表示的正截面受弯承载力设计值简称为抵抗弯矩。
1 材料图的作法A、纵向受拉钢筋全部伸入支座各截面Mu相同，材料图为矩形图。
以均布荷载作用下的简支梁为例，其设计弯矩图为抛物线。
图5-13 全部纵筋伸入支座的材料图B、部分纵向受拉钢筋弯起确定抗剪箍筋和弯筋时，考虑一根钢筋在离支座的C点弯起。
（该点到支座边缘的距离为650mm）；该钢筋弯起后，其内力臂逐渐减小，，因而其抵抗弯矩变小直至等于零。
假定该钢筋弯起后与梁轴线的交点为D，过D点后不再考虑该钢筋承受弯矩，则CD段的材料图为斜直线cd。
图5-14钢筋弯起的材料图C、部分纵向受拉钢筋截断在图4-23中，假定纵筋①抵抗控制截面A-A的部分弯矩（图中纵坐标ef），A-A为①号筋强度充分利用截面，B-B和C-C为按计算不需要该钢筋的截面，也称理论截断点，则在B-B和C-C处截面①号筋的材料图就是图中矩形阴影abcd。
为了可靠锚固，①号筋的实际截断点需延伸一段长度。
2 材料图的作用A、反映材料利用的程度材料图越贴近弯矩图，表示材料利用程度越高。
图5-15 纵筋截断的材料图B 、确定纵向钢筋的弯起数量和位置弯起钢筋的目的：斜截面抗剪；抵抗支座负弯矩只有当材料图全部覆盖住弯矩图，各正截面弯矩承载力才有保证；而要满足截面受弯承载力的要求，也必须通过作材料图才能确定弯起钢筋的数量和位置。
C 、确定纵向钢筋的截断位置③满足斜截面受弯承载力的纵向钢筋弯起位置图5-16表示弯起钢筋弯起点与弯矩图形的关系。
钢筋②在受拉区的弯起点为1，按正载面受弯承载力计算不需要该钢筋的截面为2，该钢筋强度充分利用的截面为3，它所承担的弯矩力为图中阴影部分。
当弯起点与按计算充分利用该钢筋的截面之间的距离不小于h0/2时，可以满足斜截面受弯承载力的要求（保证斜截面的受弯承载力不低于正截面的受弯承载力）自然，钢筋弯起后与梁中心线的交点应在该钢筋正截面抗弯的不需要点之外。
